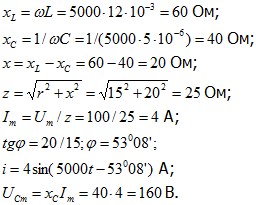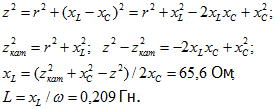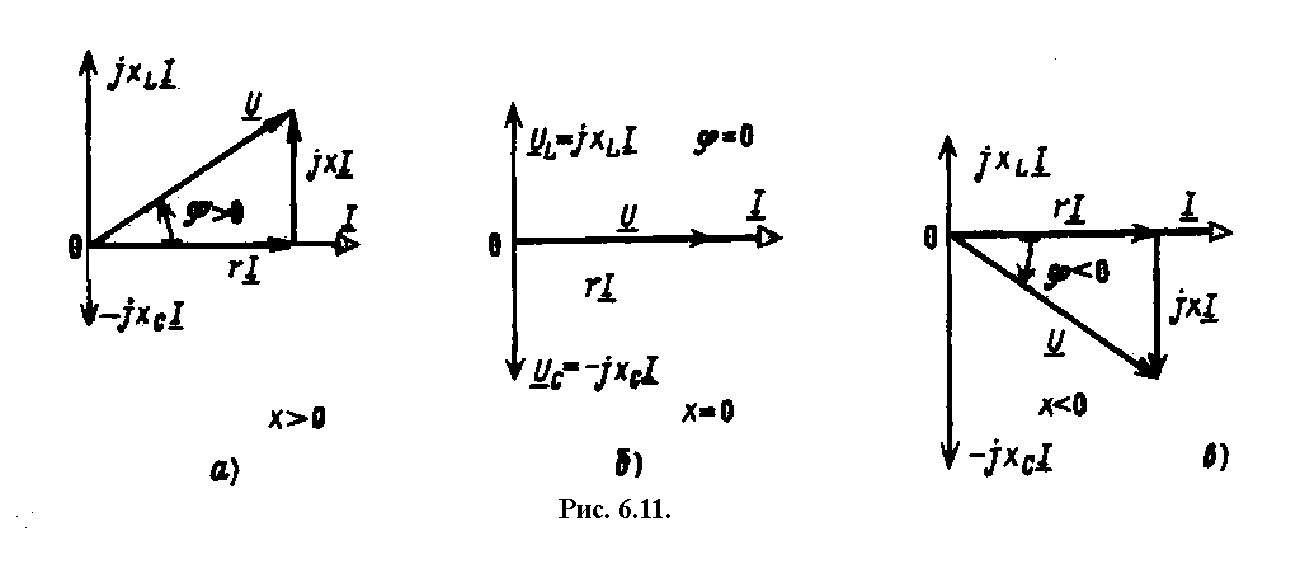Разность фаз напряжения и тока
Условимся под разностью фаз φ напряжения и тока всегда понимать разность начальных фаз напряжения и тока
(а не наоборот):
Поэтому на векторной диаграмме угол φ отсчитывается в направлении от вектора I к вектору U (рис. 3.10). Именно при таком определении разности фаз угол φ равен аргументу комплексного сопротивления. Угол φ положителен при отстающем токе () и отрицателен при опережающем токе (
).
Разность фаз между напряжением и током зависит от соотношения индуктивного и емкостного сопротивлений. При имеем
и ток отстает по фазе от напряжения,
. При
имеем
, ток совпадает по фазе с напряжением, rLC-цепь в целом проявляет себя как активное сопротивление. Это случай так называемого резонанса в последовательном контуре. Наконец, при
имеем
, ток опережает по фазе напряжение.
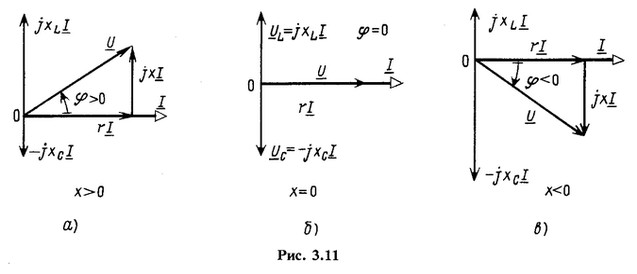
Векторные диаграммы для трех возможных соотношений даны на рис. 3.11. При построении этих диаграмм начальная фаза тока
; принята равной нулю. Поэтому
равны друг другу.
Рассматривая при заданной частоте цепь по рис. 3.8 в целом как пассивный двухполюсник, можно ее представить одной из трех эквивалентных схем: при как последовательное соединение сопротивления и индуктивности (
), при
как сопротивление r и при
как последовательное соединение сопротивления и емкости (
). При заданных L и С соотношение между
зависит от частоты, а потому от частоты зависит и вид эквивалентной схемы.
Выше, в разделе, было принято, что задан ток, а определялись напряжения на элементах и на входных выводах цепи. Однако часто бывает задано напряжение на выводах, а ищется ток. Решение такой задачи не представляет труда. Записав по заданным величинам комплексное напряжение U и комплексное сопротивление Z, определим комплексный ток
и тем самым действующий ток и начальную фазу тока.
Часто равной нулю принимается начальная фаза заданного напряжения: . В этом случае, как следует из раздела, начальная фаза тока
; равна и противоположна по знаку разности фаз φ, т. е
.
Установленные выше соотношения между амплитудами и действующими токами и напряжениями, а также выражение для сдвига фаз ф позволяют вычислить ток и не прибегая к записи закона Ома в комплексной форме. Подробно этот путь решения показан в примере 3.4.
Пример 3.4.
К цепи, состоящей из последовательно соединенных конденсатора и катушки, приложено напряжение . Емкость конденсатора С=5 мкФ, сопротивление катушки r=15 Ом, индуктивность L=12 мГн. Найти мгновенные значения тока в цепи и напряжений на конденсаторе и на катушке.
Решение.
Схема замещения цепи показана на рис. 3.8.
Напряжение на емкости отстает от тока по фазе на 90°, следовательно,
Комплексное сопротивление катушки
Комплексная амплитуда напряжения на выводах катушки
Мгновенное напряжение на катушке
Пример 3.5.
В цепи, состоящей из последовательно соединенных конденсатора и катушки, ток I=2 А, его частота f=50 Гц. Напряжение на выводах цепи U=100 В, катушки Uкат =150 В и конденсатора Uс=200 В. Определить сопротивление и индуктивность катушки и емкость конденсатора.
Решение.
Полное сопротивление цепи z=U/I=50 Ом.
Полное сопротивление катушки zкат=Uкат/I=75 Ом;
Все страницы раздела «Цепи переменного тока» на websor
Разность фаз напряжения и тока
Условимся под
разностью фаз
напряжения и тока всегда понимать
разность начальных фаз напряжения u
и тока i
{ (а не наоборот):
=u‑i. (6.28)
Поэтому на векторной
диаграмме угол
отсчитывается в направлении от вектора
I
к вектору U
(рис. 6.10). Именно при таком определении
разности фаз угол
равен аргументу комплексного сопротивления.
Угол
положителен при отстающем токе (u>i)
и отрицателен при опережающем токе
(u<i).
Разность фаз между
напряжением и током зависит от соотношения
индуктивного и емкостного сопротивлений.
При xL>xC
имеем x=xL—xC>0
и ток отстает по фазе от напряжения,
=arctg(x/r)>0.
При xL=xC
имеем x=0,
=0,
z=r,
ток совпадает по фазе с напряжением,
rLC-цепь
в целом проявляет себя как активное
сопротивление. Это случай так называемого
резонанса в последовательном контуре.
Наконец, при xL<xC
имеем x<0,
<0,
ток опережает по фазе напряжение.
Векторные диаграммы
для трех возможных соотношений xL
и xC
даны на рис. 6.11. При построении этих
диаграмм начальная фаза тока i
принята равной нулю. Поэтому
и u
равны друг другу.
Рассматривая при
заданной частоте цепь по рис. 6.8 в целом
как пассивный двухполюсник, можно ее
представить одной из трех эквивалентных
схем: при xL>xC
как последовательное соединение
сопротивления и индуктивности (r
и x‘L=xL—xC),
при xL=xC
как сопротивление r
и при xL<xC
как последовательное соединение
сопротивления и емкости (r
и x‘C=xC—xL).
При заданных L
и С
соотношение между xL,
и xC
зависит от частоты, а потому от частоты
зависит и вид эквивалентной схемы.
Выше было принято,
что задан ток, а определялись напряжения
на элементах и на входных выводах цепи.
Однако часто бывает задано напряжение
на выводах, а ищется ток. Решение такой
задачи не представляет труда. Записав
по заданным величинам комплексное
напряжение U
и комплексное сопротивление Z,
определим комплексный ток
I=U/Z
и тем самым
действующий ток и начальную фазу тока.
Часто равной нулю
принимается начальная фаза заданного
напряжения: u=0.
В этом случае, как следует из (6.28),
начальная фаза тока i
равна и противоположна по знаку разности
фаз ,
т. е. i=—.
Установленные
выше соотношения между амплитудами и
действующими токами и напряжениями, а
также выражение для сдвига фаз
позволяют вычислить ток и не прибегая
к записи закона Ома в комплексной форме.
Подробно этот путь решения показан в
примере.
Пример.
К цепи, состоящей из последовательно
соединенных конденсатора и катушки,
приложено напряжение u=100sin5000t
В. Емкость конденсатора С=5
мкФ, сопротивление катушки r=15
Ом, индуктивность L=12
мГн. Найти мгновенные значения тока в
цепи и напряжений на конденсаторе и на
катушке.
Решение.
Схема замещения цепи показана на рис.
6.8.
xL=L=50001210‑3=60
Ом;
xC=1/(С)=1/(5000510‑6)=40
Ом;
x=xL‑xC=60‑40=20
Ом;
;
Im=Um/z=100/25=4
А;
tg=20/15; =53°08′;
i=4sin(5000t‑53°08′)
А;
UCm=xCIm=404=160
В.
Напряжение на
емкости отстает от тока по фазе на 90°,
следовательно,
uC=160sin(5000t‑143°08′)
В.
Комплексное
сопротивление катушки
ZКАТ=r+jxL=15+j60=61,815°58′
Ом.
Комплексная
амплитуда напряжения на выводах катушки
UКАТm=ZКАТIm=61,875°58’4‑53°08’=247,222°50′
В.
Мгновенное
напряжение на катушке
uКАТ=247,2sin(5000t+22°50′)
В.
Пример.
В цепи, состоящей из последовательно
соединенных конденсатора и катушки,
ток I=2
А, его частота f=50
Гц. Напряжение на выводах цепи U=100
В, катушки UКАТ=50
В и конденсатора UС=200
В. Определить сопротивление и индуктивность
катушки и емкость конденсатора.
Решение.
=2f=250=314
рад/с; xC=UС/I=100
Ом и С=1/(xC)=31,8
мкФ.
Полное сопротивление
цепи z=U/I=50
Ом.
Полное сопротивление
катушки zКАТ=UКАТ/I=75
Ом;
z2=r2+(xL‑xC)2=r2+(xL)2‑2xLxC+(xC)2;
zКАТ2=r2+(xL)2; z2‑zКАТ2=‑2xLxC+(xC)2; xL=(zКАТ2+(xC)2‑z2)/2xC=65,6
Ом;
L=xL/=0,209
Гн.
Соседние файлы в папке Некие лекции по элтеху
- #
- #
- #
- #
- #
- #
- #
«Любое
препятствие
преодолевается
настойчивостью».
Леонардо
да Винчи
Задача
1.
В цепь переменного тока включена катушка с индуктивностью 75 мГн. Найдите
действующее значение напряжения на данном участке цепи, если действующее
значение силы тока равно 2 А, а частота колебаний равна 50 Гц.
|
ДАНО: |
СИ |
РЕШЕНИЕ Из закона Ома для участка цепи Тогда действующее напряжение будет равно Индуктивное сопротивление определяется по формуле Т.к. циклическая частота равна индуктивное сопротивление будет равно С учётом последней формулы действующее значение напряжения |
|
|
Ответ:
47 В.
Задача
2.
В цепь переменного тока включены резистор с сопротивлением 20 Ом и
конденсатор с ёмкостью 10 мкФ. Известно, что напряжение на конденсаторе
изменяется по закону ,
а амплитудный ток, протекающий по данному участку равен 5 А.
Какое напряжение покажет вольтметр, указанный на схеме?
|
ДАНО: |
СИ |
РЕШЕНИЕ Запишем закон Ома для цепей переменного тока Полное сопротивление определяется по формуле (с учётом Действующее значение напряжения определяется по формуле С другой стороны действующие значения напряжения и силы Тогда получим Запишем уравнение гармонических колебаний в общем виде По условию задачи задано следующее уравнение Сопоставляя эти два уравнения можно определить, что Тогда действующее значение напряжения |
|
|
Ответ:
79 В.
Задача
3.
Дана цепь переменного тока со следующими параметрами: активное сопротивление
равно 20 Ом, индуктивность равна 15 мГн, электроёмкость конденсатора равна
55 мкФ, частота равна 50 Гц, амплитудное напряжение равно 220 В.
Найдите амплитудные токи, протекающие в каждом элементе цепи, а также суммарный
ток.
|
ДАНО: |
СИ |
РЕШЕНИЕ При параллельном соединении Закон Ома для участка цепи Исходя из него, запишем Индуктивное сопротивление определяется по формуле Ёмкостное сопротивление определяется по формуле Тогда получим Циклическую частоту можно определить по формуле Тогда сила тока в резисторе, Запишем закон Ома для цепей переменного тока В котором полное сопротивление определяется как Тогда сила тока |
|
|
Задача
4.
Конденсатор и катушка индуктивности последовательно подключены к источнику
переменного напряжения. Частоту колебаний увеличивают от 50 Гц до 80 Гц. Как
изменится значение амплитудного тока? Резонансная частота колебаний равна 70
Гц.
|
ДАНО: |
РЕШЕНИЕ Запишем закон Ома для цепей переменного тока В соответствии с ним, Полное сопротивление определяется по формуле Исходя из того, что в цепи В соответствии с полученным Тогда отношение полных сопротивлений Собственная частота колебательного контура определяется по Тогда получаем, что отношение полных сопротивлений равно Т.к. циклическая частота определяется по формуле то получаем Тогда отношение полных сопротивлений равно Можно получить косвенное |
|
|
Ответ:
амплитудный ток увеличится в 6,67 раза.
Задача
5.
В цепь переменного тока последовательно включен резистор с сопротивлением 10
Ом, катушка и конденсатор с ёмкостью 200 нФ. Известно что при частотах 1 кГц и
1,5 кГц в цепи наблюдаются одинаковые амплитудные токи. Найдите индуктивность
катушки и разность фаз между током и напряжением при указанных частотах.
|
ДАНО: |
СИ |
РЕШЕНИЕ Запишем закон Ома для цепей переменного тока В соответствии с этим, Запишем теперь формулу, по На основании данной формулы Преобразуем полученное Преобразуем получившуюся формулу Циклическая частота определяется по формуле Тогда индуктивность катушки равна Разность фаз определяется по формуле В соответствии с полученной |
|
|
Сдвиг фаз между током и напряжением в цепи переменного тока
Содержание
- 1 Определения и основные формулы
- 2 ПТ и активная нагрузка
- 3 Конденсатор в цепи ПТ
- 4 Индуктивность в цепи ПТ
- 5 Видео по теме
При транспортировке электрической энергии от мест её генерации (тепловые, атомные и гидроэлектростанции) до конечных потребителей необходимо неоднократно варьировать величину напряжения (понижать или повышать). С наибольшей эффективностью эти преобразования удаётся сделать, когда в линиях электропередачи используется переменное напряжение. При этом электрический ток, возникающий в результате действия переменного электрического поля, будет также переменным, изменяясь во времени периодически с такой же частотой. Если в сети присутствуют реактивные элементы (ёмкости, индуктивности), то возникает сдвиг фаз между переменным током и напряжением.
Определения и основные формулы
Переменным принято называть ток, изменяющийся с течением времени как по величине, так и по амплитуде. В английской технической литературе используется термин alternating current (AC). Он переводится как «чередующийся ток» или ток, изменяющий свою полярность.
Периодический переменный ток (ПТ) — это ток, который через идентичные интервалы времени принимает исходную величину, совершая таким образом циклический процесс, аналогичный гармоническому колебанию маятника. Гармонические колебания описываются с помощью синусоидальной функции:
Величина, которая определяется как произведение ω на t и имеет размерность угла (в радианах угол 90 градусов соответствует π/2 радиан), называется фазой синусоидальной переменной. В данном случае тока. Формула справедлива для случая, когда измерение тока стартует с точки отсчёта t = 0. В общем случае рабочая формула выглядит так:
Используя специальный измерительный прибор — осциллограф, можно наблюдать синусоиду напряжения на экране и определять её параметры.
ПТ и активная нагрузка
Если к источнику переменного тока подключено обычное сопротивление (резистор), то согласно закону Ома ток на резисторе, равен:
В приведенной выше формуле величина I0 = U0 / R — амплитуда ПТ. Видно, что ток в цепи с активным сопротивлением изменяется с течением времени абсолютно синхронно с напряжением.
Таким образом, на активной нагрузке угол сдвига фаз между током и напряжением равен нулю.
Конденсатор в цепи ПТ
Конструкция конденсатора препятствует протеканию постоянного тока, полностью его блокируя. Поочерёдно заряжаясь и разряжаясь конденсаторные пластины поддерживают ток в цепи, поскольку по определению ток I — это изменение заряда Q за единицу времени:
Ниже представлена картинка, объясняющая подключение конденсатора С к источнику переменного напряжения U.
Напряжение на конденсаторе в любой момент времени равно напряжению:
Тогда заряд Q(t) на обкладках конденсатора определим, используя выражение:
Пользуясь формулой для тока, получим первую производную от заряда по времени, которая равна ёмкостному току Ic(t):
Из графиков, представленных на картинке ниже, видно, что максимальная амплитуда тока наступает на четверть периода раньше, чем напряжения. Из этого следует, что фаза напряжения на π/2 радиан меньше фазы электротока. То есть, в цепи синусоидального тока существует отставание напряжения по фазе (фазовый сдвиг) на π/2.
Данное явление может быть объяснено по-другому. Из курса тригонометрии известно, что:
С помощью формул, приведенных выше, можно получить такое выражение:
Данное соотношение в явном виде показывает, что фазовый сдвиг равен π/2.
Индуктивность в цепи ПТ
Катушка индуктивности в цепях СПТ является реактивным элементом, поскольку ее активное сопротивление практически равно нулю. При подключении катушки также возникает фазовый сдвиг, но его причина несколько иная, чем в цепи с емкостью.
При практически нулевом омическом сопротивлении не может возникнуть короткое замыкание (резкий рост тока), поскольку переменный характер напряжения включает иной механизм сопротивления. Согласно закону, открытому британским учёным Майклом Фарадеем, в катушке появляется переменное магнитное поле, которое создает магнитный поток F, инициирующий появление электродвижущей силы (ЭДС самоиндукции) на концах катушки индуктивности:
В соответствии с законом Фарадея:
Откуда следует, что:
Используя данную формулу, находим определение для тока на индуктивности:
Как известно,
Следовательно, в идеальном индуктивном элементе угол сдвига фаз между напряжением и током равен π/2, причём ток отстаёт по фазе от напряжения.
Из графика видно, что максимум силы тока достигается на четверть периода позже, чем максимум напряжения, что соответствует отставанию по фазе на π/2.
От угла сдвига фаз зависит, какова будет реактивная мощность и, следовательно, коэффициент мощности, который выражается через cosφ и является очень важной характеристикой для оценки эффективности работы электрооборудования. Его значение может находиться в диапазоне от нуля до единицы. Если cosφ = 0, это означает, что в электроцепи присутствуют лишь реактивные токи. На практике такая ситуация невозможна, но чтобы потери мощности, связанные с реактивными токами, были меньше, используют компенсационные устройства.
Принцип действия таких устройств основывается на свойстве конденсаторов и катушек сдвигать фазу в противоположных направлениях. Компенсаторы зачастую используют в производственных цехах, где работает большое количество электрооборудования. Это приводит к ощутимым потерям электроэнергии и ухудшению качества электротока. Устройство компенсации решает подобные проблемы. Им успешно силу тока изменяют, если что-то сдвигают. Обычно такое устройство состоит из блоков конденсаторов довольно большой емкости, которые помещаются в отдельных шкафах.
Видео по теме
Starting from the Laplace domain, the voltage across the resistor is given by:
$$V_R(s)=frac{1}{sL+R}V_{in}(s) Rightarrow frac{V_R(s)}{V_{in}(s)}=frac{1}
{sL+R} = H(s)$$ It can be seen that, as expected, the RL circuit is a stable linear system, since the (real) pole is in the left half plane.
Converting to the Fourier domain by substituting $s=jomega$ (since we are only interested in the steady state response):
$$Rightarrow H(jomega)=frac{1}{jomega{L}+R}$$
Since $H(jomega)$ represents the transfer function of a stable linear system, the response to a general input $x(t)=Acos(omega {t} + phi)$ is given by:
$$y(t)=Avert H(jomega)vert cos[omega {t} + phi + angle{H(jomega)}]$$
Therefore, for an input voltage given by
$$v_{in}(t)=86+frac{400}{pi}cdotsum_{text{n}=1}^inftyfrac{sinleft(200picdottext{n}cdot tright)}{text{n}}$$
and using the superposition principle, the voltage across the resistor is given by:
$$v_R(t)=86 + sum_{n=1}^infty {frac{400}{npi} frac{R}{sqrt{R^2+omega_n^2 L^2}} sin Big[200pi {n} {t} — tan^{-1}left( frac{omega_n L}{R} right) Big]}$$
where $$vert H(jomega)vert = frac{R}{sqrt{R^2+omega_n^2 L^2}}$$
Now, since the voltage and current across a resistor are in phase, the current through the resistor is $$i_R(t)= frac{86}{R} + sum_{n=1}^infty {frac{400}{npi} frac{1}{sqrt{R^2+omega_n^2 L^2}} sin Big[200pi {n} {t} — tan^{-1}left( frac{omega_n L}{R} right) Big]}$$
The instantaneous power dissipated by the resistor is:
$$p(t)=i_R(t)cdot v_R(t)$$
The average power dissipated by the resistor is $$ Rightarrow P_{avg}=frac{1}{T}int_0^T{i_R(t)cdot v_R(t)}mathrm{d}t=frac{1}{T}int_0^T{frac{v_R^2(t)}{R}}mathrm{d}t = frac{1}{R}Big[ frac{1}{T}int_0^T{v_R^2(t)}mathrm{d}t Big]=frac{V_{RMS}^2}{R}$$
Finally (with some careful algebra):
$$V_{RMS}^2= 86^2 + frac{1}{2}sum_{n=1}^infty {left(frac{400}{npi} frac{R}{sqrt{R^2+omega_n^2 L^2}}right)^2} $$
Substituting $R=20Omega$, $L=25mmathrm{H}$ and $omega_n = 200pi {n}$, gives the average power as:
$$P_{avg} = frac{V_{RMS}^2}{R} = frac{86^2}{20} +frac{1}{2}{frac{1}{20}sum_{n=1}^infty left(frac{400}{npi} frac{20}{sqrt{20^2+{200^2pi^2 {n^2}} times left(25times 10^{-3}right)^2}}right)^2} $$
Simplifying gives:
$$P_{avg} = frac{1849}{5} + sum_{n=1}^infty {10left( frac{400}{npi sqrt{400 + 25pi^2 n^2} } right)^2}=frac{17422}{15}-500cothleft(4right) approx 661.131W$$