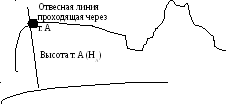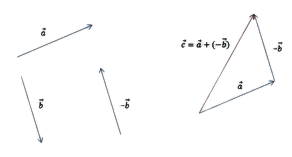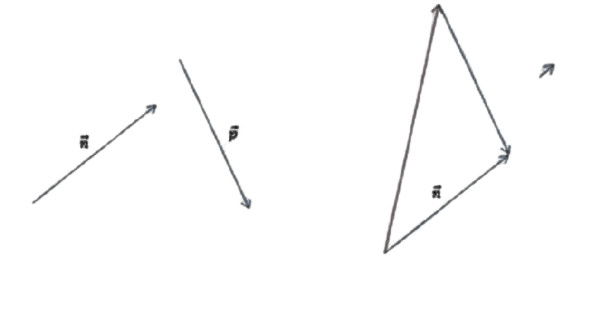Содержание:
- Формула
- Примеры нахождения разности векторов
Формула
Чтобы найти разность векторов $bar{a}-bar{b}$, заданных на плоскости координатами $bar{a}=left(a_{x} ; a_{y}right)$ и $bar{b}=left(b_{x} ; b_{y}right)$, необходимо вычесть из
координат первого вектора соответствующие
координаты второго, то есть
$$bar{a}-bar{b}=left(a_{x}-b_{x} ; a_{y}-b_{y}right)$$
В случае если векторы заданы в пространстве, то есть $bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$ и $bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$, то их разность равна
$$bar{a}-bar{b}=left(a_{x}-b_{x} ; a_{y}-b_{y} ; a_{z}-b_{z}right)$$
Примеры нахождения разности векторов
Пример
Задание. Найти разность векторов $bar{a}-bar{b}$, где
$bar{a}=(3 ; 0)$ и $bar{b}=(1 ; 2)$
Решение. Для нахождения разности векторов
$bar{a}$ и
$bar{b}$, вычтем их соответствующие координаты:
$$bar{a}-bar{b}=(3 ; 0)-(1 ; 2)=(3-1 ; 0-2)=(2 ;-2)$$
Ответ. $bar{a}-bar{b}=(2 ;-2)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти разность векторов
$bar{a}-bar{b}-bar{c}$, заданных в трехмерном пространстве своими координатами $bar{a}=(2 ;-3 ; 1), bar{b}=(1 ; 0 ;-2)$ и $bar{c}=(-1 ; 2 ; 3)$
Решение. Для нахождения искомой разности векторов вычтем их соответствующие координаты:
$$begin{aligned} bar{a}-bar{b}-bar{c}=(2 ;-3 ; 1)-(1 ; 0 ;-2)-(-1 ; 2 ; 3)=& \=(2-1-(-1) ;-3-0-2 ; 1-(-2)-3)=(2 ;-5 ; 0) end{aligned}$$
Ответ. $begin{aligned} bar{a}-bar{b}-bar{c}=(2 ;-5 ; 0) end{aligned}$
Читать дальше: как найти проекцию вектора.
В прошлых уроках Вы узнали, что такое натуральные числа — это числа, используемые при счете предметов.
Также мы успели поговорить про шкалы — линии с отмеченными на них величинами, которые помогают нам определить ту или иную величину.
Эта информация доступна зарегистрированным пользователям
Сегодня мы рассмотрим в некотором смысле “шкалу” для натуральных чисел — координатный луч, узнаем, что скрывается за этим определением.
Ответим на вопрос, почему луч подходит больше всего для обозначения натуральных чисел, а также научимся определять с помощью него длины отрезков.
Луч- это часть прямой ограниченная с одной стороны точкой, называемой началом луча.
Начертим луч с началом в точке О так, чтобы он шел слева направо, и отметим на нем точку А не очень далеко от начала.
Эта информация доступна зарегистрированным пользователям
Отрезок ОА назовем единичным отрезком.
Далее отложим от точки А следующий отрезок АВ, равный отрезку ОА.
Затем отложим от точки В отрезок ВС, также равный единичному отрезку.
Продолжим процесс, уже не называя точки.
Эта информация доступна зарегистрированным пользователям
Теперь напишем над точкой O число 0, над точкой А число 1, над точкой В число 2, над С — 3 и так далее.
Эта информация доступна зарегистрированным пользователям
Так мы получили шкалу, которую называют координатным лучом.
В самом деле, для шкалы нам необходимы были такие объекты, как штрих, деление, цена деления, посмотрим, чем они представлены в данном случае.
В роли штрихов выступают точки.
Изображая координатный луч, можно точки обозначать как небольшие штрихи, это ничуть не делает рисунок менее точным.
Делением в данном случае является отрезок между любыми соседними точками.
Этот отрезок всегда равен единичному по построению, ведь мы всегда откладывали отрезок, равный единичному.
Ценой деления в данном случае является единица.
Может быть немного непривычно, что единица идет без наименования, ведь на других шкалах обычно цена деления 1 кг, 1 см, 1 км/ч.
Но здесь идет измерение натуральных чисел, поэтому просто единица.
Так что координатный луч вполне можно считать шкалой.
Если же говорить про более конкретное определение, то вот оно.
Координатный луч — луч с указанным для него единичным отрезком.
Нередко к этому определению добавляют помимо единичного отрезка еще два объекта: точку начала отсчета и направление увеличения чисел.
В сущности они не обязательны, ведь на луче уже есть точка — точка начала луча.
А на координатном луче точка начала отсчета и точка начала луча всегда совпадают.
Направление задавать тоже нет необходимости, ведь у луча только одно вполне определенное направление: от начала.
Единичный отрезок же необходим, ведь без него не будет одинакового расстояния между соседними точками и смысла в луче не будет.
Отметим важный момент: в одном координатном луче всегда один единичный отрезок.
Эта информация доступна зарегистрированным пользователям
Мы уже поговорили про координатный луч, но важно понять, почему он “координатный” и как определены координаты в данном случае.
Обычно можно услышать слово “координаты” в географическом контексте.
Когда мы узнаем координаты, а это два числа, то можем однозначно сказать, про какую точку на карте идет речь.
Другими словами, в географическом смысле, координаты являются числами, определяющими положение точки на карте.
В случае с координатным лучом все даже проще.
Ведь если карта — двумерный объект, то есть, если перед нами лежит карта, нам нужно одно число, чтобы определить, как высоко расположена точка, а второе число, чтобы определить насколько она смещена вправо или влево, то на луче точка может быть лишь дальше или ближе от его начала.
Координата точки на координатном луче соответствует количеству единичных отрезков между этой точкой и точкой начала отсчета.
Посмотрим еще раз на рисунок из прошлой главы:
Эта информация доступна зарегистрированным пользователям
Точка А находится на расстоянии одного единичного отрезка от точки начала отсчета.
Точке А соответствует число 1
Точка В находится на расстоянии двух единичных отрезков от точки начала отсчета.
И точке В соответствует число 2
Аналогично каждой следующей точке соответствует число на единицу больше.
Число, соответствующее точке на координатном луче, называют координатой этой точки.
Заметим теперь, как соответствуют друг другу натуральный ряд и координатный луч.
За исключением точки начала отсчета, каждой точке соответствует натуральное число.
Если смотреть от начала отсчета, то координата следующей точки после данной равна следующему натуральному числу после координаты данной точки.
На том же самом рисунке мы видим, что следующее число за координатой точка В (2) , за точкой В идет точка С и координата точки С (3)
Допустим мы знаем, что точки P и Q — соседние, причем Q находится дальше от точки начала отсчета, чем P.
И также мы знаем, что координата точки P равняется 276
Тогда мы сможем сказать координату точки Q, это будет следующее натуральное число после числа 276, то есть ответ: 277
Аналогичная логика работает и в другую сторону.
Координата точки, идущей перед данной, является предыдущим натуральным числом по отношению к координате данной точки.
Эта информация доступна зарегистрированным пользователям
Так, если координата точки В — это 2, то координата точки А будет числом, на единицу меньшим, чем 2, то есть единицей.
Допустим, точки E и R соседние.
Также известно, что R находится дальше от точки начала отсчета, чем Е; а также известна координата точки R, она равна 315
Чтобы найти координату точки Е достаточно взять предыдущее натуральное число от числа 315, это будет число 314
Эти примеры показывают, как натуральный ряд ложится на координатный луч.
Отметим, что именно луч идеально соответствует натуральным числам, ведь и луч, и натуральный ряд ограничены с одной стороны (с начала), но продолжаются бесконечно.
Если же нам надо найти координату точки безотносительно соседних точек, то достаточно отсчитать количество единичных отрезков между данной точкой и точкой начала отсчета.
Эта информация доступна зарегистрированным пользователям
Найдем координату точки Н.
Между ей и точкой О (началом отсчета) 4 единичных отрезка, значит, координата точки Н равна 4
Эта информация доступна зарегистрированным пользователям
Только что в тесте было задание, в котором было необходимо найти разность координат двух точек.
Возможно, вы заметили некоторую закономерность, но если нет, сейчас разберем.
Эта информация доступна зарегистрированным пользователям
Посмотрим на разность координат точек D и C
Мы можем посчитать их координаты. В данном случае они сразу указаны, надо просто вычесть из большей меньшую.
Получится, что разность координат равна единице.
Также заметим, что между точками C и D один единичный отрезок.
Если рассмотрим разность координат точек D и В, то увидим, что разность координат равна 2, а также то, что между ними 2 единичных отрезка.
Правило: чтобы посчитать разность координат двух точек на координатном луче, достаточно посчитать, сколько между ними единичных отрезков.
Данное правило удобно, когда изначально координаты точек неизвестны, но при этом легко посчитать, сколько между ними единичных отрезков.
Теперь поговорим про измерение отрезков.
Допустим, требуется найти длину отрезка AD
Мы можем просто сосчитать количество единичных отрезков между точками А и D
Получится 3 отрезка, следовательно, длина равна 3.
Но можно сделать проще.
Правило: чтобы найти длину отрезка на координатном луче необходимо из координаты точки, дальней от точки начала отсчета, надо вычесть координаты ближней точки.
В случае с отрезком AD необходимо вычесть из координаты точки D (4) координату точки А (1)
Таким образом, длина отрезка AD равна ((mathbf{4-1=3}))
Эта информация доступна зарегистрированным пользователям
Интересно, что с математикой можно столкнуться не только в учебниках, но и в художественной литературе и даже в кинематографе.
Привычно видеть в роли главного героя в фильме какого-либо сильного человека, спортсмена, политика.
Но иногда главным харизматичным героем может быть математик, ученый.
Расскажу про одну достаточно интересную картину, повествующую о нестандартно мыслящемем математике.
А именно про “Человека, который изменил все”.
Эта информация доступна зарегистрированным пользователям
Данный фильм рассказывает про то, как менеджер одного из беднейших в американской лиге бейсбольных клубов “Окленд Атлетикс” нанимает к себе, казалось бы, далекого от спорта человека, похожего на типичного “ботаника”.
Этот человек оказывается выпускником экономического факультета, который решает отбирать игроков в клуб используя методы статистического анализа.
И здесь очень интересна концепция: нередко тот или иной клуб тратит большие деньги, чтобы нанять к себе успешного игрока.
Правда, после того как деньги потрачены, за новый клуб игрок может выступать уже не так хорошо.
Суть статистики заключалась в том, чтобы посмотреть данные множества игроков и начать выявлять таланты, которые еще не успели себя проявить.
Таким образом, клуб нанимает к себе игроков, которые в будущем становятся успешными, да еще и за не очень большие деньги.
Со статистикой можно даже идти дальше и просчитывать не только успехи отдельных игроков, но и всей команды в целом.
Так что данный фильм интересен той концепцией, которую он несет в массы.
Читайте также
Теорема доказана.
Теорема о разности векторов: Координаты разности векторов равны разности соответствующих координат этих векторов.
Доказательство.
Докажем теорему для двух векторов. Теорема для большего количества векторов доказывается аналогично. Пусть $overrightarrow=left$, $overrightarrow=$, тогда
Теорема доказана.
Теорема о произведении вектора на число: Координаты произведения вектора на число равны произведению соответствующих координат это число.
Доказательство.
Теорема доказана.
Пример задачи на нахождение координат вектора
Решение.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 05 04 2022
Определение разности двух векторов
В математике и физике студентам и школьникам зачастую попадаются задачи на векторные величины и на выполнение различных операций над ними. В чём же отличие векторных величин от привычных нам скалярных, единственная характеристика которых — это численное значение? В том, что они обладают направлением.
[block >
Определения векторной математики
Введём главные определения, используемые при выполнении линейных операций.
- Вектором называют направленный (имеющий точку начала и точку конца) отрезок.
- Длина (модуль) — это длина направленного отрезка.
- Коллинеарными называют такие два вектора, которые либо параллельны одной и той же прямой, либо одновременно лежат на ней.
- Противоположно направленными векторами называют коллинеарные и при этом направленные в разные стороны. Если же их направление совпадает, то они являются сонаправленными.
- Вектора являются равными, когда они сонаправлены и одинаковы по модулю.
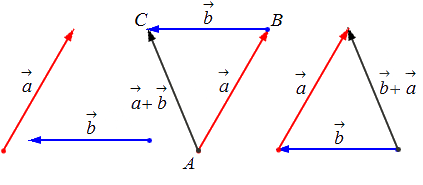
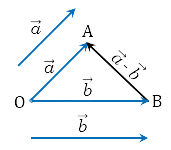
- Суммой двух векторов a и b является такой вектор c, начало которого совпадает с началом первого, а конец — с концом второго при условии, что b начинается в той же точке, в которой заканчивается a.
- Разностью векторов a и b называют сумму a и (—b), где (—b) — противоположно направленный к вектору b. Также определение разности двух векторов может быть дано следующее: разностью c пары векторов a и b называют такой c, который при сложении с вычитаемым b образует уменьшаемое a.
Аналитический метод
Аналитический способ подразумевает получение координат разности по формуле без построения. Возможно выполнить вычисление для плоского (двухмерного), объёмного (трёхмерного) или же n-мерного пространства.
Для двухмерного пространства и векторных величин a <a₁; a₂> и b <b₁; b₂> расчёты будут иметь следующий вид: c <c₁; c₂> = <a₁ — b₁; a₂ — b₂>.
В случае с добавлением третьей координаты расчёт будет проводиться аналогично, и для a <a₁; a₂; a₃> и b <b₁; b₂; b₃> координаты разности будут также получены попарным вычитанием: c <c₁; c₂; c₃> = <a₁ — b₁; a₂ — b₂; a₃ — b₃>.
Вычисление разности графически
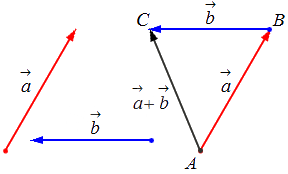
Для того чтобы построить разность графическим способом, следует воспользоваться правилом треугольника. Для этого необходимо выполнить следующую последовательность действий:
- По заданным координатам построить векторы, для которых нужно найти разность.
- Совместить их концы (т. е. построить два направленных отрезка, равных заданным, которые будут оканчиваться в одной и той же точке).
- Соединить начала обоих направленных отрезков и указать направление; результирующий будет начинаться в той же точке, где начинался вектор, являющийся уменьшаемым, и заканчиваться в точке начала вычитаемого.
[block > Результат операции вычитания показан на рисунке ниже.
Также существует метод построения разности, незначительно отличающийся от предыдущего. Его суть заключается в применении теоремы о разности векторов, которая формулируется следующим образом: для того чтобы найти разность пары направленных отрезков, достаточно найти сумму первого из них с отрезком, противоположно направленным ко второму. Алгоритм построения будет иметь следующий вид:
- Построить исходные направленные отрезки.
- Тот, что является вычитаемым, необходимо отразить, т. е. построить противоположно направленный и равный ему отрезок; затем совместить его начало с уменьшаемым.
- Построить сумму: соединить начало первого отрезка с концом второго.
Результат такого решения изображён на рисунке:
Решение задач
Для закрепления навыка разберём несколько заданий, в которых требуется рассчитать разность аналитически или графически.
Задача 1. На плоскости заданы 4 точки: A (1; —3), B (0; 4), C (5; 8), D (—3; 2). Определить координаты вектора q = AB — CD, а также рассчитать его длину.
Решение. Вначале следует найти координаты AB и CD. Для этого из координат конечных точек вычтем координаты начальных. Для AB началом является A (1; —3), а концом — B (0; 4). Рассчитаем координаты направленного отрезка:
Аналогичный расчёт выполняется для CD:
Теперь, зная координаты, можно найти разность векторов. Формула для аналитического решения плоских задач была рассмотрена ранее: для c = a — b координаты имеют вид <c₁; c₂> = <a₁ — b₁; a₂ — b₂>. Для конкретного случая можно записать:
Чтобы найти длину q, воспользуемся формулой | q | = √(q₁² + q₂²) = √((— 9)² + (— 1)²) = √(81 + 1) = √82 ≈ 9,06.
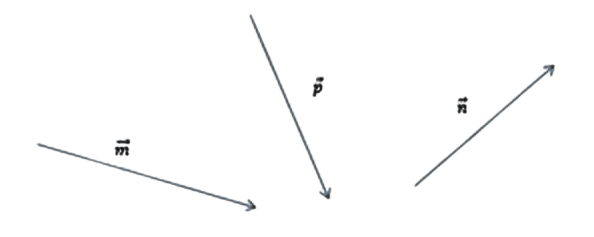
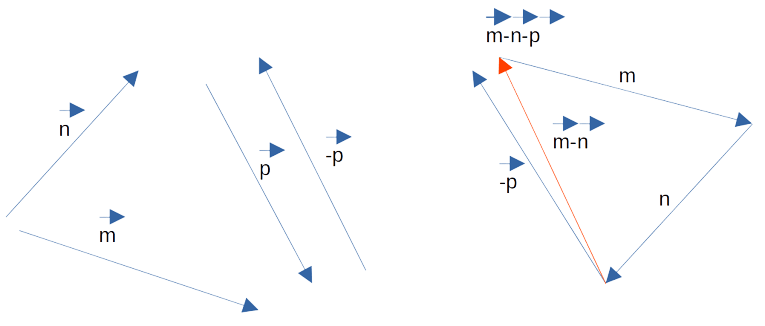
[block > Задача 2. На рисунке изображены векторы m, n и p.
Необходимо построить для них разности: p — n; m — n; m — n — p. Выяснить, какая из них обладает наименьшим модулем.
Решение. В задаче требуется выполнить три построения. Рассмотрим каждую часть задания более подробно.
Часть 1. Для того чтобы изобразить p — n, воспользуемся правилом треугольника. Для этого при помощи параллельного переноса соединим отрезки так, чтобы совпала их конечная точка. Теперь соединим начальные точки и определим направление. В нашем случае вектор разности начинается там же, где и вычитаемый n.
Часть 2. Изобразим m — n. Теперь для решения воспользуемся теоремой о разности векторов. Для этого следует построить вектор, противоположный n, а затем найти его сумму с m. Полученный результат будет выглядеть так:
[block > Часть 3. Для того чтобы найти разность m — n — p, следует разбить выражение на два действия. Поскольку в векторной алгебре действуют законы аналогичные законам арифметики, то возможны варианты:
- m — (n + p): в этом случае вначале строится сумма n + p, которая затем вычитается из m;
- (m — n) — p: здесь сначала нужно найти m — n, а затем отнять от этой разности p;
- (m — p) — n: первым действием определяется m — p, после чего из полученного результата нужно вычесть n.
Так как в предыдущей части задачи мы уже нашли разность m — n, нам остаётся лишь вычесть из неё p. Построим разность двух данных векторов при помощи теоремы о разности. Ответ показан на изображении ниже (красным цветом обозначен промежуточный результат, а зелёным — окончательный).
Остаётся определить, модуль какого из отрезков является наименьшим. Вспомним, что понятия длины и модуля в векторной математике являются идентичными. Оценим визуально длины p — n, m — n и m — n — p. Очевидно, что самым коротким и обладающим наименьшим модулем является ответ в последней части задачи, а именно m — n — p.
[block > [block >
Операции над векторами и их свойства: сложение и умножение
Прежде чем приступить к тематике статьи, напомним основные понятия.
Вектор – отрезок прямой, характеризующийся численным значением и направлением. Вектор обозначается строчной латинской буквой со стрелкой сверху. При наличии конкретных точек границ обозначение вектора выглядит как две прописные латинские буквы (маркирующие границы вектора) также со стрелкой сверху.
Нулевой вектор – любая точка плоскости, обозначается как нуль со стрелкой сверху.
Длина вектора – величина, равная или большая нуля, определяющая длину отрезка, составляющего вектор.
Коллинеарные векторы – лежащие на одной прямой или на параллельных прямых. Не выполняющие это условие векторы называют неколлинеарными.
Сложение двух векторов
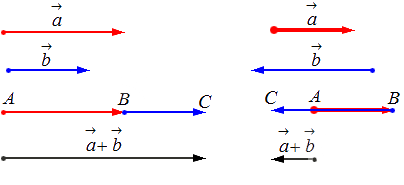
Исходные данные: векторы a → и b → . Для выполнения над ними операции сложения необходимо из произвольной точки отложить вектор A B → , равный вектору а → ; из полученной точки undefined – вектор В С → , равный вектору b → . Соединив точки undefined и C , получаем отрезок (вектор) А С → , который и будет являться суммой исходных данных. Иначе описанную схему сложения векторов называют правилом треугольника.
Геометрически сложение векторов выглядит так:
— для неколлинеарных векторов:
— для коллинеарных (сонаправленных или противоположнонаправленных) векторов:
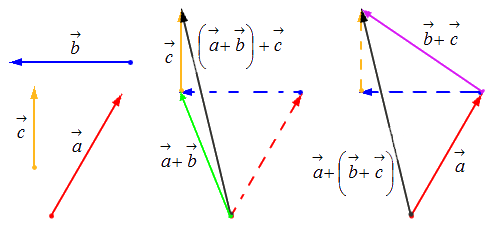
Сложение нескольких векторов
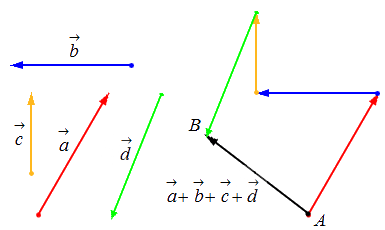
Взяв за основу описанную выше схему, мы получаем возможность произвести операцию сложения векторов в количестве более 2: поочередно прибавляя каждый последующий вектор.
Исходные данные: векторы a → , b → , c → , d → . Из произвольной точки А на плоскости необходимо отложить отрезок (вектор), равный вектору a → ; затем от конца полученного вектора откладывается вектор, равный вектору b → ; далее – по тому же принципу откладываются последующие векторы. Конечной точкой последнего отложенного вектора будет точка B , а полученный отрезок (вектор) A B → – суммой всех исходных данных. Описанную схему сложения нескольких векторов называют также правилом многоугольника .
Геометрически оно выглядит следующим образом:
Отдельной схемы действия по вычитанию векторов нет, т.к. по сути разность векторов a → и b → есть сумма векторов a → и — b → .
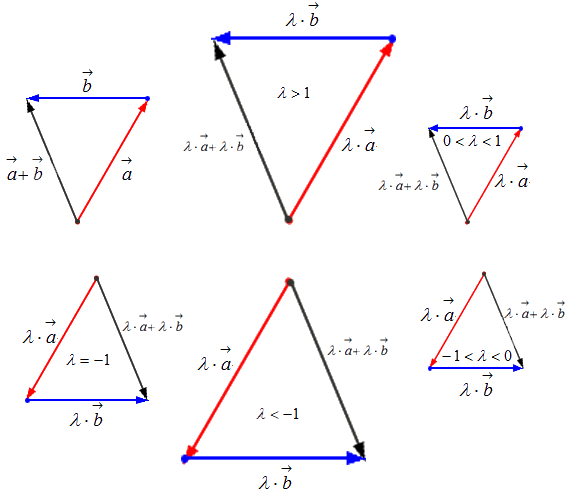
Умножение вектора на число
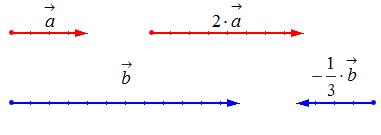
Чтобы произвести действие умножения вектора на некое число k , необходимо учитывать следующие правила:
— если k > 1 , то это число приведет к растяжению вектора в k раз;
— если 0 k 1 , то это число приведет к сжатию вектора в 1 k раз;
— если k 0 , то это число приведет к смене направления вектора при одновременном выполнении одного из первых двух правил;
— если k = 1 , то вектор остается прежним;
— если одно из множителей – нулевой вектор или число, равное нулю, результатом умножения будет нулевой вектор.
Исходные данные:
1) вектор a → и число k = 2 ;
2) вектор b → и число k = — 1 3 .
Геометрически результат умножения в соответствии с указанными выше правилами будет выглядеть следующим образом:
Свойства операций над векторами
Описанным выше операциям над векторами присущи свойства, некоторые из которых очевидны, а прочие можно обосновать геометрически.
Исходные данные: векторы a → , b → , c → и произвольные действительные числа λ и μ .
- Свойство коммутативности: a ⇀ + b → = b → + a → .
- Свойство ассоциативности: ( a → + b → ) + c → = a → + ( b → + c → ) .
- Свойство использования нейтрального элемента по сложению (нулевой вектор 0 → ⃗). Это очевидное свойство: a → + 0 → = a →
- Свойство использования нейтрального элемента по умножению (число, равное единице): 1 · a → = a → . Это очевидное свойство, не предполагающее никаких геометрических преобразований.
- Любой ненулевой вектор a → имеет противоположный вектор — a → и верным является равенство: a → + ( — a → ) = 0 → . Указанное свойство — очевидное.
- Сочетательное свойство операции умножения: ( λ · µ ) · a → = λ · ( µ · a → ) . Например, растяжение вектора при умножении на число 10 можно произвести, сначала растянув вектор в 2 раза, а затем полученный результат еще в 5 раз. Также возможен вариант умножения на число 10 при сжатии вектора в 5 раз и последующего растяжения полученного результата в 50 раз.
- Первое распределительное свойство (очевидно): ( λ + µ ) · a → = λ · a → + µ · a → .
- Второе распределительное свойство: λ · ( a → + b → ) = λ · a → + λ · b → .
Геометрически это свойство определяется подобием треугольников:
Свойства коммутативности и ассоциативности дают возможность складывать векторы в произвольном порядке.
Перечисленные свойства операций позволяют осуществлять необходимые преобразования векторно-числовых выражений аналогично привычным числовым. Рассмотрим это на примере.
Задача: упростить выражение a → — 2 · ( b → + 3 · a → )
Решение
— используя второе распределительное свойство, получим: a → — 2 · ( b → + 3 · a → ) = a → — 2 · b → — 2 · ( 3 · a → )
— задействуем сочетательное свойство умножения, выражение приобретет следующий вид: a → — 2 · b → — 2 · ( 3 · a → ) = a → — 2 · b → — ( 2 · 3 ) · a → = a → — 2 · b → — 6 · a →
— используя свойство коммутативности, меняем местами слагаемые: a → — 2 · b → — 6 · a → = a → — 6 · a → — 2 · b →
— затем по первому распределительному свойству получаем: a → — 6 · a → — 2 · b → = ( 1 — 6 ) · a → — 2 · b → = — 5 · a → — 2 · b → Краткая запись решения будет выглядеть так: a → — 2 · ( b → + 3 · a → ) = a → — 2 · b → — 2 · 3 · a → = 5 · a → — 2 · b →
Ответ: a → — 2 · ( b → + 3 · a → ) = — 5 · a → — 2 · b →
http://zaochnik.com/spravochnik/matematika/vektory/operatsii-nad-vektorami-i-ih-svojstva/
Лекция 3.
Системы координат
и высот применяемые в геодезии.
Геодезические
координаты.
Координатами
называются
угловые или линейные величины, определяющие
положение точек на плоскости, поверхности
или в пространстве относительно
направлений или плоскостей, выбранных
в качестве исходных в данной системе
координат. В геодезии применяют различные
системы координат рассмотрим лишь те
которые обозначены на топографических
картах.
1.Геодезическая
система координат.
Положение
точки на земном эллипсоиде относительно
экватора и начального (гринвичского)
меридиана описывается геодезическими
координатами широтой «В» и долготой
«L»
выражаемых в угловой мере (град, мин,
сек).
Широтой точки
(т.М, см. рис) называют угол составленный
отвесной линией , проходящей через эту
точку, и плоскостью экватора. Широты
бывают северные и южные и изменяются
от 0 градусов (на экваторе ) до 90 градусов
(на полюсах)
Долготой
точки называют двугранный угол,
заключенный между плоскостью меридиана,
проходящего через эту точку и плоскостью
начального Гринвичскоко меридиана.
Долготы бывают восточные и западные ,
изменяются (на восток и запад) от нуля
градусов (гринвичский меридиан) до 180
градусов.
Широты и долготы
точек, определяют из результатов
геодезических измерений на местности
с последующим их преобразованием на
поверхность земного эллипсоида. На
топографических картах геодезическая
система координат показана следующим
образом: в углах рамки трапеции подписаны
значения широт параллелей и значения
долгот меридианов ограничивающих данный
лист карты, между внешней и внутренней
рамками дана рамка широт и долгот в виде
чередующихся интервалов, минутный
интервал разделен точками на 10 секундные
интервалы.
2. Зональная
плоская прямоугольная система координат.
В
геодезических и топографических работах
применяется изображение поверхности
земного эллипсоида по частям — координатным
зонам в проекции Гаусса-Крюгера..
Ось абсцисс Х
т.А (XA,YA)
XA
YA
Ось ординат Y
Смещенная ось абсцисс
Начало координат
В каждой зоне
в отдельности вводится система плоских
прямоугольных координат, называемая
зональной системой координат.
За ось абсцисс
принимают средний осевой меридиан
координатной зоны, а за ось ординат –
линию изображения экватора. Такие
координаты называют прямоугольными.
Так как абсциссы
Х отсчитываются от экватора к полюсам,
то для территории России, расположенной
в северном полушарии, они будут всегда
положительными.
Ординаты в каждой
зоне будут как положительными, так и
отрицательными, в зависимости от
положения точки относительно осевого
меридиана. Для удобства в работе
избавляются от отрицательных значений
ординат в пределах каждой зоны, для чего
начало координат смещают на 500км. к
западу от осевого меридиана.
. Перед ординатой
первой цифрой в значении помечен номер
зоны. Такие ординаты называют
преобразованными. Счет зон ведется от
Гринвичского меридиана в направлении
с запада на восток (всего 60 зон). Для
удобства работы с этой системой координат
параллельно осям абсцисс и ординат
проводят линии через 1 км. Значения
координат этих линий подписывают на
картах между внешней и внутренней
рамками.
-
436068
11
12
6067
Разность
координат двух точек называют приращением
координат между точками.
D
XAB=
XВ
— XA
D
YAB=
YВ
— YA
Правило: чтобы
вычислить приращение координат между
первой и второй точками необходимо от
координаты второй точки вычесть
координату первой точки, обязательно
указать знак приращения координат.
Из определения
понятия приращения координат следует
, что
X
Это алгебраическая сумма
В =
XA+
D
XAB
YВ
= YA
+D
YAB
3. Система высот.
Высота точки
земной поверхности есть расстояние от
этой точки по отвесной линии до уровенной
поверхности принятой за начало счета
высот.
Уровенная поверхность (геоид)
Кронштадского
За уровенную
поверхность в нашей стране принят
уровень Балтийского моря (в спокойном
состоянии- Балтийская система высот.).
Этот уровень
зафиксирован Кронштадским футштоком
высота которого принята равной нулю.
Если высоты
отсчитывают от уровня Кронштадского
футштока , то такие высоты называют
абсолютные.
В инженерной
практике довольно часто используют не
абсолютные высоты, а относительные
высоты или отметки.
В этом случае за нуль высоты принимают
какую-либо характерную точку.
В
пределах небольшой территории уровенную
поверхность можно считать плоской.
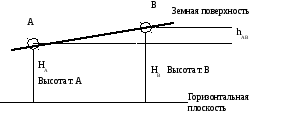
Разность высот
точек называют превышением и обозначают
буквой h.
Превышение
показывает насколько одна точка выше
(знак +) или ниже (знак-) другой.
Пусть высота точки
А равна НА
, а точки В равна НВ
. тогда
превышение меду точкой В и точкой А
равно:
hВА
= НВ—
НА
.
Если точка А выше
точки В, то превышение с точки А на точку
В имеет знак минус (превышение
отрицательное).
Если точка А ниже
точки В, то превышение с точки А на точку
В имеет знак плюс (превышение положительное).
Прямое и обратное
превышения между двумя точками равны
по величине и противоположны по знаку.
Из формулы превышения
следует , что
НВ
= НА
+hAB
(эта сумма алгебраическая).
5
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Для того, чтобы уяснить, что собой представляет разность векторов, введём понятие откладывания вектора от определённой точки и понятие суммы векторов.
Определение
Если некоторая точка A является началом вектора a, то говорят, что он является отложенным от точки A.
Теорема. От каждой точки можно отложить только один вектор, имеющий заданный модуль и направление. Докажем эту теорему.
Доказательство:
В случае, когда вектор нулевой, то теорема очевидна. Нулевые вектора в одной и той же точки совпадают между собой, т. е. являются одним и тем же вектором.
Сделаем построение. Точкой A обозначим начало вектора a, а точкой B его конец. Пусть у нас имеется некоторая точка K. Проведём через неё прямую b, которая параллельна вектору a. Отложим на данной прямой равные по своей абсолютной величине вектору a отрезки KL и KM. Из векторов, образованных этими отрезками искомым можно назвать только сонаправленный с a.
Единственность нашего вектора следует из того, что мы построили и видим.
Теорема доказана.
Определение
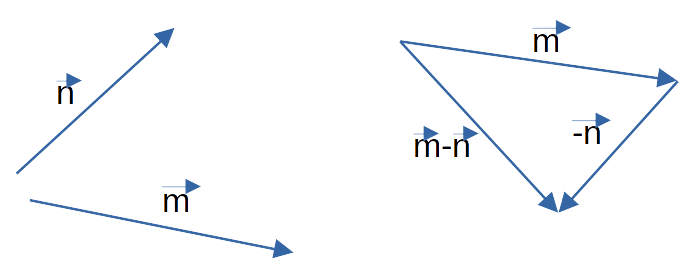
Суммой векторов a и b называется вектор с тем же началом, что вектор a и концом, как у вектора b. При этом вектор b должен начинаться в той же самой точке, в которой заканчивается вектор a.
Равные векторы, начинающиеся в разных точках, нередко обозначают одной и той же буквой. Иногда про подобные векторы говорят, как об одном и том же векторе, отложенном из разных мест.
Разность векторов
Определение
Разностью векторов a и b называется сумма вектора a c вектором, который противоположно направлен к вектору b.
По-другому это определение можно сформулировать следующим образом: разностью двух векторов a и b называется вектор c, который при сложении с вычитаемым b образует уменьшаемое, т. е. вектор a.
Формулами это записывается так:
b + c = a
a – b = c
Как найти разность векторов аналитическим способом
В двухмерном пространстве векторов a {x1, y1} и b {x2, y₂} разность векторов можно вычислить, как показано ниже:
c {x3, y3} = {x₁ — x2, y1 — y₂}.
Вычитание векторов в 3-мерном пространстве выглядит следующим образом:
c {x3; y3; z₃} = {x₁ — x2, y₂ — y₂, z1 — z2}.
Как найти разность векторов графическим способом
Нужно воспользоваться правилом треугольника. Последовательность действий следующая:
- Постройте по координатам векторы, для которых требуется найти разность;
- Совместите концы построенных векторов. Для этого нужно построить два равных заданным направленных отрезка, концы у которых будут в одной и той же точке;
- Соедините начала построенных отрезков и укажите их направление. Вектор c, называемый разностью векторов, будет иметь своё начало в той же точке, где начинается вектор, именуемый уменьшаемым и заканчивается в точке начала вычитаемого. Смотрите рисунок ниже.
Есть ещё один способ графического нахождения разности векторов. Он предусматривает следующий порядок действий:
- Постройте исходные направленные отрезки;
- Отразите вычитаемый отрезок. Для этого постройте противоположно направленный и равный ему отрезок и затем совместите начало этого отрезка с уменьшаемым;
- Постройте сумму, т. е. соедините начало первого отрезка и конец второго.
Нет времени решать самому?
Наши эксперты помогут!
Примеры вычисления разности векторов
Примеры
Вычислить вектор c, который представляет собой разность вектора a ={1;
2} и вектора b = {4; 8}.
Решение:
Действуем по выше указанному правилу
a — b = {1 — 4; 2 — 8} = {-3; -6}
Ответ: с{-3; -6}.
Вычислить вектор c, который является разностью векторов a = {1; 2; 5} и
b = {4; 8; 1}.
Решение:
Почти всё делается, как в уже рассмотренном примере, только добавляется третья координата.
a — b = {1 — 4; 2 — 8; 5 — 1} = {-3; -6; 4}
Ответ: c {-3; -6; 4}.
На рисунке векторы
Требуется построить разности: p — n, m —
n,m — n — p и найти ту из них, которая
имеет наименьший модуль.
Решение:
Для изображения p — n проще всего воспользоваться правилом треугольника. Параллельным переносом
отрезки
следует соединить таким образом, чтобы совпали их конечные точки. Далее нужно соединить начальные точки и
определить направление. В нашем случае вектор разности берёт своё начало там же, где и вычитаемый n.
Для изображения m — n правильнее будет воспользоваться вторым графическим способом нахождения разности
векторов. Сначала построим вектор противоположный n и найдём его суммы с вектором m.
Для нахождения разности m — n — p разобьём это выражение на два действия. Возможны следующие варианты:
- m — (n + p). Сначала нужно построить сумму,
затем уже вычесть её из m; - (m — n) — p. Сначала находим m — n,
осле этого от полученной разности отнимаем p; - (m— p) — n. Сначала определяем m — p, затем от
полученного результата отнимаем n.
Из вычислений выше нам известна разность m — n. Для получения решения нам нужно вычесть из неё
p.
Используя определение 3 построим разность векторов на рисунке. На нём изображён окончательный результат
и промежуточный.
Теперь нужно определить наименьший модуль. В нашем случае для этого можно лишь визуально оценить длины p — n,
m — n и m — n — p. Из построения сразу видно, что наименьшим модулем обладает вектор разности m — n —
p.