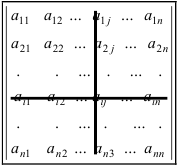
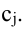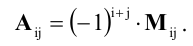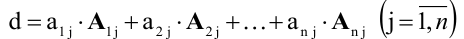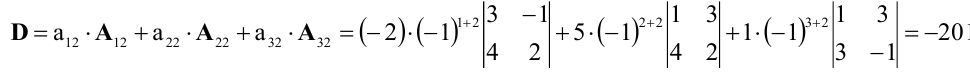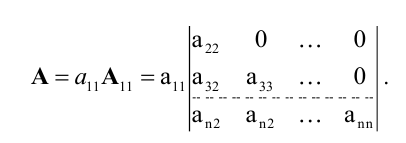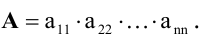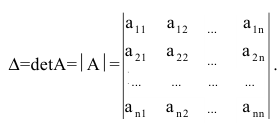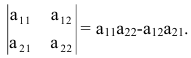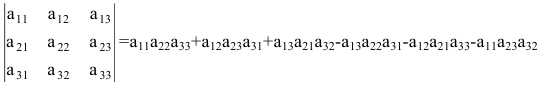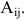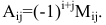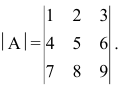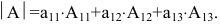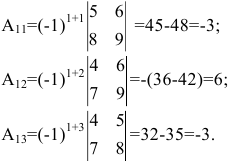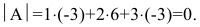Определители (детерминанты) матриц и их свойства
Пусть — квадратная матрица порядка
. Определитель (детерминант) квадратной матрицы
— это число
, которое ставится в соответствие матрице и вычисляется по ее элементам согласно следующим правилам.
1. Определителем матрицы порядка
называется единственный элемент этой матрицы:
.
2. Определителем матрицы порядка
называется число
(2.1)
где — определитель квадратной матрицы порядка
, полученной из
вычеркиванием первой строки и j-го столбца.
Определитель матрицы обозначают, заключая матрицу в «прямые» скобки:
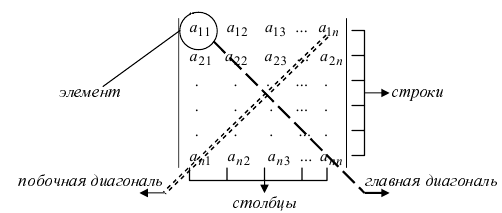
Имея в виду это обозначение, для краткости говорят о порядке определителя, строках или столбцах определителя, элементах определителя, опуская при этом слово «матрица». Например, первая строка определителя n-го порядка — это первая строка квадратной матрицы n-го порядка.
Индуктивное определение позволяет вычислить определитель любого порядка. По второму правилу (т.е. по формуле (2.1)) нахождение определителя n-го порядка сводится к вычислению и определителей (n-1)-го порядка. Нахождение каждого определителя (n-1)-го порядка сводится к вычислению определителя (n-2)-го порядка и т.д., пока не получим
определителей n-го порядка, которые находим по первому правилу. Конечно, такая процедура неудобна из-за своей громоздкости, но вполне реализуема и может быть принята в качестве определения.
Квадратную матрицу, определитель которой равен нулю, называют вырожденной {особой), в противном случае — невырожденной (неособой).
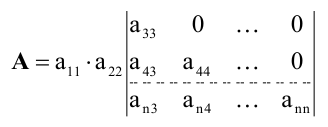
Получим формулы вычисления определителей второго и третьего порядков. По определению при
При вычеркивании первой строки и одного столбца получаем матрицу, содержащую один элемент, поэтому
Подставляя эти значения в правую часть, получаем формулу вычисления определителя второго порядка
(2.2)
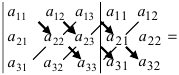
Определитель второго порядка равен разности произведения элементов, стоящих на главной диагонали, и произведения элементов, стоящих на побочной диагонали (см. схему на рис. 2.1).
Для определителя третьего порядка имеем
При вычеркивании первой строки и одного столбца получаем определители квадратных матриц второго порядка:
Эти определители второго порядка записываем по формуле (2.2) и получаем формулу вычисления определителя третьего порядка
(2.3)
Определитель (2.3) представляет собой сумму шести слагаемых, каждое из которых есть произведение трех элементов определителя, стоящих в разных строках и разных столбцах. Причем три слагаемых берутся со знаком плюс, а три других — со знаком минус.
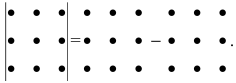
Для запоминания формулы (2.3) используется правило треугольников: надо сложить три произведения трех элементов, стоящих на главной диагонали и в вершинах двух треугольников, имеющих сторону, параллельную главной диагонали (рис. 2.2,а), и вычесть три произведения элементов, стоящих на побочной диагонали и в вершинах двух треугольников, имеющих сторону, параллельную побочной диагонали (рис. 2.2,6).
Можно также пользоваться схемой вычисления, изображенной на рис. 2.3 (правило Саррюса): к матрице приписать справа первый и второй столбцы, вычислить произведения элементов, стоящих на каждой из указанных шести прямых, а затем найти алгебраическую сумму этих произведений, при этом произведение элементов на прямых, параллельных главной диагонали, берутся со знаком плюс, а произведение элементов на прямых, параллельных побочной диагонали, — со знаком минус (согласно обозначениям на рис. 2.3).
Итак, получены формулы для вычисления определителей второго и третьего порядков. Можно продолжить вычисления по формуле (2.1) для и получить формулы для вычисления определителей четвертого, пятого и т.д. порядков. Следовательно, индуктивное определение позволяет вычислить определитель любого порядка. Другое дело, что формулы будут громоздкими и неудобными при практических вычислениях. Поэтому определители высокого порядка (четвертого и более), как правило, вычисляют на основании свойств определителей.
Пример 2.1. Вычислить определители
Решение. По формулам (2.2) и (2.3) находим ;
Формула разложения определителя по элементам строки (столбца)
Пусть дана квадратная матрица порядка
.
Дополнительным минором элемента
называется определитель матрицы порядка
, полученной из матрицы
вычеркиванием i-й строки и j-го столбца.
Алгебраическим дополнением элемента
матрицы
называется дополнительный минор
этого элемента, умноженный на
Теорема 2.1 формула разложения определителя по элементам строки (столбца). Определитель матрицы равен сумме произведений элементов произвольной строки (столбца) на их алгебраические дополнения:
(разложение по i-й строке);
(разложение по j-му столбцу).
Замечания 2.1.
1. Доказательство формулы проводится методом математической индукции.
2. При индуктивном определении (2.1) фактически использована формула разложения определителя по элементам первой строки.
Пример 2.2. Найти определитель матрицы
Решение. Разложим определитель по 3-й строке:
Теперь разложим определитель третьего порядка по последнему столбцу:
Определитель второго порядка вычисляем по формуле (2.2):
Определитель матрицы треугольного вида
Применим формулу разложения для нахождения определителя верхней треугольной матрицы
Разложим определитель по последней строке (по n-й строке):
где — дополнительный минор элемента
. Обозначим
. Тогда
. Заметим, что при вычеркивании последней строки и последнего столбца определителя
, получаем определитель
верхней треугольной матрицы такого же вида, как
, но (n-1)-го порядка. Раскладывая определитель
, по последней строке ((n-1)-й строке), получаем
. Продолжая аналогичным образом и учитывая, что
, приходим к формуле
т.е. определитель верхней треугольной матрицы равен произведению элементов, стоящих на главной диагонали.
Замечания 2.2
1. Определитель нижней треугольной матрицы равен произведению элементов, стоящих на главной диагонали.
2. Определитель единичной матрицы равен 1.
3. Определитель матрицы треугольного вида будем называть определителем треугольного вида. Как показано выше, определитель треугольного вида (определитель верхней или нижней треугольной матрицы, в частности, диагональной) равен произведению элементов, стоящих на главной диагонали.
Основные свойства определителей (детерминантов)
1. Для любой квадратной матрицы , т.е. при транспонировании определитель не изменяется. Из этого свойства следует, что столбцы и строки определителя «равноправны»: любое свойство, верное для столбцов, будет верным для строк.
2. Если в определителе один из столбцов нулевой (все элементы столбца равны нулю), то определитель равен нулю: .
3. При перестановке двух столбцов определитель меняет знак на про тивоположный (свойство антисимметричности):
4. Если в определителе имеется два одинаковых столбца, то он равен нулю:
при
5. Если определитель имеет два пропорциональных столбца, то он равен нулю:
при
6. При умножении всех элементов одного столбца определителя на число определитель умножается на это число:
7. Если j-й столбец определителя представляется в виде суммы двух столбцов , то определитель равен сумме двух определителей, у которых j-ми столбцами являются
и
соответственно, а остальные столбцы одинаковы:
8. Определитель линеен по любому столбцу:
9. Определитель не изменится, если к элементам одного столбца прибавить соответствующие элементы другого столбца, умноженные на одно и тоже число:
10. Сумма произведений элементов какого-либо столбца определителя на алгебраические дополнения соответствующих элементов другого столбца равна нулю:
при
.
Замечания 2.3
1. Первое свойство определителя доказывается по индукции. Доказательства остальных свойств проводятся с использованием формулы разложения определителя по элементам столбца. Например, для доказательства второго свойства достаточно разложить определитель по элементам нулевого столбца (предположим, что j-й столбец нулевой, т.е.
):
Для доказательства свойства 10 нужно прочитать формулу разложения определителя справа налево, а именно, сумму произведений элементов i-го столбца на алгебраические дополнения элементов j-го столбца представить как разложение по j-му столбцу определителя
у которого на месте элементов j-ro столбца стоят соответствующие элементы i-го столбца. Согласно четвертому свойству такой определитель равен нулю.
2. Из первого свойства следует, что все свойства 2-10, сформулированные для столбцов определителя, будут справедливы и для его строк.
3. По формулам разложения определителя по элементам строки (столбца) и свойству 10 заключаем, что
(2.4)
4. Пусть — квадратная матрица. Квадратная матрица
того же порядка, что и
, называется присоединенной по отношению к
, если каждый ее элемент
равен алгебраическому дополнению элемента
матрицы
. Иными словами, для нахождения присоединенной матрицы следует:
а) заменить каждый элемент матрицы его алгебраическим дополнением
, при этом получим матрицу
;
б) найти присоединенную матрицу , транспонируя матрицу
.
Из формул (2.4) следует, что , где
— единичная матрица того же порядка, что и
.
Пример 2.3. Дана матрица . Сравнить определитель матрицы
с определителями матриц
Решение. Определитель матрицы был найден в примере 2.1:
. По формуле (2.2) вычисляем определители остальных матриц:
что соответствует свойству 1;
что соответствует свойству 3, так как матрица получена из матрицы
перестановкой 1-го и 2-го столбцов;
что соответствует свойству 3, так как матрица получена из матрицы
перестановкой 1-й и 2-й строк;
что соответствует свойству 6, так как матрица получена из матрицы
умножением элементов 2-й строки на число
;
что соответствует свойству 9, так как матрица получена из матрицы
прибавлением к элементам первой строки соответствующих элементов второй строки, умноженных на
.
Пример 2.4. Дана матрица . Найти присоединенную матрицу
и вычислить произведения
и
.
Решение. Найдем алгебраические дополнения всех элементов матрицы :
Составим присоединенную матрицу, транспонируя матрицу (см. п.4 замечаний 2.3), т.е.
Вычислим произведения
что соответствует п.4 замечаний 2.3, так как (см. пример 2.1).
Пример 2.5. Найти определитель блочно-диагональной матрицы , где
— произвольная квадратная матрица,
— единичная, а
— нулевая матрица соответствующего порядка,
— транспонированная.
Решение. Разложим определитель по последнему столбцу. Так как в этом столбце все элементы нулевые, за исключением последнего, равного 1, получим определитель такого же вида, что и исходный, но меньшего порядка. Раскладывая полученный определитель по последнему столбцу, уменьшаем его порядок. Продолжая таким же образом, получаем определитель матрицы . Следовательно,
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Разность матриц
Определение:
Разностью двух матриц называется
матрица той же размерности, что и
исходные, каждый элемент которой
определяется как разность соответствующих
элементов матриц.
Пусть
и
.
Тогда
,
где
,
,
.
Разность матриц
А и В обозначается символом
.
Замечание 1.
А, В, С
– матрицы одинаковых размеров.
Замечание 2.
Разность матриц
можно определить также следующим
образом:
,
где
— матрица, противоположная матрице В.
Произведение матрицы на число
В результате
умножения матрицы на число получается
матрица такой же размерности, что и
исходная, каждый элемент которой является
результатом произведения соответствующего
элемента исходной матрицы на число.
Пусть
,
k – число. Тогда
такая, что
(17) (
,
).
Обозначения:
или
.
Пример
3.
Найти матрицу
3А-2В, если
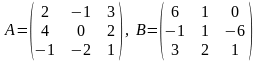
Решение
Имеем
,
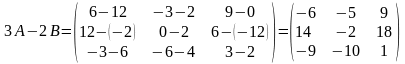
Справедливы
следующие свойства
А,
В – матрицы.
,
— числа.
Произведение матриц
Определение:
Пусть
,
.
Тогда
,
такая, что
,
,
,
.
Произведение
матрицы А на матрицу В обозначают
.
Следует
запомнить, что операция умножения
двух матриц вводится только для случая,
когда число столбцов первой матрицы
равно числу строк второй матрицы.
Следует
запомнить.
Из определения
произведения матриц следует, что элемент
матрицы АВ, стоящий в i-й
строке и k-м столбце, равен сумме
произведений элементов i-й строки
матрицы А на соответствующие элементы
k—го столбца матрицы
В.
Замечание 1.
Если матрицы А
и В квадратные одного размера, то
произведения АВ и ВА всегда
существуют.
Замечание 2.
Если матрицу А
можно умножить на матрицу В, а В
можно умножить на А, то, вообще
говоря,
.
Пример
4.
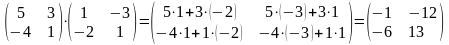
Пример
5.
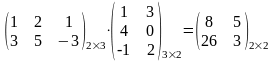
Пример
6.
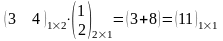
Справедливы
следующие свойства умножения матриц:
-
-
-
-
,
А – квадратная матрица, Е —
единичная матрица того же порядка.
Лекция № 2. § 2. Определители. Определитель второго порядка
Определение:
Определителем 2-го порядка называют
число, которое получается из элементов
квадратной матрицы
по указанному правилу.
Определитель
второго порядка:
.
Обозначение
определителя:
.
Определитель матрицы А также называют
ее детерминантом.
Замечание
Вычислить
определитель 2-го порядка означает найти
разность из произведения элементов,
стоящих на главной диагонали матрицы
(идущей из левого верхнего в правый
нижний угол) и произведения элементов,
находящихся на побочной, диагонали.
Пример
1.
Вычислить:

Свойства определителя второго порядка
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Определители II и III порядка
Определение: Определителем порядка n называется число (выражение), записанное в виде квадратной таблицы, имеющей n строк и n столбцов, которая раскрывается по определенному правилу.
Числа
Определение: Определителем II порядка называется число (выражение), записанное в виде квадратной таблицы размером 2×2, т.е. имеющая 2 строки и 2 столбца.
Определение: Определитель II порядка вычисляется по правилу: из произведения элементов, стоящих на главной диагонали, надо вычесть произведение элементов, стоящих на побочной диагонали:
Пример:
Определение: Определителем III порядка называется число (выражение), записанное в виде квадратной таблицы размером 3×3, то есть имеющей 3 строки и 3 столбца.
Определитель III порядка вычисляется по правилу Саррюса: за определителем выписывают первый и второй столбцы, затем из суммы произведений элементов, стоящих на главной диагонали ей параллельных диагоналях, надо вычесть сумму произведений элементов, стоящих на побочной диагонали и ей параллельных:
Пример:
Определение: Минором 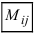
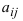
Пример:
Найти миноры элементов 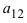
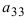
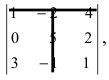
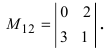
Пример:
Найти миноры элементов 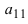
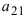
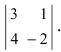
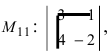
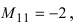
Определение: Алгебраическим дополнением 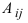
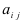
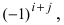
Замечание: Из определения алгебраического дополнения следует, что алгебраическое дополнение совпадает со своим минором, если сумма 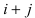
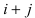
Определение: Транспонированным определителем n-го порядка называется определитель порядка n, полученный из исходного определителя путем замены строк на соответствующие столбцы, а столбцов на соответствующие строки.
Если
Пример:
Найти определитель, транспонированный к определителю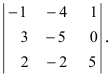
Свойства определителей
1. Величина транспонированного определителя равна величине исходного определителя. Пусть 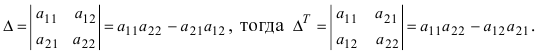
2. Перестановка местами двух строк (столбцов) изменяет знак определителя на противоположный. Пусть
Если поменять местами строки (столбцы) четное число раз, то величина и знак определителя не меняется. Нечетная перестановка местами строк (столбцов) не меняет величину определителя, но изменяет его знак на противоположный.
3. Определитель, содержащий две (или более) одинаковых строки (столбца), равен нулю. Если определитель содержит два одинаковых столбца, то 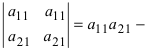
4. Для того чтобы умножить определитель на число k, достаточно умножить на это число все элементы какой-либо одной строки (столбца). Обратно: если все элементы какой-либо строки (столбца) имеют общий множитель k, то его можно вынести за знак определителя.
Докажем это свойство:
5. Если две каких-либо строки (столбца) пропорциональны, то определитель равен нулю.
Пусть в определителе II порядка первая и вторая строки пропорциональны, тогда
6. Если все элементы какой-либо строки (столбца) равны нулю, то определитель равен нулю.
Пусть в определителе II порядка все элементы первой строки равны нулю, тогда
7. Если элементы какой-либо строки (или столбца) можно представить в виде двух слагаемых, то сам определитель можно представить в виде суммы двух определителей. Если 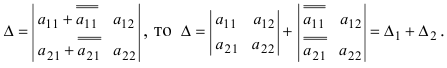
8. Если все элементы какой-либо строки (столбца) умножить на вещественное число к и прибавить k соответствующим элементам другой строки (соответственно, столбца), то величина определителя не изменится.
Умножим элементы второго столбца на вещественное число k и прибавим результат умножения к соответствующим элементам первого столбца, получим
Второй определитель равен нулю по свойству 5.
Замечание: Данное свойство применяется для обнуления всех элементов какой-либо строки (столбца) за исключением одного (метод обнуления), что существенно снижает трудоемкость вычисления определителей порядка выше 3 (см. также свойство 9.).
9. [Метод раскрытия определителя по элементам какой-либо строки (или столбца); универсальный способ вычисления определителя любого порядка]. Определитель любого порядка равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения:
Пример:
Вычислить определитель 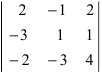
Решение:
Воспользуемся свойством 9.: раскроем определитель по элементам 3 строки 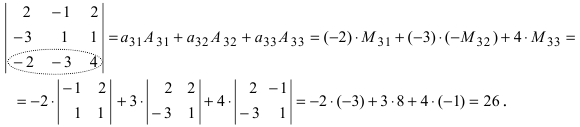
Из полученных результатов видно, что свойство 9. является универсальным методом вычисления любых определителей по элементам любой строки или столбца.
Используя свойство 8. можно обнулить все элементы какой-либо строки (столбца) за исключением одного (метод обнуления), а затем раскрыть определитель по элементам этой строки, воспользовавшись свойством 9.
Пример:
Вычислить определитель
Решение:
Обнулим элементы в третьей строке, для чего выполним следующие действия: 
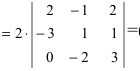
(по свойству 4. из третьего столбца вынесем множитель 0,5, тогда множитель перед определителем станет равным 1)
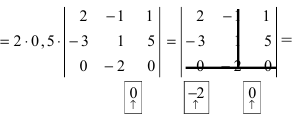
(раскроем определитель по элементам третьей строки: 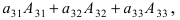
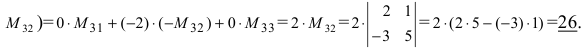
Пример:
Решить уравнение
Решение:
Вычислим определители второго и третьего порядков согласно вышеописанным правилам:
Найденные величины подставим в исходное уравнение
Пример:
Решить неравенство
Решение:
Вычислим определители второго и третьего порядков согласно вышеописанным правилам:
Найденные величины подставим в исходное неравенство
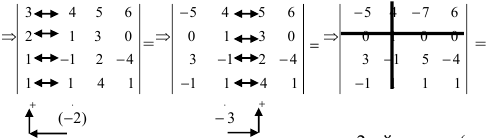
Пример:
Вычислить определитель четвертого порядка (аналогично выполнить такие же действия с определителем третьего порядка), преобразовав его так, чтобы три элемента некоторого ряда равнялись нулю, и вычислить полученный определитель по элементам этого ряда:
Решение:
Во второй строке исходного определителя присутствуют 1 и 0, поэтому обнуление элементов будем производить в этой строке (при обнулении элементов в строке действия производят со столбцами и наоборот): 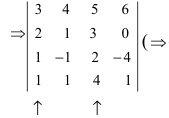
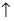
(по методу обнуления раскроем определитель по элементам 2-ой строки (
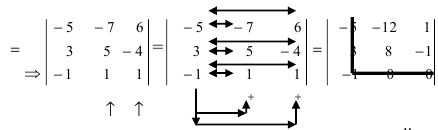
Определители
Перестановкой чисел 1, 2,…, n называется любое расположение этих чисел в определенном порядке. В элементарной алгебре доказывается, что число всех перестановок, которые можно образовать из n чисел, равно 12…n = n!. Например, из трех чисел 1, 2, 3 можно образовать 3!=6 перестановок: 123, 132, 312, 321, 231, 213. Говорят, что в данной перестановке числа i и j составляют инверсию (беспорядок), если i>j, но i стоит в этой перестановке раньше j, то есть если большее число стоит левее меньшего.
Перестановка называется четной (или нечетной), если в ней соответственно четно (нечетно) общее число инверсий. Операция, посредством которой от одной перестановки переходят к другой, составленной из тех же n чисел, называется подстановкой n-ой степени.
Подстановка, переводящая одну перестановку в другую, записывается двумя строками в общих скобках, причем числа, занимающие одинаковые места в рассматриваемых перестановках, называются соответствующими и пишутся одно под другим. Например, символ 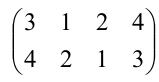
Подстановка называется четной (или нечетной), если общее число инверсий в обеих строках подстановки четно (нечетно). Всякая подстановка n-ой степени может быть записана в виде 
Пусть нам дана квадратная матрица порядка n
Рассмотрим все возможные произведения по n элементов этой матрицы, взятых по одному и только по одному из каждой строки и каждого столбца, т.е. произведений вида:
где индексы 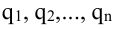
Определителем n-го порядка, соответствующим матрице (4.3), называется алгебраическая сумма n! членов вида (4.4). Для записи определителя употребляется символ 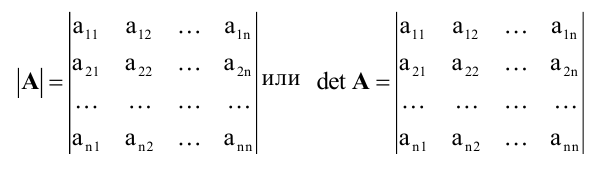
Свойства определителей:
- Определитель не меняется при транспонировании.
- Если одна из строк определителя состоит из нулей, то определитель равен нулю.
- Если в определителе переставить две строки, определитель поменяет знак.
- Определитель, содержащий две одинаковые строки, равен нулю.
- Если все элементы некоторой строки определителя умножить на некоторое число
то сам определитель умножится на
- Определитель, содержащий две пропорциональные строки, равен нулю.
- Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых
то определитель равен сумме определителей, у которых все строки, кроме i-ой, — такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов
в другом — из элементов
- Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и то же число.
Замечание. Все свойства остаются справедливыми, если вместо строк взять столбцы.
Минором 
Алгебраическим дополнением элемента 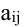
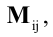
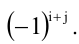
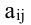
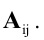
Способы практического вычисления определителей, основанные на том, что определитель порядка n может быть выражен через определители более низких порядков, дает следующая теорема.
- Заказать решение задач по высшей математике
Теорема (разложение определителя по строке или столбцу).
Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение d по элементам i-й строки 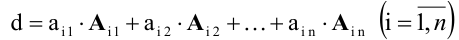
В частности, если все элементы строки (или столбца), кроме одного, равны нулю, то определитель равен этому элементу, умноженному на его алгебраическое дополнение.
Пример:
Не вычисляя определителя 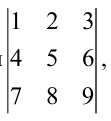
Решение:
Вычтем из второй строки первую, получим определитель 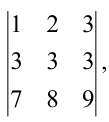
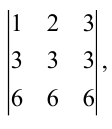
Такой определитель равен нулю.
Пример:
Вычислить определитель 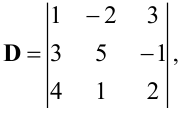
Решение:
Разложим определитель по элементам второго столбца:
Пример:
Вычислить определитель 
Решение:
Разложим определитель А по первой строке:
Определитель, стоящий справа, можно снова разложить по первой строке, тогда получим:
И так далее. После n шагов придем к равенству
Пример:
Вычислить определитель
Решение:
Если к каждой строке определителя, начиная со второй, прибавить первую строку, то получится определитель, в котором все элементы, находящиеся ниже главной диагонали, будут равны нулю. А именно, получим определитель: 
Рассуждая, как в предыдущем примере найдем, что он равен произведению элементов главной диагонали, т.е. n!. Способ, с помощью которого вычислен данный определитель, называется способом приведения к треугольному виду.
——- в вышмате
Определители. Алгебраические дополнения
Внимание! Понятие определителя вводится только для квадратной матрицы.
Матрица называется квадратной порядка n, если количество ее строк совпадает с количеством столбцов и равно n.
Элементы квадратной матрицы, имеющие одинаковые значения индексов, составляют главную диагональ. Элементы квадратной матрицы порядка n, сумма индексов каждого из которых равна n+1, составляют побочную диагональ.
Определитель матрицы 
Внимание! Определитель — это число, характеризующее квадратную мат- рицу.
Определитель матрицы второго порядка равен разности элементов главной и побочной диагоналей соответственно:
Определитель матрицы третьего порядка равен сумме элементов главной диагонали и элементов, расположенных в вершинах треугольников с основаниями, параллельными главной диагонали, а также разности элементов побочной диагонали и элементов, расположенных в вершинах треугольников с основаниями, параллельными побочной диагонали.
Схематично это правило изображается так (правило треугольника):
Например,
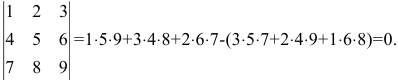
Отметим некоторые свойства определителя.
- Определитель треугольной матрицы равен произведению элементов главной диагонали.
- При транспонировании матрицы ее определитель не изменяется.
- От перестановки двух рядов (строк или столбцов) определитель меняет знак.
- Общий множитель всех элементов некоторого ряда определителя можно выносить за знак определителя.
- Если все элементы какого-нибудь ряда матрицы равны нулю, то определитель равен нулю.
- Определитель, содержащий два пропорциональных ряда, равен нулю.
- Определитель не изменится, если к элементам какого-либо ряда прибавить соответствующие элементы другого ряда, умноженные на одно и то же число.
- Определитель произведения двух матриц одинакового порядка равен произведению определителей этих матриц.
Минором элемента 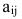
Алгебраическим дополнением элемента 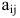
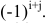
Теорема разложения.
Определитель матрицы равен сумме произведений элементов любого ряда на их алгебраические дополнения.
Пример №2
Вычислить определитель, разлагая его по элементам первой строки:
Решение:
По теореме разложения
Найдем алгебраические дополнения элементов матрицы А:
Следовательно,
Для вычисления определителя порядка выше третьего удобно пользоваться теоремой разложения (метод понижения порядка) или методом приведения определителя к треугольному виду.
Пример №3
Вычислить определитель, приведя его к треугольному виду:
Решение:
Применяя свойство 6 определителей, преобразуем последовательно второй, третий, четвертый столбцы матрицы.
- прибавили ко второму столбцу первый, умноженный на -2;
- прибавили к третьему столбцу первый, умноженный на -3;
- прибавили к четвертому столбцу первый, умноженный на -4;
- применили свойство 1 определителей.
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Экстремум функции
- Пределы в математике
- Функции многих переменных
- Уравнения прямых и кривых на плоскости
- Плоскость и прямая в пространстве
Мы уже знакомы с темой «Сложение матриц». Вычитание матриц аналогично их сложению. Данное действие требует от студентов лишь арифметических знаний и внимательности. Перед изучением новой темы рекомендуем повторить, что такое матрица. Особое внимание следует уделить ее размеру.
Онлайн-калькулятор
Приступим к рассмотрению действия над матрицами, которое называется вычитанием.
Как и при сложении, вычитать будем те матрицы, которые имеют одинаковый размер. Вычесть из матрицы «шесть на восемь» можно только матрицу «шесть на восемь», а из матрицы «два на четыре» только матрицу «два на четыре».
При вычитании матриц справедливо равенство Amn−Bmn=CmnA_{mn}-B_{mn}=C_{mn}. Оно означает, что вычитая из матрицы AA порядка m×nmtimes n матрицу BB порядка m×nmtimes n, получим матрицу CC такого же порядка.
Правило вычитания матриц
Разность матриц PP и KK получается вычитанием их соответствующих элементов. Первый элемент новой матрицы получается вычитанием из первого элемента матрицы PP первого элемента матрицы KK, второй элемент новой матрицы — вычитанием из второго элемента матрицы PP второго элемента матрицы KK. Также поступаем с остальными элементами.
Найдем разность A=(a11a12…a1na21a22…a2n…………am1am2…amn)A=begin{pmatrix}a_{11}&a_{12}&…&a_{1n}\a_{21}&a_{22}&…&a_{2n}\…&…&…&…\a_{m1}&a_{m2}&…&a_{mn}end{pmatrix} и B=(b11b12…b1nb21b22…b2n…………bm1bm2…bmn)B=begin{pmatrix}b_{11}&b_{12}&…&b_{1n}\b_{21}&b_{22}&…&b_{2n}\…&…&…&…\b_{m1}&b_{m2}&…&b_{mn}end{pmatrix}.
A−B=(a11a12…a1na21a22…a2n…………am1am2…amn)−(b11b12…b1nb21b22…b2n…………bm1bm2…bmn)A-B=begin{pmatrix}a_{11}&a_{12}&…&a_{1n}\a_{21}&a_{22}&…&a_{2n}\…&…&…&…\a_{m1}&a_{m2}&…&a_{mn}end{pmatrix}-begin{pmatrix}b_{11}&b_{12}&…&b_{1n}\b_{21}&b_{22}&…&b_{2n}\…&…&…&…\b_{m1}&b_{m2}&…&b_{mn}end{pmatrix}=
=(a11−b11a12−b12…a1n−b1na21−b21a22−b22…a2n−b2n…………am1−bm1am2−bm2…amn−bmn)= begin{pmatrix}a_{11}-b_{11}&a_{12}-b_{12}&…&a_{1n}-b_{1n}\a_{21}-b_{21}&a_{22}-b_{22}&…&a_{2n}-b_{2n}\…&…&…&…\a_{m1}-b_{m1}&a_{m2}-b_{m2}&…&a_{mn}-b_{mn}end{pmatrix}.
Алгоритм выполнения вычитания:
- определяем размеры матриц;
- если матрицы имеют одинаковый размер, выполняем вычитание (в противном случае найти разность невозможно).
Пример 1
Найти разность матриц GG и HH, если G=(39214321925171534)G=begin{pmatrix}39&21&4\32&19&25\17&15&34end{pmatrix} и H=(451915161833241610)H=begin{pmatrix}45&19&15\16&18&33\24&16&10end{pmatrix}.
Матрицы имеют размер 3×33times 3. Для нахождения разности G−HG-H из соответствующих элементов матрицы GG нужно вычесть соответствующие элементы матрицы HH:
G−H=(39214321925171534)−(451915161833241610)=(39−4521−194−1532−1619−1825−3317−2415−1634−10)=G-H=begin{pmatrix}39&21&4\32&19&25\17&15&34end{pmatrix}-begin{pmatrix}45&19&15\16&18&33\24&16&10end{pmatrix}=begin{pmatrix}39-45&21-19&4-15\32-16&19-18&25-33\17-24&15-16&34-10end{pmatrix}=
=(−62−11161−8−7−124)=begin{pmatrix}-6&2&-11\16&1&-8\-7&-1&24end{pmatrix}
Пример 2
Найти разность матриц TT и FF, если T=(243716152433461168571324)T=begin{pmatrix}24&37&16\15&24&33\46&11&68\57&13&24end{pmatrix} и F=(3954295119313491843515)F=begin{pmatrix}39&54&29\51&19&31\34&9&18\43&5&15end{pmatrix}.
Матрицы имеют размер 4×34times 3. Для нахождения разности T−FT-F из соответствующих элементов матрицы TT нужно вычесть соответствующие элементы матрицы FF:
T−F=(243716152433461168571324)−(3954295119313491843515)=(24−3937−5416−2915−5124−1933−3146−3411−968−1857−4313−524−15)=T-F=begin{pmatrix}24&37&16\15&24&33\46&11&68\57&13&24end{pmatrix}-begin{pmatrix}39&54&29\51&19&31\34&9&18\43&5&15end{pmatrix}=begin{pmatrix}24-39&37-54&16-29\15-51&24-19&33-31\46-34&11-9&68-18\57-43&13-5&24-15end{pmatrix}=
=(−15−17−13−3652122501489)=begin{pmatrix}-15&-17&-13\-36&5&2\12&2&50\14&8&9end{pmatrix}
Как видно из примеров, вычитание является таким же простым действием, как и сложение. Продолжайте изучение темы «матрицы» с нами, и тогда данная тема покажется вам очень простой.
Помощь с выполнением задач онлайн от экспертов на бирже Студворк!
Тест по теме «Вычитание матриц»
Содержание:
- Вычисления определителей второго порядка
- Методы вычисления определителей третьего порядка
- Приведение определителя к треугольному виду
- Правило треугольника
- Правило Саррюса
- Разложение определителя по строке или столбцу
- Разложение определителя по элементам строки или столбца
- Теорема Лапласа
В общем случае правило вычисления определителей
$n$-го порядка
является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.
Вычисления определителей второго порядка
Чтобы вычислить определитель матрицы 
элементов главной диагонали отнять произведение
элементов побочной диагонали:
$$left| begin{array}{ll}{a_{11}} & {a_{12}} \ {a_{21}} & {a_{22}}end{array}right|=a_{11} cdot a_{22}-a_{12} cdot a_{21}$$
Пример
Задание. Вычислить определитель второго порядка
$left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|$
Решение. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=11 cdot 5-(-2) cdot 7=55+14=69$
Ответ. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=69$
Методы вычисления определителей третьего порядка
Для вычисления определителей третьего порядка существует такие правила.
Правило треугольника
Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми,
берется со знаком «плюс»; аналогично, для второго определителя — соответствующие произведения берутся со знаком «минус», т.е.
$$left| begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \ {a_{21}} & {a_{22}} & {a_{23}} \ {a_{31}} & {a_{32}} & {a_{33}}end{array}right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-$$
$$-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ методом треугольников.
Решение. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$
$$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей
параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных,
со знаком «минус»:
$$-a_{13} a_{22} a_{31}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}$$
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ с помощью правила Саррюса.
Решение.
$$+(-1) cdot 4 cdot(-2)-(-1) cdot 1 cdot 1-3 cdot 3 cdot(-2)-3 cdot 4 cdot(-2)=54$$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Разложение определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их
алгебраические дополнения. Обычно выбирают
ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Пример
Задание. Разложив по первой строке, вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right| leftarrow=a_{11} cdot A_{11}+a_{12} cdot A_{12}+a_{13} cdot A_{13}=$
$1 cdot(-1)^{1+1} cdot left| begin{array}{cc}{5} & {6} \ {8} & {9}end{array}right|+2 cdot(-1)^{1+2} cdot left| begin{array}{cc}{4} & {6} \ {7} & {9}end{array}right|+3 cdot(-1)^{1+3} cdot left| begin{array}{cc}{4} & {5} \ {7} & {8}end{array}right|=-3+12-9=0$
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.
Пример
Задание. Вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. Выполним следующие
преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному.
$$left| begin{array}{ccc}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {4-4 cdot 1} & {5-4 cdot 2} & {6-4 cdot 3} \ {7-7 cdot 1} & {8-7 cdot 2} & {9-7 cdot 3}end{array}right|=$$
$$=left| begin{array}{rrr}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {-6} & {-12}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {2 cdot(-3)} & {2 cdot(-6)}end{array}right|=0$$
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение
к треугольному виду, либо с помощью теоремы Лапласа.
Разложение определителя по элементам строки или столбца
Пример
Задание. Вычислить определитель
$left| begin{array}{llll}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|$ , разложив его по элементам какой-то строки или какого-то столбца.
Решение. Предварительно выполним
элементарные преобразования над строками определителя, сделав
как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих,
от второй — пять третьих и от четвертой — три третьих строки, получаем:
$$left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=left| begin{array}{cccc}{9-1} & {8-0} & {7-9} & {6-18} \ {5-5} & {4-0} & {3-5} & {2-10} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|$$
Полученный определитель разложим по элементам первого столбца:
$$left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=0+0+1 cdot(-1)^{3+1} cdot left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|+0$$
Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули,
например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей — вторую:
$$left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|=left| begin{array}{rrr}{0} & {2} & {4} \ {4} & {-2} & {-8} \ {0} & {4} & {8}end{array}right|=4 cdot(-1)^{2+2} cdot left| begin{array}{ll}{2} & {4} \ {4} & {8}end{array}right|=$$
$$=4 cdot(2 cdot 8-4 cdot 4)=0$$
Ответ. $left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=0$
Замечание
Последний и предпоследний определители можно было бы и не вычислять,
а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.
Приведение определителя к треугольному виду
С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его
значение, согласно свойствам определителя, равно произведению
элементов стоящих на главной диагонали.
Пример
Задание. Вычислить определитель
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|$ приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:
$$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {2} & {-5} & {3} & {0} \ {-1} & {4} & {2} & {-3}end{array}right|$$
Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
$$Delta=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {3} & {-1} & {2} \ {0} & {2} & {5} & {-1}end{array}right|$$
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:
$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {-10} & {-10} \ {0} & {0} & {-1} & {-9}end{array}right|$$
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:
$$Delta=-10 left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {-1} & {-9}end{array}right|=$$
$$=-10 cdot left| begin{array}{cccc}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {0} & {-8}end{array}right|=(-10) cdot 1 cdot(-1) cdot 1 cdot(-8)=-80$$
Ответ. $Delta=-80$
Теорема Лапласа
Теорема
Пусть $Delta$ — определитель
$n$-го порядка. Выберем в нем произвольные
$k$ строк (или столбцов), причем
$k leq n-1$ . Тогда сумма произведений всех
миноров
$k$-го порядка, которые содержатся в выбранных
$k$ строках (столбцах), на их
алгебраические дополнения равна определителю.
Пример
Задание. Используя теорему Лапласа, вычислить определитель
$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|$
Решение. Выберем в данном определителе пятого порядка две строки —
вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):
$$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=left| begin{array}{cc}{1} & {-1} \ {4} & {-5}end{array}right| cdot(-1)^{2+4+2+4} cdot left| begin{array}{ccc}{2} & {0} & {5} \ {3} & {1} & {1} \ {1} & {2} & {1}end{array}right|+$$
$$+left| begin{array}{ll}{1} & {2} \ {4} & {0}end{array}right| cdot(-1)^{2+4+2+5} cdot left| begin{array}{rrr}{2} & {0} & {4} \ {3} & {1} & {0} \ {1} & {2} & {-2}end{array}right|+left| begin{array}{cc}{-1} & {2} \ {-5} & {0}end{array}right| cdot(-1)^{2+4+5} cdot left| begin{array}{ccc}{2} & {3} & {0} \ {3} & {2} & {1} \ {1} & {1} & {2}end{array}right|=$$
$$=-23+128+90=195$$
Ответ. $left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=195$
Читать дальше: обратная матрица.



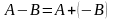



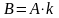




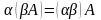
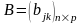



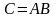
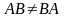

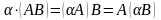
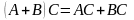
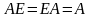
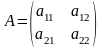





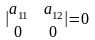
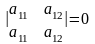


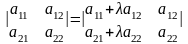
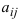
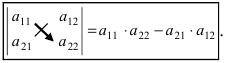
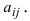
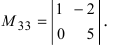
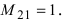
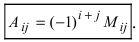

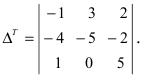
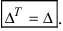
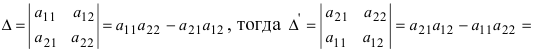
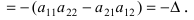
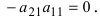
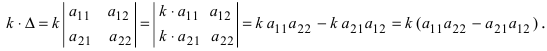
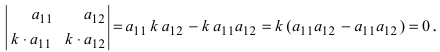
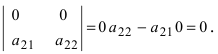
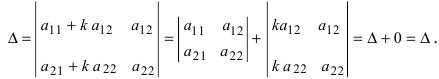
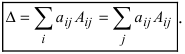
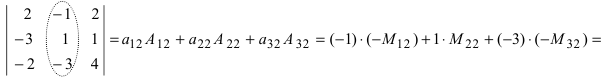
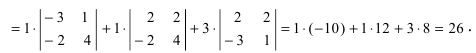
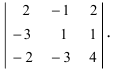
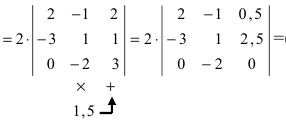
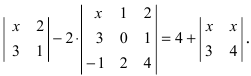
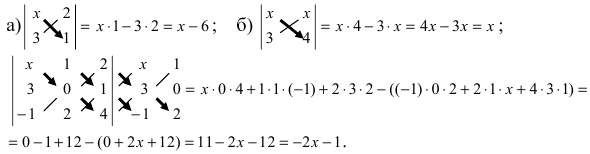
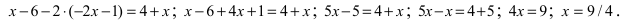

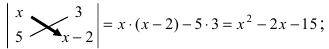
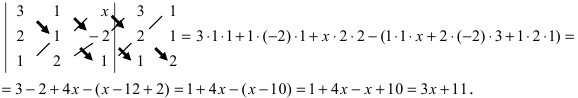
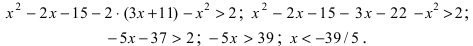

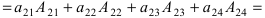
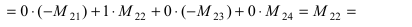
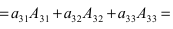
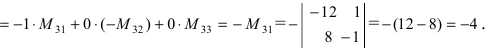
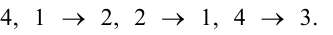


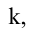 то сам определитель умножится на
то сам определитель умножится на 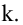
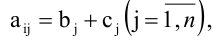 то определитель равен сумме определителей, у которых все строки, кроме i-ой, — такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов
то определитель равен сумме определителей, у которых все строки, кроме i-ой, — такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов 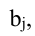 в другом — из элементов
в другом — из элементов