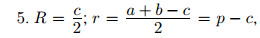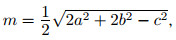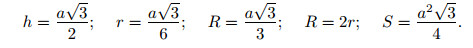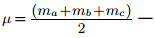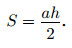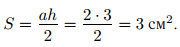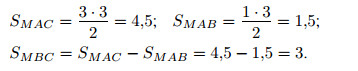Как найти разность площадей треугольников - Исправление недочетов и поиск решений вместе с Examum.ru

Сообщения без ответов | Активные темы

Автор

Сообщение

Заголовок сообщения: Найти разницу площадей двух треугольников

Добавлено: 14 окт 2021, 07:17

Beautiful Mind

Зарегистрирован:
05 апр 2021, 04:44
Сообщений: 1538
Cпасибо сказано: 217
Спасибо получено:
522 раз в 470 сообщениях
Очков репутации: 148

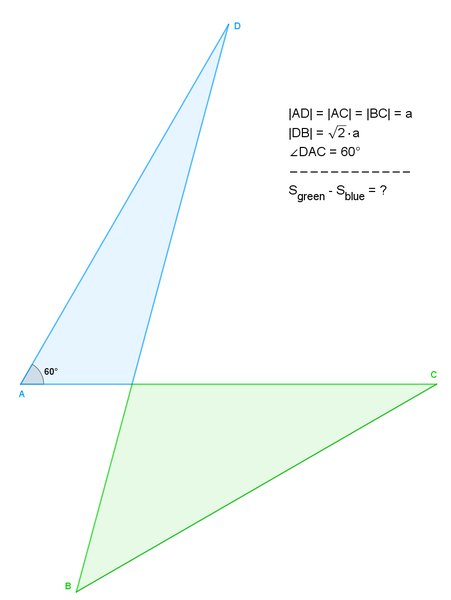
Вот, придумалась несложная задача, по-моему, симпатичная. Визуально даже великолепная. Годится для повышения самооценки учеников 8 класса. Я намеренно её упростил дабы увеличить долю удовольствия благодарным решателям.

Условие продублировано на рисунке.

[math]|AD| = |AC| = |BC| = a[/math]
[math]|DB| = sqrt{2}·a[/math]
[math]∠DAC = 60°[/math]

Надо найти разницу площадей зелёного и синего треугольников, выразив через [math]a[/math].

П.С. Если кто сочтёт эту задачу слишком простой, предлагаю решить её версию для произвольного допустимого
[math]|DB| = b[/math]; [math]frac{ sqrt{3} }{ 2 } a[/math] [math]<[/math] [math]b[/math] [math]< 2a[/math]

Вернуться к началу

За это сообщение пользователю ferma-T «Спасибо» сказали:
Glotov1

Rams	Заголовок сообщения: Re: Найти разницу площадей двух треугольников Добавлено: 14 окт 2021, 08:15
	ferma-T писал(а): П.С. Если кто сочтёт эту задачу слишком простой, предлагаю решить её версию для произвольного допустимого [math]\|DB\| = b[/math]; [math]frac{ sqrt{3} }{ 2 } a[/math] [math]<[/math] [math]b[/math] [math]< 2a[/math] ferma-T При [math]frac{ sqrt{3} }{ 2 } a[/math] [math]<[/math] [math]b[/math] [math]< a[/math] точка [math]B[/math] будет в другом положении. Вы это учитывали?
Вернуться к началу

	За это сообщение пользователю Rams «Спасибо» сказали: ferma-T

ferma-T	Заголовок сообщения: Re: Найти разницу площадей двух треугольников Добавлено: 14 окт 2021, 09:55
	Rams писал(а): Можно дать точное значение, но некрасиво, трехэтажные дроби под корнем Судя по вашему ответу с пятью синусами, вы явно решали не оптимальным способом. У меня ответ вовсе не «трехэтажные дроби под корнем«, а вполне компактный красивый ответ с одним маааааленьким корешочком. Rams писал(а): При [math]frac{sqrt{3}}{2}a < b < a[/math] точка B будет в другом положении. Я не так писал. Я писал [math]frac{sqrt{3}}{2}a < b < 2a[/math] . Но окей, не возражаю, пусть будет [math]a < b < 2a[/math] (я так и хотел сначала, но почему-то неправильно захотелось добавить возможность точке В быть прямо под точкой D но ниже [AC]). Тогда точка В уже точно будет примерно там же (в том же квадранте), что и на рисунке. Короче, поправляю условие для версии с произвольным \|DB\|: [math]\|DB\| = b; a < b < 2a[/math] Спасибо за замечание. Подождём других соискателей-энтузиастов. Последний раз редактировалось ferma-T 14 окт 2021, 10:18, всего редактировалось 4 раз(а).
Вернуться к началу

	За это сообщение пользователю ferma-T «Спасибо» сказали: Rams

Glotov1	Заголовок сообщения: Re: Найти разницу площадей двух треугольников Добавлено: 14 окт 2021, 11:22
	MihailM писал(а): А maple с вольфрамами зачем? [math]{frac{1}{2}}-{frac {sqrt {3}}{4}}[/math] Да, здесь можно увидеть, что искомая разница равна разнице между равнобедренным прямоугольным треугольником и равносторонним треугольником со стороной равной катету первого треугольника. А для b не равной аsqrt2 ответ будет (1/2)bsqrt(a^2-(b/2)^2) — a(sqrt3)/4 .
Вернуться к началу

	За это сообщение пользователю Glotov1 «Спасибо» сказали: ferma-T, Rams

Glotov1	Заголовок сообщения: Re: Найти разницу площадей двух треугольников Добавлено: 14 окт 2021, 18:25
	ferma-T писал(а): Glotov1 писал(а): А для b не равной аsqrt2 ответ будет (1/2)bsqrt(a^2-(b/2)^2) — a(sqrt3)/4 . … Только квадрат у [math]a[/math] равностороннего [math]Delta[/math] у вас зажилился.
Вернуться к началу

chebo	Заголовок сообщения: Re: Найти разницу площадей двух треугольников Добавлено: 14 окт 2021, 19:22
	[math]frac{ 2 — sqrt{3} }{ 4}a^{2}[/math] (а, написали уже… только у меня без мэпла и вольфрама, без всяких ГМО, продукт чистого разума ))
Вернуться к началу

ferma-T	Заголовок сообщения: Re: Найти разницу площадей двух треугольников Добавлено: 14 окт 2021, 21:27
	Rams писал(а): Разница площадей зелёного и синего треугольников: [math]frac{ a^{2} }{ 2 } cdot frac{ sin45^{circ} sin30^{circ}-sin15^{circ} sin60^{circ}}{ sin105^{circ} } approx 0,06699a^{2}[/math] Можно дать точное значение, но некрасиво, трехэтажные дроби под корнем. Итак, большинство соискателей нашли правильный ответ в простой форме. Но меня всё-таки раздирает любопытство, как Rams решал, how did he/she end up getting such a stunning trigonometric expression? Я сам не пробовал, но, как я понимаю, если не идти простым путём, а в лоб через тригонометрию, то там вовсе не тривиально получается. И почему у него не упростилось?
Вернуться к началу

Похожие темы	Автор	Ответы	Просмотры	Последнее сообщение
Каково соотношение площадей 2 треугольников в форуме Геометрия	Race	16	1056	01 дек 2016, 14:43
Найти отношение площадей треугольника и четырёхугольника в форуме Геометрия	dasha math	1	1023	16 апр 2014, 22:04
Найти отношение площадей сечений усечённой пирамиды в форуме Геометрия	nkshgm	11	95	22 май 2023, 12:02
Какую конечную разницу использовать? в форуме Дифференциальное исчисление	stut	3	381	25 июн 2014, 02:25
Увеличить разницу между величинами в форуме Численные методы	swdartvader	9	628	11 сен 2014, 00:17
Оценить относительную разницу значений в форуме Математическая статистика и Эконометрика	ikassenov	4	253	02 июл 2019, 12:36
Как правильно посчитать разницу в процентах? в форуме Алгебра	rema174	4	184	13 май 2019, 16:55
Объясните разницу между дискретным и континуальным ВП в форуме Комбинаторика и Теория вероятностей	Svetaaaaaa	1	374	03 янв 2018, 10:55
Решение треугольников . Найти длину стороны треугольника в форуме Геометрия	gruzik	26	559	09 фев 2021, 22:18
Сумма площадей в форуме Геометрия	FEBUS	4	191	30 ноя 2019, 23:12

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 1

Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете добавлять вложения

Источник

Все формулы по геометрии. Площади фигур

Чтобы решать задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.

Начнем с квадрата.

Площадь квадрата равна квадрату его стороны.

Площадь прямоугольника равна произведению его длины и ширины.

Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне. Она также равна произведению его сторон на синус угла между ними.

Для площади треугольника есть целых 5 формул. И все они применяются в задачах ЕГЭ.

1) Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне: $S=displaystyle frac{1}{2}ah_a=displaystyle frac{1}{2}bh_b=displaystyle frac{1}{2}ch_c.$

2) Она также равна половине произведения его сторон на синус угла между ними:

$S=displaystyle frac{1}{2}ab{sin C=displaystyle frac{1}{2}ac{sin B= } }displaystyle frac{1}{2}bc{sin A }.$

3) По формуле Герона, где $p=displaystyle frac{1}{2}left(a+b+cright)$ полупериметр.

4) Также площадь треугольника равна произведению его полупериметра на радис вписанной окружности, S = pr.

5) Еще один способ. Площадь треугольника равна произведению его сторон, деленному на 4 радиуса описанной окружности, $S=displaystyle frac{abc}{4R}.$

Есть и другие формулы для площади треугольника. Но для решения заданий ЕГЭ, и первой, и второй части, достаточно этих пяти.

Площадь прямоугольного треугольника равна половине произведения его катетов. Она также равна половине произведения гипотенузы на высоту, проведенную к этой гипотенузе:

$S=displaystyle frac{1}{2}ab=displaystyle frac{1}{2}ch_{ }$

Площадь правильного треугольника равна квадрату его стороны, умноженному на sqrt{3} и деленному на 4:

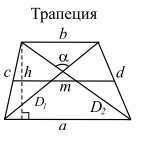
Площадь трапеции равна произведению полусуммы оснований на высоту, $S=displaystyle frac{a+b}{2}cdot h.$

Также можно сказать, что площадь трапеции равна произведению ее средней линии на высоту,

Площадь произвольного четырехугольника равна половине произведения его диагоналей на синус угла между ними, $S=displaystyle frac{1}{2}ACcdot BDcdot {sin alpha }$

Площадь ромба равна произведению квадрата его стороны на синус угла ромба. Она также равна половине произведения диагоналей:

Площадь круга равна произведению числа и квадрата радиуса круга.

Ее также можно записать как произведение числа и квадрата диаметра круга, деленного на 4:

Вспомним важные свойства площадей фигур.

Равные фигуры имеют равные площади.
Иногда фигуры, имеющие равные площади, еще называют равновеликими.
Если фигура составлена из нескольких фигур, не имеющих общих внутренних точек, то ее площадь равна сумме площадей этих фигур.

Пример. Найдем площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1см times 1см.

Решение:

Найдем площадь фигуры на рисунке как сумму площадей нескольких фигур.

На рисунке это три треугольника и трапеция, указаны их площади. Тогда площадь фигуры равна 10 + 3,5 + 1,5 + 3 = 18.

Ответ: 18.

3. Отношение площадей подобных фигур равно квадрату коэффициента подобия.

Треугольники АВС и на рисунке называются подобными.

У треугольника все стороны в k раз длиннее, чем у треугольника АВС. Высота треугольника в k раз длиннее, чем высота треугольника АВС. Тогда площадь треугольника в k^2 раз больше, чем площадь треугольника АВС.

4. На рисунке показаны треугольники АВС и BCD, имеющие общую высоту. Отношение площадей этих треугольников равно отношению АС к CD:

$displaystyle frac{S_{ABC}}{S_{BCD}}=displaystyle frac{AC}{CD}$

5. Треугольники АВС и АЕС на рисунке имеют одинаковое основание и разные высоты.

Отношение площадей этих треугольников равно отношению их высот:

$displaystyle frac{S_{ABC}}{S_{AEC}}=displaystyle frac{BD}{EH}.$

6. Медиана треугольника делит его на два равновеликих, то есть равных по площади, треугольника.

На рисунке СМ — медиана треугольника АВС. Площади треугольников АСМ и ВСМ равны.

7. Три медианы треугольника делят его на шесть равных по площади треугольников.

На рисунке все 6 треугольников, из которых состоит треугольник АВС, имеют равные лощади.

Задачи ЕГЭ и ОГЭ по теме: Площади фигур.

Задача 1. Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен ${30}^circ.$

Решение:

Площадь треугольника равна половине произведения его сторон на синус угла между ними. Поэтому

$S=displaystyle frac{1}{2}cdot 8cdot 12cdot {sin 30{}^circ =displaystyle frac{1}{2}cdot 8cdot 12cdot displaystyle frac{1}{2}=24 }.$

Ответ: 24.

Задача 2. Площадь треугольника ABC равна 4, DE — средняя линия, параллельная стороне AB. Найдите площадь треугольника CDE.

Решение:

Так как DE и АВ параллельны, треугольники CDE и САВ подобны с коэффициентом подобия $displaystyle frac{1}{2}.$ Площади подобных фигур относятся как квадрат коэффициента подобия. Тогда

$S=displaystyle frac{1}{4}cdot 4=1.$

Ответ: 1.

Задача 3. У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?

Решение:

Выразим площадь двумя способами:
$S_{ABC}=displaystyle frac{1}{2}CHcdot AB=displaystyle frac{1}{2}AKcdot CB.$

Тогда $AK=displaystyle frac{CHcdot AB}{CB}=displaystyle frac{4cdot 9}{6}=6.$

Ответ: 6.

Задача 4. Площадь треугольника ABC равна 10, DE — средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.

Решение:

Треугольник CDE подобен треугольнику CAB с коэффициентом $displaystyle frac{1}{2}.$ Площади подобных фигур относятся как квадрат коэффициента подобия, поэтому

$S_{CDE}=displaystyle frac{1}{4}cdot 10=2.5.$

Следовательно, .

Ответ: 7,5.

Задача 5. В параллелограмме ABCD AB = 3, AD = 21, ${sin A=displaystyle frac{6}{7}}$ . Найдите большую высоту параллелограмма.

Решение:

Большая высота — это DH, потому что проведена к меньшей стороне. Из треугольника АDН:

$DH=AD{sin A=21cdot displaystyle frac{6}{7}=3cdot 6=18 }.$

Ответ: 18.

Задача 6. Найдите площадь квадрата, если его диагональ равна 1.

Решение:

Квадрат — это частный случай ромба. Площадь квадрата равна половине произведения его диагоналей. Поэтому она равна 0,5.

Ответ: 0,5.

Задача 7. Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1:2.

Решение:

Площадь прямоугольника равна произведению его длины на ширину. Периметр прямоугольника равен сумме длин всех сторон. Пусть одна из сторон прямоугольника равна a, тогда вторая равна 2a. Площадь прямоугольника равна тогда одна из сторон равна 3, а другая 6. Периметр P = 2 · 3 + 2 · 6 = 18.

Ответ: 18.

Задача 8. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.

Решение:

Площадь параллелограмма равна произведению его сторон на синус угла между ними. Площадь прямоугольника равна произведению длины на ширину. Пусть одна сторона параллелограмма и прямоугольника равна вторая равна а острый угол параллелограмма равен alpha . Тогда площадь параллелограмма равна а площадь прямоугольника равна

По условию площадь прямоугольника вдвое больше:

${S_2=2S_1} .$ Следовательно, $acdot b=2acdot bcdot {sin alpha Leftrightarrow {sin alpha }=0,5 }Leftrightarrow alpha =30{}^circ.$

Ответ: 30.

Задача 9. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.

Решение:

Площадь параллелограмма равна произведению его основания на высоту, проведенную к этому основанию. Пусть высоты равны соответственно a и b. Тогда S = 5 · a = 10 · b = 40. Поэтому a = 8, b = 4. Большая высота равна 8.

Ответ: 8.

Задача 10. Найдите площадь ромба, если его высота равна 2, а острый угол 30 ${}^circ.$

Решение:

Площадь ромба равна произведению квадрата его стороны на синус угла ромба. С другой стороны, площадь ромба равна произведению его основания на высоту, проведенную к этому основанию. Пусть сторона ромба равна

Получим уравнение:

$a^2=a{sin alpha }.$

Корень уравнения a = 4, поэтому

Ответ: 8.

Задача 11. Найдите площадь ромба, если его диагонали равны 4 и 12.

Решение:

Площадь ромба равна половине произведения его диагоналей. $S=displaystyle frac{1}{2}cdot 4cdot 12=24.$

Ответ: 24.

Задача 12. Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.

Решение:

Трапеция равнобедренная, значит,

$AH=displaystyle frac{AB-DC}{2}=6;$

$AD=displaystyle frac{P_{ABCD}-left(AB+DCright)}{2}=10.$

Тогда по теореме Пифагора из треугольника ADH:

$DH=sqrt{{AD}^2-{AH}^2}=8;$

$S=displaystyle frac{AB+CD}{2}cdot DH=20cdot 8=160.$

Ответ: 160.

Задача 13. Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 45 ${}^circ.$

Решение:

Проведем высоту CH. Треугольник CHB — прямоугольный, в нем

$angle B=45{}^circ ,$ значит, он также равнобедренный, CH = HB = 4.
$S_{ABCD}=displaystyle frac{AB+CD}{2}cdot CH=4cdot 4=16.$

Ответ: 16.

Задача 14. Высота трапеции равна 5, площадь равна 75. Найдите среднюю линию трапеции.

Решение:

Средняя линия трапеции равна полусумме оснований. Выразим её из формулы площади трапеции:
$S=displaystyle frac{a+b}{2}cdot hLeftrightarrow displaystyle frac{a+b}{2}cdot 5=75Leftrightarrow displaystyle frac{a+b}{2}=15.$

Ответ: 15.

Задача 15. Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту. Пусть высота равна h, тогда

$S=displaystyle frac{27+9}{2}cdot h=72.$

Из этого уравнения получим: h = 4.

Рассмотрим прямоугольный треугольник, гипотенузой которого является боковая сторона трапеции, равная 8, а катетом — высота трапеции. Длина катета равна половине гипотенузы, следовательно, он лежит напротив угла ${30}^circ.$

Ответ: 30.

Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Задача 16. Найдем площадь четырехугольника на рисунке.

Решение:

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным 5. Высоты этих треугольников равны 2 и 3. Тогда площадь четырёхугольника равна сумме площадей двух треугольников:

Ответ: 12,5.

В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

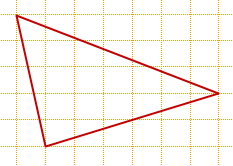
Задача 17. Найдем площадь треугольника, изображенного на клетчатой бумаге.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной 5 и трёх прямоугольных треугольников. Видите их на рисунке? Получаем:

Ответ: 10,5.

Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.

Задача 18.

Найдите площадь сектора круга радиуса 1, длина дуги которого равна 2.

Решение:

На этом рисунке мы видим часть круга. Площадь всего круга равна так как R=1. Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как R = 1), а длина дуги данного сектора равна 2, следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

Ответ: 1.

Формула Пика

Покажем, как вычислять площадь фигуры, изображенной на координатной плоскости, с помощью формулы Пика.

Задача 19. Найдите площадь многоугольника АВСDE, изображенного на рисунке.

Первый способ:

Площадь многоугольника ABCDE равна сумме площадей треугольника BCD, трапеции BKDE и треугольника AKE.

Имеем:

$S_{vartriangle BCD}=displaystyle frac{1}{2}cdot 9cdot 2=9;$

$S_{BKDE}=displaystyle frac{1}{2}cdot (9+3)cdot 2=12;$

$S_{vartriangle AKE}=displaystyle frac{1}{2}cdot 3cdot 4=6;$

$S_{ABCDE}=9+12+6= 27.$

Второй способ — применить формулу Пика.

Назовем точку координатной плоскости целочисленной, если обе ее координаты — целые числа. На нашем рисунке это точки на пересечениях линий, разделяющих клетчатую бумагу на клетки.

Площадь многоугольника с целочисленными вершинами равна

Здесь В — количество целочисленных точек внутри многоугольника, Г — количество целочисленных точек на границе многоугольника.

Главное — аккуратно посчитать. На нашем рисунке

В = 24 (показаны зеленым),

Г = 8 (показаны красным),

S = 24 + $displaystyle frac{8}{2}$ — 1 = 27.

Ответ: 27.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Все формулы по геометрии. Площади фигур» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Признаки равенства треугольников

1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны.

2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то треугольники равны.

3. Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то треугольники равны.

Признаки равенства прямоугольных треугольников

1. По двум катетам.

2. По катету и гипотенузе.

3. По гипотенузе и острому углу

4. По катету и острому углу

Теорема о сумме углов треугольника и следствия из неё

1. Сумма внутренних углов треугольника равна 180°.

2. Внешний угол треугольника равен сумме двух внутренних не смежных с ним углов.

3. Сумма внутренних углов выпуклого n-угольника равна 180°(n − 2).

4. Сумма внешних углов n-угольника равна 360°

5. Углы со взаимно перпендикулярными сторонами равны, если они оба острые или оба тупые.

6. Угол между биссектрисами смежных углов равен 90°.

7. Биссектрисы внутренних односторонних углов при параллельных прямых и секущей перпендикулярны.

Основные свойства и признаки равнобедренного треугольника

1. Углы при основании равнобедренного треугольника равны.

2. Если два угла треугольника равны, то он равнобедренный.

3. В равнобедренном треугольнике медиана, биссектриса и высота, проведённые к основанию, совпадают.

4. Если в треугольнике совпадает любая пара отрезков из тройки: медиана, биссектриса, высота, — то он является равнобедренным.

Неравенство треугольника и следствия из него

1. Сумма двух сторон треугольника больше его третьей стороны

2. Сумма звеньев ломаной больше отрезка, соединяющего начало первого звена с концом последнего.

3. Против большего угла треугольника лежит бOльшая сторона.

4. Против большей стороны треугольника лежит больший угол.

5. Гипотенуза прямоугольного треугольника больше катета

6. Если из одной точки проведены к прямой перпендикуляр и наклонные, то

1) перпендикуляр короче наклонных;

2) большей наклонной соответствует большая ´ проекция и наоборот

Средняя линия треугольника.

Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.

Теорема о средней линии треугольника.

Средняя линия треугольника параллельна стороне треугольника и равна её половине.

Теоремы о медианах треугольника

1. Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2 : 1, считая от вершины.

2. Если медиана треугольника равна половине стороны, к которой она проведена, то треугольник прямоугольный

3. Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы

Свойство серединных перпендикуляров к сторонам треугольника.

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая является центром окружности, описанной около треугольника

Теорема о высотах треугольника.

Прямые, содержащие высоты треугольника, пересекаются в одной точке.

Теорема о биссектрисах треугольника.

Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в треугольник.

Свойство биссектрисы треугольника.

Биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам

Признаки подобия треугольников

1. Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.

2. Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого, а углы, заключенные между этими сторонами, равны, то треугольники подобны.

3. Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого, то треугольники подобны.

Площади подобных треугольников

1. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

2. Если два треугольника имеют равные углы, то их площади относятся как произведения сторон, заключающих эти углы.

В прямоугольном треугольнике

1. Катет прямоугольного треугольника равен произведению гипотенузы на синус противолежащего или на косинус прилежащего к этому катету острого угла.

2. Катет прямоугольного треугольника равен другому катету, умноженному на тангенс противолежащего или на котангенс прилежащего к этому катету острого угла.

3. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.

4. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, противолежащий этому катету, равен 30°.

где a, b — катеты, а c — гипотенуза прямоугольного треугольника; r и R — радиусы вписанной и описанной окружностей соответственно

Теорема Пифагора и теорема, обратная теореме Пифагора

1. Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.

2. Если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то треугольник — прямоугольный

Средние пропорциональные в прямоугольном треугольнике

Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное проекций катетов на гипотенузу, а каждый катет есть среднее пропорциональное гипотенузы и своей проекции на гипотенузу

Метрические соотношения в треугольнике

1. Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

2. Следствие из теоремы косинусов. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

3. Формула для медианы треугольника. Если m — медиана треугольника, проведённая к стороне c, то

где a и b — остальные стороны треугольника.

4. Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов.

5. Обобщённая теорема синусов. Отношение стороны треугольника к синусу противолежащего угла равно диаметру окружности, описанной около треугольника.

Формулы площади треугольника

1. Площадь треугольника равна половине произведения основания на высоту.

2. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

3. Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.

4. Площадь треугольника равна произведению трёх его сторон, делённому на учетверённый радиус описанной окружности.

5. Формула Герона:

где p — полупериметр; a, b, c — стороны треугольника.

Элементы равностороннего треугольника

Пусть h, S, r, R — высота, площадь, радиусы вписанной и описанной

окружностей равностороннего треугольника со стороной a. Тогда

Основные формулы

Далее S — площадь фигуры, P — периметр, p — полупериметр.

Чертежи

Обозначения

Формулы

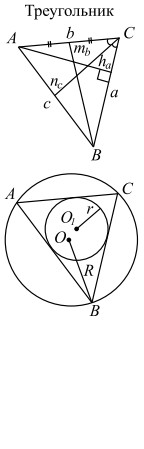a, b, c — стороны;
A, B, C — противолежащие
им углы;

h_a, h_b, h_c — высоты,
проведённые к
соответствующим
сторонам;

n_a, n_b, n_c — биссектрисы,
проведённые к
соответствующим сторонам;

b_a и b_c — отрезки, на
которые делится
биссектрисой сторона b;
m_a, m_b, m_c —
медианы, проведённые
к соответствующим
сторонам;

полусумма медиан;
R — радиус описанной
окружности;

r — радиус вписанной
окружности

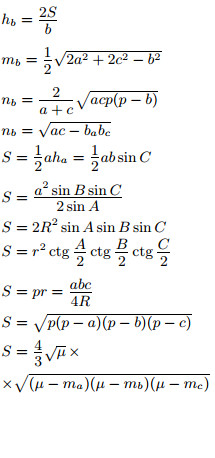Прямоугольный треугольник

Немного полезной информации

В этой главе мы рассмотрим простые виды задач по геометрии, а именно задачи, в которых нужно найти площади плоских фигур, нарисованных

на клетчатой бумаге или расположенных на координатной плоскости.

Для решения таких задач требуется знать не очень много формул, поэтому их решение доступно практически каждому.

Давайте вспомним эти формулы и разберём примеры их применения.

Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы (c) равен сумме квадратов катетов (a и b):

c² = a² + b²

Площадь прямоугольного треугольника равна половине произведения его катетов:

S =ab/2.

Напомним, что у прямоугольного

треугольника есть прямой угол, равный 90°. Сторона напротив прямого

угла (самая длинная) называется гипотенузой, две прилежащие к прямому углу стороны называют катетами.

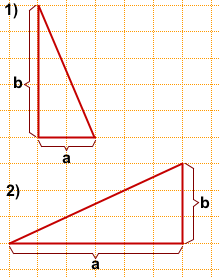
На рисунке 147 приведены чертежи некоторых прямоугольных треугольников, у которых показаны катеты a и b.

Задачи с решениями

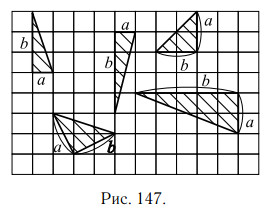
1. На клетчатой бумаге с клетками размером 1 см × 1 см изображён треугольник (см. рис. 148). Найдите его площадь в квадратных сантиметрах.

Решение.

Площадь прямоугольного треугольника равна половине произведения

его катетов. В данном треугольнике катеты равны 2 см и 6 см (посчитаем

по клеточкам), поэтому площадь

Ответ: 6

Площадь треугольника

Немного полезной информации

Площадь произвольного треугольника равна половине произведения длины его стороны (a) на высоту (h), проведённую к этой стороне:

На рисунке 152 приведены чертежи некоторых треугольников, у которых обозначены одна из сторон a и высота, проведённая к этой стороне h.

Как правило, удобно брать ту сторону, которая проходит по линиям

клетчатой бумаги (или же проходит параллельно осям координат).

Задачи с решениями

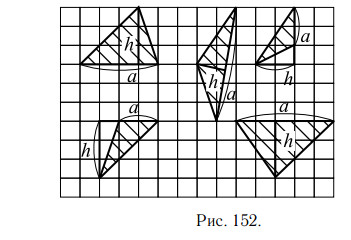
На клетчатой бумаге с клетками размером 1 см × 1 см изображён треугольник (см. рис. 153). Найдите его площадь в квадратных сантиметрах.

Решение.

1-й способ.

Площадь произвольного треугольника равна половине произведения

длины его стороны (a) на высоту (h), проведённую к этой стороне. Проведём высоту h. Треугольник тупоугольный, поэтому высота проводится вне

треугольника.

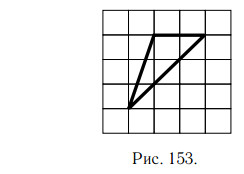
На рисунке 154 сторона a = 2 см, высота h = 3 см

Ответ: 3.

Заметим, что так как клетки имеют размер 1 см × 1 см, то площадь

в квадратных сантиметрах получится, если мы будем по рисунку считать

размер отрезков в клетках. Поэтому единицы длины в этих задачах можно

и не писать.

2-й способ.

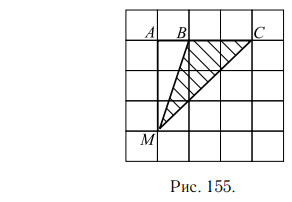
Достроим треугольник BCM до прямоугольного треугольника MCA

(см. рис. 155).

Тогда искомую площадь треугольника BCM можно найти как разность площадей двух прямоугольных треугольников MAC и MAB.

Катеты первого из них равны 3 см и 3 см, катеты второго — 3 см и 1 см.

Площадь прямоугольного треугольника равна половине произведения

его катетов, следовательно,

Ответ: 3.

Четырёхугольник

Параллелограмм.

Параллелограммом называется четырёхугольник, противоположные стороны которого попарно параллельны.

Свойства и признаки параллелограмма

1. Диагональ разбивает параллелограмм на два равных треугольника.

2. Противоположные стороны параллелограмма попарно равны.

3. Противоположные углы параллелограмма попарно равны.

4. Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.

5. Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник — параллелограмм.

6. Если две противоположные стороны четырёхугольника равны и параллельны, то этот четырёхугольник — параллелограмм.

7. Если диагонали четырёхугольника делятся точкой пересечения пополам, то этот четырёхугольник — параллелограмм.

Свойство середин сторон четырёхугольника.

Середины сторон любого четырёхугольника являются вершинами параллелограмма, площадь которого равна половине площади четырёхугольника.

Прямоугольник.

Прямоугольником называется параллелограмм с прямым углом.

Свойства и признаки прямоугольника

1. Диагонали прямоугольника равны.

2. Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник

Квадрат.

Квадратом называется прямоугольник, все стороны которого равны.

Формулы площади четырёхугольника

1. Площадь параллелограмма равна произведению основания на высоту

2. Площадь параллелограмма равна произведению его соседних сторон на синус угла между ними.

3. Площадь прямоугольника равна произведению двух его соседних сторон.

Основные формулы

Далее S — площадь фигуры, P — периметр, p — полупериметр.

Площадь четырёхугольника

Площадь прямоугольника равна произведению его смежных сторон:

S = ab.

На рисунке 156 приведены чертежи некоторых прямоугольников, у которых показаны смежные стороны a и b

Задачи с решениями

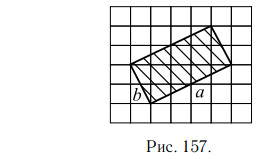
На клетчатой бумаге с клетками размером 1 см×1 см изображён прямоугольник (см. рис. 157). Найдите его площадь в квадратных сантиметрах.

Решение.

1-й способ.

Площадь прямоугольника равна произведению его смежных сторон a

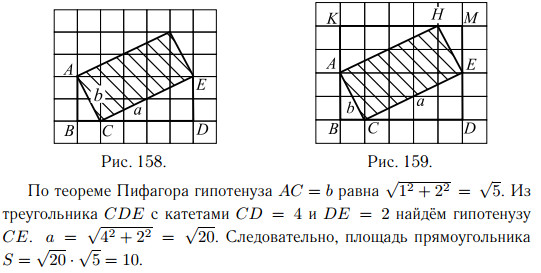
и b. Для того чтобы найти стороны прямоугольника, рассмотрим прямоугольный треугольник ABC с катетами AB = 2 и BC = 1 и гипотенузой

AC = b (см. рис. 158).

Ответ: 10.

2-й способ.

Достроим прямоугольник ACEH до прямоугольника BKMD

(см. рис. 159). Чтобы найти площадь ACEH, нужно из площади прямоугольника BKMD вычесть площади прямоугольных треугольников

AKH, HME, EDC и ABC.

Так как площадь прямоугольного треугольника равна половине произведения катетов, то площадь каждого из двух больших треугольников

(AKH и EDC) равна 4, а площадь каждого из двух маленьких треугольников (HME и ABC) равна 1. Площадь прямоугольника BKMD равна 4 · 5 = 20. Следовательно, площадь искомого прямоугольника будет равна 20 − 1 − 1 − 4 − 4 = 10.

Ответ: 10.

Заметим, что подобным «достраиванием» можно найти площадь любого многоугольника на клетчатой бумаге.

Квадрат.

Квадратом называется прямоугольник, все стороны которого равны.

Свойства и признаки ромба

1. Диагонали ромба перпендикулярны.

2. Диагонали ромба делят его углы пополам

3. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм — ромб.

4. Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.

Площадь ромба равна половине произведения его диагоналей

Основные формулы

Далее S — площадь фигуры, P — периметр, p — полупериметр.

Четырёхугольник

Параллелограмм.

Параллелограммом называется четырёхугольник, противоположные стороны которого попарно параллельны.

Свойства и признаки параллелограмма

1. Диагональ разбивает параллелограмм на два равных треугольника.

2. Противоположные стороны параллелограмма попарно равны.

3. Противоположные углы параллелограмма попарно равны.

4. Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.

5. Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник — параллелограмм.

Свойство середин сторон четырёхугольника.

Прямоугольник.

Прямоугольником называется параллелограмм с прямым углом.

Свойства и признаки прямоугольника

1. Диагонали прямоугольника равны.

2. Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник

Квадрат.

Квадратом называется прямоугольник, все стороны которого равны.

Формулы площади четырёхугольника

1. Площадь параллелограмма равна произведению основания на высоту

2. Площадь параллелограмма равна произведению его соседних сторон на синус угла между ними.

3. Площадь прямоугольника равна произведению двух его соседних сторон.

Основные формулы

Далее S — площадь фигуры, P — периметр, p — полупериметр.

Площадь четырёхугольника

Площадь прямоугольника равна произведению его смежных сторон:

S = ab.

На рисунке 156 приведены чертежи некоторых прямоугольников, у которых показаны смежные стороны a и b

Ромб

Квадрат.

Квадратом называется прямоугольник, все стороны которого равны.

Свойства и признаки ромба

1. Диагонали ромба перпендикулярны.

2. Диагонали ромба делят его углы пополам

3. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм — ромб.

4. Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.

Площадь ромба равна половине произведения его диагоналей

Основные формулы

Далее S — площадь фигуры, P — периметр, p — полупериметр.

Трапеция

Трапецией называется четырёхугольник, у которого только две противоположные стороны (основания) параллельны. Средней линией трапеции называется отрезок, соединяющий середины непараллельных сторон (боковых сторон).

1. Теорема о средней линии трапеции. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.

Замечательное свойство трапеции.

Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой.

Равнобедренная трапеция.

Трапеция называется равнобедренной, если её боковые стороны равны.

Свойства и признаки равнобедренной трапеции

1. Углы при основании равнобедренной трапеции равны.

2. Диагонали равнобедренной трапеции равны

3. Если углы при основании трапеции равны, то она равнобедренная.

4. Если диагонали трапеции равны, то она равнобедренная

5. Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали — полусумме оснований.

Основные формулы

Далее S — площадь фигуры, P — периметр, p — полупериметр.

Чертежи	Обозначения	Формулы
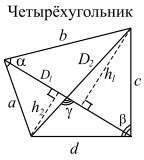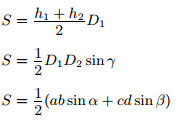	a, b, c, d — стороны; D₁, D₂ — диагонали; γ — угол между диагоналями; h₁, h₂ — длины перпендикуляров, опущенных на диагональ D₁; α, β — два противолежащих угла четырёхугольника.
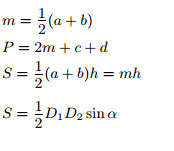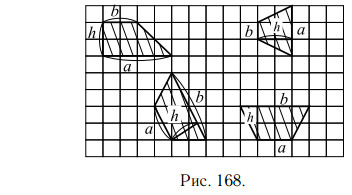
	a, b — основания; c, d — боковые стороны; D1, D2 — диагонали; α — угол между диагоналями; m — средняя линия; h — высота

Площадь трапеции равна половине произведения суммы оснований (a + b) на высоту (h):

На рисунке 168 приведены чертежи некоторых трапеций, у каждой из

которых показаны основания a и b и высота h.

Площадь четырёхугольника равна половине произведения его диагоналей на синус угла между ними.

Основные формулы

Далее S — площадь фигуры, P — периметр, p — полупериметр.

Площадь четырёхугольника равна половине произведения его диагоналей на синус угла между ними.

Основные формулы

Далее S — площадь фигуры, P — периметр, p — полупериметр.

Площади круга и сектора

Площадь круга равна произведению числа π на квадрат радиуса:

S = πR².

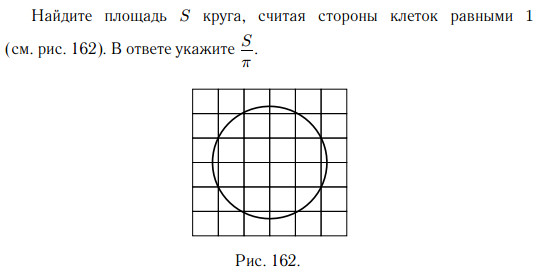
Решение.

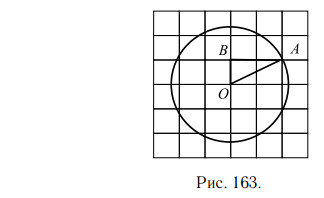
Площадь круга равна произведению числа π на квадрат радиуса. Найдём радиус. Из центра O проведём радиус OA. В треугольнике OAB сторона OA — гипотенуза, катеты равны 1 и 2 (см. рис. 163)

Найдём гипотенузу по теореме Пифагора.

Ответ: 5

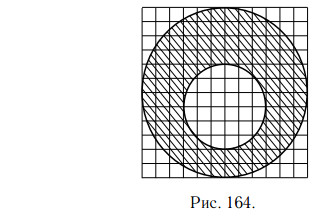
На клетчатой бумаге нарисовано два круга (см. рис. 164). Площадь

внутреннего круга равна 3. Найдите площадь заштрихованной фигуры.

Решение.

Радиус R внутреннего круга — 3 клетки, его площадь равна πR² = 3.

Радиус внешнего круга — 6 клеток, то есть 2R, поэтому его площадь равна

π · (2R)² = 3 · 4 = 12. Площадь заштрихованной фигуры равна разности 12 − 3 = 9.

Ответ: 9

Источник

Рассмотрим задачи,в которых требуется найти площадь треугольника изображённого на клетчатой бумаге.

Начнем с прямоугольных треугольников.

Задача 1

На клетчатой бумаге с размером клетки 1×1 изображен прямоугольный треугольник.

Найти его площадь.

Решение:

Площадь прямоугольного треугольника будем искать с помощью формулы

$[S = frac{1}{2}ab,]$

где a и b — катеты.

Длину катетов считаем по клеточкам.

1) a=2, b=5,

$[ S = frac{1}{2} cdot 2 cdot 5 = 5. ]$

2) a=6, b=3,

$[ S = frac{1}{2} cdot 6 cdot 3 = 9. ]$

Задача 2

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найти его площадь.

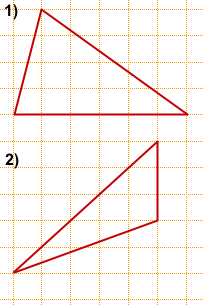
Решение:

Чаще всего площадь произвольного треугольника, изображённого на клетчатой бумаге, ищут по формуле

$[S = frac{1}{2}ah_a ,]$

где a — сторона треугольника, h_a — высота, проведённая к этой стороне.

a и h_a вычисляем по клеточкам (одна из этих величин должна лежать на горизонтальной линии, другая — на вертикальной).

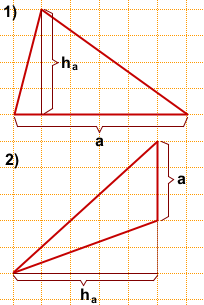
1) a=6, h_a=4,

$[ S = frac{1}{2}ah_a = frac{1}{2} cdot 6 cdot 4 = 12. ]$

2) a=3, h_a=5,

$[ S = frac{1}{2}ah_a = frac{1}{2} cdot 3 cdot 5 = 7,5. ]$

А как найти площадь, если ни одна из сторон треугольника не лежит на горизонтальной или вертикальной линии клеток?

Иногда площадь треугольника можно найти как разность площадей других фигур.

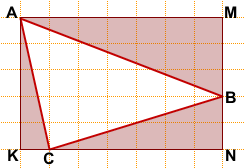
Задача 3

На клетчатой бумаге с размером клетки 1×1 изображён треугольник.

Найдите его площадь.

Решение:

Обозначим вершины треугольника, площадь которого мы ищем, через A, B и C.

Площадь треугольника ABC можно найти как разность площадей прямоугольника AMNK и треугольников AKC, AMB и CBN:

$[S_{Delta ABC} = S_{AMNK} - S_{Delta AKC} - S_{Delta AMB} - S_{Delta CBN} .]$

Площадь прямоугольника найдём по формуле S=ab.

$[ S_{AMNK} = AM cdot AK = 7 cdot 5 = 35. ]$

Площади прямоугольных треугольников найдём по формуле

$[ S = frac{1}{2}ab, ]$

где a и b — катеты.

$[S_{Delta AKC} = frac{1}{2}AK cdot KC = frac{1}{2} cdot 5 cdot 1 = 2,5;]$

$[S_{Delta AMB} = frac{1}{2}AM cdot MB = frac{1}{2} cdot 7 cdot 3 = 10,5;]$

$[S_{Delta CBN} = frac{1}{2}CN cdot BN = frac{1}{2} cdot 6 cdot 2 = 6.]$

Отсюда

$[S_{Delta ABC} = 35 - 2,5 - 10,5 - 6 = 16.]$

Источник

Все формулы по геометрии. Площади фигур

Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.

Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!

Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.

Ты нашел то, что искал? Поделись с друзьями!

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.

1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

Читайте также о задачах на тему «Координаты и векторы». Для их решения вспомните, что такое абсцисса точки (это ее координата по ) и что такое ордината (координата по ). Пригодятся также такие понятия, как координаты вектора и длина вектора (она находится по теореме Пифагора), синус и косинус угла, угловой коэффициент прямой, уравнение прямой, а также сумма, разность и скалярное произведение векторов, угол между векторами.

Как найти площадь треугольника

О чем эта статья:

8 класс, 9 класс

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные понятия

Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.

Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

Популярные единицы измерения площади:

квадратный миллиметр (мм 2 );
квадратный сантиметр (см 2 );
квадратный дециметр (дм 2 );
квадратный метр (м 2 );
квадратный километр (км 2 );
гектар (га).

Формула площади треугольника

Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.

Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.

Научиться быстро щелкать задачки на нахождение площади треугольника помогут курсы по математике от Skysmart!

Общая формула

1. Площадь треугольника через основание и высоту

, где — основание, — высота.

2. Площадь треугольника через две стороны и угол между ними

, где , — стороны, — угол между ними.

3. Площадь треугольника через описанную окружность и стороны

, где , , — стороны, — радиус описанной окружности.

4. Площадь треугольника через вписанную окружность и стороны

, где , , — стороны, — радиус вписанной окружности.

Если учитывать, что — это способ поиска полупериметра, то формулу можно записать следующим образом:

5. Площадь треугольника по стороне и двум прилежащим углам

, где — сторона, и — прилежащие углы.

6. Формула Герона для вычисления площади треугольника

Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.

, где , , — стороны, — полупериметр, который можно найти по формуле:

Для прямоугольного треугольника

Площадь треугольника с углом 90° по двум сторонам

Площадь треугольника по гипотенузе и острому углу

, где — гипотенуза, — любой из прилегающих острых углов.

Гипотенузой принято называть сторону, которая лежит напротив прямого угла.

Площадь прямоугольного треугольника по катету и прилежащему углу

, где — катет, — прилежащий угол.

Катетом принято называть одну из двух сторон, образующих прямой угол.

Площадь треугольника через гипотенузу и радиус вписанной окружности

, где — гипотенуза, — радиус вписанной окружности.

Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу

, где , — части гипотенузы.

Площадь прямоугольного треугольника по формуле Герона

, где , — катеты, — полупериметр, который можно найти по формуле:

Для равнобедренного треугольника

Вычисление площади через основание и высоту

, где — основание, — высота, проведенная к основанию.

Поиск площади через боковые стороны и угол между ними

, где — боковая сторона, — угол между боковыми сторонами.

Площадь равностороннего треугольника через радиус описанной окружности

, где — радиус описанной окружности.

Площадь равностороннего треугольника через радиус вписанной окружности

, где — радиус вписанной окружности.

Площадь равностороннего треугольника через сторону

Площадь равностороннего треугольника через высоту

Таблица формул нахождения площади треугольника

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу, использовать как закладку в тетрадке или учебнике и обращаться к ней по необходимости.

Треугольник

Треугольник произвольный

Треугольник – это многоугольник с тремя сторонами (тремя углами).

Виды треугольников :+ показать

Остроугольный треугольник – треугольник, у которого все углы острые (то есть меньше 90˚).

Тупоугольный треугольник – треугольник, у которого один из углов тупой (больше 90˚).

Прямоугольный треугольник – треугольник, у которого один из углов прямой (равен 90˚).

Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми , третья сторона называется основанием .

Равносторонний (правильный) треугольник – треугольник, у которого все три стороны равны.

Свойства

1. Против большей стороны лежит больший угол, и наоборот.

2. Против равных сторон лежат равные углы, и наоборот.

3. Сумма углов треугольника равна 180 º .

4. Внешний угол треугольника равен сумме внутренних углов,
не смежных с ним:

(Внешний угол образуется в результате продолжения одной из сторон треугольника).

5. Любая сторона треугольника меньше суммы двух других сторон.

Признаки равенства треугольников

1. Треугольники равны, если у них соответственно равны две стороны и угол между ними.

2 . Треугольники равны, если у них соответственно равны два угла и прилегающая к ним сторона.

3. Треугольники равны, если у них соответственно равны три стороны.

Биссектриса, высота, медиана

Здесь подробно о биссектрисе, высоте, медиане треугольника.

Средняя линия треугольника

Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника.

Средняя линия треугольника параллельна третьей стороне и равна ее половине.

Вписанная окружность

Центр вписанной окружности – точка пересечения биссектрис треугольника.

Описанная окружность

Центр описанной окружности – точка пересечения серединных перпендикуляров.

Соотношение сторон в произвольном треугольнике

Теорема косинусов:

Теорема синусов:

Площадь треугольника

Через сторону и высоту

Через две стороны и угол между ними

Через радиус описанной окружности

Через радиус вписанной окружности

, где – полупериметр

Смотрите также площадь треугольника здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Есть пара ошибок в формулах. В частности в формуле вычисления площади через 2 стороны и угол между ними, в теореме Синусов, в разделе “свойства”.
А вообще отличные статьи, очень выручают, всё понятно и доступно, премного благодарен

Анатолий, спасибо!
В разделе “свойства” ошибок не нашла…
В теореме синусов, – да… не пропечаталась буква гамма. Подправила.
В формуле площади треугольника, вы правы – картинка не соответствовала формуле. Исправила.
К сожалению, ошибки сразу не всегда замечаются.
Благодарю еще раз!

В разделе свойства:

Да, не хватало значка «» у А. Спасибо!

Здраствуйте! Мне нужна ваша помощь!
Задача: ВЕРШИНЫ ТРЕУГОЛЬНИКА ДЕЛЯТ ОПИСАННУЮ ОКОЛО НЕГО ОКРУЖНОСТЬ НА ТРИ ДУГИ, ДЛИНЫ КОТОРЫХ ОТНОСЯТСЯ КАК 6:7:33. НАЙДИТЕ РАДИУС ОКРУЖНОСТИ, ЕСЛИ МЕНЬШАЯ ИЗ СТОРОН РАВНА 11.

Подозреваю, у вас опечатка в условии…
Если длины дуг (а значит и их градусные меры) находятся в отношении , то выходим на уравнение Откуда Значит угол треугольника, что напротив меньшей стороны, есть
Применяем теорему синусов: , откуда

спасибо я так и думал а то не могу решить и всё
СПАСИБО!

Здравствуйте. Пожалуйста, объясните, как решить задачу:
Вписанная в теругольник ABC окружность касается сторон AB, BC и AC в точках K,L и М соответственно.Найдите KL, если AM=2, МС=3 и угол С=π/3

Очевидно,
Примите за .
Примените к треугольнику теорему косинусов:

Найдете , далее можно найти угол и из треугольника найти

Спасибо большое за ваш сайт. Очень радует, тот факт, что когда люди не понимают какую-нибудь задачу, вы помогаете решить. Спасибо. Побольше бы таких сайтов, всё понятно и доступно

источники:

http://skysmart.ru/articles/mathematic/ploshad-treugolnika

Треугольник

Источник