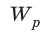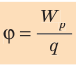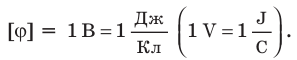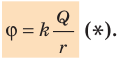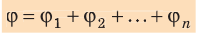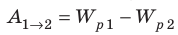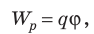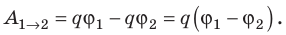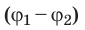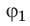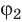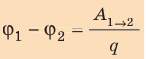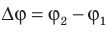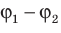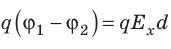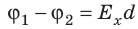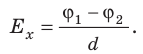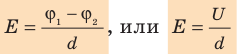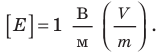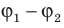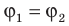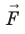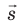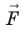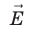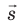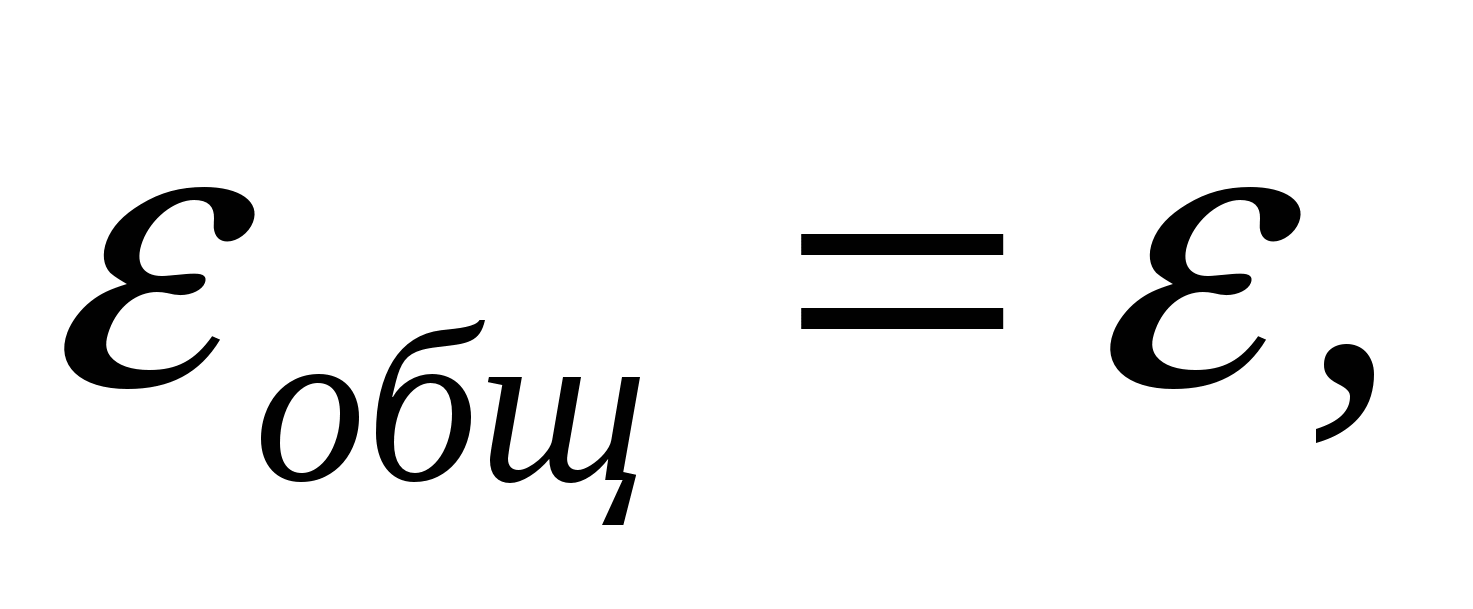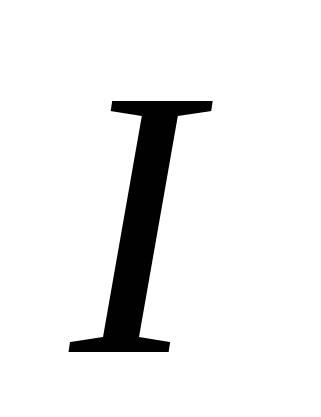Как найти разность потенциалов зная эдс - Исправление недочетов и поиск решений вместе с Examum.ru

Разность потенциалов и сложение при соединение выводов нескольких источников питания

Разность потенциалов (электрическое напряжение) — это разность уровней электрических зарядов двух тел. По другому можно сказать, что напряжение — это разность значений потенциала в начальной и конечной точках траектории. А что же такое потенциал? Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду. Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность.

Согласитесь, приведенные выше определения не так легки для восприятия. Поэтому постараемся простыми словами с примерами их изучить. Также рассмотрим интересную методику по сложению потенциалов (не путать с разностью потенциалов).

Потенциал простыми словами

Степень электризации тела характеризует величину, называемую электрическим потенциалом или просто потенциалом тела. Электризация — это процесс сообщения телу электрического заряда путем переноса с другого тела. При этом нарушается электрическая нейтральность обоих тел. Тело, заряженное положительно, станет обладать положительным потенциалом, а тело, заряженное отрицательно, — отрицательным потенциалом. Как пример, электризация эбонитовой палочки при трении о мех.

Разность потенциалов — это разность уровней электрических зарядов двух тел. Разность потенциалов также можно получить и между различными частями (точками) одного и того же тела под влиянием электростатической или электромагнитной индукции.

Электростатическая индукция — явление наведения собственного электростатического поля при действии на тело внешнего электрического поля. Явление обусловлено перераспределением зарядов внутри проводящих тел, а также поляризацией внутренних микроструктур у непроводящих тел.

Электромагнитная индукция — явление возникновения электрического тока, электрического поля или электрической поляризации при изменении магнитного поля во времени или при движении материальной среды в магнитном поле.

Далее мы будем рассматривать потенциалы только между различными частями (точками) одного и того же тела при воздействии на него магнитного поля. То есть будем анализировать разность потенциалов на выводах генератора переменного и постоянного тока.

Получение разности потенциалов на выводах генератора

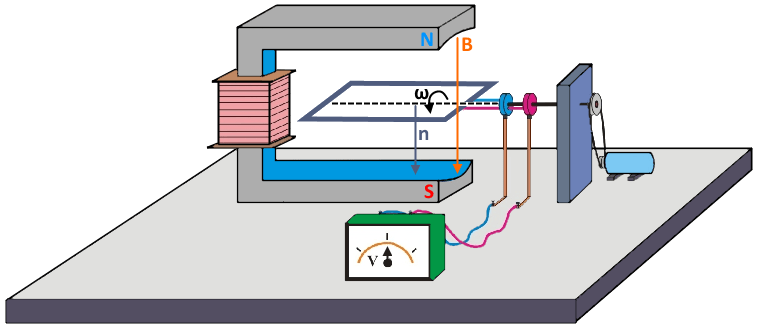
В основе практически всех генераторов тока лежит проводящая рамка, вращающаяся в магнитном поле. В этой рамке может быть много витков. Для примера упрощенно можно рассмотреть рамку, состоящую из одного витка.

При вращении рамки два ее участка постоянно пересекают силовые линии магнитного поля. При этом, когда один участок движется в одну сторону, второй движется в другую. Что происходит при этом? Под действием магнитного поля силы Лоренца перемещают электроны от одного конца (1) рамки к концу (2), потом обратно и далее уже от конца (2) к концу (1). Все это происходит за один оборот рамки. А так как рамка вращается постоянно, то на концах мы имеем переменную разность потенциалов (переменную ЭДС электромагнитной индукции).

Более подробно на данном вопросе останавливаться не будем, и далее перейдем непосредственно к основной теме — сложению и разности потенциалов.

Разность потенциалов на примере электрической цепи

Рассмотрим электрическую цепь состоящую из генератора постоянного тока, резистора (нагрузки) и соединительных проводов.

Начнем с генератора. В предыдущем пункте мы кратко рассмотрели принцип работы генератора переменного тока. Чем же отличается генератор переменного тока? Не будем углубляться в конструктивные особенности, а отметим лишь главное — на одном выводе генератора (источника) постоянного тока всегда имеется избыток электронов (отрицательный потенциал), на другом — недостаток электронов (избыток положительных зарядов, положительный потенциал).

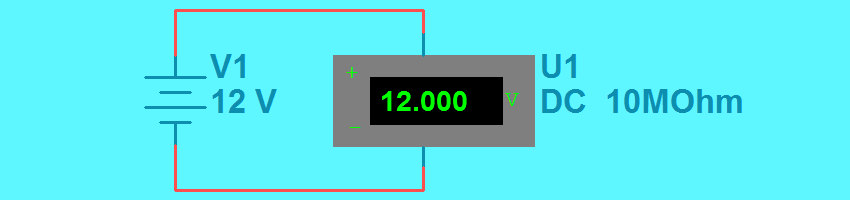
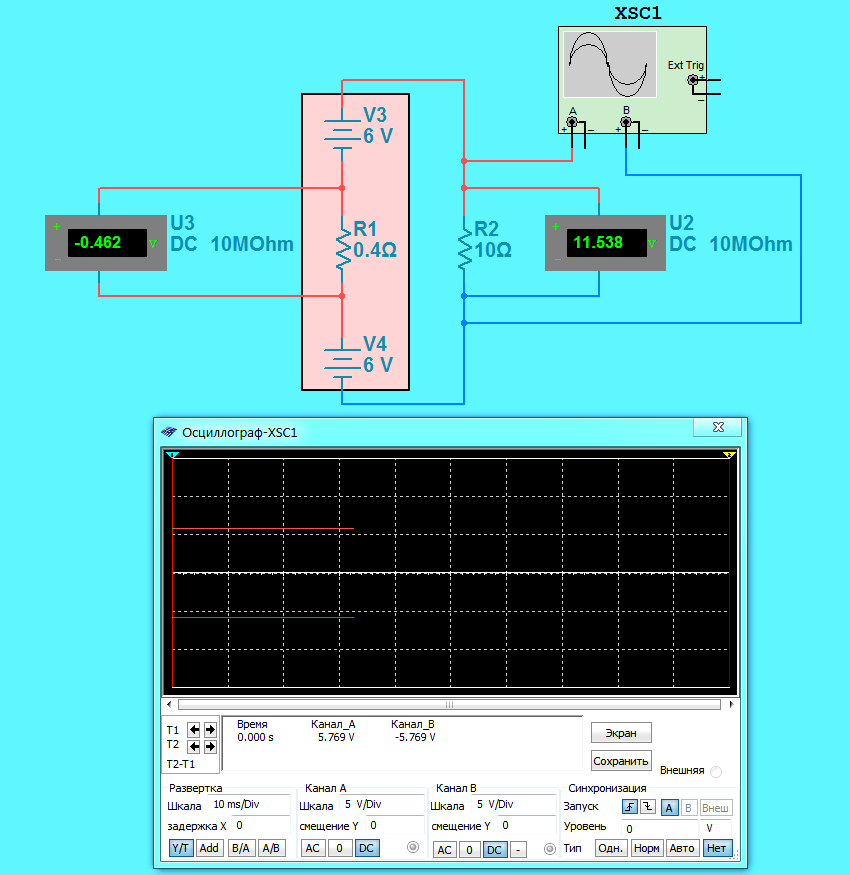
Возьмем для примера 12 вольтовый источник постоянного тока и наглядно поэкспериментируем с ним в программе Multisim:

На схеме к плюсу источника тока подключен плюс вольтметра, а к минусу источника — минус вольтметра. Вольтметр показывает напряжение между выводами источника тока. В данном случае напряжение 12 Вольт численно равно ЭДС, так как внутреннее сопротивление мы приняли равным 0 Ом. Далее мы рассмотрим пример с внутренним сопротивлением источника питания. Пока же остановимся на напряжении. Как известно, напряжение — это разность потенциалов. Если разность потенциалов 12 Вольт, то какие же потенциалы на выводах источника? Так как в источнике постоянного тока определенное количество отрицательных зарядов (электронов) скапливается на минусовом выводе, то естественно на плюсовом выводе остается такое же количество положительных зарядов. Соответственно потенциал на плюсе источника +6 Вольт, на минусе -6 Вольт, а разность потенциалов равна +6-(-6) = +12 Вольт. Почему мы отнимаем от +6? Все просто — несмотря на то, что электроны движутся от минуса к плюсу, направление тока принято брать от плюса к минусу.

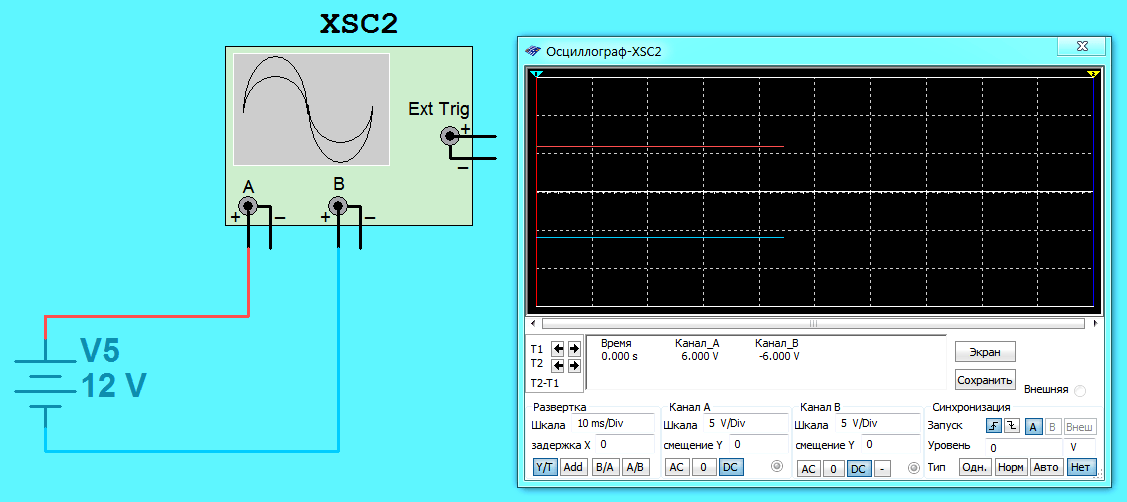
Покажем наглядно потенциалы на выводах генератора (источника) постоянного тока:

Мы подключили к плюсу источника тока канал A осциллографа, а к минусу — канал B. На экране осциллографа два графика (красная и синяя прямая), которые показывают, что потенциал на плюсовом выводе не изменяется и равен +6 Вольт, на минусовом -6 Вольт.

Теперь добавим в цепь резистор (нагрузку) и проанализируем распределение потенциалов на выводах источника с учетом его внутреннего сопротивления:

Как видно из схемы потенциалы на выводах источника вместо +6 и — 6 уменьшились до +5,769 и -5,769 Вольт. То есть напряжение на выводах уже не равно ЭДС. Происходит это за счет падения напряжения на внутреннем сопротивлении источника питания. В нашем случае падение напряжения равно +0,462 Вольт (на схеме оно со знаком минус, так как не соблюдена полярность подключения вольтметра). Если прибавить его к напряжению на выводах источника, то получим ЭДС источника тока: +0,462+(+5,769-(-5,769)) = 0,462+11,538 = 12 Вольт.

Остановимся чуть подробнее на этой схеме и разберемся, что произошло при добавлении в цепь нагрузки (резистора 10 Ом):

В первую очередь, цепь замкнулась и по ней потек ток.
В цепи находятся два последовательно соединенных резистора. Один резистор — это нагрузка во внешней цепи, второй резистор — внутреннее сопротивление источника питания (он находится во внутренней цепи и мы его как бы не видим, но он есть).
По правилу последовательного соединения сумма внутреннего сопротивления и сопротивления нагрузки во внешней цепи дает общее сопротивление Rобщ = 0,4+10 = 10,4 Ом.
Так как ЭДС определяется по формуле E = I×Rобщ, то нетрудно найти силу тока в цепи I = E/Rобщ = 12/10, 4 = 1,154 А.
Последовательное соединение резисторов — это такое взаимное расположение компонентов, при котором ток движется в одном направлении и имеет общее значение для каждого резистора. При таком соединении напряжение на каждом участке будет пропорционально сопротивлению конкретного резистора в цепи.
Зная силу тока в цепи нетрудно определить напряжения на каждом резисторе по формуле Uрез = I×Rрез. Получаем напряжение (падение напряжения) на внутреннем сопротивлении источника 0,462 Вольт и напряжение на резисторе внешней цепи 11,538 Вольт. Суммарно эти напряжения равны значению ЭДС источника тока.

Подведем итог по разности потенциалов на выводах источника постоянного тока. Любой источник (батарея, генератор) обладает некоторым внутренним сопротивлением (иногда для удобства его значением пренебрегают, то есть приравнивают его к нулю). До тех пор, пока к источнику питания не подключена внешняя нагрузка (когда цепь замыкается и по ней течет ток), разность потенциалов (напряжение) численно равно значению ЭДС. Как только цепь замыкается через нагрузку, разность потенциалов (напряжение) на выводах источника питания уже не равно ЭДС. Оно уменьшается на значение падения напряжения на внутреннем сопротивлении источника питания.

Сложение потенциалов

Теперь рассмотрим довольно интересный вопрос — сложение потенциалов при соединении выводов нескольких источников питания.

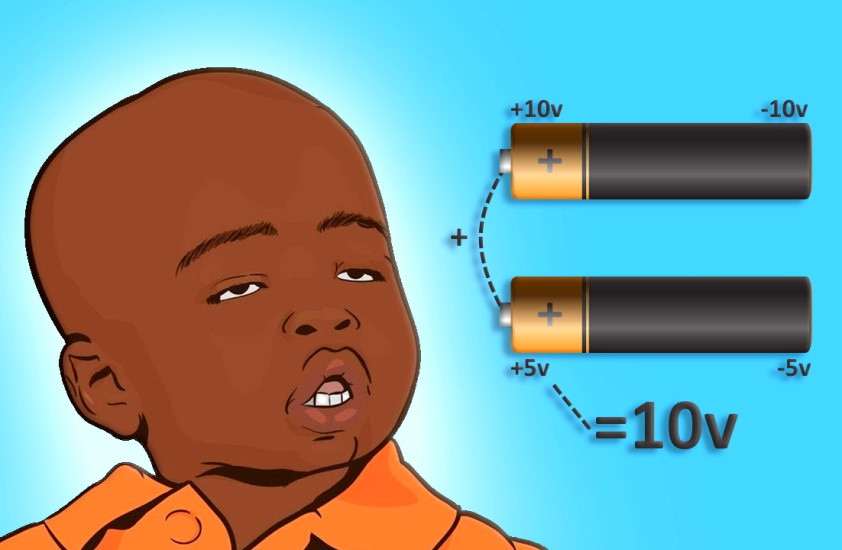
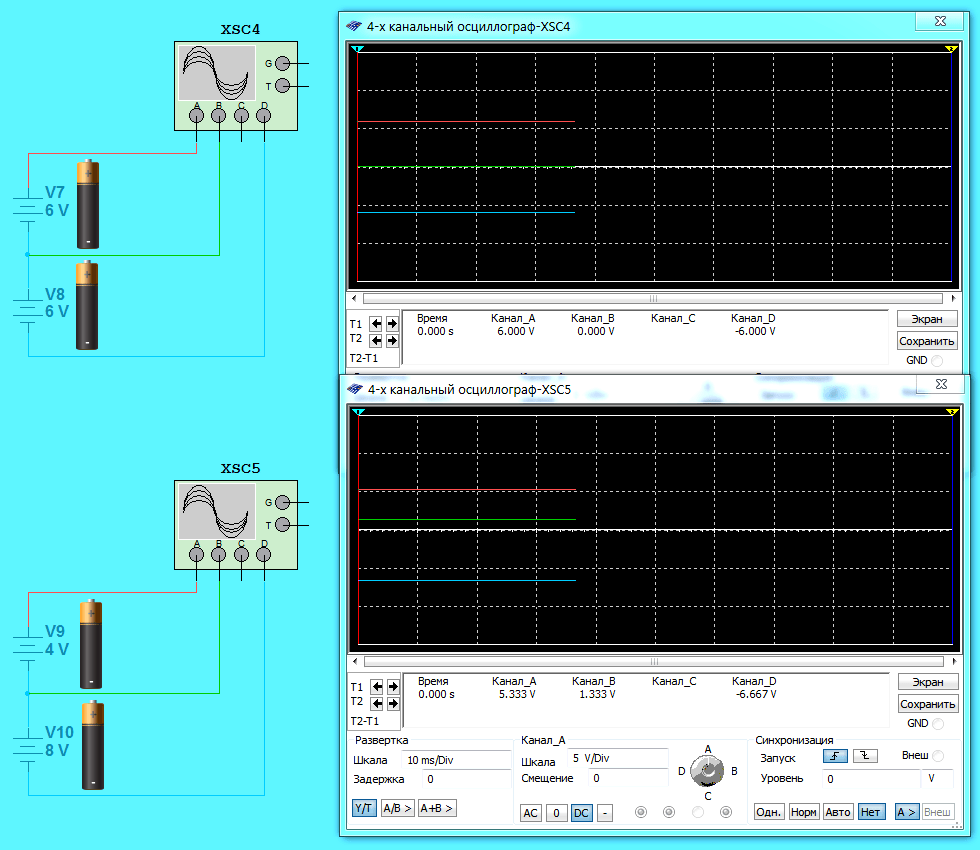
Возьмем для начала две батарейки с ЭДС 6 Вольт. Если их соединить последовательно (плюс одной батарейки с минусом другой), то ЭДС такой батареи удвоится и будет равно 12 Вольт. Потенциал в точке соединения будет 0 Вольт, а потенциалы на оставшихся выводах +6 и -6 Вольт. Это самый простой пример, так как две батарейки имеют одинаковую ЭДС и соединены разноименными полюсами.

Все становится намного сложнее, когда мы соединяем батарейки с разными ЭДС. Да, суммарное ЭДС батареи складывается из ЭДС двух батареек. Но распределение потенциалов имеет некоторую особенность. Рассмотрим это на примерах:

Сначала мы соединили две 6 вольтовые батарейки (минус одной с плюсом другой). На осциллографе точка соединения имеет потенциал 0 Вольт, а оставшиеся выводы +6 и -6 Вольт. Суммарное ЭДС такой батареи +6-(-6) = 12 Вольт.

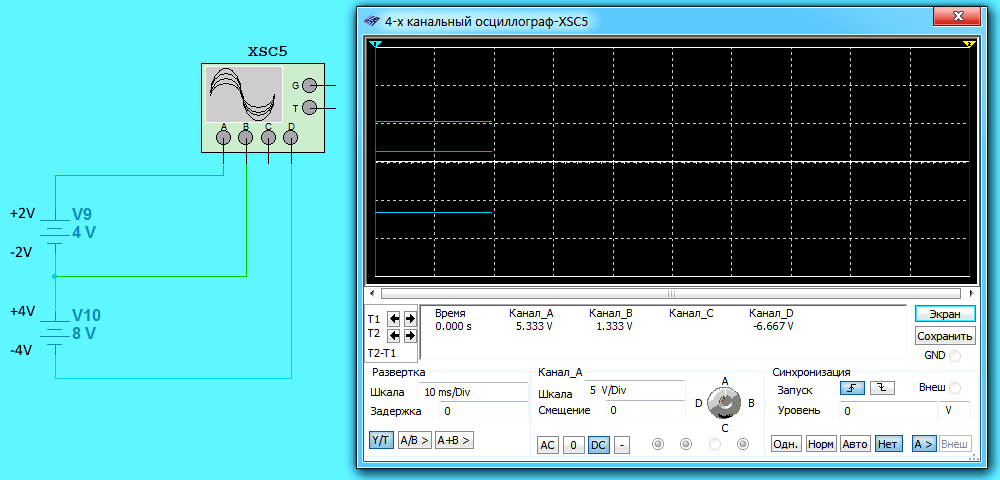
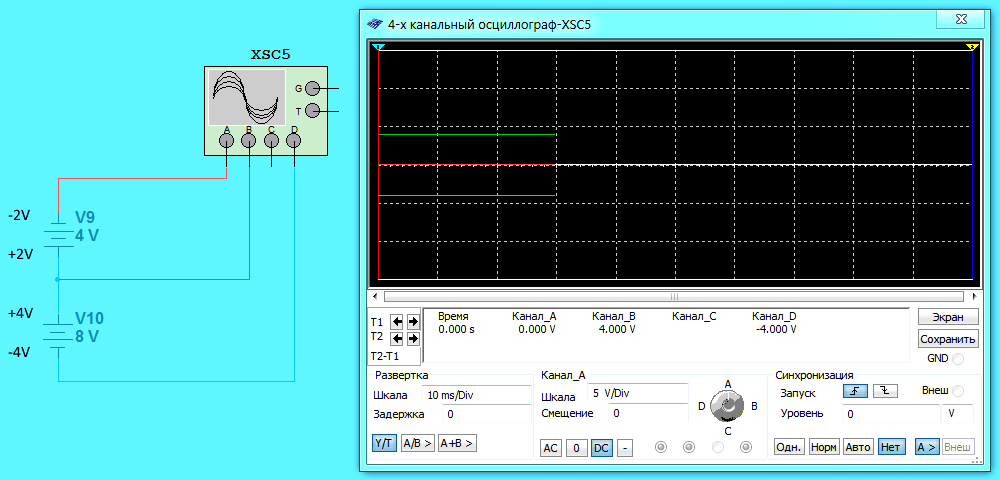
Ниже на схеме тоже батарея с ЭДС 12 Вольт. Однако ЭДС одной батарейки 4 Вольт, а другой 8 Вольт. Здесь самое интересное — распределение потенциалов. Можно было бы предположить, что потенциал в точке соединения равен -2+4 = 6 Вольт (сложили потенциал на минусе одной батарейки с потенциалом на плюсе другой). Исходя из этого потенциалы на выводах самой батареи (батарея — это соединенные вместе несколько батареек (гальванических элементов)) стали бы +10 Вольт и -2 Вольт, что в сумме тоже дает общую ЭДС 12 Вольт. Но как ни странно осциллограф показывает в точке соединения потенциал +1,333 Вольт, а на выводах батареи +5,333 и -6,667 Вольт. Как же так получилось? Давайте разбираться.

Поможет нам математика. Рассмотрим следующую схему и составим систему уравнений:

a-x = 2a’ (разность получившихся потенциалов после соединения равна удвоенному значению потенциала (ЭДС) на одном из выводов до соединения в батарею; a — потенциал на выводе батарейки после соединения в батарею; a’ — потенциал на выводе батарейки до соединения в батарею).
x-b = -2b’ (разность получившихся потенциалов после соединения равна удвоенному значению потенциала (ЭДС) на одном из выводов до соединения в батарею; со знаком минус, так как удваивается потенциал отрицательного вывода; b — потенциал на выводе батарейки после соединения в батарею; b’ — потенциал на выводе батарейки до соединения в батарею).
x = -a+(-b) (потенциал в точке соединения равен сумме потенциалов; a и b взяты со знаком минус, так как складываются потенциалы противоположных им выводов).

Выразим из первого уравнения a: a = 2a’+x. Выразим из второго уравнения b: b = x+2b’. Подставим все это в третье уравнение: x = -2a’-x-x-2b’; 3x = -2(a’+b’); x = (-2/3)×(a’+b’) = -(a’+b’)/1,5.

Простыми словами, чтобы сложить потенциалы в точке соединения двух источников питания, нужно сложить потенциалы соединяемых выводов, а затем полученное значение разделить на 1,5. Причем это правило справедливо для любых комбинаций соединения (-и+, -и-, +и+).

Закрепим материал наглядными примерами из программы и самостоятельным расчетом по формуле:

На первой схеме пример, который уже рассматривался. Здесь минус одной батарейки соединяется с плюсом другой батарейки. ЭДС первой батарейки 4 Вольт (соответственно потенциалы на выводах +2 и -2 Вольт). ЭДС второй батарейки 8 Вольт (соответственно потенциалы на выводах +4 и -4 Вольт). Воспользуемся правилом и определим потенциал в точке соединения. Сначала складываем потенциалы -2+(+4) = +2 Вольт. Затем это значение делим на 1,5. Получаем +2/1,5 = +1,333333333333333 Вольт. То же самое показывает осциллограф (канал B).

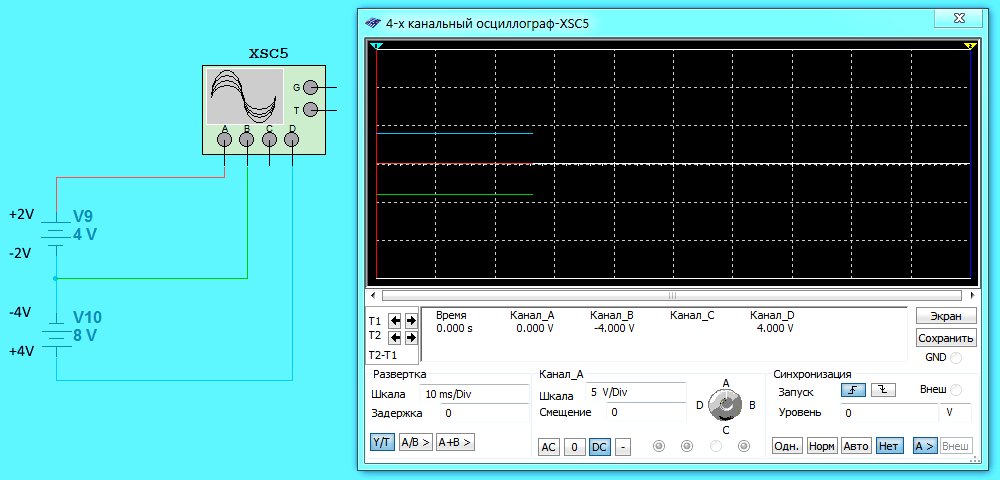
На второй схеме минус одной батарейки соединяется с минусом другой батарейки. ЭДС первой батарейки 4 Вольт (соответственно потенциалы на выводах +2 и -2 Вольт). ЭДС второй батарейки 8 Вольт (соответственно потенциалы на выводах +4 и -4 Вольт). Воспользуемся правилом и определим потенциал в точке соединения. Сначала складываем потенциалы -2+(-4) = -6 Вольт. Затем это значение делим на 1,5. Получаем -6/1,5 = -4 Вольт. То же самое показывает осциллограф (канал B).

На третьей схеме плюс одной батарейки соединяется с плюсом другой батарейки. ЭДС первой батарейки 4 Вольт (соответственно потенциалы на выводах +2 и -2 Вольт). ЭДС второй батарейки 8 Вольт (соответственно потенциалы на выводах +4 и -4 Вольт). Воспользуемся правилом и определим потенциал в точке соединения. Сначала складываем потенциалы +2+(+4) = +6 Вольт. Затем это значение делим на 1,5. Получаем +6/1,5 = +4 Вольт. То же самое показывает осциллограф (канал B).

Подведем итог. Разность потенциалов показывает напряжение между двумя точками (выводами). Сумма же потенциалов нужна для определения потенциала в точке соединения нескольких источников питания. Мы рассмотрели сумму потенциалов в точке при соединении двух источников питания. Но в цепи может быть и более двух последовательно соединенных источников питания, и здесь с распределением потенциалов также имеет свои особенности (в данном обзоре не рассматривалась такая схема). Может возникнуть вопрос — а зачем вообще нужно это сложение потенциалов? Ответ будет в одной из следующих публикаций, где будут рассмотрены особенности при переходе со звезды на треугольник.

Источник

ЭДС. Закон Ома для полной цепи

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.
Сторонняя сила
Закон Ома для полной цепи
КПД электрической цепи
Закон Ома для неоднородного участка

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.

До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.

Как мы знаем, положительный заряд :

• уходит во внешнюю цепь с положительной клеммы источника;

• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;

• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.

Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила $vec{F_E}$ , направленная против движения заряда (т.е. против направления тока).

к оглавлению ▴

Сторонняя сила

Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).

Рис. 1. Сторонняя сила

Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила $vec{F_{CT}}$ не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.

Обозначим через $A_{CT}$ работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы $A_{CT}$ называется также работой источника тока.

Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, $A_{CT}$ — это также работа сторонней силы по перемещению заряда по всей цепи.

Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.

Опыт показывает, что работа $A_{CT}$ прямо пропорциональна перемещаемому заряду . Поэтому отношение $A_{CT}/q$ уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается :

$mathcal E = frac{displaystyle A_{CT}}{displaystyle q vphantom{1^a}}.$ (1)

Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.

Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.

к оглавлению ▴

Закон Ома для полной цепи

Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.

Пусть источник тока с ЭДС, равной , и внутренним сопротивлением подключён к резистору (который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).

Рис. 2. Полная цепь

Наша задача — найти силу тока в цепи и напряжение на резисторе .

За время по цепи проходит заряд q = It . Согласно формуле (1) источник тока совершает при этом работу:

$A_{CT} = Eq = EIt.$ (2)

Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и . Данное количество теплоты определяется законом Джоуля–Ленца:

(3)

Итак, $A_{CT} = Q$ , и мы приравниваем правые части формул (2) и (3):

После сокращения на получаем:

Вот мы и нашли ток в цепи:

$I = frac{displaystyle mathcal E}{displaystyle R + r vphantom{1^a}}.$ (4)

Формула (4) называется законом Ома для полной цепи.

Если соединить клеммы источника проводом пренебрежимо малого сопротивления (R = 0) , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:

$I_{K3} = frac{displaystyle mathcal E}{displaystyle r vphantom{1^a}}.$

Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.

Зная силу тока (формула (4)), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи:

$U = IR = frac{displaystyle mathcal E R}{displaystyle R + r vphantom{1^a}}.$ (5)

Это напряжение является разностью потенциалов между точками и (рис. 2). Потенциал точки равен потенциалу положительной клеммы источника; потенциал точки равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.

Мы видим из формулы (5), что в реальной цепи будет — ведь умножается на дробь, меньшую единицы. Но есть два случая, когда .

1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При r = 0 формула (5) даёт .

2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина R + r неотличима от , и формула (5) снова даёт нам .

Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.

к оглавлению ▴

КПД электрической цепи

Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.

Количество теплоты, выделяющееся на полезной нагрузке за время , обозначим $Q_{polezn}$ .

Если сила тока в цепи равна , то

$Q_{polezn} = I^2Rt.$

Некоторое количество теплоты выделяется также на источнике тока:

$Q_{ist} = I^2rt.$

Полное количество теплоты, которое выделяется в цепи, равно:

$Q_{poln} = Q_{polezn} + Q_{ist} = I^2Rt + I^2rt = I^2(R + r)t.$

КПД электрической цепи — это отношение полезного тепла к полному:

$eta = frac{displaystyle Q_{polezn}}{displaystyle Q_{poln} vphantom{1^a}} = frac{displaystyle I^2Rt}{displaystyle I^2(R+r)t vphantom{1^a}} = frac{displaystyle R}{displaystyle R+r vphantom{1^a}}.$

КПД цепи равен единице лишь в том случае, если источник тока идеальный (r = 0) .

к оглавлению ▴

Закон Ома для неоднородного участка

Простой закон Ома U = IR справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.

Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.

На рис. 3 показан неоднородный участок, содержащий резистор и источник тока. ЭДС источника равна , его внутреннее сопротивление считаем равным нулю (если внутреннее сопротивление источника равно , можно просто заменить резистор на резистор R + r ).

Рис. 3. ЭДС «помогает» току:

Сила тока на участке равна , ток течёт от точки к точке . Этот ток не обязательно вызван одним лишь источником . Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток является результатом совокупного действия всех источников, имеющихся в цепи.

Пусть потенциалы точек и равны соответственно и . Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.

Напряжение на нашем участке равно: . За время через участок проходит заряд q = It , при этом стационарное электрическое поле совершает работу:

$A_{POL} = Uq = UIt.$

Кроме того, положительную работу совершает источник тока (ведь заряд прошёл сквозь него!):

$A_{CT} = mathcal Eq = mathcal EIt.$

Сила тока постоянна, поэтому суммарная работа по продвижению заряда , совершаемая на участке стационарным электрическим полем и сторонними силами источника, целиком превращается в тепло: $A_{POL} + A_{CT} = Q$ .

Подставляем сюда выражения для $A_{POL}$ , $A_{CT}$ и закон Джоуля–Ленца:

Сокращая на , получаем закон Ома для неоднородного участка цепи:

(6)

или, что то же самое:

(7)

Обратите внимание: перед стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки к точке .

Отметим два следствия выведенных формул (6) и (7).

1. Если участок однородный, то . Тогда из формулы (6) получаем U = IR — закон Ома для однородного участка цепи.

2. Предположим, что источник тока обладает внутренним сопротивлением . Это, как мы уже упоминали, равносильно замене на R + r :

Теперь замкнём наш участок, соединив точки и . Получим рассмотренную выше полную цепь. При этом окажется, что и предыдущая формула превратится в закон Ома для полной цепи:

Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.

Может быть и другой случай подключения, когда источник «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от к , направлен против действия сторонних сил источника.

Рис. 4. ЭДС «мешает» току:

Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!

Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:

$A_{CT} = mathcal E q = mathcal EIt.$

Тогда закон Ома для неоднородного участка примет вид:

(8)

или:

где по-прежнему — напряжение на участке.

Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:

Ток при этом течёт от точки к точке . Если направление тока совпадает с направлением сторонних сил, то перед ставится «плюс»; если же эти направления противоположны, то ставится «минус».

Повторим основные понятия и определения по теме «Закон Ома».

Напомним, что напряжение измеряется в вольтах.

Сила тока измеряется в амперах.

Сопротивление измеряется в омах. Эта единица измерения названа в честь Георга Симона Ома, открывшего взаимосвязь между напряжением, сопротивлением цепи и силой тока в этой цепи.

Основные определения, которые мы используем в решении задач:

Источник тока – это устройство, способное создавать необходимую для существования тока разность потенциалов.

Можно сказать, что источник тока действует, как насос. Он «качает» электроны по проводникам, как водяной насос воду по трубам. Эту аналогию можно продолжить. При этом источник тока совершает работу, за счёт химических реакций, происходящих внутри него.

Если эту работу разделить на переносимый источником заряд q (суммарный заряд всех проходящих через источник электронов), то мы получим величину, которую называют электродвижущей силой или сокращённо ЭДС.

Измеряется эта ЭДС, как и разность потенциалов, в вольтах и имеет примерно тот же смысл.

По определению, сила тока равна отношению суммарного заряда электронов, проходящих через сечение проводника, ко времени прохождения. Измеряется сила тока в амперах (А).

Свойство проводника препятствовать прохождению по нему тока характеризуется величиной, которую назвали электрическим сопротивлением – R. Проходя через проводник, электрический ток нагревает его.

Сопротивление измеряют в омах (Ом).

Сам источник тока тоже обладает сопротивлением. Такое сопротивление принято называть внутренним сопротивлением источника r (Ом).

Именно немецкому учёному Георгу Ому удалось установить, от чего может зависеть электрическое сопротивление проводника. Проведя многочисленные эксперименты, Ом сделал следующие выводы:

Сопротивление проводника тем больше, чем больше его длина.
Сопротивление проводника тем больше, чем меньше его толщина или площадь поперечного сечения.

Кроме того, Ом выяснил, что каждый материал обладает своим электрическим сопротивлением. Величина, которая показывает, каким сопротивлением будет обладать проводник единичной длины и единичной площади сечения из данного материала, называется удельным электрическим сопротивлением: (Ом*мм²/м). Эта величина справочная. Таким образом, получается, что электрическое сопротивление проводника равно:

Рассмотрим задачи ЕГЭ по теме «Закон Ома» для полной цепи.

Задача 1. На рисунке приведён график зависимости напряжения на концах железного провода площадью поперечного сечения 0,05 мм² от силы тока в нём. Чему равна длина провода? Ответ дайте в метрах. Удельное сопротивление железа 0,1 Ом*мм²/м.

Решение:

Из закона Ома для проводника или участка цепи без источника следует:

$displaystyle I=frac{U}{R};$

$displaystyle R=frac{U}{I}.$

По графику: при

Из формулы сопротивления выражаем и находим длину проводника:

Ответ: 10.

Задача 2. Через поперечное сечение проводников за 8 с прошло 10²⁰ электронов. Какова сила тока в проводнике? Ответ дайте в амперах.

Решение:

По определению силы тока:

$displaystyle I=frac{q}{t}.$

Заряд всех электронов: где е — модуль заряда электрона, $e=1,6cdot 10^{-19}$ Кл.

Тогда $displaystyle I=frac{Ncdot e}{t}=frac{10^{20}cdot 1,6cdot 10^{-19}}{8}=2 A.$

Ответ: 2.

Задача 3. Идеальный амперметр и три резистора общим сопротивлением 66 Ом включены последовательно в электрическую цепь, содержащую источник с ЭДС равной 5 В, и внутренним сопротивлением r=4 Ом. Каковы показания амперметра? (Ответ дайте в амперах, округлив до сотых.)

Решение:

По закону Ома для полной цепи:

Тогда $displaystyle I=frac{5}{66+4}=0,07 A.$

Ответ: 0,07.

Задача 4. ЭДС источника тока равна 1,5 В. Определите сопротивление внешней цепи, при котором сила тока будет равна 0,6 А, если сила тока при коротком замыкании равна 2,5 А. Ответ дайте в Ом, округлив до десятых.

Решение:

Сила тока короткого замыкания определяется следующим образом:

Отсюда выражаем и находим внутреннее сопротивление источника:

При внешнем сопротивлении, не равном нулю, сила тока в цепи определяется законом Ома для полной цепи:

Отсюда выражаем сопротивление резистора и находим его:

Ответ: 1,9.

Задача 5. На рисунке изображена схема электрической цепи, состоящей из источника постоянного напряжения с ЭДС 5 В и пренебрежимо малым внутренним сопротивлением, ключа, резистора с сопротивлением 2 Ом и соединительных проводов. Ключ замыкают. Какой заряд протечет через резистор за 10 минут? Ответ дайте в кулонах.

Решение:

Выражаем время в секундах: t = 10 минут = 600 с.

Определяем силу тока по закону Ома для полной цепи:

Внутреннее сопротивление пренебрежимо мало, поэтому r = 0.

По определению силы тока:

$displaystyle I=frac{q}{t}.$

Отсюда Кл.

Ответ: 1500.

Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «ЭДС. Закон Ома для полной цепи» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Понятие потенциала в физике
Понятие разности потенциалов, формула нахождения
Единица разности потенциалов
Измерение контактной разности потенциалов
Разность потенциалов на практике
Потенциал. Эквипотенциальные поверхности.
Что называют потенциалом электростатического поля
- Как определяют разность потенциалов
  - Как связаны напряженность однородного электростатического поля и разность потенциалов
  - Какие поверхности называют эквипотенциальными
Для чего нужен потенциометр электрику
Понятие потенциала, разности потенциалов
Общие сведения

Понятие потенциала в физике

Из курса физики известно, что работа некоторых сил, например силы тяжести, не зависит от траектории движения тела, а зависит лишь от величины перемещения.

Такие силы и силовые поля, в которых они действуют, называют потенциальными или консервативными.

Сила, действующая на заряд, помещенный в однородное электростатическое поле, также относится к потенциальным и определяется формулой:

Формула 1

F→=q·E→,

где q — электрический заряд, Кл;

E→ — напряженность электрического поля, В.

В механике работа определяется как произведение силы на расстояние между точками – началом и концом движения и косинусом угла α между векторами силы и скорости. Аналогично выведем формулу для определения работы электростатического поля при перемещении заряда из одного положения в другое.

Формула 2

A=F→·Δr·cosα=q·E→·Δr·cosα=q·E→·(r2-r1)·cosα=(q·E→·r2-q·E→·r1)·cosα.

Величину q·E→·r1 называют потенциальной энергией поля.

Определение 1

Потенциальная энергия является мерой работы, которую совершат силы при перемещении объекта в потенциальном поле.

Работа зависит от разницы потенциальных энергий в начальной и конечной точке. Тогда работу можно представить как:

Формула 3

A=-(W2-W1).

Примечание

Знак «минус» в выражении для работы означает, что если уменьшить потенциальную энергию с помощью силового воздействия, работа поля будет положительной. Если потенциальную энергию увеличить — работа будет отрицательной.

Поместим в некоторую точку неподвижный заряд q, чтобы создать электростатическое поле. Когда заряд q1 попадает в это поле, заряды q и q1 не взаимодействуют друг с другом, на заряд q1 действует само поле. Чтобы ввести новую характеристику поля, не зависящую от помещенных в него зарядов, необходимо поделить потенциальную энергию на заряд q. Полученную величину называют потенциалом.

Определение 2

Потенциал (от слова potentia — сила, возможность) — скалярная величина в физике, равная отношению потенциальной энергии к величине заряда.

В электрике принято следующее обозначение потенциала: φ.

Формула 4

φ=Wq.

Нулевым принято считать потенциал бесконечно удаленной точки (r→∞).

Ток в цепи всегда течет от большего потенциала к меньшему.

Формула для потенциала одного заряда приведена выше. На практике любое заряженное тело можно разделить на несколько элементов, каждый из которых будет иметь свой потенциал. Тогда потенциал системы, состоящей из двух и более зарядов:

Формула 5

φ=φ1+φ2+φ3+…

Понятие разности потенциалов, формула нахождения

Подставим выражение для потенциала в точке в формулу для работы:

Формула 6

A=-(W2-W1)=-(qφ2-qφ1)=-q(φ2-φ1).

Физическую величину, смысл которой заключается в разнице между потенциалами в начальной и конечной точках траектории, называют разностью потенциалов или напряжением (U).

Формула 7

U=φ1-φ2.

В самом простом случае, когда на рассматриваемую цепь или участок цепи действует только электростатическое поле, напряжение можно считать равным разности потенциалов. В иных случаях напряжение в проводнике определяют как сумму разности потенциалов и работу внешних сил (ЭДС), возникающих, например, в результате закона электромагнитной индукции. Тогда напряжение:

Формула 8

U=(φ1-φ2)+ЭДС.

Чтобы понять связь между напряжением и напряженностью, рассмотрим простой конденсатор в виде двух пластин с постоянной емкостью.

Между положительно и отрицательно заряженными пластинами образуется электростатическое поле напряженностью overrightarrow Е. Линии напряженности между обкладками параллельны, а модуль напряженности одинаков.

Если положительный заряд поместить рядом с положительной пластиной, он начнет двигаться в сторону отрицательной пластины, значит, поле совершит некоторую работу. Так как векторы скорости перемещения заряда и напряженности лежат на параллельных прямых, работа:A=F→·S.

Длина перемещения равна расстоянию между обкладками, а сила воздействия поля: F→=q·E→.

Тогда:A=q·E→·SиA=qU.

Приравняем выражения для работы, получим:q·E→·S=q·U.

Напряжение и напряженность связаны формулой:

Формула 9

U=E→·S

Разместим протяженный проводник в электростатическом поле. Будем считать, что линии напряженности расположены горизонтально.

Пусть проводник будет двигаться перпендикулярно линиям напряженности. В этом случае работа по перемещению заряда не совершается, так как косинус угла между векторами силы и скорости движения равен нулю. То есть все точки на поверхности проводника имеют один и тот же потенциал.

Определение 3

Эквипотенциальные поверхности — поверхности, у которых потенциалы в каждой точке одинаковы. Эквипотенциальные поверхности представляют собой плоскость для однородного поля и сферы для поля одиночного заряда.

Единица разности потенциалов

Коробка уравнивания потенциалов

В честь ученого (Алессандро Вольта), впервые доказавшего существование разницы потенциалов, единица измерения названа Вольт. В международной системе единиц напряжение обозначается символами:

В – в русскоязычной литературе;
V – в англоязычной литературе.

Кроме этого, существуют кратные обозначения:

мВ – милливольт (0.001 В);
кВ – киловольт (1000 В);
МВ – мегавольт (1000 кВ).

Измерение контактной разности потенциалов

Основная проблема заключатся в том, что контактная разность потенциалов не может быть измерена напрямую, вольтметром, хотя значение ЭДС в цепи с соединением двух различных проводников может составлять от долей до единиц вольт.

Контактная потенциальная разница существенно влияет на вольтамперную характеристику измеряемой цепи. Наглядным примером может служить полупроводниковый диод, где подобное явление возникает на границе соприкосновения полупроводников с разным типом проводимости.

Разность потенциалов на практике

С общепринятой точки зрения, разность потенциалов – это напряжение между двумя выбранными точками цепи. В то же время напряжение между каждой из этих точек и третьей точкой будет отличаться в полном соответствии с определением.

Наглядный пример:

Точка А в электрической схеме – напряжение 10 В относительно провода заземления;
В точке В напряжение составляет 25 В относительно того же провода.

Необходимо найти напряжение между точками А и В.

В данном случае искомая разность составляет:

UAB= ϕА-ϕВ=10-25=15 В.

Рассматриваемые понятия важны для минимального объема знаний в области электротехники и электроники, поскольку на них основываются все расчеты и практические решения. Без этих азов невозможно более углубленное изучение электрических дисциплин.

Потенциал. Эквипотенциальные поверхности.

В механике взаимодействие тел характеризует силой или потенциальной энергией. Электрическое поле, которое обеспечивает взаимодействие между электрически заряженными телами, также характеризуют двумя величинами. Напряженность электрического поля — это силовая характеристика. Теперь введем энергетическую характеристику — потенциал. С помощью этой величины можно будет сравнивать между собой любые точки электрического поля. Таким образом, потенциал как характеристика поля должен зависеть от значения заряда, содержащегося в этих точках. Поделим обе части формулы A = W1 — W2 на заряд q, получим

Отношение W/q не зависит от значения заряда и принимается за энергетическую характеристику, которую называют потенциалом поля в данной точке. Обозначают потенциал буквой φ.

Потенциал электрического поля φ — скалярная энергетическая характеристика поля, которая определяется отношением потенциальной энергии W положительного заряда q в данной точке поля к величине этого заряда:

Единица потенциала — вольт:

Подобно потенциальной энергии значения потенциала в данной точке зависит от выбора нулевого уровня для отсчета потенциала. Чаще всего в электродинамике за нулевой уровень берут потенциал точки, лежащей в бесконечности, а в электротехнике — на поверхности Земли.

С введением потенциала формулу для определения работы по перемещению заряда между точками 1 и 2 можно записать в виде

Поскольку при перемещении положительного заряда в направлении вектора напряженности электрическое поле выполняет положительную работу A = q (φ1 — φ2 )> 0, то потенциал φ1 больше чем потенциал φ2 . Таким образом, напряженность электрического поля направлена в сторону уменьшения потенциала.

Если заряд перемещать с определенной точки поля в бесконечность, то работа A = q (φ — φ∞ ). Поскольку φ∞ = 0, то A = qφ. Таким образом, величина потенциала φ определенной точки поля определяется работой, которую выполняет электрическое поле, перемещая единичный положительный заряд из этой точки в бесконечность,

Если электрическое поле создается точечным зарядом q, то в точке, лежащей на расстоянии r от него, потенциал вычисляют по формуле

По этой формуле рассчитывают и потенциал поля заряженного шара. В таком случае r — это расстояние от центра шара до выбранной точки поля. С этой формулы видно, что на одинаковых расстояниях от точечного заряда, который создает поле, потенциал одинаков. Все эти точки лежат на поверхности сферы, описанной радиусом r вокруг точечного заряда. Такую сферу называют эквипотенциальной поверхностью.

Эквипотенциальные поверхности — геометрическое место точек в электрическом поле, которые имеют одинаковый потенциал, — один из методов наглядного изображения электрических полей.

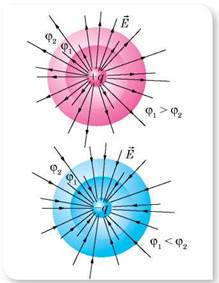
Эквипотенциальные поверхности электрических полей, созданных точечными зарядами разных знаков

Силовые линии всегда перпендикулярны эквипотенциальных поверхностей. Это означает, что работа сил поля по перемещению заряда по эквипотенциальной поверхности равна нулю.

В случае наложения электрических полей, созданных несколькими зарядами, потенциал электрического поля равен алгебраической сумме потенциалов полей, созданных отдельными зарядами, φ = φ1 + φ2 + φ3 . Эквипотенциальные поверхности таких систем имеют сложную форму. Например, для системы из двух одинаковых по значению одноименных зарядов эквипотенциальные поверхности имеют вид, изображенный на рисунке. Эквипотенциальные поверхности однородного поля явлются плоскостями.

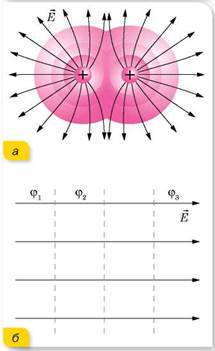
Эквипотенциальные поверхности: а — поля двух одинаковых зарядов б — однородного поля

Что называют потенциалом электростатического поля

Потенциал
электростатического поля в данной точке — это скалярная физическая величина, которая характеризует энергетические свойства поля и равна отношению потенциальной энергии
электрического заряда, помещенного в данную точку поля, к значению q этого заряда:

Единица потенциала в Си — вольт:

Из определения потенциала следует, что потенциал ϕ поля, созданного точечным зарядом Q, в точках, которые расположены на расстоянии r от данного заряда, можно рассчитать по формуле:

Из формулы ( *) видно: 1) если поле создано положительным точечным зарядом (Q > 0), то потенциал этого поля в любой точке является положительным ( ϕ > 0); 2) если поле создано отрицательным точечным зарядом (Q < 0), то потенциал этого поля в любой точке является отрицательным (ϕ < 0). Формула ( *) справедлива и для потенциала поля равномерно заряженной сферы (или шара) на расстояниях, которые больше ее радиуса или равны ему.

Если поле создано несколькими произвольно расположенными зарядами, потенциал ϕ поля в любой точке данного поля равен алгебраической сумме потенциалов
полей, созданных каждым зарядом:

Как определяют разность потенциалов

Когда в электростатическом поле заряд движется из точки 1 в точку 2, это поле совершает работу, которая равна изменению потенциальной энергии заряда, взятому с противоположным знаком:
. Поскольку
то
Выражение
называют разностью потенциалов, где
— значение потенциала в начальной точке траектории движения заряда,
— значение потенциала в ее конечной точке.

Разность потенциалов — скалярная физическая величина, равная отношению работы сил электростатического поля по перемещению заряда из начальной точки в конечную к значению этого заряда:

Единица разности потенциалов в Си — вольт:
= 1 В (V).

Разность потенциалов между двумя точками поля равна 1 В, если для перемещения между ними заряда 1 Кл электростатическое поле совершает работу 1 Дж. Обратите внимание: в подобных случаях разность потенциалов
− также называют напряжением (U). Важно не путать изменение потенциала
и разность потенциалов (напряжение)
.

Как связаны напряженность однородного электростатического поля и разность потенциалов

Рассмотрим однородное электростатическое поле на участке между точками 1 и 2, расположенными на расстоянии d друг от друга; пусть из точки 1 в точку 2 под действием поля перемещается заряд q (рис. 42.2).

Совершаемую полем работу можно найти двумя способами: 1) через разность потенциалов между точками 1 и 2: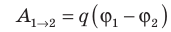<br>; 2) через напряженность поля:
— проекция вектора
на ось Ох, проведенную через точки 1 и 2.

Приравняв оба выражения для работы, получим:
, откуда:
, или

Если заряд перемещается в направлении напряженности электрического поля (
) , последняя формула примет вид:

Из последней формулы следует единица напряженности в Си — вольт на метр:

Какие поверхности называют эквипотенциальными

Для визуализации электростатического поля кроме силовых линий используют также эквипотенциальные поверхности.

Эквипотенциальная поверхность — это поверхность, во всех точках которой потенциал электростатического поля имеет одинаковое значение.

Для наглядности следует рассматривать не одну эквипотенциальную поверхность, а их совокупность. Однако графически изобразить совокупность поверхностей сложно, поэтому обычно изображают только линии пересечения эквипотенциальных поверхностей некоторой плоскостью (рис. 42.3).

Эквипотенциальные поверхности тесно связаны с силовыми линиями электростатического поля. Если электрический заряд перемещается по эквипотенциальной поверхности, то работа поля равна нулю, поскольку A=q (
), а на эквипотенциальной поверхности

Работу электростатического поля также можно представить через силу
действующую на заряд со стороны поля: A F= scosα , где α — угол между векторами
и
Поскольку A = 0, а F ≠ 0 и s ≠ 0, то cosα = 0, то есть α = 90°. Это означает, что при движении заряда вдоль эквипотенциальной поверхности вектор силы
а следовательно, и вектор напряженности
поля в любой точке перпендикулярны вектору перемещения

Таким образом, силовые линии электростатического поля перпендикулярны эквипотенциальным поверхностям (см. рис. 42.3).

Обратите внимание! Симметрия эквипотенциальных поверхностей повторяет симметрию источников поля. Так, поле точечного заряда сферически симметрично, поэтому эквипотенциальными поверхностями поля точечного заряда являются концентрические сферы; при однородном поле эквипотенциальные поверхности — это система параллельных плоскостей.

Для чего нужен потенциометр электрику

Что такое коэффициент мощности

Данный прибор широко применяется в практике для модуляции напряжения. Дело в том, что у многих источников (особенно заточенных под автономное функционирование: аккумуляторные элементы, солнечные батареи и т.д.) константное напряжение, не поддающееся управлению без специальных устройств, что может вызвать проблемы. Чтобы уменьшить исходное напряжение такого элемента, используют устройства-делители, снабженные потенциометрами.

Потенциометр-реостат

Как работает потенциометр? Он представляет собой резистор, имеющий пару выводов и подвижный ползунок с еще одним выводом. Подключаться такое переменное устройство сопротивления может двумя способами:

По типу реостата, с использованием ползункового вывода и одного из пары других. Сопротивление замеряется движением ползунка по корпусу резистора. Регуляция цепного электротока в таком случае возможна при последовательном подключении такого реостата и источника напряжения.
Потенциометрическим методом, задействующим каждый вывод из имеющейся у прибора тройки. Два главных вывода включаются параллельно источнику, снятие сниженного напряжения реализуется с ползункового механизма и одного вывода. В этом случае через резисторное устройство течет электроток, создающий спад напряжения между ползунком и боковыми выводами. В такой модели на источник питания ложится большая нагрузка, так как для точности регуляции и отсутствия сбоев необходимо, чтобы резисторное сопротивление в несколько раз уступало нагрузочному.

Потенциометрическое подключение прибора

Таким образом, понятие потенциала используется в разных областях физики: как в механике, так и в изучении электричества. В последнем случае оно выступает в качестве характеристики поля. Непосредственно рассматриваемая величина измерению не поддается, зато можно измерить разность, тогда один заряд берется за точку отсчета.

Понятие потенциала, разности потенциалов

С понятием напряжения электрического тока тесно связано понятие «потенциал» , или «разность потенциалов». Хорошо, обратимся снова к нашей водопроводной аналогии.

Наш резервуар находится на возвышенности что позволяет воде беспрепятственно стекать по трубе вниз. Так как бак с водой на высоте, то и потенциал этой точки будет более высоким или более положительным чем тот что находится на уровне земли. Видите что получается?

У нас появилось две точки имеющие разные потенциалы, точнее разную величину потенциала.

Получается, для того чтобы электрический ток мог бежать по проводу, потенциалы не должны быть равны. Ток бежит от точки с большим потенциалом к точки с меньшим потенциалом.

Помните такое выражение, что ток бежит от плюса к минусу. Так вот это все тоже самое. Плюс это более положительный потенциал а минус более отрицательный.

Кстати а хотите вопрос на засыпку? Что произойдет с током, если величины потенциалов будет периодически меняться местами?

Тогда мы будем наблюдать то как электрический ток меняет свое направление на противоположное каждый раз как потенциалы поменяются. Это получится уже переменный ток. Но его мы пока рассматривать не будем, дабы в голове сформировалось ясное понимание процессов.

Общие сведения

Электрические явления начали интересовать философов ещё со времёнДревней Греции. Существует легенда, согласно которой люди, жившие более двух тысяч лет назад, находили на острове Магнезия камни, притягивающие к себе металлические предметы. Их назвали магнитами. В то же время философ Фалес обнаружил любопытное свойство янтаря. Если его потереть об шерсть, то к нему прилипали лёгкие предметы. Благодаря этим двум явлениям природы и было открыто электричество, ранее называемое янтарностью.

Но на протяжении многих столетий учёные не могли объяснить силы, заставляющие взаимодействовать тела между собой. Существенный вклад в развитие учения внёс Отто Герик, создавший первую электромашину.

Затем Питера ван Мушенбрук смог изготовить источник электричества, названный лейденской банкой. С этого момента начался бум изучения явлений. В своё время их исследовали такие физики, как Гильберт, Кулон, Ампер, Эдисон, Франклин, Вольт, Фарадей.

Благодаря их стараниями стало известно, что электричество и магнетизм — это явления, не существующие друг без друга. Описывать их начали, ведя характеристику, названную электромагнитным полем. Возникновение же последней связано с существованием заряда и возможностью его переноса элементарными частицами. Их условно разделили на два вида:

отрицательные;
положительные.

В природе если тело находится в равновесии, то есть на него не оказывается стороннее воздействие, движение частиц происходит хаотично и обусловлено тепловыми процессами.

Но если носители заставить двигаться в одном направлении, возникнет ток. Характеризуется он силой и работой которую необходимо затратить для переноса заряда из одной точки поля в другую.

Затраченную при движении энергию называютэлектродвижущей силой, описывающейся напряжением. Величиной зависящей от изменения потенциала поля в той или иной его точке. В 1827 году Георг Ом опытным путём доказал пропорциональную зависимость силы тока и напряжения. Этот фундаментальный закон был назван его именем, записывается так: I = U / R. Правило установило, что сила электротока зависит от работы, совершаемой полем для переноса заряда из точки A в B.

РазноеДелаем токопроводящий клей из подручных материалов

РазноеЧто такое фаза в электричестве?

Источник

Силы
неэлектростатического происхождения,
действующие на заряды со стороны
источников тока называются сторонними
силами.

Электродвижущая сила

Скалярная
физическая величина, определяемая
работой, совершаемой сторонними силами
при перемещении единичного положительного
заряда, называется электродвижущей
силой
(ЭДС)
,
действующей в цепи или на ее участке:.

Напряжение

Напряжение

–
это
физическая величина, определяемая
работой, совершаемой суммарным полем
электростатических (кулоновских) и
сторонних сил при перемещении единичного
положительного заряда на данном участке
цепи.

Разность потенциалов

Напряжение
на неоднородном участке цепи

(где есть сторонние силы) равно сумме
ЭДС источника и разности потенциалов
на этом участке:

Для
однородного
участка цепи
,
где сторонние силы не действуют,

Т.е.
напряжение
совпадает с разностью потенциалов на
концах участка цепи
.

Закон
Ома для однородного участка

цепи в
интегральной

и дифференциальной форме
.
Сопротивление и его зависимость от
температуры. Сверхпроводимость.

Закон
Ома для однородного участка

цепи в
интегральной

и дифференциальной форме

Закон
Ома для однородного участка цепи:
н
емецкий
физик Георг Ом экспериментально
установил, чтосила тока в
цепи прямо пропорциональна приложенному
напряжению и обратно пропорциональна
сопротивлению проводника:.

Закон
Ома в дифференциальной форме (закон Ома
для плотности тока).
Закон
Ома в форме
относится ко всему проводнику. Представим
закон Ома в дифференциальной (т.е.
относящейся к элементу тока длиныdl
)
форме. Некоторая точка внутри проводника
характеризуется вектором плотности
тока
,
напряженностью электрического поляи свойствами материала проводника, т.е.
удельным сопротивлением.
Выделим мысленно малый объем вблизи
рассматриваемой точки и подставимв закон Ома,
получим:,
здесь
— разность потенциалов между сечениямиdS

отстоящими на расстоянии dl
.
Следовательно,.

Учтем,
что
— напряженность электростатического
поля;- плотность электрического поля;- удельная электрическая проводимость.

Тогда
из формулы (20) следует закон
Ома в дифференциальной форме
:
.

Сопротивление и его зависимость от температуры

Температурная
зависимость сопротивления может быть
представлена в виде:,

Сверхпроводимость

Сверхпроводимость

–
свойство
некоторых проводников, заключающееся
в том, что их электрическое сопротивление
скачкомпадает до
нуля при охлаждении ниже определенной
критической температуры T
к,
характерной для данного проводника.

16. Работа и мощность тока. Закон Джоуля – Ленца в интегральной и дифференциальной форме

При
протекании тока по однородному участку
цепи электрическое поле совершает
работу. За время Δt
по
цепи протекает заряд Δq
= I
Δt
.
Электрическое поле на выделенном учестке
совершает работу

выражающей закон
Ома для однородного участка цепи с
сопротивлением R
,
умножить на I
Δt
,
то получится соотношение

Закон
преобразования работы тока в тепло был
экспериментально установлен независимо
друг от друга Дж. Джоулем иЭ. Ленцем и
носит название закона
Джоуля–Ленца

.

Мощность
электрического тока равна отношению
работы тока ΔA
к
интервалу времени Δt
,
за которое эта работа была совершена:

Работа
электрического тока в СИ выражается
в джоулях

(Дж),
мощность – в ваттах

(Вт).

Закон
Джоуля-Ленца в дифференциальной форме
— удельная мощность тока равна скалярному
произведению векторов плотности тока
и напряженности электрического
поля:

где s —
удельная проводимость;

r —
удельное сопротивление среды.

Закон
Джоуля-Ленца в дифференциальной форме
носит совершенно общий характер, т. е.
не зависит от природы сил, возбуждающих
электрический ток. Закон Джоуля-Ленца,
как показывает опыт, справедлив и для
электролитов и для полупроводников.

17.
. Обобщенный закон Ома для неоднородного
участка цепи в интегральной и
дифференциальной форме. Анализ обобщенного
закона Ома. Замкнутая электрическая
цепь. Соединение сопротивлений:
последовательное и параллельное.

11 Сторонние электродвижущие силы. Закон Джоуля — Ленца

Согласно (11.4), э.д.с. численно равна работе сторонних сил,
совершаемой при перемещении единичного положительного заряда по замкнутой цепи.

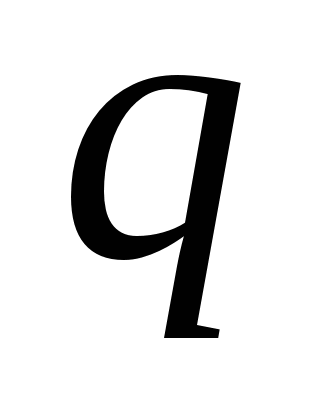
Помимо сторонних сил, на заряд действуют силы электростатического поля, имеющего напряжённость . Следовательно, результирующая сила , действующая на заряд в любой точке цепи, может быть записана в виде
Данное правило Кирхгофа является условием стационарности токов. В противном случае потенциал рассматриваемого узла изменялся бы с течением времени, и это привело бы к изменению токов в цепи.

Второе правило Кирхгофа гласит, что алгебраическая сумма произведений сил токов в отдельных участках произвольного замкнутого контура на сопротивления этих участков равна алгебраической сумме э.д.с., действующих в этом контуре:

. (11.13)
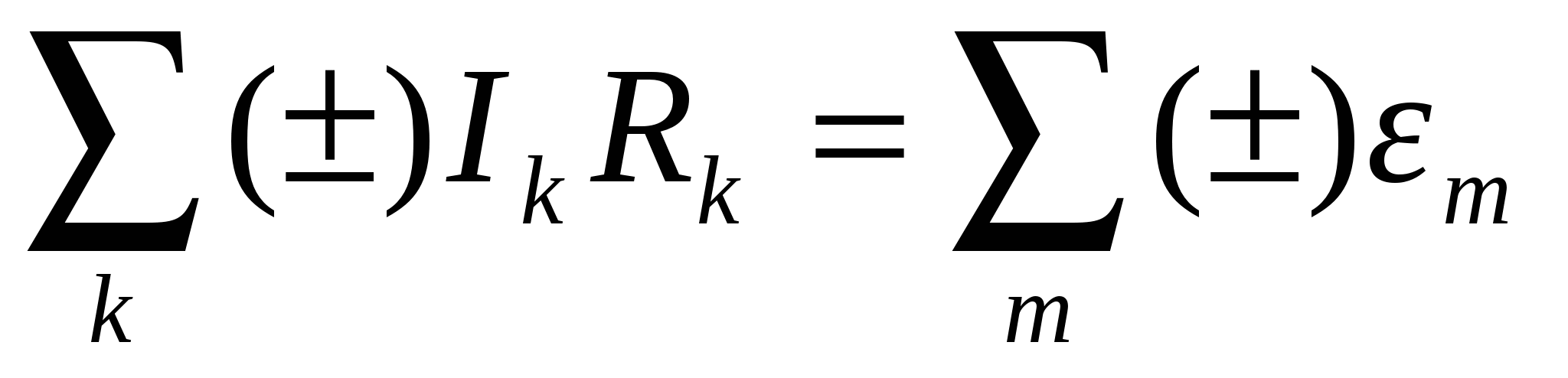
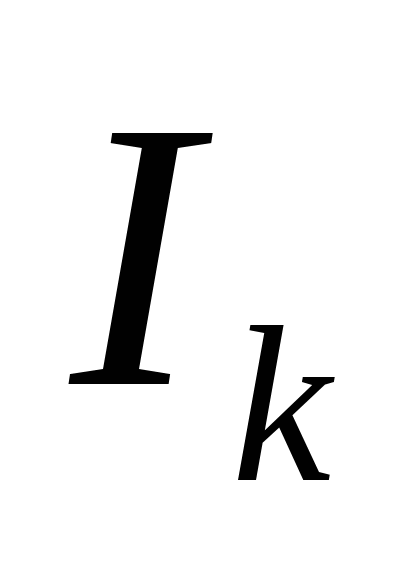
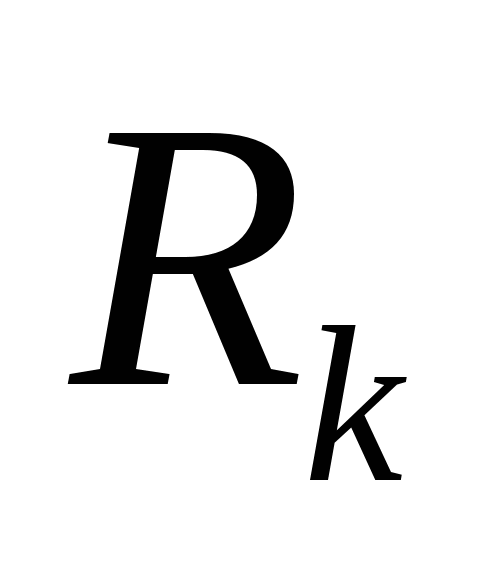
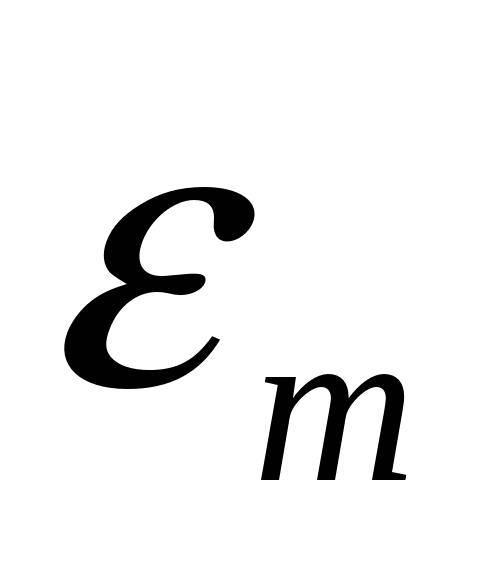
Здесь и — сила тока и сопротивление для некоторого участка замкнутой цепи, — значение э.д.с. в этой же цепи.

Второе правило Кирхгофа является следствием закона Ома для замкнутой цепи. Направление обхода замкнутого контура и направление токов на всех участках цепи выбирают произвольным образом. Сила тока записывается со знаком «+», если его направление совпадает с направлением обхода замкнутого контура, и со знаком «-» в противоположном случае. Значение э.д.с. записывается со знаком «+», если при обходе замкнутого контура движение внутри источника осуществляется от его отрицательного полюса к положительному, то есть совпадает по направлению с внутренним током источника.

Для нахождения всех неизвестных токов необходимо решить систему независимых уравнений, в которой число уравнений должно быть равно числу неизвестных токов. В результате
решения системы уравнений могут быть получены отрицательные значения силы тока. Это означает, что на рассматриваемом участке цепи реальный ток проходит в противоположном направлении относительно выбранного направления.

Например, в цепи, показанной на рисунке 16, можно выделить три замкнутых контура, для которых второе правило Кирхгофа имеет вид

(11.14)

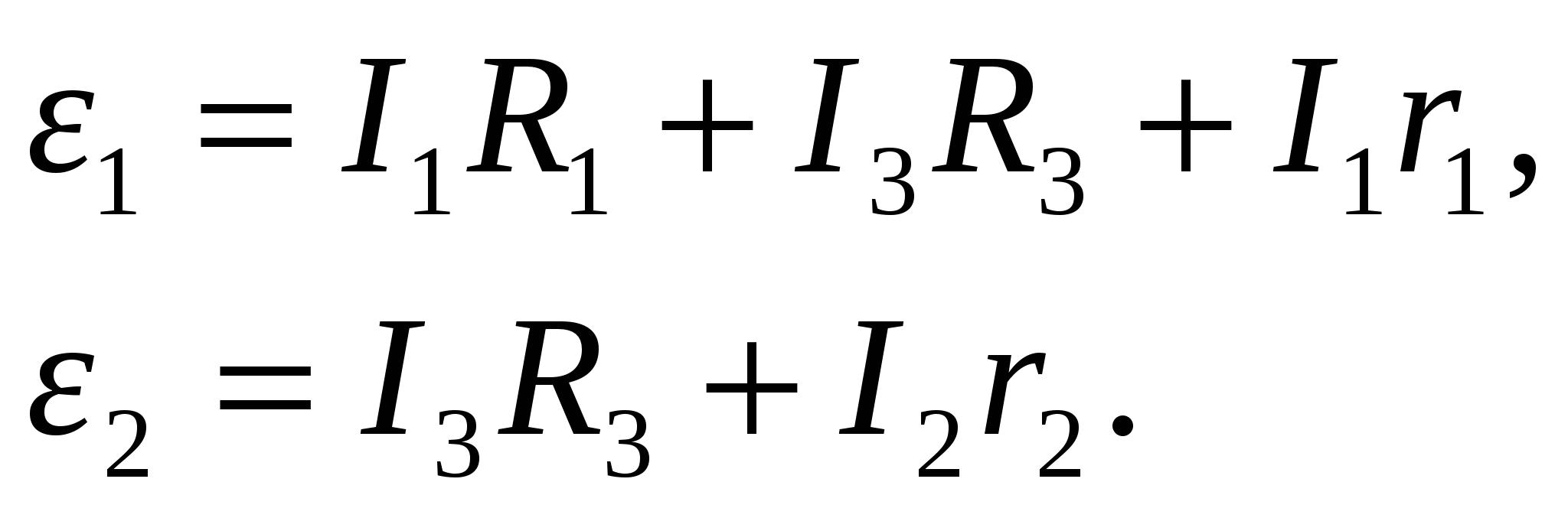
Здесь первое уравнение записано для контура

, второе уравнение – для контура

, третье уравнение – для контура

. Данная система уравнений является линейно зависимой. Поэтому для вычисления неизвестных токов I
1
,
I
2
, I
3
необходимо использовать любые два из этих трёх уравнений совместно с первым правилом Кирхгофа (11.12).

Рисунок 16 — Пример
разветвлённой цепи постоянного тока
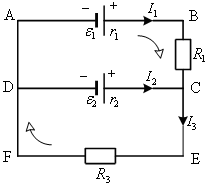
С помощью правил Кирхгофа можно рассчитать , например, э.д.с. и внутреннее сопротивление аккумуляторной батареи. Допустим, батарея состоит из нескольких источников постоянного напряжения, количество источников равно

, э.д.с. каждого источника равна , внутреннее сопротивление равно , и источники соединены последовательно. Тогда общую э.д.с. и общее внутреннее сопротивление батареи можно вычислить следующим образом:

. Если источники соединены в батарее параллельно, то

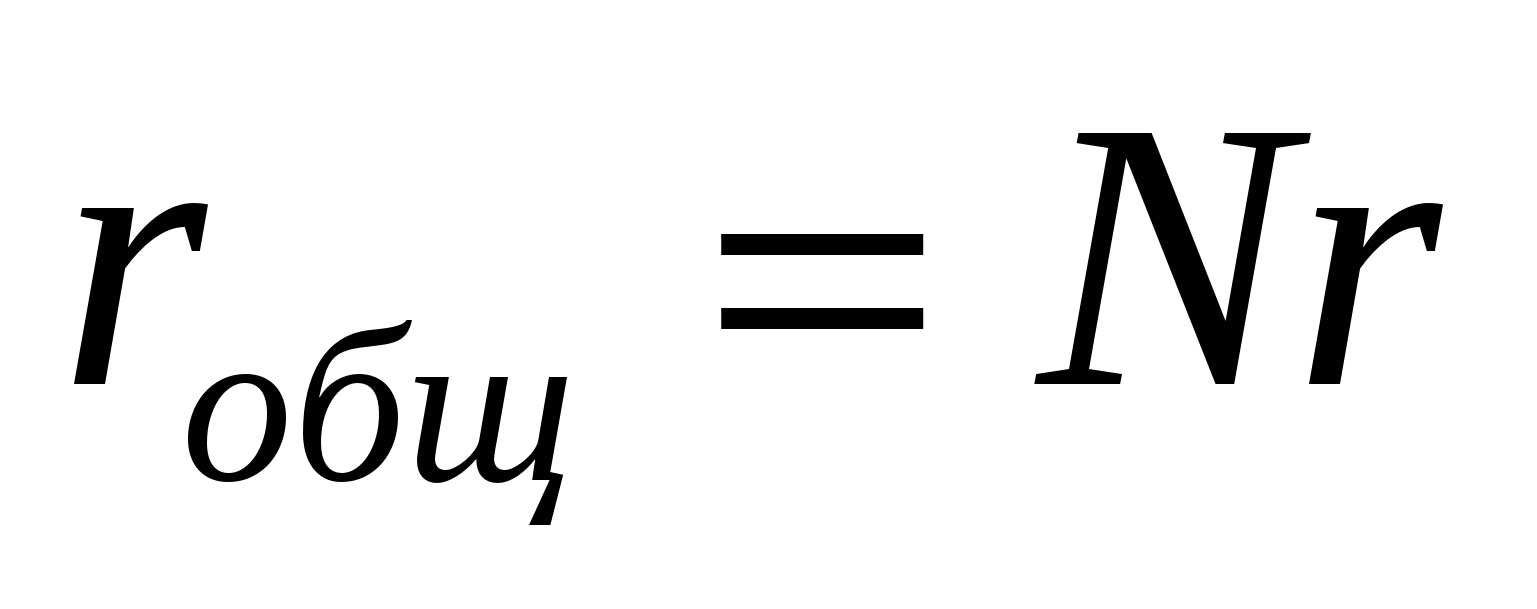
При прохождении электрического тока в цепи выделяется тепло. Этот процесс можно характеризовать с помощью понятия о тепловой мощности тока

Тепловое действие тока можно описать на основании закона Джоуля — Ленца

: тепловая мощность тока равна произведению силы тока
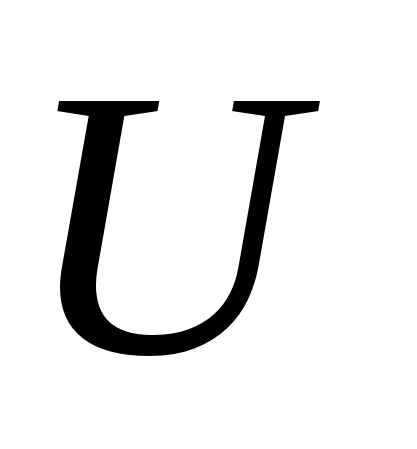
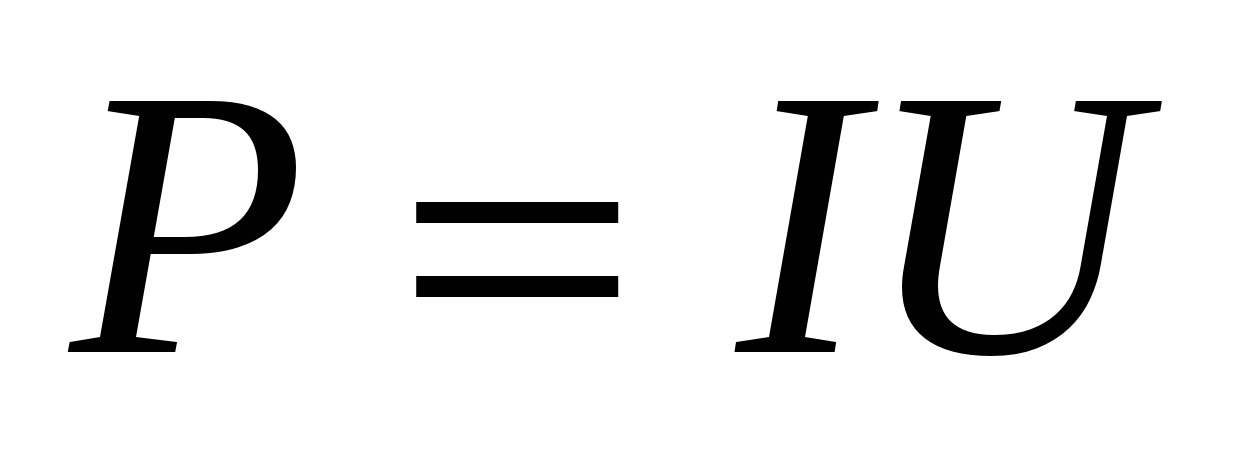
на электрическое напряжение на этом участке:

. (11.16)
Используя закон Ома для участка цепи (10.10), выражение для тепловой мощности тока (11.16) можно представить в другой форме:

. (11.17)
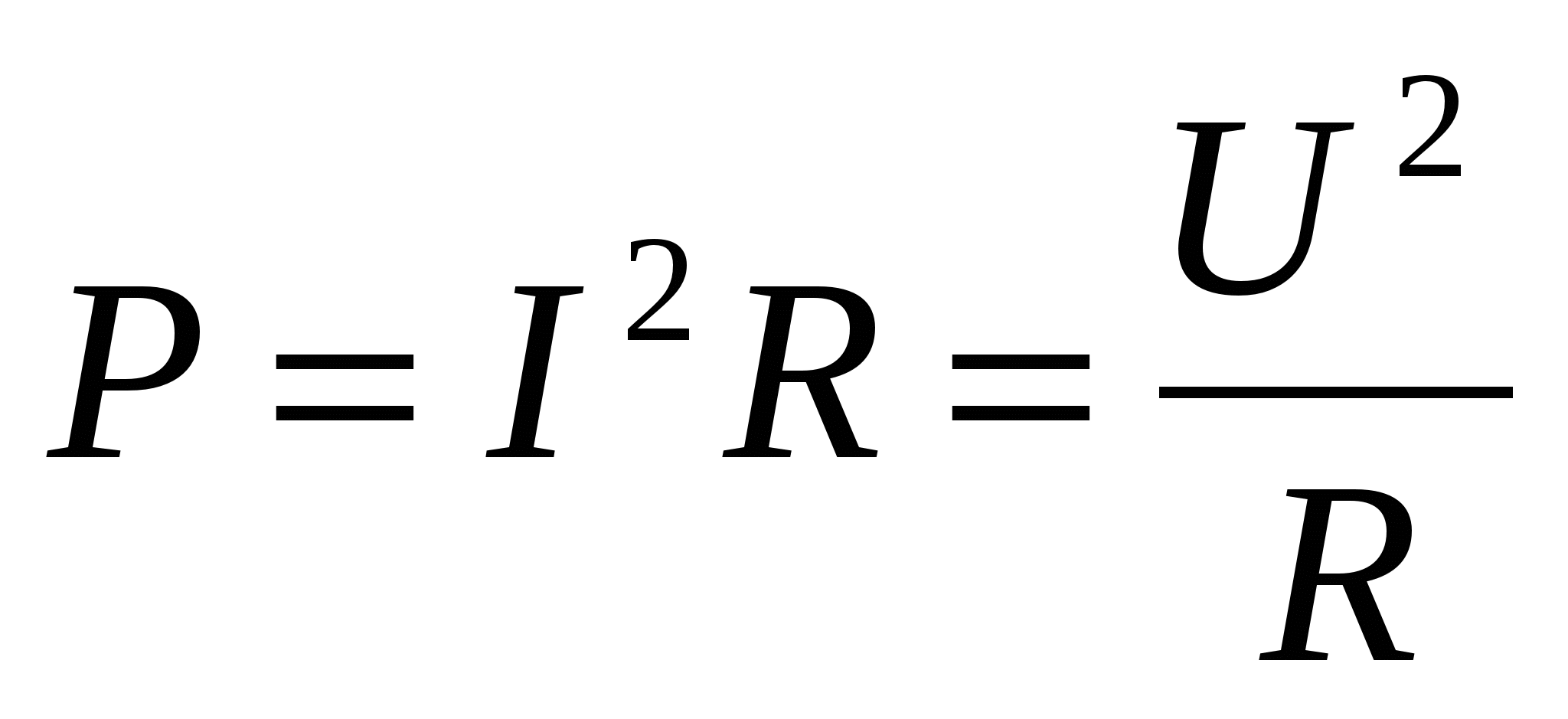
Для переменного тока тепловая мощность зависит от времени. Если ток изменяется сравнительно медленно, его называют квазистационарным. Условие квазистационарности будет сформулировано в разделе 30. В этом случае количество выделяющейся теплоты можно вычислить следующим образом:

, (11.18)
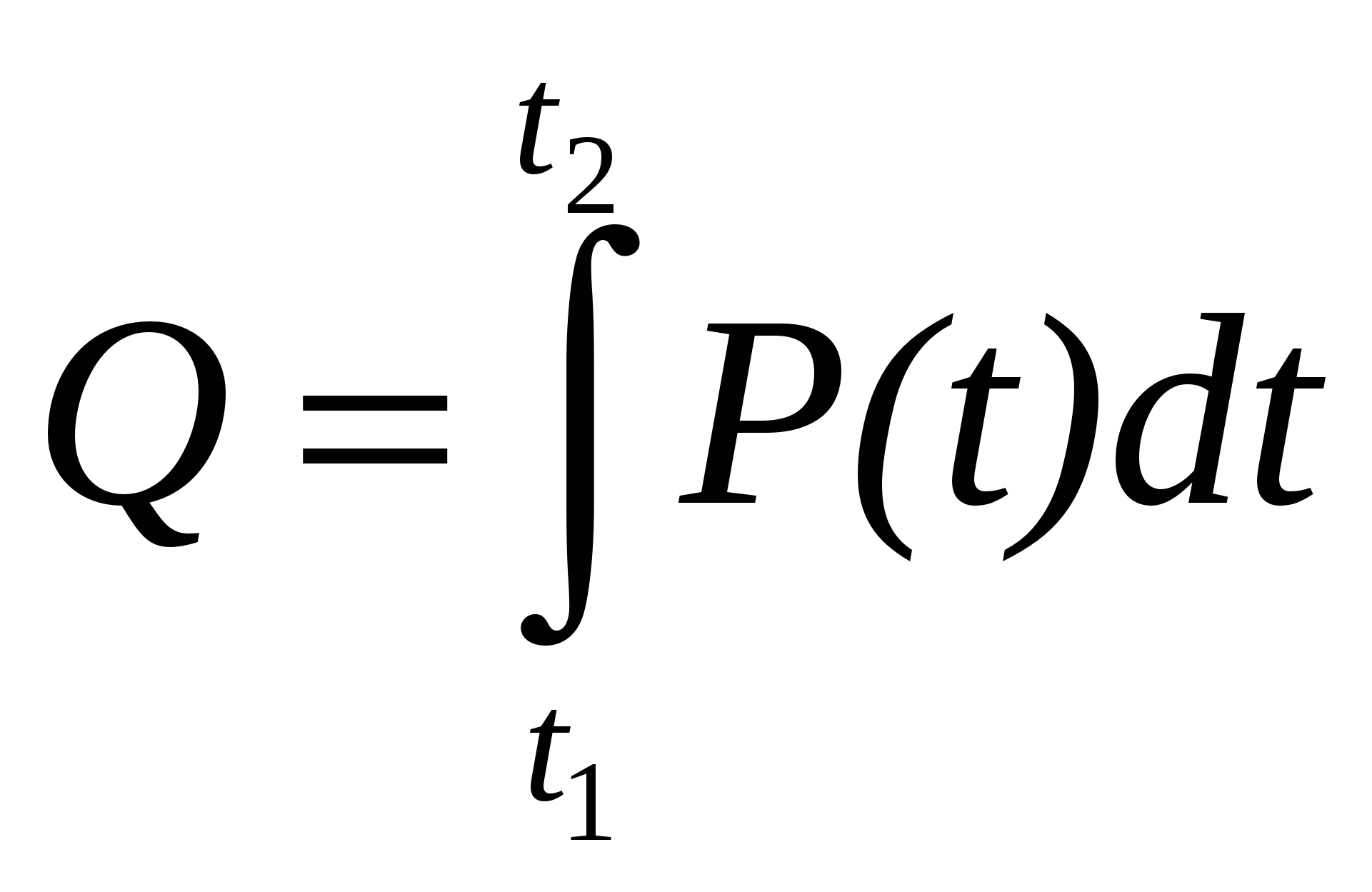
где и — начальный и конечный моменты времени.

Для постоянного тока тепловая мощность не зависит от времени, и интеграл в выражении (11.18) следует заменить произведением мощности на длительность рассматриваемого промежутка времени.

Закон Джоуля – Ленца

можно сформулировать также в дифференциальной форме.

Для этого необходимо ввести в рассмотрение объёмную плотность тепловой мощности тока

, то есть количество теплоты, выделяемой в единицу времени в единичном объеме проводника

Используя соотношение (11.16) и (11.19), получаем локальную формулировку закона Джоуля – Ленца:

. (11.20)
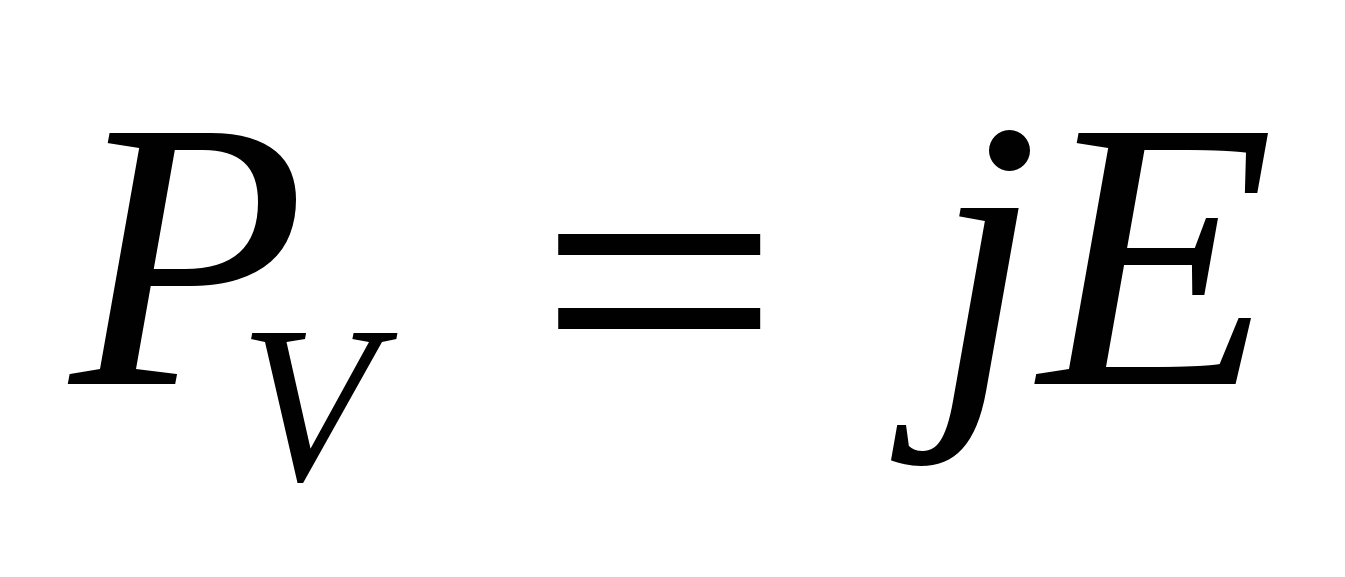
Учитывая закон Ома (10.11), закон Джоуля – Ленца в дифференциальной форме можно записать также следующим образом

. (11.21)
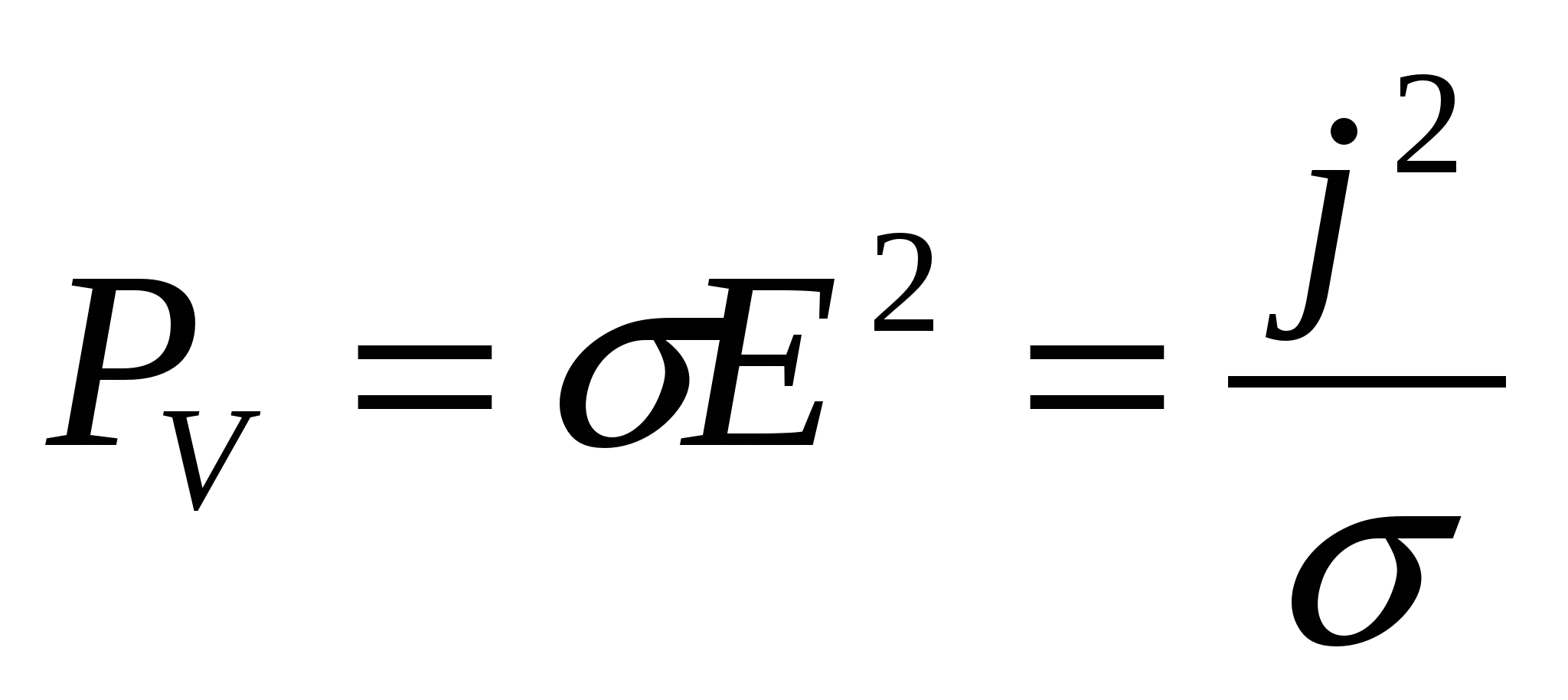
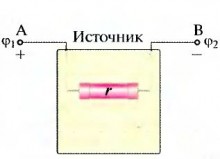
Д ля выяснения физического смысла формулы (11.20) введём в рассмотрение объёмную плотность силы, действующей со стороны электрического поля на свободные заряды

Если на концах какого-нибудь провод-ника AB создать разность потенциалов (рис. 5.16), то в нем возникнет электрическое поле напряженностью E̅.

Под действием этого поля свободные за-ряженные частицы (в металлах — это сво-бодные электроны) будут двигаться в опре-деленном направлении, не прекращая сво-его хаотического движения, создавая кратко-временный ток.

Тем не менее, на практике в подавляющем большинстве случаев необходимо иметь ток в проводниках на протяжении продолжитель-ного времени. Для этого на концах провод-ника разность потенциалов необходимо под-держивать неизменной.
Эту функцию в элект-рических цепях выполняют источники тока.

Любой источник тока имеет два полюса: положительный и отрицательный. Источ-ник, как и любой другой проводник, имеет свое сопротивление r,
которое называется внутренним сопротивлением
(рис. 5.17).

На полюсах источника на протяжении продолжительного времени существует раз-ность потенциалов. Но почему же в таком случае не возникает ток в самом источнике? В самом деле, на полюсах батареи для кар-манного фонарика довольно долго сущест-вует разность потенциалов, однако ток воз-никает лишь тогда, когда к полюсам бата-реи подсоединяется лампочка. Очевидно, что в источнике существуют какие-то силы, ко-торые стараются поддерживать разность потен-циалов на его полюсах, противодействуют электрическим силам, стремящимся выров-нять потенциалы на полюсах источника. Эти силы имеют неэлектрическое происхожде-ние, поэтому и называются сторонними.

Рис. 5.17. Источник тока

Сторонние силы обусловливают разде-ление разноименно заряженных частиц в источнике и поддерживают на его полюсах определенную разность потенциалов. В галь-ванических элементах разделение заряжен-ных частиц осуществляется за счет хими-ческой энергии, в термогенераторах — за счет тепловой и т.п.

Таким образом, сторонние силы внутри источника тока создают электрическое по-ле, которое называется полем сторонних сил
. Напряженность такого поля E ст. может измеряться силой, действующей на заря-женные частицы с суммарным зарядом в одну единицу. Материал с сайта

E ст. = F ст. / q.

Очевидно, что напряженности поля сто-ронних сил и электрических сил в источнике имеют противоположные направ-ления. Если внешняя часть цепи источника разомкнута, то напряженности обоих полей в источнике одинаковы и никакого тока в источнике нет.

Когда внешняя часть цепи ис-точника разомкнута, то напря-женность поля сторонних сил и электрических сил в источнике одинаковы по значению и про-тивоположны по направлению, поэтому и компенсируют друг друга.

Таким образом, роль источника сводится к разделению разноименно заряженных ча-стиц и к накоплению их на полюсах источ-ника.

Смещение под действием электрического поля зарядов в проводнике всегда происходит таким образом, что электрическое поле в проводнике исчезает и ток прекращается. Для протекания тока в течение продолжительного времени на заряды в электрической цепи должны действовать силы, отличные по природе от сил электростатического поля, такие силы получили название сторонних сил.

Представим стороннюю силу Fст, действующую на заряд q, в виде

Природа сторонних сил может быть различной. Источники постоянного тока могут быть основаны на химическом (гальванические элементы и аккумулятоpы) или тепловом (теpмопаpы) действии. В гальванических элементах сторонние силы возникают за счет энергии химических реакций между электродами и электролитами Гальванические элементы и аккумуляторы преобразуют химическую энергию в электрическую. В генераторе сторонние силы образуются за счет механической энергии вращения ротора генератора и т.д.,термопары преобразуют внутреннюю энергию в электрическую, фотоэлементы — световую в электрическую.

Электродвижущая сила
(ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил, то есть любых сил неэлектрического происхождения, действующих в квазистационарных цепях постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль всего контура.По аналогии с напряжённостью электрического поля вводят понятие напряжённость сторонних сил vec E_{ex}, под которой понимают векторную физическую величину, равную отношению сторонней силы, действующей на пробный электрический заряд, к величине этого заряда. Тогда в замкнутом контуре L ЭДС будет равна:

Теория Бора
была крупным шагом в развитии атомной физики и явилась важным этапом в создании квантовой механики. Однако эта теория обладает внутренними противоречиями (с одной стороны, применяет законы классической физики, а с другой основывается на квантовых постулатах). В теории Бора рассмотрены спектры атома водорода и водородоподобных систем и вычислены частоты спектральных линий, однакоэта теория не смогла объяснить интенсивности спектральных линий и ответить на вопрос: почему совершаются те или иные переходы? Серьезным недостатком теории Бора была невозможность описания с ее помощью спектра уже атома гелия — одного из простейших атомов, непосредственно следующего за атомом водорода.

Второй постулат Бора (правило частот): при переходе электрона с одной стационарной орбиты на другую излучается (поглощается) один фотон с энергией

h E E , ν = n − m (19.6)

равной разности энергий соответствующих стационарных состояний (Еn и Еm — соответственно энергии стационарных состояний атома до и после излучения (поглощения)). При Еm<Еn происходит излучение фотона (переход атома из состояния с большей энергией в состояние с меньшей энергией, т. е. переход электрона с более удаленной от ядра орбиты на более близлежащую), при Еm>Еn — его поглощение (переходатома в состояние с большей энергией, т. е. переход электрона на более удаленную отядра орбиту). Набор возможных дискретных частот v=(En -Em)/ h квантовых переходов и определяет линейчатый спектр атома.

Переме́нный ток
(англ. alternatingcurrent) — электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным. Условное обозначение на электроприборах: thicksim или thickapprox (знак синусоиды), или латинскими буквами AC.

Величина, обратная периоду, называется частотой
переменного тока:

Частота переменного тока;

Период переменного тока.

Источник