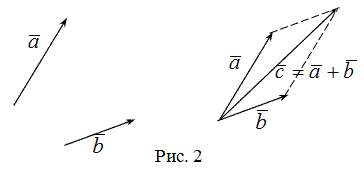
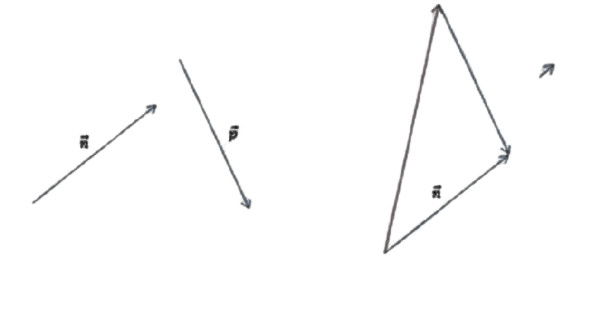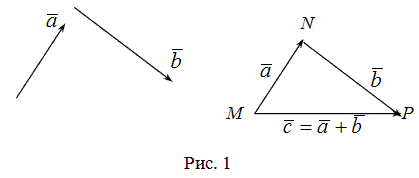Определение разности двух векторов
В математике и физике студентам и школьникам зачастую попадаются задачи на векторные величины и на выполнение различных операций над ними. В чём же отличие векторных величин от привычных нам скалярных, единственная характеристика которых — это численное значение? В том, что они обладают направлением.
[block >
Определения векторной математики
Введём главные определения, используемые при выполнении линейных операций.
- Вектором называют направленный (имеющий точку начала и точку конца) отрезок.
- Длина (модуль) — это длина направленного отрезка.
- Коллинеарными называют такие два вектора, которые либо параллельны одной и той же прямой, либо одновременно лежат на ней.
- Противоположно направленными векторами называют коллинеарные и при этом направленные в разные стороны. Если же их направление совпадает, то они являются сонаправленными.
- Вектора являются равными, когда они сонаправлены и одинаковы по модулю.
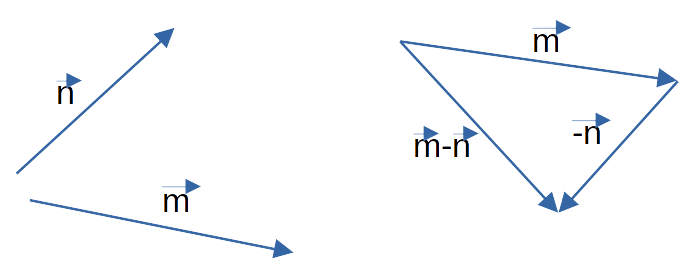
- Суммой двух векторов a и b является такой вектор c, начало которого совпадает с началом первого, а конец — с концом второго при условии, что b начинается в той же точке, в которой заканчивается a.
- Разностью векторов a и b называют сумму a и (—b), где (—b) — противоположно направленный к вектору b. Также определение разности двух векторов может быть дано следующее: разностью c пары векторов a и b называют такой c, который при сложении с вычитаемым b образует уменьшаемое a.
Аналитический метод
Аналитический способ подразумевает получение координат разности по формуле без построения. Возможно выполнить вычисление для плоского (двухмерного), объёмного (трёхмерного) или же n-мерного пространства.
Для двухмерного пространства и векторных величин a <a₁; a₂> и b <b₁; b₂> расчёты будут иметь следующий вид: c <c₁; c₂> = <a₁ — b₁; a₂ — b₂>.
В случае с добавлением третьей координаты расчёт будет проводиться аналогично, и для a <a₁; a₂; a₃> и b <b₁; b₂; b₃> координаты разности будут также получены попарным вычитанием: c <c₁; c₂; c₃> = <a₁ — b₁; a₂ — b₂; a₃ — b₃>.
Вычисление разности графически
Для того чтобы построить разность графическим способом, следует воспользоваться правилом треугольника. Для этого необходимо выполнить следующую последовательность действий:
- По заданным координатам построить векторы, для которых нужно найти разность.
- Совместить их концы (т. е. построить два направленных отрезка, равных заданным, которые будут оканчиваться в одной и той же точке).
- Соединить начала обоих направленных отрезков и указать направление; результирующий будет начинаться в той же точке, где начинался вектор, являющийся уменьшаемым, и заканчиваться в точке начала вычитаемого.
[block > Результат операции вычитания показан на рисунке ниже.
Также существует метод построения разности, незначительно отличающийся от предыдущего. Его суть заключается в применении теоремы о разности векторов, которая формулируется следующим образом: для того чтобы найти разность пары направленных отрезков, достаточно найти сумму первого из них с отрезком, противоположно направленным ко второму. Алгоритм построения будет иметь следующий вид:
- Построить исходные направленные отрезки.
- Тот, что является вычитаемым, необходимо отразить, т. е. построить противоположно направленный и равный ему отрезок; затем совместить его начало с уменьшаемым.
- Построить сумму: соединить начало первого отрезка с концом второго.
Результат такого решения изображён на рисунке:
Решение задач
Для закрепления навыка разберём несколько заданий, в которых требуется рассчитать разность аналитически или графически.
Задача 1. На плоскости заданы 4 точки: A (1; —3), B (0; 4), C (5; 8), D (—3; 2). Определить координаты вектора q = AB — CD, а также рассчитать его длину.
Решение. Вначале следует найти координаты AB и CD. Для этого из координат конечных точек вычтем координаты начальных. Для AB началом является A (1; —3), а концом — B (0; 4). Рассчитаем координаты направленного отрезка:
Аналогичный расчёт выполняется для CD:
Теперь, зная координаты, можно найти разность векторов. Формула для аналитического решения плоских задач была рассмотрена ранее: для c = a — b координаты имеют вид <c₁; c₂> = <a₁ — b₁; a₂ — b₂>. Для конкретного случая можно записать:
Чтобы найти длину q, воспользуемся формулой | q | = √(q₁² + q₂²) = √((— 9)² + (— 1)²) = √(81 + 1) = √82 ≈ 9,06.
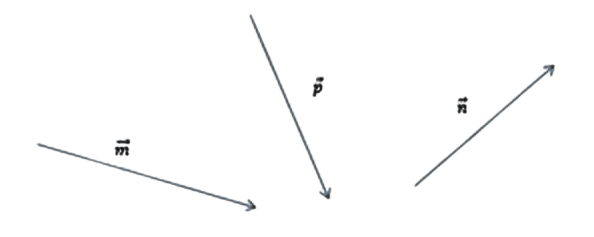
[block > Задача 2. На рисунке изображены векторы m, n и p.
Необходимо построить для них разности: p — n; m — n; m — n — p. Выяснить, какая из них обладает наименьшим модулем.
Решение. В задаче требуется выполнить три построения. Рассмотрим каждую часть задания более подробно.
Часть 1. Для того чтобы изобразить p — n, воспользуемся правилом треугольника. Для этого при помощи параллельного переноса соединим отрезки так, чтобы совпала их конечная точка. Теперь соединим начальные точки и определим направление. В нашем случае вектор разности начинается там же, где и вычитаемый n.
Часть 2. Изобразим m — n. Теперь для решения воспользуемся теоремой о разности векторов. Для этого следует построить вектор, противоположный n, а затем найти его сумму с m. Полученный результат будет выглядеть так:
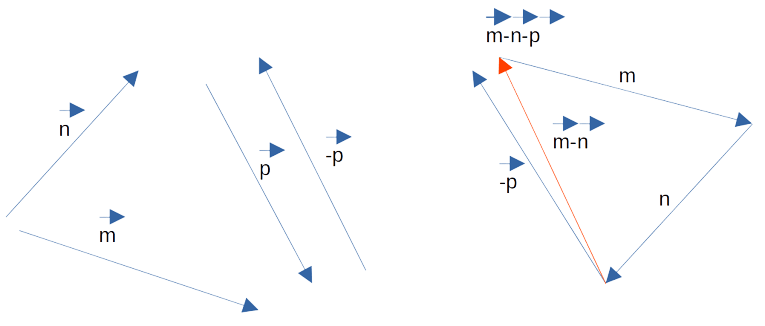
[block > Часть 3. Для того чтобы найти разность m — n — p, следует разбить выражение на два действия. Поскольку в векторной алгебре действуют законы аналогичные законам арифметики, то возможны варианты:
- m — (n + p): в этом случае вначале строится сумма n + p, которая затем вычитается из m;
- (m — n) — p: здесь сначала нужно найти m — n, а затем отнять от этой разности p;
- (m — p) — n: первым действием определяется m — p, после чего из полученного результата нужно вычесть n.
Так как в предыдущей части задачи мы уже нашли разность m — n, нам остаётся лишь вычесть из неё p. Построим разность двух данных векторов при помощи теоремы о разности. Ответ показан на изображении ниже (красным цветом обозначен промежуточный результат, а зелёным — окончательный).
Остаётся определить, модуль какого из отрезков является наименьшим. Вспомним, что понятия длины и модуля в векторной математике являются идентичными. Оценим визуально длины p — n, m — n и m — n — p. Очевидно, что самым коротким и обладающим наименьшим модулем является ответ в последней части задачи, а именно m — n — p.
[block > [block >
Сумма и разность векторов
В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.
Сумма векторов
Сложение векторов выполняется по правилу треугольника.
Геометрическая интерпретация:
Суммой a и b является вектор c , начало которого совпадает с началом a , а конец – с концом b . При этом конец вектора a должен совпадать с началом вектора b .
Для сложения векторов также используется правило параллелограмма.
Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c , совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.
Формула сложения векторов
Элементы вектора c равняются попарной сумме соответствующих элементов a и b .
» data-lang=»default» data-override=»<«emptyTable»:»»,»info»:»»,»infoEmpty»:»»,»infoFiltered»:»»,»lengthMenu»:»»,»search»:»»,»zeroRecords»:»»,»exportLabel»:»»,»file»:»default»>» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>
| Для плоских задач | a + b = x + bx; ay + by> |
| Для трехмерных задач | a + b = x + bx; ay + by; az + bz> |
| Для n-мерных векторов | a + b = 1 + b1; a2 + b2; . an + bn> |
Свойства сложения векторов
1. Коммутативность: a + b = b + a
2. Ассоциативность: ( a + b ) + c = a + ( b + c )
3. Прибавление к нулю: a + 0 = a
4. Сумма противоположных векторов: a + (- a ) = 0
Примечание: Вектор – a коллинеарен и равен по длине a , но имеет противоположное направление, из-за чего называется противоположным.
Разность векторов
Для вычитания векторов также применяется правило треугольника.
Если из вектора a вычесть b , то получится c , причем должно соблюдаться условие:
Формула вычитания векторов
Элементы вектора c равны попарной разности соответствующих элементов a и b .
» data-lang=»default» data-override=»<«emptyTable»:»»,»info»:»»,»infoEmpty»:»»,»infoFiltered»:»»,»lengthMenu»:»»,»search»:»»,»zeroRecords»:»»,»exportLabel»:»»,»file»:»default»>» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>
| Для плоских задач | a — b = x — bx; ay — by> |
| Для трехмерных задач | a — b = x — bx; ay — by; az — bz> |
| Для n-мерных векторов | a — b = 1 — b1; a2 — b2; . an — bn> |
Примеры задач
Задание 1
Вычислим сумму векторов и .
Задание 2
Найдем разность векторов и .
Как найти разность векторов
Формула
Примеры нахождения разности векторов
Задание. Найти разность векторов $bar-bar$, где $bar=(3 ; 0)$ и $bar=(1 ; 2)$
Решение. Для нахождения разности векторов $bar$ и $bar$, вычтем их соответствующие координаты:
Решение. Для нахождения искомой разности векторов вычтем их соответствующие координаты:
Остались вопросы?
Здесь вы найдете ответы.
Поможем выполнить
любую работу
Все еще сложно?
Наши эксперты помогут разобраться
Не получается написать работу самому?
Доверь это кандидату наук!
Ищещь ответ на вопрос с которым нужна помощь?
http://www.webmath.ru/poleznoe/formules_13_2.php
Радиус-вектор
Можно встретить удачные и неудачные жилые массивы: в первых ветра практически нет, независимо от погоды, а во вторых, наоборот, есть почти всегда. Это зависит от того, были ли учтены при проектировании направление и сила ветра, который преимущественно дует в данном районе. Эту информацию нужно использовать при строительстве не только жилых районов, но и аэродромов, дорог и т. д.
Чтобы ее получить, на основании многолетних наблюдений, наносят направления ветра на так называемую розу ветров (см. рис. 1). Чем чаще дует ветер в данном направлении, тем дальше соответствующая точка от точки (см. рис. 2).
Рис. 1. Роза ветров
Рис. 2. Чем чаще дует ветер в данном направлении, тем дальше соответствующая точка от точки
Рассмотрим декартову систему координат с центром в точке на плоскости. Соединяя точку
с точкой розы ветров вдоль выбранного направления
получаем вектор, который называется радиус-вектором (см. рис. 3) (чем длиннее радиус-вектор, тем чаще ветер в данной местности дует вдоль его направления).
Рис. 3. Радиус-вектор
Название «радиус-вектор» понятно – как и радиус окружности, начало любого радиус-вектора зафиксировано в одной точке, центре (начале координат) (см. рис. 4).
Рис. 4. Начало любого радиус-вектора зафиксировано в начале координат
Координаты радиус-вектора
Как описать этот вектор алгебраически? Любой точке на плоскости будет соответствовать ровно один радиус-вектор (см. рис. 5) (говорят, что точка и радиус-вектор
однозначно задают друг друга).
Рис. 5. Любой точке на плоскости соответствует ровно один радиус-вектор
Сама же точка однозначно задается своими координатами. Т. е. координаты точки
задают и саму точку, и радиус-вектор
(см. рис. 6).
Рис. 6. Координаты точки
задают и саму точку, и радиус-вектор
Но тогда почему бы координаты точки не принять и за координаты радиус-вектора
? Именно так мы и поступим. Будем называть координатами радиус-вектора
координаты
его конца
:
Координаты произвольного вектора
Мы говорили, что векторы равны (см. рис. 7), если у них равны длины и они сонаправлены:
Рис. 7. Равные векторы и
Понятно, что у равных векторов должны быть равны и координаты:
Рассмотрим произвольный вектор (см. рис. 8).
Рис. 8. Произвольный вектор
Построим вектор так, чтобы:
Получаем параллелограмм (см. рис. 9) (по признаку – две противоположные стороны равны и параллельны).
Рис. 9. Параллелограмм
Векторы (по построению), значит, координаты вектора
равны координатам радиус-вектора
и, соответственно, равны координатам точки
:
Как видим, любому вектору на плоскости можно поставить в соответствие упорядоченную пару чисел – его координаты.
Однозначное определение координат вектора
Понятно, что координаты вектора должны однозначно определяться координатами его конца и начала (т. к. начало и конец задают сам вектор).Попробуем определить, как именно.
Пусть точки и
из нашего предыдущего примера имеют координаты, соответственно,
и
. Вычислим координаты точки
, такой что радиус-вектор
(см. рис. 10).
Рис. 10. Радиус-вектор , где
,
Чтобы из точки попасть в точку
, нужно передвинуться на
единиц вправо и на
вверх (см. рис. 11).
Рис. 11. Путь из точки в точку
Такое же перемещение из начала координат приведет нас в точку (см. рис. 12).
Рис. 12. Путь из точки в точку
Значит, координаты радиус-вектора . Тогда и координаты равного ему вектора
.
Уберем вспомогательный радиус-вектор и попробуем определить координаты вектора
без его помощи. Чтобы переместиться их точки
в точку
, нам нужно переместиться на
единиц вправо и на
вверх – это и будут координаты вектора
(см. рис. 13).
Рис. 13. Чтобы переместиться их точки в точку
, нужно переместиться на
единиц вправо и на
вверх
Связанные и свободные векторы
Чтобы определить координаты радиус-вектора , нам было достаточно двух чисел – координат точки
. Чтобы определить координаты произвольного вектора
– уже четыре числа: координаты точек
и
. Есть ли в этом противоречие?
Конечно, нет. В определении радиус-вектора уже «спрятаны» две дополнительные координаты – его начало всегда совпадает с точкой , координаты которой мы знаем –
. Если перемещение из точки
в точку
по горизонтали мы искали как разность:
, то из точки
в точку
, как
. Но т. к. вычитание нуля не меняет число, то мы приравняли координаты радиус-вектора к координатам его конца (в этом удобство радиус-векторов).
Однако все же здесь есть о чем поговорить. Мы поставили в соответствие любому вектору на плоскости упорядоченную пару чисел – его координаты. Однако, вектор – направленный отрезок, который задается началом и концом. Но в этом случае, чтобы определить вектор, нужно знать четыре числа – координаты начала и конца. Так, набором из скольких чисел определяется вектор – из или
?
Рассмотрим пример из физики. Если в задаче мы можем рассматривать тело как материальную точку, то суммируем силы, которые на него действуют, независимо от точек их приложения (см. рис. 14).
Рис. 14. Если тело можно рассматривать как материальную точку, то можно суммировать силы, которые на него действуют, независимо от точек их приложения
Если же тело нельзя рассматривать как материальную точку (например, при вычислении вращающего момента), то складывать силы без учета точек их приложения уже нельзя (см. рис. 15).
Рис. 15. Если тело нельзя рассматривать как материальную точку, то нельзя суммировать силы, которые на него действуют, без учета точек их приложения
В первом случае силу можно рассматривать как пример так называемого свободного вектора, у которого начальную точку можно выбирать произвольно (или, что то же самое, которую можно произвольно переносить параллельно самим себе).
А во втором – уже как пример связанного вектора, у которого начальная точка фиксирована.
Понятно, что свободные векторы и
– это не просто равные, а одинаковые векторы. А связанные векторы
и
– нет (т. к. у них разные начала). Поэтому для задания свободного вектора нужно гораздо меньше информации, чем для задания связанного. Действительно, связанный вектор можно задать двумя элементами: точкой отсчета и свободным вектором, который от нее откладывается (отсюда
числа).
Все операции для свободных и связанных векторов определены одинаково. Единственное, для связанных векторов некоторые операции не определены, например сложение векторов с разными началами. Поэтому часто тип вектора явно не указывается.
В математике мы будем работать именно со свободными векторами (если не оговорено иное).
Нахождение координат вектора
Рассмотрим вектор (см. рис. 16).
Рис. 16. Вектор
Движемся из начала в конец: единица вправо и
единицы вверх. Координаты вектора (см. рис. 17):
Рис. 17. Вектор
Чтобы попасть из точки в точку
, двигаемся на
единицы вправо и на
вниз. Направление вниз у нас отрицательное, следовательно, координаты вектора (см. рис. 18):
Рис. 18. Вектор
Чтобы попасть из точки в точку
, двигаемся на
единиц влево (а это отрицательное направление оси
) и на
вверх (положительное направление). Координаты вектора (см. рис. 19):
Рис. 19. Вектор
Правило определения координат вектора по координатам его концов
Как мы уже сказали, у равных векторов координаты равны. Поэтому при определении координат неважно, где находится вектор, важны его длина и направление.
Мы сказали, что вектор однозначно задается началом и концом. Значит, по координатам этих двух точек можно определить координаты вектора. Как это сделать?
Рассмотрим вектор , где
, и найдем его координаты (см. рис. 20).
Рис. 20. Вектор ,
Движемся из точки на
единицы вправо (положительное направление) и на
вверх (тоже положительное направление), получаем координаты вектора (см. рис. 21):
Рис. 21. Вектор
Абсцисса точки равна
, а точки
равна
. Мы двигались вправо на
единицы, потому что
. Это и есть первая координата вектора. Аналогично разность ординат двух точек:
. Это и есть вторая координата.
Получаем правило определения координат вектора по координатам его концов: координаты вектора равны разности соответствующих координат конца и начала вектора:
Вернемся к трем рассмотренным векторам из предыдущего примера.
1. :
Тогда:
2. :
Тогда:
3. :
Тогда:
Итак, чтобы найти координаты вектора, надо из координат конца вычесть координаты начала.
Пользуясь этим алгоритмом, несложно найти координаты нуль-вектора (у которого, напомним, начало и конец совпадают) – они равны .
Пусть даны координаты вектора . Изобразим его (см. рис. 22).
Рис. 22. Вектор
Мы не знаем, где он находится. Начало этого вектора может быть в любой точке. Например, он может быть радиус-вектором и начинаться в точке . Тогда его конец будет в точке
.
Рис. 23. Вектор , где
Или он может начинаться в точке . Прибавим к координатам начала координаты векторы:
Координаты точки (см. рис. 24).
Рис. 24. Вектор , где
Обратите внимание, что мы пользуемся для нахождения координат конца следствием из сформулированного правила:

Теперь у нас есть две интерпретации вектора:
- геометрическая: вектор – это направленный отрезок;
- алгебраическая: если задана система координат, то вектор на плоскости – это упорядоченная пара чисел.
Теперь мы можем использовать обе интерпретации при работе с векторами.
Длина вектора
Раз вектор однозначно определяется своими координатами, то по ним можно вычислить и главную его характеристику – длину. Вспомним, что длина вектора равна длине отрезка с теми же концами.
Но на прошлом уроке мы доказывали, что длина отрезка , у которого
, равна:
Но – координаты вектора
. Получаем, что длина вектора
равна квадратному корню из суммы квадратов его координат:
Эту же формулу можно получить и по-другому: если построить прямоугольный треугольник, у которого вектор – это гипотенуза, то его катеты – это длины проекций вектора на оси координат, т. е. модули координат вектора (см. рис. 25).
Рис. 25. Прямоугольный треугольник, у которого вектор – гипотенуза, а катеты – модули координат вектора
Тогда достаточно использовать теорему Пифагора, чтобы получить формулу:
Например, длина вектора равна:
Координаты суммы векторов
Рассмотрим теперь различные операции с векторами. Мы уже умеем складывать векторы геометрически, используя правила треугольника или параллелограмма.
Вот два вектора (см. рис. 26): начало вектора имеет координаты
, а конец –
; начало вектора
имеет координаты
, конец –
.
Рис. 26. Векторы и
Нетрудно посчитать координаты каждого вектора: из координат конца вычитаем координаты начала:
Чтобы сложить эти два вектора по правилу треугольника, нужно перенести их так, чтобы конец одного совместился с началом другого. Переместим вектор так, чтобы его начало оказалось в начале координат. Его конец переместится тогда в точку
(см. рис. 27).
Рис. 27. Вектор перемещен так, что его начало находится в начале координат
Переместим в эту точку начало вектора (см. рис. 28).
Рис. 28. Начало вектора перемещено в конец вектора
– точку
Получим новый вектор, равный сумме по правилу треугольника (см. рис. 29).
Рис. 29. Сложение векторов по правилу треугольника
Т. к. новый вектор является радиус-вектором, то его координаты совпадают с координатами его конца. Как же найти эти координаты?
Найдем координаты конца вектора . Мы знаем координаты начала этого вектора –
. Знаем координаты самого вектора
. И знаем, что координаты вектора – это координаты конца минус координаты начала:
Тогда:
Получаем координаты точки . И, соответственно, координаты вектора:
Можно заметить, что координаты вектора суммы равны сумме координат исходных векторов: ,
. Это не случайность.
Пусть у нас есть произвольные векторы с координатами и
(см. рис. 30).
Рис. 30. Произвольные векторы и
Повторим те же операции, что и в рассмотренном примере: первый вектор отложим от начала координат, второй – от конца первого (см. рис. 31).
Рис. 31. Вектор отложен от начала координат, вектор
– от конца вектора
Тогда точка , точка
, координаты вектора
:
Получаем:
Итак, чтобы найти координаты суммы двух векторов, нужно сложить их соответствующие координаты:
Пример 1. Найти сумму векторов и
.
Решение.
Сумма векторов:
Ответ: .
Несложно доказать, что координаты суммы нескольких векторов – это суммы соответствующих координат всех векторов (например, если складываем три вектора – складываем любые два из них, получаем сумму уже двух векторов, их координаты снова нужно сложить – в итоге получаем сумму координат всех трех векторов).
Пример 2. Найти сумму векторов ,
и
.
Решение.
Получаем:
Ответ: .
Координаты разности векторов
С вычитанием дело обстоит ничуть не сложнее. Если для векторов выполняется:
То:
При этом:
Аналогично:
Получаем, что координаты разности двух векторов равны разностям соответствующих координат векторов:
Пример 3. Найти разность векторов и
.
Решение.
Получаем:
Ответ: .
Координаты вектора, умноженного на число
Что происходит с координатами вектора при умножении их на число? Умножим вектор на
. Вектор
в два раза длиннее вектора
и направлен в ту же сторону. Нетрудно увидеть, что каждая его координата тоже в два раза больше, чем у вектора
(см. рис. 32):
Рис. 32. Вектор в два раза длиннее вектора
Чтобы умножить вектор на число, нужно обе координаты вектора умножить на это число:
Это, скорее, геометрическое рассуждение. Но тот же результат можно получить и алгебраически:
Теперь мы можем сказать, что вектор:
Свойства операций с векторами
В качестве самостоятельного упражнения докажите следующие свойства операций с векторами:
При объяснении попробуйте это сделать с двух точек зрения:
- геометрической (с помощью изображения векторов как направленных отрезков, правил треугольника и параллелограмма, геометрического смысла умножения вектора на число);
- алгебраической (с помощью координат, правил сложения координат векторов, умножения координат на число).
Чтобы проверить себя или узнать доказательство свойств, которые вызвали у вас затруднения, ознакомьтесь с доказательствами ниже.
Доказательство свойств
1. .
В координатах все просто:
Верно.
Геометрическое доказательство также не составит труда, если помнить, что у нуль-вектора начало и конец совпадают (дальше можно использовать правило треугольника для сложения векторов) (см. рис. 33):
Рис. 33. Правило треугольника
2. .
Геометрическое доказательство можно провести с использованием правила параллелограмма (совместив начала векторов) – в обоих случаях получится один и тот же параллелограмм, а значит, и диагонали будут одинаковыми (см. рис. 34).
Рис. 34. Правило параллелограмма
В координатах все тоже несложно:
3. .
Геометрическое доказательство можно провести, дважды используя правило треугольника (см. рис. 35).
Рис. 35. Использование правила треугольника дважды
По пути мы начали доказывать обобщение правила треугольника – правило многоугольника. Сумма векторов, конец каждого из которых является началом следующего, – это вектор, соединяющий начало первого вектора с концом последнего.
В координатах все легко:
Верно.
4. .
В координатах все легко:
Геометрически: при умножении на число векторы сонаправлены (значит, правый и левый векторы сонаправлены) (см. рис. 36).
Рис. 36. Сонаправленные векторы
Длины обоих векторов будут равны:
Значит, векторы равны (равны длины и сонаправлены).
5. .
В координатах:
Аналогично:
Геометрически: при умножении на число векторы сонаправлены (значит, левый и правый векторы сонаправлены). Длина левого вектора:
Длина правого вектора:
Значит, векторы равны (равны длины и сонаправлены).
6. .
Геометрически: сначала складываем векторы, затем умножаем на – удлиняем диагональ в
раз. Справа – сначала удлиняем стороны параллелограмма, затем строим диагональ – получается та же диагональ, значит, векторы равны (см. рис. 37).
Рис. 37. Равные векторы и
В координатах:
Список литературы
- Александров А.Д., Вернер А.Л., Рыжик В.И. Геометрия, 9 класс. Учебник. – М.: «Просвещение», 2017.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В./Под ред. Садовничего В.А. Геометрия, 9 класс. Учебник. – М.: «Просвещение», 2018.
- Мерзляк А.Г., Полонский В.Б., Якир М.С., Геометрия, 9 класс. Учебник. – М.: издательский центр «ВЕНТАНА-ГРАФ», 2018.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал yaklass.ru (Источник)
- Интернет-портал ru.solverbook.com (Источник)
- Интернет-портал cleverstudents.ru (Источник)
Домашнее задание
1. Найти координаты и длину вектора , если
.
2. Найти координаты векторов, если
.
3. Упростить выражение:
Вычитание векторов
Содержание:
- Как происходит вычитание векторов
- Как производится вычитание векторов по координатам
-
Основные правила вычисления
- Правило треугольника
- Правило параллелограмма
- Примеры задач на понятие разности векторов
Как происходит вычитание векторов
Определение
Вычитание векторов — это арифметическое действие в геометрии, при котором из одного вектора отнимают другой.
Чтобы вычесть (overrightarrow b) из (overrightarrow а), нужно найти такой (overrightarrow с), сложение которого с вектором (overrightarrow b) составляло бы (overrightarrow а).
Таким образом, формула разности будет выглядеть так:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
(overrightarrow а-overrightarrow b=overrightarrow а+left(-overrightarrow bright))
Если задан (overrightarrow а), то можно построить противоположный ему (-overrightarrow а), равный по длине, но противоположно направленный. Тогда происходит сведение двух противоположно направленных векторов к нулевому:
(overrightarrow а+left(-overrightarrow аright)=0)
Как производится вычитание векторов по координатам
Если необходимо произвести вычитание векторов по координатам, то следует просто вычесть соответствующие точки. То есть если из (overrightarrow а) отнимается (overrightarrow b), то из X1 отнимаем X2, из Y1 Y2 и из Z1 Z2.
Проиллюстрируем координатное пространство:
Основные правила вычисления
Для того, чтобы найти значение разности векторов, можно использовать несколько способов.
Правило треугольника
Чтобы графически продемонстрировать разность, необходимо отложить от произвольной точки вектор (overrightarrow а), из его начала (overrightarrow b). Тогда вектор, начало которого совпадает с концом ( overrightarrow b), а конец — с концом (overrightarrow a), и будет искомым вектором разности (overrightarrow a;-;overrightarrow b). Проиллюстрируем это:
Правило параллелограмма
Если два неколлинеарных, то есть непараллельных вектора (overrightarrow а) и (overrightarrow b) имеют общее начало, то их разностью является вектор, совпадающий с диагональю параллелограмма, построенного на (overrightarrow а) и (overrightarrow b), причем начало этой диагонали совпадает с концом (overrightarrow b), а конец — с концом (overrightarrow а).
Если векторы (overrightarrow а) и (overrightarrow b) заданы в некотором промежутке:
(overrightarrow a=left(а_1;а_2right),;overrightarrow b=left(b_1;b_2right))
то, чтобы найти координаты их разности (overrightarrow a;-;overrightarrow b), необходимо от точек (overrightarrow a) отнять соответствующие точки (overrightarrow b):
(overrightarrow a;-;overrightarrow b=left(a_1;a_2right)-left(b_1;b_2right)=left(a_1-b_1;a_2-b_2right))
Проиллюстрируем правило многоугольника:
Примеры задач на понятие разности векторов
Задача 1
Дано
(overrightarrow a;=left(2;-1right),;overrightarrow b=left(0;2right))
Найти: (overrightarrow с=2overrightarrow a-3overrightarrow b;)
Решение
Найдем координаты (2overrightarrow a) и (3overrightarrow b). Для этого умножим каждую на два и три:
(2overrightarrow а=2timesleft(2;-1right)=left(2times2;2timesleft(-1right)right)=left(4;-2right), 3overrightarrow b=3timesleft(0;2right)=left(3times0;3times2right)=left(0;6right))
Тогда искомый вектор:
(overrightarrow с=2overrightarrow a-3overrightarrow b=left(4;-2right)-left(0;6right)=left(4-0;;-2-6right)=left(4;-8right))
Ответ: (overrightarrow с=left(4;-8right).)
Задача 2
Дано
(Аleft(1;-1;0right),;Вleft(2;3;-1right),;Сleft(0;-1;0right),;Dleft(1;0;2right))
Найти: координаты (overrightarrow{AB}-overrightarrow{CD}.)
Решение
Для начала найдем проекции (overrightarrow{AB}) и (overrightarrow{CD}).
Для этого от координат конца вектора, то есть точек B и D, нужно отнять соответствующие проекции его начала, то есть точек А и С.
(overrightarrow{AB}=left(2-1;3-left(-1right);-1-0right)=left(1;4;-1right),;overrightarrow{CD}=left(1-0;0-left(-1right);2-0right)=left(1;1;2right))
Тогда для нахождения координат разности (overrightarrow{AB}-overrightarrow{CD}), от координат первого вычтем координаты второго:
(overrightarrow{AB}-overrightarrow{CD}=left(1;4;-1right)-left(1;1;2right)=left(1-1;4-1;-1-2right)=left(0;3;-3right))
Ответ: (overrightarrow{AB}-overrightarrow{CD}=left(0;3;-3right))
Насколько полезной была для вас статья?
Рейтинг: 3.00 (Голосов: 4)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Для того, чтобы уяснить, что собой представляет разность векторов, введём понятие откладывания вектора от определённой точки и понятие суммы векторов.
Определение
Если некоторая точка A является началом вектора a, то говорят, что он является отложенным от точки A.
Теорема. От каждой точки можно отложить только один вектор, имеющий заданный модуль и направление. Докажем эту теорему.
Доказательство:
В случае, когда вектор нулевой, то теорема очевидна. Нулевые вектора в одной и той же точки совпадают между собой, т. е. являются одним и тем же вектором.
Сделаем построение. Точкой A обозначим начало вектора a, а точкой B его конец. Пусть у нас имеется некоторая точка K. Проведём через неё прямую b, которая параллельна вектору a. Отложим на данной прямой равные по своей абсолютной величине вектору a отрезки KL и KM. Из векторов, образованных этими отрезками искомым можно назвать только сонаправленный с a.
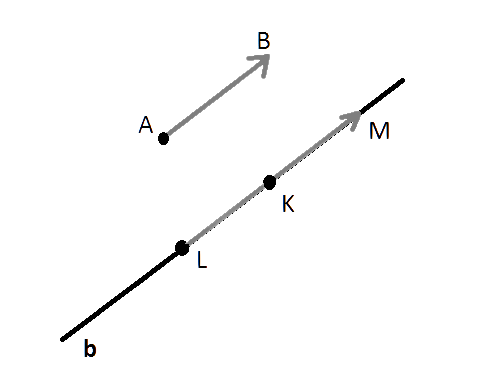
Единственность нашего вектора следует из того, что мы построили и видим.
Теорема доказана.
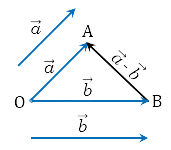
Определение
Суммой векторов a и b называется вектор с тем же началом, что вектор a и концом, как у вектора b. При этом вектор b должен начинаться в той же самой точке, в которой заканчивается вектор a.
Равные векторы, начинающиеся в разных точках, нередко обозначают одной и той же буквой. Иногда про подобные векторы говорят, как об одном и том же векторе, отложенном из разных мест.
Разность векторов
Определение
Разностью векторов a и b называется сумма вектора a c вектором, который противоположно направлен к вектору b.
По-другому это определение можно сформулировать следующим образом: разностью двух векторов a и b называется вектор c, который при сложении с вычитаемым b образует уменьшаемое, т. е. вектор a.
Формулами это записывается так:
b + c = a
a – b = c
Как найти разность векторов аналитическим способом
В двухмерном пространстве векторов a {x1, y1} и b {x2, y₂} разность векторов можно вычислить, как показано ниже:
c {x3, y3} = {x₁ — x2, y1 — y₂}.
Вычитание векторов в 3-мерном пространстве выглядит следующим образом:
c {x3; y3; z₃} = {x₁ — x2, y₂ — y₂, z1 — z2}.
Как найти разность векторов графическим способом
Нужно воспользоваться правилом треугольника. Последовательность действий следующая:
- Постройте по координатам векторы, для которых требуется найти разность;
- Совместите концы построенных векторов. Для этого нужно построить два равных заданным направленных отрезка, концы у которых будут в одной и той же точке;
- Соедините начала построенных отрезков и укажите их направление. Вектор c, называемый разностью векторов, будет иметь своё начало в той же точке, где начинается вектор, именуемый уменьшаемым и заканчивается в точке начала вычитаемого. Смотрите рисунок ниже.
Есть ещё один способ графического нахождения разности векторов. Он предусматривает следующий порядок действий:
- Постройте исходные направленные отрезки;
- Отразите вычитаемый отрезок. Для этого постройте противоположно направленный и равный ему отрезок и затем совместите начало этого отрезка с уменьшаемым;
- Постройте сумму, т. е. соедините начало первого отрезка и конец второго.
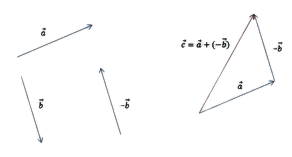
Нет времени решать самому?
Наши эксперты помогут!
Примеры вычисления разности векторов
Примеры
Вычислить вектор c, который представляет собой разность вектора a ={1;
2} и вектора b = {4; 8}.
Решение:
Действуем по выше указанному правилу
a — b = {1 — 4; 2 — 8} = {-3; -6}
Ответ: с{-3; -6}.
Вычислить вектор c, который является разностью векторов a = {1; 2; 5} и
b = {4; 8; 1}.
Решение:
Почти всё делается, как в уже рассмотренном примере, только добавляется третья координата.
a — b = {1 — 4; 2 — 8; 5 — 1} = {-3; -6; 4}
Ответ: c {-3; -6; 4}.
На рисунке векторы
Требуется построить разности: p — n, m —
n,m — n — p и найти ту из них, которая
имеет наименьший модуль.
Решение:
Для изображения p — n проще всего воспользоваться правилом треугольника. Параллельным переносом
отрезки
следует соединить таким образом, чтобы совпали их конечные точки. Далее нужно соединить начальные точки и
определить направление. В нашем случае вектор разности берёт своё начало там же, где и вычитаемый n.
Для изображения m — n правильнее будет воспользоваться вторым графическим способом нахождения разности
векторов. Сначала построим вектор противоположный n и найдём его суммы с вектором m.
Для нахождения разности m — n — p разобьём это выражение на два действия. Возможны следующие варианты:
- m — (n + p). Сначала нужно построить сумму,
затем уже вычесть её из m; - (m — n) — p. Сначала находим m — n,
осле этого от полученной разности отнимаем p; - (m— p) — n. Сначала определяем m — p, затем от
полученного результата отнимаем n.
Из вычислений выше нам известна разность m — n. Для получения решения нам нужно вычесть из неё
p.
Используя определение 3 построим разность векторов на рисунке. На нём изображён окончательный результат
и промежуточный.
Теперь нужно определить наименьший модуль. В нашем случае для этого можно лишь визуально оценить длины p — n,
m — n и m — n — p. Из построения сразу видно, что наименьшим модулем обладает вектор разности m — n —
p.
Сложение и вычитание векторов
Определение
Сложение
векторов
и
осуществляется
поправилу
треугольника.
Суммой
двух
векторов
и
называют
такой третий вектор,
начало которого совпадает с началом,
а конец — с концомпри
условии, что конец вектораи
начало векторасовпадают
(рис. 1).
Для
сложения векторов
применяется также правило параллелограмма.
Определение
Правило
параллелограмма
— если два неколлинеарных вектора
и
привести
к общему началу, то векторсовпадает
с диагональю параллелограмма, построенного
на векторахи
(рис.
2). Причем начало векторасовпадает
с началом заданных векторов.
Определение
Вектор
называетсяпротивоположным
вектором
к вектору
,
если онколлинеарен
вектору
,
равен ему по длине, но направлен в
противоположную сторону вектору.
Операция сложения векторов обладает следующими свойствами:
-
—
коммутативность -
—
ассоциативность -
-
Определение
Разностью
векторов
и
называется
вектортакой,
что выполняется условие:(рис.
3).
Умножение вектора на число
Определение
Произведением
вектора
на
число
называется
вектор,
удовлетворяющий условиям:
-
-
-
,
если
,
,
если.
Свойства умножения вектора на число:
Здесь
и
—
произвольные векторы,,
—
произвольные числа.
Евкли́дово
простра́нство
(также Эвкли́дово
простра́нство) —
в изначальном смысле, пространство,
свойства которого описываются аксиомами
евклидовой
геометрии.
В этом случае предполагается, что
пространство имеет размерность
равную 3.
В
современном понимании, в более общем
смысле, может обозначать один из сходных
и тесно связанных объектов: конечномерное
вещественное
векторное
пространство
с
введённым на нём положительно определённымскалярным
произведением,
либо метрическое
пространство,
соответствующее такому векторному
пространству. В этой статье за исходное
будет взято первое определение.
-мерное
евклидово пространство обозначается
также
часто используется обозначение(если
из контекста ясно, что пространство
обладает евклидовой структурой).
Для
определения евклидова пространства
проще всего взять в качестве основного
понятие скалярного
произведения.
Евклидово векторное пространство
определяется как конечномерное
векторное
пространство
над полем
вещественных
чисел,
на векторах которого задана
вещественнозначная
функция
обладающая
следующими тремя свойствами:
-
Билинейность:
для любых векторов
и
для любых вещественных чисели
-
Симметричность:
для любых векторов
-
Положительная
определённость: для любого
причём
Аффинное
пространство,
соответствующее такому векторному
пространству, называется евклидовым
аффинным пространством, или просто
евклидовым пространством[1].
Пример
евклидова пространства — координатное
пространство
состоящее
из всевозможныхn-ок
вещественных чисел
скалярное
произведение в котором определяется
формулой
-
Базис
и координаты вектора
Ба́зис
(др.-греч.
βασις, основа) — множество таких
векторов
в векторном
пространстве,
что любой вектор этого пространства
может быть единственным образом
представлен в виде линейной
комбинации
векторов из этого множества — базисных
векторов.
В
случае, когда базис бесконечен, понятие
«линейная комбинация» требует уточнения.
Это ведёт к двум основным разновидностям
определения:
-
Базис
Га́меля,
в определении которого рассматриваются
только конечные линейные комбинации.
Базис Гамеля применяется в основном в
абстрактной алгебре (в частности в
линейной алгебре). -
Базис
Ша́удера,
в определении которого рассматриваются
и бесконечные линейные комбинации, а
именно — разложение в ряды.
Это определение применяется в основном
в функциональном анализе, в частности
для гильбертова
пространства,
В
конечномерных пространствах обе
разновидности базиса совпадают.
Координа́ты
ве́ктора
― коэффициенты единственно возможной
линейной
комбинации
базисных
векторов
в выбранной системе
координат,
равной данному вектору.
где
—
координаты вектора.
-
Скалярное
произведение.
операция
над двумя векторами,
результатом которой является число
[когда рассматриваются векторы, числа
часто называют скалярами],
не зависящее от системы координат и
характеризующее длины векторов-сомножителей
и угол
между ними. Данной операции соответствует
умножение длины
вектора x
на проекцию
вектора y
на вектор x.
Эта операция обычно рассматривается
как коммутативная
и линейная
по каждому сомножителю.
Скалярное
произведение
двух векторов равно сумме произведений
их соответствующих координат:
-
Векторное
произведение
это
псевдовектор,
перпендикулярный
плоскости, построенной по двум
сомножителям, являющийся результатом
бинарной
операции
«векторное умножение» над векторами
в трёхмерном евклидовом
пространстве.
Векторное произведение не обладает
свойствами коммутативности
и ассоциативности
(является антикоммутативным)
и, в отличие от скалярного
произведения векторов,
является вектором. Широко используется
во многих технических и физических
приложениях. Например, момент
импульса
и сила
Лоренца
математически записываются в виде
векторного произведения. Векторное
произведение полезно для «измерения»
перпендикулярности векторов — модуль
векторного произведения двух векторов
равен произведению их модулей, если они
перпендикулярны, и уменьшается до нуля,
если векторы параллельны либо
антипараллельны.
-
Векторное
произведение
двух векторов можно вычислить с помощью
определителя
матрицы
где
-
Смешанное
произведение
Сме́шанное
произведе́ние
векторов
—скалярное
произведение
вектора
навекторное
произведение
векторов
и
:
.
Иногда
его называют тройным
скалярным произведением
векторов, по всей видимости из-за того,
что результатом является скаляр
(точнее — псевдоскаляр).
Геометрический
смысл:
Модуль смешанного произведения численно
равен объёму параллелепипеда,
образованного векторами
.смешанное
произведение
трех векторов можно найти через
определитель
-
Плоскость
в пространстве
Плоскость —
алгебраическая
поверхность
первого порядка: в декартовой
системе координат
плоскость может быть задана уравнением
первой степени.
Некоторые
характеристические свойства плоскости
-
Плоскость —
поверхность,
содержащая полностью каждую прямую,
соединяющую любые её точки; -
Две
плоскости являются либо параллельными,
либо пересекаются по прямой. -
Прямая
либо параллельна плоскости, либо
пересекает ее в одной точке, либо
находится на плоскости. -
Две
прямые, перпендикулярные одной и той
же плоскости, параллельны друг другу. -
Две
плоскости, перпендикулярные одной и
той же прямой, параллельны друг другу.
Аналогично
отрезку
и интервалу,
плоскость, не включающую крайние точки,
можно назвать интервальной плоскостью,
или открытой плоскостью.
-
Общее
уравнение (полное) плоскости
где
и
—
постоянные, причёми
одновременно
не равны нулю; ввекторной
форме:
где
—
радиус-вектор точки,
векторперпендикулярен
к плоскости (нормальный вектор).Направляющие
косинусы
вектора
:
-
Уравнение
плоскости в отрезках:
где
,
,
—
отрезки, отсекаемые плоскостью на осяхи
.
-
Уравнение
плоскости, проходящей через точку
перпендикулярно
вектору нормали
:
в
векторной форме:
-
Уравнение
плоскости, проходящей через три заданные
точки
,не
лежащие на одной прямой:
-
Нормированное
уравнение плоскости
нормальное
уравнение плоскости вида
задает
в прямоугольной системе координатOxyz
плоскость, удаленную от начала координат
на расстояние p
в положительном направлении единичного
нормального вектора плоскости
.
-
Прямая
в пространстве
Прямая
в пространстве может быть задана как
линия пересечения двух плоскостей. Так
как точка прямой прнадлежит каждой из
плоскостей, то ее координаты обязаны
удовлетворять уравнениям обеих
плоскостей, то есть удовлетворять
системе из двух уравнений.
итак,
если уравнения двух непараллельных
плоскостей —
и
,
то прямая, являющаяся их линией
пересечения, задается системой уравнений
|
|
(11.11) |
И
наоборот, точки, удовлетворяющие такой
системе уравнений, образуют прямую,
являющуюся линией пересечения плоскостей,
чьи уравнения образуют эту систему.
Уравнения (11.11)
называют общими уравнениями прямой в
пространстве.
-
Уравнение
окружности
Уравнение
окружности радиуса
с
центром вначале
координат:
-
Эллипс.
Каноническое уравнение. Эксцентриситет,
фокальный радиус.
Э́ллипс
— геометрическое
место точек
M
Евклидовой
плоскости,
для которых сумма расстояний до двух
данных точек
и
(называемыхфокусами)
постоянна и больше расстояния между
фокусами, то есть
причем
Окружность
является частным случаем эллипса. Наряду
с гиперболой
и параболой,
эллипс является коническим
сечением
и квадрикой.
Эллипс
также можно описать как пересечение
плоскости
и кругового цилиндра
или как ортогональную
проекцию
окружности
на плоскость.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #