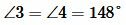Как найти разность углов при пересечении двух

Углы при пересечении двух прямых

Если какие-нибудь две прямые пересечены третьей прямой, то пересекающая их прямая называется секущей по отношению к прямым, которые она пересекает.

При пересечении двух прямых третьей, образуется два вида углов: внешние и внутренние.

На рисунке изображены две прямые a и b, пересекаемые прямой c. Прямая c по отношению к прямым a и b является секущей. Синим цветом на рисунке обозначены внешние углы (∠1, ∠2, ∠7 и ∠8), а красным — внутренние углы (∠3, ∠4, ∠5 и ∠6).

Также при пересечении двух прямых третьей, образовавшиеся углы получают попарно следующие названия:

Углы при пересечении параллельных прямых

Если секущая пересекает две параллельные прямые линии, то:

• внутренние накрест лежащие углы равны;
• сумма внутренних односторонних углов равна 180°;
• соответственные углы равны;
• внешние накрест лежащие углы равны;
• сумма внешних односторонних углов равна 180°.

Как найти разность углов параллельных прямых

§ 15. Свойства параллельных прямых

(обратная теореме 14.1)

Если две параллельные прямые пересечены секущей, то углы, образующие пару накрест лежащих углов, равны.

На рисунке 224 прямые a и b параллельны, прямая c — секущая. Докажем, что ∠ 1 = ∠ 2.

Пусть ∠ 1 ≠ ∠ 2. Тогда через точку K проведём прямую a 1 так, чтобы ∠ 3 = ∠ 2 (рис. 224). Углы 3 и 2 являются накрест лежащими при прямых a 1 и b и секущей c . Тогда по теореме 14.1 a 1 ‖ b . Получили, что через точку K проходят две прямые, параллельные прямой b . Это противоречит аксиоме параллельности прямых. Таким образом, наше предположение неверно, и, следовательно, ∠ 1 = ∠ 2.

(обратная теореме 14.3)

Если две параллельные прямые пересечены секущей, то углы, образующие пару соответственных углов, равны.

На рисунке 225 прямые a и b параллельны, прямая c — секущая. Докажем, что ∠ 1 = ∠ 2.

По теореме 15.1 углы 3 и 2 равны как накрест лежащие при параллельных прямых a и b и секущей c . Но углы 3 и 1 равны как вертикальные. Следовательно, ∠ 1 = ∠ 2.

(обратная теореме 14.2)

Если две параллельные прямые пересечены секущей, то сумма углов, образующих пару односторонних углов, равна 180° .

На рисунке 226 прямые a и b параллельны, прямая c — секущая. Докажем, что ∠ 1 + ∠ 2 = 180°.

По теореме 15.1 углы 3 и 2 равны как накрест лежащие при параллельных прямых a и b и секущей c . Но углы 3 и 1 смежные, поэтому ∠ 1 + ∠ 3 = 180°. Следовательно, ∠ 1 + ∠ 2 = 180°.

Если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой ( рис. 227 ).

Докажите это следствие самостоятельно.

Задача. Докажите, что все точки одной из двух параллельных прямых равноудалены от другой прямой.

Решение. Пусть прямые a и b параллельны (рис. 228), M и N — две произвольные точки прямой a . Опустим из них перпендикуляры MK и NP на прямую b . Докажем, что MK = NP .

Рассмотрим треугольники MKN и PNK . Отрезок KN — их общая сторона. Так как MK ⊥ b и NP ⊥ b , то MK ‖ NP , а углы MKN и PNK равны как накрест лежащие при параллельных прямых MK и NP и секущей KN .

Аналогично углы MNK и PKN равны как накрест лежащие при параллельных прямых MN и KP и секущей KN . Следовательно, треугольники MKN и PNK равны по стороне и двум прилежащим углам.

Тогда MK = NP .

Расстоянием между двумя параллельными прямыми называют расстояние от любой точки одной из прямых до другой прямой.

Например, на рисунке 228 длина отрезка MK — это расстояние между параллельными прямыми a и b .

Задача. На рисунке 229 отрезок AK — биссектриса треугольника ABC , MK ‖ AC . Докажите, что треугольник AMK — равнобедренный.

Решение. Так как AK — биссектриса треугольника ABC , то ∠ MAK = ∠ KAC .

Углы KAC и MKA равны как накрест лежащие при параллельных прямых MK и AC и секущей AK . Следовательно, ∠ MAK = ∠ MKA .

Тогда треугольник AMK — равнобедренный.

1. Каким свойством обладают накрест лежащие углы, образованные при пересечении двух параллельных прямых секущей?
2. Каким свойством обладают соответственные углы, образованные при пересечении двух параллельных прямых секущей?
3. Чему равна сумма односторонних углов, образованных при пересечении двух параллельных прямых секущей?
4. Известно, что прямая перпендикулярна одной из двух параллельных прямых. Обязательно ли она перпендикулярна другой прямой?
5. Что называют расстоянием между двумя параллельными прямыми?

326. На рисунке 230 найдите угол 1.

327. На рисунке 231 найдите угол 2.

328. Разность односторонних углов, образованных при пересечении двух параллельных прямых секущей, равна 50°. Найдите эти углы.

329. Один из односторонних углов, образованных при пересечении двух параллельных прямых секущей, в 4 раза больше другого. Найдите эти углы.

330. Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если:

1) один из этих углов равен 48°;

2) отношение градусных мер двух из этих углов равно 2 : 7.

331. Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них на 24° меньше другого.

332. На рисунке 232 m ‖ n , p ‖ k , ∠1 = 50°. Найдите ∠ 2, ∠ 3 и ∠ 4.

333. Прямая, параллельная основанию AC равнобедренного треугольника ABC , пересекает его боковые стороны AB и BC в точках D и F соответственно. Докажите, что треугольник DBF — равнобедренный.

334. На продолжениях сторон AC и BC треугольника ABC ( AB = BC ) за точки A и B отметили соответственно точки P и K так, что PK ‖ AB . Докажите, что треугольник KPC — равнобедренный.

335. Отрезки AB и CD пересекаются в точке O , AO = BO , AC ‖ BD . Докажите, что CO = DO .

336. Отрезки MK и DE пересекаются в точке F , DK ‖ ME , DK = ME . Докажите, что ∆ MEF = ∆ DKF .

337. Ответьте на вопросы.

1) Могут ли оба односторонних угла при двух параллельных прямых и секущей быть тупыми?

2) Может ли сумма накрест лежащих углов при двух параллельных прямых и секущей быть равной 180°?

3) Могут ли быть равными односторонние углы при двух параллельных прямых и секущей?

338. На рисунке 233 AB ‖ CD , BC ‖ AD . Докажите, что BC = AD .

339. На рисунке 233 BC = AD , BC ‖ AD . Докажите, что AB ‖ CD .

340. На рисунке 234 MK ‖ EF , ME = EF , ∠ KMF = 70°. Найдите ∠ MEF .

341. Через вершину B треугольника ABC (рис. 235) провели прямую MK , параллельную прямой AC , ∠ MBA = 42°, ∠ CBK = 56°. Найдите углы треугольника ABC .

342. Прямая, проведённая через вершину A треугольника ABC параллельно его противолежащей стороне, образует со стороной AC угол, равный углу BAC . Докажите, что данный треугольник — равнобедренный.

343. На рисунке 236 ∠ MAB = 50°, ∠ ABK = 130°, ∠ ACB = 40°, CE — биссектриса угла ACD . Найдите углы треугольника ACE .

344. На рисунке 237 BE ⊥ AK , CF ⊥ AK , CK — биссектриса угла FCD , ∠ ABE = 32°. Найдите ∠ ACK .

345. На рисунке 238 BC ‖ MK , BK = KE , CK = KD . Докажите, что AD ‖ MK .

346. На рисунке 239 AB = AC , AF = FE , AB ‖ EF . Докажите, что AE ⊥ BC .

347. Треугольник ABC — равнобедренный с основанием AC . Через произвольную точку M его биссектрисы BD проведены прямые, параллельные его сторонам AB и BC и пересекающие отрезок AC в точках E и F соответственно. Докажите, что DE = DF .

348. На рисунке 240 AB ‖ DE . Докажите, что ∠ BCD = ∠ ABC + ∠ CDE .

349. На рисунке 241 AB ‖ DE , ∠ ABC = 120°, ∠ CDE = 150°. Докажите, что BC ⊥ CD .

350. Через вершину B треугольника ABC провели прямую, параллельную его биссектрисе AM . Эта прямая пересекает прямую AC в точке K . Докажите, что ∆ BAK — равнобедренный.

351. Через точку O пересечения биссектрис AE и CF треугольника ABC провели прямую, параллельную прямой AC . Эта прямая пересекает сторону AB в точке M , а сторону BC — в точке K . Докажите, что MK = AM + CK .

352. Биссектрисы углов BAC и BCA треугольника ABC пересекаются в точке O . Через эту точку проведены прямые, параллельные прямым AB и BC и пересекающие сторону AC в точках M и K соответственно. Докажите, что периметр треугольника MOK равен длине стороны AC .

Упражнения для повторения

353. На отрезке AB отметили точку C так, что AC : BC = 2 : 1. На отрезке AC отметили точку D так, что AD : CD = 3 : 2. В каком отношении точка D делит отрезок AB ?

354. Отрезки AC и BD пересекаются в точке O , AB = BC = CD = AD . Докажите, что AC ⊥ BD .

355. В треугольнике MOE на стороне MO отметили точку A , в треугольнике TPK на стороне TP — точку B так, что MA = TB . Какова градусная мера угла BKP , если MO = TP , ∠ M = ∠ T , ∠ O = ∠ P , ∠ AEO = 17°?

Наблюдайте, рисуйте, конструируйте, фантазируйте

356. На рисунке 242 изображена очень сложная замкнутая ломаная. Она ограничивает некоторую часть плоскости (многоугольник). Как, отметив на рисунке любую точку, по возможности быстрее определить, принадлежит эта точка многоугольнику или нет?

Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы

Пусть прямая с пересекает параллельные прямые и . При этом образуется восемь углов. Углы при параллельных прямых и секущей так часто используются в задачах, что в геометрии им даны специальные названия.

Углы и — вертикальные. Очевидно, вертикальные углы равны, то есть

Конечно, углы и , и — тоже вертикальные.

Углы и — смежные, это мы уже знаем. Сумма смежных углов равна .

Углы и (а также и , и , и ) — накрест лежащие. Накрест лежащие углы равны.

Углы и — односторонние. Они лежат по одну сторону от всей «конструкции». Углы и — тоже односторонние. Сумма односторонних углов равна , то есть

Углы и (а также и , и , и ) называются соответственными.

Соответственные углы равны, то есть

Углы и (а также и , и , и ) называют накрест лежащими.

Накрест лежащие углы равны, то есть

Чтобы применять все эти факты в решении задач ЕГЭ, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть пару параллельных прямых и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это — один из шагов, из которых и состоит решение.

Ты нашел то, что искал? Поделись с друзьями!

1. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении , считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен .

Напомним, что биссектриса угла — это луч, выходящий из вершины угла и делящий угол пополам.

Пусть — биссектриса тупого угла . По условию, отрезки и равны и соответственно.

Рассмотрим углы и . Поскольку и параллельны, — секущая, углы и являются накрест лежащими. Мы знаем, что накрест лежащие углы равны. Значит, треугольник — равнобедренный, следовательно, .

Периметр параллелограмма — это сумма всех его сторон, то есть

2. Диагональ параллелограмма образует с двумя его сторонами углы и . Найдите больший угол параллелограмма. Ответ дайте в градусах.

Нарисуйте параллелограмм и его диагональ. Заметив на чертеже накрест лежащие углы и односторонние углы, вы легко получите ответ: .

3. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.

Мы знаем, что равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. Следовательно, равны углы при верхнем основании, а также углы при нижнем основании.

Давайте посмотрим на чертеж. По условию, , то есть .

Углы и — односторонние при параллельных прямых и секущей, следовательно,

Сравнение углов. Сложение и вычитание углов

Углы различают по их величине. Большим считается не тот угол, стороны которого длиннее, а тот, стороны которого сильнее расходятся врозь. На черт. 13 уг. EDF больше, чем угол 2, потому, что у первого стороны сильней расходятся врозь. Встречаются углы, стороны которых расходятся врозь совершенно одинаково; такие углы можно наложить один на другой так, что их вершины совпадут, а стороны сольются. Углы, которые можно таким образом наложить друг на друга, считаются равными, хотя бы стороны их были неодинаковой длины.

На черт. 13 равны, например, уг. DEH и уг. DFH, уг. 2 и уг. а; вы можете убедиться в этом, есля обведете один угол на прозрачной бумаге и покроете им другой.

Если при наложении сравниваемых углов их вершины и одна сторона совпали, вторая же сторона накладываемого угла оказалась внутри или вне другого угла, то такие углы, конечно, не равны. Тот угол, который оказался внутри другого, считается меньшим.

Рассмотрите на том же черт. 13 углы, вершины которых лежат в точке D. Здесь три угла: уг. EDF, уг. EDH и уг. HDF. Вы видите, что оба меньших угла как раз заполняют собою уг. EDF, который составляется из них, как целое из своих частей. Когда углы так расположены, то говорят, что уг. EDF есть с у м м а углов EDH и HDF. С л о ж и т ь два угла значит найти их сумму, т. е. тот угол, который составится, если приложить их друг к другу, как показано на чертеже 13.

Если на черт. 13 от угла EDF отнять угол EDH, то останется уг. HDF; этот. угол называется р а з н о с т ь ю углов EDF и EDH. Вычесть один угол из другого значит найти их разность.

Повторительные вопросы

Какие углы называются равными? – Зависит ли величина угла от длины сторон? – Покажите на чертеже, что называется суммой и разностью двух углов.

Развернутый угол

Представьте себе, что мы разводим врозь стороны какого-нибудь угла, – напр. уг. 1 (черт. 14). От этого угол станет увеличиваться: он превратится сначала в уг. 2, потом в уг. 3 и, наконец, в уг. 4, стороны которого составляют одну прямую линию. Такие углы, как уг. 4, называются р а з в е р н у т ы м и углами.

Может ли один развернутый угол быть больше или меньше другого развернутого? Конечно, нет: ведь всякие прямые линии, если их наложить одну на другую, сливаются между собою; значит, должны слиться при наложении и всякие развернутые углы. Итак:

В с е р а з в е р н у т ы е у г л ы р а в н ы м е ж д у с о б о ю.

Смежные углы. Прямой угол

На черт. 15 вы видите углы 1 и 2, которые расположены так, что вершины их совпадают (в точке А) и одна сторона (AD) у них общая, т. е. принадлежит одновременно обоим углам, другие же стороны АВ и АС этой пары углов составляют одну прямую линию. Углы, которые так расположены, называются с м е ж н ы м и. На черт. 16 вы видите несколько пар смежных углов: уг. 1 и уг. 2; уг. 3 и уг. 4; уг. 5 и у г. 6; у г. а и у г. b; уг. с и у г. d, и др.

Если углы, составляющие одну пару смежных углов, равны между собою, – как уг. 7 и 8 на черт. 16, – то каждый из них называется прямым углом. Значит:

П р я м о й у г о л е с т ь о д и н и з д в у х р а в н ы х с м е ж н ы х у г л о в.

Так как оба равных смежных угла составляют вместе один развернутый угол, то прямой угол есть половина развернутого угла. Но все развернутые углы равны друг другу; поэтому равны и их половины, т. е. прямые углы. Значит:

В с е п р я м ы е у г л ы р а в н ы д р у г д р у г у.

Прямые линии, встречающиеся под прямым углом (черт. 17), называются перпендикулярными друг к другу. На черт. 17, например, уг. 1 = уг. 2, а так как эти углы смежные и притом равные, то они – прямые. Поэтому CD перпендикулярно к АВ и АВ перпендикулярно к CD.

Слово «перпендикулярный» не надо смешивать со словом «вертикальный». В е р т и к а л ь н о й, или о т в е с н о й, называют всякую прямую линию, имеющую направление свободно свешивающейся нагруженной нити.

Все те линии, которые составляют с вертикальной линией прямой угол, называются г о р и з о н т а л ь н ым и. Горизонтальны, например, все линии, проведенные по поверхности воды (черт. 18). Отвесное направление проверяют отвесом (черт. 18); горизонтальное – плотничьим ватерпасом.

На бумаге прямой угол чертят помощью линейки и чертежного треугольника (черт. 19). Проверить, правильно ли изготовлен чертежный треугольник, можно так. Проведя по линейке прямую линию и начертив с помощью треугольника другую прямую к ней, перпендикулярную, прикладывают чертежный треугольник прямым углом к смежному углу: если эти углы равны, то треугольник изготовлен правильно.

Углы, меньшие, чем прямой, называются о с т р ы м и; большие, чем прямой, – т у п ы м и.

Повторительные вопросы к §§ 6 и 7

Какой угол называется развернутым? – Какие углы называются смежными (начертите несколько таких углов)? – Какой угол называется прямым? – Как называется угол, который равен смежному с ним? – Могут ли прямые углы иметь различную величину? – Объясните значение слов: перпендикулярный, вертикальный, отвесный, горизонтальный. – Как чертить перпендикулярные прямые помощью чертежного треугольника? – Какие углы называются острыми? Тупыми? Начертите несколько острых и несколько тупых углов.

1. Уменье чертить взаимно-перпендикулярные прямые позволяет строить так наз. «графики», т. е. ломаные (или кривые) линии, наглядно показывающие ход изменения явлений. Пусть требуется построить график температуры за неделю по следующим данным:

Изобразим эти температуры рядом перпендикуляров к одной прямой, приведенных на равных расстояниях друг от друга: длина перпендикулярных отрезков будет изображать температуру дня. Верхушки перпендикуляров соединим прямыми линиями: полученная ломаная линия и есть «график температур».

2. На черт. 20 изображены графики годового хода температуры воздуха в разных местах земного шара: на о-ве Цейлон, в Ницце, в Самаре, во Владивостоке и в Верхоянске. Рассматривая эти графики, мы можем ответить себе на ряд могущих возникнуть вопросов, например:

a) Какова температура в среднем за много лет во всех на званных местах 1 мая?

О т в е т. На Цейлоне +27° в Ницце +18°, в Самаре +15°, во Владивостоке +10°, в Верхоянске 0°.

b) Какие дни в году (в среднем) самые жаркие и самые холодные в Верхоянске?

О т в е т. 1-е июля + 15°1-е января – минус 50°

c) В каких городах в апреле средняя температура ниже0°?

О т в е т. В Верхоянске, Владивостоке и Самаре.

d) Какова разница между самой высокой и самой низкой средней температурой в Ницце? В Самаре?

О т в е т ы. В Ницце средняя температура колеблется от +9° до +24°; в Самаре – от минус 10° до +21°.

Свойство смежных углов

Сумма обоих смежных углов, очевидно, равна развернутому углу. Но развернутый угол равен двум прямым углам, взятым вместе. Поэтому:

С у м м а о б о и х с м е ж н ы х у г л о в р а в н а д в у м п р я м ы м у г л а м.

Например, на черт. 21 уг. 1 +уг. 2 = двум прямым углам.

Бывает, что по одну сторону прямой расположено не два угла, как в случае смежных углов, а несколько углов, – как на черт. 22. Легко убедиться, что сумма этих углов также равна двум прямым: из них всегда можно составить одну пару смежных углов (на черт. 22 углы АОD и DOВ, или АОЕ и ЕОВ).

Подобным же образом можно найти, чему равна сумма углов,! расположенных вокруг общей вершины, как на черт. 23. Продолжив одну из сторон за общую вершину (черт. 24), получим две группы углов: группу 1 и а, сумма которых равна двум прямым (почему?), и группу углов 2, 3, Ь, сумма которых равна также двум прямым углам; значит, сумма всех углов вокруг общей вершины равна 4 прямым углам.

Повторительные вопросы

Чему равна сумма смежных углов? – Сумма нескольких углов, расположенных по одну сторону прямой линии? – Сумма всех углов, расположенных вокруг общей вершины?

Противоположные углы

Предварительные упражнения

1) На черт. 25 уг. 1 = 48°. Найти прочие углы.

2) На черт. 25 уг. b = 136 °. Найти прочие углы.

Когда две прямые линии пересекают друг друга (черт. 25), они образуют две пары углов, стороны которых составляют продолжение одни других: одна пара – уг. 1 и уг. 2; другая – уг. а и уг. b. Особенность противоположных углов та, что углы, составляющие такую пару, всегда равны между собою: у г. 1 = уг. 2, уг. а = у г. b. Действительно, если например (черт. 25) уг. 1 = 40°, то уг. b = 180° – 40° = 140°, уг. 2 = 180° – 140° = 40°, и уг. а = 180° – 40° = 140°; мы видим, что уг. 1 = уг. 2, и уг. а = уг. b. Вообще, так как уг. 1 вместе с углом а равен двум прямым (почему?), а уг. 2 вместе с тем же углом а тоже равен двум прямым, то ясно, что уг. 1 должен равняться уг. 2. Итак:

П р о т и в о п о л о ж н ы е у г л ы р а в н ы.

Повторительные вопросы.

Какие углы называются противоположными? знаете свойство противоположных углов?

Окружность

До сих пор мы говорили только о прямых линиях. Из к р и в ы х линий остановимся на о к р у ж н о с т и (черт. 26). Окружность чертят циркулем. Острие ножки раздвинутого циркуля втыкают в бумагу, другую же ножку с карандашом вращают вокруг первой; когда карандаш сделает полный оборот, он проведет на бумаге замкнутую кривую – окружность. Та точка, в которую было воткнуто острие циркуля, называется ц е н т р о м окружности. Понятно, что все точки окружности удалены от центра на одинаковое расстояние; это расстояние называется р а д и у с о м окружности. Значит:

О к р у ж н о с т ь е с т ь к р и в а я л и н и я, в с е т о ч к и к о т о р о й о д и н а к о в о у д а л е н ы о т о д н о й

т о ч к и, н а з ы в а е м о й ц е н т р о м.

Прямая, соединяющая две точки окружности через центр, называется д и а м е т р о м.

Всякая часть окружности называется ее д у г о ю (черт. 27).

Плоская фигура, ограниченная окружностью, называется к р у г о м.

Повторительные вопросы

Что такое окружность? Центр? Радиус? Дуга? – Покажите все это на чертеже. – Все ли радиусы одной окружности равны между собою? – Что больше: диаметр или радиус? Во сколько раз?

Применения

3. Гудок завода слышен на 4 км. Начертить в масштабе 1 км в 1 см границу местности, где слышен гудок этого завода.

Р е ш е н и е. Вокруг точки, обозначающей положение завода, начертить окружность радиусом 4 см.

4. Радиус круга 100 см. Некоторая точка удалена от центра на 40 см. Лежит ли она внутри круга или вне его? Каково ближайшее расстояние от этой точки до окружности?

Р е ш е н и е. Точка лежит внутри круга. Ближайшее расстояние ее от окружности надо считать вдоль диаметра, проведенного через эту точку; оно равно 60 см. Дальнейшее расстояние (вдоль того же диаметра) – 140 см.

Источник

Вертикальные углы. Свойства вертикальных углов

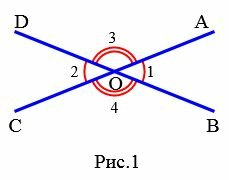
Определение 1. Вертикальными углами называются два угла, у которых стороны одного угла являются продолжениями сторон другого угла.

На Рис.1 углы AOB и COD вертикальные. Вертикальные также углы AOD и BOC.

Свойства вертикальных углов

1. Вертикальные углы равны.

2. Две пересекающие прямые образуют две пары вертикальных углов.

Доказательство пункта 1. Поскольку 1, 3 и 2, 3 смежные углы, то имеем

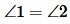
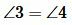
Следовательно . Аналогично доказывается, что .

Задачи и решения

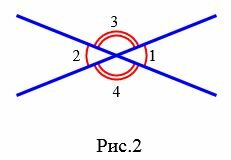
Задание 1. Угол 1 равен 32°. Найти углы 2, 3, 4 (Рис.2).

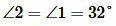
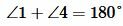
Решение. Так как углы 1 и 2 вертикальны, то . Углы 1 и 4 смежные. Следовательно . Тогда

Углы 3 и 4 вертикальные. Тогда

Ответ. .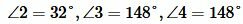

Задание 2. При пересечении двух прямых образовались четыре угла. Сумма двух углов равна 220°. Найти все углы.

Решение. Из образованных четырех углов любые две или смежные, или вертикальные. Поскольку в нашей задаче сумма двух углов равна 220°, то эти углы вертикальные (так как сумма смежных углов равна 180°). Тогда каждый из этих углов равен 220°:2=110°. Смежный по отношению угла 110° , будет угол 180°-110°=70°. Следовательно остальные два угла равны 70°. Отметим, что сумма всех четырех углов равен 360°:

.

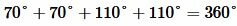
Ответ. .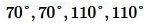

Источник

Так как разность этих углов не равна нулю, значит эти углы не равны, следовательно они в сумме дают 180 градусов. Других углов, образованных при пересечении двух параллельных прямых секущей, не может быть. Эти углы — внутренние односторонние, найдем их градусные меры:

1) 180-42 = 138 град — удвоенный меньший угол

2) 138 : 2 = 69 град — меньший угол — один из внутренних односторонних углов

3) 69+42=111 град — больший угол — другой из внутренних односторонних углов

Остальные углы либо накрестлежащие с данными и они им равны, или соответственные с данными и они им тоже равны по свойству соответствующих углов.