Как найти разность углов урок

Тема: «Сумма и разность углов»

Орг.момент.

Девиз урока:

«С малой удачи начинается большой успех»

Улыбнитесь друг другу. Подарите и мне вашу улыбку. Ведь улыбка украшает человека и дарит хорошее настроение. И пусть этот урок принесёт вам радость от новых открытий, от общения друг с другом и наполнит ваши души прекрасными чувствами.

-Что вы ждёте от этого урока?

Актуализация знаний

Сосчитайте:

Л 60 х 40 : 800 х 9 х 2=54 О 18 х 2 : 6 х 7 + 29= 71

Г 9 х 2 х 9 х 5 – 610=200 Г 4 х 40 + 280 : 70 х 5=180

Расположите ответы в порядке убывания: 200У, 180 Г,71О, 54 Л. (Оцените)

— Какие виды углов вы знаете? (развернутый, прямой, острый, тупой)

— Покажите руками: прямой угол, острый, тупой, развернутый.

Работа со спичками: постройте из спичек угол 180 гр., угол 90гр., смежные углы.

— Почему именно это слово было зашифровано? (Продолжаем измерять углы)

— С помощью какого инструмента измеряют величину угла? (транспортир)

-Назовите единицу измерения угла (градус)

Для того, чтобы измерить углы, надо вспомнить алгоритм измерения:

Совместить вершину угла с центром транспортира.

Расположить транспортир так, чтобы одна из сторон угла проходила черезнуль выбранной шкалы транспортира.

Найти штрих на шкале, через который проходит вторая сторона угла. Полученное число это и есть величина угла.

Проверить, соответствует ли полученная мера угла его виду.

2. Формулирование темы и целей.

— Вы уже догадались чем мы будем заниматься уроке? (измерять углы) Тема: Измерение углов. Еще мы будем складывать углы и вычитать. Тема: Сумма и разность углов.

3.Повторение и закрепление изученного.

1. Работу по учебнику

У.6, с.22

№1. (измерьте углы). Проверка в парах.

Физминутка

Стоп, урок! Стоп, дела! Отдыхать пришла пора!

Игра «Истина- ложь» истина – хлопаем, ложь – топаем

1.Острым называют угол, который больше прямого. (Нет)

2. Тупой угол всегда больше прямого и меньше развёрнутого? (да)

3. Единица измерения углов: килограмм? (нет)

4. Тупой угол меньше прямого угла. (нет)

5. Угол — фигура, образованная двумя лучами, выходящими из одной точки. (да)

6. биссектриса — это луч, который выходит из вершины угла и делит его пополам. (да)

7. два угла можно сравнить с помощью наложения (да)

8. величина острого угла равняется 126градусам ( Нет)

9. ар- единица измерения площади (да)

№2 (измерьте углы)

№3 (в парах)

Самостоятельно : № 12 или №1 (1столб.)

Итог урока. Рефлексия.

— Чему научились сегодня на уроке?

Какую цель ставили в начале урока? Все ли удалось?

Кому было трудно?

— Чем мы сегодня занимались на уроке? (измеряли углы, складывали, вычитали)

— Какое задание вам показалось самым сложным?

-Какое задание понравилось?

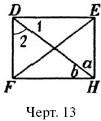
Углы различают по их величине. Большим считается не тот угол, стороны которого длиннее, а тот, стороны которого сильнее расходятся врозь. На черт. 13 уг. EDF больше, чем угол 2, потому, что у первого стороны сильней расходятся врозь. Встречаются углы, стороны которых расходятся врозь совершенно одинаково; такие углы можно наложить один на другой так, что их вершины совпадут, а стороны сольются. Углы, которые можно таким образом наложить друг на друга, считаются равными, хотя бы стороны их были неодинаковой длины.

На черт. 13 равны, например, уг. DEH и уг. DFH, уг. 2 и уг. а; вы можете убедиться в этом, есля обведете один угол на прозрачной бумаге и покроете им другой.

Если при наложении сравниваемых углов их вершины и одна сторона совпали, вторая же сторона накладываемого угла оказалась внутри или вне другого угла, то такие углы, конечно, не равны. Тот угол, который оказался внутри другого, считается меньшим.

Рассмотрите на том же черт. 13 углы, вершины которых лежат в точке D. Здесь три угла: уг. EDF, уг. EDHи уг. HDF. Вы видите, что оба меньших угла как раз заполняют собою уг. EDF, который составляется из них, как целое из своих частей. Когда углы так расположены, то говорят, что уг. EDFесть с у м м а углов EDHи HDF. С л о ж и т ь два угла значит найти их сумму, т. е. тот угол, который составится, если приложить их друг к другу, как показано на чертеже 13.

Если на черт. 13 от угла EDFотнять угол EDH, то останется уг. HDF; этот. угол называется р а з н о с т ь ю углов EDFи EDH. Вычесть один угол из другого значит найти их разность.

Повторительные вопросы

Какие углы называются равными? – Зависит ли величина угла от длины сторон? – Покажите на чертеже, что называется суммой и разностью двух углов.

Формулы суммы и разности углов тригонометрических функций онлайн

С помощю этого онлайн калькулятора можно получить формулы суммы и разности углов тригонометрических функций. Для получения формулы выберите нужную тригонометрическую функцию, нажав на «sin», выберите нужный аргумент, нажав на аргумент в формуле. В результате получится формула для этой функции и аргумента. Теоретическую часть и численные примеры смотрите ниже.

Формулы суммы и разности углов тригонометрических функций − теория, доказательство, примеры

Выведем формулы суммы и разности углов тригонометрических функций. Начнем с формулы

Как мы знаем, угол между векторами не может быть больше 180° (π). На рисунке Рис.1 угол между векторами и равен . На рисунке Рис.2 угол между векторами и равен .

Рассмотрим, теперь косинусы этих углов. Из формул приведения мы знаем (подпрбнее о формулах приведения смотрите на странице Формулы приведения тригонометрических функций онлайн):

Cкалярное произведение векторов и равно:

Так как точка имеет координаты , а имеет координаты (смотрите статью на странице Синус и косинус. Онлайн калькулятор), то скалярное произведения векторов и по координатам равно:

Поскольку левые части формул (2) и (3) равны, то равны и правые части этих формул. Следовательно выполнено равенство (1).

Докажем, далее, справедливость следующей формулы

Представим косинус суммы углов α и β в виде косинуса разности двух углов и воспользуемся формулой (1) и тем, что косинус четная функция а синус нечетная функция:

Перейдем к доказательству формул синусов суммы и разности углов:

Для доказательства формулы (5) воспользуемся формулами приведения тригонометрических функций и формулой (1):

Для доказательства формулы (6), представим разность углов в виде суммы и воспользуемся тем, что косинус четная функция а синус нечетная функция:

Формулы тангенса суммы и разности углов имееют следующий вид:

Докажем формулу (7):

Разделим числитель и знаменатель дроби в правой части уравнения (9) на (, ):

Для доказательства формулы (9) представим разность углов в виде суммы, воспользуемся формулой (8) и учтем, что тангенс нечетная функция:

Формулы котангенса суммы и разности углов имееют следующий вид:

Докажем формулу (10):

Разделим числитель и знаменатель дроби в правой части уравнения (12) на (, ):

Для доказательства формулы (11), представим разность углов α и β в виде суммы и учтем, что котангенс нечетная функция:

Умножив числитель и знаменатель в правой части уравнения (13) на −1, получим формулу (11).

Примеры использования формул суммы и разности углов тригонометрических функций

Пример 1. Найти точное значение .

Решение:

Ответ:

Пример 2. Найти косинус для угла 15°.

Решение:

Ответ:

Пример 3. Найти точное значение тангенса для угла 15° .

Решение:

Тангенсы для углов 45° и 15° известны. Подставим эти значения в (14):

Дробь в правой части уравнения (15) можно упростить, умножив числитель и знаменатель дроби на :

Ответ:

Геометрия

7 класс

Урок №5

Измерение углов

Перечень рассматриваемых вопросов:

• Измерительные инструменты.
• Градусная мера угла; биссектриса.
• Транспортир.
• Классификация углов.

Тезаурус:

Градус – угол, равный одной сто восьмидесятой части развернутого угла.

Градусная мера угла – положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.

Минута – 1/60 часть градуса.

Секунда – 1/60 часть минуты.

Луч – часть прямой, состоящий из всех точек, лежащих по одну сторону от заданной точки, которая является началом луча.

Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.

Стороны угла – лучи, из которых состоит угол.

Вершина угла – общее начало сторон угла.

Биссектриса – это луч, исходящий из вершины угла и делящий его на два равных угла.

Основная литература:

1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Дополнительная литература:

1. Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
2. Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
3. Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
4. Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
5. Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

Ранее вы уже познакомились с геометрической фигурой – уголи его составными элементами.

Сегодня мы продолжим изучать углы, познакомимся с их классификацией и будем измерять углы с помощью транспортира.

Измерение углов аналогично измерению отрезков – оно основано на сравнении, только отрезки сравнивались с отрезком, принятым за единицу измерения, а углы с углом, тоже принятым за единицу измерения.

Обычно за единицу измерения углов принимают градус.

Градус – угол, равный 1/180 части развёрнутого угла.

Положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу, называется градусной мерой угла.

Для измерения углов используют транспортир. Вспомним, как проводить измерение углов с помощью транспортира.

Транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах на той же шкале.

Например:

∠О = 50°

Но обычно говорят кратко – угол О равен 50 градусам.

Если масштабныйугол не укладываетсяцелое число раз в измеряемом угле, тоединицу измерения делят ещё на части.

Определённые части градуса носят специальные названия.

Части градуса.

Минута – 1/60 часть градуса.

Обозначается «´».

Секунда – 1/60 часть минуты.

Обозначается «´´».

Например:

∠А = 40 ° 15´ 16 ´´

Далее, аналогично понятию равные отрезки, ведём понятие равные углы.

Дваугла считаются равными, если градус и его части укладываются в этих углах одинаковое число раз, т.е. равные углы имеют равные градусные меры.

Если один угол меньше другого, то градус в нём (или его часть) укладываются в этом углу меньшее число раз, чем в другом, т.е. меньший угол имеет меньшую градусную меру.

Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.

∠АОС =∠АОL + ∠LОС,

∠АОL = 64°,

∠LОС = 64°,

∠АОС = 64° + 64° = 128°.

Далее рассмотрим классификацию углов.

Мы уже знаем, что есть развёрнутый угол, его градусная мера сто восемьдесят градусов.

Но есть и другие углы.

Например, прямой угол, его градусная мера девяносто градусов;

острый угол, его градусная мера меньше девяноста градусов;

тупой угол, его градусная мера больше девяноста градусов, но меньше ста восьмидесяти.

Выполним практическое задание – построим биссектрису угла с помощью транспортира.

Мы знаем, что биссектриса – это луч, исходящий из вершины угла и делящий его на два равных угла.

∠АОС = 128°,

128° : 2 = 64°,

OL – биссектриса ∠АОС.

Поэтому для начала определим градусную меру ∠АОС, она составляет 128°, тогда биссектриса этого угла, исходя из определения, составит 64 °.

Итак, сегодня получили представление о том, как измерять и изображать угол с помощью транспортира. Перейдем к практическим заданиям.

Способы измерения на местности.

Измерение углов на местности проводят с помощью различных приборов. Один из таких – астролябия, она состоит из диска (лимб), разбитого на градусы и вращающейся вокруг центра диска линейки (алидады). На концах алидады есть окошечки, которые нужны, чтобы устанавливать её в определённом направлении.

Опишем, как происходит измерение углов с помощью этого прибора. При измерении углов астролябию устанавливают в его вершине, например, точке О, при этом лимб должен находится горизонтально плоскости угла, а отвес, в центе диска, совпадать с вершиной угла.

Затем устанавливаем алидаду вдоль одной из сторон угла, например, АО, отмечаем деление, напротив которого находится указатель алидады.

Далее поворачиваем алидаду по часовой стрелке, пока она не совпадёт со второй стороной угла, у нас это сторона ОВ, отмечаем деление, напротив которого оказался указатель алидады. Теперь можно найти градусную меру измеряемого угла, как разность второго и первого измерения.

Тренировочные задания.

1. Луч ВК делит развернутый ∠ОВС на два угла, разность которых равна 56°. Найдите образовавшиеся углы.

Решение: нарисуем рисунок, исходя из условия задачи.

Обозначим ∠СВК за х, тогда ∠ОВК= х + 56°, исходя из условия задачи (разность углов равна 56°). Развёрнутый угол равен 180°. Составим уравнение и решим его.

х + х +56 =180,

2х= 180 – 56,

2х= 124,

х = 124:2,

х = 62° (∠СВК).

Тогда ∠ОВК= х + 56°= 62° +56° = 118°.

Ответ: ∠СВК = 62°; ∠ОВК = 118°.

2. Чему равен ∠ЕОА, если ∠ВОА = 130° 54´, а ∠ВОЕ = 105° 76´?

Решение: Найдём ∠ЕОА = ∠ВОА – ∠ВОЕ, т.к. ОЕ – луч, проведённый из вершины ∠ВОА и делящий этот угол на 2 части. Подставим в выражение градусные меры углов и найдём градусную меру ∠ЕОА. Так как в градусе 60 минут, то 105° 76´ = 106° 16´.

∠ЕОА = 130° 54´ – 106° 16´ = 24° 38´.

Ответ: ∠ЕОА = 24° 38´.

План урока:

Тригонометрические функции тупых углов

Вычисление координат точки

Вычисление площади треугольника

Площадь параллелограмма

Теорема синусов

Теорема косинусов

Тригонометрические функции тупых углов

Впервые с тригонометрическими функциями мы познакомились в 8 классе. Определить их значение можно было с помощью прямоугольного треугольника, рассматривая отношения его сторон (катетов и гипотенуз). Но такой способ определения тригонометрических функций подходит только для острых углов, попадающих в интервал от 0 до 90°. Оказывается, есть способ для вычисления значений тригонометрических функций и от больших углов.

Построим на координатной плоскости полуокружность, центр которой располагается в начале координат, а радиус равен единице. Ее называют единичной полуокружностью. Проведем из точки (0; 0) луч под некоторым углом α, который пересечет полуокружность в некоторой точке М с координатами (х; у). Заметим, что каждому значению α соответствует своя точка М на единичной полуокружности:

Опустим из М перпендикуляр на ось Ох в некоторую точку D. Тогда, если угол α острый,получается прямоугольный треугольник МOD, длины сторон которого можно определить так:

Получается, что координаты точки M как раз и являются синусом и косинусом угла α. Логично считать, что если α – не острый угол, то всё равно координаты точки M будут определять синус и косинус угла α.

Видно, что при тупом угле α точка М оказывается левее оси Оу, поэтому ее абсцисса становится отрицательной. Получается, что косинус может принимать отрицательные значения.

С помощью единичной полуокружности несложно выяснить значения синусов и косинусов для углов 0°, 90° и 180°. Они соответствуют координатам точек А, В и С на рисунке:

Так как эти точки имеют координаты (1; 0), (0; 1) и (– 1; 0), то можно записать следующее:

Используя это определение, найдем тангенс для углов 0° и 180°:

Заметим, что для 90° использовать эту формулу не удастся, так как это приведет к делению на ноль. Поэтому считается, что для 90° значение тангенса не определено, то есть его нельзя вычислить.

Единичная полуокружность является дугой окружности, чей радиус равен единице, а центр находится в начале координат. То есть она может быть задана уравнением

Тем самым мы доказали, что это тождество, которое показывает связь тригонометрических функций друг с другом, выполняется не только для острых углов, но и для всех углов из диапазона 0° ≤α ≤ 180°.

Для вычисления значений тригонометрических углов тупых углов удобно пользоваться так называемыми формулами приведения. Их довольно много, и изучаются они в основном в 10 классе, нам же хватит всего двух формул:

Например, пусть надо вычислить синус для угла 120°. Для этого мы представляем угол в виде разности, где в качестве уменьшаемого используется угол 180°:

Убедиться в справедливости этих двух формул приведения можно с помощью такого построения:

Точка М соответствует углу α, а точка K – углу (180° – α). Опустим из этих точек перпендикуляры МС и KD. Так как

Получается, что ∆OKD и ∆ОМС – прямоугольные, у них есть одинаковый острый угол α, и их гипотенузы ОК и ОМ также одинаковы как радиусы одной окружности. Тогда эти треугольники равны, и поэтому

Знак минус в первом из этих равенств показывает, что точки K отрицательная абсцисса. В итоге мы доказали две формулы приведения.

Задание. Вычислите sin 150°.

Решение. Представим угол 150° в виде разности:

Вычисление координат точки

Пусть есть некоторая точка А(х;у) с неотрицательной ординатой. Соединим ее с началом координат прямой, которая образует угол α с осью Ох. Посмотрим, как связаны координаты А со значением α.

Пусть луч ОА пересечет единичную окружность в точке М. Опустим из М и А перпендикуляры на Ох, в точки Н и С соответственно. Теперь сравним ∆ОМН и ∆ОАС. Они прямоугольные, и у них есть одинаковый угол α, следовательно, они подобны. Коэффициент подобия можно найти, поделив ОА на ОМ, при этом учтем, что ОМ = 1, так как М лежит на единичной полуокружности:

Примечание. Данное доказательство не рассматривает частные случаи, когда точка А лежит непосредственно на осях Ох и Оу, и тогда подобные треугольники ∆ОМН и ∆ОАС построить не удается. Эти случаи можно рассмотреть отдельно и показать, что для них выведенные формулы также справедливы.

Задание. Точка А находится на расстоянии 3 от начала координат (точки О), причем луч ОА образует с осью Ох угол 135°. Найдите координаты точки А.

Решение. Используя выведенные формулы, мы можем записать:

Вычисление площади треугольника

В 8 классе мы уже познакомились с одной из формул для определения площади треугольника. Однако на практике возникают ситуации, когда удобнее использовать другие формулы, одну из которых мы сейчас выведем.

Пусть в произвольном ∆АВС известны две стороны, например, ВС (обозначим ее буквой а) и АС (ее обозначим как b). Также известна величина угла между ними:

Разместим этот треугольник в системе координат так, чтобы точка С совпала с началом координат, в находилась на оси Ох и имела положительную абсциссу, А располагалась в первой четверти:

В этом случае координаты А будут определяться формулами:

Найдите площадь ∆МКН.

Решение.

Задание. Используя калькулятор, найдите площадь треугольника со сторонами 14 и 7 см, если угол между ними равен 48°. Ответ округлите до десятых долей см².

Решение. Подставляя числа в формулу, получаем:

Задание. Диагонали прямоугольника пересекаются под углом 30°, причем они равны 10 см. Вычислите площадь этого прямоугольника.

Решение.

Заметим, что диагонали прямоугольника при пересечении образуют не один, а два угла. Пусть в прямоугольнике АВСD диагонали пересекаются в точке О, и ∠АОВ = 30°. Тогда можно найти ∠ВОС, ведь он смежный с ∠АОВ:

Чтобы найти площадь прямоугольника, мы можем найти площади 4 треугольников, из которых он состоит, и потом сложить их. Для каждого из этих треугольников нам известны две стороны (они составляют по 5 см) и угол между ними:

Площадь параллелограмма

Из выведенной нами формулы площади треугольника вытекает и новая формула для площади параллелограмма. Пусть в параллелограмме нам известны смежные и угол между ними:

На рисунке смежные стороны АВ и AD обозначены буквами a и b, а угол между ними обозначен как α. Проведем диагональ BD. Площадь ∆ABD можно вычислить:

Задание. Стороны параллелограмма имеют длины 8 и 11 см, а один из углов параллелограмма равен 30°. Какова площадь этого параллелограмма?

Решение. Просто подставляем данные в формулу

Ответ: 44 см².

Задание. Известна площадь параллелограмма MNEF, одна из его сторон и угол:

Так как противоположные стороны в параллелограмме одинаковы, то MF также имеет длину 5:

MF = NE = 5

Запишем формулу для площади и подставим в нее известные данные:

Теорема синусов

Пусть есть некоторый ∆АВС, в котором стороны мы обозначим буквами:

Посчитаем его площадь, используя стороны b и c:

Также площадь треугольника можно выразить через а и с:

Полученная формула показывает, что в каждом треугольнике отношение стороны к синусу противолежащего угла – это константа, не зависящая от выбора стороны. Другими словами,в любом треугольнике стороны пропорциональны синусам углов, которые лежат против них. Это утверждение именуют теоремой синусов.

В большинстве задач достаточно выведенной формулы

Однако можно дополнить теорему синусов, выяснив, чему же именно равны все эти три отношения. Для этого впишем треугольник в окружность, после чего построим диаметр BD:

Пусть радиус этой окружности равен R, тогда диаметр BD будет вдвое больше:

Теперь рассмотрим ∆ВСD. ∠С здесь – прямой, ведь это вписанный угол, опирающийся на полуокружность, то есть дугу в 180°. По определению синуса, которое мы давали ещё в 8 классе, можно записать:

C учетом уже выведенного равенства (6) теорема синусов примет вид:

С помощью теоремы синусов у любого треугольника можно найти две неизвестные стороны, если известны третья сторона и два угла. Процесс нахождение неизвестных элементов треугольника по уже известным элементам именуется решением треугольника. Всего у треугольника 6 элементов – три стороны и три угла. Для нахождения всех элементов в общем случае достаточно знать только 3 из них, а остальные можно найти, используя теорему синусов или иные геометрические соображения.

Задание. Решите треугольник, если одна из его сторон равна 14, а прилегающие к ней углы имеют величину 60° и 40°.

Решение.

Обозначим описанный в условии треугольник как ∆МВК. Пусть МК = 14, ∠М = 60° и∠К = 40°. Тогда нам надо найти ∠В, МВ и ВК. Проще всего найти∠В, ведь в любом треугольнике все углы в сумме дают 180°:

Обратите внимание, что так как углы 40° и 80° не являются табличными, то их значения надо вычислять на калькуляторе, а результат вычисления получается приближенным. В данном случае мы округлили его до сотых.

Осталось найти сторону ВК, это также делается с помощью теоремы синусов:

Задание. В ∆SRT∠S = 30°, ∠R = 45°, а высота RM, опущенная на сторону TS, имеет длину 6. Решите ∆SRT.

Решение.

Теперь надо найти какую-нибудь сторону в ∆SRT. Для этого рассмотрим ∆RMS. Он прямоугольный, а потому для него можно записать:

Для нахождения двух оставшихся сторон можно использовать теорему синусов:

Задание. В параллелограмме MNEF∠MFE составляет 120°, а диагональ NF равна 24 и образует со стороной NE угол 40°. Найдите длину МN и MF.

Решение.

Далее заметим, что ∠FNE и ∠MFN одинаковы, ведь они накрест лежащие при параллельных отрезках NE и MF и секущей NF:

Теперь в ∆MNF известна сторона NF и все три угла. Это позволяет с помощью теоремы синусов найти и остальные две стороны:

Задание. В окружности радиусом 5 построен вписанный угол величиной 30°. Определите длину хорды, на которую он опирается.

Решение.

Решение. По теореме синусов мы можем записать, что

Теорема косинусов

Теорема синусов помогает решать треугольники, в которых известны хотя бы два угла, а также одна из сторон. Но что делать в случае, если наоборот, даны две стороны, но только один угол? Здесь необходима другая теорема, которую именуют теоремой косинусов.

Возьмем произвольный треугольник со сторонами а, b и c и поместим его на координатной плоскости так, как показано на рисунке:

Обозначим угол между а и b как α. Тогда координаты А будут определяться так:

Точка В в свою очередь будет иметь координаты (а; 0). Зная координаты А и В, мы можем найти квадрат расстояния между ними, то есть величину с²:

Полученное соотношение как раз и является теоремой косинусов.

Данная формула позволяет находить третью сторону треугольника, если известны две другие, а также угол между ними. Однако ее можно переписать так, чтобы с ее помощью можно было вычислять косинус угла, зная все три стороны треугольника:

Это позволяет решать те треугольники, для которых теоремы синусов недостаточно.

Легко заметить, что теорема косинусов похожа на теорему Пифагора. Более того, если угол α = 90°, то формула теоремы косинусов превращается в теорему Пифагора, которая, таким образом, является ее частным случаем. По этой причине иногда теорему косинусов именуют обобщенной теоремой Пифагора.

Задание. Решите ∆MNE, если

Решение. По теореме косинусов находим сторону NE:

Осталось найти ∠N и ∠Е. Для этого запишем теорему косинусов так, чтобы в ней фигурировал ∠N:

Мы нашли cosN. Чтобы вычислить сам ∠N, следует использовать особую функцию на калькуляторе или компьютере, которая называется арккосинусом и является обратной для операции «извлечение косинуса». Более подробно она изучается уже в 10 классе. С ее помощью мы узнаем, что

Обратите внимание, что обычно калькулятор выдает результат, показывая десятые и сотые доли градусы, не переводя их в минуты и секунды. Можно оставить ответ и в таком виде. При желании перевести сотые доли в минуты следует дробную часть умножить на 60:

Задание. На различных сторонах угла∠А, равного 45°, отложены точки В и С так что

Задание. Решите треугольник, если его стороны имеют длину 14, 18 и 20.

Решение.

Решение. Здесь надо дважды применить теорему косинусов, чтобы найти какие-нибудь два угла в ∆АВС:

∠C также можно найти через теорему косинусов, но проще просто вычесть из 180° два уже вычисленных угла:

Во всех рассмотренных задачах на решение треугольника мы знали три элемента треугольника и по ним однозначно вычисляли три других элемента. Однако иногда это невозможно. Так, если в задаче помимо двух сторон указан угол, который НЕ лежит между ними, то в итоге задача может иметь два решения.

Задание. В ∆MNE ∠M составляет 60°, а стороны МЕ и NE имеют длины 10 и 9 соответственно. Какова длина MN?

Решение. Теорему синусов здесь применить не удастся, так как для нее необходимо знать хотя бы два угла. Поэтому остается только записать теорему косинусов так, чтобы в ней использовался ∠M:

Получили квадратное уравнение, решить его можно через дискриминант:

В рамках данного урока мы узнали про теоремы синусов и косинусов и научились использовать их для решения треугольников. Также мы познакомились с новыми формулами для вычисления площадей треугольника и параллелограмма.