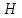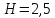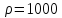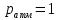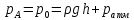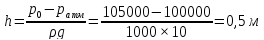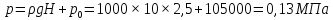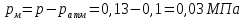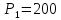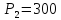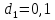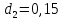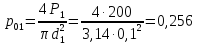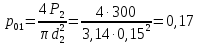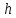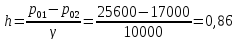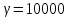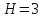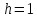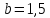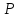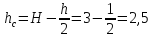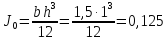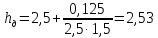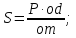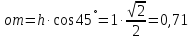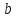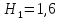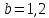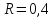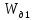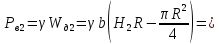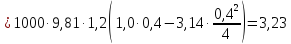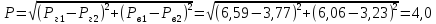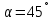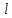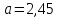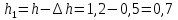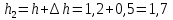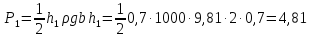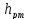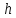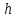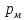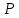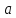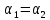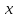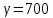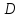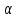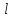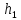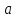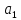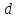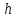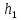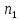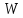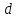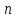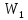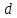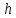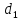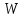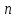В двух одинаковых
сообщающихся сосудах находится ртуть. В один из сосудов налили слой высотой 20
см, а в другой – слой масла высотой 10 см. Плотности ртути, воды и масла
соответственно равны 13600, 1000 и 800 кг/м3. Какая разность уровней
ртути в сосудах?
Решение.
Поскольку жидкости
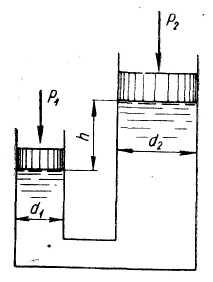
неподвижны, давление в обоих столбах жидкостей в горизонтальном сечении AB одинаковое.
В левом сосуде это давление создается столбом воды
и равно p1 = ρвghв , в правом – маслом и
ртутью высотой Dh и равно p2 + p3 = ρмghм + ρртgDh. Следовательно, p1 = p2 + p3 .
Тогда
ρвghв = ρмghм
+ ρртgDh.
Отсюда Dh = (ρвhв – ρмhм)/ρрт = 8,8 мм.
Ответ: Разность уровней
ртути в сосудах составляет 8,8 мм.
Источник: Пособие-репетитор для подготовки к централизованному тестированию. С.Н.Капельян, Л.А.Аксенович.
Задачи на Сообщающиеся сосуды
Теоретический материал, используемый для решения задачи на сообщающиеся сосуды смотрите в конспекте «Сообщающиеся сосуды. Гидравлический пресс. Шлюзы».
Сообщающиеся сосуды — два или более соединённых между собой сосудов (ниже уровни жидкости), в которых жидкость может свободно перетекать из одного сосуда в другой.
Закон сообщающихся сосудов: в открытых сообщающихся сосудах любой формы при равновесии давление жидкости на любом горизонтальном уровне одинаково.
Схематически это выглядит таким образом, что в точках А и В ⇒ рA = рB.
ρ1gh1 + ρ2gh2 = ρ3gh3 + ρ4gh4
Обратите внимание! Ниже уровня, на котором находятся точки А и В, жидкость однородна. Обозначения: р — давление, ρ — плотность, h — высота, g — ускорение свободного падения (9,8 м/с^2).
Следствие 1: в открытых сообщающихся сосудах при равновесии высоты столбов жидкостей, отсчитываемые от уровня, ниже которого жидкость однородна, обратно пропорциональны плотностям этих жидкостей.

В гидравлическом прессе сообщающиеся сосуды разных сечений S2 и S1 заполненные однородной жидкостью, используют для получения выигрыша в силе — F2/F1, равного — S2/S1.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
В левом колене сообщающихся сосудов налита вода, в правом — керосин. Высота столба керосина 20 см. Рассчитайте, на сколько уровень воды в левом колене ниже верхнего уровня керосина.
Ответ: 0,04 м (или 4 см).
Задача № 2.
В сообщающихся сосудах находятся ртуть и вода. Высота столба воды 68 см. Какой высоты столб керосина следует налить в левое колено, чтобы ртуть установилась на одинаковом уровне?
Ответ: 0,85 м (или 85 см). Чтобы увидеть решение задачи, нажмите на спойлер ниже.
Задача № 3.
Уровень жидкостей в сосудах одинаковый. В левом налита вода, в правом — керосин. Одинаковы ли давления на дно? Одинаковы ли давления на кран? Будет ли переливаться жидкость из одного сосуда в другой, если открыть кран?
ЗАДАЧИ на Сообщающиеся сосуды
Задача № 4.
В сообщающихся сосудах находятся ртуть, вода и керосин. Какова высота слоя керосина, если высота столба воды равна 20 см и уровень ртути в правом колене ниже, чем в левом, на 0,5 см?
Ответ: 0,335 м (или 33,5 см).
Смотреть РЕШЕНИЕ задачи
Задача № 5.
Площадь малого поршня гидравлического пресса равна 10 см2, большого — 50 см2. На малый поршень поместили гирю массой 1 кг. Какой груз нужно поместить на большой поршень, чтобы жидкость осталась в равновесии?
Ответ: 5 кг.
Смотреть РЕШЕНИЕ задачи

Задача № 6.
Какую высоту должен иметь столб нефти, чтобы уравновесить в сообщающихся сосудах столб ртути высотой 16 см?
Ответ: 2,7 м.
Смотреть РЕШЕНИЕ задачи
Задача № 7.
В U-образный сосуд налито 3 жидкости: вода, мед и масло. Высота воды в левом колене 40 см, высота масла в правом колене 30 см. Найдите разницу высот столбов меда в левом и правом коленах. Ответ округлить до сотых.
Ответ: ≈ 0,09 м.
Задача № 8.
В цилиндрических сообщающихся сосудах находится ртуть. Площадь поперечного сечения широкого сосуда в пять раз больше площади поперечного сечения узкого сосуда. В узкий сосуд наливают воду, которая образует столб высотой 34 см. На сколько поднимется уровень ртути в широком сосуде и на сколько опустится в узком?
Ответ: в широком сосуде на 0,42 см, в узком — на 2,1 см.
Задача № 9.
Высота воды в левом колене сообщающихся сосудов h1 = 40 см, в правом h2 = 10 см. В каком направлении будет переливаться вода, если открыть кран? На сколько изменится уровень воды в левом сосуде? Найти объем воды, который перелился из одного сосуда в другой. Левое колено сосуда имеет площадь поперечного сечения S1 = 10 см2, правое S = 20 см2.
Ответ: в правый; 0,2 м; 0,2 л.
Смотреть РЕШЕНИЕ задачи
Задача № 10.
В два колена сообщающихся сосудов налили ртуть. После установления равновесия высота ртути оказалась равна 25 см. Затем в левый сосуд (левое колено) добавили воду. Высота столба воды оказалась равна 20 см. Определите уровень ртути в левом и правом колене после добавления воды. Плотность воды 1 г/см3. Плотность ртути 13600 кг/м3.
ОТВЕТ: в левом — 0,24265 м (≈24,3 см), в правом — 0,25735 м (≈25,7 см).
Вы смотрели: Конспект урока по физике «Задачи на Сообщающиеся сосуды и Гидравлический пресс». Выберите дальнейшие действия:
- Перейти к теме: Задачи на давление твердых тел с ответами и решениями.
- Перейти к теме: Задачи на давление жидкостей с ответами и решениями.
- Вернуться к Списку конспектов по физике для 7-11 классов
- Найти конспект через Кодификатор ОГЭ по физике
- Найти конспект через Кодификатор ЕГЭ по физике
ГИДРОСТАТИКА
Задачи
и примеры их решения
|
|
|
Рис.1 |
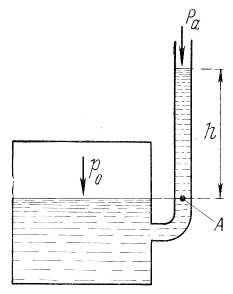
Задача
1.
В закрытом сосуде находится вода, глубина
наполнения сосуда
Давление на поверхности

Определить высоту поднятия воды
в открытой трубке над уровнем в сосуде
(давление в открытом конце трубки
атмосферное); полное и избыточное
давление у дна сосуда. Построить эпюры
гидростатического давления на плоскую
боковую стенку в закрытом сосуде (рис.1).
Решение
задачи 1:
Примем
м,
атм,
кг/м3?
атм.
Так
как жидкость находится в покое, то
гидростатическое давление в трубке на
глубине
равно давлению на поверхности жидкости
в сосуде
и определяется из основного уравнения
гидростатики следующим образом:
откуда
высота поднятия воды в открытой трубке
над уровнем в сосуде:
Для
определения полного (или абсолютного)
давления у дна сосуда воспользуемся
основным уравнением гидростатики:
Избыточное
(или манометрическое) давление есть
превышение полного (абсолютного) давления
над атмосферным, то есть:
Эпюра
дает графическое изображение изменения
гидростатического давления вдоль
поверхности. Так как избыточное
гидростатическое давление в точке
боковой стенки закрытого резервуара у
поверхности равно 0,05 атм, а в точке у
дна — 0,3 атм, для построения эпюры давления
на эту стенку необходимо восстановить
перпендикуляры в удобном масштабе к
точкам у поверхности и дна, соединить
концы перпендикуляров прямой линией,
т. к. давление изменяется с глубиной
линейно и направлено по нормали к
площадке действия.
|
|
|
Рис. |
Задача
2.
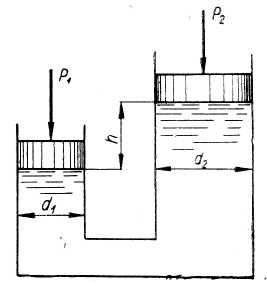
На поршень одного из сообщающихся
сосудов (рис.2), наполненных водой,
действует сила

а
на поршень второго сосуда
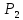
Определить
разность уровней жидкости в сосудах

если диаметр первого поршня
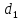
второго
поршня
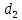
Примем
Н,
Н,
м,
м.
Давление
на единицу площади на поверхности
жидкости под первым поршнем
атм.
То
же, на поверхности жидкости под вторым
поршнем
атм.
Гидростатическое
давление во втором сосуде на глубине
определяется
по основному уравнению гидростатики
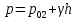
Так
как жидкость находится в покое, можно
записать

Тогда
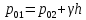
откуда
м,
где
Н/м3
— объемный вес воды.
|
|
|
Рис. |
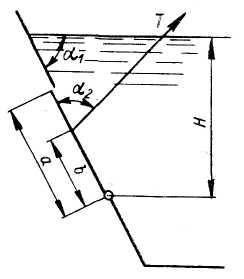
Задача
3.
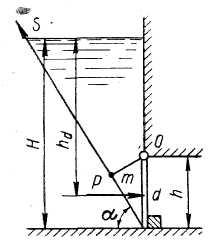
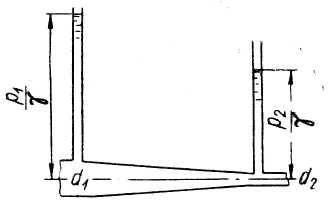
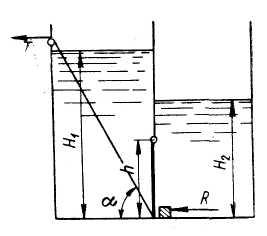
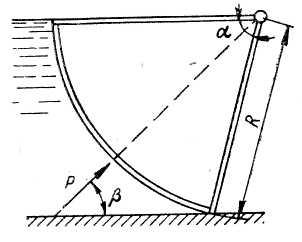
Донное отверстие плотины перекрывается
плоским прямоугольным щитом (рис.3),
шарнирно прикрепленным к телу плотины
своей верхней кромкой. Определить, какое
усилие нужно, приложить к тросу для
открытия щита, если глубина погружения
нижней кромки щита
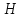
высота
щита
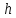
ширина
щита
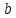
угол
между направлением троса и горизонтом
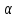
Решение задачи 3:
Примем
м,
м,
м,
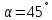
Давление
воды на щит
определяем
по формуле
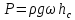
где площадь щита
м2;
глубина
погружения центра тяжести щита
м.
кН.
Глубину
погружения центра давления щита находим
по формуле:
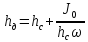
где
момент инерции площади щита
м4,
тогда
м.
Усилие
для открытия щита определится из
равенства моментов
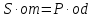
откуда
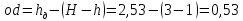
м,
кН.
|
|
|
Рис. |
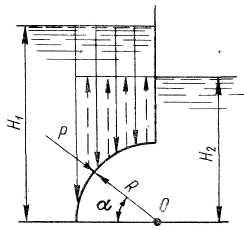
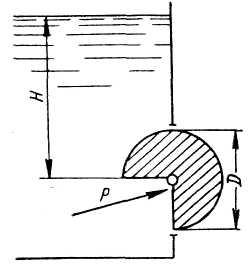
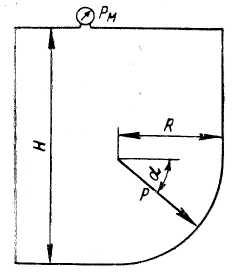
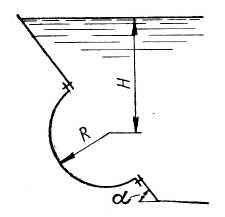
Задача
4.
В
призматическом сосуде шириной
установлена
перегородка, имеющая в своей нижней
части форму четверти цилиндрической
поверхности с радиусом
Определить
суммарное давление воды на криволинейную
часть перегородки, если глубина воды
слева
справа
Найти
точку приложения равнодействующей
давления воды.
Решение задачи 4:
Примем
м,
м,
м,
м.
Горизонтальная
составляющая давления воды слева
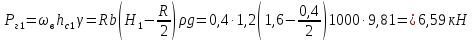
Горизонтальная
составляющая давления воды справа
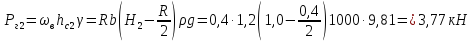
Вертикальная
составляющая давления воды слева
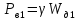
где
— объем тела давления,
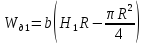
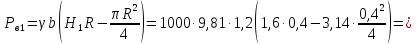
кН.
Вертикальная
составляющая давления воды справа
кН.
Суммарное
давление воды
кН.
Суммарное
давление воды направлено перпендикулярно
к поверхности перегородки, поэтому
линия ее действия должна пройти через
центр О.
Угол
наклона линии действия суммарного
давления к горизонту определяем из
соотношения
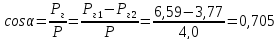

Из
центра О
проводим
линию под углом
к горизонту. Точка пересечения этой
линии с перегородкой является точкой
приложения равнодействующей давления
воды.
Задача
5.
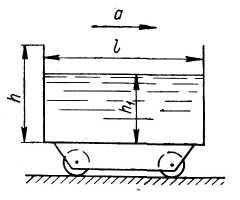
Призматический
сосуд длиной
шириной
заполнен водой на глубину
(рис.5).
Определить
силы давления воды на переднюю и заднюю
стенки сосуда при его горизонтальном
перемещении с ускорением
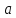
|
|
|
Рис. |
Решение
задачи 5:
Примем
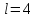
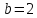
м,
м/с2.
Понижение
уровня воды у передней стенки и повышение
уровня воды у задней стенки движущегося
сосуда определяем по зависимости
м.
Глубина
воды у передней стенки
м.
Глубина
воды у задней стенки
м.
Сила
давления воды на переднюю стенку
кН.
Сила
давления воды на заднюю стенку
кН.
Задача
6.
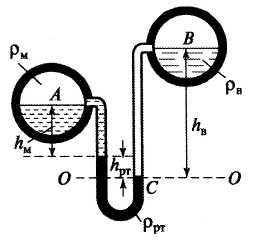
Два
горизонтальных цилиндрических
трубопровода А
и
В
содержат
соответственно минеральное масло
плотностью 900 кг/м3
и воду плотностью 1000 кг/м3.
Высоты жидкостей, представленные на
рис. 6, имеют значения:
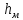
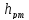
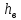
Зная, что гидростатическое давление на
оси в трубопроводе А
равно
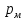
определить давление на оси трубопровода
В.
|
|
|
|
|
Рис.6 |
Рис. |
Рис. |
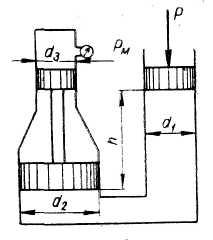
Задача
7.
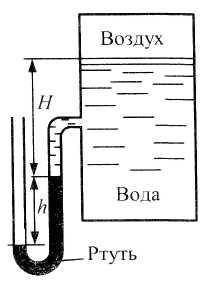
Определить абсолютное давление воздуха
в сосуде, если показание ртутного прибора
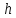
высота
(рис.7).
Плотность ртути
кг/м3.
Атмосферное давление 736 мм рт. ст.
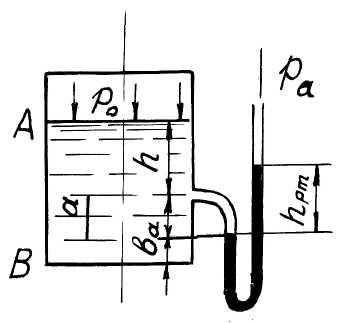
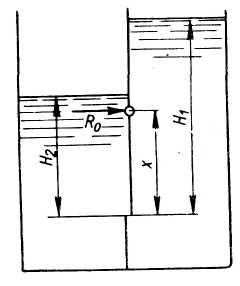
Задача
8.
Определить давление
на
поверхность воды в закрытом сосуде,
если ртутный манометр показывает
разность уровней ртути
(рис.8).
Известно:

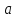
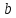
Построить
эпюру гидростатического давления на
плоскую поверхность AВ.
Задача
9. Определить
давление на свободной поверхности в
закрытом сосуде (рис.9), если в трубке,
присоединенной к сосуду, ртуть поднялась
на высоту
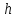
|
|
|
|
|
Рис.9 |
Рис. |
Рис. |
Задача
10.
Определить манометрическое давление
воздуха в рабочей камере кессона
(рис.10), погруженного на глубину
от поверхности воды, при условии
непроникновения воды в кессон.
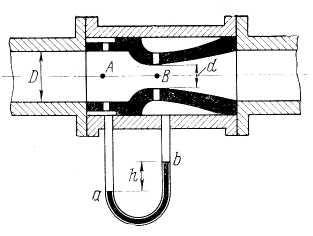
Задача
11.
Определить разность давлений в точках
А
и В расходомера Вентури, если показание
ртутно-водяного дифференциального
манометра
(рис.11).
Задача
12. Определить,
на какую высоту
поднимется
вода в пьезометрической трубке под
действием плунжеров (рис.12) при следующих
данных: диаметр плунжера
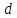
заглубление
плунжера

сила
давления на плунжер
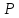
Собственный
вес плунжера не учитывать.
|
|
|
|
|
Рис.12 |
Рис. |
Рис. |
Задача
13.
На поршень одного из сообщающихся
сосудов, наполненных водой (рис.13),
действует сила
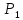
Какую
силу
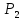
нужно
приложить ко второму поршню, чтобы
уровень воды под ним был на
выше уровня воды под первым поршнем?
Диаметр первого поршня
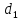
второго
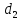
Задача
14.
Определить манометрическое давление
в верхней части одного из сообщающихся
сосудов, наполненных водой (рис.14), под
действием силы
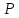
приложенной
к поршню правого сосуда. Исходные данные:
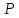
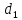
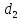
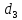

Задача
15.
Какую
силу
нужно
приложить к поршню левого сосуда,
наполненного водой, чтобы уравновесить
давление воды на поршень правого сосуда
(рис.15)? Исходные данные:
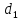
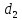

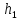
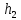
|
|
|
|
|
Рис.15 |
Рис. |
Рис. |
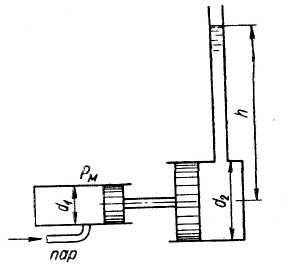
Задача
16.
Определять высоту
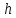
на
которую может поднять воду прямодействующий
паровой насос (рис.16) при следующих
данных: диаметр парового цилиндра
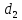
манометрическое
давление в паровом цилиндре

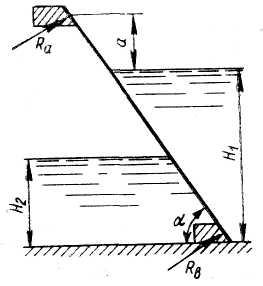
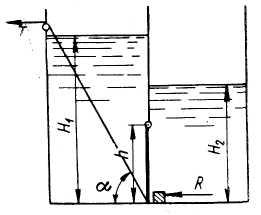
Задача
17.
Определить реакции верхнего и нижнего
опорных брусьев, на которые опирается
щит, перекрывающий прямоугольное
отверстие плотины шириной
при
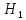

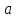
(рис.17).
Задача
18.
Квадратное
отверстие со стороной
в
наклонной
стенке резервуара с водой закрыто
поворотным щитом. Определить натяжение
каната
при
следующих данных:
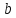

(рис. 18).
Задача
19.
В перегородке,
разделяющей резервуар на две части,
устроен вырез, который закрывается
прямоугольным щитком (рис.19). Определить,
на каком расстоянии
должна
быть расположена ось поворота щита,
чтобы он автоматически открывался при
уровне воды в правой камере
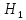
если
с другой стороны щита сохраняется
постоянный уровень
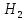
Определить
реакцию шарнира
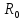
Ширина щита
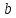
|
|
|
|
|
Рис.18 |
Рис. |
Рис. |
Задача
20.
В
перегородке, разделяющей резервуар на
две части, имеется прямоугольное
отверстие, которое закрывается поворотным
щитом высотой
и
шириной b
(рис.20).
Определить,
какую силу
нужно приложить к тросу для поворота
щита при
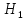


Найти
реакцию донного порога

Задача
21.
Поворотный клапан закрывает выход из
бензохранилища в трубу квадратного
сечения (рис.21). Определить, какую аилу
нужно
приложить к тросу для открытия клапана
при следующих данных:
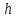
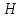
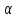
объемный вес бензина
кг/м3;
манометрическое
давление паров бензина в резервуаре
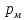
|
|
|
|
|
Рис.21 |
Рис. |
Рис. |
Задача
22.
В прямоугольном окне вертикальной
стенки резервуара установлен на цапфах
цилиндрический затвор диаметром
и шириной
(рис.22).
Определить
суммарное усилие на цапфы и момент от
воздействия воды на затвор при напоре

Задача
23.
Секторный
затвор плотины с центральным углом
имеет ось вращения, расположенную в
плоскости свободной поверхности воды
(рис.23). Определить величину и направление
суммарного давления воды на затвор,
если радиус затвора
и
ширина затвора
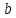
Задача
24.
Определить величину и направление
равнодействующей давления воды на
криволинейную стенку резервуара в виде
четверти цилиндрической поверхности
радиусом
шириной
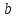
если
глубина воды в резервуаре
и давление
на поверхности
(рис.24).
|
|
|
|
|
Рис.24 |
Рис. |
Рис. |
Задача
25.
Определить
растягивающее и срезающее усилия,
действующие на болты, которыми прикреплена
полусферическая крышка, закрывающая
круглое отверстие в наклонной стенке
резервуара при следующих данных:
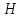
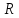
(рис.25).
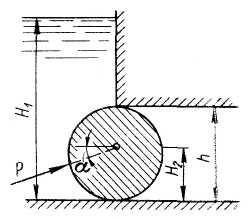
Задача
26.
Определить
величину и направление равнодействующей
давления воды на цилиндрический затвор
плотины, перекрывающий прямоугольное
донное отверстие высотой
и
шириной
(рис.26).
Глубина
воды слева

справа
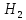
Задача
27. Призматический
резервуар длиной
и
высотой
наполнен
жидкостью на глубину
(рис.27).
С
каким наибольшим ускорением
должен
перемещаться резервуар в горизонтальном
направлении, чтобы не происходило
перелива жидкости через его заднюю
стенку? При каком ускорении
начнется
обнажение дна резервуара у его передней
стенки?
|
|
|
|
|
Рис.27 |
Рис. |
Рис. |
Задача
28.
Призматический резервуар длиной
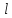
шириной
и
высотой
движется
в горизонтальном направлении с ускорением
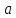
Какой
наибольший объем жидкости
можно
налить в сосуд, чтобы не происходило
перелива жидкости через его заднюю
стенку? Какой объем жидкости
останется
в сосуде при его движении с ускорением
(рис.27).
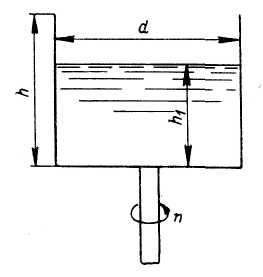
Задача
29.
Цилиндрический
сосуд диаметром
и
высотой
наполнен
жидкостью на глубину
(рис.28).
С
каким числом оборотов
нужно
вращать сосуд, чтобы жидкость поднялась
до его краев? При каком числе оборотов
начнется
обнажение дна сосуда?
Задача
30.
Определить,
какой объем жидкости
нужно
налить в цилиндрический сосуд диаметром
и
высотой
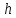
чтобы
при его вращении с числом оборотов
жидкость
поднялась до краев сосуда (рис.28). Какой
объем жидкости
останется
в сосуде при его вращении с числом
оборотов
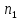
Задача
31.
В
цилиндрический сосуд диаметром
и
высотой
с
отверстием в верхней крышке диаметром
налит
объем жидкости
(рис.29).
Определить,
с каким наибольшим числом оборотов
можно
вращать сосуд, чтобы жидкость не
выливалась на него?
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Комментарии преподавателя
Закон сообщающихся сосудов
Когда жидкость находится в равновесии, ее поверхность горизонтальна — например, в стакане с чаем (рис. 1, а). Поверхность жидкости остается горизонтальной и при наклоне сосуда (рис. 1, б).
Рис. 1. Поверхность покоящейся жидкости в сосуде всегда горизонтальна
Все точки горизонтальной поверхности находятся на одном и том же уровне. А будет ли поверхность жидкости на одном уровне в различных сосудах, если жидкость может перетекать из одного сосуда в другой? Такие сосуды называют сообщающимися.
Поставим опыт
Укрепим в штативе U-образную стеклянную трубку. Ее колена представляют собой сообщающиеся сосуды. Нальем подкрашенную воду в любое колено трубки — мы увидим, что вода установится в обоих коленах на одном уровне (рис. 2, а).
Если наклонить трубку, то часть воды перельется из одного колена в другое так, что поверхность воды в коленах будет снова на одном уровне (рис. 2, б).
Рис. 2. Поверхность жидкости в сообщающихся сосудах находится всегда на одном уровне
Итак, в сообщающихся сосудах поверхность жидкости находится на одном уровне.
Это утверждение называют законом сообщающихся сосудов. Закон сообщающихся сосудов обусловлен текучестью жидкости и тем, что давление жидкости растет с увеличением глубины.
Рис. 3. Пока уровни жидкости в сообщающихся сосудах не станут одинаковыми, жидкость будет перетекать из сосуда, где уровень жидкости выше, в сосуд, где уровень жидкости ниже
Действительно, если в одном из сообщающихся сосудов уровень жидкости был бы выше, то давление жидкости у дна этого сосуда было бы больше, вследствие чего жидкость начала бы перетекать в тот сосуд, где уровень жидкости ниже (рис. 3).
Закон сообщающихся сосудов справедлив только для сосудов, содержащих одну и ту же жидкость (или разные жидкости, но с одинаковой плотностью). В разделе «Сообщающиеся сосуды с различными жидкостями» мы рассмотрим пример для жидкостей с различной плотностью.
Как работает водопровод? На рис. 4 изображена схема действия водопровода в небольшом населенном пункте. Воду из реки или озера накачивают насосами в высоко расположенный бак — его устанавливают на водонапорной башне. А из этого бака вода течет в дома, подчиняясь закону сообщающихся сосудов.
Рис. 4. Схема действия водопровода в поселке. Вода постулает в дома из высоко расположенного бака.
Сообщающиеся сосуды с различными жидкостямиРассмотрим на примере случай, когда в сообщающиеся сосуды налиты несмешивающиеся жидкости с различной плотностью. Решим задачуВ U-образной трубке находятся вода и масло (рис. 5). Высота слоя масла равна 10 см. Насколько уровень поверхности масла выше уровня поверхности воды? Будем считать, что плотность масла равна 900 кг/м3. Решение. На уровне поверхности раздела масла и воды (отмеченном пунктирной линией на рис.5) давление одинаково (иначе вода в нижней части трубки перетекала бы в сторону меньшего давления). Следовательно, давление, создаваемое слоем масла, равно давлению, создаваемому слоем воды над отмеченным уровнем. Если обозначить высоту слоя масла hм, а указанного слоя воды hв, то получим ρмghм = ρвghв, где ρм и ρв — плотность масла и воды соответственно. Отсюда hв/hм=ρм/ρв, то есть уровень жидкости выше в сосуде, содержащем, жидкость с меньшей плотностью. Найдем разность уровней жидкостей. Из выведенной формулы получаем Поскольку высота слоя масла по условию 10 см. получаем, что уровень масла на 1 см. выше уровня воды. Ответ: на 1 см. Рис. 5. Если в сообщающиеся сосуды налиты жидкости с различной плотностью, уровни жидкости в сосудах будут разными Домашняя работа Задание 1. Ответь на вопросы.
Задание 2. Реши ребус. К занятию прикреплен файл «Это интересно!». Вы можете скачать файл в любое удобное для вас время. Использованные источники: http://www.tepka.ru/fizika_7 |
На рис. 156 изображено несколько сосудов, соединенных снизу между собой трубкой. Такие сосуды называют сообщающимися. Если в сообщающиеся сосуды налить однородную жидкость, то эксперимент показывает, что поверхности жидкости во всех сосудах установятся на одной высоте h.
В сообщающихся сосудах поверхности однородной жидкости устанавливаются на одном уровне.
Это явление можно объяснить, используя выведенную формулу для расчета гидростатического давления. Поскольку жидкость находится в состоянии покоя, то ее давление в точках A, B, C и D, находящихся на одном горизонтальном уровне, должно быть одинаковым. В противном случае жидкость, находящаяся между этими точками, начала бы двигаться. Давление в рассматриваемых точках определяется атмосферным давлением, плотностью жидкости и высотой ее столба. Так как налитая жидкость однородна и атмосферное давление на поверхности жидкости во всех сосудах одинаково, то высота столбов жидкости во всех сосудах должна быть одинакова.
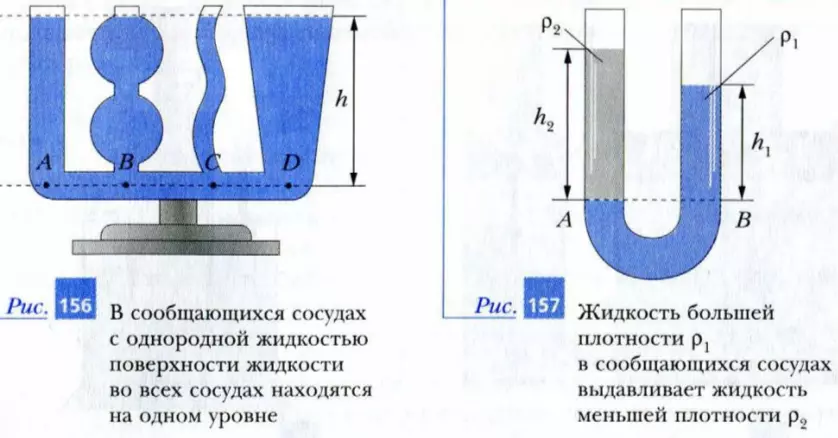
Наоборот, если в сообщающиеся сосуды налить разные по плотности жидкости, то высота столбов этих жидкостей будет разной. На рис. 157 изображена U-образная трубка, в правое колено которой налили жидкость с плотностью ρ1, а в левое колено – жидкость с плотностью ρ2. В данном случае ρ1 > ρ2. Поэтому более плотная жидкость выдавливает менее плотную и частично заполняет левое колено. Так как жидкости покоятся, то гидростатические давления в правом и левом коленах на уровне AB границы раздела жидкостей равны. Из формулы для расчета гидростатического давления находим
pA = pатм + ρ2 · g · h2 и pB = pатм + ρ1 · g · h1.
Поэтому ρ2 · g · h2 = ρ1 · g · h1, или ρ2 · h2 = ρ1 · h1.
Проанализируем полученное соотношение. Если ρ1 > ρ2 в некоторое число раз, то h12 в такое же число раз.
Разновидности сообщающихся сосудов находят широкое применение в науке и технике. Рассмотрим один из примеров — гидравлический пресс.
Принцип работы гидравлического пресса иллюстрирует устройство, показанное на рис. 158. Оно состоит из двух сообщающихся цилиндров разных диаметров, в которых могут без трения двигаться легкие поршни. Обозначим площадь меньшего поршня S1, а большего – S2. Цилиндры заполнены жидкостью, предназначенной для передачи гидростатического давления.
Если приложить к меньшему поршню силу F1 (например, поставить на него груз), то эта сила создаст в жидкости добавочное давление p1 = F1/S1. Для того чтобы устройство осталось в равновесии, ко второму поршню нужно приложить силу F2, которая создаст в жидкости давление p2 = F2/S2, равное p1. Следовательно, F2/S2 = F1/S1. Или, по-другому, F2/F1 = S2/S1. То есть F2 во столько раз больше F1, во сколько раз площадь большего поршня S2 больше площади поршня S1. Таким образом, с помощью гидравлического пресса можно получить выигрыш в силе, равный S2/S1. Иначе говоря, прикладывая к малому поршню небольшую силу, можно большим поршнем создать очень большое усилие.
В настоящее время гидравлические прессы способны развивать силу 108 Н. Они используются для штамповки деталей из листового металла, выдавливания профилей, а также для прессования различных материалов – фанеры, картона и др.
По этому же принципу работают гидравлические домкраты (рис. 159), гидравлические усилители автомобильных тормозов и гидравлические усилители руля.
Итоги
Сосуды, соединенные снизу между собой трубкой, называют сообщающимися сосудами.
В сообщающихся сосудах поверхности однородной жидкости устанавливаются на одном уровне.
Если сообщающиеся сосуды заполнены жидкостями разной плотности, то высоты столбов жидкостей над уровнем границы их раздела определяются соотношением: ρ2 · h2 = ρ1 · h1.
В гидравлическом прессе сообщающиеся сосуды разных сечений S2 и S1, заполненные однородной жидкостью, используют для получения выигрыша в силе F2/F1, равного S2/S1.
Вопросы
- Какие сосуды называют сообщающимися? Приведите примеры сообщающихся сосудов.
- От чего зависит разность уровней жидкости в сообщающихся сосудах?
- Что такое гидравлический пресс? Приведите примеры устройств, работающих по тому же принципу, что и гидравлический пресс.
- Каким образом с помощью гидравлического пресса можно получить выигрыш в силе? Можно ли с помощью гидравлического пресса получить выигрыш в работе?
Упражнения
- Найдите, во сколько раз различаются высоты столбов жидкостей над уровнем границы их раздела в сообщающихся сосудах, если плотности жидкостей различаются в два раза (см. рис. 157).
- Как с помощью сообщающихся сосудов и воды определить плотность масла? Плотность воды считать известной.
- Какой максимальный выигрыш в силе можно получить с помощью гидравлического пресса, площади поршней которого S1 = 4 см2 и S2 = 2 м2? Чему будет равен в этом случае модуль силы, действующей на большой поршень, при действии на малый поршень силы, модуль которой равен 600 Н?
- На сколько нужно переместить малый поршень пресса из упражнения 3, чтобы большой поршень переместился на 1 мм?
- Под действием силы 100 Н малый поршень гидравлического пресса опустился на 20 см. При этом большой поршень поднялся на 5 см. Какая максимальная сила гидростатического давления действовала на большой поршень?