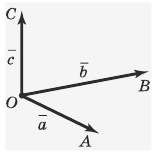
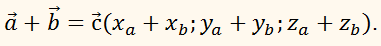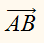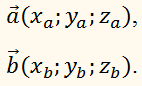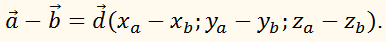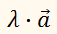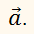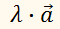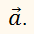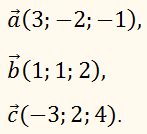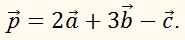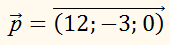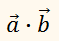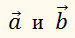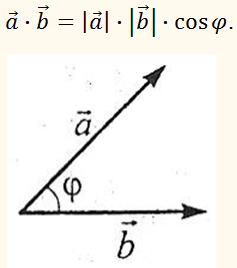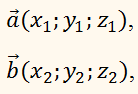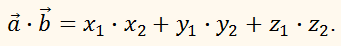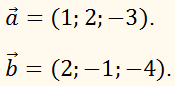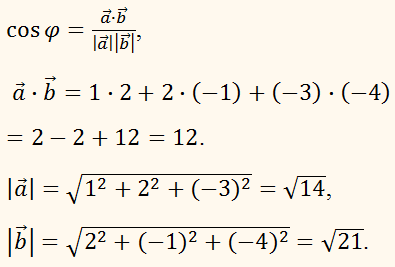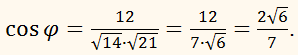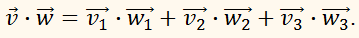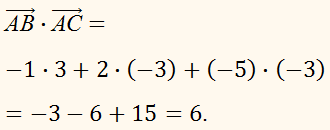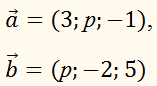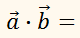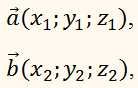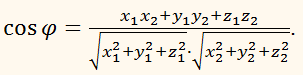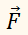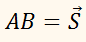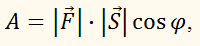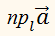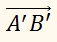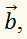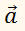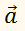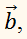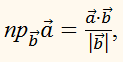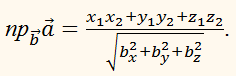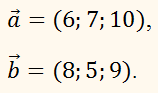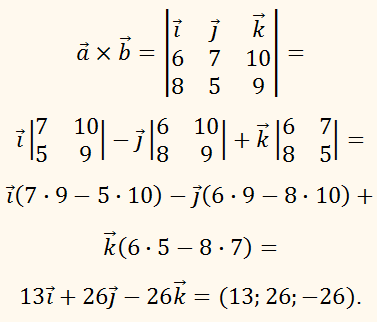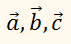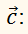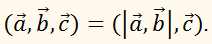Пусть нам дан вектор ( overrightarrow ) и действительное число ( k ) .
Определение Произведением вектора ( overrightarrow ) на действительное число ( k ) называется вектор ( overrightarrow ) удовлетворяющий следующим условиям:
Длина вектора ( overrightarrow ) равна ( left|overrightarrowright|=left|kright||overrightarrow| ) ;
Векторы ( overrightarrow ) и ( overrightarrow ) сонаправлены, при ( kge 0 ) и противоположно направлены, если ( kle 0 )
Обозначение: ( overrightarrow=koverrightarrow ) .
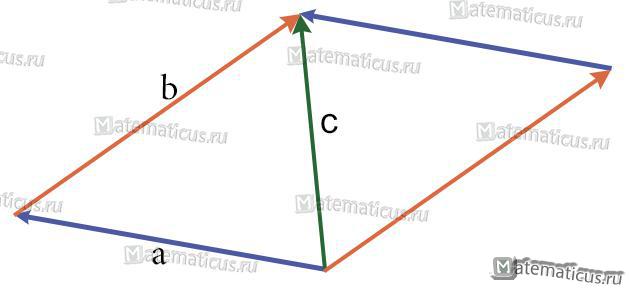
Для правила сложения трех векторов рассмотрим следующую задачу.
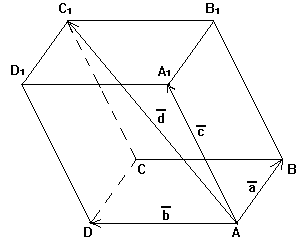
Дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Доказать, что $overrightarrow+overrightarrow+overrightarrow=overrightarrow$
Доказательство.
Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow=overrightarrow$, получим:
Из этой задачи получаем следующее правило для нахождения сложения трех векторов. Чтобы найти сумму трех векторов $overrightarrow,overrightarrow и overrightarrow$ нужно от произвольной точки $O$ отложить векторы $overrightarrow=overrightarrow$, $overrightarrow=overrightarrow$ и $overrightarrow=overrightarrow$ и построим параллелепипед на этих векторах. Тогда вектор диагонали $overrightarrow$ и будет суммой этих трех векторов. Это правило называется правилом параллелепипеда для сложения трех векторов.
Разложение вектора по двум неколлинеарным векторам
Вспомним сначала, какие векторы называются компланарными.
Два вектора, которые параллельны одной плоскости называются компланарными.
Произвольный вектор $overrightarrow
$ можно разложить по трем некомпланарным векторам $overrightarrow, overrightarrow$ и $overrightarrow$ с единственными коэффициентами разложения.
Математически это можно записать следующим образом
Доказательство.
Существование: Пусть нам даны три некомпланарных вектора $overrightarrow, overrightarrow$ и $overrightarrow$. Выберем произвольную точку $O$ и построим следующие векторы:
[overrightarrow=overrightarrow, overrightarrow=overrightarrow, overrightarrow=overrightarrow и overrightarrow
=overrightarrow]
Рассмотрим следующий рисунок:
Произведем следующие дополнительные построения. Проведем через точку $P$ прямую, которая будет параллельна вектору $overrightarrow$. Пусть эта прямая пересекает плоскость $OAB$ в точке $P_1$. Далее, проведем через точку $P_1$ прямую, которая будет параллельна вектору $overrightarrow$. Пусть эта прямая пересекает прямую $OA$ в точке $P_2$ (смотри рисунок выше).
Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow=overrightarrow$, получим:
Так как векторы $overrightarrow$ и $overrightarrow$ коллинеарны, то
Так как векторы $overrightarrow$ и $overrightarrow$ коллинеарны, то
Так как векторы $overrightarrow$ и $overrightarrow$ коллинеарны, то
Тогда, получаем, что
Существование разложения доказано.
Единственность: Предположим противное. Пусть существует еще одно разложение вектора $overrightarrow
$ по векторам $overrightarrow, overrightarrow$ и $overrightarrow$:
Вычтем эти разложения друг из друга
Из этого получаем
Теорема доказана.
Урок «Сложение и вычитание векторов»
Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Введем правило сложения двух векторов.
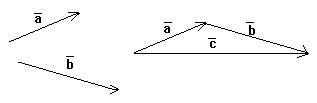
Пусть нам даны два неколлинеарных вектора a и b. Отложим от произвольной точки пространства А вектор АВ, равный вектору а. Затем от точки В отложим вектор ВС, равный вектору b. Вектор АС называется суммой векторов а и b.
Нужно отметить, что сумма векторов не зависит от выбора точки А.
Это правило сложения векторов называется правилом треугольника.
Правило треугольника: для любых трёх точек А, В, С имеет место равенство: вектор АВ плюс вектор ВС получается вектор АС.
При сложении неколлинеарных векторов можно воспользоваться правилом параллелограмма.
Пусть даны векторы а и b. От произвольной точки А отложим векторы АВ и АС, равные соответственно а и b. Достроим до параллелограмма, проведя дополнительные линии, параллельно данным векторам. Вектор AD являющийся диагональю параллелограмма, выходящий из точки А есть сумма векторов а и b.
Решим задачу №327 под буквой а.
На рисунке изображен параллелепипед ABCDA1B1C1D1.Назовите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов AB и A1D1 .
Воспользуемся правилом параллелограмма. К вектору АВ прибавим вектор АD, равный вектору A1D1.
Суммой этих векторов будет диагональ основания параллелепипеда, то есть вектор АС.
Напомним свойства сложения векторов, так как они ни чем не отличаются от свойств сложения векторов в планиметрии:
Для любых трех векторов а, бэ и це, выполняются равенства
1) переместительный закон
2) сочетательный закон
Введем определение противоположных векторов.
Два вектора называются противоположными, если их длины равны и они противоположно направлены
Вектор минус а противоположен вектору а
Вектор DF противоположен вектору FD, и равен минус вектор FD
Определим вычитание векторов
Разностью векторов и называется такой вектор, сумма которого с вектором равна вектору .
Разность векторов и можно найти как сумму вектора с противоположным вектором вектору .
Введем правило вычитания векторов.
Пусть нам даны два неколлинеарных вектора и . Отметим произвольную точку А. Отложим от точки А вектор АВ , равный вектору а и вектор АС, равный вектору b. Вектор СВ будет разностью данных векторов.
Существует правило для трех точек.
Любой вектор можно представить как разность двух векторов, проведенных из одной точки.
Добавляем третью точку (любую) и задаем разность из вектора, проведенного из этой точки в конец данного вектора минус вектор, проведенный в начало.
Решим задачу №332
На рисунке изображен параллелепипед ABCDA1B1C1D1 Представьте векторы АВ1 и DK в виде разности двух векторов, начала и концы которых совпадают с отмеченными на рисунке точками.
Рассмотрим вектор АВ1 и воспользуемся правилом трех точек. Третьей точкой удобно взять точку А1. Вектор, проведенный в конец то есть в точку В1 будет А1В1 и в начало точку А – вектор А1А. Получаем АВ1 равно А1В1 минус А1А.
Выполним это же задание для вектора DK. Здесь третьей точкой удобно взять точку D1. Вектор в конец ¬ — D1K, в начало — D1D. Получим вектор DK равен D1K минус D1D.
http://spravochnick.ru/matematika/dekartovy_koordinaty_i_vektory_v_prostranstve/pravilo_parallelepipeda_razlozhenie_vektora/
http://urokimatematiki.ru/urok-slozhenie-i-vichitanie-vektorov-951.html
Skip to content
Сложение векторов
Сложение векторов по правилу параллелограмма
Правило параллелограмма
Если слагаемые a и b не коллинеарны, то
c=a+b
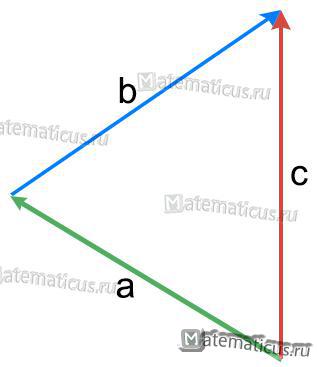
Сложение векторов по правилу треугольника
Правило треугольника
Суммой векторов a (на рисунке зелёный вектор) и b (на рисунке синий вектор) называется третий вектор c (на рисунке красный вектор) , получаемый следующее построение:
Примечание
Нельзя смешивать понятие «сумма отрезков» с понятием «сумма векторов».
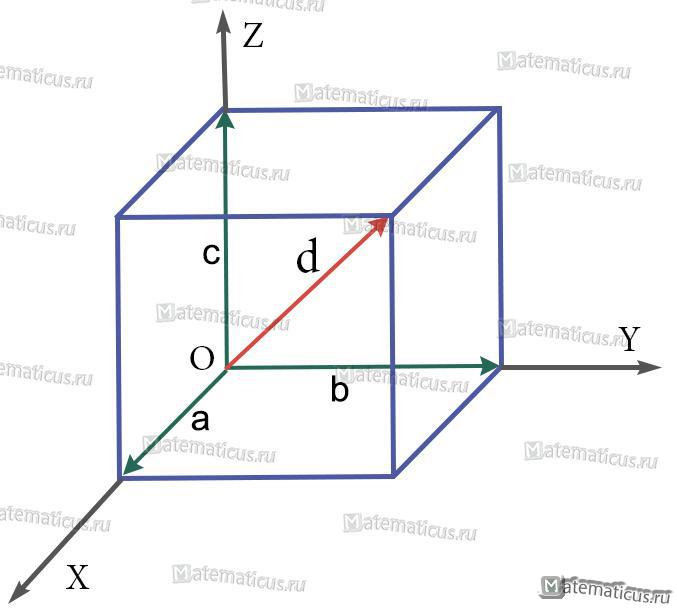
Правило параллелепипеда
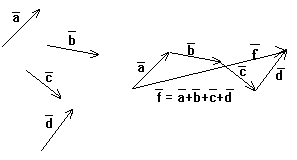
Если три вектора a, b, c после приведения к общему началу не лежат в одной плоскости , то их сумма равна диагонали параллелепипеда
d=a+b+c
Правило параллелепипеда применяется для сложения трех некомпланарных векторов.
Сложение противоположных векторов
Сумма противоположных векторов равна нуль-вектору, т.е.
a+(-a)=0
Свойство переместительности (переместительный закон)
От перестановки слагаемых сумма векторов не меняется.
с=a+b= b+a
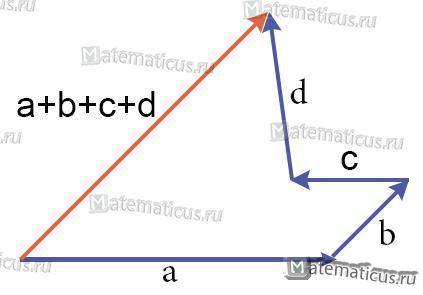
Сочетательное свойство (сочетательный закон)
Слагаемые векторы можно группировать как угодно.
a+(b+c+d) = a+b+c+d
Вычитание векторов
Вычесть вектор а (вычитаемое) из вектора b (уменьшаемое) значит найти новый вектор x (разность), который в сумме с вектором а даёт вектор b.
Разность векторов обозначается: a-b
Вычитание есть действие обратное сложению (сложение векторов).
Вычитание векторов показаны на рисунках ниже:
Примечание
Модуль разности может быть меньше модуля «уменьшаемого», но может быть и больше или равен ему. Эти случаи показаны на рисунке выше.
5719
ВИДЕО УРОК
Сумма
векторов, их разность, произведение вектора на число и скалярное произведение
векторов определяется так же, как и на плоскости. Только координат не две, а
три.
Сложение
векторов.
Для трёх
векторов (АО, ОС, ОО1), которые
не лежат в одной плоскости и имеют общее начало
О, их сумма изображается диагональю параллелепипеда
(ОВ1), построенного на этих
векторах, причём начало вектора-суммы совпадает с началом этих векторов.
Координаты
вектора-суммы векторов равны сумме соответствующих координат данных векторов.
Сложение
двух векторов производится покоординатно, то есть, если
то
c = {x3; y3; z3} =
{x1; y1; z1} + {x2; y2; z2} =
{x1 + x2; y1 + y2; z1 + z2}.
Данная
формула имеет место для произвольного конечного числа слагаемых.
Правило параллелепипеда сложения векторов.
Пусть даны три вектора
не лежащие в одной плоскости (их называют
некомпланарными).
Выполним следующие построения:
1. Отложим от
произвольной точки О векторы
2. Построим параллелепипед так, чтобы отрезки
ОА,
ОВ, ОС
были его рёбрами.
Из рисунка видно, что
Таким образом, сумма трёх векторов, не параллельных одной плоскости
представляется диагональю параллелепипеда, построенного на данных векторах,
отложенных от одной точки, как на рёбрах.
Получили правило параллелепипеда для сложения векторов в
пространстве.
ПРИМЕР:
Возьмём векторы
Сумма
векторов равна:
Вычитание векторов.
Вычитание двух векторов производится
покоординатно, аналогично сложению, то есть если
то
c = {x3; y3; z3} =
{x1; y1; z1} – {x2; y2; z2} =
{x1 – x2; y1 – y2; z1 – z2}.
Геометрически два вектора складываются по правилу
параллелограмма с учётом того, что разностью векторов является диагональ,
соединяющая концы векторов, причём результирующий вектор направлен из конца
вычитаемого в конец уменьшаемого вектора.
Важным следствием вычитания векторов является тот факт,
что если известны координаты начала и конца вектора, то для
вычисления координат вектора необходимо из координаты его конца вычесть
координаты его начала.
Любой вектор пространства
может быть представлен в
виде разности двух векторов, исходящих из начала координат:
Координаты векторов
совпадают с координатами точек А и В, так как начало координат
О(0;
0; 0).
Таким образом, по правилу вычитания векторов следует
произвести вычитание координат точки А из координат точки В.
Возьмём
векторы
Разность векторов равна:
Произведение векторов.
Умножение вектора на
число λ
покоординатно:
При λ
˃ 0 –
вектор
сонаправлен
При λ < 0 – вектор
противоположно направлен
При | λ | ˃ 1 – длина вектора
увеличивается в λ раз.
При | λ | <
1 – длина вектора
уменьшается в λ раз.
ПРИМЕР:
Даны векторы
Найдите координаты вектора:
РЕШЕНИЕ:
ОТВЕТ:
Скалярное произведение векторов.
Скалярным произведением
векторов
называется число (скаляр), равное произведению длин этих векторов на
косинус угла φ между ними, то
есть:
скалярное произведение двух векторов
Скалярное произведение двух
векторов
заданных своими
координатами, равно сумме произведений их одноимённых координат, то есть:
ПРИМЕР:
Найдите угол между векторами
РЕШЕНИЕ:
Воспользуемся формулой:
Тогда
Откуда
ОТВЕТ:
ПРИМЕР:
Найти
скалярное произведение векторов
если даны точки:
РЕШЕНИЕ:
Сначала
найдём векторы:
По формуле
Вычислим скалярное произведение
Скалярное
произведение положительно, значит, угол между пространственными векторами
является острым.
ОТВЕТ: 6
Очевидно, что скалярный квадрат любого ненулевого вектора
равен квадрату его длины, так как в этом случае угол φ = 0, поэтому его
косинус равен 1.
Необходимым и достаточным условием
перпендикулярности двух векторов является равенство нулю их скалярного
произведения.
Если скалярное произведение отличных от нуля векторов
равно нулю, то векторы перпендикулярны.
ПРИМЕР:
При каком
значении р векторы
взаимно
перпендикулярны ?
РЕШЕНИЕ:
Два
ненулевых вектора перпендикулярны тогда и только тогда, когда их скалярное произведение
равно нулю.
3 ∙ р
+ р ∙ (–2) + (–1) ∙ 5
= 3р – 2р
– 5 = р – 5,
тогда
р –
5 = 0.
Откуда р = 5.
ОТВЕТ: р =
5
Попарные скалярные произведения единичных орт
равны нулю, то есть:
С помощью скалярного произведения векторов можно
вычислить угол между ними.
Если заданы два ненулевых вектора своими
координатами
то косинус угла φ между ними:
то есть
Отсюда следует условие
перпендикулярности ненулевых векторов
х1 x2 + y1y2
+ z1z2 = 0.
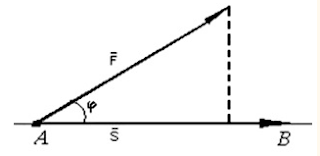
С помощью скалярного
произведения векторов находят работу постоянной силы
на прямолинейном участке пути.
Предположим, что под действием постоянной силы
материальная точка
перемещается прямолинейно из положения А в положение В. Вектор силы
образует угол φ с вектором перемещения
Физика утверждает, что
работа силы
при перемещении
равна
то есть
Следовательно, работа
постоянной силы при прямолинейном перемещении точки её приложения равна
скалярному произведению вектора силы на
вектор перемещения.
Проекции векторов.
Пусть в пространстве задана прямая (ось l), вектор
задан координатами конца и начала. Обозначим проекции
точек А и В на ось
l соответственно
через А‘ и
В‘.
Проекцией
вектора
на ось l называется длина вектора
взятая со знаком <<+>>,
если вектор
и ось l
сонаправлены, и со знаком <<–>>,
если
противоположно направлены.
Если в качестве оси l взять
некоторый другой вектор
то получим проекцию вектора
на вектор
Нахождение проекции вектора
на направление, заданное
вектором
может осуществляться по
формуле:
то есть
Некоторые основные свойства проекций.
1. Проекция вектора
на ось l равна
произведению модуля вектора
на косинус угла между
векторами и осью, то есть
2. Проекция вектора на ось положительна (отрицательна),
если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол –
прямой.
3. Проекция суммы
нескольких векторов на одну и ту же ось равна сумме проекций на эту ось.
Свойства векторного произведения.
Если векторы заданы
своими координатами:
то векторное произведение находится по формуле:
ПРИМЕР:
Найти векторное
произведение векторов:
РЕШЕНИЕ:
Составим определитель и
вычислим его:
Смешанное произведение векторов.
Смешанным произведением
трёх векторов
называется число, равное скалярному произведению
векторов
на вектор
Геометрический смысл смешанного произведения.
1.
Правилом
треугольника
Суммой двух векторов
и
называется третий вектор
,
соединяющий начало вектора
с концом вектора
,
при условии, что начало вектора
помещено в конец вектора
.
2
Правило
параллелограмм.
Если векторы
и
привести к общему началу и построить
на векторах
и
параллелограмм, то диагональ
параллелограмма, выходящая из общего
начала, называется суммой векторов
и
.
3
Правило
многоугольника. Если
векторы расположить так, чтобы начало
каждого следующего вектора поместить
в конец предыдущего, то суммой нескольких
векторов называется вектор, соединяющий
начало самого первого вектора с концом
последнего
Число слагаемых
векторов может быть любое конечное,
многоугольник в результате сложения
может быть выпуклым, а может и нет .
4.Правило
параллелепипеда. Сумма
трех некомпланарных векторов, приведенных
к общему началу, равна диагонали
параллелепипеда, построенного на этих
векторах, выходящая из общего начала.
.
Если
обозначить
,
тогда получим:
Вычитание
Правило
5 Разностью
двух векторов
и
называется третий вектор
,который
в сумме с вектором
даёт вектор
.
т.е.
.
Если
привести векторы к общему началу и
построить на них параллелограмм, то
диагональ параллелограмма, не выходящая
из общего начала, является разностью
векторов, т.е. разность векторов –
вектор, проведённый из конца вычитаемого
в конец уменьшаемого.
Свойства
(суммы и разности векторов)
Относительно
сложения имеют место законы:
1)
— коммутативный
(переместительный);
2)
— ассоциативный
(сочетательный);
3)
для любого вектора
существует нулевой вектор
,
такой,
что
;
4)
для каждого вектора существует вектор
такой, что
вектор
называется противоположным вектору
и обозначается
,
т.е.
=-
.
Умножение вектора на число
Правило
6.Произведением
вектора
на число
называется вектор
,
коллинеарный вектору
,
длина которого равна
,
а направление совпадает с вектором
,
если
,
и противоположное, если
.
.
Относительно
умножения на число имеют место законы:
а)
—распределительный;
б)
—сочетательный
;
в)
—коммутативный.
3. Проекция вектора на ось
Пусть
в пространстве задана ось l.
Опр.10
Проекцией точки М на ось l
называется
основание М1
перпендикуляра
ММ1,
опущенного из точки на ось.
Опр.11.Проекцией
вектора
на ось l
называется длина отрезка
,
взятая со знаком «+», если направление
его совпадает с направлением оси и со
знаком «-», если направление
противоположно направлению оси.
Обозначается
.
Проекция
вектора на ось равна произведению его
модуля на косинус угла
,
который вектор образует с осью.
При
этом углом
между вектором и осью называется угол,
на который нужно повернуть ось до
совмещения с вектором против хода
часовой стрелки.
4.Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы
Проекции
вектора на оси координат называются
его координатами. В этом заключается
их геометрический смысл.
Если
задана система координат на плоскости
и в пространстве, то начало вектора
можно всегда совместить с началом
координат, не меняя при этом длину и
направление. Выделим на координатных
осях единичные векторы и обозначим
.Выберем
произвольный вектор
.
Найдем проекции вектора на координатные
оси.
Проведем
через конец вектора плоскости, параллельные
координатным плоскостям. Точки пересечения
с осями обозначим соответственно через
М1,М2,М3.
Получили прямоугольный параллелепипед,
одной диагональю которого является
.
Тогда
;
;
.
По определению суммы получим, что
,
но т.к.
,то
.
Но
,
,
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вектор – это направленный прямолинейный отрезок, то есть отрезок, имеющий
определенную длину и определенное направление. Пусть точка А – начало вектора, а точка B – его конец, тогда вектор обозначается символом 
или 
. Вектор 
называется противоположным
вектору и может быть
обозначен 
.
Сформулируем ряд базовых определений.
Длиной
или модулем
вектора называется
длина отрезка и обозначается 
. Вектор нулевой длины (его суть — точка) называется нулевым 
и направления
не имеет. Вектор 
единичной длины, называется единичным. Единичный вектор,
направление которого совпадает с направлением вектора , называется ортом вектора .
Векторы
называются коллинеарными, если они лежат на одной прямой или на
параллельных прямых, записывают
. Коллинеарные векторы могут иметь совпадающие или
противоположные направления. Нулевой вектор считают коллинеарным любому
вектору.
Векторы
называются равными 
, если они коллинеарны, одинаково направлены и имеют
одинаковые длины.
Три вектора в пространстве называются компланарными,
если они лежат в одной плоскости или на параллельных плоскостях. Если среди
трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы
компланарны.
Рассмотрим в
пространстве прямоугольную систему координат 0xyz. Выделим на осях координат 0x, 0y, 0z единичные векторы (орты) и
обозначим их через 
соответственно.
Выберем произвольный вектор
пространства и совместим его начало с началом
координат. Спроектируем вектор
на координатные
оси и обозначим проекции через ax, ay, az
соответственно. Тогда нетрудно показать, что
. (2.25)
Эта
формула является основной в векторном исчислении и называется разложением
вектора по ортам координатных осей. Числа ax, ay, az называются координатами вектора . Таким образом, координаты вектора являются его
проекциями на оси координат. Векторное равенство (2.25) часто записывают в
виде
. Мы будем использовать обозначение вектора в фигурных
скобках, чтобы визуально легче различать координаты вектора и координаты точки.
С использованием формулы длины отрезка, известной из школьной геометрии, можно
найти выражение для вычисления модуля вектора
:
, (2.26)
то
есть модуль вектора равен корню квадратному из суммы квадратов его координат.
Обозначим углы между вектором
и осями
координат через α, β, γ соответственно. Косинусы этих углов называются
для вектора направляющими, и для них выполняется соотношение:
Верность данного равенства можно показать с помощью
свойства проекции вектора на ось, которое будет рассмотрено в нижеследующем
пункте 4.
Пусть в трехмерном пространстве заданы векторы 
своими
координатами. Имеют место следующие
операции над ними: линейные (сложение, вычитание, умножение на число и
проектирование вектора на ось или другой вектор); не линейные – различные
произведения векторов (скалярное, векторное, смешанное).
1. Сложение двух векторов производится покоординатно, то
есть если
.
Данная
формула имеет место для произвольного конечного числа слагаемых.
Геометрически
два вектора складываются по двум правилам:
а) правило треугольника –
результирующий вектор суммы двух векторов соединяет начало первого из них с
концом второго при условии, что начало второго совпадает с концом первого
вектора; для суммы векторов –
результирующий вектор суммы соединяет начало первого из них с концом последнего
вектора-слагаемого при условии, что начало последующего слагаемого совпадает с
концом предыдущего;
б)
правило
параллелограмма (для двух
векторов) – параллелограмм строится на векторах-слагаемых как на сторонах,
приведенных к одному началу; диагональ параллелограмма исходящая из их общего начала, является суммой
векторов.
2. Вычитание двух векторов производится
покоординатно, аналогично сложению, то есть если 
, то
.
Геометрически два
вектора складываются по уже упомянутому правилу параллелограмма с учетом того, что разностью векторов
является диагональ, соединяющая концы векторов, причем результирующий вектор
направлен из конца вычитаемого в конец уменьшаемого вектора.
Важным следствием
вычитания векторов является тот факт, что если известны координаты начала и
конца вектора, то для вычисления координат вектора необходимо из координат его конца
вычесть координаты его начала. Действительно, любой вектор пространства может быть
представлен в виде разности двух векторов, исходящих из начала координат: 
. Координаты векторов
и
совпадают с
координатами точек А и В, так как начало координат О(0;0;0). Таким образом, по правилу
вычитания векторов следует произвести вычитание координат точки А из координат точки В.
3. Умножение вектора на число λ покоординатно:
.
При λ>0
– вектор
сонаправлен ; λ<0 – вектор противоположно направлен ; |λ|>1 – длина вектора увеличивается в λ раз; |λ|<1 – длина вектора уменьшается в λ раз.
4. Пусть в пространстве задана
направленная прямая (ось l), вектор 
задан
координатами конца и начала. Обозначим проекции точек A и B на ось l
соответственно через A’ и B’.
Проекцией 
вектора на ось l называется длина вектора 
, взятая со
знаком «+», если вектор и ось l сонаправлены, и со
знаком «–», если и l противоположно направлены.
Если
в качестве оси l взять некоторый другой вектор 
, то получим проекцию вектора на вектор .
Рассмотрим некоторые
основные свойства проекций:
1) проекция вектора на ось l равна произведению модуля
вектора на косинус угла
между вектором и осью, то есть 
;
2.) проекция вектора на ось
положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и
равна нулю, если этот угол – прямой;
3) проекция суммы нескольких
векторов на одну и ту же ось равна сумме проекций на эту ось.
Сформулируем определения и
теоремы о произведениях векторов, представляющих нелинейные операции над
векторами.
5. Скалярным произведением 
векторов и называется
число (скаляр), равное произведению длин этих векторов на косинус угла φ между
ними, то есть
. (2.27)
Очевидно, что скалярный квадрат любого ненулевого вектора равен квадрату его длины, так как в этом случае угол 
, поэтому его косинус (в 2.27) равен 1.
Теорема 2.2. Необходимым и достаточным условием
перпендикулярности двух векторов является равенство нулю их скалярного
произведения 
Следствие. Попарные скалярные произведения единичных орт равны нулю, то есть 
Теорема 2.3. Скалярное произведение двух векторов 
,
заданных своими координатами, равно сумме произведений их одноименных координат, то есть
(2.28)
С помощью скалярного произведения векторов можно
вычислить угол между ними.
Если заданы два ненулевых вектора
своими координатами , то косинус угла φ между ними:
(2.29)
Отсюда
следует условие перпендикулярности ненулевых векторов
и :
(2.30)
Нахождение проекции вектора на направление,
заданное вектором , может осуществляться по формуле
(2.31)
С помощью скалярного произведения векторов находят
работу постоянной силы 
на
прямолинейном участке пути.
Предположим, что под действием постоянной силы материальная точка перемещается прямолинейно из
положения А в положение B. Вектор силы образует угол φ с вектором перемещения 
(рис. 2.14). Физика утверждает, что работа силы при перемещении 
равна 
.
Следовательно, работа постоянной силы
при прямолинейном перемещении точки ее приложения равна скалярному произведению
вектора силы на вектор перемещения.
Пример
2.9. С
помощью скалярного произведения векторов найти угол при вершине A параллелограмма ABCD, построенного на векторах 
Решение. Вычислим модули векторов и их скалярное произведение
по теореме (2.3):
Отсюда согласно формуле (2.29) получим косинус
искомого угла
Пример 2.10. Затраты сырьевых и материальных ресурсов, используемых
на производство одной тонны творога, заданы в таблице 2.2 (руб.).
Какова общая цена этих ресурсов, затрачиваемых на изготовление одной
тонны творога?
Таблица 2.2
Решение. Введем в рассмотрение два вектора: вектор затрат
ресурсов на тонну продукции 
и вектор цены единицы
соответствующего ресурса 
.
Тогда 
. Общая цена
ресурсов 
, что представляет собой скалярное произведение
векторов 
. Вычислим его по формуле (2.28) согласно теореме 2.3:
Таким образом, общая цена затрат на производство одной
тонны творога составляет 279 541,5 рублей
Примечание. Действия с векторами, осуществленные в примере 2.10,
можно выполнить на персональном компьютере. Для нахождения скалярного
произведения векторов в MS Excel используют функцию СУММПРОИЗВ( ), где в качестве
аргументов указываются адреса диапазонов элементов матриц, сумму произведений
которых необходимо найти. В MathCAD
скалярное произведение двух векторов выполняется при помощи соответствующего
оператора панели инструментов Matrix
Пример 2.11. Вычислить работу, произведенную силой 
, если точка ее приложения перемещается прямолинейно
из положения A(2;4;6) в положение A(4;2;7). Под каким углом к AB направлена сила ?
Решение. Находим вектор перемещения, вычитая из координат его конца координаты
начала
. По формуле (2.28) 
(единиц работы).
Угол φ между и
находим по
формуле (2.29), то есть
6. Три некомпланарных вектора 
, взятые в указанном порядке, образуют правую
тройку, если при наблюдении из конца третьего вектора 
кратчайший
поворот от первого вектора ко второму
вектору совершается против часовой стрелки, и левую,
если по часовой стрелке.
Векторным
произведением 
вектора на вектор называется
вектор , удовлетворяющий следующим условиям:
– перпендикулярен векторам и ;
– имеет длину, равную 
, где φ – угол, образованный векторами
и ;
– векторы образуют правую
тройку (рис. 2.15).
Теорема 2.4. Необходимым и достаточным
условием коллинеарности двух векторов является равенство нулю их векторного
произведения
Теорема 2.5. Векторное произведение векторов 
, заданных своими координатами, равно определителю
третьего порядка вида
(2.32)
Примечание. Определитель (2.25)
раскладывается по свойству 7 определителей
Следствие 1. Необходимым и достаточным условием коллинеарности двух
векторов является пропорциональность их соответствующих координат
Следствие 2. Векторные произведения единичных орт равны 
Следствие 3. Векторный квадрат любого вектора равен нулю
Геометрическая
интерпретация векторного произведения состоит в том, что длина результирующего
вектора численно равна площади S
параллелограмма, построенного на векторах–сомножителях как на сторонах,
приведенных к одному началу. Действительно, согласно определению, модуль
векторного произведения векторов равен 
. С другой стороны, площадь параллелограмма,
построенного на векторах и , также равна 
. Следовательно,
. (2.33)
Также с помощью векторного произведения можно
определить момент силы относительно точки и линейную скорость вращения.
Пусть в точке A приложена
сила 
и пусть O –
некоторая точка пространства (рис. 2.16). Из курса физики известно, что моментом
силы относительно
точки O называется вектор 
, который проходит через точку O и удовлетворяет следующим условиям:
— перпендикулярен плоскости, проходящей через точки O, A, B;
— его модуль численно равен произведению силы на плечо 
.
— образует правую тройку с векторами и .
Следовательно,
момент силы относительно
точки O представляет собой векторное произведение
. (2.34)
Линейная скорость 
точки М твердого тела, вращающегося с
угловой скоростью 
вокруг
неподвижной оси, определяется формулой Эйлера 
, O – некоторая неподвижная
точка оси (рис. 2.17).
Пример 2.12. С помощью
векторного произведения найти площадь треугольника ABC, построенного на векторах
, приведенных к одному началу.
Решение. Найдем векторное произведение заданных векторов по
формуле (2.32).
. Согласно формуле (2.33) модуль векторного
произведения двух неколлинеарных векторов численно равен площади
параллелограмма, построенного на данных векторах как на сторонах, приведенных к
общему началу, то есть 
. Тогда площадь треугольника 
. Следовательно, искомая площадь равна 
(единиц
площади)
7. Рассмотрим произведение трех векторов , составленное следующим образом: 
. Здесь первые два вектора перемножаются векторно, а
результирующий вектор – скалярно на третий. Такое произведение 
называется смешанным
произведением трех векторов
(векторно–скалярным произведением).
Теорема 2.6. Необходимым и достаточным условием компланарности
трех векторов является равенство нулю их смешанного произведения
Теорема 2.7. Если три вектора 
заданы своими координатами, то их смешанное
произведение представляет собой определитель третьего порядка, составленный из
координат векторов- сомножителей соответственно, то есть
(2.35)
Нетрудно показать, что объем параллелепипеда,
построенного на векторах как на
сторонах, приведенных к общему началу, численно равен модулю смешенного
произведения этих векторов 
.
Объем треугольной пирамиды, построенной на этих же
векторах, равен
(2.36)
Пример 2.13. Вершинами пирамиды служат точки 
. Вычислить объем пирамиды.
Решение. Найдем
координаты векторов
. Вычислим смешанное произведение этих векторов: 
По формуле (2.36) объем пирамиды, построенной на
векторах 
равен
(единиц объема)
Рассмотрим очень важный вопрос о
разложении вектора по базису. Приведем
следующие определения.
Система векторов 
называется
линейно зависимой, если существуют такие числа 
, хотя бы одно из которых отлично от нуля, что имеет
место равенство
(2.37)
Отсюда всегда можно один из линейно
зависимых векторов выразить через линейную комбинацию остальных. Действительно,
допустим для определенности, что 
. Тогда на это число разделим равенство (2.37), имеем:
получим выражение вектора 
через
остальные векторы 
Линейно независимыми называют векторы, если равенство
(2.37) выполняется только тогда, когда
все
В системе векторов число линейно
независимых векторов равняется рангу матрицы, которая составлена из координат
этих векторов (смотри раздел I.5).
Базисом n – мерного
пространства En называют любую совокупность линейно независимых векторов n – мерного пространства.
Произвольный вектор 
n
– мерного пространства можно представить
в виде линейной комбинации векторов базиса
таким образом:
Числа
называются координатами
вектора в базисе
векторов .
Линейное пространство называется
конечномерным и имеет размерность n, если в этом
пространстве существует система из n линейно независимых векторов (базис) такая,
что каждое ее расширение приводит к линейной зависимости системы.
Например, в трехмерном пространстве
существует базис единичных орт такой, что любое расширение этой системы
линейно независимых векторов, то есть каждый вектор трехмерного
пространства, приводит к линейной зависимости векторов (является линейной
комбинацией орт ):
Коэффициенты {x1, x2, x3} такого разложения вектора
по ортам являются координатами вектора в трехмерном
пространстве.
Вопросы для самопроверки