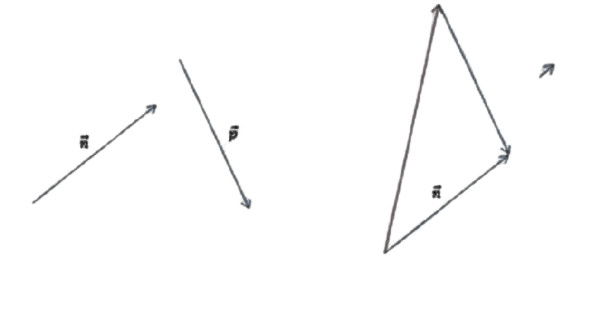Чтобы лучше понять закон вычитания векторов, нужно вспомнить свойство математических действий: сложения и вычитания.
Такое же свойство справедливо и для действий с векторами.
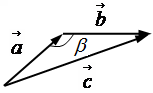
Чтобы вычесть вектор
b→
из вектора
a→
, нужно найти такой вектор
c→
, сумма которого с вектором
b→
составляла бы вектор
a→
.
Обрати внимание!
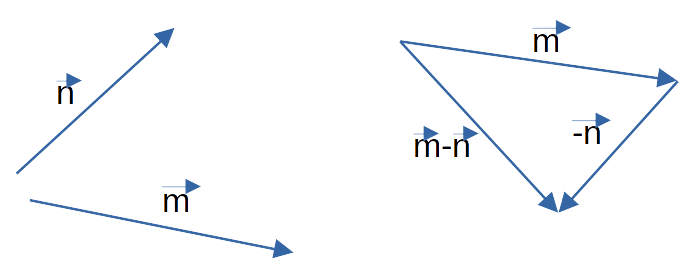
Легче запомнить, как найти разность векторов
a→
и
b→
, следующим образом:
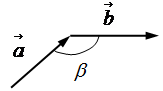
1) векторы нужно привести к общему началу (A);
2) соединить конечные точки (B) и (C);
3) отметить направление вектора разности от конечной точки уменьшителя к конечной точке уменьшаемого вектора.
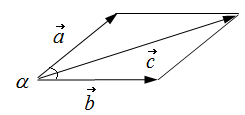
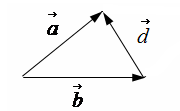
Вспомним закон параллелограмма для сложения векторов. По этому закону вектор суммы двух векторов, лежащих на сторонах параллелограмма с общей вершиной, проходит по длинной диагонали параллелограмма. Очевидно, что вектор разности проходит по короткой диагонали параллелограмма.
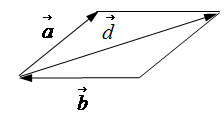
Заметим, что при вычитании вектора
a→
из вектора
b→
вектор разности
d→
будет противоположен вектору
c→
, то есть
d→=−c→
.
Сложение
и вычитание векторов.
Сумма
двух векторов. Законы сложения векторов. Правило параллелограмма.
Представим себе такую ситуацию.
Направляясь из школы домой, вам захотелось пить и вы решили зайти сначала в
магазин, а затем уже домой. Цель достигнута: вы из школы добрались домой.
Сейчас мы описали принцип первого правила сложения векторов.
Правило треугольника.
Чтобы найти вектор суммы двух векторов и
, нужно:
1) совместить параллельным переносом начало вектора с концом
вектора ;
2) провести вектор из начала вектора в конец
вектора ;
3) получившийся вектор и есть вектор суммы: .

Если к вектору прибавить
нулевой вектор по правилу
треугольника, то получим вектор , т.е.
справедливо равенство: .
Утверждение. Если и
–
произвольные точки, то .
Например, .
Сложение векторов подчиняется алгебраическим законам.
ТЕОРЕМА.
Для любых векторов и
справедливы
равенства:
(переместительный
закон)
(сочетательный
закон).
Дано:
Доказать: 1)
2)
Доказательство.
Доказательство теоремы в случае, когда
векторы коллинеарны достаточно простое. Его вы можете провести самостоятельно.
Мы рассмотрим случай, когда данные векторы неколлинеарны.
1). Отметим произвольную точку и отложим от этой точки
вектор . Воспользуемся правилом
треугольника и прибавим к нему вектор . Вектором суммы этих двух
векторов является вектор . (Рисунок слева).
Теперь от точки и отложим вектор
. По правилу треугольника
прибавим к нему вектор . Вектором суммы этих двух
векторов является вектор . (Рисунок справа).
– параллелограмм и точка
совпадает с точкой
. Значит,
, т.е.
 |
2). От точки отложим вектор
, от точки
отложим вектор
, а от точки
– вектор
. Найдём суммы векторов по
правилу треугольника.
Теорема доказана.
При доказательстве первой формулы получился параллелограмм,
причём, из точки выходят два вектора
и
, а вектор их суммы является
диагональю параллелограмма. На основе этого возникает второе правило
геометрического сложения векторов.
Правило параллелограмма.
Чтобы найти вектор суммы двух векторов и
, нужно:
1) совместить параллельным переносом начала векторов и
;
2) на этих векторах достроить параллелограмм;
3) вектором суммы является
вектор, который лежит на диагонали параллелограмма, имеющий своё начало в
начале исходных векторов.
Сумма
нескольких векторов.
Сложение нескольких векторов происходит по принципу правила
треугольника. Складываются два вектора, к вектору суммы прибавляется следующий
вектор и т.д. Приведём пример.
Сложить векторы .

и отложим от неё вектор
. Прибавим к нему вектор
по правилу треугольника.
. Теперь к вектору
прибавим вектор
.
. К вектору
прибавляем вектор
.
. Осталось к вектору
прибавить вектор
.
.
Итак, . Значит, суммой векторов
является вектор, с началом
в начале первого вектора и концом – в конце последнего. Такое сложение векторов
называется правилом многоугольника.
Правило многоугольника.
Чтобы найти вектор суммы нескольких векторов, нужно:
1) последовательно совместить параллельным переносом начало
последующего вектора с концом предыдущего;
2) вектором суммы всех векторов является вектор, с началом в
начале первого вектора и концом – в конце последнего.
Вычитание
векторов.
Определение. Разностью
двух векторов и
называется такой вектор
, что при
сложении его с вектором получается
вектор .

векторов можно производить, руководствуясь двумя понятиями: следствием из
правила треугольника сложения векторов; определением разности двух чисел. Разберём
каждое из них.
Сложим векторы и
по правилу треугольника. По
рисунку видно, что . Отсюда,
и
. Значит, разность двух
векторов можно составить, совмещая их начала, либо совмещая их концы. Отсюда
два правила:
I правило
вычитания векторов.
Чтобы найти вектор разности двух векторов, нужно:
1) совместить параллельным переносом начала этих векторов;
2) вектором разности является вектор с началом в конце второго вектора
и концом в конце первого вектора.
II правило
вычитания векторов.
Чтобы найти вектор разности двух векторов, нужно:
1) совместить параллельным переносом концы этих векторов;
2) вектором разности является вектор с началом в начале первого
вектора и концом в начале второго вектора.
Далее, из алгебры мы знаем, что для того, чтобы
из числа вычесть
число , нужно к числу
прибавить
число, противоположное числу , т.е.
. Такое же
правило справедливо и для векторов.
ТЕОРЕМА.
Для любых векторов справедливо
равенство:

Дано:
Доказать:
Доказательство.
1. Найдём разность векторов по
I правилу. Вектором разности является
вектор (рисунок слева). А теперь
найдём сумму векторов по правилу
треугольника, где – вектор,
противоположный вектору . Вектором
суммы является вектор (рисунок
справа). Не трудно заметить, что . Они сонаправлены и имеют
одинаковые модули.
2. А теперь докажем то же самое аналитически. По определению
разности векторов,
Что и требовалось доказать.
Из этой теоремы следует третье правило
вычитания векторов.
III правило
вычитания векторов.
Чтобы найти вектор разности двух векторов, нужно к первому вектору прибавить вектор, противоположный
второму.
Используя это правило вычитания векторов,
способ сложения векторов выбирается произвольно.
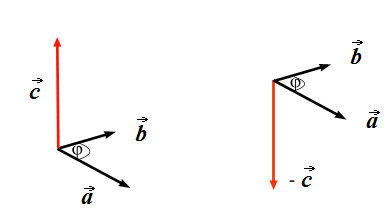
1. 
является суммой векторов
и
. Определите, какой из четырёх рисунков верный.
2. Проведите векторы . Какая геометрическая фигура у вас
получилась?
3. 
является разностью векторов
и
. Определите, какой из четырёх рисунков
верный.
4. 
является суммой векторов
и
. Определите, какой из четырёх рисунков
верный.
5. 
вектор через векторы
, используя рисунок.
6. 
вектор через векторы
, используя рисунок.
7. Упростите выражения:
8. Длина вектора равна
, а длина вектора
равна
. Сколько различных целых значений может
принимать длина вектора ?
9. Длина вектора равна
, а длина вектора
равна
. Сколько различных целых значений может
принимать длина вектора ?
10. Длина вектора равна
, а длина вектора
равна
. Сколько различных целых значений может
принимать длина вектора ?
11. Длина вектора равна
, а длина вектора
равна
. Сколько различных целых значений может
принимать длина вектора ?
12. Длина вектора равна
, а длина вектора
равна
. Сколько различных целых значений может
принимать длина вектора ?
13. В квадрате проведены диагонали
и
. Укажите номера верных утверждений.
|
1) |
2) |
3) |
|||
|
4) |
5) |
6) |
|||
|
7) |
|
||||
14. – параллелограмм. Найдите сумму векторов
.
15. – прямоугольник. Диагонали
и
пересекаются в точке
. Укажите номера верных утверждений.
|
1) |
2) |
3) |
|||
|
4) |
5) |
6) |
|||
|
7) |
|
9) |
10) |
||
16. – параллелограмм. Выразите векторы
и
через векторы
и
.
17. – параллелограмм. Выразите векторы
и
через векторы
и
.
18. – прямоугольник. Выразите векторы
и
через векторы
и
.
19. – параллелограмм. Выразите векторы
и
через векторы
и
.
20. 
векторов , изображённых на клетчатой бумаге с
размерами клетки 1 х 1.
21. 
прямоугольника равны 20 и 21. Найдите длину суммы
векторов и
.
22. 
прямоугольника равны 7 и 24. Найдите длину разности
векторов и
.
23. 
найдите длину вектора (размеры клетки 1 х 1).
24. 
найдите длину суммы векторов и
(размеры клетки 1 х 1).
25. 
найдите длину разности векторов и
, изображённых на клетчатой бумаге с
размерами клетки 1 х 1.
Вычитание векторов
Содержание:
- Как происходит вычитание векторов
- Как производится вычитание векторов по координатам
-
Основные правила вычисления
- Правило треугольника
- Правило параллелограмма
- Примеры задач на понятие разности векторов
Как происходит вычитание векторов
Определение
Вычитание векторов — это арифметическое действие в геометрии, при котором из одного вектора отнимают другой.
Чтобы вычесть (overrightarrow b) из (overrightarrow а), нужно найти такой (overrightarrow с), сложение которого с вектором (overrightarrow b) составляло бы (overrightarrow а).
Таким образом, формула разности будет выглядеть так:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
(overrightarrow а-overrightarrow b=overrightarrow а+left(-overrightarrow bright))
Если задан (overrightarrow а), то можно построить противоположный ему (-overrightarrow а), равный по длине, но противоположно направленный. Тогда происходит сведение двух противоположно направленных векторов к нулевому:
(overrightarrow а+left(-overrightarrow аright)=0)
Как производится вычитание векторов по координатам
Если необходимо произвести вычитание векторов по координатам, то следует просто вычесть соответствующие точки. То есть если из (overrightarrow а) отнимается (overrightarrow b), то из X1 отнимаем X2, из Y1 Y2 и из Z1 Z2.
Проиллюстрируем координатное пространство:
Основные правила вычисления
Для того, чтобы найти значение разности векторов, можно использовать несколько способов.
Правило треугольника
Чтобы графически продемонстрировать разность, необходимо отложить от произвольной точки вектор (overrightarrow а), из его начала (overrightarrow b). Тогда вектор, начало которого совпадает с концом ( overrightarrow b), а конец — с концом (overrightarrow a), и будет искомым вектором разности (overrightarrow a;-;overrightarrow b). Проиллюстрируем это:
Правило параллелограмма
Если два неколлинеарных, то есть непараллельных вектора (overrightarrow а) и (overrightarrow b) имеют общее начало, то их разностью является вектор, совпадающий с диагональю параллелограмма, построенного на (overrightarrow а) и (overrightarrow b), причем начало этой диагонали совпадает с концом (overrightarrow b), а конец — с концом (overrightarrow а).
Если векторы (overrightarrow а) и (overrightarrow b) заданы в некотором промежутке:
(overrightarrow a=left(а_1;а_2right),;overrightarrow b=left(b_1;b_2right))
то, чтобы найти координаты их разности (overrightarrow a;-;overrightarrow b), необходимо от точек (overrightarrow a) отнять соответствующие точки (overrightarrow b):
(overrightarrow a;-;overrightarrow b=left(a_1;a_2right)-left(b_1;b_2right)=left(a_1-b_1;a_2-b_2right))
Проиллюстрируем правило многоугольника:
Примеры задач на понятие разности векторов
Задача 1
Дано
(overrightarrow a;=left(2;-1right),;overrightarrow b=left(0;2right))
Найти: (overrightarrow с=2overrightarrow a-3overrightarrow b;)
Решение
Найдем координаты (2overrightarrow a) и (3overrightarrow b). Для этого умножим каждую на два и три:
(2overrightarrow а=2timesleft(2;-1right)=left(2times2;2timesleft(-1right)right)=left(4;-2right), 3overrightarrow b=3timesleft(0;2right)=left(3times0;3times2right)=left(0;6right))
Тогда искомый вектор:
(overrightarrow с=2overrightarrow a-3overrightarrow b=left(4;-2right)-left(0;6right)=left(4-0;;-2-6right)=left(4;-8right))
Ответ: (overrightarrow с=left(4;-8right).)
Задача 2
Дано
(Аleft(1;-1;0right),;Вleft(2;3;-1right),;Сleft(0;-1;0right),;Dleft(1;0;2right))
Найти: координаты (overrightarrow{AB}-overrightarrow{CD}.)
Решение
Для начала найдем проекции (overrightarrow{AB}) и (overrightarrow{CD}).
Для этого от координат конца вектора, то есть точек B и D, нужно отнять соответствующие проекции его начала, то есть точек А и С.
(overrightarrow{AB}=left(2-1;3-left(-1right);-1-0right)=left(1;4;-1right),;overrightarrow{CD}=left(1-0;0-left(-1right);2-0right)=left(1;1;2right))
Тогда для нахождения координат разности (overrightarrow{AB}-overrightarrow{CD}), от координат первого вычтем координаты второго:
(overrightarrow{AB}-overrightarrow{CD}=left(1;4;-1right)-left(1;1;2right)=left(1-1;4-1;-1-2right)=left(0;3;-3right))
Ответ: (overrightarrow{AB}-overrightarrow{CD}=left(0;3;-3right))
Насколько полезной была для вас статья?
Рейтинг: 3.00 (Голосов: 4)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Правило параллелограмма для сложения двух векторов:
1
.
Нарисуем вектор
.
2.
Нарисуем вектор
так,
что его начало совпадает с началом
вектора
;
угол между векторами равен
(см. рисунок).
3.
Через конец вектора
проведем прямую линию, параллельную
вектору
.
4.
Через конец вектора
проведем прямую линию, параллельную
вектору
.
Мы
построили параллелограмм. Стороны этого
параллелограмма – составляющие векторы
и
.
5.
Проведем диагональ параллелограмма из
общей точки начала вектора
и начала вектора
.
6.
Модуль результирующего вектора
равен длине диагонали параллелограмма
и определяется по формуле:
;
начало
вектора
совпадает
с началом вектора
и началом вектора
(направление
вектора
показано на рисунке).
Правило треугольника для сложения двух векторов:
1.
Нарисуем составляющие векторы
и
так, что начало вектора
совпадает с концом вектора
.
При этом угол между векторами равен
.
2.
Результирующий вектор
направлен
так, что его начало совпадает с началом
вектора
,
а конец совпадает с концом вектора
.
3.
Модуль результирующего вектора находим
по формуле:
2.2.3 Вычитание векторов
Вычитание векторов
– это действие, обратное сложению:
Найти разность
вектора
и вектора
— это тоже самое, что найти сумму вектора
и вектора
,
противоположного вектору
.
Мы можем найти вектор разности
геометрически по правилу параллелограмма
или по правилу треугольника (см. рис.).
Правило параллелограмма.
Стороны параллелограмма
— вектор
и вектор —
;
диагональ параллелограмма — вектор
разности
.
Правило треугольника.
Вектор разности
соединяет конец вектора
и конец вектора
(начало
вектора
совпадает с концом вектора
).
2.2.4 Умножение вектора на скаляр
Пусть заданы вектор
и скаляр n.
Найдем произведение вектора
и скалярного вектора n.
В
результате умножения вектора на скаляр
мы получаем новый вектор
:
Направление
вектора
такое же, как направление вектора
при
.
Направление
вектора
противоположно направлению вектора
при
.
Модуль
вектора
в n
раз больше модуля вектора
,
если
.
2.3. Скалярное и векторное произведения
2.3.1 Скалярное произведение
Из
двух векторов
и
можно
образовать скаляр по правилу:
Это
выражение называется скалярным
произведением векторов
и
и обозначается одним из символов
,
или
.
Следовательно,
.
=
.
По определению
скалярное произведение обладает
следующими свойствами:
1)
,
2)
,
3)
2.3.2 Векторное произведение
Из двух векторов
и
можно
образовать новый вектор:
,
где
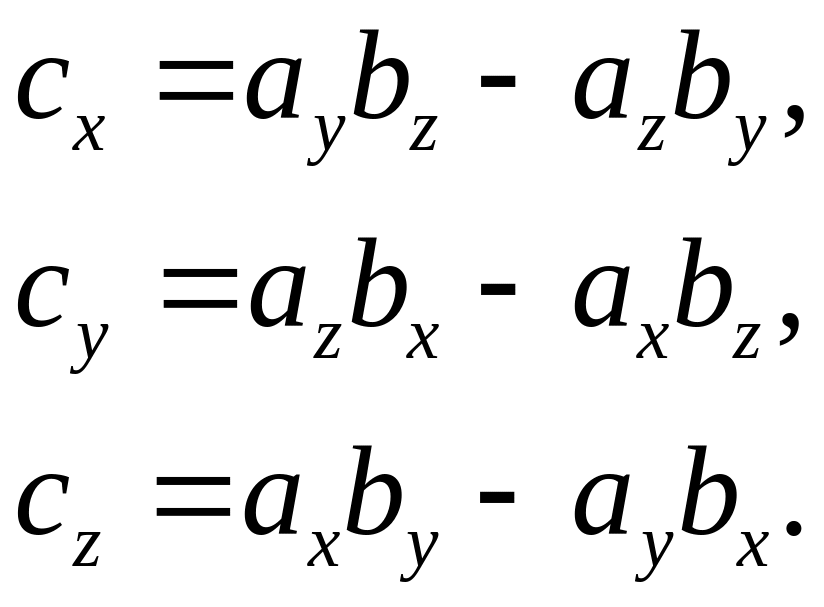
Модуль
нового результирующего вектора находим
по формуле:
.
Эта операция
называется векторным произведением
векторов
и
и обозначается одним из символов
или
.
Также общеизвестна
формула
,
где
— угол между векторами
и
.
Направление
вектора
можно найти, используя следующий прием.
Мысленно совмещаем продольную ось
буравчика (правого винта, штопора) с
перпендикуляром к плоскости, в которой
лежат перемножаемые векторы (в данном
примере – векторы
и
). Затем начинаем вращать головку винта
(ручку штопора) по направлению кратчайшего
поворота от первого сомножителя ко
второму, то есть от вектора
к вектору
.
Направление движения тела винта и будет
являться направлением вектора
.
Этот прием называется правилом
правого винта или правилом буравчика
(см.
рис.).
В терминах векторного
произведения выражаются момент силы,
момент импульса и др. Говоря о векторе,
всегда имеем ввиду его компоненты.
Вектор, в отличие от скаляра, определяется
тремя числами. Поэтому такие операции
как сложение, вычитание, скалярное и
векторное произведения сводятся к
привычным действиям с компонентами.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Для того, чтобы уяснить, что собой представляет разность векторов, введём понятие откладывания вектора от определённой точки и понятие суммы векторов.
Определение
Если некоторая точка A является началом вектора a, то говорят, что он является отложенным от точки A.
Теорема. От каждой точки можно отложить только один вектор, имеющий заданный модуль и направление. Докажем эту теорему.
Доказательство:
В случае, когда вектор нулевой, то теорема очевидна. Нулевые вектора в одной и той же точки совпадают между собой, т. е. являются одним и тем же вектором.
Сделаем построение. Точкой A обозначим начало вектора a, а точкой B его конец. Пусть у нас имеется некоторая точка K. Проведём через неё прямую b, которая параллельна вектору a. Отложим на данной прямой равные по своей абсолютной величине вектору a отрезки KL и KM. Из векторов, образованных этими отрезками искомым можно назвать только сонаправленный с a.
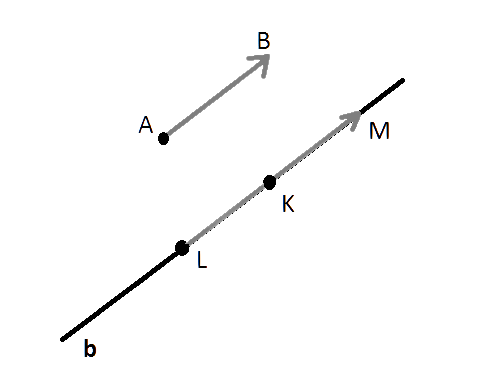
Единственность нашего вектора следует из того, что мы построили и видим.
Теорема доказана.
Определение
Суммой векторов a и b называется вектор с тем же началом, что вектор a и концом, как у вектора b. При этом вектор b должен начинаться в той же самой точке, в которой заканчивается вектор a.
Равные векторы, начинающиеся в разных точках, нередко обозначают одной и той же буквой. Иногда про подобные векторы говорят, как об одном и том же векторе, отложенном из разных мест.
Разность векторов
Определение
Разностью векторов a и b называется сумма вектора a c вектором, который противоположно направлен к вектору b.
По-другому это определение можно сформулировать следующим образом: разностью двух векторов a и b называется вектор c, который при сложении с вычитаемым b образует уменьшаемое, т. е. вектор a.
Формулами это записывается так:
b + c = a
a – b = c
Как найти разность векторов аналитическим способом
В двухмерном пространстве векторов a {x1, y1} и b {x2, y₂} разность векторов можно вычислить, как показано ниже:
c {x3, y3} = {x₁ — x2, y1 — y₂}.
Вычитание векторов в 3-мерном пространстве выглядит следующим образом:
c {x3; y3; z₃} = {x₁ — x2, y₂ — y₂, z1 — z2}.
Как найти разность векторов графическим способом
Нужно воспользоваться правилом треугольника. Последовательность действий следующая:
- Постройте по координатам векторы, для которых требуется найти разность;
- Совместите концы построенных векторов. Для этого нужно построить два равных заданным направленных отрезка, концы у которых будут в одной и той же точке;
- Соедините начала построенных отрезков и укажите их направление. Вектор c, называемый разностью векторов, будет иметь своё начало в той же точке, где начинается вектор, именуемый уменьшаемым и заканчивается в точке начала вычитаемого. Смотрите рисунок ниже.
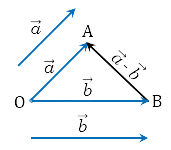
Есть ещё один способ графического нахождения разности векторов. Он предусматривает следующий порядок действий:
- Постройте исходные направленные отрезки;
- Отразите вычитаемый отрезок. Для этого постройте противоположно направленный и равный ему отрезок и затем совместите начало этого отрезка с уменьшаемым;
- Постройте сумму, т. е. соедините начало первого отрезка и конец второго.
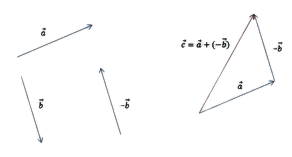
Нет времени решать самому?
Наши эксперты помогут!
Примеры вычисления разности векторов
Примеры
Вычислить вектор c, который представляет собой разность вектора a ={1;
2} и вектора b = {4; 8}.
Решение:
Действуем по выше указанному правилу
a — b = {1 — 4; 2 — 8} = {-3; -6}
Ответ: с{-3; -6}.
Вычислить вектор c, который является разностью векторов a = {1; 2; 5} и
b = {4; 8; 1}.
Решение:
Почти всё делается, как в уже рассмотренном примере, только добавляется третья координата.
a — b = {1 — 4; 2 — 8; 5 — 1} = {-3; -6; 4}
Ответ: c {-3; -6; 4}.
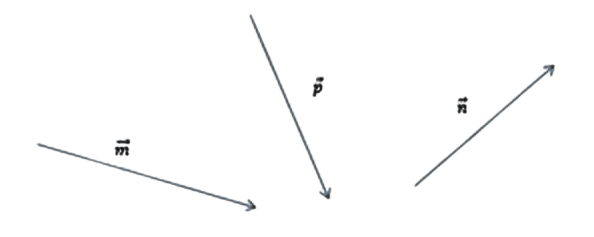
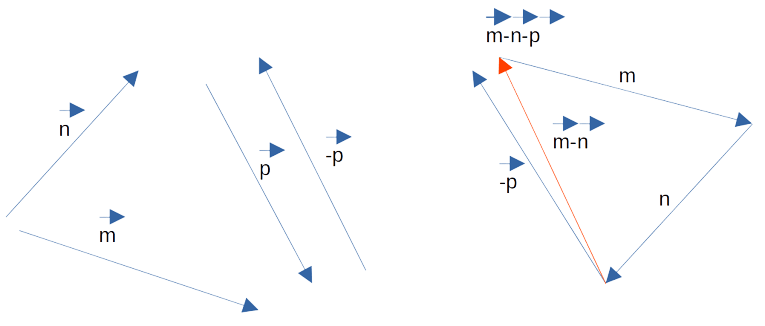
На рисунке векторы
Требуется построить разности: p — n, m —
n,m — n — p и найти ту из них, которая
имеет наименьший модуль.
Решение:
Для изображения p — n проще всего воспользоваться правилом треугольника. Параллельным переносом
отрезки
следует соединить таким образом, чтобы совпали их конечные точки. Далее нужно соединить начальные точки и
определить направление. В нашем случае вектор разности берёт своё начало там же, где и вычитаемый n.
Для изображения m — n правильнее будет воспользоваться вторым графическим способом нахождения разности
векторов. Сначала построим вектор противоположный n и найдём его суммы с вектором m.
Для нахождения разности m — n — p разобьём это выражение на два действия. Возможны следующие варианты:
- m — (n + p). Сначала нужно построить сумму,
затем уже вычесть её из m; - (m — n) — p. Сначала находим m — n,
осле этого от полученной разности отнимаем p; - (m— p) — n. Сначала определяем m — p, затем от
полученного результата отнимаем n.
Из вычислений выше нам известна разность m — n. Для получения решения нам нужно вычесть из неё
p.
Используя определение 3 построим разность векторов на рисунке. На нём изображён окончательный результат
и промежуточный.
Теперь нужно определить наименьший модуль. В нашем случае для этого можно лишь визуально оценить длины p — n,
m — n и m — n — p. Из построения сразу видно, что наименьшим модулем обладает вектор разности m — n —
p.