Как найти разрешающую способность дифракционной решетки

С
помощью дифракционной решетки можно
производить очень точные измерения
длины волны. Если период d
решетки известен, то определение длины
сводится к измерению угла _m,
соответствующего направлению на
выбранную линию в спектре m-го
порядка. На практике обычно используются
спектры 1-го или 2-го порядков.

Если
в спектре исследуемого излучения имеются
две спектральные линии с длиной волн
λ₁
и λ₂,
то решетка в каждом спектральном порядке
(кроме m = 0)
может отделить одну волну от другой.

Спектральной
разрешающей способностью
R
решетки,
характеризующей
возможность разделения с ее помощью
двух близких спектральных линий с
длинами волн λ и λ + Δλ, называется
отношение длины волны λ к минимально
возможному значению Δλ, т.е.

.
(4)

Максимум
m-го
порядка для длины волны ₂:

.
(5)

При
переходе к соседнему минимуму с длиной
волны ₁
разность хода меняется на
,
где N

число щелей решетки, поэтому

.
(6)

По критерию Рэлея
соседние максимум и минимум совпадают,
поэтому

(4)

, (7)

т.е.
разрешающая способность решетки
пропорциональна порядку спектра m
и числу щелей N.

Пусть
решетка имеет период d = 10^–3 мм,
ее длина L = 10 см.
Тогда, N = 10⁵
(это хорошая решетка). В спектре 2-го
порядка разрешающая способность решетки
оказывается равной R = 2·10⁵.
Это означает, что минимально разрешимый
интервал длин волн в зеленой области
спектра (λ = 550 нм) равен
Δλ = λ / R ≈ 2,8·10^–3 нм.

3. Понятие о голографии

Голография
(«полная запись» 
греч.) это
особый способ записи и последующего
восстановления волнового поля, основан­ный
на регистрации интерференционной
картины.

Авторы:
Д. Габор (1900 – 1979 г., Англия), опубликовал
в 1947 г., Нобелевская премия 1971 г.; Ю.Н.
Денисюк (СССР), реализовал в 1962 г. После
изобретения лазеров

источников света высокой степени
когерентности Э. Лейт Ю. Упатниекс (США)
экспериментально осуществили голографию.

Рассматривая
голограмму из разных направлений, можно
заглянуть за ближние предметы. Это
объясняется тем, что, перемещая голову,
мы воспринимаем лучи, отраженные от
скрытых частей предмета.

Применение
голографии

• Запись
  и хранение информации с высокой
  плотностью;

• Компьютеры
  с голографической памятью;

• Голографическое
  кино, телеви­де­ние, электронный
  микроскоп,…

Глава 3.
Оптика

Волновая оптика

3.11. Поляризация света

В
начале XIX века, когда Т. Юнг
и О. Френель
развивали волновую теорию света, природа
световых волн была неизвестна. На первом
этапе предполагалось, что свет представляет
собой продольные волны, распространяющиеся
в некоторой гипотетической среде –
эфире.
При изучении явлений интерференции и
дифракции вопрос о том, являются ли
световые волны продольными или
поперечными, имел второстепенное
значение. В то время казалось невероятным,
что свет – это поперечные волны, так
как по аналогии с механическими волнами
пришлось бы предполагать, что эфир –
это твердое тело (поперечные механические
волны не могут распространяться в
газообразной или жидкой среде).

Однако,
постепенно накапливались экспериментальные
факты, свидетельствующие в пользу
поперечности световых волн. Еще в конце
XVII века было обнаружено, что кристалл
исландского шпата (CaCO₃)
раздваивает проходящие через него лучи.
Это явление получило название двойного
лучепреломления
(рис. 3.11.1).

Рисунок 3.11.1. Прохождение света через кристалл исландского шпата (двойное лучепреломление). Если кристалл поворачивать относительно направления первоначального луча, что поворачиваются оба луча, прошедшие через кристалл.

В
1809 году французский инженер Э. Малюс
открыл закон, названный его именем. В
опытах Малюса свет последовательно
пропускался через две одинаковые
пластинки из турмалина (прозрачное
кристаллическое вещество зеленоватой
окраски). Пластинки могли поворачиваться
друг относительно друга на угол φ
(рис. 3.11.2).

Рисунок 3.11.2. Иллюстрация к закону Малюса.

Интенсивность
прошедшего света оказалась прямо
пропорциональной cos² φ:

I ~ cos2 φ.

Ни
двойное лучепреломление, ни закон Малюса
не могут найти объяснение в рамках
теории продольных волн. Для продольных
волн направление распространения луча
является осью симметрии. В продольной
волне все направления в плоскости,
перпендикулярной лучу, равноправны. В
поперечной волне (например, в волне,
бегущей по резиновому жгуту) направление
колебаний и перпендикулярное ему
направление не равноправны (рис. 3.11.3).

Рисунок 3.11.3. Поперечная волна в резиновом жгуте. Частицы колеблются вдоль оси y. Поворот щели S вызовет затухание волны.

Таким
образом, асимметрия относительно луча
является решающим признаком, который
отличает поперечную волну от продольной.
Впервые догадку о поперечности световых
волн высказал Т. Юнг
(1816 г.). Френель,
независимо от Юнга, также выдвинул
концепцию поперечности световых волн,
обосновал ее многочисленными экспериментами
и создал теорию двойного лучепреломления
света в кристаллах.

В
середине 60-х годов XIX века Максвелл
сделал вывод о том, что свет – это
электромагнитные
волны.
Этот вывод был сделан на основе совпадения
известного значения скорости света со
скоростью распространения предсказанных
Максвеллом электромагнитных волн. К
тому времени, когда Максвелл сделал
вывод о существовании электромагнитных
волн, поперечность световых волн уже
была доказано экспериментально. Поэтому
Максвелл справедливо полагал, что
поперечность электромагнитных волн
является еще одним важнейшим доказательством
электромагнитной природы света.

В
электромагнитной теории света исчезли
все затруднения, связанные с необходимостью
введения особой среды распространения
волн – эфира, который приходилось
рассматривать как твердое тело.

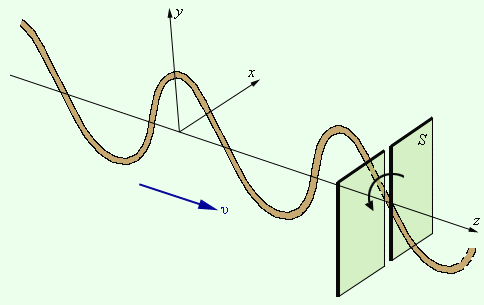
В
электромагнитной волне вектора
и
перпендикулярны
друг другу и лежат в плоскости,
перпендикулярной направлению
распространения волны (рис. 2.6.3). Во
всех процессах взаимодействия света с
веществом основную роль играет
электрический вектор
поэтому
его называют световым
вектором.
Если при распространении электромагнитной
волны световой вектор сохраняет свою
ориентацию, такую волну называют
линейно-поляризованной
или плоско-поляризованной
(термин поляризация
волн
был введен Малюсом применительно к
поперечным механическим волнам).
Плоскость, в которой колеблется световой
вектор
называется
плоскостью
колебаний
(плоскость yz
на рис. 2.6.3), а плоскость, в которой
совершает колебание магнитный вектор
–
плоскостью
поляризации
(плоскость xz
на рис. 2.6.3).

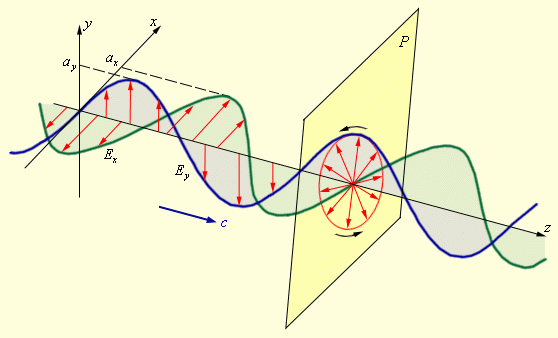
Если
вдоль одного и того же направления
распространяются две монохроматические
волны, поляризованные в двух взаимно
перпендикулярных плоскостях, то в
результате их сложения в общем случае
возникает эллиптически-поляризованная
волна
(рис. 3.11.4).

Рисунок 3.11.4. Сложение двух взаимно перпендикулярно поляризованных волн и образование эллиптически поляризованной волны.

В
эллиптически-поляризованной волне в
любой плоскости P,
перпендикулярной направлению
распространения волны, конец результирующего
вектора
за
один период светового колебания обегает
эллипс, который называется эллипсом
поляризации.
Форма и размер эллипса поляризации
определяются амплитудами a_x
и a_y
линейно-поляризованных волн и фазовым
сдвигом Δφ между ними. Частным случаем
эллиптически-поляризованной волны
является волна с круговой
поляризацией
(a_x = a_y,
Δφ = ± π / 2).

Рис. 3.11.5
дает представление о пространственной
структуре эллиптически-поляризованной
волны.

Рисунок 3.11.5. Электрическое поле в эллиптически-поляризованной волне.

Линейно-поляризованный
свет испускается лазерными источниками.
Свет может оказаться поляризованным
при отражении или рассеянии. В частности,
голубой свет от неба частично или
полностью поляризован. Однако, свет,
испускаемый обычными источниками
(например, солнечный свет, излучение
ламп накаливания и т. п.), неполяризован.
Свет таких источников состоит в каждый
момент из вкладов огромного числа
независимо излучающих атомов (см. § 3.2)
с различной ориентацией светового
вектора в излучаемых этими атомами
волнах. Поэтому в результирующей волне
вектор
беспорядочно
изменяет свою ориентацию во времени,
так что в среднем все направления
колебаний оказываются равноправными.
Неполяризованный
свет
называют также естественным
светом.

В
каждый момент времени вектор
может
быть спроектирован на две взаимно
перпендикулярные оси (рис. 3.11.6).

Рисунок 3.11.6. Разложение вектора по осям.

Это
означает, что любую волну (поляризованную
и неполяризованную) можно представить
как суперпозицию двух линейно-поляризованных
во взаимно перпендикулярных направлениях
волн:
Но
в поляризованной волне обе составляющие
E_x(t)
и E_y(t)
когерентны, а в неполяризованной –
некогерентны (см. § 3.2),
т. е. в первом случае разность фаз
между E_x(t)
и E_y(t)
постоянна, а во втором она является
случайной функцией времени.

Явление
двойного лучепреломления света
объясняется тем, что во многих
кристаллических веществах показатели
преломления для двух взаимно перпендикулярно
поляризованных волн различны. Поэтому
кристалл раздваивает проходящие через
него лучи (рис. 3.11.1). Два луча на выходе
кристалла линейно поляризованы во
взаимно перпендикулярных направлениях.
Кристаллы, в которых происходит двойное
лучепреломление, называются анизотропными.

С
помощью разложения вектора
на
составляющие по осям можно объяснить
закон
Малюса (рис. 3.11.2).

У
многих кристаллов поглощение света
сильно зависит от направления
электрического вектора в световой
волне. Это явление называют дихроизмом.
Этим свойством, в частности, обладают
пластины турмалина, использованные в
опытах Малюса. При определенной толщине
пластинка турмалина почти полностью
поглощает одну из взаимно перпендикулярно
поляризованных волн (например, E_x)
и частично пропускает вторую волну
(E_y).
Направление колебаний электрического
вектора в прошедшей волне называется
разрешенным
направлением
пластинки. Пластинка турмалина может
быть использована как для получения
поляризованного света, так и для анализа
характера поляризации света (поляризатор
и анализатор).
В настоящее время широко применяются
искусственные дихроичные пленки, которые
называются поляроидами.
Поляроиды почти полностью пропускают
волну разрешенной поляризации и не
пропускают волну, поляризованную в
перпендикулярном направлении. Таким
образом, поляроиды можно считать
идеальными поляризационными
фильтрами.

Рассмотрим
прохождение естественного света
последовательно через два идеальных
поляроида П₁
и П₂
(рис. 3.11.7), разрешенные направления
которых развернуты на некоторый угол
φ. Первый поляроид играет роль поляризатора.
Он превращает естественный свет в
линейно-поляризованный. Второй поляроид
служит для анализа падающего на него
света.

Рисунок 3.11.7. Прохождение естественного света через два идеальных поляроида. yy’ – разрешенные направления поляроидов.

Если
обозначить амплитуду линейно-поляризованной
волны после прохождения света через
первый поляроид через
то
волна, пропущенная вторым поляроидом,
будет иметь амплитуду E = E₀ cos φ.
Следовательно, интенсивность I
линейно-поляризованной волны на выходе
второго поляроида будет равна

Таким
образом, в электромагнитной теории
света закон Малюса находит естественное
объяснение на основе разложения вектора
на
составляющие.

Дифракционная решетка

Оптический элемент с периодической структурой, способный влиять на распространение световых волн так, что энергия волны, которая прошла через решетку, сосредоточивается в определенных направлениях.

Направления распространения этих пучков зависят от периода решетки и длины световых волн, то есть дифракционная решетка работает как дисперсионный элемент. Монохроматический световой пучок, падающий на решетку, тоже разделится на несколько пучков, которые распространяются в разных направлениях. Дифракционные решетки широко применяются в монохроматорах и спектрометрах.

Как правило, дифракционные решетки — это квадраты размером 50 х 50 мм с 1 200 бороздками на мм; суммарная длина бороздок составляет при этом 3 км.

Бороздки в них делаются механическим процарапыванием алмазными инструментами по стеклу. В настоящее время чаще применяются отражающие дифракционные и голографические решетки (интерференционные). Их получают посредством двух расширяющихся и пересекающихся лазерных лучей, например аргонового, с длиной волны 488 нм, которые образуют интерференционную картину в форме требуемой решетки. Затем соответствующим фотохимическим процессом бороздки (штрихи) протравливаются и покрываются защитным слоем SiO₂ (напылением). Голографические решетки изготавливают до 6 600 штрихов на мм с помощью удвоения частоты лазерной аргоновой линии 257 нм и на любой искривленной поверхности (вогнутые решетки).

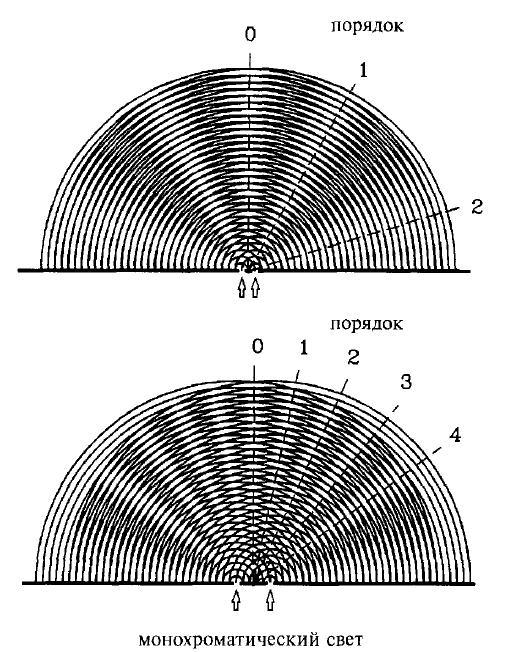
Интерференционная картина в дифракционной решетке

Если параллельный пучок света падает на две щели с размерами и расстояниями между ними, сопоставимыми с длиной волны света, возникает эффект интерференции.

В соответствии с законом Гюйгенса, обе щели являются источниками простых или сферических волн, которые взаимодействуют друг с другом в пространстве, т.е. возникает интерференция:

Рис. 1. Наложение только двух сферических волн монохроматического света образует в зависимости от относительного расстояния между ними (постоянной решетки а) типичную интерференционную картину с обозначенными максимумами (пересечение линий) и минимумами в различных направлениях (пересечение пропусков между линиями). Относительно нормали наблюдаются максимумы 0-го, 1-гo, 2-го, и т. д. порядков интерференции. Чем больше расстояние от щелей, тем больше порядков перекрывается.

Интерференционные решетки не имеют действительного «угла блеска», существующего у линейчатых решеток, поэтому они не достигают их эффективности, составляющей ~95%. Однако они демонстрируют пониженную, но более эффективную степень проходимости света (светосилу) во всем спектральном диапазоне. Даже при очень высокой плотности штрихов у этих решеток не наблюдается ошибок. Поэтому они не дают ложных спектральных линий («духов»), и уровень рассеянного света у них по крайней мере в 100 раз ниже, чем у высококачественных линейчатых решеток. Это существенно увеличивает их динамический, т.е. фотометрический, диапазон.

Разрешающая способность решетки

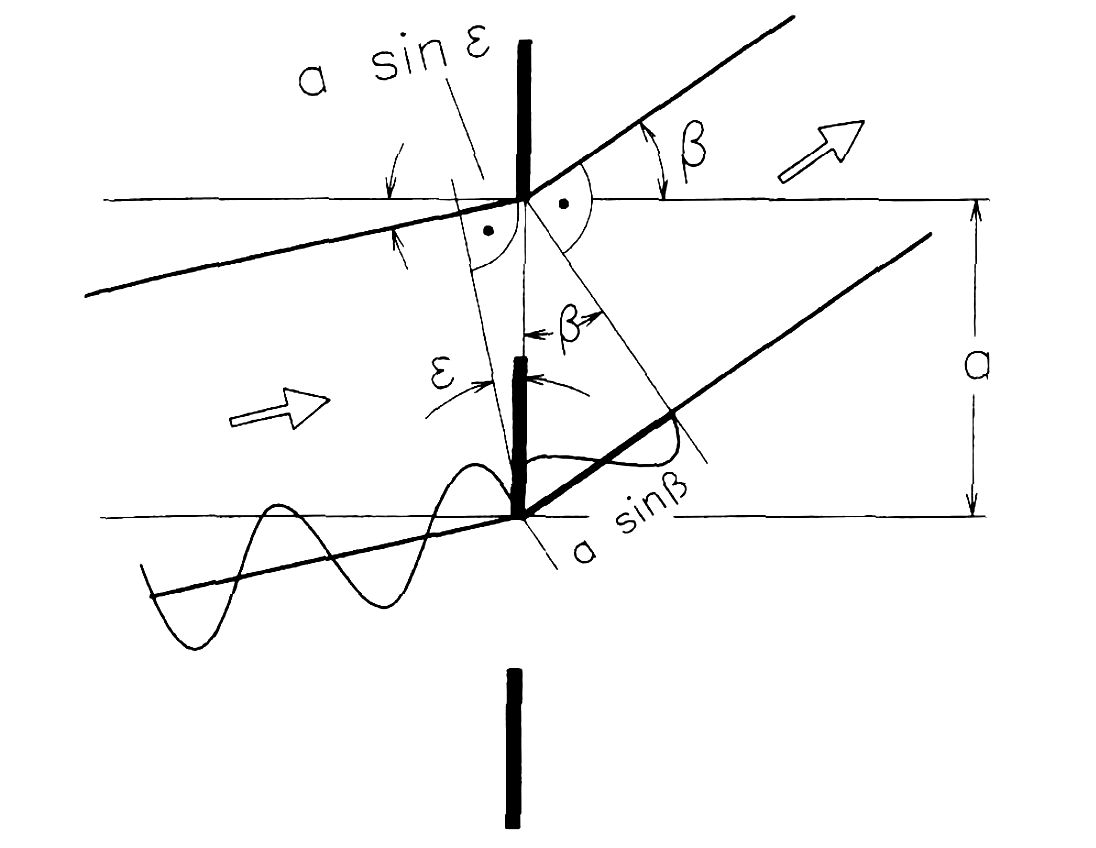
Направление максимумов определяется тем фактом, что, согласно рис. 2, гомологичные лучи отличаются только на одну длину волны или кратно ей (уравнение решетки).

Рис. 2. Математическое описание результатов, продемонстрированных на рис. 1.

sin⁡β−sin⁡ε=±mλasin beta -sin varepsilon =pm mfrac{lambda }{a}
β=arcsin⁡(±mλa+sin⁡ε)beta =arcsin left( pm mfrac{lambda }{a}+sin varepsilon right)

Знак «+» относится к прозрачным, а знак «-» — к отражающим решеткам.

Разрешающая способность решетки R — это ее способность разделять две соседние спектральные линии. В соответствии с законом Релея, это тот случай, когда максимум одной волны падает на минимум второй. Если N — общее количество штрихов решетки, тогда

R=λdλ=mNR=frac{lambda }{dlambda }=mN

Чем выше порядок т и больше количество штрихов, тем выше разрешающая способность решетки.

Пример

Например, решетка с 600 линиями на мм и шириной 50 мм дает для первого порядка интерференции числовое разрешение R = 600 х 50 = 30 000.

Тест по теме «Дифракционные решетки»

0 Пользователей и 1 Гость просматривают эту тему.

---

---

Введение

Дифракционные решетки — очень полезный и популярный инструмент в спектроскопии. Благодаря свойству преломлять свет под различными углами, можно получать монохроматические пучки от обычных источников белого cвета. Связь между углами падения, дифракции и длиной волны описывается с помощью общеизвестного уравнения дифракционной решетки, из которого путем простых алгебраических операций можно найти рассеяние, разрешение и область свободной дисперсии конкретного элемента.

Уравнение решетки

Пучок света при попадании на решетку подвергается дифракции, то есть раскладывается на несколько частей. Направление каждой компоненты зависит от длины волны и угла, под которым излучение попадает на решетку. Также имеет значение профиль и глубина штрихов, нанесенных на решетку.

Уравнение решетки полностью описывает свойства прибора, его можно записать как:

        (1) 

где α — угол падения, β_m — угол дифракции (за положительное направление принимается угол против часовой стрелки, за отрицательное — по часовой), m — порядок дифракции (любое целое число), d — период решетки или частота штрихов (обычно измеряется как число штрихов на миллиметр, в исключительных случаях приводится пересчет в нанометры), λ — длина волны падающего излучения.

Порядок дифракции

Нулевой порядок дифракции означает равенство угла падения α углу дифракции β₀, и все уравнение преобразуется в известный закон отражения. Это решение всегда возможно, но на практике отраженный луч не особенно важен. Отраженное излучение — причина потерь излучения при прохождении через решетку. В монохроматорах, спектрометрах и спектрографах в основном используется порядок дифракции m = -1. Решетки с малой частотой штрихов (соответствует большим периодам) создают больше порядков дифракции. Дифракционные решетки могут использоваться как делители монохроматических пучков одного или двух источников.

Светорассеяние

Угловая дисперсия характеризует величину изменения угла дифракции за единицу изменения длины волны. Измеряется как угловое расстояние между смежными длинами волн. Выражение угловой дисперсии определяется как производная левой части уравнения решетки при фиксированном угле падения:

         (2)

Повысить дисперсию возможно с помощью увеличения частоты штрихов либо с помощью решетки с крупно нарезанными штрихами. В основном используются решетки с мелкими штрихами, поскольку для практических применений обычно необходим более широкий спектр.

Волновая дисперсия выходной щели спектроскопического прибора обычно определяется как обратная линейная дисперсия в нано- или миллиметре. Фокусное расстояние прибора обозначается как f, и тогда общая формула обратной линейной дисперсии принимает вид:

         (3)

Габариты оптической системы зависят в том числе и от фокусного расстояния. Наиболее компактными считаются голографические дифракционные решетки с высокой частотой штрихов.

Рассеяние света также важная характеристика дифракционных решеток. Данная характеристика определяет предел обнаружения.

Голографические решетки отличаются меньшим светорассеянием и полным отсутствием «ложных» спектров на картине, поскольку метод голографической записи дает более точные промежутки между интерференционными полосами (штрихами). Однако если используются источники рассеянного света, светорассеяние голографической решетки повысится.

Область свободной дисперсии

Из уравнения дифракционной решетки можно вывести следующую закономерность: длина волны падающего света λ соответствует первому порядку дифракции, λ/2 – второму порядку дифракции, λ/3 – третьему и т. д. Очень часто при использовании решеток нужно каким-либо образом ограничивать порядки дифракции: например, с помощью полосового фильтра, либо используя ограниченный диапазон длин волн источника света или приемника.

Область свободной дисперсии дифракционных решеток, или свободная спектральная область – это максимальный интервал длин волн, который можно наблюдать при использовании данной дифракционной решетки (и в конкретном порядке дифракции) без переналожения соседних порядков спектра. Если λ₁ — нижний предел (наименьшая длина волны), λ₂ — верхний предел (наибольшая длина волны), тогда область свободной дисперсии выражается с помощью уравнения:

        (4) 

Очевидно, свободная спектральная область уменьшается пропорционально росту порядка дифракции. Так, например, порядок дифракции решетки m = -1 соответствует области свободной дисперсии величиной λ₂/2. Это значит, что в диапазоне от λ₁ до 2λ₁ не будет наблюдаться переналожения спектров до второго порядка.

Разрешающая способность

Спектральное разрешение дифракционной решетки Δλ определяется как расстояние между двумя пиками спектральных полос, которые только могут быть обнаружены приемником как раздельные. Из теории известно, что дифракционные решетки имеют предел разрешения, обусловленный свойствами конкретного прибора и источника.

Разрешающая способность дифракционной решетки есть безразмерное число R. Краткая формула имеет вид:

        (5) 

где m – порядок дифракции, N – общее число штрихов на рабочей поверхности решетки. Как видно из формулы, существует предел произведения порядка дифракции и количества штрихов.

Теоретическое значение разрешающей способности решетки всегда несколько выше реального, поскольку существуют дефекты поверхности решетки и профиля пучка.

В качестве расчетного примера рассмотрим 110-миллиметровую решетку с частотой 1800 штрихов/мм. В первом порядке дифракции теоретическая разрешающая способность равна 198000, спектральное разрешение составляет 0.03 нм при длине волны 500 нм.

Эффективность дифракционной решетки

Абсолютная эффективность определяется как величина падающего потока, который дифрагирует в заданном порядке дифракции. Относительная эффективность связана с коэффициентом отражения зеркала, покрытого тем же составом, что и решетка. Следует отметить, что относительная эффективность всегда выше, чем абсолютная.

В большинстве приложений используется только один порядок дифракции, где «идеальная» решетка обеспечивала бы стопроцентную абсолютную эффективность. Однако эффективность реальной решетки, как правило, является сложной функцией длины волны и поляризации падающего света, также зависит от частоты штрихов, профиля и материала решетки. В случае излучения с поперечной магнитной поляризацией, когда вектор электрического поля перпендикулярен штрихам решетки, можно наблюдать быстрые скачки эффективности даже при небольшом изменении длины волны. Этот феномен был впервые обнаружен Р. В. Вудом в 1902 году, поэтому скачки эффективности дифракционной решетки обычно называют аномалиями Вуда.

Синусоидальные решетки

Синусоидальный профиль штрихов характерен для голографического метода изготовления дифракционных решеток. Кривая эффективности голографической решетки в отличие от решетки, изготовленной традиционным методом нарезки, более гладкая и однородная.

Эффективность рассчитывается для конкретной спектральной области, аналогично рассчитывается глубина штрихов. Большую глубину нарезки имеют решетки с высокой частотой штрихов. Когда расстояние между канавками менее, чем в 1.25 раз меньше рабочей длины волны, существуют только порядки дифракции -1 и 0, а если решетка имеет соответствующий профиль штрихов, большая часть дифрагированного света переходит в порядок -1. В этой области голографические дифракционные решетки дают более 50% абсолютной эффективности.

Отражательная дифракционная решетка

Отражательные дифракционные решетки предназначены для конкретной длины волны, рабочий диапазон варьируется от угла решетки. Абсолютная эффективность резко снижается в диапазонах, отличных от рабочего, при этом в рабочей области может составлять примерно 70%.

Перестраивание длины волны лазерного источника

Голографические решетки часто используются для перестраивания длины волны лазера. Решетка выполняет роль селективного торцевого зеркала в резонаторе. При использовании дифракционной решетки для перестраивания длины волны лазерного излучения применяются две основные конфигурации – схема Литтроу и схема скользящего падения (также известна как схема Литтмана).

Конфигурация Литтроу

Решетка установлена так, чтобы свет желаемой длины волны дифрагировал в обратном направлении вдоль падающего излучения, а длина волны распознается вращением решетки. Внутри резонатора обычно используется ахроматическая линза, которая расширяет лазерный пучок, чтобы заполнить как можно большую площадь решетки. В качестве выходного излучения принимается излучение нулевого порядка дифракции. Недостатком этой конфигурации является то, что направление пучка меняется вместе с поворотом решетки.

Конфигурация Литтмана

Решетка фиксируется под углом падения примерно 90°, а длина волны настраивается вращением специального настраивающего зеркала. Дополнительная линза для расширения пучка не требуется, и поэтому можно использовать меньшую решетку. Однако больший угол падения подразумевает, что габаритная ширина решетки должна быть значительно больше, чем протяженность штрихов.

Эффективность схемы Литтмана может быть очень высокой, в особенности если используется входное излучение с поляризацией, перпендикулярной штрихам решетки (поперечной магнитной поляризацией). В случае поперечной электрической поляризации эффективность заметно снижается. 

Компрессия импульса

Когда короткий лазерный импульс передается через оптическое волокно, импульс как бы растягивается или «чирпируется» из-за нелинейных эффектов (явление так называемой фазовой автомодуляции).

Например, импульс падает на решетку с нормальной оптической дисперсией, то есть длинноволновая часть излучения проходит через оптическую систему быстрее, чем коротковолновая. Используя пару решеток, можно найти такое расположение, чтобы длинноволновая часть импульса проходила более длинный путь. В оптимальном случае на выходе образуется ограниченный импульс. Пара решеток не только компенсирует уширение импульса в волокне, но и сокращает его растяжение. Сжатие может достигать 90 раз.

Усиление чирпированного импульса

Очень короткие импульсы (~ 100 фс) генерируются лазерами с синхронизацией мод. Эти импульсы имеют слишком низкую пиковую мощность. Техника усиления чирпированных импульсов позволяет достичь пиковых мощностей порядка ТВт.

Усилитель представляет собой лазерный кристалл внутри резонатора. Чтобы избежать влияния нелинейных эффектов, разрушающих кристаллы, входной импульс расширяется во времени, что приводит к снижению пиковой мощности. Далее чирпированный импульс снова усиливается и затем сжимается для достижения высокой мощности. Нужно также отметить, что длительность выходного импульса в результате практически равна длительности входного.

Расширение и сжатие

Как при растяжении, так и при сжатии используются пары решеток, расположенные в субтрактивном дисперсионном режиме: то есть так, что угловая дисперсия первой решетки вычитается второй решеткой. Два параллельных пучка с разными длинами волн, падающие на первую решетку, остаются параллельными и после прохождения сквозь вторую решетку, несмотря на разницу пройденных расстояний.

Пара решеток, расположенная параллельно, будет вводить отрицательную дисперсию групповой скорости, то есть длинноволновые части излучения приходят позже, чем коротковолновые.

Для достижения положительной дисперсионной задержки необходима более сложная схема, в этом случае система афокальных линз (телескоп) размещается между решетками. Телескоп регулирует знак углов так, чтобы пучки падали на вторую решетку под тем же углом, что и на первую.

Расширитель и компрессор пучка обычно используются в двухпроходном режиме. Из преимуществ этого режима: удвоение дисперсии. Все длинноволновые компоненты пучка становятся коллинеарными, а не линейными, как это происходило бы в режиме одного прохода.

Инструменты для спектроскопии

Стандартный набор для спектроскопических исследований в основном состоит из входной апертуры, коллиматора, рассеивающего элемента, фокусирующих оптических компонентов, в отдельных случаях набор дополняется выходной апертурой. Свет, попадающий на входную щель, в коллиматоре (обычно вогнутое зеркало) преобразуется в параллельный пучок.

Рассеивающий элемент (решетка) отклоняет излучение под углом, зависящим от длины волны. Рассеянный свет фокусируется на плоскости изображения, где и формируется спектр (серия монохроматических изображений входной щели).

Монохроматоры

В монохроматоре установлена выходная апертура, с помощью которой передается очень узкая часть спектра. Входная и выходная щели жестко закреплены, сканирование спектра осуществляется вращением решетки. Итак, решетка работает с постоянным угловым отклонением между падающим и рассеянным светом. Данная схема реализована в большинстве монохроматоров типа Черни-Тернера, Эберта и Литтроу.

Волоконная оптика

Голографические решетки отлично подходят для приложений волоконной оптики благодаря компактным размерам, высокой частоте штрихов, эффективности и угловой дисперсии.

Рамановская спектроскопия и эксперименты по рассеянию лазерного излучения

В исследованиях, связанных с рассеянием лазерного излучения (рамановская спектроскопия и рассеяние Томсона), где требуется диагностика плазмы, требования к решетке очень высоки. Образец освещается лазерным излучением, резонансное рассеяние приводит к появлению слабых спектральных линий, близких к основной полосе. В рамановской спектроскопии интенсивность спектральной картины наиболее низкая, что и является основной проблемой данного метода.

Требуемое разрешение достигается с помощью крупногабаритных приборов с большим фокусным расстоянием, при этом все оптические поверхности должны иметь высочайшее качество. При работе в непосредственной близости от интенсивной спектральной линии аберрации оптической системы и дифракция Фраунгофера от упоров апертуры могут провоцировать значительное светорассеяние.

Решетки Spectrogon с низким уровнем светорассеяния изготавливаются на подложках высокого качества, потому такая решетка практически не будет вносить аберрации. Подобные решетки часто устанавливаются в масс-спектрометрах с двойной или тройной фокусировкой для уменьшения рассеянного света.

Голографические решетки становятся распространенным предпочтением. Нарезные решетки, несмотря на высокое качество, все равно порождают ложные спектры, сильно искажающие исследуемые сигналы.

Спектроскопия поглощения

Абсорбционная спектроскопия является еще одним приложением, в котором низкий уровень светорассеяния голографических решеток имеет большое преимущество. Уровень рассеянного света напрямую связан с диапазоном поглощения прибора, и чем меньше рассеянного света, тем более точный спектр поглощения можно получить.

Источник света в абсорбционной спектроскопии обычно представляет собой широкополосный источник, и поэтому рассеянный свет будет состоять из сплошного спектра. Каждый компонент длины волны падающего света порождает спектр рассеяния, в центре которого находится фактическая длина волны. Результирующий рассеянный свет является суммой всех длинноволновых компонентов.

© Spectrogon

Компания INSCIENCE помогает своим заказчикам решать любые вопросы и потребности по продукции Spectrogon на территории РФ