Как найти разрешающую способность микроскопа

Качество изображения

Разрешающая способность микроскопа

Качество изображения определяется разрешающей способностью микроскопа, т.е. минимальным расстоянием, на котором оптика микроскопа может различить раздельно две близко расположенные точки. разрешающая способность зависит от числовой апертуры объектива, конденсора и длины волны света, которым освещается препарат. Числовая апертура (раскрытие) зависит от угловой апертуры и показателя преломления среды, находящейся между фронтальной линзой объектива и конденсора и препаратом.

Угловая апертура объектива — это максимальный угол (AOB), под которым могут попадать в объектив лучи, прошедшие через препарат. Числовая апертура объектива равна произведению синуса половины угловой апертуры на показатель преломления среды, находящейся между предметным стеклом и фронтальной линзой объектива. N.A. = n • sinα где, N.A. — числовая апертура; n — показатель преломления среды между препаратом и объективом; sinα — синус угла α равного половине угла АОВ на схеме.

Таким образом, апертура сухих систем (между фронтальной линзой объектива и препаратом-воздух) не может быть более 1 (обычно не более 0,95). Среда, помещаемая между препаратом и объективом, называется иммерсионной жидкостью или иммерсией, а объектив, рассчитанный для работы с иммерсионной жидкостью, называют иммерсионным. Благодаря иммерсии с более высоким показателем преломления чем у воздуха, можно повысить числовую апертуру объектива и, следовательно, разрешающую способность.

Числовая апертура объективов всегда гравируется на их оправах.
Разрешающая способность микроскопа зависит также от апертуры конденсора. Если считать апертуру конденсора равной апертуре объектива, то формула разрешающей способности имеет вид R=λ/2NA, где R — предел разрешения; λ — длина волны; N.A — числовая апертура. Из этой формулы видно, что при наблюдении в видимом свете (зеленый участок спектра — λ=550нм), разрешающая способность (предел разрешения) микроскопа не может быть > 0,2мкм

Влияние числовой апертуры объектива микроскопа на качество изображения

Пути повышения оптической разрешающей способности

Выбор большого угла светового конуса, как со стороны объектива, так и со стороны источника освещения. Благодаря этому, возможно, собрать в объективе более преломленные лучи света от очень тонких структур. Таким образом, первый путь повышения разрешения — это использование конденсора, числовая апертура которого соответствует числовой апертуре объектива.

Второй способ — использование иммерсионной жидкости между фронтальной линзой объектива и покровным стеклом. Так мы воздействуем на показатель преломления среды n, описанный в первой формуле. Его оптимальное значение, рекомендуемое для иммерсионных жидкостей, составляет 1.51.

Иммерсионные жидкости

Иммерсионные жидкости необходимы для увеличения числовой апертуры и соответственно повышения разрешающей способности иммерсионных объективов, специально рассчитанных для работы с этими жидкостями и, соответствующим образом, маркированными. Иммерсионные жидкости, помещенные между объективом и препаратом, имеют более высокий показатель преломления, чем воздух. Поэтому, отклоненные мельчайшими деталями объекта лучи света, не рассеиваются, выходя из препарата, и попадают в объектив, что приводит к повышению разрешающей способности.

Существуют объективы водной иммерсии (маркированные белым кольцом), масляной иммерсии (черное кольцо), глицериновой иммерсии (желтое кольцо), монобромнафталиновой иммерсии (красное кольцо). В световой микроскопии биологических препаратов применяются объективы водной и масляной иммерсии. Специальные кварцевые объективы глицериновой иммерсии пропускают коротковолновое ультрафиолетовое излучение и предназначены для ультрафиолетовой (не путать с люминесцентной) микроскопии (то есть для изучения биологических объектов, избирательнопоглощающих ультрафиолетовые лучи). Объективы монобромнафталиновой иммерсии в микроскопии биологических объектов не используются.

В качестве иммерсионной жидкости для объектива водной иммерсии используется дистиллированная вода, масляной иммерсии — природное (кедровое) или синтетическое масло с определенным показателем преломления.

В отличие от других иммерсионных жидкостей масляная иммерсия является гомогенной, так как имеет показатель преломления равный или очень близкий показателю преломления стекла. Обычно этот показатель преломления (n) рассчитан для определенной спектральной линии и определенной температуры и указывается на флаконе с маслом. Так, например, показатель преломления иммерсионного масла для работы с покровным стеклом для спектральной линии D в спектре натрия при температуре =20°С равен 1,515 (nD 20 = 1,515 ), для работы без покровного стекла (nD 20 = 1,520).

Для работы с объективами-апохроматами нормируется также дисперсия, то есть разность показателей преломления для различных линий спектра.

Использование синтетического иммерсионного масла предпочтительнее, поскольку его параметры более точно нормируются, и оно в отличие от кедрового, не засыхает на поверхности фронтальной линзы объектива.

Учитывая вышесказанное, ни в коем случае нельзя пользоваться суррогатами иммерсионного масла и, в частности, вазелиновым маслом. При некоторых способах микроскопии для увеличения апертуры конденсора, иммерсионная жидкость (чаще дистиллированная вода) помещается между конденсором и препаратом.

Разрешающая способность микроскопа

Технически
возможно создать оптические микроскопы,
объективы и окуляры которых дадут общее
увеличение 1500-2000 и больше. Однако это
нецелесообразно, так как возможность
различить мелкие детали предмета
ограничивается дифракционными явлениями.
Вследствие этого изображение мельчайших
деталей предмета теряет резкость, может
возникнуть нарушение геометрического
подобия изображения и предмета, соседние
точки будут сливаться в одну, возможно
полное исчезновение изображения. Поэтому
в оптике существуют следующие
понятия, которые
характеризуют
качество микроскопа:

Разрешающая
способность микроскопа
— свойство
микроскопа давать раздельно изображение
мелких деталей рассматриваемого
предмета.

Предел
разрешения
— это наименьшее
расстояние между двумя точками, которые
видны в микроскопе раздельно.

Чем
меньше предел разрешения, тем выше
разрешающая способность микроскопа!

Предел
разрешения обусловливает наименьший
размер деталей, которые могут различаться
в препарате с помощью микроскопа.

Теорию
разрешающей способности микроскопа
разработал директор завода К.Цейса в
Йене профессор-оптик Э.Аббе (1840-1905). В
качестве простейшего микропрепарата
он взял дифракционную решетку ( рис. 2),
изучил механизм формирования изображения
в микроскопе и показал следующее.

1. 

   Пучок вторичных
   световых волн после дифракции на объекте
   DD
   попадает в объектив и создает в результате
   интерференции в его фокальной плоскости
   FF
   дифракционную картину — систему главных
   максимумов
   

   и минимумов.

2. Рис.
   2

   Далее в формировании
   изображения участвуют только лучи,
   образующие главные максимумы. Они
   пересекаются в соответствующей плоскости
   и дают изображение объекта D^’D^’.

Введем
понятие
апертурного
угла — это
угол между крайними лучами конического
светового пучка, идущего от середины
объекта в объектив ( рис. 3,а).
Для создания изображения, то есть для
разрешения объекта, достаточно, чтобы
в объектив попали лучи, образующие
максимумы только нулевого и первого
порядка хотя бы с одной стороны (
рис. 2 и 3,б).
Участие в образовании изображения лучей
от большего количества максимумов
повышает качество изображения, его
контраст. Поэтому лучи, образующие эти
максимумы, должны быть в пределах
апертурного угла объектива.

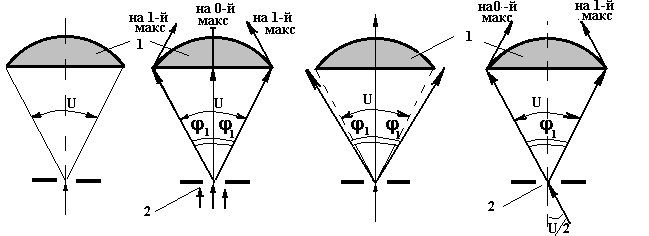
а)
б) в)
г)

1- фронтальная
линза объектива, 2 — объектив

Рис .3

Таким
образом, если объектом является
дифракционная решетка с периодом d
и свет падает на нее нормально ( рис.2 и
3,б),
то в формировании изображения обязательно
должны участвовать лучи, образующие
максимумы нулевого и первого порядков
с обеих сторон, а угол ₁
— угол
отклонения лучей, образующих максимум
первого порядка, соответственно должен
быть, в крайнем случае, равен углу U/2.

Если
же взять решетку с меньшим периодом d’,
то угол ’₁
будет больше
угла U/2
и изображение не возникнет. Значит
период решетки d
можно принять за предел разрешения
микроскопа Z.
Тогда, используя формулу дифракционной
решетки, запишем для k=1:

.

Заменяя
d
на Z,
а ₁
на U/2,
получим

.
(6)

Во
время микроскопии световые лучи падают
на объект под разными углами. При
наклонном падении лучей (рис.3,г)
предел разрешения уменьшается, так как
в формировании изображения будут
участвовать только лучи, образующие
максимумы нулевого порядка и первого
порядка с одной стороны, а угол ₁
будет равен апертурному углу U.
Расчеты показывают, что формула для
предела разрешения в этом случае
принимает следующий вид:

.
(7)

Если
пространство между объектом и объективом
заполнить иммерсионной средой с
показателем преломления n,
который больше показателя преломления
воздуха, то длина волны света _n
= 

n
. Подставляя
это выражение в формулу для предела
разрешения (7), получим

,
или

. (8)

Таким
образом, формула (7) определяет предел
разрешения для микроскопа с сухим
объективом, а формула (8) -для микроскопа
с иммерсионным объективом. Величины
sin
0,5U
и nsin
0,5U
в этих
формулах называют числовой апертурой
объектива и обозначают буквой А.
Учитывая это, формулу предела разрешения
микроскопа в общем виде записывают так
:

.
( 9)

Как видно из формул
(8) и (9), разрешающая способность микроскопа
зависит от длины волны света, величины
апертурного угла, показателя преломления
среды между объективом и объектом, угла
падения световых лучей на объект, но
она не зависит от параметров окуляра.
Окуляр никакой дополнительной информации
о структуре объекта не дает, качества
изображения не повышает, он лишь
увеличивает промежуточное изображение.

Разрешающая
способность микроскопа может быть
повышена за счет использования иммерсии
и уменьшения длины волны света. Повышение
разрешающей способности при использовании
иммерсии можно пояснить следующим
образом. Если между объективом и объектом
находится воздух (сухой объектив), то
световой луч при переходе из покровного
стекла в воздух, среду с меньшим
показателем преломления, значительно
изменяет свое направление в результате
преломления, поэтому меньше лучей
попадает в объектив. При использовании
иммерсионной среды, показатель преломления
которой приблизительно равен показателю
преломления стекла, изменение хода
лучей в среде не наблюдается и большее
количество лучей попадает в объектив.

В
качестве иммерсионной жидкости берут
воду (n=1,33),
кедровое масло (n=1,515)
и др. Если максимальный апертурный угол
у современных объективов достигает
140⁰
, то для сухого объектива А=0,94,
а для объектива с масляной иммерсией
А=1,43.
Если при расчете использовать длину
волны света 
= 555 нм, к которой наиболее чувствителен
глаз, то предел разрешения сухого
объектива составит 0,30 мкм, а с масляной
иммерсией — 0,19 мкм. Значение числовой
апертуры указывается на оправе объектива:
0,20; 0,40; 0,65 и др.

Повышение разрешающей
способности оптического микроскопа за
счет уменьшения длины волны света
достигается при использовании
ультрафиолетового излучения. Для этого
имеются специальные ультрафиолетовые
микроскопы с кварцевой оптикой и
приспособлениями для наблюдения и
фотографирования объектов. Так как в
этих микроскопах используется свет с
длиной волны примерно в два раза меньше,
чем у видимого света, то они способны
разрешать структуры препарата размерами
около 0,1мкм. Ультрафиолетовая микроскопия
имеет еще одно преимущество — с ее помощью
можно исследовать неокрашенные препараты.
Большинство биологических объектов
прозрачны в видимом свете, так как не
поглощают его. Однако они обладают
избирательным поглощением в ультрафиолетовой
области и, следовательно, легко различимы
в ультрафиолетовых лучах.

Наибольшая
разрешающая способность у электронного
микроскопа, так как длина волны при
движении электрона в 1000 раз меньше длины
световой волны.

Соседние файлы в предмете Физика

• #
• #
• #

Микроскоп – сложная оптическая система, позволяющая увеличивать изображение исследуемого объекта с десятки и сотни раз. У всех них есть принцип действия, а также характеристики, от которых зависит сфера работы каждого увеличительного прибора.

Увеличение микроскопа

Работа со световым микроскопом проводится для получения изображения под увеличением. Различают несколько его типов: объектив, окуляр, а также диапазон увеличения. Также у современного оборудования есть и цифровое.

Во сколько раз увеличивает световой микроскоп?

В обычном устройстве установлены две линзы, которые являются короткофокусными. Это окуляр и объектив.

Окуляр – это часть увеличительного прибора, устанавливаемая в окулярный узел, куда непосредственно смотрит исследователь. Его кратность в среднем составляет 10-20, величина этого параметра зависит от марки и вида прибора. Эти элементы могут быть съемные, а могут и быть установлены стационарно.

Как определить увеличение светового микроскопа?

Увеличение изображения, обеспечиваемое световым микроскопом, соответствуют произведению усиления окуляра и объектива. То есть изображение, которое мы видим при увеличении объекта, является совместной работой одного и второго элемента.

Объективы же – это элементы, которые также имеют в совеем составе увеличительные линзы. Данная конструкция закреплена на револьверном блоке, на котором может быть несколько объективов.

Поле зрения микроскопа

Поле зрения является параметром, характеризующий предельно максимальный диаметром области, который может быть визуализирован человеческим глазом при исследовании через окуляр. Зависит поле зрения от:

• Характеристик окуляра;
• Особенностей объектива;
• Диаметра тубуса.

Данную величину можно рассчитать в миллиметрах, если исследовать миллиметровую шкалу линейки через микроскоп, при этом поле зрения не зависит от кратности увеличения окуляра.

Диаметр выходного зрачка микроскопа

Для того, чтобы определить такой показатель, как диаметр выходного зрачка, необходимо применение динаметра Рамсдена. Также для измерения такой величины может использоваться диоптрийная трубка со стеклянной шкалой. В фокальной плоскости анной лупы расположена сетка, цена деления которой составляет 0,1 миллиметр.

Разрешающая способность

Важными параметрами для увеличительного оборудования является и разрешающая способность светового микроскопа.

Смыслом определения разрешающая способность светового микроскопа, является возможность оптической системы четко различать две рядом расположенные точки. Это минимальное расстояние, расположенное между двумя точками, различающимися отдельно друг от друга.

Есть пределы разрешения светового микроскопа.

Максимальная разрешающая способность равна 0,25 мкм, это предел разрешающей способности светового микроскопа.

Если не достигнут предел разрешения светового микроскопа, то ее можно увеличить. Это возможно путем увеличения апертуры объектива или уменьшением длины волны света.

Полезное увеличение

Это показатель, который определяет увеличение, способное увидеть глазом исследователя, равное разрешающей способности прибора.

Это означает, что разрешающая способность человеческого глаза равна такому же показателю увелиивающего устройства. Для того, чтобы определить максимальную разрешающую способность объектива, необходимо подобрать от 500 до 1000 крат.

Минимальное полезное увеличение – это числовая апертура, помноженная на 500. Соответственно, максимальное увеличение – это числовая апертура, умноженная на 1000. Использование значений, менее минимальных, не даст возможности использовать разрешающую способность в полном объеме, а работа на больших параметрах не дать более четкого изображения изучаемого объекта.

Какие органоиды можно увидеть в световой микроскоп?

При помощи него можно довольно детально изучить структуру и строение клетки и ее органелл. В стандартный световой микроскоп можно увидеть рибосомы, комплекс Гольджи, который был открыт именно при помощи данного оборудования Камилло Гольджи, ядро, вакуоли, митохондрии, хлоропласт. Также прекрасно визуализируется клеточная стенка.

При выборе такой аппаратуры очень важно понимать ее сферу применения, так как для школьной лаборатории вполне достаточными параметрами обладает обычный световой микроскоп, а для научно-исследовательской, медицинской лаборатории, его мощности будет недостаточно для достижения всех поставленных целей. Среди такой техники можно выделить оптические, электронные, рентгеновские микроскопы, сканирующие оптические микроскопы ближнего поля и другие.

Wave optics, also known as Physical optics, deals with the study of various phenomena such as diffraction, polarization, interference, resolution, and other occurrences. Wave optics is the segment of optics that focuses on the study and behavior of light and its wave characteristics. Wave optics particularly describes the connection between waves and rays of light. According to the wave theory of light, light is a form of energy, it travels through a medium in the form of transverse wave motion. The speed of light traveling through a medium depends upon the nature of the medium.

Here, the approximation is carried out by using ray optics for the estimation of the field on a surface. Integrating ray-estimated field over a mirror, lens, or aperture for the calculation of the scattered or transmitted field also gets involved later on. Wave optics stands as a witness to the scientific study of understanding the nature of light. One is the particle nature of light and the other is the wave nature of light.

What is Resolving Power?

The resolving power of an optical instrument is defined as the capacity of the instrument to distinguish between two objects that are close together and produce distinct images of the two objects.

In other words, resolving power changes in inverse proportion to the distance between the two objects to be resolved when viewed from an optical instrument. The images of two close-lying objects appear distinct and separate when viewed from the device. When a telescope is used to view two stars located close to each other; the telescope’s resolving power will depend on its capacity to resolve the images of the two stars. The resolving power of a lens used in a telescope can be determined by its ability to differentiate two lines or points in an object. 

Resolving Power of Optical Instrument

Human eyes are not much powerful. They need some help in some cases. This is where optical instruments come into play. These instruments have a major role in various scientific fields. From the depths of space to the layers of hair, to see all the details we require these instruments, as we cannot see them using the naked eye. One of the important aspects of optical instruments is their resolving power.

Resolving Power is a quantity that characterizes the ability of optical instruments to produce distinct images of two points of an object that are placed nearby. Devices like microscopes and telescopes have various lenses and their combination is used to generate images of different objects. Limit of resolution is defined as the smallest linear or angular distance between the two points at which their images begin to merge. The inverse to the limit of resolution is called the resolving power.

In an ideal optical system (one without aberrations), the image of a point is not a point but a central disk of light surrounded by rings, it occurs due to the diffraction of light at the edges of optical components, which are alternately dark and bright in monochromatic light and rainbow-colored in white light.

What is Resolution?

Resolution is the quality of the image which is decided by the diffraction effect. The resolving power of an instrument depends on its resolution. The resolution of an optical instrument is defined as the smallest distance between two points that can be distinguished by the observer’s eye or the lens installed in the optical device. Scientifically, the precision with which an optical device can record or measure a specimen’s variables under observation is also known as resolution.

It is measured by the smallest distance which could be seen clearly without blur due to diffraction. The diffraction or aberration reduces the resolution of an instrument and often creates a blurred image. Diffraction is associated with the wave nature of light. Light interferes with itself when it passes through a lens and creates a ring-shaped diffraction pattern called the Airy pattern. Such a pattern is obtained only when the wavefront of the light source is spherical or plane at the aperture’s exit point.

What is Magnification?

Magnification is the process of enlarging an object only by appearance and not by actual physical size. This enlargement can be calibrated by calculated numbers known as magnification. The magnified image does not actually become large but it appears to be large. Various lenses are used for this process of magnification. This concept of magnification is used in microscopes and telescopes. The magnification in the microscope helps in the study of the structure and composition of different microbes. whereas, the magnification in the telescope is observing the stars and planets. 

Resolution Vs Magnification

Magnification is the ability to make small objects larger to see their details properly, like making microscopic organisms visible. It is the process of enlarging an object only by appearance and not by the actual physical size. Resolution is the ability to distinguish between two objects from each other. The term magnification is often confused with resolution. Resolution determines the ability of the instrumentation system to show details in the object that is being imaged. On the other hand, magnification means without high resolution may make small microbes visible. Magnification magnifies the object’s size while resolution distinguishes between two objects. Magnification doesn’t allow the observer to distinguish between two objects. In order to distinguish between two different objects under a microscope, it should be first magnified to a specified point at which the resolution becomes much more relevant. The magnification and resolution of an optical instrument are inversely related to each other. When magnification increases, the resolution decreases, and vice versa.

Rayleigh’s Criterion

The minimum distances between images must be such that the central maximum of the first image lies on the first minimum of the second and vice versa. Such an image viewed from an optical device is calculated using Rayleigh’s criterion.

When two objects placed at a distance from each other are separated by an angular separation θ, the diffraction patterns of the two objects will overlap each other. They would appear as one when the two central maxima overlap. This defines Rayleigh’s resolution criterion. It can be shown that, for a circular aperture of a given diameter, the first minimum in the diffraction pattern occurs at, 

θ = 1.22(λ/D)

Where,
θ: the angular separation measured in radians
λ: the wavelength of light
D: the diameter of the aperture

Resolving Power of Telescope

Objects such as binary stars, individual stars, distant galaxies, and planets subtend small angles on a telescope. A larger aperture is needed to resolve these small angles and improve the resolving power of the telescope. Rayleigh’s criterion can be used to determine the resolving power of the telescope. The resolving power is inversely proportional to the angular separation between two distant objects. According to Rayleigh’s resolving power of optical instruments formula,

Δθ = 1.22(λ/d)

The resolving power is the reciprocal of angular separation:

Resolving Power = 1/Δθ = 1 / (1.22λ/d) = d/1.22λ

Thus, the higher the value of d or the diameter of the aperture, the better will be the resolution of the telescope. Astronomical optical telescopes have mirror diameters as large as 10 m to obtain the best resolution. 

Resolving Power of Optical Microscope

The resolving power of a microscope determines how far apart points can be seen separately. In the case of the Microscope, The resolving power is inversely proportional to the distance between the two objects. Its resolving power can also be determined by its resolving range. The resolution limit of a microscope is the shortest distance between two nearby objects when the images formed by the microscope are properly differentiated. The smaller the distance higher is the resolving power of the microscope. Using Ernst Abbe’s criterion, the resolution power of a microscope can be given by, 

 Δd = λ/(2nsinθ)

Here, the resolution Δd (smallest resolvable distance between two objects) of a microscope varies with the angular aperture.

Mathematically, the resolving power of an optical microscope can be given as:

Resolving Power = 1/Δd = (2nsinθ)/λ

where,
n is the refractive index of the medium
θ is the half-angle of the lens, which depends on the focal length and diameter of the lens.
λ wavelength of light

What is Diffraction Limit?

When we observe a point object using a circular aperture, like a lens or iris the image formed of the point object is not a point but a diffracted pattern is formed. This phenomenon is more pronounced when the size of the object is comparable to the wavelength of light, the smallest object which can be seen is termed the Diffraction Limit.

Solved Examples on Resolving Power

Example 1: A space telescope’s primary mirror has a diameter of 3.2 m. Determine the angle between two just-resolvable point light sources. Assume the average wavelength of light as 550 nm. 

Solution: 

Given,

Diameter (D) = 3.2 m

Wavelength of light (λ) =550 nm = 550 x 10^-9 m 

Using Rayleigh’s criterion, 

θ = 1.22 (λ/D)

θ = 1.22 (550 x 10^-9 / 3.2)

= 2.097 x 10^-7 m

Example 2: Assume that light of wavelength 400nm is coming from a star. The limit of resolution of a telescope whose objective has a diameter of 2.6m is.

Solution:

Given, 

Diameter of Objective Telescope (D) = 2.6 m = 100 x 2.6 cm = 260 cm

The wavelength of light (λ) = 400 nm = 4 x 10^-5 cm 

Limit of Resolution of telescope, 

dθ = 1.22λ / D = 1.22 x 4 x 10^-5/ 260

= 1.877 x 10^-7 radian

Example 3: The diameter of the objective of a telescope is 1.8m. Its resolving limit for the light of wavelength 3462 A, will be

Solution: 

Given, 

Diameter of objective telescope (D) = 1.8 m

Wavelength of light (λ) = 3462 A = 3462 x 10^-10 m 

Resolving limit (dθ) = 1.22λ / D 

= 1.22 x 3462 x 10^-10 / 1.8

= 2.346 x 10^-7 rad. 

Example 4: The limit of resolution of the microscope, if the numerical aperture of the microscope is 0.26, and the wavelength of light used is 900 nm, is

Solution: 

 Given,

Numerical Aperture (A) = 0.26 

Wavelength of light (λ) = 900 nm

For a microscope, the limit of resolution is given by,

X = λ/2A

= 900 / (2 x 0.26)

= 1.73 μm

Example 5: Calculate the resolving power of the microscope if its numerical aperture is 0.12 and wavelength of light is 5000 A. 

Solution: 

Given, 

Numerical Aperture (A) = 0.12

Wavelength of light (λ) = 5000 A

Resolving Power of Microscope (RP) = 2μsinθ / λ

                                                        = 2A / λ                                  …(Since, μsinθ = Numerical Aperture)

                                                        = 2 x 0.12 / 5000 x 10^-10

                                                        = 4.8 x 10⁵ m^-1

FAQs on Resolving Power

Question 1: What is Wave Optics?

Answer:

In Physics, Wave Optics is the branch of optics where the phenomenon like ray approximation of geometric optics is not valid such as diffraction, polarization or interference, etc.

Question 2: Explain the resolving power of an optical device.

Answer: 

The resolving power of an optical instrument is the ability of the device to distinguish between two objects that are close together and produce distinct images of these objects.

Question 3: Define the angular limit of resolution.

Answer:

The angular limit of resolution or angular resolution is the angle subtended by the two distinct objects at the objective lens of the optical instrument, when these two objects are just observed as separate objects. 

Question 4: What are Airy Discs?

Answer:

A diffraction pattern of concentric rings which is created by circular apertures, and grows dimmer as we go away from the center. These concentric circles are known as Airy discs. 

Question 5: What is the resolving power of the Human Eyes?

Answer: 

The resolution power of human eyes is about 1′ that means Human eyes can see objects placed at a distance of about 100 km apart. 

Related Resources

• Laws of Refraction of Light
• Concave and Convex Mirrors
• Reflection of Light at Plane Surface