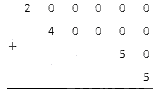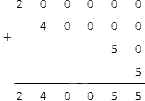Для того, чтобы выполнить некоторые действия над натуральными числами необходимо представить эти числа в виде суммы разрядных составляющих или, как говорят, разложить натуральные числа на цифры. Не менее важен и обратный процесс, который заключается в записи натурального числа в виде суммы разрядных составляющих.
Как найти натуральное число, если известна его подобная сумма?
Для того, чтобы проделывать некоторые действия, нужно представлять начальные выражения в виде сложенных чисел – другим языком, необходимо разложить числа по разрядам. Противоположный процесс также безгранично важен при решении задач и упражнений.
Определение
Разрядные слагаемые – это такие числа, которые состоят исключительно из нулей и единственной цифры, отличной от нуля. Такие натуральные числа, как 5, 20, 400, 100, принадлежат данной категории, а числа 55, 213, 680, 324, 458, 25, 694, 25 и другие – не относятся.
Число разрядных слагаемых у некоторого числа равно тому числу, сколько цифр содержатся в записи. Представление числа 61 в виде суммы разрядных слагаемых, станет выглядеть как 6 и 1, они отличаются от 0. Когда есть необходимость разложить 55050 как сумму слагаемых разрядов, оно будет представлено в виде трех слагаемых. Три пятерки, что присутствуют в записи, отличны от нуля.
Необходимо помнить, что каждое разрядное слагаемое содержит отличное от других количество знаков в собственной записи.
Сумма разрядных слагаемых числа, принадлежащего к классу натуральных, обязательно эквивалентна данному числу.
Натуральные числа, в записи которых присутствует цифра, что отлична от нуля, называются разрядными слагаемыми.
Количество чисел обязано быть равно количеству тех цифр, которые не равных нулю. Каждое слагаемое может быть записано с разным количеством знаков. Если необходимо разложить по разрядам, то при сложении получившихся цифр, мы получим число равно данному числу.
При анализе понятия, можно сформулировать вывод, что многозначные и однозначные числа, которые полностью состоят из нулей за исключением первой цифры, нельзя представлять в виде суммы. Это происходит в том случае, когда такие числа сами будут разрядными слагаемыми для каких-то чисел.
Исключая данные числа, все остальные примеры могут раскладываться на слагаемые.
Правила разложения чисел
Чтобы разложить число на сумму разрядных слагаемых, необходимо вспомнить, что каждое натуральное число связано с количеством определенных элементов. При записи числа разложение зависит от числа единиц, десятков, сотен, тысяч и т.д. К примеру, если взять число 937, то можно увидеть, что ему соответствует 9 сотен, 3 десятка и 7 единиц. Число 245 500 соответствует 2 сотням тысяч, 4 десяткам тысяч, 5 тысячам и 5 сотням. Эти числа можно представить в виде равенств — 900 + 30 + 8 = 938 и 245 500 = 200 000 + 40 000 + 5 000 + 500. В данных примерах можно наглядно увидеть, как число можно разделить на сумму цифр. Рассматривая этот пример, мы можем представить всевозможное натуральное число в виде суммы его разрядных членов. Вот еще один пример. Представим натуральное число 724 как сумму составляющих цифр. 724 равно 7 сотням, 2 десяткам и 4 единицам, поэтому 724 = 700 + 20 + 4. Однако сумма 312 + 412 не является суммой составляющих цифр числа 724, потому что нельзя иметь два числа, которые состоят из одинакового количества цифр. Мы уже рассматривали ключевое понятие. Разрядные слагаемые названы так потому, что они принадлежат к конкретному разряду.
Нет времени решать самому?
Наши эксперты помогут!
Примеры задач
Пример 1. Известна сумма разрядов, как же найти само число?
Чтобы решить этот пример, давайте рассмотрим обратную задачу. Представим, что мы знаем сумму слагаемых цифр. Нам нужно найти заданное натуральное число.
Например, сумма 300 + 40 + 9 равна 349, а сумма 30 000 + 3 000 + 600 + 20 + 7 соответствует натуральному числу 33627. Поэтому легко определить натуральное, если вы знаете сумму его вспомогательных слагаемых.
Другой способ найти натуральное — сложить столбцы сумм цифр. Этот пример не должен вызвать у вас затруднений. Рассмотрим его более подробно.
Пример 2. Нужно найти исходное число, когда дана сумма разрядных концов 300 000 + 50 000 + 2000+ 400 + 40 + 7.
Далее приступим к решению. Необходимо записать числа 300 000, 50 000, 2000, 400, 40, 7 сложить в столбик: осталось лишь сложить все числа в столбик. Важно помнить о том, что сумма нулей равна нулю и что сумма нулей и натурального числа равна натуральному числу.
Таким образом, выполнив сумму, мы получаем натуральное — 352447, сумма цифр которого равна 300 000 + 50 000 + 2000 + 400 + 40 + 7.
Поговорим еще об одном методе. Если мы научились делить числа и преобразовывать их в виде суммы понятий с цифрами, мы также можем представлять данные числа в виде некоторой суммы без цифр.
Пример 3. Разложение числа 5825 представляется как 49565 = 40000 + 9000 + 500 + 60 + 5, а сумма разрядных компонентов 5000 + 800 + 20 + 5 может быть представлена как (40000 + 9000) + (500 + 60) + 5 = 49565 или (40000 + 9000 + 500 + 60) + 5 = 49565 или 40000 + (9000 + 500 + 60) + 5 = 49565 и многие другие способы. Иногда сложные расчеты можно немного упростить. Приведем еще один небольшой пример для наилучшего закрепления представленной информации.
Пример 4. Вычтите числа 67838 и 780. Сначала представим — 67838 как сумму разрядных компонентов: 67838 = 60000 + 7000 + 800 + 30 + 8. Выполнив операцию, можно сделать вывод, что сумма (60000+7000)+ (800 + 30 + 
Стоит рассмотреть обратную задачу более подробно. Считайте, что у нас есть сумма разрядных составляющих натурального числа, и нам нужно найти это число.
Например, сумма 300+20+9 является разложением разрядных чисел 329, а сумма разрядных слагаемых вида 3 000 000 + 40 000 + 4 000 + 500 соответствует натуральному числу 3 044 500.
То есть 600 + 20 + 9 = 629, а 3 000 000 + 30 000 + 4 000 + 500 = 3 034 500.
Чтобы найти положительное число по известной сумме разрядных слагаемых, можно сложить эти разрядные слагаемые в столбик (при необходимости обратитесь к материалу по сложению целых положительных чисел в столбик). Рассмотрим решение этого примера.
Найдите целое положительное, если сумма разрядных составляющих равна 200 000 + 40 000 + 50 + 5.
Запишите числа 200 000, 40 000, 50 и 5 так, как того требует метод сложения в столбик:
Осталось только сложить все эти числа в столбик:
Под горизонтальной чертой мы получили искомое натуральное число.
В заключение мы хотели бы обратить ваше внимание еще на один момент. Умение раскладывать натуральные числа на цифры и умение выполнять обратное действие позволяет представить натуральное в виде суммы слагаемых, которые не являются разрядными.
Например, разрядное сложение целых положительных чисел 643 имеет следующий вид 643 = 600 + 40 + 3, а сумма разрядных слагаемых 700 + 20 + 5 в силу свойств сложения целых положительных чисел может быть представлена как (600 + 40) + 5 = 640 + 3 или 600+(40 + 3) = 600 + 43, или (600 + 3) + 40 = 603 + 40.
Возникает логичный вопрос: «Для чего это нужно? Ответ на него прост: в некоторых случаях это может упростить вычисления.
Пример 4. Вычтем целые положительные числа 5 799 и 790.
Сначала представим вычитаемое как сумму разрядных компонентов: 5 799 = 5 000 + 700 + 90 + 9.
Легко увидеть, что сумма разрядных компонентов равна сумме (5000 + 9) + (700 + 90) = 5009 + 790.
Тогда 5 799 — 790 = (5 009 + 790) — 790 = 5 009 + (790 — 790) =5 009 + 0=5 009.
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Разрядные слагаемые
Поддержать сайт
Любое натуральное многозначное число можно представить в виде суммы разрядных слагаемых.
Например, число «64» состоит из
6 десятков и 4 единиц.
64 = 6 десятков
+ 4 единицы = 6 · 10 + 4 = 60 + 4
Числа «60» и «4» называются разрядными слагаемыми.
Запомните!
Представление числа в виде:
425 = 400 + 20 + 5
называется разложением числа на разрядные слагаемые или суммой разрядных слагаемых.
Примеры.
356 = 3 сотни + 5 десятков + 6 единиц = 3 · 100
+ 5 · 10 + 6 = 300 + 50 + 6
8 092 = 8 тысяч + 0 сотен
+ 9 десятков + 2 единицы =
8 · 1 000 + 0 · 100 + 9 · 10 + 2 =
8 000 + 90 + 2
Числа 1, 10, 100, 1000 и т.д. — называются
разрядными единицами. Так, 1 — это единица разряда единиц; 10
— единица разряда десятков; 100 — единица разряда сотен и т.д.
Часто в заданиях требуется не только разложить число на разрядные слагаемые, но и определить количество
всех единиц какого-либо разряда. В этом случае советуем сделать подробный разбор числа.
Пример подробного разбора многозначного числа «2 038 479» (два
миллиона тридцать восемь тысяч четыреста семьдесят девять).
- Вначале разложим число на сумму разрядных слагаемых.
2 038 479 = 2 · 1 000 000 + 0 · 100 000 +
3 · 10 000 + 8 · 1 000 + 4 · 100 +
+ 7 · 10 + 9 =
2 000 000 + 30 000 + 8 000 + 400 + 70 + 9
- Это число состоит из:
- двух единиц миллионов (2 · 1 000 000);
- трёх десятков тысяч (3 · 10 000);
- восьми единиц тысяч (8 · 1000);
- четырёх сотен (4 · 100);
- семи десятков (7 · 10);
- девяти единиц (9).
- Определим сколько в числе «2 038 479» всего единиц с помощью таблицы.
|
Сколько в числе всего единиц? Чтобы определить количество единиц, записываем всё число, включая сам разряд единиц. |
2 038 479 |
|
Сколько в числе всего десятков? Чтобы определить количество десятков, записываем всё число без разряда единиц (то есть разряда до десятков). |
203 847 _ |
|
Сколько в числе всего сотен? Чтобы определить количество сотен, записываем всё число без разрядов десятков и единиц (то есть разрядов до сотен). |
203 84 _ _ |
|
Сколько в числе всего единиц тысяч? Чтобы определить количество единиц тысяч, записываем всё число без разрядов сотен, десятков и единиц (то есть разрядов до единиц тысяч). |
2 038 _ _ _ |
|
Сколько в числе всего десятков тысяч? Чтобы определить количество десятков тысяч, записываем всё число без разрядов единиц тысяч, сотен, десятков и единиц (то есть разрядов до десятков тысяч). |
2 03 _ _ _ _ |
|
Сколько в числе всего сотен тысяч? Чтобы определить количество сотен тысяч, записываем всё число без разрядов десятков тысяч, единиц тысяч, сотен, десятков и единиц (то есть разрядов до сотен тысяч). |
2 0 _ _ _ _ _ |
|
Сколько в числе всего единиц миллионов? Чтобы определить количество единиц миллионов, записываем всё число без разрядов сотен тысяч, десятков тысяч, единиц тысяч, сотен, десятков и единиц (то есть разрядов до единиц миллионов) |
2 _ _ _ _ _ _ |
- В этом числе содержится:
- 2 единицы класса миллионов (третьего класса)
- 38 единицы класса тысяч (второго класса)
- 479 единицы класса единиц (первого класса)
Важно!
Советуем обратить особое внимание на данную тему, так как умение раскладывать
числа на разрядные слагаемые поможет вам при устном счёте и решении примеров с многозначными числами.
Для проверки своих результатов
вы также можете воспользоваться нашим калькулятором
разложения числа на разрядные слагаемые онлайн.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
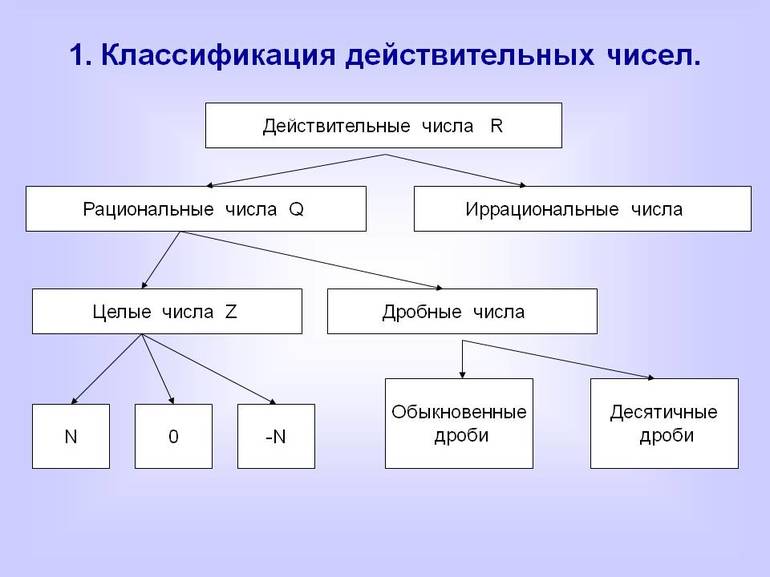
Натуральные числа и их классификация
Натуральными называют естественные величины, которые используются для счета (цифры и их комбинации: 1, 2, 3, 4, 5 и так далее), а также для расстановки по очереди (порядковые числительные: первый, второй, третий, четвертый и так далее). В совокупности они образуют так называемый ряд натуральных чисел. Его обозначением служит латинская буква N.
Главной особенностью этого ряда считается его бесконечность. Она обусловлена тем, что самого большого числа не существует. У любой составляющей ряда есть «старшие товарищи» — величины, которые по своему значению больше.
Распределение по категориям
Составляющие ряда натуральных чисел подразделяются на разряды и классы. Каждая из этих категорий неразрывно связана с другими. Разрядная классификация состоит из следующих групп (в скобках приведены слагаемые, соответствующие каждому разряду):
- единицы (1, 2, …, 9);
- десятки (10, 20, …, 90);
- сотни (100, 200, …, 900);
- тысячи (1000, 2000, …, 9000) и так далее.
Разряд числа — это положение, которое оно занимает в цифровой записи. Таким образом, любое числовое значение можно представить посредством разрядных слагаемых по математической формуле следующего вида: nnnn = n000 + n00 + n0 + n, где n означает любую цифру от 0 до 9. Для наглядного примера стоит разбить на составляющие число 4698 = 4000 + 600 + 90 + 8. Получается, что оно состоит из четырех разрядов, отображенных соответствующими составляющими:
- 4000 (четыре тысячи) — это первое слагаемое;
- 600 (шесть сотен) — второе;
- 90 (девять десятков) — третье;
- 8 (восемь простых единиц) — четвертое.
Разряд первого слагаемого называют высшим. Цифра, которой он обозначается, всегда больше нуля. Количество разрядов числа, как и количество его разрядных составляющих, всегда соответствует количеству в нем цифр, отличных от 0. Например, число 7052 состоит из трех разрядов, несмотря на свою четырехзначность. Это связано с тем, что в его составе отсутствуют сотни. Его слагаемые — семь тысяч, пять десятков и две простых единицы (7000 + 50 + 2 = 7052).
Разрядные составляющие — это натуральные числа, содержащие только одну цифру, отличную от нуля. Примеры разрядных слагаемых: 7, 30, 200, 4000 и тому подобные. Числа такого вида, как 12, 21, 475, 3500 и так далее, не могут быть отнесены к этой категории. Они подлежат математическому разложению на составляющие.
Название разрядных слагаемых обусловлено принадлежностью каждого из них к определенному разряду. Тысяча считается единицей четвертого разряда, сотня — единицей третьего разряда, десяток — второго, единица — первого. То есть нумерация разрядов начинается от наименьшей составляющей. Единицы первого разряда называются простыми, так как они однозначные. Составляющие прочих разрядов относятся к составным.
Каждый разряд состоит из десяти единиц, но обозначаться он может только девятью, так как десятая единица обеспечивает переход на следующий более высокий разряд. Не может быть разрядной составляющей типа десяти сотен — эта единица обозначается как одна тысяча.
Комплектация разрядов
В целях упрощения записи представления числа через разрядные составляющие единицы разрядов принято группировать в классы. В состав каждого из них входит три разряда:
- единицы;
- десятки;
- сотни.
Для удобства между классами разрешается ставить пробел. Особенно это необходимо для представлений очень больших величин (от миллиона), чтобы они не выглядели бесконечным набором цифр, и в процессе их разложения не возникло путаницы. На классы число разбивается строго по три цифры справа налево.
Первый класс — это единицы. Он включает от одного до трех разрядов. Это значит, что к нему относятся все натуральные числа от 1 до 999. Второй класс — это тысячи. В него входят от четырех до шести разрядов. То есть единицы, принадлежащие к этому классу, есть во всех величинах от 1000 и больше. Дальнейшее распределение по классам:
- третий — миллионы (с седьмого по девятый разряды);
- четвертый — миллиарды (с десятого по двенадцатый);
- пятый — триллионы (с тринадцатого по пятнадцатый);
- шестой — квадриллионы (с шестнадцатого по восемнадцатый);
- седьмой — квинтиллионы (с девятнадцатого по двадцать первый) и так далее.
Распределение по классовым и разрядным категориям отображено в таблице:
| Классы | Разряды |
| Миллиарды |
|
| Миллионы |
|
| Тысячи |
|
| Единицы |
|
Особенности разложения
Чтобы лучше понять, что такое разрядные слагаемые в математике и как их использовать, стоит подробно рассмотреть процесс разложения натуральных величин на эти составляющие. В основе большинства задач с разрядными слагаемыми лежит разложение натурального числа, то есть его представление в виде суммы разрядов через сложение количеств всех разрядных единиц.
Преобразить в сумму разрядных слагаемых можно каждую натуральную величину составного типа, то есть многозначную (двузначную, трехзначную и так далее). Чтобы разложить число на разрядные слагаемые корректно, необходимо соблюдать основные правила. Первое — нули не учитываются в разрядном составе числа. Второе — слагаемые записываются в порядке старшинства, то есть от старшего к младшему — вначале тысячи, затем сотни и десятки, последними фиксируются простые единицы.
Разрядный состав можно записать в трех вариантах разбора:
- базовый — простое сложение: 852768 = 800 000 + 50 000 + 2000 + 700 + 60 + 8;
- подробный — сложение с умножением единиц разряда на их количество: 852768 = 8*100 000 + 5*10 000 + 2*1000 + 7*100 + 6*10 + 8*1.
- словесный — текстовая расшифровка: 852768 = восемь сотен тысяч, пять десятков тысяч, две тысячи, семь сотен, шесть десятков, восемь простых единиц.
Вне зависимости от выбранного способа разложить число на составляющие по разрядам не составит особого труда. Конечно, чем больше число, тем выше риск запутаться и совершить ошибку. Упражняться лучше сперва на двузначных числах, а затем постепенно повышать разрядность.
Упражнения для тренировки
Для лучшего усвоения материала стоит разобрать несколько тренировочных упражнений. Несколько примеров, какими бывают математические задания по этой теме:
- 75 = 70 + 5;
- 324 = 300 + 20 + 4;
- 8434 = 8000 + 400 + 30 + 4;
- 68 486 = 60 000 + 8000 + 400 + 80 + 6;
- 575 783 = 500 000 + 70 000 + 5000 + 700 + 80 + 3;
- 8 633 087 = 8 000 000 + 600 000 + 30 000 + 3000 + 80 + 7.
Нередки упражнения с обратным процессом, то есть такие, в которых нужно найти число по его составляющим:
- 500 + 60 + 5 = 565;
- 8000 + 300 + 4 = 8304;
- 900 000 + 50 000 + 7000 + 80 + 2 = 957 082.
Стоит отметить, что не все задачи с разрядными составляющими решаются путем сложения. Многие упражнения содержат прием их вычитания. Но сложными такие задания кажутся только на первый взгляд. Их суть проста. В скобках приводятся составляющие двух чисел — уменьшаемого и вычитаемого. Требуется найти их разность: (500 + 40 + 1) — (400 + 20) = (100 + 20 + 1) = 121.
Процессы разложения чисел по разрядам и обратного сложения имеют огромное значение для решения различных математических задач и упражнений. Очень важно уметь быстро раскладывать числа любой величины по разрядному составу. Это умение поможет в устном счете и оперировании многозначными числами.
Изучение натуральных чисел и разрядного состава входит в базовую программу по математике. Этот материал проходится учащимися в начальных классах школы.
Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
Разрядные слагаемые числа
- Сумма разрядных слагаемых
- Калькулятор разложения числа на разрядные слагаемые
Сумма разрядных слагаемых
Любое натуральное число можно записать в виде суммы разрядных слагаемых.
Как это делается, видно из следующего примера: число 999 состоит из 9 сотен, 9 десятков и 9 единиц, поэтому:
999 = 9 сотен + 9 десятков + 9 единиц = 900 + 90 + 9.
Числа 900, 90 и 9 — разрядные слагаемые. Разрядное слагаемое — это количество единиц в данном разряде.
Сумму разрядных слагаемых также можно записать следующим образом:
999 = 9 · 100 + 9 · 10 + 9 · 1.
Числа, на которые выполняется умножение (1, 10, 100, 1000 и т. д.), называются разрядными единицами. Так, 1 — это единица разряда единиц, 10 — единица разряда десятков, 100 — единица разряда сотен и т. д. Числа, которые умножаются на разрядные единицы выражают количество разрядных единиц.
Запись любого числа в виде:
12 = 1 · 10 + 2 · 1 или 12 = 10 + 2
называется разложением числа на разрядные слагаемые (или суммой разрядных слагаемых).
Сумма разрядных слагаемых — это запись многозначного числа в виде сложения количеств его разрядных единиц.
Пример 1. Запишите числа в виде суммы разрядных слагаемых: 3278, 5031, 3700.
1) 3278 = 3 · 1000 + 2 · 100 + 7 · 10 + 8 · 1 = 3000 + 200 + 70 + 8;
2) 5031 = 5 · 1000 + 0 · 100 + 3 · 10 + 1 · 1 = 5000 + 30 + 1;
3) 3700 = 3 · 1000 + 7 · 100 + 0 · 10 + 0 · 1 = 3000 + 700.
Обратите внимание, что разрядные единицы могут быть записаны в виде степени числа 10:
1) 3278 = 3 · 103 + 2 · 102 + 7 · 101 + 8 · 1;
2) 5031 = 5 · 103 + 0 · 102 + 3 · 101 + 1 · 1 = 5 · 103 + 3 · 101 + 1;
3) 3700 = 3 · 103 + 7 · 102 + 0 · 101 + 0 · 1 = 3 · 103 + 7 · 102.
Пример 2. Записать число, представленное в виде суммы разрядных слагаемых:
а) 3 · 102 + 2 · 10 + 7 = 300 + 20 + 7 = 327;
б) 5 · 103 + 0 · 102 + 4 · 10 + 1 = 5000 + 40 + 1 = 5041;
в) 8 · 102 + 0 · 10 + 5 = 800 + 5 = 805;
г) 1 · 103 + 6 · 102 + 7 · 10 = 1000 + 600 + 70 = 1670.
Калькулятор разложения числа на разрядные слагаемые
Представить число в виде суммы разрядных слагаемых, вам поможет данный калькулятор. Просто введите нужное число и нажмите кнопку Разложить
.
Разрядные единицы в виде степени: