Как найти реакции опор фермы

Содержание:

1. Ферма и их расчет
2. Метод вырезания узлов
3. Метод Риттера
4. Расчет плоских ферм
5. Основные понятия о плоских фермах
6. Условие жесткости фермы
7. Статически определенные фермы
8. Метод вырезания узлов
9. Метод Риттера
10. Фермы. Способы определения усилий в стержнях ферм
11. Простейшие фермы
12. Определение усилий в стержнях фермы
13. Способ вырезания узлов
14. Способ Риттера

Фермой называется шарнирно-стержневая геометрически неизменяемая конструкция. 

Плоская ферма – частный случай пространственной конструкции, у которой один из поперечных размеров либо мал по сравнению с другими размерами, либо не существенен для распределения внутренних усилий.

Реальная ферма, может не иметь идеальных шарнирных соединений в узлах, соединения стержней между собой в узлах являются жесткими, а не шарнирными, с помощью сварки, заклепок, болтов или других скреплений.

Плоские фермы конструируют таким образом, что приложенная к ферме нагрузка передается в узлах, вследствие чего, в сечениях элементов ферм не возникают поперечные силы и изгибающие моменты, стержень работает только на продольные усилия – растяжение или сжатие, и, следовательно, реакции стержней будут направлены вдоль этих стержней.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Ферма и их расчет

Ферма — это жесткая конструкция, которая состоит из прямолинейных стержней, соединенных между собой шарнирами. Место, где стержни соединяются друг с другом, носит название узла фермы. Внешняя нагрузка прикладывается к ферме только в ее узлах. Ферма состоит из идеальных стержней, то есть тонких, однородных, невесомых
стержней, на концах которых шарниры, которые работают на растяжение или на сжатие.
Мы будем рассматривать фермы, в которых оси всех стержней и векторы внешних сил содержатся в одной плоскости, то есть, плоские фермы. Помимо этого, конструктивно ферма состоит из стержней, которые образуют собой треугольники, то есть в конструкции фермы нет лишних стержней. такие фермы являются жесткими и статически определенными. В них число стержней n и число узлов m всегда связано таким соотношением

n = 2m – 3 .

Расчет фермы сводится к определению ее опорных реакций и усилий в стержнях.

Рассмотрим простую плоскую ферму (рис. 1.26).

Как видно из схемы — это плоская конструкция, которая состоит из 7 стержней, которые соединяются в 5 узлах. В узлах I и V ферма имеет опоры (в I-ом узле — неподвижная шарнирная опора; в V-м — подвижная шарнирная опора), к II и к IV узлу фермы приложены внешние нагрузки в виде сосредоточенных сил  и ( = 30 kH; = 10 kH). Линейные и угловые размеры фермы данные на схеме (α = 45º). Оси плоской декартовой системы координат I xy показаны на схеме фермы.

Первый этап расчета фермы — это определение ее опорных реакций. Определяют опорные реакции, рассматривая ферму в целом, как твердое тело с приложенными внешними силами. Тогда, условно освобождая ферму от связей (опор) и заменяя их соответствующими реакциями (в узле I это реакции _I, _I; в узле V — _V), имеем плоскую систему произвольных сил, для которой можно использовать условия равновесия и составить систему уравнений равновесия:

Из первого уравнения системы вычисляем неизвестную реакцию X_I. она равна

X_I = P₂ = 10 kH.

Из последнего уравнения вычисляем реакцию R_V:

Далее, из второго уравнения является возможность вычислить последнюю неизвестную
величину Y_I. Она будет равняться

Y_I = P₁ – R_V = 30 – 5 = 25 kH.

Таким образом, вычислено искомые реакции опор фермы. Теперь необходимо определить неизвестные усилия в стержнях фермы. существует несколько способов определения этих усилий, графические и аналитические. Мы рассмотрим два аналитические методы: метод вырезания узлов и метод сечений (или метод Риттера). Рассмотрим последовательно эти методы.

Метод вырезания узлов

Этот метод заключается в последовательном вырезании (мысленно) узлов фермы,
начиная с узла где совпадают два стержня с неизвестными внутренними усилиями. Таким образом, каждый узел — это плоская система сходящихся сил, для которой можно составить два уравнения равновесия, из которых определяют неизвестные усилия в этих двух стержнях.

При применении этого метода принимается правило, согласно которому реакции
стержней направляются от узлов. Если же при определении реакции стержня произойдет, что она имеет отрицательный знак, то этот стержень сжат и действительное направление его реакции ориентировано к узлу.

Определим данным методом усилия в стержнях фермы, приведенной на рис. 1.26. Вырезаем сначала узел I (рис. 1.27). Кроме реакций _I и _I  к нему приложены неизвестные реакции стержней 1 и 2, которые обозначаются и и направление которых, по правилу, от узла. Покажем в этом вырезанном узле I оси координат xIy и угол α. Как видно из схемы, узел и находится в равновесии под действием плоской системы сходящихся сил с двумя неизвестными усилиями: и . Составим для узла и уравнения равновесия,
используя условия равновесия для плоской системы сходящихся сил в виде. Будем иметь

Из второго уравнения определяем усилия S₁. Оно равно

Как видим, стержень 1 сжатый усилиям 35,3 kH. С первого уравнения определим неизвестное усилие S₂

S₂ = – X_I – S₁ sinα = –10 – (– 35,3 · 0,707) = – 10 + 25,00 = 15,00 kH .

Таким образом, стержень 2 растянутый усилием 15,00 kH.

Далее вырезаем узел ІІ (рис. 1.28). В этом узле сосредоточены внешняя сила и усилия трех стержней ,  и . Причем неизвестные усилия только в двух стержнях — в 3 () и в 4 (). Также предварительно считаем, что стержни 3 и 4 растянуты, и их усилия и
направлены от узла ІІ. Усилия же в стержне 1 уже определено ранее, при вырезании первого узла, и не только установлено ​​его значение, но и то, что он сжат, поэтому направление его реакции будет к узлу ІІ. Проведем через узел ІІ оси координат xy и покажем угол α.

Составим для узла ІІ уравнения равновесия, также используя условия, аналогичные предыдущим.

Из второго уравнения определяем усилия S₃. Оно будет равняться

Как видим, стержень 3 сжатый усилиям 7,00 kH. Направление реакции S₃ — к узлу ІІ.

Из первого уравнения находим усилия S₄. Оно равно

S₄ = –S₁ sinα – S₃ cosα = – 35,30 · 0,707 – (–7,00)0,707 = – 25,00 + 5,0 = – 20,00 kH.

Таким образом, стержень 4 сжатый усилием 20,00 kH.

Далее вырезаем узел IV (рис. 1.29). Он находится под действием внешней силы и усилий в стержнях 4, 5 и 7. Усилия в стержне 4 определено и его направление — к узлу, а потому неизвестны — только усилия  и . Проведем через узел IV оси координат xy и покажем угол α. Направления усилий в стержнях 5 и 7 — от узла IV. Составим для узла IV уравнения равновесия, также используя условия равновесия:

Решаем систему, для чего из второго уравнения выразим усилия S₅ через усилия S₇. Оно будет равняться

Теперь подставим значение S₅ в первое уравнение системы. Будем иметь

S₇ cosα – (– S₇)cosα – P₂ + S₄ = 0.

Отсюда

Стержень 7 сжатый усилием 7,00 kH. Теперь есть возможность найти усилие S₅. Оно равно

S5 = – S₇ = 7,00 kH.

Стержень 5 растянутый усилием 7,00 kH.

Теперь, для окончательного определения усилий в стержнях фермы, что рассматривается, необходимо вырезать узел V. К узлу V приложена реакция , усилия , которое направлено к узлу, и неизвестно усилию , которое направляем от узла. Составим для узла V уравнения равновесия, используя условия равновесия:

Как видим, для определения последнего неизвестного усилия S₆  достаточно решить первое уравнение системы. Найдем S₆ :

S₆  = S₇ cosα = 7,00 · 0,707 = 5,00 kH.

Стержень 6 растянутый усилием 5,00 kH.

Данные расчетов заносим в таблицу 1.1. Знак при определенном усилии в стержне показывает характер его нагрузки. Если он положительный («+»), То стержень растянут, если отрицательный («–»), то стержень сжат.

Метод Риттера

Рассмотрим второй аналитический метод определения усилий в стержнях плоской фермы. Это метод Риттера, или метод сечений.

Данный метод имеет несколько преимуществ по сравнению с рассмотренным ранее
методом вырезания узлов. Здесь нет необходимости составлять большое количество уравнений равновесия узлов, особенно когда ферма многостержневая. Кроме того, в случае неточности расчета какого-то стержня, в дальнейшем эта ошибка накапливается при расчетах других стержней. Метод Риттера лишен этих неудобств.

Особенность применения этого метода состоит в том, что условно делается сечение всей фермы, при этом в сечении должно быть не больше, чем три стержня с неизвестными усилиями. Тогда рассматривается равновесие одной из частей фермы, а вторая часть отбрасывается. Действие стержней, которые попали в сечение, заменяем их реакциями. предварительно считается, что эти стержни также растянуты, то есть их усилия направлены от узлов. Опорные реакции фермы определяются так же, как и при
применении метода вырезания узлов.

Определим усилия в 4, 5 и 6 стержнях фермы, сделав сечение и рассматривая равновесие правой части фермы (рис. 1.31). Вместо указанных стержней прикладываем в узле IV усилия и а в узле V — усилие . Направления указанных усилий — от узлов. К данной части фермы приложена внешняя сила и реакция . Покажем оси прямоугольной декартовой системы координат Vxy и угол α. Как видим, данная часть
фермы находится в равновесии под действием плоской системы произвольных сил, а
для этого составим для нее уравнения равновесия, используя условия равновесия. Согласно методу Риттера надо составлять уравнения равновесия, как суммы моментов сил относительно тех точек, где пересекаются линии действия большего количества неизвестных усилий. В данном случае такими точками будут точки ІІІ и IV. В отношении этих точек возьмем моменты сил.

Будем иметь

Вычислим неизвестные усилия. Из первого уравнения — усилия S₅:

Из второго уравнения — усилия S₄. Оно будет равняться

Таким образом, стержень 4 сжатый усилиям 20,00 kH, направление усилия S₄ будет противоположный тому, который был показан на рис. 1.31.

Расчет плоских ферм

Фермой называется конструкция, состоящая из стержней, соединённых между собой на концах шарнирами и образующих геометрически неизменяемую систему. Шарнирные соединения стержней фермы называют её узлами. Если оси всех стержней фермы лежат в одной плоскости, то ферма называется плоской.

Основные понятия о плоских фермах

Фермой называется геометрически неизменная конструкция, состоящая из прямолинейных стержней, соединенных в узлах шарнирами (рис. 8.1).

Основная задача, о которой будет идти речь далее, заключается в определении внутренних усилий, возникающих в стержнях фермы под действием внешних активных сил.

Приведенное определение фермы имеет одно существенное упрощение, которое позволяет усилия в стержнях фермы находить методами теоретической механики. Этим упрощением является допущение о шарнирном соединение стержней фермы.

В реальных фермах стержни соединены жестко с помощью электросварки, клепки и тому подобное. Однако, как показывают исследования в строительной механике, сделано допущение о способе соединения стержней фермы  позволяет найти приближенное значение усилий с достаточной точностью.

Фермы используются в качестве несущих конструкций в различных сооружениях: в мостах, в перекрытиях зданий, в подъемных кранах, каркасах самолетов тому подобное.

Места соединения стержней фермы называются узлами, а те узлы, которыми ферма опирается на основу — опорными узлами. Стержни, размещены по верхнему контуру фермы, образуют верхний пояс, а по нижнем — нижний пояс (См. Рис. 8.1).

Вертикальные стержни называются стойками, а наклонены — раскосами.

Фермы бывают пространственные и плоские. Если оси всех стержней фермы лежат в одной плоскости, такая ферма называется плоской, если нет — то пространственной. В этом разделе ограничимся рассмотрением только плоских ферм.

Расчет ферм существенно упрощается, если сделать такие допущения:
1) трения в шарнирах отсутствует;
2) заданные силы, действующие на ферму, лежат в плоскости фермы и приложенные в узлах;
3) собственный вес стержней малый по сравнению с заданными силами и ею можно пренебречь.

Если выполнять эти условия, каждый стержень фермы будет работать на растяжение или сжатие и не испытывать деформации изгиба, в чем и есть преимущество фермы как строительной конструкции. Действительно, при условии, что все усилия приложены в узлах фермы и отсутствует трение в шарнирах, каждый стержень будет находиться под действием только двух сил, которые приложены к его концов. Согласно с первой аксиомой статики, при равновесии линия действия этих сил должна проходить через их точки приложения. Итак, силы, приложенные к стержню фермы, будут обязательно направлены вдоль стержня, и поэтому приводить его сжатие или растяжение.

Сделанные допущения оправданы тем, что, во-первых, трения в шарнирах малое по сравнению с заданными силами и им можно пренебречь; во-вторых, если сила приложена не у узле фермы, то ее можно разложить на составляющие, которые будут приложены в узлах.

Для того чтобы ферму можно было использовать как несущую конструкцию в инженерных сооружениях, необходимо обеспечить ее жесткость.

Определим условия, при которых ферма будет жесткой (геометрически неизменной).

Условие жесткости фермы

Найдем наименьшее число стержней N, необходимых для построения геометрически неизменяемой (жесткой) фермы, которая имеет n узлов.

Простой, геометрически неизменной фермой является конструкция, состоит из трех узлов, соединенных тремя стержнями. для жесткого присоединения каждого из последующих узлов необходимо два стержня (Рис. 8.2). Полученная таким образом новая конструкция  также будет геометрически неизменной фермой.

Следовательно, для обеспечения жесткости фермы (т.е. исключения относительных
перемещений стержней) необходимо, чтобы число стержней равнялось

то есть 

Пример неизменной жесткой фермы показано на рис. 8.3, а.

Если число стержней то конструкция будет геометрически переменной (рис. 8.3, б), а если то ферма будет содержать лишние стержни (рис. 8.3, в).

Уравнение (8.1) называется условием жесткости фермы. Заметим, что равенство (8.1) является необходимым условием жесткости фермы, но не достаточным. Для конструкции, изображенной на рис. 8.3, г, условие (8.1) выполняется, но эта система геометрически переменная. Для обеспечения геометрической неизменности фермы условие (8.1) должно выполняться как для всей фермы, так и для отдельных ее частей (решеток).

Статически определенные фермы

Статическую определенность фермы устанавливают по количеству реакций опор и числом стержней фермы.

Заметим, что ферма является неизменной системой, поэтому, как известно из предыдущего, неизвестных опорных реакций не должно быть более трех. В противном случае задача определения опорных реакций для данной фермы является статически неопределенной.

Рассчитывая фермы, кроме трех неизвестных реакций, нужно еще определить усилия в стержнях фермы. Выясним, сколько независимых уравнений статики можно составить для определения этих неизвестных сил. для этого используем метод вырезания узлов.

На каждый вырезанный узел фермы будет действовать плоская система сходящихся сил, которая состоит из внешних сил (активных и реакций связей) и внутренних усилий в стержнях. Поэтому система сил, приложенная к узлу, должна удовлетворять двум уравнениям равновесия  

Следовательно, при равновесии фермы, которая имеет n узлов, все действующие на ферму
внешние силы и усилия в стержнях должны удовлетворять 2n уравнением.

С равновесия отдельных узлов фермы следует равновесие фермы в целом, а потому три уравнения равновесия  записанные для всей фермы, будут линейными комбинациями первых уравнений, которые являются независимыми.

К 2n уравнениям будут входить три неизвестные реакции связей и внутренние усилия в стержнях. Из этих уравнений можно найти — неизвестных внутренних усилий в стержнях. Если число стержней фермы эти усилия могут быть определены из уравнений статики, и такая ферма называется статически определенной; если усилия в стержнях с помощью одних лишь уравнений статики абсолютно твердого тела определить невозможно и ферма будет статически неопределенной. Заметим, что условие жесткости фермы (8.1) действительно для плоской фермы и является условием статической определенности.

Методы нахождения усилий в стержнях статически неопределенных ферм рассматриваются в курсах сопротивления материалов и строительной механики. В курсе
теоретической механики рассматривают только статически определенные фермы.

Существует три основных метода нахождения усилий в стержнях статически определенных ферм: вырезания узлов Риттера и графический (построения
диаграммы Максвелла-Кремоны).
Остановимся только на двух аналитических методах.

Метод вырезания узлов

Суть метода вырезания узлов заключается в том, что рассматриваем равновесие каждого узла в отдельности. Для этого вырезаем узлы фермы, прикладываем к ним соответствующие внешние силы и реакции стержней и составляем уравнение
равновесия сил, приложенных к каждому узлу. Поскольку в начале расчета фермы неизвестно, какие стержни фермы растянуты, а какие сжаты, условно допускаем, что все стержни растянуты. В этом случае реакции стержней направляем от узлов. Если в результате вычислений получим значение реакций некоторых стержней со знаком минус, то это будет означать, что эти стержни сжаты. Найденные реакции стержней по модулю равны внутренним усилием в стержнях.

Последовательность рассмотрения узлов определяется по условию: число неизвестных сил, приложенных к узлу, не должно превышать количества уравнений равновесия сил, то есть двух.

Проиллюстрируем этот метод на конкретном примере.

Задача 1. Найти усилия в стержнях фермы, изображенной на рис. 8.4, методом вырезания узлов, если к узлу D фермы приложено вертикальную силу

Решение. В этой ферме число узлов n = 8, а число стержней N = 13. Итак, условие (8.1) выполняется и ферма является жесткой без лишних стержней, то есть статически определенной.

Составим уравнения равновесия для всей фермы и найдем реакции опор А и В:

Переходим к определению усилий в стержнях. Условно вырежем все узлы фермы, сохраняя последовательность, указанную выше. реакции стержней обозначим через (рис. 8.5). На основе закона равенства действия и противодействия

Для сил, которые совпадают в каждом узле, составим последовательно уравнения равновесия. Расчет начнем с узла А, в котором приложены только две неизвестные силы и 

Равновесие последнего узла В можно не рассматривать, поскольку все усилия  найдены. Если правильно найдены все усилия, то условия равновесия узла В будут выполняться тождественно.

Полученные усилия в стержнях 1, 4, 8 и 12 отрицательные, и это означает, что стержни сжаты.

Усилия в отдельных стержнях загруженной фермы, как видно из приведенного примера, могут равняться нулю. Такие стержни принято называть нулевыми.

Сформулируем леммы, которые позволяют найти нулевые стержни плоской фермы, не проводя ее расчета.

Лемма 1. Если в незагруженном узле плоской фермы сходятся два стержни, то усилия в этих стержнях равны нулю.
Лемма 2. Если в незагруженном узле плоской фермы сходятся три стержни, два из которых расположены на одной прямой, то усилия в третьем стержни равна нулю. Усилия в первых двух стержнях равны между собой.
Лемма 3. Если в узле плоской фермы сходятся два стержня и к узлу приложена внешняя сила, линия действия которой совпадает с осью одного из стержней, то усилия в этом стержни равна по модулю приложенной силе, а усилия во втором стержне равна нулю.

Довести эти леммы предлагается самостоятельно.

Методом вырезания узлов выгодно пользоваться тогда, когда нужно найти усилия во всех стержнях фермы. Этот метод хоть и простой, но громоздкий и нерациональный в тех случаях, когда нужно найти усилия не во всех стержнях фермы, а только в отдельных. Например, для нахождения усилий только в одном стержне приходится рассматривать
последовательно равновесие определенного количества узлов, пока не будет найдено усилия в нужном стержни. Этот недостаток отсутствует в методе Риттера.

Метод Риттера

Метод Риттера состоит в том, что после нахождения реакций опор ферму условно разрезают на две части так, чтобы в сечении было не более трех стержней с неизвестными усилиями, и рассматривают равновесие одной из частей фермы. Действие отброшенной части заменяют соответствующими силами, направляя их вдоль разрезанных стержней от узлов, то есть считают, что стержни розтянути (как в методе вырезания узлов).

На часть фермы, которую рассматриваем в равновесии, будут действовать внешние силы и реакции разрезанных стержней. Для полученной плоской системы сил составляем три уравнения равновесия.

Уравнение выгодно записывать в виде равенства нулю суммы моментов всех сил относительно трех разных центров,которые являются точками, в которых попарно пересекаются разрезанные стержни или их продолжение. Эти точки носят название точек Риттера. В каждое из уравнений моментов относительно трех точек Риттера будет входить лишь одно неизвестное, а именно усилия в том стержни, ось которого через эту точку не проходит. Покажем это на примере.

Задача 2. Методом Риттера найти усилия в стержнях 4, 5 и 6 фермы, изображенной на рис. 8.4.

Решение.Реакции опор фермы найдены в предыдущем примере Условным сечением разделим ферму на две части по стержнях 4, 5, 6 (рис. 8.4) и рассмотрим равновесие левой от сечения части фермы.

Действие правой части на левую заменяем реакциями и(Рис. 8.6).

Для плоской системы сил, которая действует на левую часть фермы, составляем три уравнения равновесия:

где и  — точки Риттера, которые показаны на рис. 8.6.

Индексация точек Риттера  выбрана так, что уравнение моментов, записанное относительно каждой точки , содержит только одно неизвестное усилиев стержне под номером

Решая эту систему уравнений, получим:

Величины найденных усилий совпадают с полученными ранее методом вырезания узлов.

Аналогично можно найти усилия и в других стержнях фермы. Из приведенного примера видно, что уравнение равновесия не связаны между собой, а потому для нахождения усилий в одном стержне достаточно составить лишь одно из этих уравнений.

Фермы. Способы определения усилий в стержнях ферм

Основными способами определения усилий в стержнях ферм являются: — способ вырезания узлов; — способ сечений Риттера; — графический способ определения усилий в стержнях фермы с помощью построения диаграммы Максвелла-Кремоны; — метод построения веревочного многоугольника.

Простейшие фермы

Фермами называются конструкции, которые состоят из прямолинейных стержней, которые соединены между собой шарнирами и образуют неизменную геометрическую фигуру (рис. 4.1). При расчете ферм весом стержней пренебрегают и считают, что шарниры размещены только на концах стержней; нагрузки, действующие на ферму, приложенные в шарнирах (т.е. в узлах фермы). В этом случае каждый стержень фермы испытывает усилия, действующие вдоль оси стержня, то есть будет растянут или сжат.

С всего класса геометрически неизменных ферм без лишних стержней выделим простые фермы. Их построение происходит так: рассматривается основной треугольник, к нему двумя стержнями присоединяется новый шарнир (узел) и и. д. В дальнейшем будем изучать простые, плоские фермы, где их стержни расположены в одной плоскости.
 По своему назначению зачастую фермы делятся на мостовые, стропильные и крановые (рис. 4.1). Установим зависимость между количеством стержней и количеством шарниров (узлов) в простых фермах.
 Рассуждаем так: для образования основного треугольника нужно три стержня и три шарнира. Для образования каждого из остальных шарниров (узлов) необходимо два стержня для постоянного соединения с основой фермы. Итак, общее количество стержней в простой ферме с учетом трех стержней основного треугольника определяется так:

                                                                                                             (4.1)

Основной задачей расчета простых ферм является определение усилий в стержнях фермы, которые являются внутренними силами, возникающими в стержнях под действием внешних сил. Эту задачу можно решить методами теоретической механики.

Определение усилий в стержнях фермы

Ограничимся двумя способами определения усилий в стержнях простой фермы: способом
вырезания узлов (графически-аналитический метод) и способом Риттера (аналитический метод).

Способ вырезания узлов

Этот способ заключается в том, что каждый узел вырезается из
фермы и рассматривается отдельно как таковой, что находится в равновесии под действием приложенных к нему внешних сил и усилий разрезанных стержней. Система сил, действующей на узел, является плоской системой сходящихся сил, которая находится в равновесии; следовательно, силовой многоугольник, построенный из этих сил, должен быть замкнутым. Построение силовых многоугольников (треугольников) следует начинать с узла, в которых сходятся два стержня, тогда построением замкнутого треугольника (третья сторона отвечает известной заданной силе, прилагаемой в узле) найдутся усилия в этих двух стержнях. После этого можно переходить к следующему узлу и т. Д. Каждый следующий узел выбирается так, чтобы в нем сходилось не более двух стержней с неизвестными усилиями. Так графически будут определены усилия во всех стержнях. Если усилия разрезанных стержней направлены по стержнях в сторону узла, то они сжимающие, в противном случае — растяжимые.
 Формально условия равновесия узлов фермы включают в себя условия равновесия фермы в целом, то есть позволяют найти и внешние реакции. Более того, предварительное определение внешних реакций фермы существенно упрощает решения задачи. Рассмотрим способ вырезания узлов на примере расчета усилий в стержнях фермы, показанной на рис. 4.2.

Пример 1. В узле В фермы приложена сила  Опорами фермы будут шарнир А и каток С. Определить: реакции опор , усилия стержней в узлах А и D.
 Решение. Рассмотрим ферму как твердое тело, которое находится в равновесии под действием плоской системы параллельных сил  (в этом случае реакция шарнира  будет параллельная силам  и , иначе система сил , а следовательно, сама ферма не была бы в равновесии). Проведем ось параллельно силам системы и составим условия равновесия в виде (3.21)

откуда найдем 

Определение усилий в стержнях начнем с рассмотрения узла А, в котором сходятся два стержня: 1 и 7. Строим замкнутый треугольник из сил ,  (рис. 4.2). Для этого в соответствующем масштабе строим вектор, равный вектору реакции , с конца которого проводим прямую, параллельную стержню АВ, а с начала — прямую, параллельную стержню AD. С построенного треугольника находим усилия  и . Изображая эти усилия в узле А,  видим, что направлено к узлу А по стержню АВ, следовательно, оно — тяговое, а усилия S7 направлено от узла А по стержню AВ, то есть оно — растяжимое. Растяжимое усилия обозначается знаком плюс, а сжимающее — знаком минус. Теперь рассмотрим равновесие сил в узле , в котором остаются только две неизвестные силы:   и . Реакция стержня 7, который выходящий из узла равна и противоположная по направлению его же реакции, но приложена в узле А. Опять строим замкнутый треугольник сил: откладываем силу  , с ее конца проводим прямую, параллельную стержню 2, сначала — прямую, параллельную стержню 6, и определяем величины и направления усилий и . Аналогично можно определить другие усилия:

Неудобство этого способа заключается в его громоздкости, поскольку приходится строить  столько многоугольников, сколько узлов в ферме. Объединение разных многоугольников сил в одну диаграмму осуществили независимо друг от друга английский физик Максвелл и итальянский геометр Кремона, в честь которых эту диаграмму назван диаграммой Максвелла — Кремоны.

Способ Риттера

Этот способ позволяет найти усилия в любом стержни фермы независимо от усилий в других стержнях. Однако предварительно необходимо определить реакции опор фермы.
Способ Риттера состоит в том, что ферма рассекается на две части так, чтобы в сечении было не более трех стержней с неизвестными усилиями,  которые не сходятся в одном узле. Отвергая отсеченную часть фермы и рассматривая равновесие той части, оставшейся под действием приложенных внешних сил и усилий, которые заменяют действие рассеченных стержней, получим для этой части фермы три уравнения равновесия с тремя неизвестными усилиями. Чаще всего эти уравнения являются условиями равенства нулю алгебраических сумм моментов  сил относительно  трех разных центров моментов, за которые выбирают точки парного пересечения рассеченных стержней с числа перерезанных. Эти точки называются точками Риттера.
Если два стержня из трех рассеченных параллельны, то одна точка Риттера удаляется в бесконечность. Тогда  составляют два уравнение моментов сил и одно уравнение проекций сил на ось,  перпендикулярную к параллельным стержням.

Пример 2. Определить усилия в стержнях 1, 2, 3 фермы, если  а другие размеры показано на рис. 4.3.
 Решение. Найдем реакции в опорах фермы и . Реакция катка В направлена ​​по нормали к опорной плоскости, а поскольку на ферму действует система параллельных сил то и реакция шарнира А будет параллельной этим:

Отсюда находим  Проведем сечение через стержни 1,2,3 и рассмотрим равновесие той части рассеченной фермы, в которой приложено меньшее количество сил. В рассматриваемом случае — это правая часть фермы. Усилия в рассеченных стержнях условно считаем растяжимыми и направлением в сторону части, отбрасываются. Итак, в отсеченной части фермы уравновешивается плоская система сил 

Для определения усилия соответствующей точкой Риттера будет точка К, а уравнение равновесия примет вид:

Для определения усилия точкой Риттера является точка В, для определения усилия — точка D, а соответствующие уравнения равновесия имеют вид:

Подставляя необходимые данные, находим 
Итак, усилия — растяжимое, — сжимающее (тяговое) , — нулевое (при заданной нагрузке стержень 2 не работает, но с конструкции его изъять нельзя, поскольку нарушится жесткость конструкции и не выполнится условие (4.1)). В завершение сравним методы Максвелла — Кремоны и Риттера, несмотря на их различие, которое заключается в том, что первый метод относится к графическим, а второй — к аналитическим. Как видно из предыдущего изложения, усилия методом вырезания узлов определяются последовательно, переходя от одного узла к соседнему. Поэтому неизбежно накопление ошибок, связанных с неточностью проведение параллельных прямых. Следует отметить, что накопление этих ошибок можно избежать при решении задачи чисто аналитическим способом, составляя уравнения равновесия для системы сходящихся сил, приложенных в узлах фермы.

Но, с другой стороны, взаимосвязь между построением новых вершин диаграммы Максвелла — Кремоны и положением предыдущих, следует рассматривать как определенное ограничение погрешностей, позволяет избежать грубых
ошибок.
 Метод Риттера в отличие от предыдущего не приводит к накоплению ошибок, так как все усилия определяются независимо друг от друга, но одновременно не дает возможности заметить грубые ошибки, которые могут случиться при исчислении.

Очевидно, лучшая методика определения усилий в стержнях фермы заключаться в сочетании методов Максвелла — Кремоны и Риттера. Например, все усилия определяются по методу Максвелла — Кремоны и некоторые из них проверяются методом Риттера.

Услуги по теоретической механике:

1. Заказать теоретическую механику
2. Помощь по теоретической механике
3. Заказать контрольную работу по теоретической механике

Учебные лекции:

1. Статика
2. Система сходящихся сил
3. Момент силы
4. Пара сил
5. Произвольная система сил
6. Плоская произвольная система сил
7. Трение
8. Расчет усилий в стержнях фермы
9. Пространственная система сил
10. Произвольная пространственная система сил
11. Плоская система сходящихся сил
12. Пространственная система сходящихся сил
13. Равновесие тела под действием пространственной системы сил
14. Естественный способ задания движения точки
15. Центр параллельных сил
16. Параллельные силы
17. Система произвольно расположенных сил
18. Сосредоточенные силы и распределенные нагрузки
19. Кинематика
20. Кинематика твердого тела
21. Движения твердого тела
22. Динамика материальной точки
23. Динамика механической системы
24. Динамика плоского движения твердого тела
25. Динамика относительного движения материальной точки
26. Динамика твердого тела
27. Кинематика простейших движений твердого тела
28. Общее уравнение динамики
29. Работа и мощность силы
30. Обратная задача динамики
31. Поступательное и вращательное движение твердого тела
32. Плоскопараллельное (плоское) движение твёрдого тела
33. Сферическое движение твёрдого тела
34. Движение свободного твердого тела
35. Сложное движение твердого тела
36. Сложное движение точки
37. Плоское движение тела
38. Статика твердого тела
39. Равновесие составной конструкции
40. Равновесие с учетом сил трения
41. Центр масс
42. Колебания материальной точки
43. Относительное движение материальной точки
44. Статические инварианты
45. Дифференциальные уравнения движения точки под действием центральной силы и их анализ
46. Динамика системы материальных точек
47. Общие теоремы динамики
48. Теорема об изменении кинетической энергии
49. Теорема о конечном перемещении плоской фигуры
50. Потенциальное силовое поле
51. Метод кинетостатики
52. Вращения твердого тела вокруг неподвижной точки

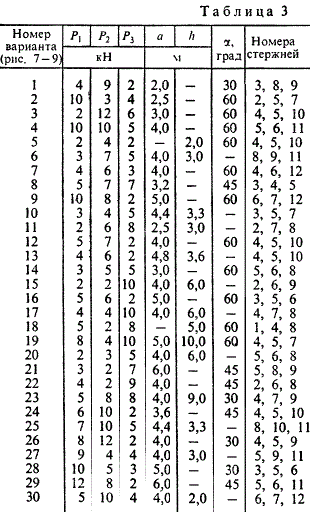
Определить реакции опор фермы от заданной нагрузки, а также силы во всех ее стержнях способом вырезания узлов. Схемы ферм показаны на рис. 7 — 9. Необходимые для расчета данные приведены в табл. 3.

Решение	Формат	Размер	Наличие
Вариант 1	doc / pdf	655 КБ / 225 КБ	Готово
Вариант 2	doc / pdf	624 КБ / 236 КБ	Готово
Вариант 3	doc / pdf	641 КБ / 243 КБ	Готово
Вариант 4	doc / pdf	669 КБ / 240 КБ	Готово
Вариант 5	doc / pdf	660 КБ / 240 КБ	Готово
Вариант 6	doc / pdf	594 КБ / 239 КБ	Готово
Вариант 7	doc / pdf	615 КБ / 238 КБ	Готово
Вариант 8	doc / pdf	541 КБ / 231 КБ	Готово
Вариант 9	doc / pdf	763 КБ / 317 КБ	Готово
Вариант 10	pdf / doc	311 КБ / 610 КБ	Готово
Вариант 11	doc / pdf	634 КБ / 236 КБ	Готово
Вариант 12	doc / pdf	649 КБ / 239 КБ	Готово
Вариант 13	doc / pdf	697 КБ / 242 КБ	Готово
Вариант 14	doc / pdf	709 КБ / 243 КБ	Готово
Вариант 15	doc / pdf	682 КБ / 250 КБ	Готово
Вариант 16	doc / pdf	654 КБ / 234 КБ	Готово
Вариант 17	doc / pdf	832 КБ / 323 КБ	Готово
Вариант 18	doc / pdf	577 КБ / 230 КБ	Готово
Вариант 19	doc / pdf	932 КБ / 248 КБ	Готово
Вариант 20	doc / pdf	720 КБ / 244 КБ	Готово
Вариант 21	doc / pdf	620 КБ / 233 КБ	Готово
Вариант 22	doc / pdf	654 КБ / 236 КБ	Готово
Вариант 23	doc / pdf	658 КБ / 249 КБ	Готово
Вариант 24	doc / pdf	555 КБ / 231 КБ	Готово
Вариант 25	doc / pdf	679 КБ / 241 КБ	Готово
Вариант 26	doc / pdf	653 КБ / 240 КБ	Готово
Вариант 27	doc / pdf	631 КБ / 236 КБ	Готово
Вариант 28	doc / pdf	586 КБ / 238 КБ	Готово
Вариант 29	doc / pdf	649 КБ / 241 КБ	Готово
Вариант 30	doc / pdf	868 КБ / 245 КБ	Готово

Выберем
координатные оси ХУ
с началом координат в узле 1. Разложим
силу F₂
на
проекции по осям координат и нанесём
проекции на схему:

Освободим
ферму от связей. Вместо неподвижного
шарнира в точке (в узле) 1 введём две
реакции Х₁
и У₁,
а вместо подвижного шарнира – одну
реакцию У₆
(в положительном направлении координатных
осей). Для определения трёх неизвестных
реакций опор составим и решим три
уравнения равновесия.

Первым
составим уравнение суммы моментов всех
сил относительно точки 1. В это уравнение
войдёт только одна неизвестная У₆:

,
откуда

Из
уравнения суммы проекций всех сил на
ось Х
найдём неизвестную Х₁:

откуда .

Из
уравнения суммы проекций всех сил на
ось У
найдём У₁:

Положительные
знаки у Х₁;
У₁;
У₆
указывают, что направление реакций на
схеме выбрано правильно.

Для
проверки правильности определения
реакций опор составим и решим уравнение
моментов относительно узла 3, чтобы в
это уравнение вошли все три реакции:

Следовательно,
реакции опор определены правильно.

2. Определение усилий в стержнях фермы.

Вначале
проверяем ферму на наличие «нулевых»
стержней. По лемме 1 в незагруженном
узле 5 усилия в стержнях 5-6 и 5-4 равны
нулю: S_5-6=0;
S_5-4=0.
По лемме 2 в незагруженном узле 3 усилие
в стержне 3-8 равно нулю, а усилия в
стержнях 2-3 и 3-4 равны, то есть: S_3-8=0;
S_2-3=S_3-4.
Полученные значения усилий S_5-4;
S_5-6;
S_3-8
заносим в итоговую таблицу 1.3.

Для
определения усилий в стержнях методом
«вырезания» пригодны узлы 1 и 6, так как
в них сходятся по два стержня с неизвестными
усилиями (в узле 6 из трёх стержней один
S_5-6=0
).

Вырезаем
узел 1 и
изображаем схему действующих сил
(рисунок 1.11).

	Известными являются силы опорных реакций: Х1=7,3 кН; У1=15,8 кН. Неизвестными являются усилия в перерезанных стержнях: S1-2 и S1-8, которые для наглядности обводим прямоугольной рамкой. Определяем неизвестные усилия аналитически из уравнений равновесия:
.
.
Отрицательные значения усилий указывают, что стержни 1-2 и 1-8 сжаты. Полученные значения S1-2 и S1-8 с учётом их знаков заносим в итоговую таблицу №1.3.
Рисунок 1.11. Схема сил узла 1

Вырезаем
узел 2 и
изображаем схему действующих сил
(рисунок 1.12а).

	Известными являются: внешняя сила F1 =10 кН и усилие в стержне S1-2 = =S2-1 = –15,8 кН. Неизвестными являются усилия в перерезанных стержнях: S2-3 и S2-8. Определение неизвестных усилий произведём графическим способом. Для построения многоугольника сил примем масштаб: в 1 см 5 кН. Выберем произвольную точку О и отложим в масштабе от неё два вектора известных сил: S1-2 и F1, параллельно линиям действия этих сил и с учётом знаков. Вектор S1-2 (≈3,1 см длиной) откладываем от точки О вверх и в конце этого вектора пристраиваем вектор F1 (2 см вправо). Затем из точки О и из конца вектора F1 проводим линии параллельно линиям действия S2-3 и S2-8 до их пересечений. Получилось две точки пересечений К и К’, которые равнозначны для образования замкнутого многоугольника сил. Примем для образования замкнутого многоугольника точку К. Тогда вектор S2-8 должен «войти» стрелкой в точку К, а вектор S2-3 «войти» стрелкой в точку О, чтобы получился замкнутый многоугольник сил с одинаковой ориентацией всех векторов (в данном случае – по часовой стрелке). Из направлений действия векторов видно, что S2-8 имеет положительное значение, а S2-3 – отрицательное
Рисунок 1.12а Схема сил узла 2
Рисунок 1.12б Многогранник сил узла 2
(направлен к узлу). По результатам измерений получилось, что длина вектора S2-3 равна ≈5,1 см, а длина вектора S2-8 – около 4,5 см, что приближённо соответствует значениям сил: S2-3 = – 25,5 кН, S2-8=22,5 кН. Графический метод по сравнению с аналитическим является менее точным, поэтому полученные значения усилий подлежат проверке.

Метод
Риттера
применим для определения усилий в
стержнях 3-4; 8-4; 8-7, для чего «рассечём»
ферму по этим стержням и отбросим правую
часть (рисунок 1.13).

Для
определения усилий в стержне 3-4 необходимо
составить уравнение моментов относительно
точки 8, так как в ней пересекаются два
других неизвестных усилия S_4-8
и S_7-8:

	откуда
. Следовательно, стержень 3-4 сжат. Для определения усилия S8-4 составляем уравнения проекций на ось Y, перпендикулярную двум другим неизвестным усилиям S3-4 и S8-7: , то есть стержень 8-4 сжат.
Рисунок 1.13. Левая часть рассечённой фермы

Для
нахождения усилия в стержне 8-7 следует
составить уравнение моментов относительно
точки 4, где пересекаются два других
усилия S_3-4
и S_8-4:

,
откуда

,

Полученные
значения S_3-4,
S_8-7
и S_8-4
заносим в итоговую таблицу. При этом
учтём, что согласно лемме 2 усилие S_3-4
равно усилию S_2-3.

Поскольку значение
S_2-3
по графическому методу было равно –25,5
кН, а по методу Риттера (более точному)
получилось равным –25,8
кН, то в итоговую таблицу заносим значения
S_2-3
=
S_3-4
= –25,8
кН.

Вырезаем
узел 8
и изображаем схему действующих
сил (рисунок 1.14).

	По результатам предыдущих вычислений все силы в этом узле известны, однако значение S2-8=22,5 кН определено графическим способом, поэтому нуждается в проверке. Для уточнения этого значения определим величину S2-8 аналитически из условия равновесия сил узла 8: Из при S8-3= = 0 имеем S8-2 = –S8-4 = 22,3 кН. Ранее при графическом решении в узле 2 было получено S2-8 ≈ 22,5 кН, поэтому за истинное значение принимаем S2-8 = =S8-2=22,3 кН, полученное аналитически.
Рисунок 1.14. Схема сил узла 8
Вырезаем узел 7 и изображаем схему действующих сил (рисунок 1.15).
	Известными являются: внешняя сила F3=30 кН и усилие в стержне 7-8 S7-8 = 24,3 кН. Неизвестными являются S7-6 и S7-4. Определим их значения аналитически из условий равновесия:
из .
из . Полученные значения заносим в итоговую таблицу.
Рисунок 1.15. Схема сил узла 7

Вырезаем
узел 4 и
изображаем схему действующих сил
(рисунок 1.16).

	Известными силами являются: внешняя сила F2=20 кН (или F2X=17,3 кН; F2Y=10 кН). S3-4=–25,8 кН; S4-8=–22,3 кН; S4-7=30 кН; S4-5=0. Неизвестной является одна сила S4-6.
из
Полученное значение заносим в итоговую таблицу, в которой теперь содержаться значения усилий во всех стержнях. Для дополнительного контроля правильности определения усилий в стержнях фермы рассмотрим равновесие сил в узле 6.
Рисунок 1.16. Схема сил узла 4

Вырезаем
узел 6 и
изображаем схему действующих сил
(рисунок 1.17).

	Значения всех сил известны по результатам предыдущих вычислений, поэтому если усилия вычислены правильно, то уравнения равновесия должны обратиться в тождество типа 0=0: Следовательно, усилия в стержнях определены правильно.
Рисунок 1.17. Схема сил узла 6

11

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Яблонский. Задание С.2. Определение реакций опор и сил в стержнях плоской фермы.
Определить реакции опор фермы от заданной нагрузки, а также силы во всех ее стержнях способом вырезания узлов. Схемы ферм показаны на рисунках 7-9. Необходимые для расчета данные приведены в таблице 3.
Дополнительно определить в трех стержнях фермы силы от той же нагрузки способом Риттера (номера стержней указаны в таблице 3).

Пример решения;
Вариант 1;
Вариант 2;
Вариант 3;
Вариант 4;
Вариант 5;
Вариант 6;
Вариант 7;
Вариант 8;
Вариант 9;
Вариант 10;
Вариант 11;
Вариант 12;
Вариант 13;
Вариант 14;
Вариант 15;
Вариант 16;
Вариант 17;
Вариант 18;
Вариант 19;
Вариант 20;
Вариант 21;
Вариант 22;
Вариант 23;
Вариант 24;
Вариант 25;
Вариант 26;
Вариант 27;
Вариант 28;
Вариант 29;
Вариант 30;