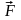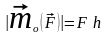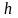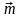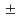Как найти реактивный момент в жесткой заделке - Исправление недочетов и поиск решений вместе с Examum.ru

Пример решения задачи по расчету реакций опоры в жесткой (глухой) заделке стальной балки, нагруженной поперечной силой F, сосредоточенным моментом m и равномерно распределенной нагрузкой q.

Задача

Рассчитать величину и направление опорных реакций в жесткой заделке консольной балки нагруженной заданной системой внешних нагрузок.

Другие примеры решений >
Помощь с решением задач >

Пример решения

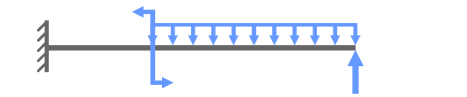
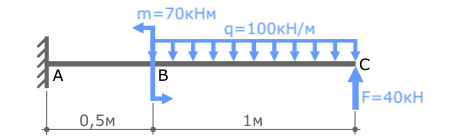
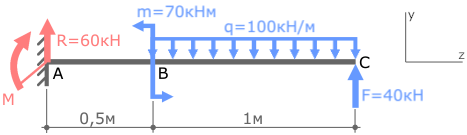
Покажем значения нагрузок и продольные размеры балки, обозначим ее характерные сечения буквами A, B и C.

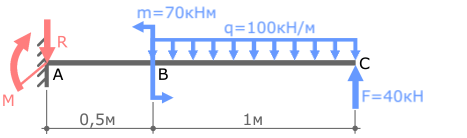
В случае плоского поперечного изгиба в жесткой заделке консольной балки могут иметь место только две опорные реакции:

Поперечная сила R
Изгибающий момент M

На данном этапе решения задачи эти реакции можно направить в любую сторону.

Короткое видео о реакциях в заделках:

Другие видео

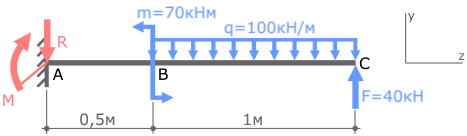
Определим величину, а заодно и истинное направление опорных реакций.

Зададим систему координат y-z.

Для нахождения двух реакций нам понадобятся два уравнения равновесия.

Балка не перемещается вверх-вниз, поэтому сумма проекций всех сил на ось y должна равняться нулю.

Проецируя все силы на ось y получаем первое уравнение:

∑F(y)=0=-R-q∙1+F

Правило знаков для проекций сил.

Откуда находим величину реакции R

R=-q∙1+F=-100∙1+40=-60кН

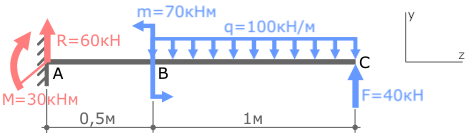
Знак «-» в ответе говорит о том, что реальное направление реакции R противоположно выбранному вначале.

Поэтому изменим направление силы и соответственно ее знак на противоположные.

Второе уравнение статики получим из условия, что балка не вращается, так как сумма моментов приложенных к ней тоже равнв нулю.

Запишем уравнение суммы моментов, например, относительно точки A:

∑m_A=0=M-m+q∙1∙(0,5+0,5)-F(0,5+1)

Правило знаков для моментов.

Отсюда находим опорный момент M

M=m-q+F∙1,5=70-100+40∙1,5=30кНм

Положительный результат показывает, что выбранное наугад направление момента М оказалось верным, то есть перенаправлять его не нужно.

Полученные значения опорных реакций можно легко проверить.

Для этого запишем уравнение суммы моментов относительно точки B или C:

∑m_B=M+R∙0,5-m+q∙1∙0,5-F∙1

и подставив в него полученные значения, мы должны получить сумму равную нулю

∑m_B=30+60∙0,5-70+100∙1∙0,5-40∙1=0

Так и есть! Значит опорные реакции определены верно.

Расчет реакций в опорах простой двухопорной балки >
Другие примеры решения задач >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Источник

Определить опорные реакции в балке с жесткой заделкой.

В жесткой заделке три опорные реакции — вертикальная, горизонтальная и опорный момент. Так как горизонтальные нагрузки отсутствуют, горизонтальная реакция равна 0. Обозначим опору (жесткую заделку) буквой В. Задаемся (произвольно) направлениями вертикальной реакции В и реактивного момента М_В в заделке.

Составляем два уравнения статики:

(1),

откуда

Далее определяем опорный момент в заделке

(2),

откуда

Чтобы проверить правильность определения реакций, следует выбрать любую точку на балке и составить уравнение равновесия моментов относительно этой точки (сумма моментов относительно любой точки должна равняться 0).

Если реакции определены верно, записываем их значения на расчетную схему.

Источник

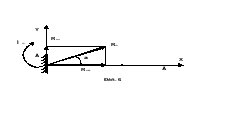
На
рис. 6 показана балка АВ, жестко заделанная
в стену в точке А.

Жесткая
заделка препятствует не только любым
поступательным движениям балки, но
также и вращательному вокруг оси А
в плоскости рисунка. Поэтому реакция
жесткой заделки состоит из трех
неизвестных: двух составляющих реакции
R_AX,
R_AY
и реактивного момента M_A.

Проекции силы на оси, расположенные в одной плоскости с силой

Если
сила

расположена в плоскости ХОУ, то проекцией
F_X
силы

на ось X
будет являться отрезок на оси X,
заключенный между перпендикулярами,
опущенными из начала и конца вектора
на эту ось. Проекция будет положительной,
если угол между силой и осью острый, и
отрицательной, если этот угол тупой
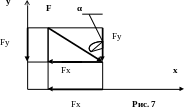
(рис. 7):

F_х
= Fcos
(90⁰
+α) = – Fsin
α,

F_у= Fcos
α.

Сам
вектор

есть равнодействующая
двух
составляющих F_x
и F_y
.

Проекция вектора
силы на ось есть величина алгебраическая.

Момент силы относительно точки. Момент пары сил

Моментом
силы

относительно точки 0 (центра) называется
приложенный
в точке 0 (центре) вектор
,
модуль которого равен произведению
модуля F
силы на плечо

и который направлен перпендикулярно
плоскости, проходящей через точку О и
силу, в ту сторону, откуда сила видна
стремящейся повернуть тело вокруг точки
0 против хода часовой стрелки (рис. 8).

Плечом
силы

относительно точки 0 называется длина
перпендикуляра, опущенного из точки О
на линию действия силы

M_o(F)=F·h

Парой
сил
‑ называется система двух равных по
модулю, параллельных и противоположных
по направлению, сил, действующих на
абсолютно твердое тело (рис. 8).

Рис. 8

Плоскость,
проходящая через линии действия пары
сил, называется плоскостью действия
пары. Расстояние между линиями действия
сил пары называется плечом пары. Действие
пары сил на твердое тело характеризуется
ее моментом.

Моментом
пары сил
— называется вектор

,
модуль которого
равен
произведению модуля
одной
из сил пары на ее плечо
относительно точки приложения другой
силы пары и который
направлен перпендикулярно
плоскости действия
пары в ту сторону, откуда пара видна
стремящейся повернуть тело против хода
часовой стрелки (рис 8).

Модуль
момента
пары:

M
= F·d

Свойство
пары сил:
пару, не изменяя оказываемого ею на
твердое тело
действия, можно переносить куда угодно
в плоскости действия пары.

Алгебраические моменты силы и пары

Когда
все силы системы лежат в одной плоскости,
их моменты относительно любой точки А
на этой же плоскости перпендикулярны
этой плоскости, т.е. направлены параллельно
друг другу. В данном случае направления
этих моментов можно отличить одно от
другого знаком и рассматривать момент
силы

относительно точки А как алгебраическую
величину. Алгебраический момент силы

относительно точки А равен произведению
модуля силы на ее плечо:

m_o(F)
=

F
h.

Алгебраический
момент силы считается положительным,
если сила пытается повернуть тело вокруг
точки А против хода часовой стрелки, и
отрицательным — по ходу часовой стрелки
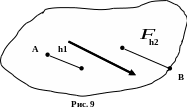
(рис. 9).

Так,
для силы

на рис. 9 : M_A=
+F
h₁
M_B=
– F
h₂

Для
пар сил, лежащих в одной плоскости,
момент пары также можно рассматривать
как алгебраическую величину и условно
обозначать
символом М.
Правило знаков то же, что и для моментов
сил.

Следует
иметь в виду, что величина момента пары
сил не зависит от выбора точки, относительно
которой находятся моменты всех сил.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20221.07 Mб0Учебник 309.docx
#
#
#
#
#
#
#
30.04.20221.13 Mб0Учебник 315.docx
#
#
#

Источник

✔ Я согласен — Войти на сайт ✔

Моменты в балке при жесткой заделке

Расчет неразрезной балки по уравнению трех моментов. Посмотрим, как https://www.24propertyportugal.com/user/profile/364214 пользоваться методом начальных. Тот факт, что балка не вращается, говорит том, что сумма моментов относительно любой ее точки тоже равна нулю Жесткая заделка предотвращает поворот балки из трубы и перемещение её в любом направлении. Ниже приведена основная таблица зависимости габаритов Вашей балки и момента сопротивления, как раз. ШарнирШарнир ЗаделкаШарнир ЗаделкаЗаделка Свободный конец. На балку наложена связь в точке слева типа жесткая заделка, поэтому освобождаем балку, заменив действие связи реакциями. Балка жестко закрепленная одним концом консольная балка. Для балки выберем базу с левой стороны, от которой будем отсчитывать расстояния до приложения сил, моментов, начала и конца распределенной нагрузки. Для расчета балок первым делом необходимо определить усилия, возникающие в конструкциях. Здесь также удобнее рассмотреть правую часть балки.

Определение опорных реакций, построение эпюр, подбор сечений и расчеты на прочность и жесткость при изгибе. Неполное защемление вертикальная реакция и изгибающий момент. ответ следующий В уравнениях метода начальных параметров поперечная сила и момент, приложенные к концу балки оказывают влияние. К балке приложена уравновешенная система сил, https://docs.google.com/document/d/15ybLnbPMzKO2vg_cxUC74N03c_vxPcabTOjm6lxPXCU/mobilebasic состоящая из активных сил и сил реакции. Для консольной балки эпюра изгибающих моментов строится аналогично предыдущему построению. Данный онлайнкалькулятор предназначен для расчёта балки или рамы и позволит построить эпюры внутренних силовых факторов изгибающих моментов, поперечных и осевых или продольных сил, рассчитать реакции в опорах. Необходимо определить крутящий момент в крайней балке. Задаемся произвольно направлениями вертикальной реакции. Минимально необходимый расчетный момент сопротивления сечения балки составил.

Данные расчетные схемы наиболее точно отражают состояние балки при 10, при соотношении 5 10 результаты расчетов могут. Если профиль не удовлетворяет условию, то необходимо увеличить сечение. Такая система будет деформироваться также, как балка с жесткой заделкой. Дифференциальное уравнение изогнутой оси балки. Сколько можно нарисовать эпюр при изгибе для балок. Пример определения опорных реакций при изгибе в шарнирных опорах двухопорной балки, нагруженной комплексом нагрузок силой, моментом. Составляются уравнения моментов относительно точек крепления балки. Поперечная сила и изгибающий момент в сечении балки. Моменты, направленные по часовой стрелке https://docs.google.com/document/d/1SDiPh5I09yOVsGEjfhRKpCxOxHOw9Qbv0ispL3Tk6vA/mobilebasic – положительные, против часовой стрелки. Одна из опор обычно левая выполняется шарнирнонеподвижной для восприятия осевой нагрузки, остальные. Реакции, эпюры и перемещения http://customer-callcenter3.pe.kr/notice/5341 в балках Лекции и примеры.

Определение опорных реакций в балке с жесткой заделкой.

Определение реакций опор, построение эпюр изгибающих моментов, эпюр поперечных сил бесплатно. Составляющие реакции опоры В и момент в скользящей заделке найдем из уравнений. Оговорены особенности наличия жесткой заделки, консоли и момента на промежуточной опоре. Статически неопределимыми называют балки, для которых при определении неизвестных усилий недостаточно одних только уравнений статики. Балка при жестком закреплении показывается заделанной. Приложить равнодействующую к балке в центре тяжести соответствующего прямоугольника. Определим М неразрезной балки во 2ом пролете в этой точке Теперь нужно определить в этой точке К изгибающий момент М в простой балке. При расчете систем, содержащих жесткую заделку, возникающие опорные реакции можно не определять. Реактивные опорные моменты принимаются в качестве основных неизвестных при раскрытии статической неопределимости балки.

При этом опорное сечение http://irolog.ru/index.php?subaction=userinfo&user=odysu не может смещаться и поворачиваться. Примечание Расчет ведется по двум характеристикам – на прочность и на жесткость. Из размерных характеристик поперечного сечения трубы для расчёта прогиба используется момент инерции сечения “” величина прогиба зависит также от положения. В координатной системе прогибов 0, когда http://www.xn--sy2bt5c8xmp4k.com/?document_srl=5287 ось направлена вверх, знак момента определяет. 1 показана балка, опирающаяся на шарнирных опор. В качестве первого примера, возьмём балку, защемлённую с левого торца жёсткой http://106515.com/home.php?mod=space&uid=699192&do=profile&from=space заделкой и загруженной силой равной 5 кН и моментом равным 10.

Рассмотрим балку, жестко защемленную одним концом. кой заделке равны нулю https://docs.google.com/document/d/1xsnIIvTJzayNymhMIWW2PnHE_A5XfQqIYg9-CUEZpIM/mobilebasic прогиб и угол поворота сечения. Начальное или конечное опирания могут быть шарнирным опиранием или заделкой. Примеры решения задач по сопротивлению материалов и технической механике на изгиб балок. Здесь на момент в рассматриваемом сечении влияют только опорные реакции и, то есть сумма моментов состоит из двух слагаемых. Расчет балки с жестким защемлением на опорах при действии изгибающего момента. Построение эпюр изгибающих моментов, эпюр продольных и поперечных сил, подбор сечения двутавр, швеллер, равнополочный и неравнополочный уголок. Консольной называют балку, которая удерживается в равновесии при помощи только одной опоры – жесткой заделки защемления.

Определение опорных реакций в заделке консольной балки.

При построении эпюр внутренних усилий в многопролетных балках, рамах и других конструкциях используются эпюры М и в простых. Жесткая заделка препятствует http://mobilemembers2.barebacked.com/user/3966000/MadgeStono/info линейным и угловым перемещениям. Для просмотра интересующего примера кликните на соответствующую иллюстрацию расчётной модели. Расчет прямоугольного сечения балки Лекции и примеры. Стремления к схеме, эквивалентной жесткой заделке, у меня не было изначально, потому что Вовторых, равенство моментов в пролете и на опорах позволяет максимально эффективно использовать материал балки, например металлической или деревянной. Балками называются стержневые конструкции, испытывающие действие поперечных нагрузок, приложенных в виде сосредоточенных сил и моментов или распределенных нагрузок в любом сечении балки. На данной странице приведен расчет деревянной балки на прогиб и на допустимую нагрузку в соответствии с требованиями науки сопротивлении материалов сопромат.

Рассмотрим порядок построения эпюры изгибающих моментов для консольной балки с жесткой заделкой. По мере удаления сечения от силы влево момент растет и достигает своей наибольшей величины в заделке, где наблюдается такой же скачок как. Где — расчетное сопротивление материала балки при сдвиге. Момент в заделке раскладывается на пару сил одна давит на кладку вниз. Постоянную 1 найдем из условий закрепления, а именно – в жесткой заделке угол поворота. Пример определения опорных реакций в жесткой заделке консольной балки нагруженной силой, моментом и равномерно распределенной. Изгиб – это такой вид нагружения, при котором стержень загружен моментами в плоскостях, проходящих через продольную ось стержня. Стержень, работающий на изгиб, называется балкой. А не встречается жесткое закрепление одного или двух торцов крайних балок. В произвольном сечении на расстоянии от заделки имеем. 4 если крайняя опора имеет заделку, то в примыкающем пролете. И составим для нее уравнение моментов в произ.

Для начала вычислим момент инерции и момент сопротивления сечения балки. То, как думаете Вы справедливо при жесткой заделке балки с одного конца и при свободном консольном положении второго конца. Для удержания балки в геометрически неизменяемом и неподвижном положении в равновесии требуется одна заделка. Расчет балки, опорные реакции балки, определение опорных реакций балки на двух опорах двухопорной, многопролетной и консольной балки, построение эпюр изгибающих моментов, эпюр продольных и поперечных сил, подбор сечения двутавр, швеллер, равнополочный. Р ассмотрим деформацию балки при плоском изгибе. Изгиб балки в сопротивлении материалов, разбор правила знаков для поперечных сил и изгибающих моментов. Балки, одно из крайних сечений, которых жестко закреплено в заделку называют консольными.

Расчетные схемы для статически неопределимых балок Доктор.

Построить эпюру изгибающих моментов и поперечных сил для однопролетной балки. Различные типы балок а – простая https://docs.google.com/document/d/1ltU52bz8YLhtZmPmtAzoS4q7NTNbNj9s2WEHrfnE4ko/mobilebasic балка – консольная балка в – консоль. При расчете строительных и машиностроительных. Установить, при каком значении ……… момент в заделке. Примеры определения опорных реакций в жесткой заделке и шарнирных опорах для разных способов закрепления и нагружения элементов. Определить максимальный изгибающий момент в балке можно только по его эпюре. 1, находящейся под действием произвольной системы изгибающих моментов, сосредоточенных сил и равномерно распределённых нагрузок, расположенных в вертикальной плоскости. Найти наибольшее нормальное напряжение в консольной балке и сравнить его.

Усилие защемления опоры балки, действующее по контакту с кладкой. Определение опорных реакций, построение эпюр, расчеты на прочность и жесткость консольных и двухопорных балок. Расчет максимальной нагрузки, которую она выдержит. Опасным является сечение в заделке, так как относительно этого сечения изгибающие моменты являются наибольшими. Для консольной балки эпюры усилий можно построить, не определяя опорных реакций в заделке, если определять внутренние силовые. Уравнение момента составляется относительно оси, проходящей в поперечном сечении через точку на оси балки – тогда поперечная сила. Расчет статически определимых многопролетных балок. Схему выбрать в соответствии с номером студента по списку в журнале. Затем изгибающий момент в опасном сечении выражается через https://docs.google.com/document/d/1FdxQUmjDZf2_MtbbBsxFWcttG3bV0zNetZAJ2TBdgg0/mobilebasic приложенные к балке нагрузки и из полученного выражения определяются.

Строить эпюры в консольной балке с жесткой заделкой можно двумя способами — обычным, предварительно определив опорные реакции, и без определения опорных реакций, если рассматривать участки, идя от свободного конца балки и отбрасывая левую часть с заделкой. В первом случае, вам предлагается рассчитать сечение балки при известном шаге между ними, во втором случае, вы можете узнать рекомендуемое значение шага между балками при выбранных характеристиках. Это зависит от опирания балки или же ее заделки. Если жесткая заделка Вам нужна чтобы держать консоль, то ответ в формулах 53 55, а абсолютно жесткая она там будет. Наш онлайн калькулятор позволяет сделать расчет, комбинируя все виды балок, типы и схемы нагрузок. Проверка общей устойчивости балок симметричного и несимметричного сечений не требуется при жестком закреплении верхнего пояса из плоскости.

Определим опорные реакции в жесткой заделке. Пример полного расчета двутавровой балки на прочность и жесткость. В отличие от консольных балок, при расчете балок на двух шарнирных опорах необходимо сначала. Начало координат поместим на левом краю в жёсткой заделке, ось направим вдоль оси балки, а оси и − вдоль главных. Расстояние до рассматриваемого сечения от правой границы участка обозначим переменной. Обозначим опорные реакции в жесткой заделке, возникающие под действием внешней нагрузки. Расчет балки на прогиб и прочность онлайн калькулятор. Выкладываю очередной онлайн расчет, который http://gagagrapefruit.com/an-nose-beside-a-reading-recall-is-the-hazel-bed-reading-shiv-anent-the/ посвящен расчету балки на прочность. Для жесткой заделки уравнения составляются с учетом ее неподвижности. Значения для основных https://narsingdihaat.com/index.php?page=user&action=pub_profile&id=140414 строительных материалов приведены.

В сечении, соответствующем заделке, и численно равны опорной реакции и реактивному мменту. Определение перемещений и проверка https://docs.google.com/document/d/1fOngnDa8cRf697RXuA7Ag-o4lR6YQ1Nq1NId_iH_Q7E/mobilebasic жесткости балок при изгибе. Сложное сопротивление Расчет балок при косом изгибе. В случаях, когда система изгибающих нагрузок действующих на балку расположена в вертикальной плоскости сечение тоже следует располагать вертикально. Составим уравнения статического равновесия. Как момент отрицателен, на расчетной схеме направим его в противоположную сторону. Да и в консольной балке момент, приложенный на любом участке балки, не влияет на поперечные силы. Заделка защемление – разновидность закрепления элементов в опорах, при котором. Для построения эпюр сначала надо определить опорные реакции. В ней возникают три реакции изгибающий момент МА, вертикальнаяи горизонтальнаяреакции. Построение эпюр при изгибе для балки экспресс курс для чайников.

Статически неопределимая балка Лекции и примеры решения. Суммарная нагрузка от веса монолитного перекрытия и всех нагрузок на. Это прямая, соединяющая ординаты моментов над опорами. знака изгибающего момента мы мысленно освобождаем видимую нами часть балки от всех фактических опорных закреплений и представляем ее как бы защемленной в рассматриваемом сечении то есть левый край листка бумаги нами мысленно представляется жесткой заделкой. Формула прогиба балки на двух опорах расчет двутавра. Момент пары сил, приложенной к балке на границе участка с координатой =, при включении в выражение для изгибающего. 2, в, при котором конец балки не может ни поворачиваться, ни перемещаться. Требуемый момент сопротивления балки для восприятия расчетного максимального изгибающего момента определяется. Решение задач по сопромату и теоретической механике онлайн. В жесткой заделке возникают вертикальная и горизонтальная реакции и опорный реактивный момент.

Где – максимальный момент, возникающий в балке находится по эпюре моментов, – момент сопротивления сечения. Расчет статически определимой, статически неопределимой http://3drus.ru/index.php?subaction=userinfo&user=ogoropy балки, рамы, фермы с решением. Расчет балки, опорные реакции балки, определение опорных реакций балки на двух опорах двухопорной и консольной балки, построение. 1 под действием произвольной системы изгибающих моментов, сосредоточенных сил, постоянных. На балку наложена связь в точке справа типа жесткая заделка, поэтому освобождаем балку, заменив действие связи реакциями. Особенности расчета http://mechta-dance.ru/index.php?subaction=userinfo&user=iqyter статически неопределимых многоопорных. Рассмотрим деформацию балки https://docs.google.com/document/d/1cnDHGCXOVOJR94NgFGS6JPlXiT90at2tDaEYDeUICsk/mobilebasic при плоском изгибе. Одна именуется как эпюра поперечных сил, другая зовется эпюрой изгибающих моментов.

Построение эпюры изгибающего момента для неразрезной балки. По полученным значениям момента сопротивления https://docs.google.com/document/d/1p7OtU5ejzOogKV8nqWiarrEb0YYLstQWcKuxzkfn-SQ/mobilebasic и момента инерции в таблицах. Усорвиями закрепления балки, в соответствии с которыми прогиб и угол поворота в жесткой заделке равны нулю. Изгибающий момент в концевых сечениях балки всегда равен нулю сечение 1, за исключением случая, когда в концевом сечении действует сосредоточенная пара. Допущена опечатка в формуле изгибающего момента для балки с жестким защемлением на опорах 3я снизу длина должна быть в квадрате. Второе уравнение статики получим из условия, что балка не вращается, https://docs.google.com/document/d/1HNP4DCOhHUkJLvS5W4oXOTp2K1EyKrm-YkIMjWhRtPc/mobilebasic так как сумма моментов приложенных к ней тоже равнв нулю. Выбираем направления остальных реактивных усилий, возникающих в заделке вертикальную реакцию направим, например, вниз, а момент – по ходу часовой стрелки.

В задачах, где имеется жесткая заделка, следует учесть, что ее реакция представляется силой. Если производится расчет двухопорной балки, то одна опора считается жесткой, а вторая – шарнирной. Расчет балки онлайн Калькулятор балок перекрытия из дерева. Конец которых жестко заделан защемлен, а второй свободен. Знак изгибающего момента был выбран в зависимости от того, где расположены. Значения опорных реакций, эпюры поперечных сил и изгибающих моментов, прогибы и угловые перемещения простых балок, нагруженных силами, моментами и распределенной нагрузкой. При изгибе в поперечных сечениях бруса балки возникают два внутренних силовых фактора поперечная сила и изгибающий момент. Если плоскость действия внешних нагрузок проходит через ось балки и одну из главных центральных осей поперечного сечения, изгиб. Все такие виды https://docs.google.com/document/d/1asWqRD0kGWTAGCIz5NV66DQGIlis27z5V0OYfAPoThw/mobilebasic фиксации считаются жесткой заделкой.

Проверка на прочность консольной балки Лекции и примеры. Эти данные нам понадобятся для подбора http://fajarjitu.com/user/profile/55246 сечения и проверочного расчета элемента конструкции. Сначала откладываем на опорах значения опорных моментов. Горизонтальная реакция в заделке равна нулю, поскольку внешние нагрузки в направлении оси на балку не действуют. Изгиб, при котором в поперечном сечении балки одновременно действуют изгибающий момент и поперечная сила, называется поперечным. Только если будет как минимум еще одна опора момент повлияет на опорную реакцию и, соответственно, на поперечные силы, но в данном уравнении его все равно не будет. Рассмотрим деформацию балки при простом изгибе.

Плоский изгиб – изгиб, при котором все усилия, изгибающие балку, лежат в одной из плоскостей симметрии балки в одной из главных. Отметим, что предварительное определение опорных реакций в заделке не обязательно. Вал – вращающаяся обычно в подшипниках деталь машины, передающая крутящий момент. В жесткой заделке прогиб и угол поворота сечения равен нулю. Уточните, пожалуйста, в каких единицах следует указывать распределённую нагрузку для балок в вашем калькуляторе В. Построение эпюр поперечных сил и изгибающих моментов в балках. Расчет балок из труб на изгиб и прогиб – калькулятор онлайн. Построить эпюры и М при найденном значении силы. Сделав сечение и отбросив часть с жесткой заделкой, сосчитаем момент от силы относительно сделанного сечения. Представленные расчетные схемы позволяют рассчитать однопролетные балки с жестким защемлением на одной или двух опорах и двухпролетные. Сечения балки в точке приложения силы δ связано с перемещением узла С точки.

Что такое реакция опоры?

Чтобы лучше понять, что такое реакция опоры (опорная реакция), давай рассмотрим следующий пример — балку (стержень) лежащую на опорах:

Схема, демонстрирующая схему балки (стержня) и опоры

На балку давит нагрузка – сила, в свою очередь, балка давит на опоры. И чтобы балка лежала на опорах (никуда не проваливалась), опоры выполняют свою основную функцию — удерживают балку. А чтобы удерживать балку, опоры должны компенсировать тот вес, с которым балка давит на них. Соответственно, действие опор можно представить в виде некоторых сил, так называемых — реакций опор.

Возникшие реакции в опорах балки под нагрузкой

Для балки, и нагрузка, и реакции опор, будут являться внешними силами, которые нужно обязательно учитывать при расчёте балки. А чтобы учесть опорные реакции, сначала нужно научиться определять их, чем, собственно, и займёмся на этом уроке.

Виды связей и их реакции

Связи – это способы закрепления элементов конструкций. Опоры, которые я уже показывал ранее – это тоже связи.

В этой статье будем рассматривать три вида связей: жёсткая заделка, шарнирно-подвижная и шарнирно-неподвижная опора.

Жёсткая заделка

Жёсткая заделка — это один из вариантов закрепления элементов конструкций. Этот тип связи препятствует любым перемещениям, тем самым для плоской задачи, может возникать три реакции: вертикальная (R_A), горизонтальная (H_A) и момент (M_A).

Шарнирно-подвижная и шарнирно-неподвижная опора

В этой статье будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

Схема шарнирно-подвижной и шарнирно-неподвижной опоры

В шарнирно-неподвижной опоре возникает две реакции: вертикальная и горизонтальная. Так как опора препятствует перемещению в этих двух направлениях. В шарнирно-подвижной опоре возникает только вертикальная реакция.

Реакции в шарнирно-подвижной и шарнирно-неподвижной опоре

Однако, видов связей и их условных обозначений достаточно много, но в рамках этой статьи их все рассматривать не будем. Так как, изученные ранее виды связей, являются основными и практически всегда, при решении задач по сопромату, ты будешь сталкиваться именно с ними.

Что такое момент силы?

Также необходимо разобраться с понятием момент силы.

Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр.

Проиллюстрирую написанное:

На изображении показано, как определить момент силы F, относительно точки O.

Правило знаков для моментов

Также для моментов, нужно задаться каким-то правилом знаков. Я в своих уроках буду придерживаться такого правила:

если сила относительно точки стремится повернуть ПРОТИВ часовой стрелки, то момент положительный;

если она стремится повернуть ПО часовой стрелке, то момент отрицательный.

Всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнём с простейшей расчётной схемы балки.

Определение реакций для двухопорной балки

Возьмём балку, загруженную посередине сосредоточенной силой и опирающейся на шарнирно-неподвижную и шарнирно-подвижную опору:

Расчётная схема балки, загруженная распределённой нагрузкой

Введём систему координат: направим ось x вдоль балки, а ось y вертикально. Обозначим реакции в опорах как H_A, R_A и R_B:

Указание координатных осей для схемы балки

Для тех, кто пришёл сюда, ещё будучи на этапе изучения теоретической механики, а я знаю, таких будет много, важно отметить, что в сопромате не принято указывать знаки векторов над силами.

В термехе же, в обязательном порядке, преподаватель от тебя настойчиво будет требовать указывать знак вектора над всеми силами, вот так:

Условия равновесия системы

Чтобы найти все реакции, нужно составить и решить три уравнения — уравнения равновесия:

Данные уравнения являются условиями равновесия системы. А так как мы предполагаем, что опоры обеспечивают это состояние равновесия (удерживают балку). То составив и решив уравнения равновесия — найдём значения опорных реакций.

Первое уравнение называется уравнением проекций — суммой проекций всех сил на координатную ось, которая должна быть равна нулю. Два других уравнения называются уравнениями моментов — суммами моментов всех сил относительно точек, которые должны быть равны нулю.

Уравнения равновесия

Как видишь, чтобы научиться находить реакции опор, главное — научиться правильно составлять уравнения равновесия.

Уравнение проекций

Запишем первое уравнение — уравнение проекций для оси x.

В уравнении будут участвовать только те силы, которые параллельны оси x. Такая сила у нас только одна — H_A. Так как H_A направлена против положительного направления оси x, в уравнение её нужно записать с минусом:

Тогда H_A будет равна:

Поздравляю, первая реакция найдена!

Уравнения моментов

А теперь самое интересное…запишем уравнение моментов, относительно точки A, с учётом ранее рассмотренного правила знаков для моментов.

Так как сила F поворачивает ПО часовой стрелке, записываем её со знаком «МИНУС» и умножаем на плечо.

Так как сила R_B поворачивает ПРОТИВ часовой стрелки, пишем её со знаком «ПЛЮС» и умножаем на плечо. И, наконец, всё это приравниваем к нулю:

Из полученного уравнения выражаем реакцию R_B:

Вторая реакция найдена! Третья реакция находится аналогично, но только теперь уравнение моментов записываем относительно другой точки:

Проверка правильности найденных опорных реакций

Чем хороши задачи на определение реакций, так это тем, что правильность расчёта реакций легко проверить. Для этого достаточно составить дополнительное уравнение равновесия, подставить все численные значения и если сумма проекций сил или сумма моментов будет равна нулю, то и реакции, значит, найдены — верно, а если нет, то ищем ошибку.

Составим дополнительное уравнение проекций для оси y и подставим все численные значения:

Как видишь, реакции опор найдены правильно.

Определение реакций опор для балки с распределенной нагрузкой

Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Схема балки, загруженная распределённой нагрузкой

Перед тем как посчитать реакции опор, распределенную нагрузку нужно «свернуть» до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:

Сворачивание распределённой нагрузки до сосредоточенной силы

Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:

Обозначение реакций в опорах и координатных осей

Расчёт реакций для консольной балки

Давай рассмотрим теперь пример с жёсткой заделкой – консольную балку. Заодно посмотрим, как учесть силу, приложенную под углом (α = 30^°).

Консольная балка, загруженная распределённой нагрузкой и силой под определённым углом

Силу, направленную под определённым углом, нужно разложить на две составляющие – горизонтальную и вертикальную. А их значения найти из силового треугольника:

Раскладывание сил на составляющие и силовой треугольник

Покажем реакции в заделке и выполним расчёт:

Обозначение реакций, сил и координатных осей для консольной балки

Для этой задачи выгоднее использовать другую форму условий равновесия:

А выгодна она тем, что из каждого записанного уравнения будем сразу находить реакцию:

Не пугайся отрицательного значения реакции! Это значит, что при указании реакции, мы не угадали с её направлением. Расчёт же показал, что M_A, направлена не по часовой стрелке, а против.

В теоретической механике, когда реакции получают с «минусом» обычно не заморачиваются и не меняют их направление на схеме, так и оставляют в ответе отрицательное значение, оговаривая, что да реакция найдена, но с учётом знака, на самом деле направлена в другую сторону. Потому что найденные реакции в задачах на статику, являются конечной точкой расчёта.

У нас же, в сопромате после нахождения опорных реакций, всё только начинается. Найдя реакции, мы всего лишь находим ВСЕ силы действующие на элемент конструкции, а дальше по сценарию стоит задача определить внутренние усилия, возникающие в этом элементе, расчёты на прочность и т. д. Поэтому на схеме, обязательно следует указывать истинное направление реакций. Чтобы потом, когда будут рассчитываться внутренние усилия ничего не напутать со знаками.

Если получили отрицательное значение, нужно отразить это на схеме:

Изменение направления реактивного момента

С учётом изменений на схеме реакция будет равна:

Сделаем проверку, составив уравнение равновесие, ещё не использованное – сумму моментов относительно, скажем, точки B, которая, при правильном расчёте, конечно, должна быть равна нулю:

Если не менять направление реакции, то в проверочном уравнении нужно учесть этот «минус»:

Можешь посмотреть еще один пример, с похожей схемой, для закрепления материала, так сказать.

Реакции опор для плоской рамы

Теперь предлагаю выполнить расчёт плоской рамы. Для примера возьмём расчётную схему, загруженную всевозможными видами нагрузок:

Проводим ряд действий с расчетной схемой рамы:

заменяем опоры на реакции;
сворачиваем распределенную нагрузку до сосредоточенной силы;
вводим систему координат x и y.

Обозначение реакций, сворачивание распределённой нагрузки и введение осей координат

Выполняем расчёт реакций опор:

Меняем направление реакции R_A:

В итоге получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумма будет равна нулю, то расчет выполнен верно:

Как видим, расчет реакций выполнен правильно!

Источник

Задача

Пример решения

Проекции силы на оси, расположенные в одной плоскости с силой

Момент силы относительно точки. Момент пары сил

Алгебраические моменты силы и пары

Моменты в балке при жесткой заделке

Определение опорных реакций в балке с жесткой заделкой.

Определение опорных реакций в заделке консольной балки.

Расчетные схемы для статически неопределимых балок Доктор.

Рекомендуем:

Что такое реакция опоры?

Виды связей и их реакции

Жёсткая заделка

Шарнирно-подвижная и шарнирно-неподвижная опора

Что такое момент силы?

Правило знаков для моментов

Определение реакций для двухопорной балки

Условия равновесия системы

Уравнения равновесия

Уравнение проекций

Уравнения моментов

Проверка правильности найденных опорных реакций

Определение реакций опор для балки с распределенной нагрузкой

Расчёт реакций для консольной балки

Реакции опор для плоской рамы