Как найти ребра треугольной пирамиды взаимно перпендикулярны

Решить эту задачу можно и длиннее, но гораздо более «традиционным» способом! Итак:

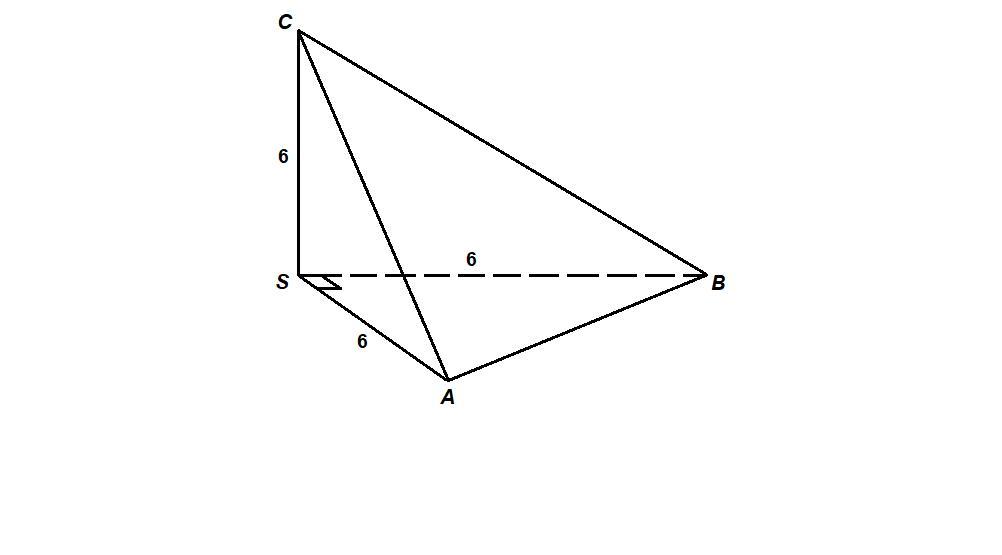
1) Т.к. по усл. SA=SB=SC=L=3, то по т. Пифагора в ∆ASB: AB=√(3^2+3^2 )=3√2

Аналогично для ∆ASC и ∆BSC. Поэтому ∆ABC, леж-й в основании — равностор-й, со стороной a=3√2.

2) S(∆ABC)=(a^2 √3)/4=…=4,5√3 (она же — площадь основания). Осталось найти высоту. Доп.постр: SO⊥(ABC), причём т.к. АВС-равностор-й (что было док. выше), то т. О — центр мед., бисс., и высот этого треугольника.

Найдём высоту основания СК, причём О∈СК и SK∩CK=K (SK-мед., бис и выс. равноб треуг. ASB).

3) С одной стороны: S(∆ABC)=(a^2 √3)/4=…=4,5√3

С другой стороны: S(∆ABC)=1/2*AB*CK

Откуда (с уч. того, что AB=a=3√2), получим

CK=(a√3)/2=…=1,5√6

Считая что медианы точкой пересеч-я делятся в отношении 2 к 1 считая от вершины, найдём ОК=1/3*CK=0,5√6

4) Практически всё! Последний «рывок»:

∆ASК (т. Пиф): SK^2=3^2-(a/2)^2=9-18/4=4,5 (не извлекаю корень из SK, т.к. следующим действием всё равно «обратно» возводить.

∆SКО (т. Пиф): (SO)^2=(SK)^2-(OK)^2=9/2-6/4=3, значит искомая высота h=SO=√3, и вот тогда

5) V=1/3*Sосн*h=1/3*(4,5√3)*√3=4,5

Победа!!!

Ответ:
36
Объяснение:
Пирамида SABC, ребра при вершине S взаимно перпендикулярны.
Можно повернуть пирамиду на боковую грань и рассмотреть пирамиду с основанием SAB.
∠ASB = 90°

Ребро CS перпендикулярно ребрам основания SA и SB, значит оно перпендикулярно плоскости основания, т.е. CS — высота пирамиды.

Видео по теме

---

Задача 1. В правильной четырехугольной пирамиде   точка   – центр основания,   – вершина,   Найдите длину отрезка .

Решение: + показать

---

Задача 2.  В правильной четырехугольной пирамиде   точка  – центр основания,  – вершина,   Найдите боковое ребро

Решение: + показать

---

Задача 3. Стороны основания правильной четырехугольной пирамиды равны боковые ребра равны Найдите площадь поверхности этой пирамиды.

Решение: + показать

---

Задача 4.  В правильной четырёхугольной пирамиде   точка   —  центр основания,  — вершина,   Найдите длину отрезка

Решение: + показать

---

Задача 5. Основанием пирамиды является прямоугольник со сторонами и Ее объем равен Найдите высоту этой пирамиды.

Решение: + показать

---

Задача 6. В правильной четырёхугольной пирамиде   с основанием  боковое ребро  равно сторона основания равна  Найдите объём пирамиды.

Решение: + показать

---

Задача 7. В правильной четырёхугольной пирамиде все рёбра равны Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых рёбер.

Решение: + показать

---

Задача 8.  Даны две правильные четырёхугольные пирамиды. Объём первой пирамиды равен У второй пирамиды высота в раза больше, а сторона основания в раза больше, чем у первой. Найдите объём второй пирамиды.

Решение: + показать

---

Задача 9.  В правильной четырёхугольной пирамиде боковое ребро равно а тангенс угла между боковой гранью и плоскостью основания равен  Найти сторону основания пирамиды.

Решение: + показать

---

Задача 10. Основанием пирамиды является прямоугольник со сторонами и Ее объем равен Найдите высоту этой пирамиды.

Решение: + показать

---

Задача 11. Стороны основания правильной четырехугольной пирамиды равны боковые ребра равны Найдите площадь поверхности этой пирамиды.

Решение: + показать

---

Задача 12. В правильной треугольной пирамиде   медианы основания  пересекаются в точке . Площадь треугольника   равна объем пирамиды равен Найдите длину отрезка .

Решение: + показать

---

Задача 13.  В правильной треугольной пирамиде  точка  — середина ребра  — вершина. Известно, что а . Найдите площадь боковой поверхности пирамиды.

Решение: + показать

---

Задача 14. Найдите объем правильной треугольной пирамиды, стороны основания которой равны а высота равна  

Решение: + показать

---

Задача 15.  Найдите высоту правильной треугольной пирамиды, стороны основания которой равны а объем равен

Решение: + показать

---

Задача 16. Стороны основания правильной шестиугольной пирамиды равны боковые ребра равны Найдите площадь боковой поверхности этой пирамиды.

Решение: + показать

---

Задача 17. Объем правильной шестиугольной пирамиды Сторона основания равна Найдите боковое ребро.

Решение: + показать

---

Задача 18. Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в два раза?

Решение: + показать

---

Задача 19. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в раз?

Решение: + показать

---

Задача 20.  Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в пять раз?

Решение: + показать

---

Задача 21. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом °. Высота пирамиды равна Найдите объем пирамиды.

Решение: + показать

---

Задача 22. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно Найдите объем пирамиды.

Решение: + показать

---

Задача 23. От треугольной призмы, объем которой равен отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.

Решение: + показать

---

Задача 24. Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен Найдите объем шестиугольной пирамиды. Видео по теме 1 2 

Решение: + показать

---

Задача 25.  Сторона основания правильной шестиугольной пирамиды равна 8, боковое ребро равно 16. Найдите объём пирамиды.

Решение: + показать

---

Задача 26. Сторона основания правильной шестиугольной пирамиды равна а угол между боковой гранью и основанием равен Найдите объем пирамиды.

Решение: + показать

---

Задача 27. Найдите объём правильной шестиугольной пирамиды если объём треугольной пирамиды равен

Решение: + показать

---

Задача 28.  Объем параллелепипеда  равен Найдите объем треугольной пирамиды  

Решение: + показать

---

Задача 29. Объем куба равен Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

---

Задача 31. Объем правильной четырехугольной пирамиды  равен Точка  — середина ребра . Найдите объем треугольной пирамиды .

Решение: + показать

---

Задача 32. От треугольной пирамиды, объем которой равен отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

Решение: + показать

---

Задача 33.  Ребра тетраэдра равны Найдите площадь сечения, проходящего через середины четырех его ребер.

Решение: + показать

---

  Вы можете пройти тест