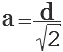Найти стороны квадрата через диагональ поможет теорема Пифагора.
Впрочем, если это квадрат, то нужно искать не стороны квадрата, а одну его сторону, поскольку все стороны равны.
Диагональ делит квадрат на два треугольника, для каждого треугольника (а они — прямоугольные), диагональ является гипотенузой, а стороны квадрата — катетами.
Чтобы не вводить лишние буквенные обозначения я так и обозначу: гипотенузу буквой «г», а сторону квадрата буквой «с».
По теореме Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
г2 = с2 + с2 (с2 — это с в квадрате, не знаю как записать точнее )
г2 = 2 с2
с2 = г2/2 (г в квадрате, делённое на 2)
с = квадратному корню из г2/2
Г — диагональ квадрата, она известна; подставляем в формулу
/
/
/ Длина стороны квадрата
Длина стороны квадрата
Установить Длина стороны квадрата на мобильный
Найти длину стороны квадрата
зная площадь
|
||
| Площадь квадрата S | ||
|
|
||
| Результат |
Вычислить длину стороны квадрата
зная диагональ
|
||
| Диагональ квадрата d | ||
| Результат |
Скачать калькулятор
Рейтинг: 2.5 (Голосов 24)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Сообщить об ошибке
Смотрите также
| Сторона треугольника | Стороны прямоугольного | Стороны равнобедренного | Стороны равностороннего |
| Стороны прямоугольника | Стороны ромба | Стороны параллелограмма | Ребро куба |
Александра
531 дн. назад
Клас клас клас!!! Не могла понять (сломала голову
- reply
Наталья
828 дн. назад
Класс!!! Не люблю считать. Вообще… Спасибо!!!
- reply
Николай
1027 дн. назад
Супер. И быстро. Мне нравится.
- reply
Добавить комментарий:
Я не робот
Введите данные:
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
Cторона квадрата, диаметр вписанной окружности (L)
Диагональ квадрата, диаметр описанной окружности (M)
Радиус вписанной окружности (R1)
Радиус описанной окружности (R2)
Округление:
* — обязательно заполнить
Диагональ, диаметр описанной окружности (M) = 10
Cторона, диаметр вписанной окружности (L) = (sqrt{frac{M^{2}}{2}}) = (sqrt{frac{10^{2}}{2}}) = 7.07
Радиус вписанной окружности (R1) = (frac{L}{2}) = (frac{7.07}{2}) = 3.54
Радиус описанной окружности (R2) = (frac{M}{2}) = (frac{10}{2}) = 5
Периметр (P) = (L*4) = (7.07*4) = 28.28
Площадь (S) = (L^{2}) = (7.07^{2}) = 49.98
Квадрат, наряду с кругом, считается идеальной геометрической фигурой. Квадрат является не только параллелограммом, но и ромбом, и прямоугольником одновременно, так как у него все стороны равны и все углы прямые. Более того, квадрат является представителем ряда правильных многоугольников, поэтому к нему относятся и их свойства тоже. Вычислить сторону квадрата можно несколькими различными способами: через периметр квадрата, через площадь квадрата или через диагональ квадрата, а также радиусы вписанной и описанной окружностей.
Поскольку все стороны квадрата между собой равны, а периметр многоугольника – это сумма всех его сторон, то найти сторону можно, разделив периметр на четыре (количество равных сторон):
Площадь квадрата – это его сторона, возведенная во вторую степень, следовательно, если нам нужно найти сторону через площадь, то необходимо извлечь из нее квадратный корень:
Если дана диагональ квадрата, то исходя из теоремы Пифагора в прямоугольном треугольнике, который образует диагональ, сторона будет равна диагонали, деленной на корень из двух:
a2+a2=d2
2a2=d2
Как найти сторону квадрата, если известна его диагональ
Квадрат является одной из наиболее простых геометрических фигур в плане вычисления его параметров — длин сторон и диагоналей, площади и периметра. Это определяется тем, что в отличие от других многоугольников, всегда известны величины всех его углов, а также достаточно знать длину всего одной стороны. Нахождение длины стороны квадрата по известной длине диагонали, как в общем виде, так и с практическими расчетами не представляет сложности.
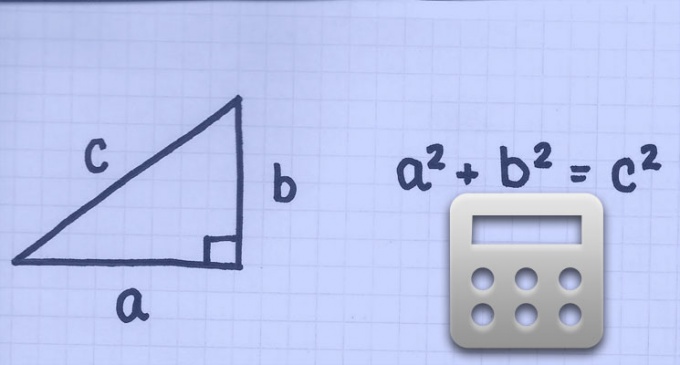
Инструкция
Используйте теорему Пифагора, алгебраическая формулировка которой утверждает, что в прямоугольном треугольнике сумма квадратов длин катетов равна квадрату длины гипотенузы: a² + b² = c². Так как диагонали квадрата делят его на два именно таких прямоугольных треугольника, у которых к тому же еще и длины катетов одинаковы, то можно сформулировать такое свойство квадрата, как геометрической фигуры: квадрат длины диагонали равен удвоенному квадрату длины стороны (2a²=c²). Из этого вытекает, что длина стороны равна квадратному корню из половины квадрата длины диагонали: a=√(c²/2).
Воспользуйтесь встроенным в поисковую систему Google калькулятором для практических расчетов по вычислению длины стороны квадрата. Например, если известная длина диагонали равна 15 сантиметрам, то перейдя на сайт поисковика, введите такой запрос: «корень из ((15 в квадрате)/2)». Если вы привыкли использовать символ ^ для обозначения операции возведения в степень и sqrt для обозначения операции извлечения квадратного корня, то Google правильно поймет и такой запрос: «sqrt (15^2/2)». В любом случае ответ будет одинаков: длина стороны квадрата равна 10,6066017 сантиметров.
Используйте, например, программный калькулятор из стандартного набора программ операционной системы Windows в качестве альтернативного способа для расчета длины стороны квадрата. Ссылка на его запуск упрятана довольно глубоко в главное меню системы — после щелчка по кнопке «Пуск» нужно раскрыть раздел «Все программы», перейти в подраздел «Стандартные», кликнуть секцию «Служебные» и выбрать пункт «Калькулятор». Более быстрый способ — нажать сочетание клавиш WIN + R, ввести команду calc и нажать клавишу Enter.
Введите известную длину стороны, затем нажмите клавишу со звездочкой и Enter — так вы выполните операцию возведения в квадрат. Затем нажмите клавишу с косой чертой, введите двойку и нажмите Enter. После этого щелкните кнопку с надписью sqrt и увидите искомую длину стороны квадрата — 10,606601717798212866012665431573 сантиметров.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.