Скачать материал

Скачать материал


- Сейчас обучается 39 человек из 28 регионов


- Сейчас обучается 75 человек из 34 регионов


- Сейчас обучается 104 человека из 36 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
ТЕМА ПИРАМИДА Кониченко Елена Михайловна учитель 1 категории школа № 4 им. А.Н. Кесаева г. Севастополь
-
2 слайд
ЦЕЛИ УРОКА : а) образовательные: познакомить учащихся с понятием –пирамида; познакомить учащихся с элементами пирамиды; научить учащихся находить грани, ребра, вершины пирамиды; научить учащихся выполнять построение пирамиды и ее развертки; научить учащихся вычислять длину ребер пирамиды; б) развивающие: развитие пространственного воображения; формирование способности сравнивать геометрические фигуры, обобщать полученные знания, формирование логического мышления; в) воспитательные: привитие навыка аккуратности при построении чертежа; активизация интереса учащихся к получению новых знаний; воспитание трудолюбия. Тип урока: изучение нового материала.
-
3 слайд
УСТНЫЙ СЧЕТ Вычислите и запишите результаты по возрастанию чисел. Поставьте соответствующие буквы и прочитайте название темы урока. 1) 20 x 7 4) 23 + 47 7) 100 — 10 — 50 : 7 x 90 : 5 x 16 + 1900 + 33 — 90 : 100 = … М = … И = … Д 2) 100 – 77 5) 620 + 190
54 : 6 x 3 : 90 + 34 + 51 x 20 x 2 : 12 — 180 — 56 = … И = … П = … А 3) 200 : 4 6) 4 x 40 + 70 + 260 x 5 : 6 – 240 — 45 = … А = … Р
-
4 слайд
ОТВЕТЫ 1) 51 2) 10 3) 360 4) 70 5) 0 6) 25 7) 100
30 По возрастанию : 0 , 10 , 25 , 30 , 51 , 70 , 100, 360 П И Р А М И Д А
-
5 слайд
Назовите представленные на картинках предметы: 1) 2) 3) 4)
-
6 слайд
Все эти предметы дают представление о пирамиде:
-
-
8 слайд
Многоугольники Назовите виды многоугольников на рисунках: 1 2 3 4 5 6 7 8
-
9 слайд
ВИДЫ ПИРАМИД S S Треугольная пирамида SABC Четырехугольная Шестиугольная Пятиугольная Усеченная четырехугольная A B C D A B C D E F A B C D P K M N
-
10 слайд
ПИРАМИДА – слово греческого происхождения, означает “костер”,”огонь”. Пирами́да —многогранник, основание которого — многоугольник, а остальные грани — треугольники (боковые грани), имеющие общую вершину. По числу углов основания различают пирамиды треугольные, четырёхугольные и т.д. Вершины многоугольника называют вершинами основания, а ребра многоугольника – ребрами основания пирамиды. Количество вершин, ребер и граней зависит от вида пирамиды.
-
11 слайд
На рисунке пирамида , назовите: Вершину пирамиды. Вершины основания. Основание пирамиды. Ребра основания. Боковые ребра пирамиды. Боковые грани пирамиды. Грани, которые проходят через вершину пирамиды. Вид пирамиды. S K P R T
-
12 слайд
Сколько вершин, ребер и граней у пирамиды: s s A B C A B C D E F 1) 2) 3)
-
13 слайд
О Т В Е Т Ы Вершин – 7 2) Вершин – 5 3) Вершин — 4 Ребер — 12 Ребер — 8 Ребер — 6 Граней — 7 Граней — 5 Граней — 4
-
14 слайд
РАЗВЕРТКА четырехугольной пирамиды 3 см 3 см 4 см 2 см Постройте в тетради развертку этой пирамиды.
-
15 слайд
ФИЗКУЛЬТМИНУТКА Потрудились-отдохнем, Встанем, глубоко вздохнем. Руки в стороны, вперед, Влево, вправо, поворот. Три наклона, прямо встать. Руки вниз и вверх поднять. Руки плавно опустили, Всем улыбки подарили.
-
16 слайд
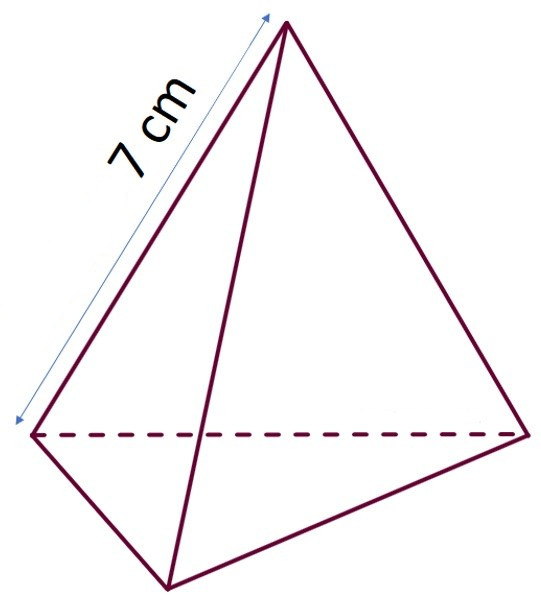
Какой длины потребуется проволока для изготовления каркаса данной пирамиды? 1) 2) 3) Длина каждого ребра равна 3см Длина ребра основания 5 см, длина бокового ребра 7 см Длина бокового ребра 10 см; длина ребра основания 9 см
-
17 слайд
ОТВЕТЫ: 1) 8 x 3 = 24 ( см ) 2) 5 x 5 + 5 x 7 = 25 + 35 = 60 ( см ) 3) 6 x 9 + 6 x 10 = 54 + 60 = 114 ( см )
-
18 слайд
На каждой парте стоят фигуры разных видов пирамиды. Заполните таблицу по одной из пирамид:
-
19 слайд
Задание: по данным своей таблицы заполните пропуски в тексте Число вершин пирамиды на ________ больше числа вершин в ее основании. Ребер боковых граней _________, сколько их в основании. Число боковых граней _________ числу сторон основания.
-
20 слайд
Проверьте свои выводы: Число вершин пирамиды на единицу больше числа вершин в ее основании. Ребер боковых граней столько же, сколько их в основании. Число боковых граней равно числу сторон основания.
-
21 слайд
ПИРАМИДЫ вокруг нас
-
-
23 слайд
Спасибо за урок .
Краткое описание документа:
•ЦЦели презентацииа)образовательные:
•познакомить учащихся с понятием –пирамида;
•познакомить учащихся с элементами пирамиды;
•научить учащихся находить грани, ребра, вершины пирамиды;
•научить учащихся выполнять построение пирамиды и ее развертки;
•научить учащихся вычислять длину ребер пирамиды;
•б) развивающие:
•развитие пространственного воображения;
•формирование способности сравнивать геометрические фигуры, обобщать полученные знания, формирование логического мышления;
•в) воспитательные:
•привитие навыка аккуратности при построении чертежа;
•активизация интереса учащихся к получению новых знаний;
•воспитание трудолюбия.
•
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 263 482 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
Рейтинг:
5 из 5
- 18.11.2014
- 5566
- 19
Рейтинг:
4 из 5
- 18.11.2014
- 13968
- 164
- 18.11.2014
- 1885
- 0
Рейтинг:
4 из 5
- 18.11.2014
- 5803
- 259
Рейтинг:
5 из 5
- 18.11.2014
- 9427
- 163
- 18.11.2014
- 1339
- 0
- 18.11.2014
- 3784
- 11
Учебник: Математика 5 класс. Г.В.Дорофеев, И.Ф.Шарыгин, С.В.Суворова и др. ФГОС.
Тип урока: урок применения полученных знаний в практике.
Форма урока: урок-исследование.
Цель урока: организация работы по формированию знаний и исследованию пирамиды, построение развёртки и моделирование пирамиды.
Задачи: определить элементы пирамиды, исследовать особенности пирамиды, изучить виды пирамид, построить развёртку пирамиды, изготовить модель пирамиды.
Образовательные: продолжить изучение основных элементов пирамиды, научить учащихся находить грани, рёбра, вершины пирамиды, познакомить с развёрткой пирамиды и научить моделировать пирамиду.
Развивающие: развивать пространственное воображение, формировать способности сравнивать геометрические фигуры, обобщать полученные знания, формировать логическое мышление и навыки грамотной математической речи.
Воспитательные: прививать навыки аккуратности при построении чертежа, воспитывать положительную мотивацию к учению, умение выслушивать товарища, высказывать свою точку зрения, активизация интереса учащихся к получению новых знаний, воспитание трудолюбия.
Оборудование: компьютер с проектором, презентация, ролик, карточки, учебники, модели пирамид, развертки пирамид, ножницы, картон, клей, раздаточный материал.
Планируемые образовательные результаты:
|
Личностные |
Метапредметные |
Предметные |
||
|
Умение выдвигать гипотезы и отстаивать свою позицию. Находчивость и активность при выполнении исследовательской работы. Осознание личной ответственности за общее дело. Умение признавать собственные ошибки. |
Регулятивные |
Коммуникативные |
Познавательные |
Формулировать определение пирамиды, распознавать пирамиду на чертежах, рисунках, в окружающем мире; определять количество граней, ребер, вершин пирамиды; моделировать пирамиду, используя трубочки и пластилин; моделировать пирамиду из разверток. |
|
Умение определять тему, цель, организовать выполнение заданий учителя, преодолевать трудности на пути достижения цели, адекватно их оценивая, уметь контролировать свое время при выполнении задания. |
Умение работать в составе группы, планировать успешное сотрудничество, аргументировать свою точку зрения, задавать вопросы с целью получения нужной информации |
Вырабатывать умение работать с различными источниками информации, работать с таблицами, дополнять их необходимыми данными, структурировать учебный материал, грамотно формулировать выводы, делать умозаключения, представлять результаты работы классу. |
Технологическая карта урока
Приложение
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Вопросы к параграфу
1. Какие предметы дают представление о прямоугольном параллелепипеде?
Коробка, кирпич, спичечный коробок, ящик, пакет молока или сока, платяной шкаф и т.д.
2. Из каких фигур состоит поверхность прямоугольного параллелепипеда?
Из шести прямоугольников.
3. Сколько граней имеет прямоугольный параллелепипед?
Шесть граней.
4. Сколько пар противолежащих граней имеет прямоугольный параллелепипед?
У прямоугольного параллелепипеда три паны противолежащих граней.
5. Каким свойством обладают противолежащие грани прямоугольного параллелепипеда?
Противолежащие грани прямоугольного параллелепипеда равны.
6. Как называют стороны граней прямоугольного параллелепипеда?
Стороны граней прямоугольного параллелепипеда называют рёбрами.
7. Как называют вершины граней прямоугольного параллелепипеда?
Вершины граней прямоугольного параллелепипеда называют вершинами.
8. Сколько вершин имеет прямоугольный параллелепипед?
Прямоугольный параллелепипед имеет 8 вершин.
9. Сколько рёбер имеет прямоугольный параллелепипед?
Прямоугольный параллелепипед имеет 12 рёбер.
10. Какое общее название имеют длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину?
Измерения.
11. Какие названия измерений прямоугольного параллелепипеда используют для их различия?
Длина, ширина, высота.
12. Какую фигуру называют кубом?
Куб — это прямоугольный параллелепипед, у которого все измерения равны.
13. Из каких фигур состоит поверхность куба?
Из шести равных квадратов.
14. Из каких фигур состоит поверхность пирамиды?
Поверхность пирамиды состоит из боковых граней — треугольников, имеющих общую вершину, и основания.
15. Какую пирамиду называют треугольной? Четырёхугольной?
Треугольной пирамидой называют пирамиду, у основания которой три стороны, то есть основание является треугольником.
Четырехугольной пирамидой называют пирамиду, у основания которой четыре стороны, то есть основание является четырёхугольником.
16. Что называют вершиной пирамиды?
Вершиной пирамиды называют общую вершину боковых граней.
17. Что называют рёбрами основания пирамиды?
Стороны основания пирамиды называют рёбрами основания пирамиды.
18. Что называют боковыми рёбрами пирамиды?
Боковыми рёбрами пирамиды называют стороны боковых граней, не принадлежащие основанию.
Решаем устно
1. Вычислите:
- 13 • 4 • 25 = 13 • (4 • 25) = 13 • 100 = 1 300
- 4 • 5 • 78 • 5 = (4 • 5) • 78 • 5 = (20 • 5) • 78 = 100 • 78 = 7 800
- 125 • 943 • 8 = (125 •
• 943 = 1 000 • 943 = 943 000
2. Упростите выражение:
- 3a • 16b = 48 ab
- 4m •9n •5k = 180 mnk
- 7a •2b •50c •8d = 5600 abcd
3. Раскройте скобки:
- 2(a + b) = 2a + 2b
- (3 — b) • 5 = 3 • 5 — b • 5 = 15 — 5b
- 6m(7n + 8p) = 6m • 7n + 6m • 8p = 42 mn + 48 mp
4. Найдите периметр прямоугольника, площадь которого равна 28 см², а одна из его сторон — 7 см.
1) 28 : 7 = 4 (см) — длина второй стороны прямоугольника.
2) (4 + 7) • 2 = 11 • 2 = 22 (см) — периметр прямоугольника.
Ответ: периметр равен 22 см.
5. В магазине разложили 6 ц яблок в ящики так, что в каждом ящике оказалось по 12 кг яблок. Сколько ящиков заполнили яблоками?
6ц = 600 кг.
600 : 12 = 50 (ящиков) — заполнили яблоками.
Ответ: 50 ящиков.
6. Во сколько раз площадь квадрата, сторона которого равна 6 см, больше площади квадрата со стороной 2 см?
1) 6 • 6 = 36 (см²) — площадь квадрата со стороной 6 см.
2) 2 • 2 = 4 (см²) — площадь квадрата со стороной 2 см.
3) 36 : 2 = 18 (раз) — площадь квадрата со стороной 6 см больше площади квадрата со стороной 2 см.
Ответ: в 18 раз.
Упражнения
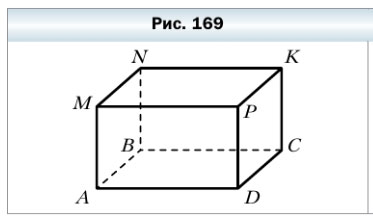
598. На рисунке 169 изображён прямоугольный параллелепипед ABCDMNKP. Назовите:
1) грани, которым принадлежит вершина С — ABCD, NKCB, PKCD
2) рёбра, равные ребру ВС — AD, MP, NK
3) верхнюю грань — MNKP
4) вершины, принадлежащие нижней грани — A, B, C, D
5) грани, имеющие общее ребро AM — AMNB, AMPD
6) грань, равную грани DPKC — AMNB
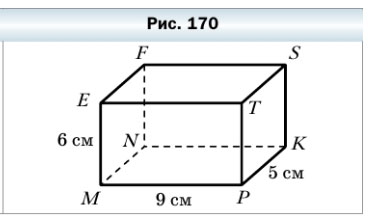
599. Измерения прямоугольного параллелепипеда MNKPEFST (рис. 170) равны 9 см, 5 см и 6 см. Вычислите сумму длин всех его рёбер и площадь его поверхности.
В прямоугольном параллелепипеде MNKPEFST всего 12 рёбер:
- рёбро EM = FN = SK = TP = 6 см
- рёбро MP = ET = FS = NK = 9 см
- рёбро PK = MN = EF = TS = 5 см
6 • 4 + 9 • 4 + 5 • 4 = 24 + 36 + 20 = 80 (см) — длина всех рёбер прямоугольного параллелепипеда MNKPEFST.
Поверхность прямоугольного параллелепипеда состоит из 6 граней:
- площадь грани EFST = MNKP = 5 • 9 = 45 см²
- площадь грани EFNM = TSKP = 6 • 5 = 30 см²
- площадь грани ETPM = FSKN = 9 • 6 = 54 см²
45 • 2 + 30 • 2 + 54 • 2 = 90 + 60 + 108 = 258 (см²) — площадь поверхности прямоугольного параллелепипеда MNKPEFST.
Ответ: длина всех рёбер 80 см, площадь поверхности 258 см².
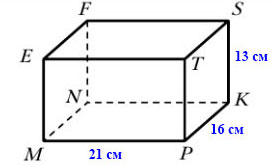
600. Найдите сумму длин всех рёбер прямоугольного параллелепипеда, измерения которого равны 13 см, 16 см, 21 см.
В прямоугольном параллелепипеде MNKPEFST всего 12 рёбер:
- рёбро EM = FN = SK = TP = 13 см
- рёбро MP = ET = FS = NK = 21 см
- рёбро PK = MN = EF = TS = 16 см
13 • 4 + 16 • 4 + 21 • 4 = 52 + 64 + 84 = 200 (см) — длина всех рёбер прямоугольного параллелепипеда MNKPEFST.
Ответ: длина всех рёбер 200 см.
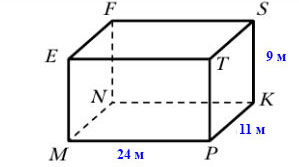
601. Найдите площадь поверхности прямоугольного параллелепипеда, измерения которого равны 9 м, 24 м, 11 м.
Поверхность прямоугольного параллелепипеда состоит из 6 граней:
- площадь грани EFST = MNKP = 24 • 11 = 264 м²
- площадь грани EFNM = TSKP = 9 • 11 = 99 м²
- площадь грани ETPM = FSKN = 24 • 9 = 216 м²
264 • 2 + 99 • 2 + 216 • 2 = 528 + 198 + 432 = 1 158 (м²) — площадь поверхности прямоугольного параллелепипеда MNKPEFST.
Ответ: площадь поверхности 1 158 м².
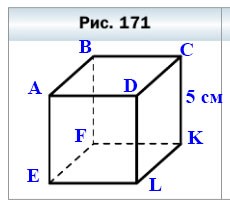
602. Вычислите площадь поверхности и сумму длин всех рёбер куба (рис. 171), ребро которого равно 5 см.
В кубе ABCDEFKL всего 12 рёбер и они все равны 5 см.
5 • 12 = 60 (см) — длина всех рёбер куба ABCDEFKL.
Поверхность куба состоит из 6 граней и они все равны 5 • 5 = 25 см²
25 • 6 = 150 (см²) — площадь поверхности куба ABCDEFKL.
Ответ: длина всех рёбер 60 см, площадь поверхности 150 см².
603. Найдите сумму длин всех рёбер и площадь поверхности куба, если его ребро равно 7 см.
В кубе ABCDEFKL всего 12 рёбер и они все равны 7 см.
7 • 12 = 84 (см) — длина всех рёбер куба ABCDEFKL.
Поверхность куба состоит из 6 граней и они все равны 7 • 7 = 49 см²
49 • 6 = 294 (см²) — площадь поверхности куба ABCDEFKL.
Ответ: длина всех рёбер 84 см, площадь поверхности 294 см².
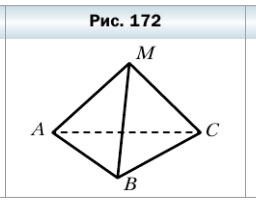
604. На рисунке 172 изображена пирамида МАВС. Укажите:
1) основание пирамиды — ABC
2) вершину пирамиды — M
3) боковые грани пирамиды — AMB, AMC, BMC
4) боковые рёбра пирамиды — AM, BM, CM
5) рёбра основания пирамиды — AB, BC, AC
605. На рисунке 173 изображена пирамида SABCD. Укажите:
1) основание пирамиды — ABCD
2) вершину пирамиды — S
3) боковые грани пирамиды — ADS, DCS, CBS, ABS
4) боковые рёбра пирамиды — AS, BS, CS, DS
5) рёбра основания пирамиды — AB, BC, CD, DA
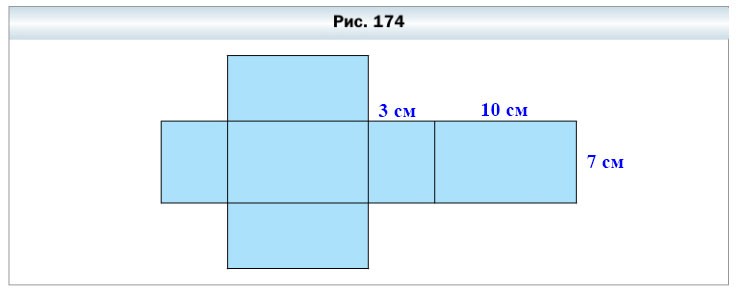
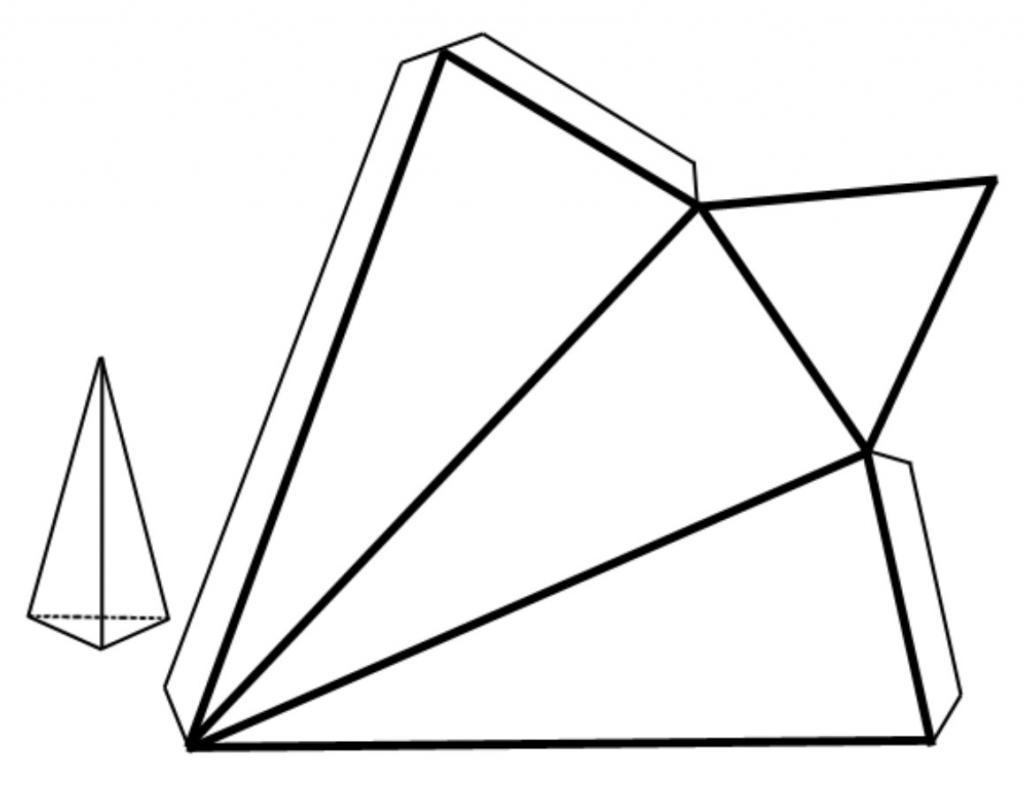
606. На рисунке 174 изображена развёртка прямоугольного параллелепипеда.
1) Из скольких прямоугольников состоит развёртка? — из 6 прямоугольников.
2) Сколько пар равных прямоугольников содержит развёртка? — 3-х пары равных прямоугольников.
3) Какова площадь этой развёртки, если измерения параллелепипеда равны 10 см, 7 см и 3 см?
S = (10 • 7) • 2 + (3 • 10) • 2 + (7 • 3) • 2 = 70 • 2 + 30 • 2 + 21 • 2 = 140 + 60 + 42 = 242 см²
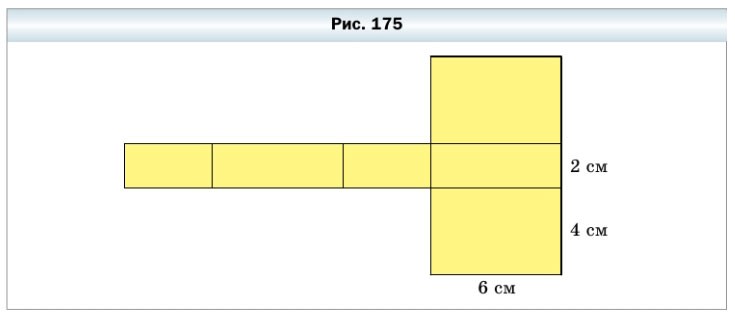
607. Вычислите площадь поверхности прямоугольного параллелепипеда, развёртка которого изображена на рисунке 175.
S = (6 • 4) • 2 + (6 • 2) • 2 + (4 • 2) • 2 = 24 • 2 + 12 • 2 + 8 • 2 = 48 + 24 + 16 = 88 см²
Ответ: площадь поверхности равна 88 см².
608. Высота прямоугольного параллелепипеда равна 20 см, что на 5 см больше его ширины и в 3 раза меньше его длины. Вычислите площадь поверхности параллелепипеда.
1) 20 — 5 = 15 (см) — ширина прямоугольного параллелепипеда.
2) 20 • 3 = 60 (см) — длина прямоугольного параллелепипеда
3) (60 • 20) • 2 + (60 • 15) • 2 + (20 • 15) • 2 = 1 200 • 2 + 900 • 2 + 300 • 2 = 2 400 + 1 800 + 600 = 4 800 (см²) — площадь поверхности прямоугольного параллелепипеда.
Ответ: S = 4 800 см².
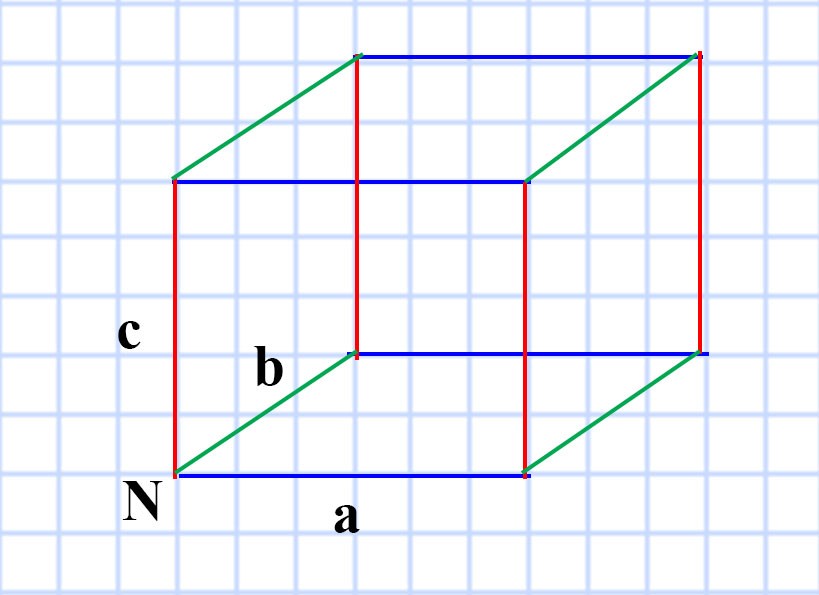
609. Сумма длин всех рёбер прямоугольного параллелепипеда равна 28 см. Найдите сумму длин трёх его рёбер, имеющих общую вершину.
В прямоугольном параллелепипеде всего 12 ребер. Причём:
- 4 ребра равны длине a — рёбра синего цвета
- 4 ребра равны ширине b — рёбра зелёного цвета
- 4 ребра равны ширине c — рёбра красного цвета
Мы знаем, что сумма длин всех рёбер этого прямоугольного параллелепипеда равна 28 см.
Значит, можно записать:
4a + 4b + 4с = 28
4 (a + b + с ) = 28
a + b + с = 28 : 4
a + b + с = 7 (см)
Так как рёбра a, b и с сходятся в общей вершине N, то искомая сумма длин трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину равна 7 см.
Ответ: 7 см.
610. Прямоугольный параллелепипед и куб имеют равные площади поверхностей. Длина параллелепипеда равна 18 м, что в 2 раза больше, чем его ширина, и на 8 м больше, чем его высота. Найдите ребро куба.
1) 18 : 2 = 9 (м) — ширина параллелепипед.
2) 18 — 8 = 10 (м) — высота параллелепипеда.
3) (18 • 9) • 2 + (18 • 10) • 2 + (10 • 9) • 2 = 162 • 2 + 180 • 2 + 90 • 2 = 324 + 360 + 180 = 864 (м²) — площадь поверхности параллелограмма.
Значит площадь поверхности куба равна 864 м². Так как у куба всего 6 граней и все они одинаковы, то можно найти площадь грани куба.
4) 864 : 6 = 144 (м²) — площадь грани куба.
Для того, чтобы найти длину ребра куба, надо подобрать такое число, квадрат которого будет равняться числу 144. Это число 12 (12 • 12 = 144).
Значит длина ребра куба равна 12 м.
Ответ: 12 метров.
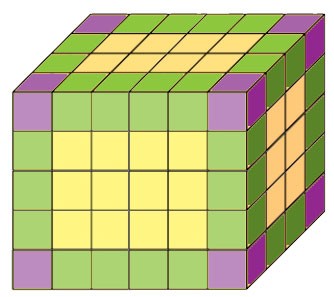
611. Брусок, имеющий форму прямоугольного параллелепипеда с измерениями 4 см, 5 см и 6 см, покрасили со всех сторон и разрезали на кубики с ребром 1 см. Сколько получилось кубиков, у которых:
1) окрашено три грани — 8 кубиков (фиолетовые), которые расположены по вершинам прямоугольного параллелепипеда.
2) окрашено две грани — 36 кубков (зелёные), которые расположены по рёбрам параллелепипеда, но не являются его вершинами (4 • 4 + 3 • 4 + 2 • 4 = 16 + 12 + 8 = 36):
- по 4 кубика на 4 рёбрах длиной 6 см
- по 3 кубика на 4 рёбрах длиной 5 см
- по 2 кубика на 4 рёбрах длиной 4 см
3) окрашено одна грань — 52 кубика (жёлтые), которые не примыкают ни к вершинам, ни к рёбрам параллелепипеда (12 • 2 + 8 • 2 + 6 • 2 = 24 + 16 + 12 = 52):
- 4 • 3 = 12 кубиков на двух гранях размерами 6 см х 5 см
- 4 • 2 = 8 кубиков на двух гранях размерами 6 см х 4 см
- 3 • 2 = 6 кубиков на двух гранях размерами 5 см х 5 см
Упражнения для повторениях
612. Скорость космического корабля «Восток», на котором Юрий Гагарин совершил свой полёт, равна 8 км/с.
1) За сколько минут он пролетал 960 км?
960 : 8 = 120 (с) — нужно кораблю для преодоления 960 км.
120 с = 2 мин
Ответ: 2 минуты.
2) Какое расстояние он пролетал за 1 ч?
1 ч = 60 мин = 3 600 с
8 • 3 600 = 28 800 (км) — пролетает корабль за 1 час.
Ответ: 28 800 км.
613. Из листа картона можно вырезать шесть одинаковых квадратов. Сколько листов картона надо для того, чтобы вырезать 50 таких квадратов?
50 = 6 • 8 + 2
Значит нужно 8 + 1 = 9 листов.
Ответ: 9 листов.
614. Поезд отправился со станции в 16 ч со скоростью 54 км/ч. В 19 ч с этой же станции в противоположном направлении отправился второй поезд. В 24 ч расстояние между ними было равно 642 км. С какой скоростью двигался второй поезд?
1) 24 — 16 = 8 (часов) — двигался первый поезд.
2) 54 • 8 = 432 (км) — проехал первый поезд за 8 часов.
3) 24 — 19 = 5 (часов) — двигался второй поезд.
4) 642 — 432 = 210 (км) — проехал второй поезд за 5 часов.
5) 210 : 5 = 42 (км/ч) — скорость второго поезда.
Ответ: 42 км/ч.
615. Решите уравнение:
Задача от мудрой совы
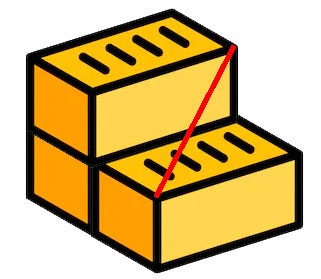
616. Как с помощью линейки измерить диагональ кирпича, имея ещё несколько таких кирпичей? (Диагональ параллелепипеда — это отрезок, соединяющий две его вершины, не принадлежащие одной грани.)
Для этого нам потребуется как минимум 3 кирпича:
- Сложим кирпичи лесенкой
- Линейкой измерим расстояние так, как показано на рисунке.
- Измеренное расстояние будет точно соответствовать длине диагонали кирпича.
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
План урока:
Понятие пирамиды
Правильная пирамида
Усеченная пирамида
Типичные задачи на пирамиды
Понятие пирамиды
Построим на некоторой плос-ти α произвольный многоугольник А1А2…Аn. Далее отметим в пространстве точку Р, не принадлежащую плос-ти α. Соединив точку Р с вершинами многоуг-ка получим многогранник, который именуется пирамидой (в различной литературе может использоваться сокращение пирам-а).
Та единственная точка Р, не находящаяся в одной плос-ти со всеми остальными вершинами, именуется вершиной пирам-ы. Многоугольник, образованный остальными вершинами – это основание пирамиды.
Основанием пирам-ы может быть многоугольник с любым количеством сторон. Если в основании лежит, например, пятиугольник, то и пирам-у называют пятиугольной. Если же в основании находится десятиугольник, то это будет уже десятиугольная пирам-а. В общем случае пирам-у, у которой в основании располагается n-угольник, именуется n-угольной. Ясно, что треугольная пирам-а и тетраэдр – это по сути одна и та же фигура.
Все грани пирам-ы, за исключением ее основания, именуются боковыми гранями. Понятно, что каждая боковая грань – это треугольник. Ребра пирамиды, выходящие из ее вершины, именуются боковыми ребрами пирамиды.
Посчитаем количество ребер, вершин и граней пирам-ы. Если она n-угольная, то у неё (n + 1) вершин (n точек в основании и ещё одна точка, не лежащая в основании). Также у нее (n + 1) граней, из них одна – это основание, а остальные n – боковые грани пирамиды (по одной на каждую сторону n-угольника). Наконец, у пирам-ы n ребер находятся в плос-ти основания, а ещё n ребер являются боковыми. Итого имеем 2n ребер. Теперь можно убедиться, что теорема Эйлера для пирам-ы выполняется:
Из вершины пирам-ы можно опустить перпендикуляр на плос-ть основания. Он будет именоваться высотой пирамиды.
Как и в случае с призмой, можно подсчитать площадь боковой поверхности призмы, которую обозначают как Sбок. Если же к ней ещё добавить и площадь основания (Sосн), то в сумме получится уже площадь полной поверхности призмы (Sполн). Эту связь между величинами можно представить в виде формулы:
Правильная пирамида
Особый интерес и в геометрии, и в реальной жизни представляют так называемые правильные пирамиды. Их отличают две особенности:
1) в их основании находится правильный многоугольник;
2) высота пирам-ы падает на основание в точке, являющейся центром этого правильного многоуг-ка.
Напомним, что центром правильного многоуг-ка считается центр описанной около него окружности, который одновременно является и центром вписанной окружности.
Действительно, опустим из вершины Р правильной пирам-ы высоту РО. Тогда О будет центром описанной окружности:
Примечание. На рисунках, показывающих объемные фигуры, окружности искажают свою форму и выглядят как эллипсы, то есть овалы.
Построим из О радиусы ОА1, ОА2, ОА3,… Они все будут одинаковы, ведь это радиусы одной и той же окружности. Также заметим, что высота правильной пирамиды РО будет перпендикулярна каждому из этих радиусов, ведь она перпендикулярна и всей плос-ти. Это значит, что ∆РОА1, ∆РОА2, ∆РОА3… – прямоугольные. При этом у них есть общий катет РО, а катеты ОА1, ОА2, ОА3… одинаковы. Значит, эти треугольники равны. Отсюда и вытекает, что их гипотенузы, то есть боковые ребра РА1, РА2, РА3…, также одинаковы, ч. т. д.
Заметим, что можно доказать и почти противоположное утверждение – если у пирам-ы боковые ребра одинаковы, а в основании находится правильный многоуг-к, то она является правильной. Для доказательства предположим, что ребра РА1, РА2, РА2… одинаковы. Опустим из Р высоту, которая упадет в некоторую точку О. Теперь соединим эту точку с вершинами А1, А2, А3… Получатся прямоугольные ∆РОА1, ∆РОА2, ∆РОА3… У них есть общий катет (высота РО) и одинаковые гипотенузы. Значит, эти треугольники равны, и потому одинаковы отрезки ОА1, ОА2, ОА3… Это значит, что точка О равноудалена от вершин многоуг-ка, и если из нее провести окружность радиусом ОА1, то она также пройдет через остальные вершины многоуг-ка. То есть эта окружность окажется описанной. Это и означает, что точка О – центр многоуг-ка, и тогда вся пирам-а оказывается по определению правильной.
Из равенства боковых ребер напрямую вытекает и тот факт, что все боковые грани правильной пирам-ы – одинаковые равнобедренные треугольники. Высоты, проведенные в этих равнобедренных треугольниках к основанию правильной пирамиды, именуются апофемами.
Ещё раз уточним, что понятие апофемы применимо только к правильной пирам-е. У других пирамид тоже можно на боковых гранях провести высоты к основанию, но они просто не будут называться апофемами пирамиды.
Ясно, что раз в правильной пирам-е все боковые грани – равные друг другу равнобедренные треуг-ки, то и их высоты, то есть апофемы, одинаковы. Также можно утверждать, что каждая апофема делит ребра, на которое она падает, пополам, ведь высоты в равнобедренном треуг-ке – это ещё и медианы.
Апофема используется для вычисления площади боковой поверхности пирам-ы, так как существует такая теорема:
Докажем ее. Пусть у правильной n-угольной пирам-ы в основании находится многоуг-к со стороной а. Тогда его периметр Р вычисляется так:
Каждая боковая грань пирам-ы – это треугольник. Проведем на них апофемы, которые одновременно окажутся и высотами для этих треугольников. Если мы обозначим длину апофемы как d, то площадь каждой грани можно рассчитать по простейшей формуле площади треугольника:
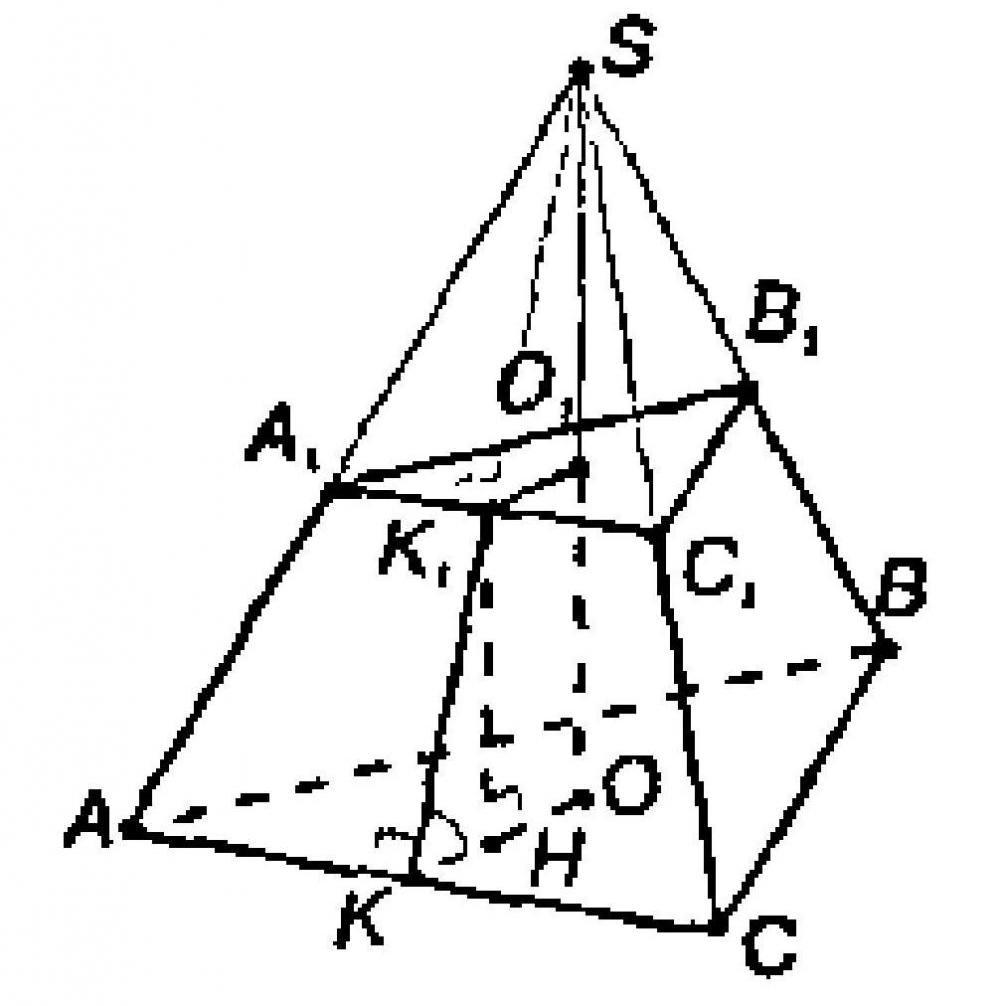
Усечённая пирамида
Возьмем произвольную пирам-у, а далее секущую плоскость, которая будет параллельна основанию, причем она будет пересекать ребра РА1, РА2, РА3… в точках В1, В2, В3… соответственно. В результате, отбросив «верхушку» пирам-ы, мы получим новую фигуру, которая именуется усеченной пирамидой.
У усеченной пирам-ы уже не одна, а две грани считаются основаниями, и они параллельны друг другу. Большее из них именуют нижним основанием, а меньшее – верхним основанием.
Докажем, что боковые грани любой усеченной пирам-ы – это трапеции. Действительно, обозначим плос-ть верхнего основания как α, нижнее основание как β, а произвольную грань как γ:
Нам надо доказать, что А1А2В2В1 – это трапеция. Действительно, прямые А1А2 и В1В2 не могут скрещиваться, ведь они располагаются в единой плос-ти γ. Не могут они и пересекаться, ведь тогда точка их пересечения была бы общей для плос-тей α и β, а эти плос-ти параллельны. Остается один вариант: А1А2||В1B2. Две другие стороны грани, А1В1 и А2В2, будут пересекаться в точке Р, вершине исходной пирам-ы. Тогда по определению две четырехугольник А1А2В2В1 будет трапецией, ведь у него две стороны параллельны, а две другие – нет.
Отдельно отметим, что усеченная пирам-а, полученная из правильной пирам-ы, также называется правильной, а высоты ее боковых граней также именуются апофемами. Докажем одну теорему:
Действительно, пусть из правильной пирам-ы с вершиной в Р получена правильная усеченная пирамида с основаниями А1А2А3…An и В1В2В3…Bn:
Так как исходная пирам-а – правильная, то ее грани – равные равнобедренные треугольники, у которых одинаковы углы при основаниях:
Мы уже знаем, что грани А1А2В2В1 и А2А3В3В2 – трапеции. Раз у них одинаковы углы при основании, то можно утверждать, что эти трапеции – равнобедренные. Это значит, что любые два боковых ребра, находящиеся на одной грани, одинаковы. Значит, одинаковы вообще все боковые ребра. Получается, что все боковые грани – это равнобедренные трапеции с одинаковыми основаниями, боковыми сторонами и углами при основании. Этого достаточно для того, чтобы считать эти трапеции равными, ч. т. д.
Из этой теоремы вытекает тот факт, что стороны многоуг-ка, образующего верхнее основание, одинаковы. Более того, углы этого многоуг-ка равны таким же углам в нижнем основании. Например, ∠А1А2А3 = ∠В1В2В3. Действительно, мы знаем, что А1А2||В1В2 и А2А3||B2B3, и потому стороны углов ∠А1А2А3 = ∠В1В2В3 оказываются сонаправленными лучами.
Так как в нижнем многоуг-ке А1А2А3…An все углы одинаковы (ведь он правильный), то и в верхнем многоуг-ке В1В2В3…Bn также будут одинаковы углы. В итоге можно утверждать, что верхнее основание усеченной пирамиды является правильным многоуг-ком, также как и нижнее.
Отметим ещё один факт. При построении секущей плос-ти пирам-а делится на две части. Нижняя из них – это усеченная пирам-а, а верхняя – это обычная пирам-а, меньшая исходной. Докажем, что если исходная пирам-а РА1А2А3…Рn была правильной, то оставшаяся после отсечения «верхушка» также будет правильной пирам-ой. Мы уже выяснили, что ее основание В1В2В3…Вn– правильный многоуг-к. Отрезки РА1, РА2, РА3… одинаковы как боковые ребра исходной правильной пирам-ы. В свою очередь отрезки А1В1, А2В2, А3В3 одинаковы как боковые ребра правильной усеченной пирам-ы. Но отсюда получается, что одинаковы также и отрезки РВ1, РВ2, РВ3… Значит, в пирам-е РВ1В2В3…Вn в основании лежит правильный многоуг-к, а ее боковые ребра одинаковы. Из этого вытекает, что эта пирам-а – правильная.
Ещё одна теорема позволяет вычислять площадь боковой поверхности правильной усеченной пирам-ы:
Действительно, каждая грань такой пирам-ы – это трапеция. Обозначим длину ее верхнего основания буквой а, а нижнего – буквой b.Тогда, если основания пирам-ы – это многоуг-ки с n сторонами, периметр этих оснований будет вычисляться так:
Теперь проведем на каждой боковой грани апофему, чья длина будет обозначаться как d. Тогда, используя формулы площади трапеции, сможем вычислить площадь грани:
Типичные задачи на пирамиды
Рассмотрим несколько задач, в которых фигурируют пирам-ы. Перед просмотром решения попытайтесь решить их самостоятельно.
Задание. Существует ли пирамида, у которой ровно 999 ребер?
Решение. Если в основании пирам-ы находится n-угольник, то у нее 2n ребер. Так как n– целое число, то 2n будет уже четным числом. То есть количество ребер у любой пирам-ы всегда четно. Поэтому не существует пирам-ы с 999 ребрами, ведь 999 – нечетное число.
Задание. Верно ли, что всякий правильный тетраэдр одновременно является и правильной пирам-ой? И наоборот, является ли каждая правильная треугольная пирам-а правильным тетраэдром?
Решение. Напомним, что правильный тетраэдр – это тетраэдр, у которого все ребра одинаковы. Если одну из вершин тетраэдра принять за вершину пирам-ы, то получится, что в ее основании равносторонний треугольник, который, как мы знаем, является правильным многоуг-ком. Также окажется, что все боковые ребра пирам-ы также одинаковы. Это значит, что она – правильная.
Теперь посмотрим на произвольную правильную треугольную пирам-у. Будет ли она обязательно правильным тетраэдром? Нет, ведь ее боковые ребра могут отличаться по длине от ребер, находящихся в основании. Например, в основании может находиться равносторонний треуг-к со стороной 5 см, а боковое ребро правильной пирамиды может иметь длину 10 см. Таким образом, можно считать правильный тетраэдр лишь частным случаем правильной пирам-ы.
Задание. В основании пирам-ы находится ромб со стороной 5 см.Одна из его диагоналей имеет длину 8 см. Высота пирам-ы имеет длину 7 см и проходит через точку, в которой пересекаются диагонали ромба. Вычислите длину боковых ребер.
Решение.
Обозначим ромб в основании как АВСD, а вершину пирам-ы буквой Р. Пусть диагонали пересекаются в точке О, тогда РО – высота. Также пусть диагональ АС равна 8 см. По свойству ромба О будет серединой диагоналей, поэтому
Отрезок OD будет иметь ту же длину 3 см, ведь О – середина BD.
Так как высота РО перпендикулярна всем прямым в плос-ти основания, то ∆АОР, ∆ВОР, ∆СОР, ∆DOP – прямоугольные, и боковые ребра пирам-ы будут гипотенузами этих треугольников. Вычислим АР по теореме Пифагора:
Задание. В основании пирам-ы лежит квадрат, а одно из ее боковых ребер перпендикулярно основанию. Одна из боковых граней образует с плос-тью основания угол в 45°. Длина длиннейшего ребра пирам-ы составляет 12 см. Определите высоту пирам-ы и площадь ее боковой поверхности.
Решение.
Обозначим квадрат, находящийся в основании, как АВСD, а вершину пирам-ы как Р. Пусть ребро PD перпендикулярно основанию. Тогда PD⊥AD и PD⊥CD. Ясно, что PD как раз и является искомой нами высотой пирам-ы.
Теперь надо понять, какие углы в пирам-е составляют 45° и какое ребро равно 12 см. Грани ADP и СDP проходят через перпендикуляр PDк основанию, а потому они перпендикулярны основанию. Значит, угол в 45° с основанием образует либо грань АВР, либо грань СВР.
Заметим, что АВ⊥AD (это смежные стороны квадрата), а AD – это проекция ребра АР на основание. Тогда по теореме о трех перпендикулярах АВ⊥АР. Аналогично из того факта, что ВС⊥СD, вытекает, что ВС⊥СР. Также заметим, что ∆ADP и ∆СDP прямоугольные, имеют общий катет PD и одинаковые катеты AD и CD (это стороны квадрата). Значит, это равные треугольники, и
∠PAD = ∠PCD
Грань АВР пересекается c основанием по прямой АВ, причем AD⊥АВ и АР⊥АВ. Значит, ∠РАD – это угол между гранью АВР и основанием. Аналогично и ∠РСD является углом между гранью СВР и основанием. Но эти углы одинаковы. Значит, каждый из этих углов будет равен 45°, иначе в пирам-е не останется угла между плос-тями, который мог бы составлять 45°.
Ясно, что ребро АР длиннее ребра РD, ведь в прямоугольном ∆ADP АР – это гипотенуза, а РD катет (гипотенуза всегда длиннее катета). Теперь заметим, что ∆РАВ и ∆РСВ – также прямоугольные, ведь АВ⊥АР и ВС⊥СР. Но в них гипотенузой является уже РВ, то есть РВ длиннее АВ, ВС, АР и РС. Так как отрезки AD и AC равны АВ как стороны квадрата, получаем, что именно ребро РВ – длиннейшее в пирам-е, то есть его длина составляет 12 см.
В прямоугольном ∆ADP∠PAD = 45°. Это значит, что ∆ADP является прямоугольным и равнобедренным, то есть AD = PD. Обозначим искомую нами длину РD как x. Теперь проведем диагональ BD:
Её длину можно вычислить из ∆ADB:
Итак, высоту нашли, теперь нужно рассчитать боковую площадь. Но для этого предварительно найдем АР из ∆АРD:
Такую же длину имеет и РС, ведь ∆АРD и ∆СРD равны.
Мы уже выяснили, что каждая боковая грань – прямоугольный треугольник. Зная длины катетов, легко найдем площадь каждой грани:
Задание. В правильной шестиугольной пирам-е ребро при основании равно 3 см. Высота этой пирам-ы составляет 4 см. Вычислите длину апофемы этой пирам-ы, а также угол, который ее боковые грани образуют с основанием.
Решение.
Основание пирам-ы обозначим как АВСDEF, а вершину как Р. Пусть РО – высота, тогда О – центр описанной окружности. Напомним, что у правильного шестиугольника радиус описанной окружности совпадает с длиной его стороны, то есть
Теперь надо найти угол между гранью АВР и основанием. Они пересекаются по прямой АВ. РН⊥АВ, ведь РН – апофема. ОН – это проекция РН на основание. Так как АВ⊥РН, то по обратной теореме о трех перпендикулярах и ОН⊥АВ. Значит, ∠ОНР и является искомым углом между гранью АВР и основанием. Для его вычисления применим тригонометрию к ∆ОНР:
Задание. В правильной шестиугольной пирам-е все ребра имеют длину, равную единице. Найдите угол между прямыми АР и BD:
Решение. Для нахождения угла между АР и BD, у которых нет общей точки, можно вычислить угол между прямыми, которые будут им параллельны. Легко заметить, что АЕ||BD. Докажем это, рассмотрев основание пирам-ы:
Каждый угол правильного шестиугольника составляет 120°. В частности, это относится к ∠F и ∠С. ∆АFЕ – равнобедренный, ведь его стороны FE и AF одинаковы. Тогда и углы при основании будут одинаковыми. Найдем их:
Аналогично можно определить, что все углы четырехугольника АВDE прямые, то он представляет собой прямоугольник. Его противоположные стороны параллельны, в частности, АЕ||BD. Это означает, что искомый нами угол – это ∠РАЕ:
Для его вычисления необходимо вычислить длины сторон ∆РАЕ. Ребра РА и РЕ по условию равны единице. Длину ЕА найдем из ∆FAE, применив теорему косинусов:
Задание. В правильной шестиугольной пирам-е боковые ребра имеют длину 2, а ребра в основании равны 1. Вычислите угол между плос-тями РFA и PDE:
Решение. Сначала надо найти прямую, по которой эти две грани пересекаются. Мы видим одну их общую точку – Р. Продолжим ребра FA и ED до тех пор, пока они не пересекутся в некоторой точке К. Эта точка K также будет общей для плос-тей, проходящих через грани PFA и РЕD. Значит, они пересекаются по прямой РК:
Найдем углы в ∆КЕF, помня при этом, что все в шестиугольнике АВСDEF составляют по 120°:
Получили, что все углы в ∆КЕF составляют по 60°, то есть он равносторонний, и поэтому стороны KE и KF одинаковы. Но также одинаковы и грани FA и DE. Отсюда получаем и равенство отрезков АК и DK:
Теперь сравним ∆АРК и ∆KPD. КР – их общая сторона, АР = РD как боковые ребра правильной пирам-ы, и АК = DK. Получается, что эти треугольники равны.
Далее в ∆АРК опустим высоту АН. Из равенства ∆АРК и ∆KPD вытекает, что и HD будет высотой в ∆PHD, ведь в равных треугольниках высоты должны делить равные стороны в одном и том же отношении. Тогда по определению двугранного угла ∠AHD и будет искомым углом между гранями, ведь KP – линия их пересечения, АН⊥KP и DH⊥KP.
∆AKP – равнобедренный, ведь отрезки АК и АР оказались одинаковыми. Значит, АН не только высота, но и медиана. Поэтому
Отрезок AD окажется диаметром окружности, описанной около шестиугольника. Мы знаем, что радиус такой окружности равен длине стороны шестиугольника, то есть единице. Тогда диаметр будет вдвое больше:
Сегодня мы познакомились с ещё одним видом многогранника –пирамидой. Они нередко встречаются в задачах ЕГЭ, посвященных стереометрии. Особо часто используются правильные пирамиды, поэтому важно помнить их основные свойства.
Пирамида и ее боковые ребра. Формулы. Боковое ребро пирамиды Хеопса
Одной из геометрических фигур, свойства которых изучают в школах в курсе стереометрии, является пирамида. Рассмотрим, что собой представляет эта фигура, а также подробно охарактеризуем важный линейный параметр — боковое ребро пирамиды.
Пирамида как фигура геометрии
Прежде чем рассматривать понятие о боковом ребре пирамиды, следует дать определение этой пространственной фигуры. Если говорить коротко, то пирамида представляет собой поверхность, ограниченную одним n-угольником и n треугольниками. Рисунок ниже показывает один из возможных вариантов этой фигуры.
С геометрической точки зрения получить пирамиду можно таким способом: взять n-угольник и соединить все его углы с некоторой точкой в пространстве, которая не должна лежать в плоскости n-угольника.
Заметим, что, независимо от количества сторон n в исходном многоугольнике, всегда при соединении его углов с единственной точкой получаются треугольники. Их совокупность образует боковую поверхность пирамиды, а исходный многоугольник является ее основанием. Точка, в которой соединяются все треугольники, получила название вершины пирамиды.
Элементы пирамиды
Каждая пирамида образована тремя главными элементами:
- гранями;
- ребрами;
- вершинами.
Граней или сторон у фигуры всегда n + 1. Это легко видеть на приведенном в предыдущем пункте рисунке. Шестиугольное основание является одной гранью. Оставшиеся 6 сторон представляют собой треугольники, опирающиеся на стороны основания и пересекающиеся в вершине пирамиды.
Ребра представляют собой совокупность точек пересечения соседних граней. Фигура имеет два типа этих элементов:
- ребра основания;
- боковые ребра пирамиды.
Их количества, независимо от числа сторон n основания, всегда равны друг другу, то есть фигура имеет 2 × n ребер. Если с ребрами основания все понятно (они являются сторонами n-угольника), то для боковых ребер следует уточнить, что они представляют собой отрезки, соединяющие углы основания с высотой рассматриваемой фигуры.
Наконец, третьим типом элементов пирамиды будут вершины. У фигуры имеется n + 1 вершина. Однако n из них образованы основанием и двумя боковыми гранями. Лишь одна единственная вершина не связана с основанием. Она играет важную роль при изучении количественных характеристик пирамиды, например, ее высоты или апофемы.
Правильные пирамиды
Пирамиды могут быть наклонными и прямыми, правильными и неправильными, выпуклыми и вогнутыми. Все названные типы фигур отличаются друг от друга многоугольным основанием и особенностями поведения высоты.
Предположим, что имеется пирамида, у которой высота (опущенный из вершины к основанию перпендикуляр) падает на многоугольник точно в его геометрическом центре. В этом случая фигура называется прямой. Если же многоугольник является равносторонним, то помимо прямой, пирамида также будет правильной. Напомним, что центр геометрический плоской фигуры аналогичен центру масс в физике. Для квадрата он совпадает с точкой пересечения диагоналей, а для треугольника — с точкой, где медианы пересекаются.
Пирамиды правильные удобно изучать ввиду их симметрии. Так, боковые ребра правильной пирамиды и ее боковые грани равны друг другу. Частным случаем является ситуация, когда боковые грани будут образованы равносторонними треугольниками.
Далее рассмотрим, какими формулами следует пользоваться, чтобы определить размеры боковых ребер пирамид — правильной четырехугольной и треугольной.
Треугольная пирамида
Существуют четыре линейных параметра, которые описывают размеры правильной пирамиды. К ним относятся сторона основания a, боковое ребро b, высота h и апофема hb. Ниже приведем формулы, которые позволяют рассчитать длину бокового ребра для треугольной пирамиды правильной. Основание этой фигуры представляет треугольник с равными сторонами, что позволяет записать следующие равенства:
Обе формулы являются следствием теоремы Пифагора для треугольников, в которых боковое ребро b является гипотенузой.
Четырехугольная пирамида
Эта фигура, пожалуй, является самой известной среди остальных пирамид благодаря величественным древним египетским сооружениям. Боковое ребро пирамиды четырехугольной правильной можно определить по таким формулам:
Как и в предыдущем случае, эти выражения являются следствием свойства катетов и гипотенузы прямоугольного треугольника.
Отметим, что формула расчета бокового ребра правильной пирамиды четырехугольной через ее апофему и сторону основания аналогична таковой для треугольной фигуры. Это совпадение не является случайным, поскольку боковые грани обеих пирамид — это равнобедренные треугольники.
Задача на определение бокового ребра пирамиды Хеопса
Каждый человек знает, что первое чудо света — пирамида Хеопса, обладает головокружительными размерами. Она является самой большой из всех пирамид, находящихся в египетской Гизе. Стороны ее основания образуют квадрат с точностью до нескольких десятков сантиметров. Средняя длина стороны пирамиды оценивается в 230,363 метра. Высота пирамиды в настоящее время составляет около 137 метров, однако исходная высота каменного гиганта была 146,50 метров.
Воспользуемся приведенными выше цифрами, чтобы определить, чему равно боковое ребро правильной пирамиды четырехугольной, посвященной фараону Хеопсу.
Поскольку нам известна высота h и длина стороны a монумента, то следует применить такую формулу для b:
Подставляя в нее известные данные, получаем, что боковое ребро правильной четырехугольной пирамиды равно 273 метра, что немногим меньше периметра футбольного поля (300 метров).
Формулы и свойства правильной треугольной пирамиды. Усеченная треугольная пирамида
Объемной фигурой, которая часто появляется в геометрических задачах, является пирамида. Самая простая из всех фигур этого класса — треугольная. В данной статье разберем подробно основные формулы и свойства правильной пирамиды треугольной.
Геометрические представления о фигуре
Прежде чем переходить к рассмотрению свойств правильной пирамиды треугольной, разберемся подробнее, о какой фигуре идет речь.
Предположим, что имеется произвольный треугольник в трехмерном пространстве. Выберем в этом пространстве любую точку, которая в плоскости треугольника не лежит, и соединим ее с тремя вершинами треугольника. Мы получили треугольную пирамиду.

Она состоит из 4-х сторон, причем все они являются треугольниками. Точки, в которых соединяются три грани, называются вершинами. Их у фигуры также четыре. Линии пересечения двух граней — это ребра. Ребер у рассматриваемой пирамиды 6. Рисунок ниже демонстрирует пример этой фигуры.
Поскольку фигура образована четырьмя сторонами, ее также называют тетраэдром.
Правильная пирамида
Выше была рассмотрена произвольная фигура с треугольным основанием. Теперь предположим, что мы провели перпендикулярный отрезок из вершины пирамиды к ее основанию. Этот отрезок называется высотой. Очевидно, что можно провести 4 разные высоты для фигуры. Если высота пересекает в геометрическом центре треугольное основание, то такая пирамида называется прямой.
Прямая пирамида, основанием которой будет треугольник равносторонний, называется правильной. Для нее все три треугольника, образующих боковую поверхность фигуры, являются равнобедренными и равны друг другу. Частным случаем правильной пирамиды является ситуация, когда все четыре стороны являются равносторонними одинаковыми треугольниками.
Рассмотрим свойства правильной пирамиды треугольной и приведем соответствующие формулы для вычисления ее параметров.
Сторона основания, высота, боковое ребро и апотема
Любые два из перечисленных параметров однозначно определяют остальные две характеристики. Приведем формулы, которые связывают названные величины.
Предположим, что сторона основания треугольной пирамиды правильной равна a. Длина ее бокового ребра равна b. Чему будут равны высота правильной пирамиды треугольной и ее апотема.
Для высоты h получаем выражение:
Эта формула следует из теоремы Пифагора для прямоугольного треугольника, сторонами которого являются боковое ребро, высота и 2/3 высоты основания.
Апотемой пирамиды называется высота для любого бокового треугольника. Длина апотемы ab равна:
Из этих формул видно, что какими бы ни были сторона основания пирамиды треугольной правильной и длина ее бокового ребра, апотема всегда будет больше высоты пирамиды.
Представленные две формулы содержат все четыре линейные характеристики рассматриваемой фигуры. Поэтому по известным двум из них можно найти остальные, решая систему из записанных равенств.
Объем фигуры
Для абсолютно любой пирамиды (в том числе наклонной) значение объема пространства, ограниченного ею, можно определить, зная высоту фигуры и площадь ее основания. Соответствующая формула имеет вид:
Применяя это выражение для рассматриваемой фигуры, получим следующую формулу:
Где высота правильной треугольной пирамиды равна h, а ее сторона основания — a.
Не сложно получить формулу для объема тетраэдра, у которого все стороны равны между собой и представляют равносторонние треугольники. В таком случае объем фигуры определится по формуле:
То есть он определяется длиной стороны a однозначно.
Площадь поверхности
Продолжим рассматривать свойства пирамиды треугольной правильной. Общая площадь всех граней фигуры называется площадью ее поверхности. Последнюю удобно изучать, рассматривая соответствующую развертку. На рисунке ниже показано, как выглядит развертка правильной пирамиды треугольной.
Предположим, что нам известны высота h и сторона основания a фигуры. Тогда площадь ее основания будет равна:
Получить это выражение может каждый школьник, если вспомнит, как находить площадь треугольника, а также учтет, что высота равностороннего треугольника также является биссектрисой и медианой.
Площадь боковой поверхности, образованной тремя одинаковыми равнобедренными треугольниками, составляет:
Данное равенство следует из выражения апотемы пирамиды через высоту и длину основания.
Полная площадь поверхности фигуры равна:
S = So + Sb = √3/4*a2 + 3/2*√(a2/12+h2)*a
Заметим, что для тетраэдра, у которого все четыре стороны являются одинаковыми равносторонними треугольниками, площадь S будет равна:
Свойства правильной усеченной пирамиды треугольной
Если у рассмотренной треугольной пирамиды плоскостью, параллельной основанию, срезать верх, то оставшаяся нижняя часть будет называться усеченной пирамидой.
В случае правильной пирамиды с треугольным основанием в результате описанного метода сечения получается новый треугольник, который также является равносторонним, но имеет меньшую длину стороны, чем сторона основания. Усеченная треугольная пирамида показана ниже.
Мы видим, что эта фигура уже ограничена двумя треугольными основаниями и тремя равнобедренными трапециями.
Предположим, что высота полученной фигуры равна h, длины сторон нижнего и верхнего оснований составляют a1 и a2 соответственно, а апотема (высота трапеции) равна ab. Тогда площадь поверхности усеченной пирамиды можно вычислить по формуле:
S = 3/2*(a1+a2)*ab + √3/4*(a12 + a22)
Здесь первое слагаемое — это площадь боковой поверхности, второе слагаемое — площадь треугольных оснований.
Объем фигуры рассчитывается следующим образом:
V = √3/12*h*(a12 + a22 + a1*a2)
Для однозначного определения характеристик усеченной пирамиды необходимо знать три ее параметра, что демонстрируют приведенные формулы.
Геометрические фигуры. Правильная пирамида.
Правильная пирамида — когда основанием пирамиды является правильный многоугольник, а высота проецируется в центр основания (или проходит через него).
В правильной пирамиде все боковые ребра имеют одинаковую величину, и каждая боковая грань является равнобедренными треугольниками одного размера.
Правильная пирамида обладает следующими свойствами:
Формулы для правильной пирамиды.
V — объем пирамиды,
S — площадь основания пирамиды,
h — высота пирамиды,
Sb — площадь боковой поверхности пирамиды,
a — апофема (не путать с α) пирамиды,
P — периметр основания пирамиды,
n — число сторон основания пирамиды,
b — длина бокового ребра пирамиды,
α — плоский угол при вершине пирамиды.
Ниже указанная формула определения объема используется лишь для правильной пирамиды:
V — объем правильной пирамиды,
h — высота правильной пирамиды,
n — количество сторон правильного многоугольника, основания правильной пирамиды,
a — длина стороны правильного многоугольника.
Боковое ребро правильной пирамиды находят по формуле:
где b — боковое ребро правильной пирамиды (SA, SB, SC, SD либо SE),
n — количество сторон правильного многоугольника (основание правильной пирамиды),
a — сторона правильного многоугольника (AB, BC, CD, DE либо EA) — основания правильной пирамиды,
h — высота правильной пирамиды (OS).
Указания к решению задач. Свойства, которые мы перечислили выше, помогают при практическом решении. Когда нужно определить углы наклона граней, их поверхность и так далее, значит общая методика сводится к разбиению всей объемной фигуры на отдельные плоские фигуры и применение их свойств для определения отдельных элементов пирамиды, так как большинство элементов оказываются общими для нескольких фигур.
Нужно разбить всю объемную фигуру на отдельные элементы — треугольники, квадраты, отрезки. Дальше, к отдельным элементам применяем знания из курса планиметрии, что очень упрощает определение ответа.
Правильная треугольная пирамида.
Правильная треугольная пирамида — это пирамида, у которой основанием оказывается правильный треугольник, а вершина опускается в центр основания.
Формулы для правильной треугольной пирамиды.
Формула для нахождения объема правильной треугольной пирамиды:
V — объем правильной пирамиды, которая имеет в основании правильный (равносторонний) треугольник,
h — высота правильной пирамиды,
a — длина стороны основания правильной пирамиды.
Так как правильная треугольная пирамида — это частный случай правильной пирамиды, значит, формулы, верные для правильной пирамиды, оказываются верными и для правильной треугольной.
Еще одним частным случаем правильно пирамиды является тетраэдр.
http://1ku.ru/obrazovanie/41519-formuly-i-svojstva-pravilnoj-treugolnoj-piramidy-usechennaja-treugolnaja-piramida/
http://www.calc.ru/Geometricheskiye-Figury-Pravilnaya-Piramida.html



 54 : 6 x 3 : 90 + 34 + 51 x 20 x 2 : 12 — 180 — 56 = … И = … П = … А 3) 200 : 4 6) 4 x 40 + 70 + 260 x 5 : 6 – 240 — 45 = … А = … Р
54 : 6 x 3 : 90 + 34 + 51 x 20 x 2 : 12 — 180 — 56 = … И = … П = … А 3) 200 : 4 6) 4 x 40 + 70 + 260 x 5 : 6 – 240 — 45 = … А = … Р