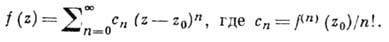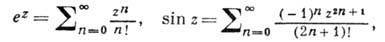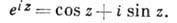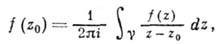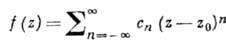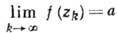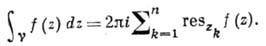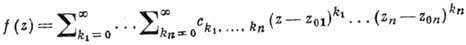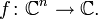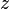Математический
аппарат квантовой механики
Со школьных времен
вам знакомо понятие функции:
функция – это правило, согласно которому
всякому числу
x
(из области определения) ставится в
соответствие число
y.
Нам в нашем курсе понадобятся функции,
вообще говоря, комплексные, отвечающие
требованиям регулярности:
они должны быть конечны
во всей области определения, однозначны
и непрерывны.
Эти условия необходимы (хотя и недостаточны)
для выполнения еще одного важного
требования: эти функции должны быть
квадратично
интегрируемы,
т.е. если
– регулярная функция, а *
– ее комплексно сопряженную, то интеграл
должен
иметь конечное значение.
Если такой интеграл
равен единице, функцию называют
нормированной.
Пару функций, для
которых
,
называют ортогональными.
2. Операторы
При обсуждении
законов квантовой механики наряду с
функциями удобно ввести еще один класс
математических объектов – операторы.
Оператор – это
правило, согласно которому уже каждой
функции f
ставится в соответствие другая функция
.
(обратите внимание:
операторы часто обозначают такой
«шляпкой»). Пусть, например, оператор
задает дифференцирование функции. Тогда
для функции
действие
такого оператора даст
,
т.е. наш оператор переводит функцию sin
x
в новую функцию cos
x.
Все ли понимают,
что на другую функцию этот оператор
будет действовать по-другому? Например,
во что превратится функция u(x)
= sin 2x?
Понятно, что не на
всякую функцию можно подействовать
оператором. Так, наш оператор
дифференцирования можно применять
только к дифференцируемым функциям.
Кстати, а кто-нибудь
может привести пример недифференцируемой
функции? Ну, например, y(x)
= | x
|. Заодно запомним: Не всякая непрерывная
функция дифференцируема, а любая
дифференцируемая функция непрерывна.
Поэтому, задавая
оператор, определяют класс функций, на
которые он действует. Говорят, что
оператор
определен
на классе
дифференцируемых функций.
Приведем еще
несколько примеров.
-
Пусть f(x)
– функция одной переменной, а оператор
.
Тогда
.
Действие оператора сводится к умножению
функции на аргумент. -
Действие оператора
приводит
к
. -
Заметим, что наша
функция может быть функцией многих
переменных, тогда
,
оператор
задает
дифференцирование по переменной x.
Вы, наверное,
догадываетесь, что функцию можно
подвергнуть и нескольким преобразованиям.
Определим сумму
операторов как
.
Под произведением
операторов будем понимать
.
Пусть, например,
,
,
тогда
.
При этом произведение
,
т.е. умножение
операторов некоммутативно.
Оператор (AB
– BA),
обозначаемый [A,B],
называется коммутатором. Если [A,B]
= 0, то говорят, что операторы коммутируют.
Найдем коммутатор
наших операторов
:
.
Таким
образом, коммутатор равен 1.
Полезно ввести
понятия единичного
оператора, такого, что для любой функции
,
и обратного
оператора А–1,
такого что А–1А
= AA–1
= I.
3. Линейные операторы.
В квантовой механике
нам придется иметь дело только с линейными
операторами, т.е. с такими, что
и
Эти условия можно
объединить, и записать:
Легко видеть, что
оператор дифференцирования линеен, а
оператор возведения в квадрат – нет.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
-
-
August 20 2009, 21:49
Listens: Phantom of the opera
- IT
- Cancel
ТФКП. Найти регулярную (аналитическую) функцию по заданой мнимой части
Найти регулярную фунцию f(z)=u(x,y)+iv(x,y), для которой
и
Аналитическую функцию можно будет восстановить, если мнимая часть будем гармонической функцией, т.е если для нее будет выполнятся уравнение Лапласа.
Необходимо найти частные производные функции v. Можно это делать и в таком виде, но удобне перейти в полярные координаты.
В полярных координатах уравнение Лапласа выглядит, как
Получится
Находим частные производные первого и второго порядков
Найдем теперь сумму
Функция v гармоническая. Теперь можно восстанавливать регулярную функцию.
Запишем условие Коши-Римана для полярных координат.
Получаем систему
Из первого уравнения
И тогда
Откуда
И тогда фунция u
Или, переходя в обратно в декартовы координаты
Тогда регулярная фунция f
Впринипе, фунция f найдена, но будет лучше если она будет зависить от z. Для этого рассмотрим эту функцию на оси OX. Тогда y=0.
Получим
И теперь обратно, x=z. Получаем
Теперь найдем f(i)
И ответ
§ 12. СВОЙСТВА РЕГУЛЯРНЫХ ФУНКЦИЯ 93
Из теоремы
2 и п. 3 § 7 вытекает
Следствие 5. Гармоническая в области функция бесконечно
дифференцируема.
3. Достаточные условия
регулярности. Теорема 1 утверждает, что достаточным условием регулярности
функции /(z) в области D является дифференцируемость этой функции. Рассмотрим
другие достаточные условия.
Теорема 3 (теорема Морера). Пусть
функция /(z) непрерывна в односвязной области D и пусть интеграл от функции
f(z) no любому замкнутому контуру, лежащему в D, равен нулю. Тогда
функция f(z)
регулярна в области D.
Доказательство. В силу следствия
3 § 9 функция f(z) имеет
первообразную, т. е. существует дифференцируемая функция F(z) такая, что F'(z)==f(z)
для всех z e D. Согласно теореме 1
функция F (г) регулярна в области D, и,
следовательно, ее производная—регулярная в D функция, т. е. функция/(z)== == F’ (z) регулярна в области D.
Теорема 4 (первая теорема
Вейерпгтрасса). Пусть функции fn[z) (п = 1, 2, …) регулярны в области D, и пусть ряд
/(г)
=2/„(г) (9)
n=l
равномерно
сходится в каждой замкнутой области, лежащей в D. Тогда функция /(z) регулярна в D.
Доказательство. Пусть Zo — произвольная точка области D.
Рассмотрим круг К: lz—Zol <
б, лежащий вместе со своей границей в области D. По условию, ряд (9)
равномерно сходится в К, а значит, и в К. Кроме того, функции /n(z) (п == = 1, 2, …) регулярны и, следовательно,
непрерывны в К. Поэтому функция /(z) непрерывна в К как сумма
равномерно сходящегося ряда, составленного из непрерывных функций.
Пусть «f — любой замкнутый контур, лежащий в
круге К. Интегрируя почленно равномерно сходящийся на у ряд (9),
получаем
f/(z)dz=
I J/„(z)dz. , «=i„
По
интегральной теореме Коши /n(z)riz==0 (га = 1, 2, …) и,
Г v следовательно, ) / (z) dz
= 0. В силу теоремы Морера, функция
v
/(z) регулярна в круге К и, в частности, в точке Zy. Так как Zo—произвольная
точка области D, то функция /(z) регулярна в области D. Теорема
доказана.
94 ГЛ. II. РЕГУЛЯРНЫЕ ФУНКЦИИ
Теорема 5 (вторая теорема
Вейерштрасса). В условиях предыдущей теоремы ряд (9) можно дифференцировать
почленно любое число раз. Получаемые при этом ряды равномерно сходятся в каждой
замкнутой области Д, лежащей в области D.
Мы ограничимся формулировкой второй теоремы Вейерштрасса
(доказательство ее содержится, например, в .[11]).
Другие достаточные условия регулярности, относящиеся к
интегралам, зависящим от параметра, будут даны в § 15.
В заключение п. 3 приведем краткую сводку основных свойств
регулярных функций. Заметим, что наряду с термином «регулярная функция» в
литературе используются другие эквивалентные термины:
{регулярная функция} ^{голоморфная функция}==
^{однозначная аналитическая функция}.
Критерии (необходимые
и достаточные условия} регулярности функции f(z) в области D:
1) дифференцируемость функции /(z)
в области D;
2) условия Коши — Римана.
Достаточные условия
регулярности функции /(z) в области D дают теорема Морера и первая
теорема Вейерштрасса. Свойства регулярных функций:
1) сумма, разность, произведение
регулярных функций /(z) и g'(z),
а также их частное (при g(z)^O) и суперпозиция являются регулярными функциями;
2) регулярная функция бесконечно
дифференцируема;
3) для регулярной функции
справедливы интегральная теорема Коши и интегральная формула Коши;
4) первообразная регулярной в одпосвязной
области функции регулярна.
4. Некоторые приемы разложения
в степенной ряд. Всякая функция /(z), регулярная в круге |z—а|<р,
разлагается в сходящийся в этом круге (см. следствие 3 из теоремы 1) степенной
ряд
/(z)= 1с„(2-а)», (10)
Asked
3 years, 11 months ago
Viewed
48 times
$begingroup$
If I am given the expression $lim_{hto 0}frac{2^{3+h}-2^3}{h}$, how do I find what $g(x)$ (or the regular function) is and what point we are evaluating the slope at (or where the tangent line will touch the curve of $g(x)$)? Online problems tend to create the limit expression using the regular function and point of the tangent rather than creating the regular function and point of the tangent from the limit expression. So I don’t really know how to approach this problem. Could someone outline their step by step process to solving problems like these, any help is appreciated.
asked Jun 8, 2019 at 1:51
$endgroup$
$begingroup$
What you have there: $$L=lim_{hto 0}frac{2^{3+h}-2^3}{h}$$ is the derivative of the the function $f(x)=2^x$ at $x=3$. Thus, this limit $L$ calculates the slope of the tangent line to $f(x)$ at $x=3$.
Your tangent line is given by $$y-f(3)=L(x-3)$$
answered Jun 8, 2019 at 1:54
coreyman317coreyman317
2,97913 silver badges43 bronze badges
$endgroup$
6
You must log in to answer this question.
Привет, сегодня поговорим про голоморфная функция, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
голоморфная функция, регулярная функция, аналитическая функция, функция комплексного переменного , настоятельно рекомендую прочитать все из категории Комплексный анализ и операционное исчисление (теория функций комплексного переменного).
голоморфная функция , иногда называемая регулярной функцией —
функция комплексного переменного , определенная на открытом подмножестве комплексной плоскости 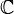
В отличие от вещественного случая, это условие означает, что функция бесконечно дифференцируема и может быть представлена сходящимся к ней рядом Тейлора.
Голоморфные функции также называют иногда аналитическими, хотя второе понятие гораздо более широкое, так как
аналитическая функция не обязана быть определена на множестве комплексных чисел. Тот факт, что для комплекснозначных функций комплексной переменной множества голоморфных и аналитических функций совпадают, является нетривиальным и весьма замечательным результатом комплексного анализа.
АНАЛИТИЧЕСКАЯ ФУНКЦИЯ (голоморфная функция) — функция f(z) комплексной переменной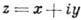
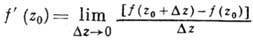
Классификация особенностей аналитическая функция позволяет во многом охарактеризовать и свойства ф-ции в целом. Ф-ции комплексной переменной использовались уже в 18 в., в частности в работах Л. Эйлера (L. Euler). Окончательно теория аналитическая функция. одной переменной оформилась в работах О. Коши (А. Саuchy), К. Вейерштрасса (К. Weierstrass) и Б.Римана (В. Riemann) в 19 в. Теория аналитическая функция. многих переменных продолжает интенсивно развиваться.
Одна из причин широкого применения аналитическая функция. в физике связана с физ. требованиями типа причинности. Так, в квантовой теории поля аналитичность Уайтмена функций и амплитуд рассеяния вытекает из исходных постулатов теории. Метод дисперсионных соотношений целиком базируется на теории аналитическая функция, ур-ния Янга — Миллса можно записать как условия аналитичности нек-рых ф-ций. Большое число приложений аналитическая функция связано также с двумерными задачами электростатики, гидродинамики и т. д., где используются, напр., конформные отображения.
Определение
Пусть 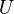
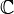
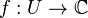
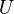
Другое определение
Определению голоморфной функции можно придать несколько другой вид, если воспользоваться операторами 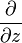
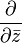
где 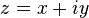
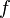
что эквивалентно условиям Коши — Римана.
История
Термин «голоморфная функция» был введен двумя учениками Коши, Брио (1817—1882) и Буке (1819—1895), и происходит от греческих слов őλoς (холос), что значит «целый», и μoρφń (морфе) — форма, образ.
Сегодня многие математики предпочитают термин «голоморфная функция» вместо «аналитическая функция», так как второе понятие более общее. Кроме того, одним из важных результатом комплексного анализа является то, что любая голоморфная функция является аналитической, что не очевидно из определения. Термин «аналитический» употребляют обычно для более общих функций, заданных не обязательно на комплексной плоскости.
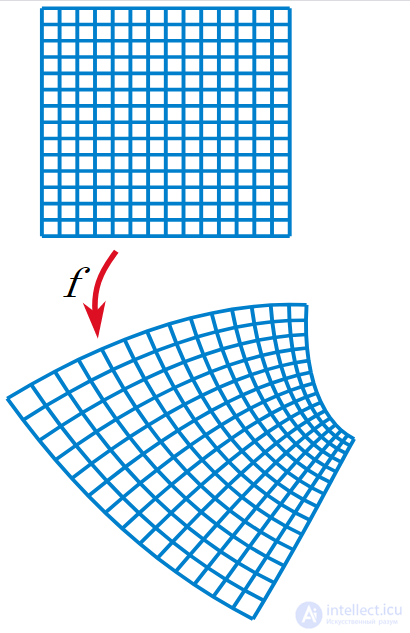
Голоморфная функция осуществляет конформное отображение, преобразуя ортогональную сетку в ортогональную (там где комплексная производная не обращается в нуль).
Связанные определения
Свойства
- Комплексная функция
является голоморфной тогда и только тогда, когда выполняются условия Коши — Римана
и частные производные 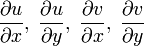
- Сумма и произведение голоморфных функций — голоморфная функция, что следует из линейности дифференцирования и выполнения правила Лейбница. Частное голоморфных функций также голоморфно во всех точках, где знаменатель не обращается в 0.
- Производная голоморфной функции опять является голоморфной, поэтому голоморфные функции являются бесконечно дифференцируемыми в своей области определения.
- Голоморфные функции являются аналитическими, то есть могут быть представлены в виде сходящегося в некоторой окрестности каждой точки ряда Тейлора . Об этом говорит сайт https://intellect.icu . Таким образом, для комплексных функций комплексной переменной множества голоморфных и аналитических функций совпадают.
- Из любой голоморфной функции можно выделить ее вещественную и мнимую часть, каждая из которых будет решением уравнения Лапласа в
. То есть если
— голоморфная функция, то
и
— гармонические функции.
- Если абсолютная величина голоморфной функции достигает локального максимума во внутренней точке своей области определения, то функция постоянна (предполагается, что область определения связна). Отсюда следует, что максимум (и минимум, если он не равен нулю) абсолютной величины голоморфной функции могут достигаться лишь на границе области.
- В области, где первая производная голоморфной функции не обращается в 0, а функция однолистна, она осуществляет конформное отображение.
- Интегральная формула Коши связывает значение функции во внутренней точке области с ее значениями на границе этой области.
- С алгебраической точки зрения, множество голоморфных на открытом множестве функций — это коммутативное кольцо и комплексное линейное пространство. Это локально выпуклое топологическое векторное пространство с полунормой, равной супремуму на компактных подмножествах.
- Согласно теореме Вейерштрасса, если ряд голоморфных функций в области
равномерно сходится на любом компакте в
то его сумма также голоморфна, причем ее производная является пределом производных частичных сумм ряда .
Основные свойства. Если 
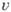
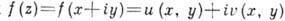
из к-рых следует, что 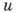
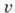
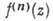
Радиус сходимости этого ряда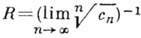
Пример: для распространенных элементарных ф-ций ez, sin z и cos z имеют место след. разложения в точке z0=0:
из к-рых, в частности, вытекает ф-ла Эйлера
Специфичны и интегральные св-ва А. ф. Если замкнутый контур Y целиком лежит в области аналитичности D ф-ции / (z) и там его можно стянуть в точку, то интеграл от /(z) по этому контуру равен нулю. Это свойство также вполне характеризует А. ф.: если 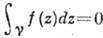
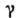
справедливая для любой точки z0, к-рая лежит в области, ограниченной контуром 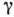
Для А. ф. имеет место принцип максимума модуля, согласно к-рому модуль А. ф., отличной от постоянной, не может достигать своего макс. значения ни в какой внутр. точке области аналитичности D. Напр., если А. ф. задана в единичном шаре 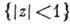
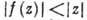
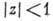
Пусть f(z) аналитична в секторе 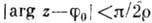
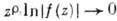
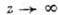
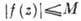
Понятие аналитичности имеет смысл также и на множествах более сложных, чем области комплексной плоскости С, но локально устроенных как последние. Напр., добавляя к С бесконечно удаленную точку, получают расширенную комплексную плоскость С. Комплексная структура в окрестности бесконечно удаленной точки задается отображением 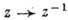
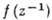
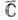
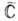
Особые точки. Точки, в к-рых нарушается аналитичность ф-ции f(z), наз. ее особыми точками. Если f(z) аналитична во всех точках нек-рой окрестности точки z0, кроме, быть может, ее самой, то z0 наз. изолиров. особой точкой. В окрестности изолиров. особой точки f(z) разлагается в абсолютно сходящийся ряд Лорана, содержащий, быть может, отрицат. степени (z-z0):
Различают три типа изолиров. особых точек: устранимую особую точку, полюс и существенно особую точку. Точка z0 наз. устранимой, если f(z) ограничена в нек-рой ее окрестности. Полагая 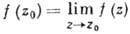
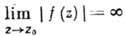
В этом случае лишь конечное число членов лорановского разложения f(z) в z0 с отрицат. степенями (z — z0) отлично от нуля. Коэф. c_j наз. вычетом функции f(z) в точке z0 и обозначается 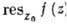

Пусть 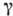
Эта формула является основой теории вычетов и служит эфф. инструментом для вычисления определ. интегралов. Ф-ция, аналитическая во всей комплексной плоскости, за исключением, быть может, полюсов, наз. мероморфной. Ф-ция, не имеющая в С особых точек, наз. целой.
Многозначные функции. Всякая А. ф. однозначно восстанавливается по своим значениям в любом сколь угодно малом открытом подмножестве области аналитичности. Более того, если две аналитические в D ф-ции совпадают в счетном числе точек из D, имеющих хотя бы одну предельную точку, также принадлежащую D, то эти ф-ции совпадают и всюду в D. Типичной является ситуация, когда А. ф. первоначально задана в нек-рой области D, но продолжается до А. ф. в существенно большей области. Т. о., возникает задача об аналитическом продолжении заданной А. ф. до А. ф. в максимально возможной области.
Чтобы эта задача была разрешима в классе однозначных ф-ций, приходится расширить понятие области, допустив возможность ее самоналожений. Это приводит к понятию неоднолистных областей, в частности римановой поверхности данной А. ф. Пусть f(z) — А. ф. в области D к 

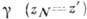
Если f(z) аналитически продолжается вдоль двух путей 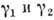
Пусть f(z) аналитична в нек-рой области D и аналитически продолжается (вообще говоря, неоднозначно) вдоль любого пути, не содержащего фиксиров. точку z0 (такая точка наз. точкой ветвления). Если провести разрез плоскости С, соединяющий точку z0 с бесконечно удаленной точкой, то можно получить конечное или счетное число ф-ций, аналитичных в плоскости С с разрезом, получающихся из f(z) аналитич. продолжением вдоль путей, огибающих z0 заданное число раз. Риманову поверхность ф-ции f(z) можно представить себе как конечное или счетное число экземпляров плоскостей С с разрезом (листов), склеенных вдоль берегов разрезов таким образом, что каждый оборот вокруг z0 переводит точку на новый лист.
А. ф., заданная в области D, наз. однолистной в D, если она осуществляет взаимно однозначное отображение D на ее образ 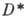

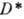
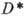

Функции многих переменных. Теория А. ф. мн. комплексных переменных по сравнению с одномерной теорией обладает новыми специфич. чертами. Ф-ция f(z), z=(z1, …, zn) наз. аналитической (голоморфной) в области D n-мерного комплексного пространства 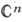
По теореме Гартогса f(z) аналитична в D тогда и только тогда, когда она аналитична по каждому переменному в отдельности при фиксированных остальных в соответствующих сечениях области D.
Важное отличие многомерной теории от одномерной состоит в существовании таких областей, что голоморфные в них ф-ции обязательно аналитически продолжаются в существенно большие области. В частности, при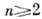
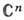
Свойство области быть областью голоморфности есть локальное свойство ее границы, обобщающее понятие выпуклости. Если D не является областью голоморфности, то все ф-ции, голоморфные в D, одноврем. продолжаются в нек-рую большую область. Вопрос об отыскании такой наибольшей области (оболочки голоморфности), как и в случае аналитич. продолжения заданной функции, приводит к многолистным областям наложения над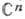
Др. пример неожиданного «принудительного» продолжения многомерных А. ф. дает теорема об острие клина (получена Н. Н. Боголюбовым в 1956), играющая важную роль в теории дисперсионных соотношений и аксиоматич. квантовой теории поля. По этой теореме две ф-ции, аналитические каждая в своей спец. вида трубчатой области и совпадающие на n-мерном чисто вещественном открытом множестве соприкосновения этих областей (т. е. на множестве вдвое меньшей размерности), аналитически продолжаются в комплексную окрестность G этого множества и представляют собой единую А. ф. Вид области G можно найти с помощью теоремы о С-выпуклой оболочке (получена В. С. Владимировым в 1964).
Вариации и обобщения
Многомерный случай
Существует также определение голоморфности функций многих комплексных переменных
Для определения используются понятия 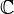
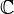
С-линейность[править ]
Функция 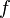
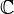
(для 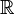
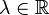
С-дифференцируемость[править ]
Функция 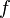
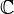
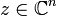
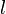

где 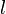
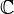
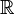
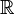
Голоморфность[править ]
Функция 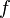
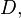
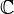
Примеры
Все полиномиальные функции от z с комплексными коэффициентами голоморфны на C , как и синус , косинус и экспоненциальная функция . (Тригонометрические функции на самом деле тесно связаны с экспоненциальной функцией и могут быть определены с помощью формулы Эйлера ). Главная ветвь функции комплексного логарифма голоморфна на множестве C ∖ { z ∈ R : z ≤ 0}. Функция квадратного корня может быть определена как
и поэтому голоморфен везде, где стоит логарифм log ( z ). Функция 1 / z голоморфна на { z : z ≠ 0}.
Как следствие уравнений Коши – Римана , вещественнозначная голоморфная функция должна быть постоянной. Таким образом, абсолютное значение г , то аргумент о г , то действительная часть из г и мнимая часть из г не голоморфны. Другой типичный пример непрерывной функции, которая не является голоморфной, — комплексно сопряженная функция z, образованная комплексным сопряжением .
Ссылки
- ↑ А. В. Домрин, А. Г. Сергеев. Лекции по комплексному анализу. Первое полугодие. — М.: МИАН, 2004. — С. 79. — ISBN 5-98419-007-9.
- ↑ Markushevich A. I., Silverman, Richard A. (ed.) Theory of functions of a Complex Variable. — М.: Американское математическое общество, 2-е изд. — ISBN 0-8218-3780-X, .
Литература
- Шабат Б. В. Введение в комплексный анализ. — М.: Наука, 1969. — 577 с.
- Титчмарш Е. Теория функций: Пер. с англ. — 2-е изд., перераб. — М.: Наука, 1980. — 464 с.
- Привалов И. И. Введение в теорию функций комплексного переменного: Пособие для высшей школы. — М.-Л.: Государственное издательство, 1927. — 316 с.
- Евграфов М. А. Аналитические функции. — 2-е изд., перераб. и дополн. — М.: Наука, 1968. — 472 с.
Вау!! 😲 Ты еще не читал? Это зря!
- Антиголоморфная функция
- Вычет
- Первообразная ( комплексный анализ )
- Антиголоморфная функция
- Биголоморфия
- Голоморфная отделимость
- Мероморфная функция
- Квадратурные области
- Гармонические карты
- Гармонические морфизмы
- Производные Виртингера
Напиши свое отношение про голоморфная функция. Это меня вдохновит писать для тебя всё больше и больше интересного. Спасибо Надеюсь, что теперь ты понял что такое голоморфная функция, регулярная функция, аналитическая функция, функция комплексного переменного
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Комплексный анализ и операционное исчисление (теория функций комплексного переменного)

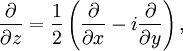
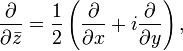
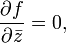
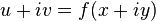 является голоморфной тогда и только тогда, когда выполняются условия Коши — Римана
является голоморфной тогда и только тогда, когда выполняются условия Коши — Римана
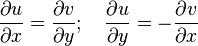
 . То есть если
. То есть если 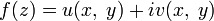 — голоморфная функция, то
— голоморфная функция, то 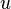 и
и 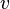 — гармонические функции.
— гармонические функции. равномерно сходится на любом компакте в
равномерно сходится на любом компакте в