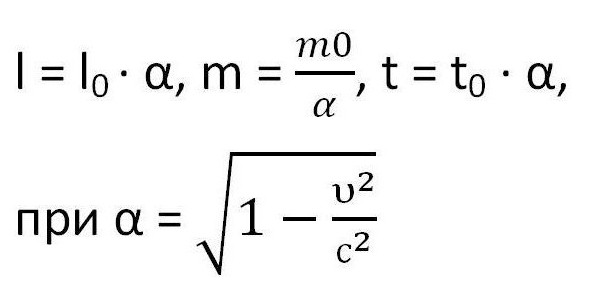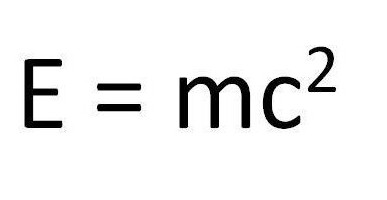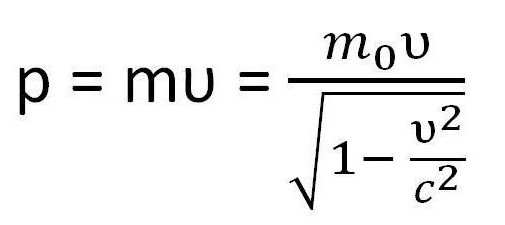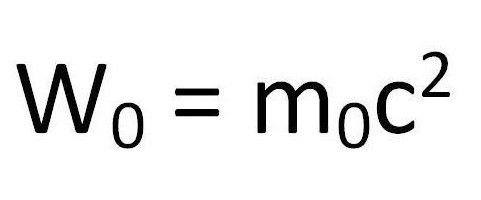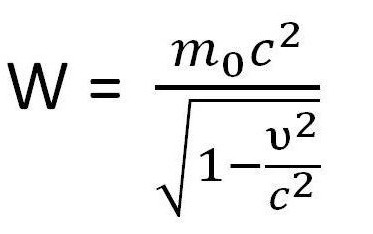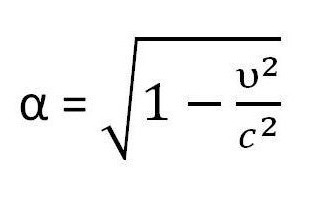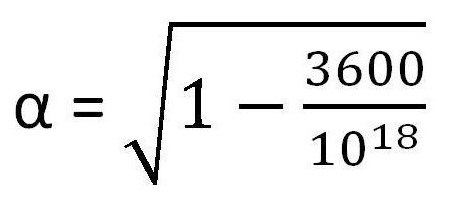Как найти релятивистскую массу - Исправление недочетов и поиск решений вместе с Examum.ru

In physics, the mass idea discourse is quite common. When there are comparisons of length and time in distinct frames, the well-known special theory of relativity says a lot more about relativistic mass. When the body is moving, the relative change in mass is also experienced. This is referred to as relativistic mass. When an item is moving, it experiences mass increase, which is similar to length contraction and time dilation.

Relativistic Mass

The mass of an object that varies with its own speed as the said object approaches the speed of light is called its relativistic mass. It rises with speed and approaches infinity as the speed rises to the speed of light. Its unit of measurement is meters per second (m/s) and the dimensional formula is given by [M¹ L⁰ T⁰].

In particle and nuclear physics, the phrase “relativistic mass” is rarely used, and special relativity writers prefer to refer to the relativistic energy of the object instead.

Example

The weight of the particle accelerator + electrons system can be raised by the translational weight of an electron, not through the electron’s resting mass, if an electron in a cyclotron moves in circles with a translational velocity.

Formula

m = $frac{m_0}{sqrt{1-frac{v^2}{c^2}}}$

where,

m_o denotes the rest mass of the object

v denotes the velocity of the moving body

c denotes the velocity of light

Sample Problems

Problem 1: A 10 kg object travels in the air at a velocity of 0.77 c. Calculate its rest mass.

Solution:

Given: m = 10 kg, v = 0.77 c and c = 3 × 10⁸ m/s.

Since, m = $frac{m_0}{sqrt{1-frac{v^2}{c^2}}}$

$10=frac{m_0}{sqrt{1-frac{(0.77)^2c^2}{c^2}}}$

10 = m₀/0.6830

m_o= 6.3 kg

Problem 2: A 20 kg object travels in the air at a velocity of 0.67 c. Calculate its rest mass.

Solution:

Given: m = 20 kg, v = 0.67 c and c = 3 × 10⁸m/s.

Since, $m = frac{m_0}{sqrt{1-frac{v^2}{c^2}}}$

$20=frac{m_0}{sqrt{1-frac{(0.67)^2c^2}{c^2}}}$

20 = m₀/0.7423

m_o = 14.8 kg

Problem 3: A 10 kg object travels in the air at a velocity of 0.99 c. Calculate its rest mass.

Solution:

Given: m = 10 kg, v = 0.99 c and c = 3 × 10⁸ m/s.

Since, $m = frac{m_0}{sqrt{1-frac{v^2}{c^2}}}$

$10=frac{m_0}{sqrt{1-frac{(0.99)^2c^2}{c^2}}}$

10 = m₀/0.1410

m_o = 1.41 kg

Problem 4: A 10 kg object travels in the air at a velocity of 0.43 c. Calculate its rest mass.

Solution:

Given: m = 10 kg, v = 0.43 c and c = 3 × 10⁸ m/s.

Since, $m = frac{m_0}{sqrt{1-frac{v^2}{c^2}}}$

$10=frac{m_0}{sqrt{1-frac{(0.43)^2c^2}{c^2}}}$

10 = m₀/0.9028

m_o = 18.056 kg

Problem 5: A 10 kg object travels in the air at a velocity of 0.33 c. Calculate its rest mass.

Solution:

Given: m = 10 kg, v = 0.33 c and c = 3 × 10⁸ m/s.

Since, $m = frac{m_0}{sqrt{1-frac{v^2}{c^2}}}$

$10=frac{m_0}{sqrt{1-frac{(0.33)^2c^2}{c^2}}}$

10 = m_o/0.9439

m_o = 9.4 kg

Problem 6: Calculate the mass of a particle at a velocity of 0.21 c if its rest mass is 10 kg.

Solution:

Given: m_o = 10 kg, v = 0.21 c and c = 3 × 10⁸ m/s.

Since,

$m = frac{m_0}{sqrt{1-frac{v^2}{c^2}}}$

$m=frac{10}{sqrt{1-frac{(0.21)^2c^2}{c^2}}}$

m = 10.22 kg

Problem 7: Calculate the mass of a particle at a velocity of 0.45 c if its rest mass is 20 kg.

Solution:

Given: m_o = 20 kg, v = 0.21 c and c = 3 × 10⁸ m/s.

Since,

$m = frac{m_0}{sqrt{1-frac{v^2}{c^2}}}$

$m=frac{20}{sqrt{1-frac{(0.45)^2c^2}{c^2}}}$

m = 22.39 kg

Last Updated :
14 Jun, 2022

Like Article

Save Article

Источник

Эйнштейн показал,
что масса тела зависит от его скорости:

где
m₀–
масса тела в той системе отсчета, где
тело покоится (масса покоя); m – масса
тела в той системе, относительно которой
тело движется (релятивистская масса);

– скорость тела относительно системы
отсчета, в которой определяется масса
m.

Релятивистский
импульс

где m – релятивистская масса.

Закон взаимосвязи
массы и энергии:

где
m – релятивистская масса; Е – полная
энергия материального объекта.

Кинетическая
энергия объекта

где
–
полная энергия;–
энергия покоя.

Из
закона взаимосвязи массы и энергии
следует, что всякое изменение массы
тела на m
сопровождается изменением его энергии
на E:

E=mc².

Примеры решения задач

Задача
1 Уравнение
движения точки по прямой имеет вид: x =
A+Bt+Ct³,
где А = 4 м, В = 2 м/c, С = 0,2 м/с³.
Найти: 1) положение точки в моменты
времени t = 2 c и t = 5 с; 2) среднюю скорость
за время, протекшее между этими моментами;
3) мгновенные скорости в указанные
моменты времени; 4) среднее ускорение
за указанный промежуток времени; 5)
мгновенные ускорения в указанные
моменты времени.

Дано:

x
= A + Bt + Ct³

A
= 4 м

B
= 2 м/c

C
= 0,2 м/c³

t₁
= 2 c; t₂
= 5 c

Решение

1.
Чтобы найти координаты точки, надо в
уравнение движения подставить
значения t₁
и t₂:

x₁=
(4+22+0,22³)
м
=
9,6 м,

x₂=
(4+25+0,25³)
м
=
39 м.

x₁,
x₂,
<>-
?

₁,
₂
— ?

<a>,
a₁,
a₂
— ?

2.
Средняя скорость,

м/с = 9,8 м/с.

3.
Мгновенные скорости найдем,
продифференцировав по времени уравнение
движения:

₁= (2+30,22²)
м/с = 4,4 м/c;

₂= (2+30,25²)
м/с = 17 м/с.

4.
Среднее ускорение
,

м/c²= 4,2 м/с².

5.
Мгновенное ускорение получим, если
продифференцируем по времени выражение
для скорости: a = 23Ct
= 6Ct.

a₁= 60,22
м/c²=
2,4 м/с²;

a₂= 60,25
м/с²=
6 м/с².

Ответ:
x₁=
9,6 м; x₂=
39 м; 
= 9,8 м/с; ₁= 4,4 м/c; ₂= 17 м/с; а
= 4,2 м/с²;
a₁=
2,4 м/с²;
a₂=
6 м/с².

Задача
2 Маховик
вращается равноускоренно. Найти угол
,
который составляет вектор полного
ускорения
любой
точки маховика с радиусом в тот момент,
когда маховик совершит первые N=2 оборота.

Дано:

₀
= 0

N = 2

 =
const

Решение

Разложив
вектор
точки М на тангенциальноеи нормальноеускорения, видим, что искомый
угол определяется соотношением
tg=a_/a_n.

 —
?

Поскольку
в условии дано лишь число оборотов,
перейдем к угловым величинам. Применив
формулы: a_= R,
a_n=
²R,
где R – радиус маховика, получим

tg
=

так
как маховик вращается равноускоренно,
найдем связь между величинами 
и ;

Поскольку
₀= 0; 
= 2N,
то ²= 22N
= 4N.

Подставим
это значение в формулу, получим:

 2,3.

Ответ:


2,3.

Задача
3 Две гири
с массами m₁= 2 кг и m₂= 1 кг
соединены нитью, перекинутой
через невесомый блок. Найти ускорение
a, с которым движутся гири, и силу натяжения
нити
. Трением в блоке пренебречь.

Дано:

m₁
= 2 кг

m₂
= 1 кг

Решение

Воспользуемся
для решения задачи основным законом
динамики

где

– равнодействующая всех сил,
действующих на тело.

a,
F_Н—
?

На тело 1 и тело 2 действуют только две
силы – сила тяжести и сила

натяжения
нити. Для первого тела имеем

(1)

для второго тела

.
(2)

Так
как сила трения в блоке отсутствует,

Ускорения
тел а₁
и а₂
направлены в противоположные стороны
и равны по модулю:

Получаем
из выражений (1) и (2) систему уравнений

Выберем
ось Х, как показано на рисунке и запишем
полученную систему уравнений

в
проекции на ось Х

Решая
эту систему относительно а и F_Н,
получаем:

=
3,3 м/с²;

=
13 Н.

Ответ:
a
= 3,3 м/c²
; F_H
= 13 Н.

Задача
4 К ободу
однородного диска радиусом R=0,2 м
приложена касательная сила
F=98,1 Н. При вращении на диск
действует момент сил трения

М_ТР=4,9
Нм.
Найти массу m диска, если известно, что
диск вращается с угловым ускорением
=100
рад/с².

Дано:

R
= 0,2 м

F
= 98,1 Н

M_ТР
= 4,9 Нм

 =
100 рад / c²

Решение

Воспользуемся
основным законом динамики вращательного
движения, записанным для оси вращения,
направление которой совпадает с
направлением угловой скорости: ,

где


момент сил, приложенных к телу,

m
— ?

относительно
выбранной оси ( M_F— момент
силы F, M_тр
– момент сил трения);

момент
инерции диска.

Учитывая,
что M_F=FR,
получаем
.

Отсюда
;
m = 7,4 кг.

Ответ:
m
= 7,4 кг.

Задача 5

Вагон массой 20 т,
движущийся равнозамедленно, под действием
силы трения в 6 кН через некоторое время
останавливается. Начальная скорость
вагона равна 54 км/ч. Найти работу сил
трения и расстояние, которое вагон
пройдет до остановки.

Дано:

m
= 20 
10 ³
кг

F_тр
=
6 
10 ³
Н

 =
15 м/c

Решение

По закону сохранения
механической энергии изменение полной
механической энергии определяется
работой неконсервативных сил, то есть

A_ТР— ?
r
— ?

Так
как механическая энергия вагона равна
его кинетической энергии, в качестве
неконсервативной силы выступает сила

трения.
Так как в конце пути скорость вагона
равна нулю, то

Итак:
=-2250
кДж.

По
определению, для работы, совершаемой
постоянной силой трения:

м.

Ответ:
r
= 375 м.

Задача
6 После
упругого удара нейтрона о ядро атома
углерода он движется в направлении,
перпендикулярном начальному. Считая,
что масса М ядра углерода в n=12 раз больше
массы m нейтрона, определить, во сколько
раз уменьшается энергия нейтрона в
результате удара.

Дано:

Решение

Ведем
обозначения: ₁
– скорость нейтрона до удара, ₁
– после удара; ₂
– скорость ядра углерода после удара
(до удара она равна нулю).


—
?

По
законам сохранения импульса и энергии
соответственно имеем:

По
условию задачи требуется найти отношение

Из
треугольника импульсов (смотри рисунок)

имеем:
(m₁)²+(m₁)²=(M₂)².

С
учетом записанных выражений, а также
соотношения n=M/m получим

₁²-₁²=n₂²;

₁²+₁²=n²₂².

Разделив
почленно последние равенства, получаем

Отсюда

=1,18.

Ответ:

= 1,18.

Задача
7 Круглая
платформа радиусом R=1,0 м, момент инерции
которой J=130
кгм²,
вращается по инерции вокруг вертикальной
оси, делая n₁=1,0
об/с. На краю платформы стоит человек,
масса которого m=70 кг. Сколько оборотов
в секунду n₂
будет совершать платформа, если человек
перейдет в её центр? Момент инерции
человека рассчитывать как для материальной
точки.

Дано:

R= 1м

J
= 130 кг 
м²

n₁
= 1c^-1

m
= 70 кг

Решение

Согласно условию задачи,
платформа с человеком вращается по
инерции. Это означает, что результирующий
момент всех внешних сил, приложенных
к вращающейся системе, равен нулю.
Следовательно, для системы “платформа
+ человек” выполняется закон сохранения
момента импульса, который запишем в
скалярной форме:

n₂
— ?

L₁= L₂
,
(1)

где
L₁

импульс системы «платформа + человек
на краю платформы»,
L₂

импульс системы
«платформа + человек в центре платформы».

L₁=
J₁₁=
(J+mR²)2n₁,
(2)

L₂=
J₂₂=
J2n₂,
(3)

где
mR²

момент инерции человека, J₁= J+mR²

момент инерции системы «платформа +
человек на краю платформы», J₂

момент инерции системы «платформа +
человек в центре платформы», ₁
и ₂

соответствующие угловые скорости
системы. Решая систему уравнений (1) 
(3), получаем

n₂= n₁(J+mR²)/J
= 1,5 об/с.

Ответ:
n₂
= 1,5 с^-1.

Задача 8

Определить
кинетическую энергию (в электронвольтах)
и релятивистский импульс электрона,
движущегося со скоростью 
= 0,9 c (с = 310⁸
м/с 
скорость света в вакууме).

Дано:

 =
0,9 c

Решение

Так
как скорость частицы сопоставима по
значению со скоростью света в вакууме,
то частицу нельзя считать классической.
Для нахождения кинетической энергии
воспользуемся формулой:

Е_К,
р — ?

где

масса покоя электрона.

Получаем

Так
как
,то

Можно
было найти значение кинетической энергии
сразу в электрон вольтах, учитывая, что
энергия покоя электрона

Релятивистский
импульс находим по формуле

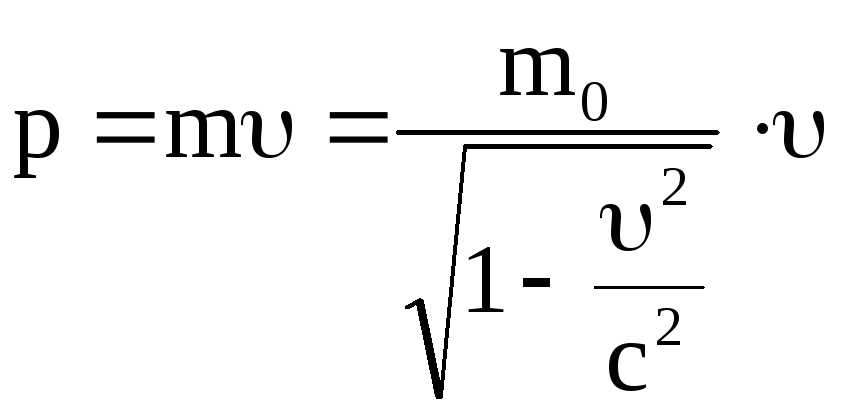
Ответ:
E_K
0,66 МэВ; р 
5,6 10^-22кгм/c.

Соседние файлы в папке Физика лр. Механика

Источник

В 1905 году Альберт Эйнштейн опубликовал свою теорию относительности, которая несколько изменила представление науки об окружающем мире. Исходя из его предположений была получена формула релятивистской массы.

Специальная теория относительности

Вся суть заключается в том, что в системах, движущихся относительно друг друга, любые процессы протекают несколько по-разному. Конкретно это выражается, например, в увеличении массы с увеличением скорости. Если скорость движения системы гораздо меньше скорости света (υ << c = 3 · 10⁸ ), то эти изменения практически не будут заметны, так как они будут стремится к нулю. Однако если скорость движения близка к скорости света (например, равна одной десятой от нее), то такие показатели, как масса тела, его длина и время любого процесса, изменятся. С помощью следующих формул возможно рассчитать эти значения в движущейся системе отсчета, в том числе — масса релятивистской частицы.

Здесь l₀, m₀ и t₀ — длина тела, его масса и время процесса в неподвижной системе, а υ — скорость движения объекта.

По теории Эйнштейна, ни одно тело не способно развивать скорость большую, чем скорость света.

Масса покоя

Вопрос массы покоя релятивистской частицы возникает именно в теории относительности, когда масса тела или частицы начинает изменяться в зависимости от скорости. Соответственно, массой покоя называется масса тела, которое в момент измерения содержится в покое (при отсутствии движения), то есть скорость его равняется нулю.

Релятивистская масса тела является одним из основных параметров при описании движения.

Принцип соответствия

После появления теории относительности Эйнштейна потребовался некоторый пересмотр используемой в течении нескольких веков механики Ньютона, которая уже не могла использоваться при рассмотрении систем отсчета, движущихся со скоростью, сравнимой со скоростью света. Поэтому потребовалось изменить все уравнения динамики, используя преобразования Лоренца — изменение координат тела или точки и времени процесса при переходе между инерциальными системами отсчета. Описание данных преобразований основывается на том, что в каждой инерциальной системе отсчета все физические законы работают одинаково и равноправно. Таким образом, законы природы никаким образом не зависят от выбора системы отсчета.

Из преобразований Лоренца и выражается основной коэффициент релятивистской механики, который описан выше и назван буквой α.

Сам принцип соответствия достаточно прост — он говорит о том, что любая новая теория в каком-то определенном частном случае будет давать те же результаты, что и предыдущая. Конкретно в релятивистской механике это отражается тем фактом, что при скоростях, которые много меньше скорости света, используются законы классической механики.

Релятивистская частица

Релятивистской частицей называется частица, которая движется со скоростью, сравнимой со скоростью света. Их движение описывается специальной теорией относительности. Существует даже группа частиц, существование которых возможно только при движении со скоростью света — такие называются частицами без массы или просто безмассовыми, так как в состоянии покоя их масса равняется нулю, поэтому это уникальные частицы, которые не имеют никакого аналогичного варианта в нерелятивистской, классической механике.

То есть, масса покоя релятивистской частицы может равнятся нулю.

Частицу можно назвать релятивистской, если ее кинетическая энергия может быть сравнима с энергией, которая выражается следующей формулой.

Данная формула обуславливает условие необходимой скорости.

Энергия частицы также может быть и больше своей энергии покоя — такие называют ультрарелятивистскими.

Для описания движения подобных частиц используется квантовая механика в общем случае и квантовая теория поля для более обширного описания.

Появление

Подобные частицы (и релятивистские, и ультрарелятивистские) в естественном виде существуют только в космическом излучении, то есть излучение, источник которого находится вне Земли, электромагнитной природы. Человеком же они искусственно создаются в специальных ускорителях — с помощью них же были найдены несколько десятков видов частиц, и данный список постоянно обновляется. Подобной установкой является, например, Большой Адронный Коллайдер, находящийся в Швейцарии.

Появляющиеся при β-распаде электроны также могут иногда достигать достаточной скорости для того, чтобы отнести их к классу релятивистских. Релятивистская масса электрона также может быть найден по указанным формулам.

Понятие массы

Масса в механике Ньютона обладает несколькими обязательными свойствами:

Гравитационное притяжение тел возникает из-за их массы, то есть непосредственно зависит от нее.
Масса тела не зависит от выбора системы отсчета и не меняется при ее перемене.
Инерция тела измеряется его массой.
Если тело находится в системе, в которой не происходят никакие процессы и которая является замкнутой, то его масса практически не будет меняться (кроме диффузионной передачи, которая у твердых тел происходит очень медленно).
Масса составного тела складывается из масс отдельных его частей.

Принципы относительности

Принцип относительности Галилея.

Данный принцип был сформулирован для нерелятивистской механики и выражается следующим образом: вне зависимости от того, находится ли системы в состоянии покоя или же совершают они какое-либо движение, все процессы в них протекают одинаково.

Принцип относительности Эйнштейна.

Данный принцип базируется на двух постулатах:

Принцип относительности Галилея используется и в данном случае. То есть, в любой СО абсолютно все законы природы работают одинаково.
Скорость света абсолютно всегда и во всех системах отсчета одинакова, вне зависимости от скорости движения источника света и экрана (приемника света). Для доказательства данного факта был проведен ряд экспериментов, которые полностью подтвердили первоначальную догадку.

Масса в релятивистской и в ньютоновской механике

В отличие от механики Ньютона, в релятивистской теории масса не может являться мерой количества материала. Да и сама релятивистская масса определяется некоторым более обширным способом, оставляя возможным объяснить, например, существование частиц без массы. В релятивистской механики особое внимание уделяется скорее энергии, чем массе — то есть основным фактором, определяющим какое-либо тело или элементарную частицу, является его энергия или же импульс. Импульс возможно найти по следующей формуле.

Однако при этом масса покоя частицы является очень важной характеристикой — ее значение является очень небольшим и нестабильным числом, поэтому к измерениям подходят с максимальной скоростью и аккуратностью. Энергию покоя частицы можно найти по следующей формуле.

Аналогично теориям Ньютона, в изолированной системе масса тела является постоянной, то есть, не изменяется со временем. Также не меняется она и при переходе от одной СО к другой.
Не существует абсолютно никакой меры инерции движущегося тела.
Релятивистская масса движущегося тела не определяется воздействием на него гравитационными силами.
Если масса тела равна нулю, то оно обязательно должно двигаться со скоростью света. Обратное утверждение неверно — скорости света могут достигать не только безмассовые частицы.
Полную энергию релятивисткой частицы возможно с помощью следующего выражения:

Природа массы

До некоторого времени в науке считалось, что масса любой частицы обусловлена электромагнитной природой, однако к настоящему моменту стало известно, что таким образом возможно объяснить лишь малую ее часть — основной же вклад вносится природой сильных взаимодействий, возникающих из-за глюонов. Однако данным способом невозможно объяснить массу десятка частиц, природа которой все еще не была выяснена.

Релятивистское увеличение массы

Результат всех описанных выше теорем и законов можно выразить в достаточно понятном, хоть и удивительном процессе. Если одно тело движется относительно другого с какой-либо скоростью, то его параметры и параметры тел, находящихся внутри, если первоначальное тело представляет собой систему, меняются. Безусловно, на малых скоростях это практически не будет заметно, однако данный эффект все равно будет присутствовать.

Можно привести простой пример — другое истечение времени в движущемся со скоростью 60 км/ч поезде. Тогда по следующей формуле рассчитывается коэффициент изменения параметров.

Данная формула также была описана выше. Подставив все данные в нее (при c ≈ 1·10⁹ км/ч), получится следующий результат:

Очевидно, что изменение чрезвычайно мало и не меняет показатели часов так, чтобы это было заметно.

Источник

Физика > Релятивистские энергия и масса

Изучите массу и энергию релятивистской частицы в специальной теории относительности. Рассмотрите роль скорости света, формулы релятивистской массы и энергии.

В специальной теории относительности, если движение объекта приближается к скорости света, то энергия и импульс возрастают без ограничений.

Задача обучения

Охарактеризовать возможность движения объекта со световой скоростью.

Основные пункты

Термины

Специальная теория относительности: световая скорость остается неизменной во всех системах отсчета.
Масса покоя – масса тела, когда оно не перемещается по отношению к наблюдателю.
Коэффициент Лоренца – используется для определения степени временного замедления, сокращения длины и релятивистской массы.

Релятивистские энергия и масса

В специальной теории относительности Эйнштейна, если объект наделен массой, то не способен достигать световой скорости. По мере приближения к отметке, его энергия и импульс будут возрастать без ограничений. Релятивистские поправки для энергии и массы нужны, потому что световая скорость в вакууме остается стабильной во всех системах отсчета.

Сохранение массы и энергии – общепринятые физические законы. Чтобы они действовали, должна функционировать специальная теория относительности. Если скорость объекта ниже световой, то выражения для значений релятивистских энергии и массы будут примерно сходиться с ньютоновскими вариантами.

Здесь показана связь между релятивистской и ньютоновской кинетической энергией и скоростью объекта. Релятивистская будет возрастать до бесконечности, если объект приближается к световой скорости. А вот показатель Ньютона продолжит расти по мере увеличения скорости объекта

Релятивистская масса

В 1934 году массу релятивистской частицы определил Ричард К. Толман. Для частички с нулевой массой покоя выступает коэффициент Лоренца (v – относительная скорость между инерциальными системами отсчета, c – световая скорость).

Ричард К. Толман и Альберт Эйнштейн (1932 год)

Если относительная скорость приравнивается к нулю, то достигает 1, а релятивистская масса сводится к массе покоя. По мере возрастания скорости к световой, знаменатель правой стороны стремится к нулю, то есть, к бесконечности.

В уравнении для импульса масса будет релятивистской. То есть, это постоянная пропорциональности между скоростью и импульсом.

Стоит отметить, что несмотря на действенность второго закона Ньютона, производная форма будет недействительной, потому что не выступает постоянной.

Релятивистская энергия

Релятивистская энергия связана с массой покоя через формулу:

Это квадрат эвклидовой формы для различных векторов импульса в системе.

В современном мире предсказания релятивистской энергии и массы регулярно подтверждаются в экспериментах с ускорителями частиц. Можно не только точно определить рост релятивистских импульса и энергии, но их также используют для понимания поведения циклотронов и синхротрона.

Источник

Определение релятивистских длин, масс, плотностей

Задачи все предлагаю простые: такие есть в каждом учебнике. Но каждая тема всегда начинается с разминки: с простого. Ну а дальше — дальше все интереснее и интереснее!

Скорость света

Задача 1. Частица движется со скоростью . Во сколько раз релятивистская масса частицы больше массы покоя?

Запишем отношение масс:

Ответ:

Задача 2. При какой скорости релятивистская масса движущейся частицы вдвое больше массы покоя этой частицы ?
Теперь используем формулу предыдущей задачи «в обратную сторону»:

Ответ: м/с
Задача 3. На сколько увеличится релятивистская масса частицы при увеличении ее начальной скорости от до скорости ?

Ответ: на .

18.15. Скорость частицы Мм/с. На сколько процентов релятивистская масса движущейся частицы больше массы покоящейся частицы?

Ответ: на 0,5 %
Задача 4. С какой скоростью должен лететь протон (а.е. м.)‚ чтобы его релятивистская масса была равна массе покоя -частицы (а. е. м.)?

То есть, иными словами, нас спрашивают, с какой скоростью должен лететь протон, чтобы его масса возросла вчетверо?

Ответ: м/с

Задача 5. Во сколько раз изменится плотность тела при его движении со скоростью ?

Плотность тела зависит не только от его массы, но и от объема, а тот, в свою очередь, функция куба линейных размеров. Тогда исходная плотность тела (плотность покоя):

Релятивистская плотность:

Где

Тогда отношение плотностей (или во сколько раз изменится плотность):

Ответ: плотность возрастет в 2,8 раза.
Задача 6. При движении с некоторой скоростью продольные размеры тела уменьшились в раза. Во сколько раз изменилась масса тела?

Ответ: масса выросла вдвое.
Задача 7. Отношение заряда движущегося электрона к его массе, определенное из опыта, Кл/кг. Определить релятивистскую массу электрона и его скорость.