Как найти решение если система неопределенная

Система m
линейных алгебраических уравнений с n
неизвестными (или, линейная система,
также употребляется аббревиатура СЛА́У)
в линейной алгебре — это система
уравнений вида

Совместная
СЛУ– СЛУ, имеющая одно или несколько
решений.

Неопределенная
СЛУ– совместная СЛУ, имеющая более
одного решения.

Решается методом
Жордана – Гаусса. Решения выражаются
по средством свободных членов.

10) Однородные системы линейных уравнений

СЛАУ называется
однородной, если все её свободные члены
равны 0.

Теорема 1 (о
нетривиальных решениях однородной
системы)

Однородная
линейная система с квадратной матрицей
имеет нетривиальное решение тогда и
только тогда, когда определитель системы
равен нулю.

Доказательство
По теореме Крамера
тогда и только тогда, когда система с
квадратной матрицей имеет единственное
решение (т.е. векторы – столбцы системы
– линейно зависимы). В случае если задана
система линейных однородных уравнений,
это решение – тривиальное (0,0,…0). Значит,
нетривиальные решения имеются тогда и
только тогда, когда(т.е. решений системы бесконечное
множество).

Любое решение
СЛОУ выражается в виде линейной комбинации

векторов (если):

,
…,.

Покажем, что
вектора
– линейно независимы. Для этого составим
матрицуиз их координат:

.

Ниже черты
расположен минор порядка
,
отличный от нулястолбцов матрицылинейно независимы.

Следовательно,
вектора
– линейно независимы, т.е. эти вектора
образуют базис подпространства.

Условие
нетривиальной совместности:

Для того, чтобы
однородная система имела нетривиальное
решение, необходимо и достаточно, чтобы
ранг ее основной матрицы был меньше
числа неизвестных

Теоре́ма
Кро́некера — Капе́лли— критерий
совместности системы линейных
алгебраических уравнений:

Система линейных
алгебраических уравнений совместна
тогда и только тогда, когда ранг её
основной матрицы равен рангу её
расширенной матрицы, причём система
имеет единственное решение, если ранг
равен числу неизвестных, и бесконечное
множество решений, если ранг меньше
числа неизвестных.

11. Векторы. Линейные операции над векторами

Геометрическим
вектором (или просто вектором) называетсянаправленный отрезок.

Вектор называется
нулевым, если начало и конец его совпадают.
Нулевой

вектор не имеет
определенного направления и имеет
длину, равную нулю. Это

позволяет при
записи отождествлять нулевой вектор с
вещественным числом

нуль.

Векторы
называются коллинеарными, если они
лежат либо на од-

ной прямой,
либо на параллельных прямых.

Два вектора
называются равными, если они коллинеарны,
имеют оди-

наковую длину
и одинаковое направление.

Линейные
операции над векторами.

Линейными
операциями принято называть операцию
сложения векторов и опе-

рацию умножения
векторов на вещественные числа.

Суммойa +
b двух векторов a и b называется вектор,
идущий

из начала
вектора a в конец вектора b при условии,
что вектор b

приложен к
концу вектора a.

1. a + b = b + a
(переместительное свойство);

2. (a + b) + c= a + (b +
c) (сочетательное свойство);

3. а+0=а

4. а+(-а)=0

Разностьюa — b вектора a и вектора b называется такой
вектор

c, который в
сумме с вектором b дает вектор a.

Произведениемα a (или aα) вектора a на вещественное
число α

называется
вектор b, коллинеарный вектору a, имеющий
длину,

равную |α|·|a| ,
и имеющий направление, совпадающее с
направле-

нием вектора
a в случае α > 0 и противоположное
направлению

вектора a в
случае α < 0.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #

  29.05.20154.35 Mб56начерталка.rar.pdf

• #
• #
• #
• #
• #
• #
• #
• #

From Wikipedia, the free encyclopedia

In mathematics, particularly in algebra, an indeterminate system is a system of simultaneous equations (e.g., linear equations) which has more than one solution (sometimes infinitely many solutions).^[1] In the case of a linear system, the system may be said to be underspecified, in which case the presence of more than one solution would imply an infinite number of solutions (since the system would be describable in terms of at least one free variable^[2]), but that property does not extend to nonlinear systems (e.g., the system with the equation ).

An indeterminate system by definition is consistent, in the sense of having at least one solution.^[3] For a system of linear equations, the number of equations in an indeterminate system could be the same as the number of unknowns, less than the number of unknowns (an underdetermined system), or greater than the number of unknowns (an overdetermined system). Conversely, any of those three cases may or may not be indeterminate.

Examples[edit]

The following examples of indeterminate systems of equations have respectively, fewer equations than, as many equations as, and more equations than unknowns:

Conditions giving rise to indeterminacy[edit]

In linear systems, indeterminacy occurs if and only if the number of independent equations (the rank of the augmented matrix of the system) is less than the number of unknowns and is the same as the rank of the coefficient matrix. For if there are at least as many independent equations as unknowns, that will eliminate any stretches of overlap of the equations’ surfaces in the geometric space of the unknowns (aside from possibly a single point), which in turn excludes the possibility of having more than one solution. On the other hand, if the rank of the augmented matrix exceeds (necessarily by one, if at all) the rank of the coefficient matrix, then the equations will jointly contradict each other, which excludes the possibility of having any solution.

Finding the solution set of an indeterminate linear system[edit]

Let the system of equations be written in matrix form as

where is the coefficient matrix, is the vector of unknowns, and is an vector of constants. In which case, if the system is indeterminate, then the infinite solution set is the set of all vectors generated by^[4]

where is the Moore–Penrose pseudoinverse of and is any vector.

See also[edit]

• Indeterminate equation
• Indeterminate form
• Indeterminate (variable)
• Linear algebra
• Simultaneous equations
• Independent equation
• Identifiability

References[edit]

Further reading[edit]

• Lay, David (2003). Linear Algebra and Its Applications. Addison-Wesley. ISBN 0-201-70970-8.

Методы решения систем линейных алгебраических уравнений (СЛАУ) с примерами

Содержание:

Методы решения систем линейных алгебраических уравнений (СЛАУ)

Метод Крамера

Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение

Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы

Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на для этого умножим все элементы первого столбца на эту неизвестную:

Второй столбец умножим на третий столбец — на -ый столбец — на и все эти произведения прибавим к первому столбцу, при этом произведение не изменится:

Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.

Определение: Определитель называется первым вспомогательным определителем СЛАУ.

Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:

31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.

Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины Проанализируем полученные формулы:

Пример:

Решить СЛАУ методом Крамера

Решение:

Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом

Найдем главный определитель СЛАУ (раскрываем по первой строке)

Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя

Воспользуемся формулами Крамера

Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.

Выполним проверку Отсюда видно, что СЛАУ решена верно.

Матричный способ решения СЛАУ

Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных матpицы-столбцы неизвестных и свободных коэффициентов

Тогда СЛАУ можно записать в матричном виде Матричный способ решения СЛАУ состоит в следующем: умножим слева матричное уравнение на обратную матрицу к матрице А, получим в силу того, что произведение найдем Таким образом, для нахождения неизвестных матричным способом, надо найти обратную к А матрицу после чего надо умножить эту матрицу на матрицу-столбец свободных коэффициентов.

Пример:

Решить СЛАУ матричным способом

Решение:

Введем в рассмотрение следующие матрицы

Найдем матрицу (см. Лекцию № 2): найдем детерминант матрицы А.

Пример:

Решение:

Найдем алгебраические дополнения всех элементов Запишем обратную матрицу (в правильности нахождения обратной матрицы убедиться самостоятельно). Подействуем пай денной матрицей на матрицу-столбец свободных коэффициентов В:

Отсюда находим, что х = 1; y = l; z = l.

Метод Гаусса

Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:

Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.

Обменяем в расширенной матрице первую и вторую строки местами, получим Приведем матрицу к треугольному виду, выполнив следующие преобразования: умножим элементы первой строки на (-2) и прибавим к соответствующим элементам второй строки Разделим все элементы второй строки на (-5), получим эквивалентную матрицу

Умножим элементы первой строки на (—1) и прибавим к соответствующим элементам третьей строки Разделим все элементы третьей строки на (-3), получим Таким образом, эквивалентная СЛАУ имеет вид (напомним, что первый столбец это коэффициенты при неизвестной х, второй — при неизвестной у, третий — при неизвестной z, а за вертикальной чертой находится столбец свободных коэффициентов):

Из первого уравнения находим, что х = 1.

Вывод: Из вышеизложенного материала следует, что вне зависимости от

способа решения СЛАУ всегда должен получаться один и тот же ответ.

Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.

Ранг матрицы. Теорема Кронекера-Капелли

Определение: Рангом матрицы называется наивысший порядок отличного от нуля минора этой матрицы.

Если то среди всевозможных миноров этой матрицы есть хотя бы один минор порядка r, который отличен от нулю, а все миноры порядков больших, чем r, равны нулю.

При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.

Пример:

Найти ранг матрицы

Решение:

Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например, среди миноров третьего порядка также есть миноры, которые не равны нулю, например, Очевидно, что определитель четвертого порядка равен нулю, так как он будет содержать строку, состоящую из одних нулей (см. свойство для определителей). Следовательно, ранг матрицы А равен 3.

Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.

Следствия из теоремы Кронекера — Капелли

Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).

Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).

В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.

Рекомендую подробно изучить предметы:

Математика Алгебра Линейная алгебра Векторная алгебра Высшая математика Дискретная математика Математический анализ Математическая логика

Ещё лекции с примерами решения и объяснением:

• Скалярное произведение и его свойства
• Векторное и смешанное произведения векторов
• Преобразования декартовой системы координат
• Бесконечно малые и бесконечно большие функции
• Критерий совместности Кронекера-Капелли
• Формулы Крамера
• Матричный метод
• Экстремум функции

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Исследование СЛАУ. Общие сведения

В данной статье мы расскажем о методах, видах, условиях и определениях исследований решений систем линейных уравнений, что такое метод Кронекера-Капели, а также приведем примеры.

Общие сведения (определения, условия, методы, виды)

Системы линейных алгебраических уравнений с n неизвестными могут иметь:

• единственное решение;
• бесконечное множество решение (неопределенные СЛАУ);
• ни одного решения (несовместные СЛАУ).

Пример 1

Система x + y + z = 1 2 x + 2 y + 2 z = 3 не имеет решений, поэтому она несовместна.

Система x + y = 1 2 x + 7 y = — 3 имеет единственное решение x = 2 ; y = 1 .

Система x + y = 1 2 x + 2 y = 2 3 x + 3 y = 3 имеет бесконечное множество решений x = t y = 1 — t при — ∞ t ∞ .

Перед решением системы уравнений необходимо исследовать систему, т.е. ответить на следующие вопросы:

• Совместна ли система?
• Если система совместна, то, какое количество решений она имеет — одно или несколько?
• Как найти все решения?

Если система малоразмерна при m = n , то ответить на поставленные вопросы можно при помощи метода Крамера:

• если основной определитель системы, то система совместна и имеет единственное решение, которое вычисляется методом Крамера;
• если, и один из вспомогательных определителей, то система не является совместной, т.е. не имеет решений;
• если и все, и один из коэффициентов СЛАУ, то система не является определенной и имеет бесконечное множество решений.

Ранг матрицы и его свойства

Бывают случаи, которые выбиваются из представленных вариантов решения СЛАУ, например, линейные уравнения с большим количеством уравнений и неизвестных.

Для такого варианта решения существует ранг матрицы, который представляет собой алгоритм действий в случае решения системы матрицы, когда

В математике выделяют следующие подходы к определению ранга матрицы:

• при помощи понятия линейной зависимости/независимости строк/столбцов матрицы. Ранг равен максимальному количеству независимых строк (столбцов) матрицы
• при помощи понятия минора матрицы в качестве наивысшего порядка минора, который отличается от нуля. Минор матрицы порядка k — определитель k-го порядка, составленный из элементов, которые стоят на пересечении вычеркиваемых k-строк и k-столбцов матрицы;
• при помощи метода Гаусса. По завершении прямого хода ранг матрицы равняется количеству ненулевых строк.

Обозначение ранга матрицы: r ( A ) , r g ( A ) , r A .

Свойства ранга матрицы:

1. квадратная невырожденная матрица обладает рангом, который отличается от нуля;
2. если транспонировать матрицу, то ранг матрицы не изменяется;
3. если поменять местами 2 параллельные строки или 2 параллельных столбца, ранг матрицы не изменяется;
4. при удалении нулевого столбца или строки ранг матрицы не изменяется;
5. ранг матрицы не изменяется, если удалить строку или столбец, которые являются линейной комбинацией других строк;
6. при умножении все элементов строки/столбца на число k н е р а в н о н у л ю ранг матрицы не изменяется;
7. ранг матрицы не больше меньшего из ее размеров: r ( А ) ≤ m i n ( m ; n ) ;
8. когда все элементы матрицы равны нулю, то только тогда r ( A ) = 0 .

Пример 2

А 1 = 1 1 1 2 2 2 3 3 3 , B 1 = 1 0 0 0 0 0

r ( A 1 ) = 1 , r ( B 1 ) = 1

А 2 = 1 2 3 4 0 5 6 7 0 0 0 0 ; В 2 = 1 1 3 1 2 1 4 3 1 2 5 0 5 4 13 6

Примеры решения СЛАУ

Методы решения систем линейных уравнений широко используются в задачах математики, экономики, физики, химии и других науках. На практике, они позволяют не делать лишних действий, а записать систему уравнений в более компактной форме и сократить время выполнения задач. Поэтому, будущим специалистам очень важно понять основные методы решения и научиться выбирать оптимальный.

Перед изучением примеров решения задач советуем изучить теоретический материал по СЛАУ, прочитать все теоремы и методы решения. Список тем находится в правом меню.

Примеры по темам:

СЛАУ: основные понятия, виды

Задание. Проверить, является ли набор $<0,3>$ решением системы $left<begin 3 x-2 y=-6 \ 5 x+y=3 endright.$

Решение. Подставляем в каждое из уравнений системы $x=0$ и $y=3$ :

$$3 x-2 y=-6 Rightarrow 3 cdot 0-2 cdot 3=-6 Rightarrow-6=-6$$ $$5 x+y=3 Rightarrow 5 cdot 0+3=3 Rightarrow 3=3$$

Так как в результате подстановки получили верные равенства, то делаем вывод, что заданный набор является решением указанной СЛАУ.

Ответ. Набор $<0,3>$ является решением системы $left<begin 3 x-2 y=-6 \ 5 x+y=3 endright.$

Задание. Систему $left<begin x-y+z-4 t=0 \ 5 x+y+t=-11 endright.$ записать в матричной форме и выписать все матрицы, которые ей соответствуют.

Решение. Заданную СЛАУ записываем в матричной форме $A cdot X=B$ , где матрица системы:

$$A=left(begin 1 & -1 & 1 & -4 \ 5 & 1 & 0 & 1 endright)$$

$$A=left(begin 1 & -1 & 1 & -4 \ 5 & 1 & 0 & 1 endright)$$

вектор-столбец свободных коэффициентов:

то есть, запись СЛАУ в матричной форме:

$$left(begin 1 & -1 & 1 & -4 \ 5 & 1 & 0 & 1 endright)left(begin x \ y \ z \ t endright)=left(begin 0 \ -11 endright)$$

Задание. Записать матрицу и расширенную матрицу системы $left<begin 2 x_<1>+x_<2>-x_<3>=4 \ x_<1>-x_<2>=5 endright.$

Решение. Матрица системы $A=left(begin 2 & 1 & -1 \ 1 & -1 & 0 endright)$ , тогда расширенная матрица $tilde=(A mid B)=left(begin 2 & 1 & -1 & 4 \ 1 & -1 & 0 & 5 endright)$

Критерий совместности системы

Задание. При каких значениях $lambda$ система $left<begin 2 x_<1>-x_<2>+x_<3>+x_<4>=1 \ x_<1>+2 x_<2>-x_<3>+x_<4>=2 \ x_<1>+7 x_<2>-4 x_<3>+2 x_<4>=lambda endright.$ будет совместной?

Решение. Ранг матрицы равен количеству ненулевых строк после приведения этой матрицы к ступенчатому виду. Поэтому записываем расширенную матрицу системы $tilde$ (слева от вертикальной черты находится матрица системы $A$ ):

и с помощью элементарных преобразований приводим ее к ступенчатому виду. Для этого вначале от второй строки отнимаем две вторых строки, а от третьей вторую, в результате получаем:

Третью строку складываем с первой:

и меняем первую и вторую строки матрицы местами

Квадратные СЛАУ. Матричный метод решения

Теоретический материал по теме — матричный метод решения.

Задание. Найти решение СЛАУ $left<begin5 x_<1>+2 x_<2>=7 \ 2 x_<1>+x_<2>=9endright.$ матричным методом.

Решение. Выпишем матрицу системы $left<begin 5 x_<1>+2 x_<2>=7 \ 2 x_<1>+x_<2>=9 endright.$ и матрицу правых частей $B=left(begin 7 \ 9 endright)$ . Найдем обратную матрицу для матрицы системы. Для матрицы второго порядка обратную можно находить по следующему алгоритму: 1) матрица должна быть невырождена, то есть ее определитель не должен равняться нулю: $|A|=1$ ; 2) элементы, стоящие на главной диагонали меняем местами, а у элементов побочной диагонали меняем знак на противоположный и делим полученные элементы на определитель матрицы. Итак, получаем, что

$$X=left(begin x_ <1>\ x_ <2>endright)=A^ <-1>B=left(begin 1 & -2 \ -2 & 5 endright) cdotleft(begin 7 \ 9 endright)=$$ $$=left(begin -11 \ 31 endright) Rightarrowleft(begin x_ <1>\ x_ <2>endright)=left(begin -11 \ 31 endright)$$

Две матрицы одного размера равны, если равны их соответствующие элементы, то есть в итоге имеем, что $x_<1>=-11$, $x_<2>=31$

Ответ. $x_<1>=-11$, $x_<2>=31$

Задание. Решить с помощью обратной матрицы систему $left<begin 2 x_<1>+x_<2>+x_<3>=2 \ x_<1>-x_<2>=-2 \ 3 x_<1>-x_<2>+2 x_<3>=2 endright.$

Решение. Запишем данную систему в матричной форме:

где $A=left(begin 2 & 1 & 1 \ 1 & -1 & 0 \ 3 & -1 & 2 endright)$ — матрица системы, $X=left(begin x_ <1>\ x_ <2>\ x_ <3>endright)$ — столбец неизвестных, $B=left(begin 2 \ -2 \ 2 endright)$ — столбец правых частей. Тогда

Найдем обратную матрицу $A^-1$ к матрице $A$ с помощью союзной матрицы:

Определитель матрицы $A$

$$Delta=left|begin 2 & 1 & 1 \ 1 & -1 & 0 \ 3 & -1 & 2 endright|=2 cdot(-1) cdot 2+1 cdot(-1) cdot 1+1 cdot 0 cdot 3-$$ $$-3 cdot(-1) cdot 1-(-1) cdot 0 cdot 2-1 cdot 1 cdot 2=-4 neq 0$$

Отсюда искомая матрица

Метод / Теорема Крамера

Теоретический материал по теме — метод Крамера.

Задание. Найти решение СЛАУ $left<begin 5 x_<1>+2 x_<2>=7 \ 2 x_<1>+x_<2>=9 endright.$ при помощи метода Крамера.

Решение. Вычисляем определитель матрицы системы:

$$Delta=left|begin 5 & 2 \ 2 & 1 endright|=5 cdot 1-2 cdot 2=1 neq 0$$

Так как $Delta neq 0$ , то по теореме Крамера система совместна и имеет единственное решение. вычислим вспомогательные определители. Определитель $Delta_<1>$ получим из определителя $Delta$ заменой его первого столбца столбцом свободных коэффициентов. Будем иметь:

$$Delta_<1>=left|begin 7 & 2 \ 9 & 1 endright|=7-18=-11$$

Аналогично, определитель $Delta_<2>$ получается из определителя матрицы системы $Delta$ заменой второго столбца столбцом свободных коэффициентов:

$$Delta_<2>=left|begin 5 & 7 \ 2 & 9 endright|=45-14=31$$

Тогда получаем, что

Ответ. $x_<-1>=-11$, $x_ <2>= 31$

Задание. При помощи формул Крамера найти решение системы $left<begin 2 x_<1>+x_<2>+x_<3>=2 \ x_<1>-x_<2>=-2 \ 3 x_<1>-x_<2>+2 x_<3>=2 endright.$

Решение. Вычисляем определитель матрицы системы:

$$Delta=left|begin 2 & 1 & 1 \ 1 & -1 & 0 \ 3 & -1 & 2 endright|=2 cdot(-1) cdot 2+1 cdot(-1) cdot 1+1 cdot 0 cdot 3-$$ $$-3 cdot(-1) cdot 1-(-1) cdot 0 cdot 2-1 cdot 1 cdot 2=-4 neq 0$$

Так как определитель матрицы системы неравен нулю, то по теореме Крамера система совместна и имеет единственное решение. Для его нахождения вычислим следующие определители:

$$Delta_<1>=left|begin 2 & 1 & 1 \ -2 & -1 & 0 \ 2 & -1 & 2 endright|=2 cdot(-1) cdot 2+(-2) cdot(-1) cdot 1+$$ $$+1 cdot 0 cdot 2-2 cdot(-1) cdot 1-(-1) cdot 0 cdot 2-(-2) cdot 1 cdot 2=4$$ $$Delta_<2>=left|begin 2 & 2 & 1 \ 1 & -2 & 0 \ 3 & 2 & 2 endright|=2 cdot(-2) cdot 2+1 cdot 2 cdot 1+2 cdot 0 cdot 3-$$ $$-3 cdot(-2) cdot 1-2 cdot 0 cdot 2-1 cdot 2 cdot 2=-4$$ $$Delta_<3>=left|begin 2 & 1 & 2 \ 1 & -1 & -2 \ 3 & -1 & 2 endright|=2 cdot(-1) cdot 2+1 cdot(-1) cdot 2+$$ $$+1 cdot(-2) cdot 3-3 cdot(-1) cdot 2-(-1) cdot(-2) cdot 2-1 cdot 1 cdot 2=-12$$

Метод Гаусса. Метод последовательного исключения неизвестных

Теоретический материал по теме — метод Гаусса.

Задание. Решить СЛАУ $left<begin 2 x_<1>+x_<2>+x_<3>=2 \ x_<1>-x_<2>=-2 \ 3 x_<1>-x_<2>+2 x_<3>=2 endright.$ методом Гаусса.

Решение. Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее строками приведем эту матрицу к ступенчатому виду (прямой ход) и далее выполним обратный ход метода Гаусса (сделаем нули выше главной диагонали). Вначале поменяем первую и вторую строку, чтобы элемент $a_<1>$ равнялся 1 (это мы делаем для упрощения вычислений):

Далее делаем нули под главной диагональю в первом столбце. Для этого от второй строки отнимаем две первых, от третьей — три первых:

Все элементы третьей строки делим на два (или, что тоже самое, умножаем на $frac<1><2>$:

Далее делаем нули во втором столбце под главной диагональю, для удобства вычислений поменяем местами вторую и третью строки, чтобы диагональный элемент равнялся 1:

От третьей строки отнимаем вторую, умноженную на 3:

Умножив третью строку на $left(-frac<1><2>right)$ , получаем:

Проведем теперь обратный ход метода Гаусса (метод Гассу-Жордана), то есть сделаем нули над главной диагональю. Начнем с элементов третьего столбца. Надо обнулить элемент $$tilde simleft(begin 1 & -1 & 0 & -2 \ 0 & 1 & 0 & 1 \ 0 & 0 & 1 & 3 endright)$$

Далее обнуляем недиагональные элементы второго столбца, к первой строке прибавляем вторую:

Полученной матрице соответствует система

$left<begin x_<1>+0 cdot x_<2>+0 cdot x_<3>=-1 \ 0 cdot x_<1>+x_<2>+0 cdot x_<3>=1 \ 0 cdot x_<1>+0 cdot x_<2>+x_<3>=3 endright.$ или $left<begin x_<1>=-1 \ x_<2>=1 \ x_<3>=3 endright.$

Однородные СЛАУ. Фундаментальная система решений

Теоретический материал по теме — однородные СЛАУ.

Задание. Выяснить, имеет ли однородная СЛАУ $left<begin 3 x-2 y=-1 \ x+3 y=7 endright.$ ненулевые решения.

Решение. Вычислим определитель матрицы системы:

$$Delta=left|begin 3 & -2 \ 1 & 3 endright|=9-(-2)=9+2=11 neq 0$$

Так как определитель не равен нулю, то система имеет только нулевое решение $x=y=0$

Ответ. Система имеет только нулевое решение.

Задание. Найти общее решение и ФСР однородной системы $Delta=left|begin 3 & -2 \ 1 & 3 endright|=9-(-2)=9+2=11 neq 0$

Решение. Приведем систему к ступенчатому виду с помощью метода Гаусса. Для этого записываем матрицу системы (в данном случае, так как система однородная, то ее правые части равны нулю, в этом случае столбец свободных коэффициентов можно не выписывать, так как при любых элементарных преобразованиях в правых частях будут получаться нули):

$$A=left(begin 1 & 1 & 0 & -3 & -1 \ 1 & -2 & 2 & -1 & 0 \ 4 & -2 & 6 & 3 & -4 \ 2 & 4 & -2 & 4 & -7 endright)$$

с помощью элементарных преобразований приводим данную матрицу к ступенчатому виду. От второй строки отнимаем первую, от третьей — четыре первых, от четвертой — две первых:

$$A simleft(begin 1 & 1 & 0 & -3 & -1 \ 0 & -2 & 2 & 2 & 1 \ 0 & -6 & 6 & 15 & 0 \ 0 & 2 & -2 & 10 & -5 endright)$$

Обнуляем элементы второго столбца, стоящие под главной диагональю, для этого от третьей строки отнимаем три вторых, к четвертой прибавляем вторую:

$$A simleft(begin 1 & 1 & 0 & -3 & -1 \ 0 & -2 & 2 & 2 & 1 \ 0 & 0 & 0 & 9 & -3 \ 0 & 0 & 0 & 12 & -4 endright)$$

От четвертой строки отнимем $$frac<4><3>$$ третьей и третью строку умножим на $$frac<1><3>$$ :

$$A simleft(begin 1 & 1 & 0 & -3 & -1 \ 0 & -2 & 2 & 2 & 1 \ 0 & 0 & 0 & 3 & -1 \ 0 & 0 & 0 & 0 & 0 endright)$$

Нулевые строки можно далее не рассматривать, тогда получаем, что

$$A simleft(begin 1 & 1 & 0 & -3 & -1 \ 0 & -2 & 2 & 2 & 1 \ 0 & 0 & 0 & 3 & -1 endright)$$

Далее делаем нули над главной диагональю, для этого от первой строки отнимаем третью, а ко второй строке прибавляем третью:

$$A simleft(begin 1 & 1 & 0 & -6 & 0 \ 0 & -2 & 2 & 5 & 0 \ 0 & 0 & 0 & 3 & -1 endright)$$

то есть получаем систему, соответствующую данной матрице:

Или, выразив одни переменные через другие, будем иметь:

Здесь $x_<2>, x_<4>$ — независимые (или свободные) переменные (это те переменные, через которые мы выражаем остальные переменные), $x_<1>,x_<3>,x_<5>$ — зависимые (связанные) переменные (то есть те, которые выражаются через свободные). Количество свободных переменных равно разности общего количества переменных $n$ (в рассматриваемом примере $n=5$ , так как система зависит от пяти переменных) и ранга матрицы $r$ (в этом случае получили, что $r=3$ — количество ненулевых строк после приведения матрицы к ступенчатому виду): $n-r=5-3=2$

Так как ранг матрицы $r=3$ , а количество неизвестных системы $n=5$ , то тогда количество решений в ФСР $n-r=5-3-2$ (для проверки, это число должно равняться количеству свободных переменных).

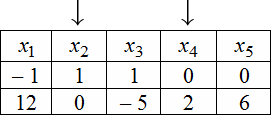
Для нахождения ФСР составляем таблицу, количество столбцов которой соответствует количеству неизвестных (то есть для рассматриваемого примера равно 5), а количество строк равно количеству решений ФСР (то есть имеем две строки). В заголовке таблицы выписываются переменные, свободные переменные отмечаются стрелкой. Далее свободным переменным придаются любые, одновременно не равные нулю значений и из зависимости между свободными и связанными переменными находятся значения остальных переменных. Для рассматриваемой задачи эта зависимость имеет вид:

Тогда придавая в первом случае, например, независимым переменным значения $x_<2>=1$ , $x_<4>=0$ получаем, что $left<begin x_<1>=-1+6 cdot 0=-1 \ x_<3>=1-frac<5> <2>cdot 0=1 \ x_<5>=3 cdot 0=0 endright.$ . Полученные значения записываем в первую строку таблицы. Аналогично, беря $x_<2>=0$ , $x_<4>=2$, будем иметь, что $x_<1>=12,x_<3>=-5,x_<5>=6$ , что и определяет второе решение ФСР. В итоге получаем следующую таблицу:

Эти две строчки и есть фундаментальным решением заданной однородной СЛАУ. Частное решение системы:

Общее решение является линейной комбинацией частных решений:

$$X=C_ <1>X_<1>+C_ <2>X_<2>=C_<1>left(begin -1 \ 1 \ 1 \ 0 \ 0 endright)+C_<2>left(begin 12 \ 0 \ -5 \ 2 \ 6 endright)$$

где коэффициенты $C_<1>, C_<2>$ не равны нулю одновременно. Или запишем общее решение в таком виде:

Придавая константам $C_<1>, C_<2>$ определенные значения и подставляя их в общее решение, можно будет находить частные решения однородной СЛАУ.

Базисные (основные) и свободные (неосновные) переменные. Общее и базисное решения системы линейных алгебраических уравнений. Первая часть.

В теме «Теорема Кронекера-Капелли» было указано, что если ранг расширеной матрицы системы $widetilde{A}$ и ранг матрицы системы $A$ равны между собой, то заданная система линейных алгебраических уравнений (СЛАУ) совместна, т.е. имеет решение. Вопрос о количестве этих решений разрешим с помощью следствия из теоремы Кронекера. Согласно ему, если $rang A=rangwidetilde{A} = n$ ($n$ – количество неизвестных), то СЛАУ имеет единственное решение. Если же $rang A=rangwidetilde{A} < n$, то количество решений заданной СЛАУ бесконечно.

Особый интерес представляет именно случай $rang A=rangwidetilde{A} < n$, которым и займёмся в этой теме. Так как $rang A=rangwidetilde{A}$, то обозначим эти ранги просто буквой $r$, т.е. $rang A=rangwidetilde{A}=r$. Итак, $r < n$ и система неопределена, т.е. имеет бесконечное количество решений.

Что означает фраза «ранг матрицы равен $r$»? Она означает, что есть хотя бы один минор $r$-го порядка, который не равен нулю. Напомню, что такой минор называется базисным. Базисных миноров может быть несколько. При этом все миноры, порядок которых выше $r$, равны нулю или не существуют.

Если коэффициенты при $r$ переменных совместной СЛАУ образуют базисный минор матрицы системы $A$, то эти $r$ переменных называют базисными или основными. Остальные $n-r$ переменных именуют свободными или неосновными.

Выбрать $r$ базисных переменных в общем случае можно различными способами. В примерах я покажу наиболее часто используемый способ выбора.

Решение СЛАУ, в котором все свободные переменные равны нулю, называется базисным.

Во всех изложенных ниже примерах матрицу системы будем обозначать буквой $A$, а расширенную матрицу системы – буквой $widetilde{A}$.

Пример №1

Решить СЛАУ $
left { begin{aligned}
& 3x_1-6x_2+9x_3+13x_4=9\
& -x_1+2x_2+x_3+x_4=-11;\
& x_1-2x_2+2x_3+3x_4=5.
end{aligned} right.$. Если система является неопределённой, указать базисное решение.

Решение

Итак, мы имеем СЛАУ, у которой 3 уравнения и 4 переменных: $x_1$, $x_2$, $x_3$, $x_4$. Так как количество переменных больше количества уравнений, то такая система не может иметь единственное решение (чуть позже мы строго докажем это предложение на основе теоремы Кронекера-Капелли). Найдём решения СЛАУ, используя метод Гаусса:

$$
left( begin{array} {cccc|c}
3 & -6 & 9 & 13 & 9 \
-1 & 2 & 1 & 1 & -11 \
1 & -2 & 2 & 3 & 5 end{array} right) rightarrow
left|begin{aligned}
& text{поменяем местами первую и третью}\
& text{строки, чтобы первым элементом}\
& text{первой строки стала единица.}
end{aligned}right| rightarrow \

rightarrowleft( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 5\
-1 & 2 & 1 & 1 & -11 \
3 & -6 & 9 & 13 & 9
end{array} right)
begin{array} {l} phantom{0} \ r_2+r_1\ r_3-3r_1 end{array} rightarrow

left( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 5\
0 & 0 & 3 & 4 & -6 \
0 & 0 & 3 & 4 & -6
end{array}right)
begin{array} {l} phantom{0} \ phantom{0}\r_3-r_2end{array} rightarrow \

rightarrowleft( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 5\
0 & 0 & 3 & 4 & -6 \
0 & 0 & 0 & 0 & 0
end{array}right)
$$

Мы завершили прямой ход метода Гаусса, приведя расширенную матрицу системы к ступенчатому виду. Слева от черты расположены элементы преобразованной матрицы системы, которую мы также привели к ступенчатому виду. Напомню, что если некая матрица приведена к ступенчатому виду, то её ранг равен количеству ненулевых строк.

И матрица системы, и расширенная матрица системы после эквивалентных преобразований приведены к ступенчатому виду; они содержат по две ненулевых строки. Вывод: $rang A=rangwidetilde{A} = 2$.

Итак, заданная СЛАУ содержит 4 переменных (обозначим их количество как $n$, т.е. $n=4$). Кроме того, ранги матрицы системы и расширенной матрицы системы равны между собой и равны числу $r=2$. Так как $r < n$, то согласно следствию из теоремы Кронекера-Капелли СЛАУ является неопределённой (имеет бесконечное количество решений).

Найдём эти решения. Для начала выберем базисные переменные. Их количество должно равняться $r$, т.е. в нашем случае имеем две базисные переменные. Какие именно переменные (ведь у нас их 4 штуки) принять в качестве базисных? Обычно в качестве базисных переменных берут те переменные, которые расположены на первых местах в ненулевых строках преобразованной матрицы системы, т.е. на «ступеньках». Что это за «ступеньки» показано на рисунке:

На «ступеньках» стоят числа из столбцов №1 и №3. Первый столбец соответствует переменной $x_1$, а третий столбец соответствует переменной $x_3$. Именно переменные $x_1$ и $x_3$ примем в качестве базисных.

В принципе, если вас интересует именно методика решения таких систем, то можно пропускать нижеследующее примечание и читать далее. Если вы хотите выяснить, почему можно в качестве базисных взять именно эти переменные, и нельзя ли выбрать иные – прошу раскрыть примечание.

Примечание. показатьскрыть

Базисные переменные выбраны: это $x_1$ и $x_3$. Остальные $n-r=2$ переменных (т.е. $x_2$ и $x_4$) являются свободными. Нам нужно выразить базисные переменные через свободные.

Я предпочитаю работать с системой в матричной форме записи. Для начала очистим полученную матрицу $left( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 5\
0 & 0 & 3 & 4 & -6 \
0 & 0 & 0 & 0 & 0
end{array}right)$ от нулевой строки:

$$
left( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 5\
0 & 0 & 3 & 4 & -6
end{array}right)
$$

Свободным переменным, т.е. $x_2$ и $x_4$, соответствуют столбцы №2 и №4. Перенесём эти столбцы за черту. Знак всех элементов переносимых столбцов изменится на противоположный:

Почему меняются знаки? Что вообще значит это перенесение столбцов? показатьскрыть

А теперь продолжим решение обычным методом Гаусса. Наша цель: сделать матрицу до черты единичной. Для начала разделим вторую строку на 3, а потом продолжим преобразования обратного хода метода Гаусса:

$$
left( begin{array} {cc|ccc}
1 & 2 & 5 & 2 & -3\
0 & 3 & -6 & 0 & -4
end{array}right)
begin{array} {l} phantom{0} \ 1/3cdot{r_2} end{array} rightarrow
left( begin{array} {cc|ccc}
1 & 2 & 5 & 2 & -3\
0 & 1 & -2 & 0 & -4/3
end{array}right)
begin{array} {l} r_1-2r_2 \ phantom{0} end{array} rightarrow \

rightarrow left(begin{array} {cc|ccc}
1 & 0 & 9 & 2 & -1/3\
0 & 1 & -2 & 0 & -4/3
end{array}right).
$$

Матрица до черты стала единичной, метод Гаусса завершён. Общее решение найдено, осталось лишь записать его. Если вспомнить, что четвёртый столбец соответствует переменной $x_2$, а пятый столбец – переменной $x_4$, то получим:

$$
left{begin{aligned}
& x_1=9+2x_2-frac{1}{3}x_4;\
& x_2in R;\
& x_3=-2-frac{4}{3}x_4;\
& x_4 in R.
end{aligned}right.
$$

Нами получено общее решение заданной СЛАУ. Чтобы найти базисное решение, нужно все свободные переменные приравнять к нулю. Т.е. полагая $x_2=0$ и $x_4=0$, будем иметь:

$$
left{begin{aligned}
& x_1=9;\
& x_2=0;\
& x_3=-2;\
& x_4=0.
end{aligned}right.
$$

Решение $x_1=9$, $x_2=0$, $x_3=-2$, $x_4=0$ и является базисным решением данной СЛАУ. В принципе, задавая свободным переменным иные значения, можно получить иные частные решения данной системы. Таких частных решений бесконечное количество. Например, принимая $x_2=-4$ и $x_4=1$, получим такое частное решение: $left{begin{aligned}
& x_1=frac{2}{3};\
& x_2=-4;\
& x_3=-frac{10}{3};\
& x_4=1.
end{aligned}right.$. Базисное решение, которые мы нашли ранее – лишь одно из бесконечного множества частных решений заданной СЛАУ.

Если есть желание, то полученное решение можно проверить. Например, подставляя $x_1=9+2x_2-frac{1}{3}x_4$ и $x_3=-2-frac{4}{3}x_4$ в левую часть первого уравнения, получим:

$$
3x_1-6x_2+9x_3+13x_4=3cdot left(9+2x_2-frac{1}{3}x_4right)-6x_2+9cdot left(-2-frac{4}{3}x_4right)+13x_4=9.
$$

Проверка первого уравнения увенчалась успехом; точно так же можно проверить второе и третье уравнения.

Ответ: Общее решение: $left{begin{aligned}
& x_1=9+2x_2-frac{1}{3}x_4;\
& x_2in R;\
& x_3=-2-frac{4}{3}x_4;\
& x_4 in R.
end{aligned}right.$, базисное решение: $
left{begin{aligned}
& x_1=9;\
& x_2=0;\
& x_3=-2;\
& x_4=0.
end{aligned}right.$.

Пример №2

Решить СЛАУ

$$left{begin{aligned}
& x_1-2x_2+4x_3+2x_5=0;\
& 4x_1-11x_2+21x_3-2x_4+3x_5=-1; \
& -3x_1+5x_2-13x_3-4x_4+x_5=-2.
end{aligned}right.$$

Если система является неопределённой, указать базисное решение.

Решение

Похожий пример уже был решен в теме «метод Крамера» (пример №4). Переменные $x_4$ и $x_5$ были перенесены в правые части, а дальше применялись стандартные операции метода Крамера. Однако такой метод решения не гарантирует достижения результата. Например, мы переносим некие переменные в правую часть, а оставшийся определитель оказывается равным нулю, – что тогда? Решать перебором? Поэтому гораздо удобнее применять преобразования метода Гаусса, как и в предыдущем примере.

$$
left( begin{array} {ccccc|c}
1 & -2 & 4 & 0 & 2 & 0\
4 & -11 & 21 & -2 & 3 & -1\
-3 & 5 & -13 & -4 & 1 & -2
end{array} right)
begin{array} {l} phantom{0} \r_2-4r_1\r_3+3r_1end{array} rightarrow

left( begin{array} {ccccc|c}
1 & -2 & 4 & 0 & 2 & 0\
0 & -3 & 5 & -2 & -5 & -1\
0 & -1 & -1 & -4 & 7 & -2
end{array} right) rightarrow \

rightarrow left|begin{aligned}
& text{поменяем местами вторую и третью}\
& text{строки, чтобы диагональным элементом}\
& text{второй строки стало число (-1).}
end{aligned}right|rightarrow

left( begin{array} {ccccc|c}
1 & -2 & 4 & 0 & 2 & 0\
0 & -1 & -1 & -4 & 7 & -2\
0 & -3 & 5 & -2 & -5 & -1
end{array} right)
begin{array} {l} phantom{0} \ phantom{0}\r_3-3r_1end{array} rightarrow \

rightarrow left( begin{array} {ccccc|c}
1 & -2 & 4 & 0 & 2 & 0\
0 & -1 & -1 & -4 & 7 & -2\
0 & 0 & 8 & 10 & -26 & 5
end{array} right).
$$

Матрица системы и расширенная матрица системы приведены к трапециевидной форме. Ранги этих матриц равны между собой и равны числу 3, т.е. $rang A=rangwidetilde{A} = 3$. Так как ранги равны между собой и меньше, чем количество переменных, то согласно следствию из теоремы Кронекера-Капелли данная система имеет бесконечное количество решений.

Количество неизвестных $n=5$, ранги обеих матриц $r=3$, поэтому нужно выбрать три базисных переменных и $n-r=2$ свободных переменных. Применяя тот же метод «ступенек», что и в предыдущем примере, выберем в качестве базисных переменных $x_1$, $x_2$, $x_3$, а в качестве свободных переменных – $x_4$ и $x_5$.

Столбцы №4 и №5, которые соответствуют свободным переменным, перенесём за черту. После этого разделим третью строку на 8 и продолжим решение методом Гаусса:

$$
left( begin{array} {ccc|ccc}
1 & -2 & 4 & 0 & 0 & -2\
0 & -1 & -1 & -2 & 4 & -7\
0 & 0 & 8 & 5 & -10 & 26
end{array} right)
begin{array} {l} phantom{0} \ phantom{0}\1/8cdot{r_3}end{array} rightarrow

left( begin{array} {ccc|ccc}
1 & -2 & 4 & 0 & 0 & -2\
0 & -1 & -1 & -2 & 4 & -7\
0 & 0 & 1 & 5/8 & -5/4 & 13/4
end{array} right)
begin{array} {l}r_1-4r_3 \r_2+r_3\ phantom{0}end{array} rightarrow \

left( begin{array} {ccc|ccc}
1 & -2 & 0 & -5/2 & 5 & -15\
0 & -1 & 0 & -11/8 & 11/4 & -15/4\
0 & 0 & 1 & 5/8 & -5/4 & 13/4
end{array} right)
begin{array} {l} phantom{0} \ -1cdot{r_2}\ phantom{0}end{array} rightarrow

left( begin{array} {ccc|ccc}
1 & -2 & 0 & -5/2 & 5 & -15\
0 & 1 & 0 & 11/8 & -11/4 & 15/4\
0 & 0 & 1 & 5/8 & -5/4 & 13/4
end{array} right)
begin{array} {l}r_1+2r_2 \ phantom{0}\ phantom{0}end{array} rightarrow\

rightarrowleft( begin{array} {ccc|ccc}
1 & 0 & 0 & 1/4 & -1/2 & -15/2\
0 & 1 & 0 & 11/8 & -11/4 & 15/4\
0 & 0 & 1 & 5/8 & -5/4 & 13/4
end{array} right)
$$

Из последней матрицы имеем общее решение заданной СЛАУ: $left{begin{aligned}
& x_1=frac{1}{4}-frac{1}{2}x_4-frac{15}{2}x_5;\
& x_2=frac{11}{8}-frac{11}{4}x_4+frac{15}{4}x_5;\
& x_3=frac{5}{8}-frac{5}{4}x_4+frac{13}{4}x_5;\
& x_4 in R;\
& x_5 in R.
end{aligned}right.$. Базисное решение получим, если приравняем свободные переменные к нулю, т.е. $x_4=0$, $x_5=0$:

$$
left{begin{aligned}
& x_1=frac{1}{4};\
& x_2=frac{11}{8};\
& x_3=frac{5}{8};\
& x_4=0;\
& x_5=0.
end{aligned}right.
$$

Ответ: Общее решение: $left{begin{aligned}
& x_1=frac{1}{4}-frac{1}{2}x_4-frac{15}{2}x_5;\
& x_2=frac{11}{8}-frac{11}{4}x_4+frac{15}{4}x_5;\
& x_3=frac{5}{8}-frac{5}{4}x_4+frac{13}{4}x_5;\
& x_4 in R;\
& x_5 in R.
end{aligned}right.$, базисное решение: $left{begin{aligned}
& x_1=frac{1}{4};\
& x_2=frac{11}{8};\
& x_3=frac{5}{8};\
& x_4=0;\
& x_5=0.
end{aligned}right.$.

Продолжение этой темы рассмотрим во второй части, где разберём ещё два примера с нахождением общего решения.

Как решать систему уравнений

О чем эта статья:

8 класс, 9 класс, ЕГЭ/ОГЭ

Основные понятия

Алгебра в 8 и 9 классе становится сложнее. Но если изучать темы последовательно и регулярно практиковаться в тетрадке и онлайн — ходить на уроки математики будет не так страшно.

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в исходное уравнение получилось верное числовое равенство.

Например, возьмем 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.

Уравнением можно назвать, например, равенство 3 + x = 7 с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Система уравнений — это несколько уравнений, для которых надо найти значения неизвестных, каждое из которых соответствует данным уравнениям.

Так как существует множество уравнений, составленных с их использованием систем уравнений также много. Поэтому для удобства изучения существуют отдельные группы по схожим характеристикам. Рассмотрим способы решения систем уравнений.

Линейное уравнение с двумя переменными

Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.

Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому уравнению и обращает его в верное числовое равенство.

Теорема, которую нужно запомнить: если в линейном уравнение есть хотя бы один не нулевой коэффициент при переменной — его графиком будет прямая линия.

Вот алгоритм построения графика ax + by + c = 0, где a ≠ 0, b ≠ 0:

Дать переменной 𝑥 конкретное значение x = x₁, и найти значение y = y₁ при ax₁ + by + c = 0.

Дать x другое значение x = x₂, и найти соответствующее значение y = y₂ при ax₂ + by + c = 0.

Построить на координатной плоскости xy точки: (x₁; y₁); (x₂; y₂).

Провести прямую через эти две точки и вуаля — график готов.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Система двух линейных уравнений с двумя переменными

Для ax + by + c = 0 можно сколько угодно раз брать произвольные значение для x и находить значения для y. Решений в таком случае может быть бесчисленное множество.

Система линейных уравнений (ЛУ) с двумя переменными образуется в случае, когда x и y связаны не одним, а двумя уравнениями. Такая система может иметь одно решение или не иметь решений совсем. Выглядит это вот так:

Из первого линейного уравнения a₁x + b₁y + c₁ = 0 можно получить линейную функцию, при условии если b₁ ≠ 0: y = k₁x + m₁. График — прямая линия.

Из второго ЛУ a₂x + b₂y + c₂ = 0 можно получить линейную функцию, если b₂ ≠ 0: y = k₂x + m₂. Графиком снова будет прямая линия.

Можно записать систему иначе:

Множеством решений первого ЛУ является множество точек, лежащих на определенной прямой, аналогично и для второго ЛУ. Если эти прямые пересекаются — у системы есть единственное решение. Это возможно при условии, если k₁ ≠ k₂.

Две прямые могут быть параллельны, а значит, они никогда не пересекутся и система не будет иметь решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ ≠ m₂.

Две прямые могут совпасть, и тогда каждая точка будет решением, а у системы будет бесчисленное множество решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ = m₂.

Метод подстановки

Разберем решение систем уравнений методом подстановки. Вот алгоритм при переменных x и y:

Выразить одну переменную через другую из более простого уравнения системы.

Подставить то, что получилось на место этой переменной в другое уравнение системы.

Решить полученное уравнение, найти одну из переменных.

Подставить поочередно каждый из найденных корней в уравнение, которое получили на первом шаге, и найти второе неизвестное значение.

Записать ответ. Ответ принято записывать в виде пар значений (x; y).

Потренируемся решать системы линейных уравнений методом подстановки.

Пример 1

Решите систему уравнений:

x − y = 4
x + 2y = 10

Выразим x из первого уравнения:

x − y = 4
x = 4 + y

Подставим получившееся выражение во второе уравнение вместо x:

x + 2y = 10
4 + y + 2y = 10

Решим второе уравнение относительно переменной y:

4 + y + 2y = 10
4 + 3y = 10
3y = 10 − 4
3y = 6
y = 6 : 3
y = 2

Полученное значение подставим в первое уравнение вместо y и решим уравнение:

x − y = 4
x − 2 = 4
x = 4 + 2
x = 6

Ответ: (6; 2).

Пример 2

Решите систему линейных уравнений:

x + 5y = 7
3x = 4 + 2y

Сначала выразим переменную x из первого уравнения:

x + 5y = 7
x = 7 − 5y

Выражение 7 − 5y подставим вместо переменной x во второе уравнение:

3x = 4 + 2y
3 (7 − 5y) = 4 + 2y

Решим второе линейное уравнение в системе:

3 (7 − 5y) = 4 + 2y
21 − 15y = 4 + 2y
21 − 15y − 2y = 4
21 − 17y = 4
17y = 21 − 4
17y = 17
y = 17 : 17
y = 1

Подставим значение y в первое уравнение и найдем значение x:

x + 5y = 7
x + 5 = 7
x = 7 − 5
x = 2

Ответ: (2; 1).

Пример 3

Решите систему линейных уравнений:

x − 2y = 3
5x + y = 4

Из первого уравнения выразим x:

x − 2y = 3
x = 3 + 2y

Подставим 3 + 2y во второе уравнение системы и решим его:

5x + y = 4
5 (3 + 2y) + y = 4
15 + 10y + y = 4
15 + 11y = 4
11y = 4 − 15
11y = −11
y = −11 : 11
y = −1

Подставим получившееся значение в первое уравнение и решим его:

x − 2y = 3
x − 2 (−1) = 3
x + 2 = 3
x = 3 − 2
x = 1

Ответ: (1; −1).

Метод сложения

Теперь решим систему уравнений способом сложения. Алгоритм с переменными x и y:

При необходимости умножаем почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами.

Складываем почленно левые и правые части уравнений системы.

Решаем получившееся уравнение с одной переменной.

Находим соответствующие значения второй переменной.

Запишем ответ в в виде пар значений (x; y).

Система линейных уравнений с тремя переменными

Системы ЛУ с тремя переменными решают так же, как и с двумя. В них присутствуют три неизвестных с коэффициентами и свободный член. Выглядит так:

Решений в таком случае может быть бесчисленное множество. Придавая двум переменным различные значения, можно найти третье значение. Ответ принято записывать в виде тройки значений (x; y; z).

Если x, y, z связаны между собой тремя уравнениями, то образуется система трех ЛУ с тремя переменными. Для решения такой системы можно применять метод подстановки и метод сложения.

Решение задач

Разберем примеры решения систем уравнений.

Задание 1. Как привести уравнение к к стандартному виду ах + by + c = 0?

5x − 8y = 4x − 9y + 3

5x − 8y = 4x − 9y + 3

5x − 8y − 4x + 9y = 3

Задание 2. Как решать систему уравнений способом подстановки

Выразить у из первого уравнения:

Подставить полученное выражение во второе уравнение:

Найти соответствующие значения у:

Задание 3. Как решать систему уравнений методом сложения

1. Решение систем линейных уравнений начинается с внимательного просмотра задачи. Заметим, что можно исключить у. Для этого умножим первое уравнение на минус два и сложим со вторым:

1. Решаем полученное квадратное уравнение любым способом. Находим его корни:

1. Найти у, подставив найденное значение в любое уравнение:

1. Ответ: (1; 1), (1; -1).

Задание 4. Решить систему уравнений

Решим второе уравнение и найдем х = 2, х = 5. Подставим значение переменной х в первое уравнение и найдем соответствующее значение у.

Задание 5. Как решить систему уравнений с двумя неизвестными

При у = -2 первое уравнение не имеет решений, при у = 2 получается:

Уравнения с двумя переменными (неопределенные уравнения)

Разделы: Математика

Обращение автора к данной теме не является случайным. Уравнения с двумя переменными впервые встречаются в курсе 7-го класса. Одно уравнение с двумя переменными имеет бесконечное множество решений. Это наглядно демонстрирует график линейной функции, заданный в виде ax + by=c. В школьном курсе учащиеся изучают системы двух уравнений с двумя переменными. В результате из поля зрения учителя и, поэтому ученика, выпадает целый ряд задач, с ограниченными условиями на коэффициент уравнения, а также методы их решения.

Речь идет о решении уравнения с двумя неизвестными в целых или натуральных числах.

В школе натуральные и целые числа изучаются в 4-6-х классах. К моменту окончания школы не все ученики помнят различия между множествами этих чисел.

Однако задача типа “решить уравнение вида ax + by=c в целых числах” все чаще встречается на вступительных экзаменах в ВУЗы и в материалах ЕГЭ.

Решение неопределенных уравнений развивает логическое мышление, сообразительность, внимание анализировать.

Я предлагаю разработку нескольких уроков по данной теме. У меня нет однозначных рекомендаций по срокам проведения этих уроков. Отдельные элементы можно использовать и в 7-м классе (для сильного класса). Данные уроки можно взять за основу и разработать небольшой элективный курс по предпрофильной подготовке в 9-м классе. И, конечно, этот материал можно использовать в 10-11 классах для подготовки к экзаменам.

Цель урока:

повторение и обобщение знаний по теме “Уравнения первого и второго порядка”
• воспитание познавательного интереса к учебному предмету
• формирование умений анализировать, проводить обобщения, переносить знания в новую ситуацию

Урок 1.

Ход урока.

1) Орг. момент.

2) Актуализация опорных знаний.

Определение. Линейным уравнением с двумя переменными называется уравнение вида

mx + ny = k, где m, n, k – числа, x, y – переменные.

Определение. Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.

Уравнения с двумя переменными, имеющими одни и те же решения, называются равносильными.

1. 5x+2y=12 (2)y = -2.5x+6

Данное уравнение может иметь сколько угодно решений. Для этого достаточно взять любое значение x и найти соответствующее ему значение y.

Пусть x = 2, y = -2.5•2+6 = 1

x = 4, y = -2.5•4+6 =- 4

Пары чисел (2;1); (4;-4) – решения уравнения (1).

Данное уравнение имеет бесконечно много решений.

3) Историческая справка

Неопределенные (диофантовы) уравнения – это уравнения, содержащие более одной переменной.

В III в. н.э. – Диофант Александрийский написал “Арифметику”, в которой расширил множество чисел до рациональных, ввел алгебраическую символику.

Так же Диофант рассмотрел проблемы решения неопределенных уравнений и им даны методы решения неопределенных уравнений второй и третьей степени.

4) Изучение нового материала.

Определение: Неоднородным диофантовым уравнением первого порядка с двумя неизвестными x, y называется уравнение вида mx + ny = k, где m, n, k, x, y Z k0

Если свободный член k в уравнении (1) не делится на наибольший общий делитель (НОД) чисел m и n, то уравнение (1) не имеет целых решений.

Пример: 34x – 17y = 3.

НОД (34; 17) = 17, 3 не делится нацело на 17, в целых числах решения нет.

Пусть k делится на НОД (m, n). Делением всех коэффициентов можно добиться, что m и n станут взаимно простыми.

Если m и n уравнения (1) взаимно простые числа, то это уравнение имеет по крайней мере одно решение.

Если коэффициенты m и n уравнения (1) являются взаимно простыми числами, то это уравнение имеет бесконечно много решений:

где (; ) – какое-либо решение уравнения (1), t Z

Определение. Однородным диофантовым уравнением первого порядка с двумя неизвестными x, y называется уравнение вида mx + ny = 0, где (2)

m, n, x, y Z

Если m и n – взаимно простые числа, то всякое решение уравнения (2) имеет вид

5) Домашнее задание. Решить уравнение в целых числах:

9x – 18y = 5

x + y= xy

Несколько детей собирали яблоки. Каждый мальчик собрал по 21 кг, а девочка по 15 кг. Всего они собрали 174 кг. Сколько мальчиков и сколько девочек собирали яблоки?

Замечание. На данном уроке не представлены примеры решения уравнений в целых числах. Поэтому домашнее задание дети решают исходя из утверждения 1 и подбором.

Урок 2.

1) Организационный момент

2) Проверка домашнего задания

5 не делится нацело на 9, в целых числах решений нет.

Методом подбора можно найти решение

3) Составим уравнение:

Пусть мальчиков x, x Z, а девочек у, y Z, то можно составить уравнение 21x + 15y = 174

Многие учащиеся, составив уравнение, не смогут его решить.

Ответ: мальчиков 4, девочек 6.

3) Изучение нового материала

Столкнувшись с трудностями при выполнении домашнего задания, учащиеся убедились в необходимости изучения их методов решений неопределенных уравнений. Рассмотрим некоторые из них.

I. Метод рассмотрения остатков от деления.

Пример. Решить уравнение в целых числах 3x – 4y = 1.

Левая часть уравнения делится на 3, следовательно, должна делиться и правая часть. Рассмотрим три случая.

1. Если y = 3m, m Z, то 4y + 1= 4•3m + 1 = 12m + 1 не делится на 3.
2. Если y = 3 m + 1, то 4y +1 = 4• (3m + 1)+1 = 12m + 5 не делится на 3.
3. Если y = 3 m + 2, то 4y +1 = 4• (3m + 2)+1 = 12m + 9 делится на 3, поэтому 3x = 12m + 9, следовательно, x = 4m + 3, а y = 3m + 2.

Ответ: где m Z.

Описанный метод удобно применять в случае, если числа m и n не малы, но зато разлагаются на простые сомножители.

Пример: Решить уравнения в целых числах.

Пусть y = 4n, тогда 16 — 7y = 16 – 7•4n = 16 – 28n = 4*(4-7n) делится на 4.

y = 4n+1, тогда 16 – 7y = 16 – 7• (4n + 1) = 16 – 28n – 7 = 9 – 28n не делится на 4.

y = 4n+2, тогда 16 – 7y = 16 – 7• (4n + 2) = 16 – 28n – 14 = 2 – 28n не делится на 4.

y = 4n+3, тогда 16 – 7y = 16 – 7• (4n + 3) = 16 – 28n – 21 = -5 – 28n не делится на 4.

Следовательно, y = 4n, тогда

4x = 16 – 7•4n = 16 – 28n, x = 4 – 7n

Ответ: , где n Z.

II. Неопределенные уравнения 2-ой степени

Сегодня на уроке мы лишь коснемся решения диофантовых уравнений второго порядка.

И из всех типов уравнений рассмотрим случай, когда можно применить формулу разности квадратов или другой способ разложения на множители.

Пример: Решить уравнение в целых числах.

13 – простое число, поэтому оно может быть разложено на множители лишь четырьмя способами: 13 = 13•1 = 1•13 = (-1)(-13) = (-13)(-1)

Рассмотрим эти случаи

а) =>

б) =>

в) =>

г) =>

4) Домашнее задание.

Примеры. Решить уравнение в целых числах:

а)

2x = 4	2x = 5	2x = 5
x = 2	x = 5/2	x = 5/2
y = 0	не подходит	не подходит
2x = -4	не подходит	не подходит
x = -2
y = 0

б)

в)

Итоги. Что значит решить уравнение в целых числах?

Какие методы решения неопределенных уравнений вы знаете?

Упражнения для тренировки.

1) Решите в целых числах.

а) 8x + 12y = 32	x = 1 + 3n, y = 2 — 2n, n Z
б) 7x + 5y = 29	x = 2 + 5n, y = 3 – 7n, n Z
в) 4x + 7y = 75	x = 3 + 7n, y = 9 – 4n, n Z
г) 9x – 2y = 1	x = 1 – 2m, y = 4 + 9m, m Z
д) 9x – 11y = 36	x = 4 + 11n, y = 9n, n Z
е) 7x – 4y = 29	x = 3 + 4n, y = -2 + 7n, n Z
ж) 19x – 5y = 119	x = 1 + 5p, y = -20 + 19p, p Z
з) 28x – 40y = 60	x = 45 + 10t, y = 30 + 7t, t Z

2) Найти целые неотрицательные решения уравнения:

а) 8x + 65y = 81	x = 2, y = 1
б) 17x + 23y = 183	x = 4, y = 5

3) Найти все пары целых чисел (x; y), удовлетворяющие следующим условиям

а) x + y = xy	(0;0), (2;2)
б)	(1;2), (5;2), (-1;-1), (-5;-2)

Число 3 можно разложить на множители:

в)	(11;12), (-11;-12), (-11;12), (11;-12)
г)	(24;23), (24;-23), (-24;-23), (-24;23)
д)	(48;0), (24;1), (24;-1)
е)	x = 3m; y = 2m, mZ
ж) y = 2x – 1	x = m: y = 2m – 1, m Z
з)	x = 2m; y = m; x = 2m; y = -m, m Z
и)	решений нет

4) Решить уравнения в целых числах

	(-3;-2), (-1;1), (0;4), (2;-2), (3;1), (5;4)
(x — 3)(xy + 5) = 5	(-2;3), (2;-5), (4;0)
(y + 1)(xy – 1)=3	(0;-4), (1;-2), (1;2)
	(-4;-1), (-2;1), (2;-1), (4;1)
	(-11;-12), (-11;12), (11;-12), (11;12)
	(-24;23), (-24;23), (24;-23), (24;23)

5) Решить уравнения в целых числах.

Детская энциклопедия “Педагогика”, Москва, 1972 г.

Алгебра-8, Н.Я. Виленкин, ВО “Наука”, Новосибирск, 1992 г.

Конкурсные задачи, основанные на теории чисел. В.Я. Галкин, Д.Ю. Сычугов. МГУ, ВМК, Москва, 2005г.

Задачи повышенной трудности в курсе алгебры 7-9 классов. Н.П. Косрыкина. “Просвещение”, Москва, 1991 г.

Алгебра 7, Макарычев Ю.Н., “Просвещение”.

Исследование СЛАУ. Общие сведения

В данной статье мы расскажем о методах, видах, условиях и определениях исследований решений систем линейных уравнений, что такое метод Кронекера-Капели, а также приведем примеры.

Общие сведения (определения, условия, методы, виды)

Системы линейных алгебраических уравнений с n неизвестными могут иметь:

• единственное решение;
• бесконечное множество решение (неопределенные СЛАУ);
• ни одного решения (несовместные СЛАУ).

Пример 1

Система x + y + z = 1 2 x + 2 y + 2 z = 3 не имеет решений, поэтому она несовместна.

Система x + y = 1 2 x + 7 y = — 3 имеет единственное решение x = 2 ; y = 1 .

Система x + y = 1 2 x + 2 y = 2 3 x + 3 y = 3 имеет бесконечное множество решений x = t y = 1 — t при — ∞ t ∞ .

Перед решением системы уравнений необходимо исследовать систему, т.е. ответить на следующие вопросы:

• Совместна ли система?
• Если система совместна, то, какое количество решений она имеет — одно или несколько?
• Как найти все решения?

Если система малоразмерна при m = n , то ответить на поставленные вопросы можно при помощи метода Крамера:

• если основной определитель системы, то система совместна и имеет единственное решение, которое вычисляется методом Крамера;
• если, и один из вспомогательных определителей, то система не является совместной, т.е. не имеет решений;
• если и все, и один из коэффициентов СЛАУ, то система не является определенной и имеет бесконечное множество решений.

Ранг матрицы и его свойства

Бывают случаи, которые выбиваются из представленных вариантов решения СЛАУ, например, линейные уравнения с большим количеством уравнений и неизвестных.

Для такого варианта решения существует ранг матрицы, который представляет собой алгоритм действий в случае решения системы матрицы, когда

В математике выделяют следующие подходы к определению ранга матрицы:

• при помощи понятия линейной зависимости/независимости строк/столбцов матрицы. Ранг равен максимальному количеству независимых строк (столбцов) матрицы
• при помощи понятия минора матрицы в качестве наивысшего порядка минора, который отличается от нуля. Минор матрицы порядка k — определитель k-го порядка, составленный из элементов, которые стоят на пересечении вычеркиваемых k-строк и k-столбцов матрицы;
• при помощи метода Гаусса. По завершении прямого хода ранг матрицы равняется количеству ненулевых строк.

Обозначение ранга матрицы: r ( A ) , r g ( A ) , r A .

Свойства ранга матрицы:

1. квадратная невырожденная матрица обладает рангом, который отличается от нуля;
2. если транспонировать матрицу, то ранг матрицы не изменяется;
3. если поменять местами 2 параллельные строки или 2 параллельных столбца, ранг матрицы не изменяется;
4. при удалении нулевого столбца или строки ранг матрицы не изменяется;
5. ранг матрицы не изменяется, если удалить строку или столбец, которые являются линейной комбинацией других строк;
6. при умножении все элементов строки/столбца на число k н е р а в н о н у л ю ранг матрицы не изменяется;
7. ранг матрицы не больше меньшего из ее размеров: r ( А ) ≤ m i n ( m ; n ) ;
8. когда все элементы матрицы равны нулю, то только тогда r ( A ) = 0 .

Пример 2

А 1 = 1 1 1 2 2 2 3 3 3 , B 1 = 1 0 0 0 0 0

r ( A 1 ) = 1 , r ( B 1 ) = 1

А 2 = 1 2 3 4 0 5 6 7 0 0 0 0 ; В 2 = 1 1 3 1 2 1 4 3 1 2 5 0 5 4 13 6