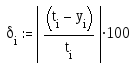Как найти решение краевой задачи

Численные методы решения краевых задач

Постановка задачи и основные положения

Рассмотрим двухточечные краевые задачи, часто встречающиеся в приложениях, например, при решении задач вариационного исчисления, оптимального управления, механики жидкости и газа и др. Пусть дано обыкновенное дифференциальное уравнение

[math]F bigl(x,y(x),y'(x),ldots,y^{(n)}(x)bigr)=0,quad a leqslant x leqslant b,qquad (7.1)[/math]

и краевые условия

[math]begin{gathered}varphi_{i}bigl(y(a),y'(a),ldots,y^{(n-1)}(a)bigr)=0,quad i=1,2,ldots,L,\[2pt] psi_{j}bigl(y(b),y'(b),ldots,y^{(n-1)}(b)bigr)=0,quad j=L+1,ldots,n, end{gathered}qquad (7.2)[/math]

где [math]F bigl(x,y,y’,ldots,y^{(n)}bigr);~ varphi_{i}bigl(y,y’,ldots,y^{(n-1)}bigr),~ i=overline{1,L};~ psi_{j}bigl(y,y’,ldots,y^{(n-1)}bigr),~ j=overline{L+1,n}[/math] — функции указанных аргументов, заданные в некоторой области их изменения; [math]L[/math] и [math](n-L)[/math] — число условий на левом и правом концах отрезка [math][a,b][/math] соответственно. Общее количество условий равно порядку дифференциального уравнения. Требуется найти функцию [math]y=y(x)[/math], которая на отрезке [math][a,b][/math] удовлетворяет уравнению (7.1), а на концах отрезка — краевым условиям (7.2).

Если уравнения (7.1),(7.2) линейны относительно искомой функции и ее производных, то краевая задача называется линейной.

Для простоты ограничимся частным случаем линейной краевой задачи для дифференциального уравнения второго порядка [math](n=2)[/math], которая наиболее часто ставится в вычислительной практике и записывается в виде

где [math]p(x),, q(x),, f(x)in C_2[a,b][/math] — заданные функции, а [math]alpha_0,,alpha_1,, beta_0,, beta_1,,A,,B[/math] — заданные числа, [math]alpha_{j}^2+beta_{j}^2>0,~ j=0;1[/math]. Требуется найти функцию [math]y(x)[/math], удовлетворяющую уравнению (7.3) и краевым условиям (7.4). Краевые условия при [math]alpha_{j}ne0,~ beta_{j}ne0,~ j=0;1[/math], задают линейную связь между значениями искомого решения и его производной на концах отрезка [math][a,b][/math].

В простейшем случае, когда [math]beta_0=0,~ beta_1=0[/math], краевые условия задают на концах отрезка [math][a,b][/math] только значения функции [math]y(a),,y(b)[/math]. Такие функциональные условия называют краевыми условиями первого рода. В этом случае краевая задача называется первой краевой задачей.

В случае, когда [math]alpha_0=0,~ alpha_1=0[/math], т.е. на концах отрезка заданы только значения производных, краевые условия являются дифференциальными. Такие краевые условия называют условиями второго рода или «мягкими». Последнее название обусловлено тем, что они определяют на концах отрезка [math][a,b][/math] всего лишь наклоны интегральных кривых, а не значения функции [math]y(x)[/math]. В этом случае задача (7.3),(7.4) называется второй краевой задачей.

В общем случае, когда [math]alpha_0[/math] и (или) [math]alpha_1;~beta_0[/math] и (или) [math]beta_1[/math] не равны нулю, краевые условия носят функционально-дифференциальный характер и называются условиями третьего рода. Тогда задача (7.3),(7.4) называется третьей краевой задачей.

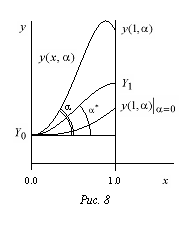
Например, условия [math]y(a)=A,~ y(b)=B[/math] являются условиями первого рода. Геометрически это означает, что при решении первой краевой задачи требуется найти интегральную кривую уравнения (7.3), проходящую через данные точки [math](a,A),, (b,B)[/math] (рис. 7.1,а). Условия [math]y'(a)=A,, y'(b)=B[/math] являются условиями второго рода. Геометрически вторая краевая задача сводится к отысканию интегральной кривой уравнения, пересекающей прямые [math]x=a,~ x=b[/math] под заданными углами [math]alpha,,beta[/math], где [math]operatorname{tg}alpha=A,~ operatorname{tg}beta=B[/math] (рис. 7.1,6). Условия [math]y'(a)=A,~ y(b)=B[/math] являются частным случаем краевых условий третьего рода, так как [math]alpha_0=0,~ beta_0=1,[/math] [math]alpha_1=1,~ beta_1=0[/math]. Геометрически данная краевая задача сводится к отысканию интегральной кривой уравнения, проходящей через точку [math](b,B)[/math] и пересекающей прямую [math]x=a[/math] под данным углом [math]alpha[/math], где [math]operatorname{tg}alpha= A[/math] (рис. 7.1,в).

В общем случае краевая задача может:

а) иметь единственное решение;

б) не иметь решений;

в) иметь несколько или бесконечно много решений.

Утверждение 7.1 (о существовании и единственности решения краевой задачи (7.3),(7.4)). Для того чтобы существовало единственное решение краевой задачи (7.3),(7.4), необходимо и достаточно, чтобы однородная краевая задача

[math]begin{gathered}y»+p(x)y’-q(x)y=0,quad a leqslant x leqslant b,\ alpha_0cdot y(a)+ beta_0cdot y'(a)=0,\ alpha_1cdot y(b)+ beta_1cdot y'(b)=0 end{gathered}[/math]

имела только тривиальное решение [math]y(x)equiv0[/math].

Пример 7.1. Найти аналитическое решение следующих краевых задач:

а) [math]y»+y=1,~ 0 leqslant x leqslant frac{pi}{2},~ y'(0)=0,~ y! left(frac{pi}{2}right)-y’! left(frac{pi}{2}right)=2[/math] (третья краевая задача);

б) [math]y»+y=-x,~ 0 leqslant x leqslant 1,~ y(0)=0,~ y(1)=0[/math] (первая краевая задача).

Решение

Рассмотренный метод нахождения аналитического решения краевых задач применим для ограниченного класса задач. Поэтому в вычислительной практике используются численные и приближенно-аналитические методы, позволяющие найти приближенное решение краевых задач, точные аналитические решения которых не могут быть найдены.

---

Метод сеток

Рассмотрим линейную краевую задачу с краевыми условиями первого рода (первую краевую задачу):

где [math]p(x),q(x),f(x)in C_2[a,b][/math] — заданные функции; [math]A,,B[/math] — заданные числа.

Очевидно, любой отрезок [math][a,b][/math], на котором ищется решение краевой задачи, можно привести к отрезку [math][0;1][/math] с помощью линейного преобразования [math]widetilde{x}= frac{x-a}{b-a}[/math]. Действительно, тогда новая переменная [math]widetilde{x}in [0;1][/math]. В результате без ограничения общности краевая задача (7.5) может быть решена сначала на отрезке [math][0;1][/math], а затем это решение с помощью преобразования [math]x=a+(b-a)cdot widetilde{x}[/math] может быть записано на отрезке [math][a,b][/math]. То же относится и к исследованию свойств полученного решения.

Утверждение 7.2 (о единственности решения краевой задачи (7.5)). Если функции [math]p(x),q(x),f(x)[/math] принадлежат классу [math]C_2[a,b],~ q(x) geqslant 0[/math] на [math][0;1][/math], то краевая задача (7.5) имеет единственное решение [math]y(x)in C_4[0;1][/math].

Для решения задачи (7.5) применим метод сеток, получаемый путем аппроксимации первой и второй производных. Введем равномерную сетку (где [math]n[/math] — число отрезков разбиения)

[math]Omega_n= bigl{x_0,x_1,ldots,x_nbigr},quad x_{i}=x_0+icdot h,quad i=overline{0,n}lquad h=frac{b-a}{n},.[/math]

Функции [math]p(x),q(x),f(x)[/math] заменяются их проекциями на сетку [math]Omega_n[/math], то есть [math]p(x)to p(x_{i})=p_i,[/math] [math]q(x)to q(x_{i})=q_i,[/math] [math]f(x)to f(x_{i})= f_i,[/math]. Вместо точного решения [math]y(x)[/math] отыскивается некоторое приближение [math]widehat{y}_{i}= widehat{y}(x_{i})approx y(x_{i}),~ i=overline{0,n}[/math]. Первая и вторая производные аппроксимируются на трехточечном шаблоне [math](x_{i-1},x_{i},x_{i+1})[/math] по формулам второго порядка (5.10),(5.14):

Краевые условия для этой задачи аппроксимируются точно, т.е. [math]y(a)[/math] и [math]y(b)[/math] заменяются на [math]widehat{y}_{0}[/math] и [math]widehat{y}_{n}[/math]. После замены от дифференциальной задачи (7.5) переходим к разностной схеме:

[math]frac{widehat{y}_{i+1}-2widehat{y}_{i}+ widehat{y}_{i-1}}{h^2}+ p_{i} frac{}{}-q_{i}widehat{y}_{i}= f_{i},quad i=overline{1,n-1},quad widehat{y}_{0}=A,~ widehat{y}_{n}=B,[/math]

представляющей собой систему алгебраических уравнений трехдиагонального вида:

где [math]alpha_{i}=frac{1}{h^2}-frac{p_{i}}{2h},~ gamma_{i}=frac{1}{h^2}+ frac{p_{i}}{2h},~ beta_{i}= frac{2}{h^2}+q_{i},~ delta_{i}=f_{i}[/math]. Здесь система (7.6) записана для внутренних узлов сетки [math]Omega_n[/math]. Она является трехдиагональной системой линейных алгебраических уравнений и решается методом прогонки.

Замечания

1. Изложенный метод сеток допускает обобщение. Например, его можно применять для решения нелинейной краевой задачи:

где [math]F(x,y)[/math] — нелинейная по [math]y[/math] функция (в общем случае, который здесь не рассматривается, функция [math]F[/math] зависит также и от [math]y'[/math]).

Рассуждая аналогично рассмотренному выше способу, перейдем к разностной задаче:

В силу нелинейности правой части полученная алгебраическая система является нелинейной и для ее решения нельзя использовать метод прогонки в том виде, в каком он изложен для линейной задачи. Поэтому для ее решения используем метод простых итераций, с помощью которого при фиксированном [math]k[/math] (номер итерации) система алгебраических уравнений (7.8) превращается в линейную, так как величины, входящие в правую часть системы, известны из предыдущей итерации. Действительно, для k-й итерации получается система (которая решается на каждой итерации методом прогонки)

[math]widehat{y}_{i-1}^{(k)}-2widehat{y}_{i}^{(k)}+ widehat{y}_{i+1}^{(k)}= h^2F bigl(x_{i}, widehat{y}_{i}^{(k-1)}bigr),quad i=overline{1,n-1},quad widehat{y}_{0}^{(k)}=A,~ widehat{y}_{n}^{(k)}=B.[/math]

Можно показать, что итерации сходятся при выполнении условия [math]q=frac{1}{8}(x_n-x_0)^2M_1<1,[/math] [math]M_1=max_{[a,b]}left|frac{partial F}{partial y}right|[/math] с линейной скоростью.

2. Краевые условия второго и третьего рода в задаче, аналогичной (7.5), могут быть аппроксимированы несколькими способами.

Первый способ. Использование аппроксимационных формул (5.4) первого порядка

В силу первого порядка этих аппроксимаций метод сеток в этом случае также будет иметь первый порядок аппроксимации.

Второй способ. Применение формулы Тейлора и ее преобразование с использованием дифференциального уравнения. Таким способом может быть достигнут второй порядок аппроксимации.

Третий способ. Применение левосторонней (5.8) и правосторонней (5.9) формул, аппроксимирующих производные со вторым порядком:

3. Порядок аппроксимации схемы определяется минимальным порядком аппроксимации дифференциального уравнения и краевых условий.

---

Алгоритм применения метода сеток

1. Задать сетку [math]Omega_n[/math] на отрезке [math][a,b][/math] или сформировать ее из условий достижения требуемой точности.

2. Используя аппроксимационные формулы (5.10),(5.14) и один из трех способов аппроксимации краевых условий (в случае, если они второго или третьего рода), перейти от исходной дифференциальной задачи к системе алгебраических уравнений (разностной схеме), неизвестными в которой являются величины, «близкие» к решению краевой задачи в узлах сетки.

3. Найти решение разностной задачи путем решения трехдиагональной системы уравнений и таким образом определить приближенное решение краевой задачи.

Пример 7.2. Найти приближенное решение краевой задачи [math]y»+y=1,~ 0 leqslant x leqslant frac{pi}{2},[/math] [math]y'(0)=0,[/math] [math]y! left(frac{pi}{2}right)-y’! left(frac{pi}{2}right)=2[/math] при [math]n=3[/math], используя первый способ аппроксимации краевых условий. Записать разностные схемы для второго и третьего способов при произвольном [math]n[/math].

Решение

---

Методы минимизации невязки

Описываемые здесь методы относятся к приближенно-аналитическим и могут применяться при решении достаточно широкого класса задач. На основе одного из приближенно-аналитических методов (метода Галеркина) строится метод конечных элементов, излагаемый в разд. 7.5.

Рассмотрим линейную краевую задачу (7.3),(7.4). Ее решение будем искать в виде

где [math]varphi_0(x), varphi_1(x), ldots, varphi_m(x)[/math] — элементы заданной системы функций; [math]a_1,ldots,a_m[/math] — неопределенные коэффициенты. Заданная система функций называется базисной, и ее элементы должны удовлетворять условиям:

а) [math]varphi_{j}(x)in C_2[a,b],~ j=overline{0,m}[/math];

б) при любом конечном [math]m[/math] функции [math]varphi_1(x), ldots, varphi_m(x)[/math] линейно независимы на отрезке [math][a,b][/math];

в) [math]varphi_0(x)[/math] удовлетворяет краевым условиям (7.4)

г) [math]varphi_1(x), ldots, varphi_m(x)[/math] удовлетворяют условиям

Функция

называется невязкой. Она равна разности левой и правой частей уравнения (7.3), образующейся при подстановке [math]widehat{y}_{m}(x)[/math] вместо [math]y(x)[/math] в дифференциальное уравнение, и характеризует степень отклонения функции [math]widehat{y}_{m}(x)[/math] от точного решения краевой задачи. Если при некоторых значениях коэффициентов [math]a_1,ldots,a_m[/math] невязка тождественно равна нулю на отрезке [math][a,b][/math], а именно

то функция [math]widehat{y}_{m}(x)[/math] совпадает с точным решением краевой задачи (7.3),(7.4), так как удовлетворяются и уравнение, и краевые условия.

Однако при решении краевых задач, как правило, не удается получить невязку тождественно равной нулю. Поэтому ставится задача: вычислить коэффициенты [math]a_1,ldots,a_m[/math] таким образом, чтобы невязка в каком-либо смысле стала меньшей. Полученные в результате коэффициенты определяют приближенное решение (7.11).

Выражение для невязки [math]varepsilon(x; a_1,ldots, a_m)[/math] с учетом (7.11) удобно записывать в следующей эквивалентной форме:

где [math]Lwidehat{y}_{m}equiv widehat{y},»_{m}(x)+ p(x)widehat{y},’_{m}(x)-q(x) widehat{y}_{m}(x),~ L[/math] — линейный оператор задачи (7.3),(7.4) (выполняются равенства [math]L(y+z)= Ly+Lz,[/math] [math]L(Cy)=Ccdot Ly[/math] для любых [math]y,,z[/math] и постоянной [math]C[/math]).

Рассмотрим различные методы, минимизирующие невязку.

А. Метод коллокации. На интервале [math](a,b)[/math] задаются т точек [math]x_1,ldots, x_n[/math] (точек коллокации) и требуется, чтобы в каждой из них невязка (7.14) обращалась в нуль:

С учетом (7.16) эта система принимает вид

Если полученная система [math]m[/math] линейных уравнений совместна, то из нее определяются коэффициенты [math]a_1,ldots, a_m[/math], которые затем подставляются в (7.11).

Б. Метод наименьших квадратов (непрерывный вариант). Неизвестные коэффициенты [math]a_1,ldots, a_m[/math] должны обеспечивать минимум интеграла от квадрата невязки:

[math]I= intlimits_{a}^{b} varepsilon^2(x,a_1,ldots, a_m),dxto min_{a_1,ldots, a_m}.[/math]

Для решения задачи применяются необходимые условия безусловного экстремум:

Подставляя (7.16) в (7.19), получаем систему [math]m[/math] линейных алгебраических уравнений для нахождения коэффициентов [math]a_1,ldots, a_mcolon[/math]

где [math]textstyle{langle f,grangle= intlimits_{a}^{b} f(x)g(x)dx}[/math] — скалярное произведение. В системе (7.20) все скалярные произведения предварительно вычисляются.

В. Метод наименьших квадратов (дискретный вариант). Неизвестные коэффициенты [math]a_1,ldots,a_m[/math] должны обеспечивать минимум суммы квадратов значений невязки в заданном наборе точек [math]x_1,ldots,x_n;~ n geqslant m[/math], то есть [math]x_{i}in (a,b),~ i=overline{1,n}colon[/math]

[math]S= sumlimits_{i=1}^{n} varepsilon^2(x_{i}, a_1,ldots,a_m)to min_{a_1,ldots,a_m}.[/math]

Для решения задачи применяются необходимые условия безусловного экстремума

Отсюда следует система [math]m[/math] линейных уравнений для нахождения коэффициентов [math]a_1,ldots,a_m[/math], которая по форме записи совпадает с (7.20), но скалярное произведение определяется по формуле [math]textstyle{(f,g)= sumlimits_{i=1}^{n} f(x_{i})g(x_{i})}[/math].

Замечание. При [math]n=m[/math] результаты, полученные точечным методом наименьших квадратов и методом коллокации, совпадают. В этом случае точки [math]x_1,ldots, x_n[/math] являются точками коллокации.

Г. Метод моментов (взвешенных невязок). Неизвестные коэффициенты ах,…,ат находятся из условия равенства нулю /и моментов невязки:

где [math]psi_{j}(x),~ j=overline{1,m}[/math] — функции, удовлетворяющие условиям:

а) [math]psi_{j}(x)in C[a,b],~ j=overline{1,m}[/math];

б) функции [math]psi_{j}(x)[/math] являются элементами системы степеней [math]x[/math] или системы тригонометрических функций.

Функции [math]psi_{j}(x),~ j=overline{1,m}[/math] называются весовыми, а условие (7.22) является условием ортогональности невязки к весовым функциям.

Д. Метод Галсркина. Он является частным случаем метода моментов, когда в качестве весовых функций используются базисные. Коэффициенты [math]a_1,ldots,a_m[/math] находятся из условия ортогональности функций базисной системы [math]varphi_1(x),ldots, varphi_{m}(x)[/math] к невязке:

Отсюда следует система [math]m[/math] линейных уравнений для нахождения коэффициентов:

где [math]textstyle{langle f,grangle= intlimits_{a}^{b} f(x)g(x)dx}[/math] — скалярное произведение. В системе (7.24) все скалярные произведения предварительно вычисляются.

Известно, что при достаточно большом [math]m[/math] условие (7.23) обеспечивает малость невязки в среднем.

---

Алгоритм применения методов минимизации невязки

1. В выражении (7.11) выбрать систему базисных функций, задать число [math]m[/math] в зависимости от требуемой точности.

2. Найти коэффициенты [math]a_1,ldots,a_m[/math] путем решения одной из систем алгебраических уравнений (7.18),(7.20),(7.24) в зависимости от выбранного метода.

3. Выписать приближенное решение краевой задачи по формуле (7.11).

Пример 7.3. Найти приближенное решение краевой задачи [math]y»+y=-x,~0 leqslant x leqslant 1,[/math] [math]y(0)=0,~ y(1)=0[/math] методом коллокации, интегральным методом наименьших квадратов, методом Галеркина

Решение

Пример 7.4. Найти приближенное решение краевой задачи [math]y»+2xy’-2y=2x^2,~ 0 leqslant x leqslant 1,[/math] [math]y'(0)=-2,~ y(1)+y'(1)=0[/math] методом Галеркина.

Решение

---

Методы сведения краевой задачи к задаче Коши

Метод стрельбы. Суть этого метода заключается в сведении решения краевой задачи к многократному решению задачи Коши. Принцип построения метода стрельбы рассмотрим на примере нелинейной краевой задачи:

где [math]f(x,y,y’)[/math] — нелинейная функция, обусловливающая нелинейность дифференциального уравнения (7.25).

При введении новой переменой [math]z=y'[/math] уравнение (7.25) записывается в нормальной форме Коши, а краевые условия видоизменяются:

где[math]eta=y'(a)=operatorname{tg}alpha[/math] — параметр, равный тангенсу угла наклона интегральной кривой в точке [math]x=a[/math]. Угол [math]alpha[/math] (параметр [math]eta[/math]) в процессе многократного решения краевой задачи должен принять такое значение, чтобы интегральная кривая «попала в цель», т.е. в точку [math](b,B)[/math] (рис.7.2 ,а). В общем случае полученное при некотором значении [math]eta[/math] решение [math]y(x,eta)[/math] не будет удовлетворять условию [math]y(b,eta)=B[/math] на правом конце отрезка.

Следовательно, требуется найти такое значение параметра [math]eta[/math], чтобы оно было корнем нелинейного уравнения [math]Phi(eta)= y(b,n)-B=0[/math]. Для решения этого уравнения, как правило, используются методы половинного деления или секущих. В случае использования метода половинного деления сначала делают «пробные» выстрелы при выбранных наугад или в соответствии с некоторым алгоритмом значениях [math]eta[/math] до тех пор, пока среди значений [math]Phi(eta)[/math] не окажется двух противоположных по знаку. Им соответствует начальный интервал неопределенности, который далее последовательно сокращается путем деления пополам. При применении метода секущих используется формула

[math]eta^{(k+1)}=eta^{(k)}-frac{Phi(eta^{(k)})cdot bigl[eta^{(k)}-eta^{(k-1)}bigr]}{Phi(eta^{(k)})-Phi(eta^{(k-1)})},quad k=1,2,ldots[/math]

где [math]eta^{(0)},,eta^{(1)}[/math] — начальные значения параметра, [math]k[/math] — номер итерации. Итерации прекращаются при выполнении условия окончания [math]bigl|Phi(eta^{(k)})bigr| leqslant varepsilon[/math] или [math]bigl|eta^{(k+1)}-eta^{(k)}bigr| leqslant varepsilon[/math] с некоторым положительным [math]varepsilon[/math], характеризующим точность решения задачи.

Замечание. Точность решения краевой задачи зависит не только от точности определения параметра [math]eta[/math], но также и от точности решения соответствующей задачи Коши. Поэтому одновременно с уточнением параметра [math]eta[/math] рекомендуется уменьшать шаг при решении задачи Коши, либо выбирать более точный метод.

Рассмотрим применение метода стрельбы для решения линейной краевой задачи (7.3),(7.4):

[math]begin{gathered}y»+p(x)y’-q(x)y=f(x),quad a leqslant x leqslant b,\ alpha_0y(a)+ beta_0y'(a)=A,\ alpha_1y(b)+ beta_1y'(b)=B. end{gathered}[/math]

Методика решения линейной краевой задачи

1. Решить две задачи Коши

при условии

а именно при [math]beta_0ne0[/math] задается [math]y(a)=eta[/math], тогда [math]y'(a)= frac{A-alpha_0eta}{beta_0}[/math], а при [math]beta_0=0[/math] задается [math]y'(a)=eta[/math] и тогда [math]y(a)=frac{A}{alpha_0}[/math] с разными произвольными значениями [math]eta[/math], то есть [math]eta=eta^{(0)}[/math] и [math]eta=eta^{(1)}[/math].

2. Найти значения [math]Phi(eta^{(0)}),, Phi(eta^{(1)})[/math] функции [math]Phi(eta)= alpha_1cdot y(b,eta)+ beta_1cdot y'(b,eta)-B[/math] и новое значение параметра:

[math]eta^{(2)}=eta^{(1)}-frac{Phi(eta^{(1)})cdot bigl[eta^{(1)}-eta^{(0)}bigr]}{Phi(eta^{(1)})-Phi(eta^{(0)})},.[/math]

3. Решить краевую задачу (7.28),(7.29) при [math]eta=eta^{(2)}[/math]. В результате получится приближенное решение исходной линейной краевой задачи, точность которого определяется точностью решения задачи Коши при значении [math]eta=eta^{(2)}[/math].

Таким образом, в силу линейности поставленной краевой задачи соответствующая задача Коши решается только три раза.

Пример 7.5. Методом стрельбы найти приближенное решение нелинейной краевой задачи

[math]ycdot y»-y’^2=0,quad y(0)=1,quad y(1)=2,!718.[/math]

Соответствующую задачу Коши решить явным методом Эйлера с шагом [math]h=0,!01[/math], а параметр [math]eta[/math] вычислить методом половинного деления.

Решение

Пример 7.6. Найти приближенное решение краевой задачи [math]y»+y=-x,~0 leqslant x leqslant 1,[/math] [math]y(0)=0,~ y(1)=0[/math] методом стрельбы.

Решение

---

Метод дифференциальной прогонки

Отличие метода дифференциальной прогонки от вышеизложенного метода стрельбы заключается в том, что решаются вспомогательные задачи Коши не для исходного дифференциального уравнения, а для других уравнений меньшего порядка. Рассмотрим его применение для решения линейной краевой задачи (7.3),(7.4).

Методика решения линейной краевой задачи

Первый случай: [math]beta_0ne0[/math].

Прямая прогонка. Решить две независимые друг от друга задачи Коши относительно [math]Z_1(x)[/math] и [math]Z_2(x)[/math] на отрезке [math][a,b]colon[/math]

[math]begin{aligned}&Z’_1=-Z_1^2-p(x)Z_1+q(x),quad Z_1(a)=-frac{alpha_0}{beta_0},;\ &Z’_2=-Z_2cdot bigl[Z_1+p(x)bigr]+f(x),quad Z_2(x)=frac{A}{beta_0},. end{aligned}[/math]

Обратная прогонка. Решить задачу Коши

[math]y’=Z_1(x)y+ Z_2(x),quad a leqslant x leqslant b;qquad y(b)=frac{B-beta_1Z_2(b)}{alpha_1+ beta_1Z_1(b)},.[/math]

Второй случай: [math]alpha_0ne0[/math].

Прямая прогонка. Решить две независимые друг от друга задачи Коши:

[math]begin{aligned}& u’_1=-u_1^2q(x)+ u_1p(x)+1,quad a leqslant x leqslant b,& & u_1(a)=-frac{beta_0}{alpha_0},;\ & u’_2=-u_1(x)cdot bigl[u_2q(x)+ f(x)bigr],quad a leqslant x leqslant b,& & u_2(a)=-frac{A}{alpha_0},.end{aligned}[/math]

Обратная прогонка. Решить задачу Коши

[math]u_1(x)y’=y-u_2(x),quad a leqslant x leqslant b;qquad y(b)=frac{Bu_1(b)+ beta_1u_2(b)}{beta_1+ alpha_1u_1(b)},.[/math]

Обратная прогонка в обоих случаях дает приближенное решение исходной краевой задачи.

Пример 7.7. Найти приближенное решение краевой задачи [math]y»+(x+1)y’-2y=2,~ 0 leqslant x leqslant 1,[/math] [math]y(0)-y'(0)=-1,[/math] [math]y(1)=4[/math] методом дифференциальной прогонки. При прямой и обратной прогонке использовать явный метод Эйлера с шагом [math]h=0,!02[/math].

Решение

---

Метод конечных элементов

Метод конечных элементов нашел широкое практическое применение при решении уравнений с частными производными. Здесь описывается его применение к решению линейной краевой задачи (7.3),(7.4) для обыкновенного дифференциального уравнения, в которой искомая функция зависит от одной переменной.

Суть метода конечных элементов заключается в следующем:

а) область определения функции [math]y(x)[/math], удовлетворяющей дифференциальному уравнению и краевым условиям, разбивается на конечное число подобластей, называемых конечными элементами;

б) в каждом элементе фиксируется конечное число узловых точек, общих с узловыми точками соседних элементов, в которых должны быть найдены узловые значения искомой функции;

в) искомая функция на каждом элементе аппроксимируется линейной комбинацией базисных функций с коэффициентами, равными узловым значениям искомой функции;

г) для нахождения коэффициентов применяется метод взвешенных невязок (метод Галеркина).

Разобьем отрезок [math][a,b][/math] на [math]n[/math] конечных элементов (в рассматриваемой задаче ими являются отрезки) [math]e_1,e_2,ldots,e_n[/math] с [math](n+1)[/math] нумерованными узлами [math]x_1,x_2,ldots,x_{n+1}[/math] (рис. 7.3).

Каждому нумерованному узлу [math]x_{i},~ i=overline{1,n+1}[/math], поставим в соответствие кусочно-линейную глобальную базисную функцию [math]varphi_{i}(x)[/math], принимающую в данном узле значение единица, а в остальных — нулевое значение (рис. 7.4):

Для обеспечения унифицированного определения глобальных базисных функций необходимо ввести в рассмотрение дополнительные узлы [math]x_{0}[/math] и [math]x_{n+2}[/math]. Тогда глобальные базисные функции [math]varphi_1(x),, varphi_{n+1}(x)[/math] будут определены на отрезках [math][x_0,x_2][/math] и [math][x_{n},x_{n+2}][/math] соответственно. Значения функций [math]varphi_1(x),, varphi_{n+1}(x)[/math] на отрезках [math][x_0,x_1][/math] и [math][x_{n+1}, x_{n+2}][/math], примыкающих к отрезку [math][a,b][/math], в дальнейших расчетах не используются.

Используя глобальные базисные функции, будем искать решение краевой задачи в виде (где [math]widehat{y}_{i}[/math] — значения искомой функции в узлах [math]x_{i},~ i=overline{1,n+1}[/math] (коэффициенты))

Требуется найти такие значения [math]widehat{y}_{i},~ i=overline{1,n+1}[/math], чтобы выполнялось условие (7.23) (см. метод Галеркина). Функция, аппроксимирующая искомое решение на каждом конечном элементе, называется функцией элемента. Для элемента [math]e_{i}[/math] с узлами [math]x_{i}[/math] и [math]x_{i+1}[/math] определим локальные базисные функции (рис. 7.5):

где нижний индекс у базисной функции соответствует номеру узла, а верхний -номеру конечного элемента. На каждом элементе [math]e_{i},~ i=overline{1,n}[/math], обе локальные базисные функции линейны, причем в узлах этого элемента одна из них равна единице, т.е. [math]varphi_{i}^{e_{i}}(x_{i})=1[/math] и [math]varphi_{i+1}^{e_{i}}(x_{i+1})=1[/math]. Функция элемента е, может быть выражена с помощью локальных базисных функций и узловых значений [math]widehat{y}_{i}[/math] и [math]widehat{y}_{i+1}[/math] по формуле

Тогда приближенное решение (7.31) краевой задачи можно представить в форме

В силу свойств локальных базисных функций на элементе [math]e_{i}[/math] функция элемента является линейной и принимает в узле [math]x_{i}[/math] значение [math]widehat{y}_{i}[/math], а в узле [math]x_{i+1}[/math] значение [math]widehat{y}_{i+1}[/math] (рис. 7.5). Если в краевой задаче заданы условия первого рода, т.е. [math]y(a)=A,~ y(b)=B[/math], то при рассмотрении элемента [math]e_1[/math] следует положить [math]widehat{y}_1=A[/math], так как [math]x_1=a[/math], а при рассмотрении элемента [math]e_n[/math] положить [math]widehat{y}_{i+1}=B[/math], поскольку [math]x_{n+1}=b[/math]. Тогда краевые условия первого рода для решения, записанного в виде (7.31) или эквивалентном ему (7.34), выполняются автоматически. Для учета условий второго и третьего рода применяется обобщенный подход (см. пример 7.8). В целом аппроксимация (7.31) является кусочно-линейной. На рис. 7.6 показано применение формулы (7.31) для аппроксимации некоторой произвольной функции [math]y=y(x)[/math].

Рассмотрим некоторые теоретические аспекты применения метода конечных элементов на типовом примере линейной краевой задачи с краевыми условиями первого рода.

Пример 7.8. Найти приближенное решение краевой задачи [math]y»-y=0,~ 0 leqslant x leqslant 1,[/math] [math]y(0)=0,~ y(1)=1[/math] методом конечных элементов, полагая число конечных элементов, равным трем.

Решение

---

Алгоритм применения метода конечных элементов

1. Разбить отрезок [math][a,b][/math] на [math]n[/math] конечных элементов [math]e_1,ldots, e_n[/math] и представить решение в виде (7.31).

2. Для каждого конечного элемента составить матрицу [math]K^{i},~ i=overline{1,n}[/math], по формуле (7.42), элементы которой вычисляются согласно (7.41).

3. Сформировать матрицу [math]K[/math] в результате суммирования матриц [math]K^{i}[/math], вектор [math]f[/math] с учетом (7.40) и составить систему (7.38).

4. Учесть краевые условия и решить систему (7.38). В результате найти значения [math]widehat{y}_1,ldots, widehat{y}_{n+1}[/math] и выписать приближенное решение по формуле (7.31).

Теперь применим описанную методику к решению поставленной задачи.

1. Положим [math]n=3[/math] при равномерной сетке. Тогда [math]h=x_{i+1}-x_{i}= frac{1}{3}= text{const}[/math], a глобальные базисные функции, определяемые по формулам (7.30), изображены на рис. 7.7.

Решение задачи ищется в форме (где [math]widehat{y}_1, widehat{y}_2, widehat{y}_3, widehat{y}_4[/math] подлежат определению)

2. Составим матрицу [math]K^{i}[/math] для каждого элемента [math]e_1,e_2,e_3[/math]. С этой целью вычислим отдельные элементы матрицы по формулам (7.41). Для конечного элемента ех[math]e_1[/math]получим

[math]begin{aligned}K_{1,1}^{e_1}&= intlimits_{x_1}^{x_2}! left[left(frac{d varphi_1^{e_1}(x)}{dx} right)^2+ bigl(varphi_1^{e_1}(x) bigr)^2right]!dx= intlimits_{0}^{1!not{phantom{|}},,3}! left(left[frac{d}{dx}frac{x_2-x}{x_2-x_1}right]^2+ left(frac{x_2-x}{x_2-x_1}right)^2right)!dx=\ &=intlimits_{0}^{1!not{phantom{|}},,3}! left[9+ 9!left(frac{1}{3}-xright)^2right]!dx= left.{left[9x-frac{9}{3}! left(frac{1}{3}-xright)^2right]}right|_{0}^{1!not{phantom{|}},,3}= frac{28}{9},;\[4pt] K_{1,2}^{e_1}&= intlimits_{x_1}^{x_2}! left[frac{d varphi_1^{e_1}(x)}{dx}cdot frac{d varphi_2^{e_1}(x)}{dx}+ varphi_1^{e_1}(x)cdot varphi_2^{e_1}(x)right]!dx=\ &= intlimits_{0}^{1!not{phantom{|}},,3}! left[frac{d}{dx}! left(frac{x_2-x}{x_2-x_1}right)cdot frac{d}{dx}! left(frac{x-x_1}{x_2-x_1}right)+ frac{x_2-x}{x_2-x_1}cdot frac{x-x_1}{x_2-x_1}right]!dx=\ &= intlimits_{0}^{1!not{phantom{|}},,3}! left[-3cdot3+ 9! left(frac{1}{3}-xright)!(x-0)right]!dx=-frac{53}{18},;\[4pt] &quad K_{2,1}^{e_1}= K_{1,2}^{e_1};quad K_{2,2}^{e_1}=K_{1,1}^{e_1}.end{aligned}[/math]

Здесь нижние индексы соответствуют связям узлов для элемента, указанного в верхнем индексе. В результате для конечного элемента [math]e_1[/math] получаем

[math]K^1= begin{pmatrix}dfrac{28}{9}&-dfrac{53}{18}&0&0\[9pt]-dfrac{53}{18}& dfrac{28}{9}&0&0\[8pt] 0&0&0&0\ 0&0&0&0 end{pmatrix}[/math]

Так как сетка равномерная, дифференциальное уравнение с постоянными коэффициентами и базисные функции «одинаковые», то для конечных элементов е2,е3 в Решаемой задаче аналогично имеем

[math]K^2=begin{pmatrix}0&0&0&0\[5pt] 0&dfrac{28}{9}&-dfrac{53}{18}&0\[9pt] 0&-dfrac{53}{18}& dfrac{28}{9}&0\[8pt] 0&0&0&0 end{pmatrix}!,qquad K^3= begin{pmatrix} 0&0&0&0\ 0&0&0&0\[5pt] 0&0& dfrac{28}{9}&-dfrac{53}{18}\[9pt] 0&0&-dfrac{53}{18}& dfrac{28}{9}end{pmatrix}!.[/math]

3. Складывая матрицы элементов [math]e_1,,e_2,,e_3[/math], находим результат ансамблирования:

[math]K= begin{pmatrix} dfrac{28}{9}&-dfrac{53}{18}&0&0\[9pt]-dfrac{53}{18}& dfrac{56}{9}&-dfrac{53}{18}&0\[9pt] 0&-dfrac{53}{18}& dfrac{56}{9}&-dfrac{53}{18}\[9pt] 0&0&-dfrac{53}{18}& dfrac{28}{9}end{pmatrix}!.[/math]

По формуле (7.40) с учетом (7.43) определим компоненты вектора / правой части системы (7.38):

[math]f_1= left.{varphi_1(x)cdot frac{dwidehat{y}(x)}{dx}}right|_{0}^{1}=left.{-frac{d widehat{y}(x)}{dx}}right|_{x=0}[/math], поскольку [math]varphi_1(1)=0[/math] и [math]varphi_1(0)=0[/math];

[math]f_2= left.{varphi_2(x)cdot frac{dwidehat{y}(x)}{dx}}right|_{0}^{1}=0[/math], так как [math]varphi_2(1)=0[/math] и [math]varphi_2(0)=0[/math];

[math]f_3= left.{varphi_3(x)cdot frac{dwidehat{y}(x)}{dx}}right|_{0}^{1}=0[/math], так как [math]varphi_3(1)=0[/math] и [math]varphi_3(0)=0[/math];

[math]f_4= left.{varphi_4(x)cdot frac{dwidehat{y}(x)}{dx}}right|_{0}^{1}=left.{frac{d widehat{y}(x)}{dx}}right|_{x=0}[/math], поскольку [math]varphi_4(1)=1[/math] и [math]varphi_4(0)=0[/math];

С учетом полученных результатов запишем систему (7.38):

Из краевых условий [math]y(0)=0,~ y(1)=1[/math] следует, что [math]widehat{y}_1= y(0)=0,~ widehat{y}_4= y(1)=1[/math]. Тогда в системе (7.44) можно исключить первое и четвертое уравнения, положив в остальных [math]widehat{y}_1=0,~ widehat{y}_4=1[/math]. В итоге получим систему

[math]begin{pmatrix}dfrac{56}{9}&-dfrac{53}{18}\[9pt]-dfrac{53}{18}& dfrac{56}{9} end{pmatrix}!cdot! begin{pmatrix}widehat{y}_2\[6pt] widehat{y}_3end{pmatrix}= begin{pmatrix}0\[6pt] dfrac{53}{18}end{pmatrix}!.[/math]

Отсюда [math]widehat{y}_2=0,!2885;~ widehat{y}_3=0,!6088[/math]. Точные значения [math]y(x_2)= y(1!!not{phantom{|}},3)=0,!2889;[/math] [math]y(x_3)= y(2!!not{phantom{|}},3)= 0,!6102[/math]. Приближенное решение задачи имеет вид

[math]widehat{y}(x)= 0,!2885cdot varphi_2(x)+ 0,!6088cdot varphi_3(x)+ varphi_4(x).[/math]

Замечание. В случае краевых условий второго или третьего рода следует воспользоваться более общей схемой метода Галеркина с учетом невязки краевых условий, содержащих производные. Например, рассмотрим задачу [math]y»-y=0,[/math] [math]y(0)=0,~ y'(1)=1[/math]. Вместо (7.35) используем следующее условие:

где [math]widetilde{varphi}_{j}(x)=0,~ j=overline{1,n+1}[/math] — весовые функции, задаваемые в общем случае независимо от функций [math]varphi_{j}(x)=0,~ j=overline{1,n+1}[/math]. Как и ранее, краевое условие первого рода на левом конце может быть выполнено автоматически. Далее интегрируем по частям:

[math]intlimits_{0}^{1}! left[frac{d widehat{y}(x)}{dx}cdot frac{d varphi_{j}(x)}{dx}+ widehat{y}(x)cdot varphi_{j}(x)right]!dx+ left.{varphi_{j}(x)frac{d widehat{y}(x)}{dx} }right|_{0}^{1}+ left.{left[widetilde{varphi}_{j}(x)left(frac{d widehat{y}(x)}{dx}-1right)right]}right|_{x=1}=0.[/math]

Базисные функции [math]widetilde{varphi}_{j}(x),~ j=overline{1,n+1}[/math], следует подбирать так, чтобы члены, содержащие краевые условия с производными, и члены с производными первого порядка, возникающими в той же точке в процессе интегрирования по частям, уничтожились. Положим [math]widetilde{varphi}_{j}(x)=-varphi_{j}(x),[/math] [math]j=overline{1,n+1}[/math]. Тогда имеем

[math]intlimits_{0}^{1}! left[frac{d widehat{y}(x)}{dx}cdot frac{d varphi_{j}(x)}{dx}+ widehat{y}(x)cdot varphi_{j}(x)right]!dx= left.{-varphi_{j}(x)frac{d widehat{y}(x)}{dx} }right|_{x=0}+ varphi_{j}(1),quad j=overline{1,n+1}.[/math]

Полагая [math]n=3[/math] и рассуждая аналогично случаю краевых условий первого рода с учетом равенств

[math]varphi_1(0)=1,~ varphi_2(0)=0,~ varphi_3(0)=0,~ varphi_4(0)=0,qquad varphi_1(1)=0,~ varphi_2(1)=0,~ varphi_3(1)=0,~ varphi_4(1)=0,[/math]

получаем систему

[math]begin{pmatrix} dfrac{28}{9}&-dfrac{53}{18}&0&0\[9pt]-dfrac{53}{18}& dfrac{56}{9}&-dfrac{53}{18}&0\[9pt] 0&-dfrac{53}{18}& dfrac{56}{9}&-dfrac{53}{18}\[9pt] 0&0&-dfrac{53}{18}& dfrac{28}{9}end{pmatrix}!cdot! begin{pmatrix}widehat{y}_1\[6pt] widehat{y}_2\[6pt] widehat{y}_3\[6pt] widehat{y}_4end{pmatrix}= begin{pmatrix} left.{-dfrac{d widehat{y}(x)}{dx}}right|_{x=0}\[6pt] 0\[6pt] 0\[6pt]1 end{pmatrix}!.[/math]

Краевое условие [math]y(0)=0[/math] на левом конце учитывается вычеркиванием первого уравнения и приравниванием [math]widehat{y}_1=0[/math] в остальных уравнениях.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

10.4. Краевая задача для дифференциального уравнения второго порядка

Как было сказано в п. 10.1, в силу основной теоремы су­ществования и единственности решения для уравнения второ­го порядка

Определена задача Коши, когда в точке Х = X0 заданы значения неизвестной функции и ее производной:

Если выполнены условия теоремы 10.1, то задача Коши (10.13), (10.14) однозначно определяет частное решение.

Однако существует и другой тип задач для дифференци­альных уравнений второго порядка — значения неизвестной функции задаются в двух разных точках. Иными словами, при решении уравнения (10.13) на интервале (А, B) рассмотрим Гра­ничные условия наиболее простого вида на концах интервала

В этом случае уравнение (10.13) совместно с условиями (10.14) называется Первой краевой задачей для уравнения второго по­рядка. Поскольку второе условие в (10.15) равносильно второ­му условию в (10.14), то указанная краевая задача может иметь единственное решение, т. е. определять единственным образом частное решение дифференциального уравнения (10.13), прохо­дящее через точки (X1, Y1), (X2, Y2). Так, для линейного диффе­ренциального уравнения второго порядка первая краевая зада­ча имеет решение, если определитель системы линейных алгеб­раических уравнений относительно произвольных постоянных C1 и С2

Реализующей краевые условия (10.15), отличен от нуля. Здесь в соответствии с теоремой 10.4 (X) — частное решение не­однородного уравнения, У1(х) и У2(х) — линейно независимые решения соответствующего однородного уравнения. В таком случае краевая задача с условиями (10.15) однозначно опреде­ляет частное решение дифференциального уравнения (10.8).

Пример 1. Найти частное решение уравнения

Удовлетворяющее краевым условиям

Общее решение этого уравнения было найдено в примере 4 и. 10.3:

Для отыскания частного решения, соответствующего данным краевым условиям, подставим это решение в эти краевые усло­вия. Получаем систему линейных уравнений относительно про­извольных постоянных С1 и С2

Нетрудно видеть, что определитель этой системы не равен ну­лю, т. е. данная краевая задача имеет решение. Вычитая из второго уравнения первое, умноженное на 2, получаем С2, а затем из первого уравнения — С1:

Отсюда решение данной краевой задачи как частное решение дифференциального уравнения, проходящее через точки (0, 1) и (ln 2, 2), имеет вид

Лекция 4. Краевые задачи для дифференциальных уравнений. Задача Штурма-Лиувилля.

Будем рассматривать однородное линейное уравнение второго порядка

Ly ≡ a₂(x)y» + a₁(x)y’ + a₀(x)y = 0. Его можно записать по-другому:

Однородное уравнение Ly = 0 и неоднородное Ly = f, как известно, имеют бесконечное множество решений. На практике часто бывает нужно из множества решений выделить только одно. Для этого задают некоторые дополнительные условия. Если это начальные условия у(х₀) = у_o, y'(x_o) = y₁, то получают задачу Коши. Если задают дополнительные условия на концах некоторого отрезка, то получают задачу, которая называется краевой задачей. Условия, которые задаются на концах отрезка, называются краевыми условиями. Краевые условия иногда именуют также граничными условиями и тогда говорят о граничной задаче.
Мы будем задавать линейные краевые условия вида

где α₁, α₂, β₁, β₂, A, B — заданные числа, причем по крайней мере одно из чисел α₁, α₂, и одно из чисел β₁, β₂, отличны от нуля. Если в (16) хотя бы одно из чисел А и В не равно нулю, то краевые условия называют неоднородными. Если А = В = 0, то условия (16) называются однородными. Краевая задача называется однородной, если рассматривается однородное уравнение (15) Ly = 0 и однородные краевые условия (16). Решением краевой задачи называется такое решение дифференциального уравнения, которое удовлетворяет заданным краевым условиям. Заметим сразу, что однородная краевая задача всегда имеет решение у ≡ 0 (тривиальное решение).

Наряду с уравнением (15) рассмотрим уравнение

содержащее некоторый числовой параметр λ. Здесь функции р(х), q(x), r(x) действительные, а число λ может быть, вообще говоря, и комплексным. Краевая задача (17), (16) при А = В = 0 является однородной. Поэтому при любых λ она имеет тривиальное решение. Нас будут интересовать такие значения λ, при которых эта задача обладает не только тривиальными решениями.

Задача Штурма-Лиувилля. Найти те значения параметра λ, при которых уравнение (17) имеет нетривиальное решение, удовлетворяюшее однородным краевым условиям (16). В дальнейшем будем ее записывать в виде

λy = 0, l₁y = 0, l₂y = 0>.
Те значения параметра λ, при которых задача Штурма-Лиувилля имеет ненулевое решение, называются собственными значениями (собственными числами) задачи, а сами эти решения — собственными функциями. Задачу Штурма-Лиувилля называют также задачей на собственные значения. В силу однородности уравнения и краевых условий собственные функции задачи Штурма-Лиувилля определены с точностью до постоянного множителя. Это означает, что если y(х) -собственная функция при некотором значении λ, то произведение Cy(x), где С — произвольная постоянная, также является собственной функцией при том же значении параметра λ. В связи с этим часто в качестве собственной функции рассматривают нормированную функцию у <х), у которой ||у(х)|| = 1. Такая собственная функция определена, по существу, однозначно (с точностью до знака ±). Далее мы подробно изучим наиболее простой случай задачи Штурма-Лиувилля, когда уравнение имеет вид

Из множества краевых условий вида (16) ограничимся тремя частными случаями:

1) краевые условия первого рода

2) краевые условия второго рода

3) краевые условия третьего рода

Общая задача Штурма-Лиувилля будет обладать свойствами, очень похожими на свойства в этих простых случаях, если на коэффициенты уравнения (17) наложить дополнительные условия: р(х), q(x), f(x) -непрерывные функции, причем р(х) имеет, кроме того, непрерывную производную на [а, b], р(х) > 0, q(x) ≥ 0.

Основные свойства собственных значений и собственных функций задачи Штурма-Лиувилля.

Лемма. Определитель Вронского двух собственных функций задачи Штурма-Лиувилля на концах отрезка [а, b] равен нулю.

Доказательство. Напомним, что определителем Вронского функций у = y₁(x) и у = у₂(x) называется определитель вида

Рассмотрим однородные краевые условия общего вида (16). Пусть у₁(x) и у₂(x) — две любые собственные функции. Это означает, что в точке x = а выполняются равенства

Числа α₁, и α₂ не могут одновременно равняться нулю. Значит, алгебраическая система двух однородных уравнений с двумя неизвестными имеет ненулевое решение. Это возможно только в том случае, когда определитель этой системы равен нулю:

Этот определитель совпадает с определителем Вронского в точке x = а, то есть W(a) = 0.

Аналогичные рассуждения, проведенные для точки x = b, показывают, что W(b) = 0.

Свойство 1. Две собственные функции задачи Штурма-Лиувилля, соответствующие одному и тому же собственному значению λ, линейно зависимые.

Доказательство. Так как собственные функции являются решениями одного и того же однородного уравнения (17) (по условию число λ одно), то в случае их линейной независимости определитель Вронского не равен нулю ни в одной точке отрезка [а, b]. Это противоречит только что доказанной лемме. Следовательно, y₁(x) и у₂(x) — линейно зависимые функции.

Свойство 2. Две собственные функции у₁(x) и у₂(x), соответствующие различным собственным значениям λ₁ и λ₂ (λ₁ ≠ λ₂), на отрезке [а, b] ортогональны.

Доказательство этого свойства проведем для собственных функций такой задачи, в которой уравнение имеет вид (18). Составим определитель Вронского функций у₁ и у₂ и продифференцируем его:

Так как у₁ и у₂ — решения уравнения (18) при λ = λ₁ и λ = λ₂, соответственно, то получим

Проинтегрируем по отрезку [а, b] левую и правую части полученного равенства. С учетом леммы будем иметь

По условию λ₁ — λ₂ ≠0, следовательно
Функции y₁(x) 0 и у₂(х) 0, поэтому
Значит, y₁(x) и у₂(х) на отрезке [а, b] ортогональны.

Если уравнение, входящее в задачу Штурма-Лиувилля, имеет вид (17), где r(х) > 0 и r(x) 1, то под ортогональностью функций в этом случае подразумевают ортогональность с весом r(х): две функции y₁(x) и у₂(х) ортогональны на отрезке [а, b] с весом r(x), если

Под нормой функции ||у(x)|| в этом случае также подразумевают весовую норму:

Свойство 3. Собственные функции, соответствующие различным собственным значениям, образуют линейно независимую систему функций.

Это утверждение вытекает из попарной ортогональности собственных функций, соответствующих различным собственным значениям (см. свойство 2).

Свойство 4. Собственные значения задачи Штурма-Лиувилля действительные.

Доказательство. Предположим, что задача Штурма-Лиувилля λy = 0, l₁y = 0, l₂y = 0> имеет комплексное собственное значение λ = α + βi,β ≠ 0. Пусть ему соответствует собственная функция у(х) (вообще говоря, тоже комплекснозначная). Так как все коэффициенты уравнения и краевых условий имеют действительные значения, то

Здесь черта означает переход к комплексно сопряженному выражению. В нашем случае

Значит число также является собственным значением той же задачи Штурма-Лиувилля и ему соответствует собственная функция . Так как в силу свойства 2 функции y(x) и ортогональны на [а, b], то

Отсюда следует, что у(x) ≡ 0 на [а, b]. Значит ни одно комплексное число λ не может быть собственным значением.

Свойство 5. Пусть коэффициенты уравнения (17) удовлетворяют условиям: р(х), q(x), r(x) — непрерывные функции и, кроме того, р(х) имеет непрерывную производную на [а, b], р(х) > 0, q(x) > 0, r(х) > 0. Тогда задача Штурма-Лиувилля _λ y = 0, l₁ y = 0, l₂ y = 0> имеет бесконечное число собственных значений λ ₁, λ₂, . λ_n, . Если краевые условия имеют вид (19) или (20), или (21), то собственные значения соответствующей задачи Штурма-Лиувилля удовлетворяют неравенствам

Теорема Стеклова.Всякая непрерывная функция f(x), удовлетворяющая однородным краевым условиям : l₁f = 0 и l₂f = 0 , и имеющая непрерывные производные до второго порядка на отрезке [а, b], разлагается на этом отрезке в сходящийся ряд Фурье по собственным функциям y_n(х) задачи Штурма-Лиувилля _λ y = 0, l₁ y = 0, l₂ y = 0> :

где коэффициенты Фурье С_n вычисляются по формулам:

Эта теорема применяется при решении уравнений математической физики методом Фурье.

Решение задач Штурма-Лиувилля

Вначале рассмотрим уравнение (18) y» + λy = 0. и краевые условия первого рода (19) y(a) = y(b) = 0. Для удобства будем считать, что a = 0 и b = l > 0. К такой задаче можно всегда свести данную задачу, если сделать замену переменной x’ = x — a, при этом вид уравнения не изменится.

Вид общего решения уравнения (18) зависит от значений параметра λ. Разберем три случая: 1) λ 0. В первом случае обозначим λ = — k 2 . Тогда характеристическое уравнение r 2 — k 2 = 0 будет иметь действительные различные корни r₁ = k, r₂ = — k: Поэтому, общее решение дифференциального уравнения запишется в виде y = C₁e kx + C₂e -kx . Подставим краевые условия в общее решение и получим

Определитель этой системы равен

Следовательно, система имеет только нулевое (тривиальное) решение C₁ = C₂ = 0. Значит, при λ 2 и получим характеристическое уравнение r 2 + k 2 = 0. Оно имеет комплексные корни r₁ = ki и r₂ = -ki и общее решение дифференциального уравнения в этом случае запишется в виде y = C₁cos kx + C₂sin kx. Подставим краевые условия в общее решение:

Для того, чтобы эта система имела нетривиальные решения, необходимо и достаточно, чтобы sin kl = 0. Следовательно kl = πn, то есть Так как то можно ограничиться только положительными значениями n = 1, 2, . . Таким образом, собственные значения данной задачи имеют вид При этих значениях алгебраическая система (22) имеет решения:C₁ = 0, C₂ — любое действительное число. Подставим эти значения в общее решение дифференциального уравнения и получим собственные функции задачи

Обычно постоянный множитель выбирают либо равным единице, либо из условия нормировки:

По тому же алгоритму решаются задачи Штурма-Лиувилля следующего вида:

и

Эти задачи так же, как и предыдущая, при λ 0 не имеют собственных значений. В случае λ > 0 общее решение уравнения записывается в виде y = C₁cos kx +C₂sin kx, где После подстановки у в краевые условия, получим:

а) для задачи (23)

Для того, чтобы эти системы уравнений имели нетривиальные решения, необходимо и достаточно, чтобы coskl = 0. Следовательно, то есть Отрицательные значения n можно не рассматривать, так как Таким образом, собственные значения у этих задач одинаковые

Собственные функции задачи (23) имеют вид А у задачи (24) они другие:

Некоторые отличия возникают при решении задачи Штурма-Лиувилля в случае краевых условий второго рода

y» + λy = 0, y'(0) = y'(l) = 0.

(25)

Рассуждениями, аналогичными тем, которые проводились для краевых условий первого рода, можно показать, что задача (25) при λ 0. В этом случае, общее решение уравнения имеет вид y = C₁cos kx + C₂sin kx, Найдем производную этой функции и подставим в нее краевые условия (25):

Эта алгебраическая система имеет нетривиальные решения тогда и только тогда, когда, sinkl = 0 то есть kl = πn или Таким образом, числа также являются собственными значениями задачи. Собственные функции при этих значениях имеют вид . Окончательно, задача (25) имеет собственные значения и собственные функции

Для задачи Штурма-Лиувилля с краевыми условиями третьего рода (21) уже не удается получить собственные значения в явном виде. В качестве примера рассмотрим одну такую задачу, когда

y» + λy = 0, y'(0) = y(0), y'(l) = 0.

(26)

При задача (26) не имеет собственных значений и собственных функций. Доказательство этого проводится так же, как и для краевых условий первого рода. При λ > 0 общее решение уравнения записывается в виде y = C₁coskx + C₂sinkx, где . После дифференцирования этой функции и подстановки её производной и самой функции в краевые условия (26) будем иметь:

или

Получившаяся алгебраическая система будет иметь нетривиальные решения только в том случае, когда

coskl — ksinkl = 0 или

Уравнение (28) является трансцендентным уравнением относительно k. Оно не решается в явном виде. Однако, построив графики левой и правой частей уравнения (28), видно, что оно имеет бесконечно много решений (см. рис.13). Обозначим корни уравнения (28) через r_n, n = 1,2, . . Тогда при

Рис.13

Численными методами можно найти приближенные значения r_n. Из системы (27) при k = r_n получим C_1n = r_nC_2n , где C_2n -произвольные постоянные. При этих значениях постоянных решения дифференциального уравнения будут иметь вид

Они являются собственными функциями краевой задачи (26) с собственными значениями

«Краевая задача для дифференциального уравнения 2-го порядка. Примеры»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Ленинградский государственный университет имени А.С.Пушкина

Кафедра высшей математики

Курсовая работа по дифференциальным уравнениям на тему:

«Краевая задача для дифференциального уравнения 2-го порядка. Примеры»

студентки 3 курса,

физики и информатики

(ФИО, уч степень, уч звание, долж-ть)

Санкт-Петербург, 2010 г.

Цель курсовой работы исследовать дифференциальные уравнения второго порядка, в частности проанализировать решение краевых задач для дифференциального уравнения второго порядка.

В данной курсовой работе речь пойдет о дифференциальных уравнениях второго порядка и краевых задачах для данного типа уравнений. Мы рассмотрим следующие понятия:

Дифференциальные уравнения второго порядка;

Так же рассмотрим применение краевых задач в практической жизни человека, на примере уравнения колебаний струны.

Глава 1. Краевая задача для дифференциального уравнения второго порядка стр.5

§1. Общие сведения о дифференциальных уравнениях второго порядка стр.5

п.1.1. Общие понятия стр.5

п.1.2. Механический смысл дифференциального уравнения второго порядка

§2. Введение в краевые задачи стр.8

п.2.1.Определение краевой задачи стр.8

п.2.2.Постановка краевой задачи стр.8

§3. Линейная краевая задача. Сведение ее к задаче Коши стр.11

§4. Функция Грина стр.14

Глава 2. Применение краевых задач на практике стр.15

§1. Краевая задача для дифференциального уравнения второго порядка, в частных производных стр.15

п.1. Дифференциальные уравнения в частных производных стр.15

п.2. Вывод уравнения колебаний струны. Понятие о граничных и начальных условиях стр.17

§2. Решение обыкновенных дифференциальных уравнений второго порядка с заданными краевыми условиями стр.20

Список литературы стр.25

Дифференциальные уравнения – это уравнения, содержащие искомые функции, их производные различных порядков и независимые переменные. Теория дифференциальных уравнений возникла в конце 17 века, под влиянием потребностей механики и других естественнонаучных дисциплин, по существу одновременно с интегральным и дифференциальным исчислением.

Простейшие дифференциальные уравнения встречались уже в работах И.Ньютона и Г.Лейбница; термин «дифференциальные уравнения» принадлежит Лейбницу.

Под обыкновенным дифференциальным уравнением понимается равенство, содержащее независимую переменную, неизвестную функцию от этой переменной и ее производные. Порядком старшей производной, входящей в состав уравнения задается порядок дифференциального уравнения. Функцией, имеющей соответствующие производные и обращающие уравнение в тождество, определяется решение дифференциального уравнения. Процесс нахождения решений дифференциального уравнения называют его интегрированием.

В данной курсовой работе рассмотрим обыкновенные дифференциальные уравнения второго порядка, в частности краевые задачи для дифференциального уравнения второго порядка. А так же во второй главе познакомимся с дифференциальными уравнениями в частных производных, на примере уравнения колебания струны.

Для достижения цели, представленной в предисловии необходимо выполнить следующие задачи:

Ознакомиться с дифференциальными уравнениями второго порядка;

Ввести понятие краевой задачи;

Рассмотреть функцию Грина, и метод отыскания периодических решений;

Исследовать применение данных задач к практике.

Глава 1. Краевая задача для дифференциального уравнения второго порядка

В данной главе, мы познакомимся с обыкновенными дифференциальными уравнениями второго порядка, рассмотрим общие понятия о дифференциальных уравнения данного порядка (общие понятия и механический смысл). Также введем понятие краевой задачи и краевых условий для дифференциального уравнения второго порядка.

§1. Общие сведения о дифференциальных уравнениях второго порядка

п.1.1. Общие понятия

Дифференциальное уравнение второго порядка с неизвестной функцией у=у(х) имеет вид:

где F — данная функция.

Предполагая, что данное уравнение может быть однозначно разрешено относительно производной , получим:

, где f – некоторая функция.

Общее решение этого уравнения содержит две произвольные постоянные С ₁ и С ₂ . Поэтому через данную точку М ₀ (х ₀ ,у ₀ ), проходит пучок интегральных кривых, (рис.1) так как одна из произвольных постоянных остается неопределенной.

Чтобы выделить определенную интегральную кривую, кроме точки М ₀ , достаточно задать направление касательной в точке М ₀ к искомой интегральной кривой:

Таким образом, имеем следующие начальные условия:

Из начальных условий вытекает, что постоянные С ₁ и С ₂ должны удовлетворять системе уравнений:

.

Теорема о существовании и единственности решений:

Если в некоторой области где а, b , с – положительные числа, функция непрерывна и имеет ограниченные частные производные то существует единственное решение дифференциального уравнения , удовлетворяющее начальным условиям и определенное на некотором отрезке .

п.1.2. Механический смысл дифференциального уравнения второго порядка

Пусть по оси Ох движется материальная точка массы m (рис.2), причем действующая сила зависит от времени t , координаты точки x и ее скорости . На основании закона Ньютона имеем дифференциальное уравнение движения:

Следовательно, всякое дифференциальное уравнение второго порядка, разрешенное относительно старшей производной, можно рассматривать как дифференциальное уравнение прямолинейного движения материальной точки. Начальные условия принимают следующий вид:

,

т.е. в начальный момент t ₀ задаются: х ₀ – начальное положение точки и — ее начальная скорость.

§2. Введение в краевые задачи

п.2.1. Определение краевой задачи

Рассмотрим дифференциальное уравнение второго порядка, имеющее вид:

, (1)

Уравнение такого вида могут иметь бесконечное множество решений. Но на практике необходимо из множества решений выделять только одно. Для этого задают дополнительные условия на концах некоторого отрезка и получают задачу, которую называют краевой задачей.

Условия, которые задаются на концах отрезка называются краевыми условиями. Будем задавать линейные краевые условия вида:

Решением краевой задачи называется такое решение дифференциального уравнения, которое удовлетворяет заданным краевым условиям.

Однородная краевая задача всегда имеет решение: y ≡0 (тривиальное решение).

п.2.2. Постановка краевой задачи

Рассмотрим дифференциальное уравнение второго порядка: (3)

где у — искомая функция; х — независимая переменная; f — функция, определенная и непрерывная в некоторой замкнутой области D изменения своих аргументов.

Общее решение такого дифференциального уравнения содержит две произвольные постоянные. Если для их нахождения задать при х=x ₀ значения у(х ₀ ) искомой функции у(х) и ее производной у'(х ₀ ) , то придем к постановке задачи Коши для дифференциального уравнения (3) с двумя начальными условиями. Если же потребовать, чтобы искомое решение у(х) удовлетворяло также двум условиям:

(4),

но в двух различных точках х=а и х= b , то получим одну из возможных постановок краевой задачи, называемую двухточечной . Соотношения вида (4) называют краевыми условиями данной задачи. Геометрически постановка задачи с краевыми условиями (4) означает, что требуется найти такую интегральную кривую у(х) дифференциального уравнения (3), которая проходит через точки А(а,у _а ) и В( b ,у _b ) (рис. 3).

Возможно видоизменение постановки краевой задачи: найти такое решение y=y(x) дифференциального уравнения (3), чтобы в точках х=а и х=b были выполнены краевые условия для производной функции у(х) :

(5)

где и

Такая постановка краевой задачи с геометрической точки зрения соответствует поиску интегральной кривой у(х) дифференциального уравнения (1), пересекающей прямые х=а и х= b под заданными углами и (рис.4), где, согласно геометрическому смыслу производной функции у(х) , и .

Условия (4) и (5) принято называть краевыми условиями первого и второго рода соответственно. Очевидно, имеет смысл и постановка смешанной двухточечной краевой задачи, когда в точках х=а и х= b заданы краевые условия разного рода.

Необходимо отметить, что в отличие от задачи Коши, для которой теорема Коши гарантирует при выполнении определенных условий существование и единственность решения дифференциального уравнения, краевая задача для того же дифференциального уравнения может не иметь решения или иметь несколько решений (в том числе и бесконечное множество решений).

§3. Линейная краевая задача. Сведение ее к задаче Коши

Рассмотрим линейное неоднородное обыкновенное дифференциальное уравнение второго порядка:

(6)

Функции p ( x ), q ( x ), f ( x ) предполагаем непрерывными на отрезке [ a , b ]. Требуется найти на этом отрезке решение y ( x ) дифференциального уравнения (6), удовлетворяющее краевым условиям:

(7)

где , В – постоянные, причем такой вариант краевых условий является линейной комбинацией краевых условий первого и второго рода, его называют краевыми условиями третьего рода . В частном случае и соотношения (7) переходят в краевые условия (4) первого рода, а при , — в краевые условия (5) второго рода.

Постановка двухточечной краевой задачи в виде (6), (7) включает линейное дифференциальное уравнение второго порядка и линейные относительно значений искомой функции и ее производных краевые условия. В таком случае говорят о линейной двухточечной краевой задаче. Ее называют однородной, если f(x)=0 и А=В=0 , и неоднородной — в противном случае.

Однородная краевая задача всегда имеет тривиальное решение у(х)≡0 . Однако в прикладных исследованиях часто для однородной задачи представляют интерес решения у(х)0 . В этом случае в дифференциальных уравнениях или краевые условия (7) вводят параметр, изменяя который можно добиться, чтобы при некоторых его значениях однородная краевая задача помимо тривиального имела решение, отличное от тождественно нулевого. В некоторых случаях такой параметр уже присутствует в исходной формулировке краевой задачи и имеет вполне определенный физический, механический или геометрический смысл. Эти исключительные значения параметра, при которых однородная краевая задача имеет решение, отличное от тривиального, называют собственными значениями, а отвечающие им решения — собственными функциями этой задачи.

Нахождение собственных значений и собственных функций составляет содержание так называемой задачи на собственные значения, или задачи Штурма — Лиувилля.

Краевую задачу (6), (7) можно свести к задачам Коши для того же дифференциального уравнения (6) второго порядка и соответствующего ему однородного дифференциального уравнения:

(8)

Для этого решение краевой задачи будем искать в виде

(9)

где u = u ( x ) — нетривиальное решение однородного дифференциального уравнения (8), a v(x) — решение неоднородного дифференциального уравнения (6). Ясно, что (9) как линейная комбинация решений неоднородного дифференциального уравнения и соответствующего ему однородного уравнения также является решением дифференциального уравнения (6).

Потребуем, чтобы первое из краевых условий (7) было выполнено для у(х) при любом значении μ. Подставив (9) в это краевое условие, запишем

Это равенство будет выполнено при любом значении μ, если приравнять нулю коэффициент при μ, что приведет к двум равенствам

для выполнения которых достаточно, например, положить:

(10)

(11)

В случае  ₀ =0 вместо (11) положим

v ( a )=0 , (12)

Таким образом, u (х) есть решение задачи Коши для однородного дифференциального уравнения (8), удовлетворяющее начальным условиям (10), а v(x)- решение задачи Коши для неоднородного дифференциального уравнения (6), удовлетворяющее начальным условиям (11) или (12). При этом для любого μ функция у(х)=μu(x) + v(x) удовлетворяет первому из краевых условий (7) (при х=а ). Постоянную μ выбирают так, чтобы функция у(х) удовлетворяла второму из краевых условий (7) (при х= b ), т.е.

(13)

Если выполнено неравенство

(14)

то из (13) находим

(15)

Следовательно, краевая задача (6), (7) сведена к двум задачам Коши относительно функций u (х) и v(x) для однородного (8) и неоднородного (6) дифференциальных уравнений соответственно. Эти дифференциальные уравнения удовлетворяют всем условиям теоремы Коши о существовании и единственности решения задачи Коши, т.е. существует единственное решение u (х) дифференциального уравнения (8), удовлетворяющее начальным условиям (10), и единственное решение v(x) дифференциального уравнения (6), удовлетворяющее начальным условиям (11) или (12). Поэтому при выполнении неравенства (14) существует решение рассматриваемой линейной краевой задачи (7), (8).

Отметим, что если исходное дифференциальное уравнение (6) будет однородным, т.е. f(x)=0 , и в (7) А=0 , то в силу начальных условий (11) или (12) имеем v(a)=0 и v'(a)=0 , и поэтому v(x)=0. Тогда при выполнении неравенства (14) получим где u (х)- решение дифференциального уравнения (8), удовлетворяющее начальным условиям (10).

Сведение задачи с краевыми условиями к задаче Коши рассмотрим на примере 7, главы 2, §2.

§4. Функция Грина

Определение: Функцией Грина называется функция G ( x , s ) , определенная при и при каждом фиксированном обладающая свойствами:

1. при функция G ( x , s ) удовлетворяет уравнению:

3. при x = s функция G ( x , s ) непрерывна по x , а ее производная по x терпит разрыв первого рода со скачком, равным 1/а( s ) , т.е. G ( s +0, s )= G ( s -0, s ), (17)

Чтобы найти функцию Грина краевой задачи (16) с краевыми условиями (2), необходимо найти два решения y ₁ ( x ) и y ₂ (х) , отличные от y ( x )≡0 , уравнение (16), удовлетворяет соответственно первому и второму из краевых условий (2).

Если y ₁ ( x ) не удовлетворяет одновременно обоим краевым условиям, то функция Грина G ( x , s ) существует и ее можно представить в виде:

(18)

где функции и подбираются так, чтобы функция (18) удовлетворяла условиям (17), т.е. чтобы

Если найдена функция Грина G ( x , s ), то решение краевой задачи (16), с краевыми условиями (2) выражается формулой:

Замечание: Из определения функции Грина еще не следует ее существование для каждой краевой задачи.

Глава 2. Применение краевых задач на практике

Краевые задачи на практике применяются:

в изучении течения жидкостей в каналах;

уравнение колебаний струны;

рассеяние волн областью с неровной поверхностью

В данной главе мы рассмотрим, как можно физическую задачу свести к математической задаче.

А так же рассмотрим примеры решения уравнений для обыкновенных дифференциальных уравнений второго порядка.

§1. Краевая задача для дифференциального уравнения второго порядка в частных производных

п.1. Дифференциальные уравнения в частных производных

В главе 1 данной курсовой работы были рассмотрены дифференциальные уравнения, в которых участвовали искомые функции от одной независимой переменной, вместе с их производными. Эти уравнения носят названия обыкновенные дифференциальные уравнения.

Однако, в различных технических вопросах наиболее часто встречается искомой функция, u , от двух независимых переменных, x и t :

причем условия поставленного вопроса дают для ее определения некоторое соотношение, связывающее не только величины x , t , y , но и частные производные:

т.е. соотношение вида:

. (1)

Такое соотношение называется дифференциальным уравнением в частных производных ; порядок его определяется порядком наивысшей встречающейся в нем производной. Число независимых переменных может оказаться более двух. Для техники наибольшую важность представляют линейные уравнения в частных производных второго или высшего порядка.

Уравнение (1) называется линейным , если оно первой степени относительно искомой функции и всех производных и не содержит их произведений, т.е. это уравнение может быть записано в виде

Причем коэффициенты A , B , C , a , b , c зависят только от x и y .

Если эти коэффициенты не зависят от x и y , то уравнение (2) представляет собой линейное дифференциальное уравнение с постоянными коэффициентами .

Пусть D = B 2 -4 AC – дискриминант уравнения. В зависимости от значения D уравнение (2) относится к одному из следующих типов:

D > 0 – эллиптический тип;

D = 0 – параболический тип;

D — гиперболический тип;

D не сохраняет постоянного знака – смешанный тип.

Дифференциальное уравнение с частными производными имеет в общем случае бесчисленное множество решений. Для конкретного решения уравнения нужны дополнительные условия – начальные или краевые условия. Начальные условия характеризуют процесс в начальный момент времени. Краевые условия описывают состояние физического процесса в граничных (краевых) областях (точках).

Краевые задачи ставятся следующим образом: найти функция u , которая удовлетворяет уравнению Лапласа:

Во всех внутренних точках области S , а на границе области — некоторому условию. В зависимости от вида условия различают следующие краевые задачи:

— задача Дирихле;

— задача Неймана.

В следующем пункте представлена краевая задача для дифференциального уравнения второго порядка в частных производных, на примере уравнения колебания струны.

п.2. Вывод уравнения колебаний струны. Понятие о граничных и начальных условиях

Рассмотрим натянутую струны, т.е. тонкую гибкую упругую нить, расположенную в плоскости Oxu , которая в результате известного возмущения была выведена из положения равновесия Ox . Изучим поперечные колебания струны, полагая, что при таком колебании струны ее точки движутся перпендикулярно оси Ox .

Обозначим через u = u ( x , t ) – смещение точки струны с абсциссой х в момент времени t относительно оси Ох (рис.5).

Тогда функцией u ( x , t ) при опишется процесс колебаний струны: для любого фиксированного момента времени t = t ₁ выражением u = u ( x , t ₁ ) определяется мгновенной профиль струны.

Сделаем следующие допущения:

Предположим, что струна совершает малые колебания, т.е. ее форма в процессе колебаний незначительно отличается от прямой u =0 . Будем предполагать, что наклон касательной к графику функции u ( x , t ) , t = const , т.е. , есть малая по модулю величина по сравнению с единицей. Отсюда получаем, что и

К концам участка струны приложены направленные по касательной упругие силы натяжения (рис.5), модули которых равны: и являются практически постоянными, т.е. Т ₀ не зависит от х и t .

На струну действуют непрерывно распределенные внешние силы, перпендикулярные оси Ox , с плотностью (нагрузкой) p(x,t) , рассчитанной на единицу длины.

Вырежем из струны бесконечно малый элемент , абсциссами которого являются х и х+ dx . Воздействие отброшенной левой и правой частей струны заменим соответствующими силами натяжения. Тогда элемент можно рассматривать, как свободную материальную точку, находящуюся под действием упругих сил и внешней силы — орт оси О u .

Пусть — линейная плотность струны в точке х. Так в положении равновесия масса элемента равна , то в силу сохранения массы, элемент имеет ту же массу. Обозначим через и углы, образованные с осью Ох касательными к профилю струны в момент времени t в точках М и соответственно. Проектируя на ось Ou силы, приложенные к элементу , в силу закона Ньютона и предположения 2) получим:

(1)

Согласно предположению 1) углы и малы, поэтому:

(2)

(2*).

Для подсчета (2*) используем следующую формулу: , справедливую с точностью до бесконечно малых высших порядков.

(3)

Подставляя выражение (2) и (3) в формулу (1), получим:

(4)

Мы получили искомое уравнение малых вынужденных поперечных колебаний струны.

В случае постоянной плотности () это уравнение принимает вид:

. (5),

где , а — плотность силы, отнесенная к единице массы.

При отсутствии внешней силы ( P ( x , t ) =0) мы получаем уравнение малых свободных колебаний струны:

(6)

Уравнение (4), как показано выше, имеет бесчисленное множество решений. Поэтому для однозначной характеристики процесса колебаний необходимо к уравнению присоединить некоторые дополнительные условия, вытекающие их физического смысла данной задачи. Эти условия могут быть весьма разнообразными. В простейшем случае, как и в динамике точки, задается положение и скорость точек струны в начальный момент времени:

(7)

Эти условия, которым должно удовлетворять решение u ( x , t ) при t =0, называются начальными условиями.

Если струна ограничена, то необходимо задать условия на ее концах. В частности, для струны, концы которой x =0 и x = l закреплены,

(8)

при всяком . Условия (8) – граничные (краевые) условия.

Таким образом, физическая задача о колебаниях струны, закрепленной на концах, свелась к следующей математической задаче: найти решение u ( x , t ) уравнения (4), удовлетворяющее начальным условиям (7) и граничным условиям (8). Такая задача называется смешанной краевой задачей для уравнения колебания. К ней также можно прийти при изучении одномерных колебаний идеального газа или одномерных продольных колебаний стержня.

§2. Решение обыкновенных дифференциальных уравнений второго порядка с заданными краевыми условиями

Пример 1 . Найти решение уравнения , удовлетворяющее краевым условиям y (0)=3,

Все решения данного дифференциального уравнения выражаются формулой , где C ₁ , C ₂ – произвольные постоянные. Подберем C ₁ и C ₂ так, чтобы удовлетворялись заданные краевые условия, т.е. определим постоянные C ₁ и C ₂ из уравнений C ₁ + C ₂ =3, C ₁ + C ₂ e — C ₂ e =1. Отсюда С ₁ =1, С ₂ =2. Таким образом, решением краевой задачи является функция

Пример 2. Найти решение уравнения удовлетворяющее краевым условиям

Решение: Общее решение данного дифференциального уравнения имеет вид Условие y (0)=0 удовлетворяется при С ₁ =0, при этом y = C ₂ sinx . Если , где n – целое число, то из второго граничного условия находим: , .

Следовательно, в этом случае существует единственное решение данной краевой задачи:

.

Если , то из второго краевого условия имеет бесконечное множество решений: , где С ₂ может принимать любые значения.

В случае, если , а указанным краевым условиям не удовлетворяет ни одно решение данного дифференциального уравнения, т.е. краевая задача решений не имеет.

Пример 3: Решить краевую задачу:

Решение: Общее решение данного уравнения имеет вид:

Подставим общее решение в заданные краевые условия, получим систему уравнений относительно постоянных C ₁ и C ₂ :

Следовательно,

Пример 4: Решить краевую задачу

Решение: Общее решение данного уравнения имеет вид:

Так как то из общего решения следует, что Из краевого условия следует, что

В результате получаем:

Пример 5: Построить функцию Грина для краевой задачи

Решение: Общее решение уравнения есть Условию y (-1)=0 удовлетворяет, например, решение , а второму краевому условию – решение

Функцию Грина для указанной краевой задачи ищем в виде:

где функции и определяются из условий Отсюда

Таким образом, искомая функция Грина имеет вид:

Построив функцию Грина G ( x , s ) , запишем решение данной краевой задачи:

Пример 6: Решить краевую задачу ограничена при

Решение: Построим функцию Грина для этой задачи. Общее решение уравнения есть Решение удовлетворяет первому краевому условию, а решение удовлетворяет второму краевому условию, поэтому функцию Грина ищем в виде:

Функции и определяем из условий

, т.е. Отсюда получаем:

Искомое решение имеет вид:

Пример 7: Решить краевую задачу

На примере этой краевой задачи проиллюстрируем метод приведения краевых задач к задачам Коши. В данном случае такое приведение не эффективно, но во многих случаях, особенно в связи с методами численного решения, этот прием оказывается полезным. Найдем решение указанной краевой задачи в виде:

где соответственно решения таких задач Коши: Решив каждую из этих задач Коши, находим:

Подберем в выражении

коэффициенты  и  так, чтобы это выражение удовлетворяло краевым условиям. Подставляя в краевые условия, получаем уравнения для определения  и  :  =  , 6  +  =7.

Отсюда  =  =1. Таким образом, искомое решение имеет вид:

Теория дифференциальных уравнений является одним из самых больших разделов современной математики. Чтобы охарактеризовать ее место в современной математической науке, прежде всего необходимо подчеркнуть основные особенности теории дифференциальных уравнений, состоящей из двух обширных областей математики: теории обыкновенных дифференциальных уравнений и теории уравнений с частными производными.

Важная особенность — это непосредственная связь теории дифференциальных уравнений с приложениями. Характеризуя математику как метод проникновения в тайны природы, можно сказать, что основным путем применения этого метода является формирование и изучение математических моделей реального мира. Изучая какие-либо физические явления, исследователь прежде всего создает его математическую идеализацию или, другими словами, математическую модель, то есть, пренебрегая второстепенными характеристиками явления, он записывает основные законы, управляющие этим явлением, в математической форме. Очень часто эти законы можно выразить в виде дифференциальных уравнений. Такими оказываются модели различных явлений механики сплошной среды, химических реакций, электрических и магнитных явлений и др.

В данной курсовой работе мы познакомились с понятиями дифференциального уравнения, краевых условий; рассмотрели применение дифференциальных уравнений второго порядка к практике.

Агафонов С.А., Герман А.Д., Муратова Т.В. Диффенциальные уравнения. Математика в техническом университете. Выпуск 8. Изд-во МГТУ им.Н.Э.Баумана. 2003 – 348.

Демидович Б.П., Моденов В.П. Дифференциальные уравнения: Учебное пособие. 3-е изд.,стер. – Спб.: Издательство «Лань», 2008. – 288 с.

Егоров А.И. Обыкновенные дифференциальные уравнения с приложениями. – М.: Физматлит, 2005. – 384 с.

Камке Э. Справочник по обыкновенным дифференциальным уравнения. М., 1965. – 704 с.

Кисилев А.И., Краснов М.Л., Макаренко Г.И. Сборник задач по обыкновенным уравнениям. – М.: Изд-во «Высшая школа», 1965. – 235 с.

Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2000. – 176 с.

Фихтенгольц Г.М. Математика для инженеров, часть вторая, выпуск второй. Государственное технико-теоретическое издательство Ленинград, Москва 1933 г.

источники:

http://vicaref.narod.ru/ODE/lec4.html

http://infourok.ru/kraevaya-zadacha-dlya-differencialnogo-uravneniya-go-poryadka-primeri-3802878.html

Решение краевых задач

Двухточечные
краевые задачи

Примером
двухточечной краевой задачи является
задача:

(4)

с
граничными условиями на обоих концах
отрезка
на
котором надо найти решение
Если
функция
линейна по аргументамуи
то
мы имеем линейную краевую задачу, иначе
– нелинейную краевую задачу.

Метод
стрельбы

2.6. Метод стрельбы

Метод
стрельбы для решения краевой задачи
(4) базируется на том, что имеются удобные
способы численного решения задачи Коши,
т. е.
задачи следующего вида

  , (5)

где  —
ордината точки  из
которой выходит интегральная кривая; –угол наклона интегральной
кривой к оси x при
выходе из точки  (рис. 1).

Рис.
1. Метод стрельбы решения краевой задачи

При
фиксированном  
решение задачи (4) имеет
вид  При  решение  зависит
только от :

Используя
указанное замечание о решении задачи
Коши (5), можно задачу (4) переформулировать
следующим образом: найти такой угол  при
котором интегральная кривая, выходящая
из точки  под
углом
к
оси абсцисс, попадет в точку 

(6)

Решение
задачи (5) при этом  совпадает
с искомым решением задачи (4). Таким
образом, дело сводится к решению уравнения
(6). Уравнение (6) — это уравнение вида

где 

Оно
отличается от привычных уравнений лишь
тем, что функция  задана
не аналитическим выражением, а с помощью
алгоритма численного решения задачи
(5).

Для
решения уравнения (6) можно использовать
любой метод, пригодный для уточнения
корней нелинейного уравнения, например,
метод деления отрезка пополам, метод
Ньютона (касательных) и др. Метод Ньютона
здесь предпочтительнее (если имеется
достаточно хорошее начальное приближение)
из-за высокой стоимости вычисления
одного значения функции F(a)
(нужно решить задачу Коши (5) с данным a).

Метод
стрельбы, сводящий решение краевой
задачи (4) к вычислению решений задачи
Коши (5), хорошо работает в том случае,
если решение  «не
слишком сильно» зависит от .
В противном случае он становится
вычислительно неустойчивым, даже если
решение задачи (4) зависит от входных
данных «умеренно».

При
решении уравнений  методом
деления отрезка пополам, мы задаем  и  так,
чтобы разности  и  имели
разные знаки. Затем полагаем

Вычисляем  Затем
вычисляем  по
одной из формул:

             
или               

в
зависимости от того, имеют ли
разности  и  соответственно
разные или одинаковые знаки. Затем
вычисляем  Процесс
продолжаем до тех пор, пока не будет
достигнута требуемая точность 

В
случае использования для решения
уравнения  метода
Ньютона задаем  а
затем последующие  вычисляем
по рекуррентной формуле

             n = 0,
1, …

Производная  может
быть вычислена по одной из формул
численного дифференцирования, например,
первого порядка аппроксимации:

Метод
прогонки

При
применении метода конечных разностей
к крае­вым задачам для уравнений
второго порядка получается “трехчленная
система” линейных алгебраических
уравнений, каждое из которых содержит
три соседних неизвестных. Для решения
такой системы разработан специальный
метод, называемый методом прогонки.
Рассмотрим линейное дифференциальное
уравнение

(7)

на
интервале [a,b]с условиями на границе

(8)

(9)

От
уравнения (7) перейдем к конечно-разностному.
Для этого:

1.
Дискретизируем задачу, т.е. вводим сетку
по переменной x:

i:=0…
n

2.
Заменяем исходное уравнение (7)
конечно-разностным во внутренних узлах:

Это
уравнение приводим к каноническому
трехдиагональному виду

(10)

где
.

Линейную
систему (10) можно решать обычным способом,
однако более короткий путь — использовать
метод прогонки. В этом случае решение
ищется в виде:

j
= n, n — 1,…2(11)

где
_j,_j— прогоночные коэффициенты, которые
необходимо предварительно вычислить.
Решение реализуется в два этапа.

1.
Прямой ход –от
левого края заданного интервала[a,b]до правого в узлах сетки вычисляются_j,_j,j = 1, . . .,n.

2.
Обратный ход –от правого края до левого по формуле
(11) в тех же узлах находится искомое
решение.

Прямой
ход реализуется рекуррентными формулами
для прогоночных коэффициентов, которые
получаются из (10) и (11) при k=1..n-1:

,

Начальные
значения коэффициентов для этих
рекуррентных формул можно найти из (11)
и левого краевого условия (8):

После
того как получены прогоночные коэффициенты,
можно приступать к обратному ходу по
формуле (11), но предварительно необходимо
найти значение
.
Из (11) и правого краевого условия (9)
получаем

а

, теперь, собственно обратный ход —
искомую функцию находим по рекуррентной
формуле

Пример.

Использование
этого метода рассмотрим на примере
краевой задачи для уравнения

на
интервале [0,1] с граничными условиями

Замечание:
данное уравнение имеет точное решение

которое
будет служить тестом для отладки
программы.

Прямой
ход

Чтобы
начать обратный ход прогонки найдем из
правого краевого условия:

dt1=1,
dt2=0, dt=1+e

и
граничное значение искомой функции

Обратным
ходом рассчитываем значения функции в
остальных узлах:

Полученное
решение можно представить графиком

Рис.
2. Численное решение краевой задачи
методом прогонки

Для
сравнения построим точное решение

Рис.
3. Аналитическое решение краевой задачи

Вычислим
относительную погрешность:

Результаты
численного и точного решения и погрешность
приведем в таблице

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

АОУ
ВПО

Ленинградский
государственный университет имени А.С.Пушкина

Кафедра
высшей математики

Курсовая
работа по дифференциальным уравнениям на тему:

«Краевая
задача для  дифференциального уравнения 2-го порядка. Примеры»

студентки 3 курса,

дневного отделения

факультета математики,

физики и информатики

Шишикиной Е.А.

(ФИО, уч степень, уч звание, долж-ть)

Санкт-Петербург, 2010 г.

Предисловие

Цель курсовой работы исследовать
дифференциальные уравнения второго порядка, в частности проанализировать
решение краевых задач для дифференциального  уравнения второго порядка.

В данной курсовой работе речь пойдет
о дифференциальных уравнениях второго порядка и краевых задачах для данного
типа уравнений. Мы рассмотрим следующие понятия:

Ø  
Дифференциальные уравнения второго
порядка;

Ø  
Краевая задача;

Ø  
Краевые условия;

Ø  
Функция Грина.

Так же рассмотрим применение краевых
задач в практической жизни человека, на примере уравнения колебаний струны.

Содержание

Предисловие………………………………………………………………………………………… стр.2

Содержание………………………………………………………………………………………….. стр.3

Введение………………………………………………………………………………………………. стр.4

Глава
1. Краевая задача для дифференциального уравнения второго порядка. стр.5

§1.
Общие сведения о дифференциальных уравнениях второго порядка………. стр.5

п.1.1.
Общие понятия…………………………………………………………………………….. стр.5

п.1.2.
Механический смысл дифференциального уравнения второго порядка

……………………………………………………………………………………………………………. стр.6

§2.
Введение в краевые задачи……………………………………………………………….. стр.8

п.2.1.Определение
краевой задачи…………………………………………………………… стр.8

п.2.2.Постановка
краевой задачи…………………………………………………………….. стр.8

§3.
Линейная краевая задача. Сведение ее к задаче Коши…………………………… стр.11

§4.
Функция Грина………………………………………………………………………………… стр.14

Глава
2. Применение краевых задач на практике………………………………………. стр.15

§1.
Краевая задача для дифференциального уравнения второго порядка, в частных производных………………………………………………………………………………………… стр.15

п.1.
Дифференциальные уравнения в частных производных ………………………. стр.15

п.2.
Вывод уравнения колебаний струны. Понятие о граничных и начальных условиях ……………………………………………………………………………………………………………. стр.17

§2.
Решение обыкновенных дифференциальных уравнений второго порядка с заданными
краевыми условиями…………………………………………………………….. стр.20

Заключение………………………………………………………………………………………….. стр.24

Список
литературы……………………………………………………………………………….. стр.25

Введение

Дифференциальные уравнения – это уравнения,
содержащие искомые функции, их производные различных порядков и независимые
переменные. Теория дифференциальных уравнений возникла в конце 17 века, под
влиянием потребностей механики и других естественнонаучных дисциплин, по
существу одновременно с интегральным  и дифференциальным исчислением.

Простейшие дифференциальные уравнения
встречались уже в работах И.Ньютона и Г.Лейбница; термин «дифференциальные
уравнения» принадлежит Лейбницу.

Под обыкновенным дифференциальным
уравнением понимается равенство, содержащее независимую переменную, неизвестную
функцию от этой переменной и ее производные. Порядком старшей производной,
входящей в состав уравнения задается порядок дифференциального уравнения.
Функцией, имеющей соответствующие производные и обращающие уравнение в
тождество, определяется решение дифференциального уравнения. Процесс нахождения
решений дифференциального уравнения называют его интегрированием.

В данной курсовой работе рассмотрим обыкновенные
дифференциальные уравнения второго порядка, в частности краевые задачи для
дифференциального уравнения второго порядка. А так же во второй главе
познакомимся с дифференциальными уравнениями в частных производных, на примере
уравнения колебания струны.

Для достижения цели, представленной в
предисловии необходимо выполнить следующие задачи:

1.     Ознакомиться
с дифференциальными уравнениями второго порядка;

2.     Ввести
понятие краевой задачи;

3.          
Рассмотреть функцию Грина, и метод
отыскания периодических решений;

4.     Исследовать
применение данных задач к практике.

Глава 1. Краевая задача для
дифференциального уравнения второго порядка

В данной главе, мы познакомимся с
обыкновенными дифференциальными уравнениями второго порядка, рассмотрим общие
понятия о дифференциальных уравнения данного порядка (общие понятия и
механический смысл). Также введем понятие краевой задачи и краевых условий для
дифференциального уравнения второго порядка.

§1. Общие сведения о дифференциальных
уравнениях второго порядка

п.1.1. Общие понятия

Дифференциальное уравнение второго
порядка с неизвестной функцией у=у(х) имеет вид:

где
F—
данная функция.

Предполагая, что данное уравнение
может быть однозначно разрешено относительно производной , получим:

, где f
– некоторая функция.

Общее решение этого уравнения  содержит две произвольные постоянные С₁
и С₂. Поэтому через данную точку М₀(х₀,у₀),
проходит пучок интегральных кривых, (рис.1) так как одна из произвольных
постоянных остается неопределенной.

Рис.1

Чтобы выделить определенную
интегральную кривую, кроме точки М₀, достаточно задать
направление касательной в точке М₀ к искомой интегральной
кривой:

Таким образом, имеем следующие
начальные условия:

Из начальных условий вытекает, что
постоянные С₁ и С₂ должны удовлетворять
системе уравнений:

.

Теорема о существовании и
единственности решений:

Если в некоторой области где а, b,
с – положительные числа, функция  непрерывна и имеет ограниченные частные
производные то существует единственное решение  дифференциального уравнения , удовлетворяющее начальным условиям  и определенное на некотором отрезке .

п.1.2. Механический смысл
дифференциального уравнения второго порядка

Пусть по оси Ох движется
материальная точка массы m (рис.2),
причем действующая сила зависит от времени t,
координаты точки x и
ее скорости .  На основании закона Ньютона имеем
дифференциальное уравнение движения:

Рис.2

Следовательно, всякое
дифференциальное уравнение второго порядка, разрешенное относительно старшей
производной, можно рассматривать как дифференциальное уравнение прямолинейного
движения материальной точки. Начальные условия принимают следующий вид:

 ,

т.е. в начальный момент t₀
задаются: х₀ – начальное положение точки и  — ее начальная скорость.

§2. Введение в краевые задачи

п.2.1. Определение краевой задачи

Рассмотрим дифференциальное уравнение
второго порядка, имеющее вид:

  
, (1)

где                  
  .

Уравнение такого вида могут иметь
бесконечное множество решений. Но на практике необходимо из множества решений
выделять только одно. Для этого задают дополнительные условия на концах
некоторого отрезка и получают задачу, которую называют краевой задачей.

Условия, которые задаются на концах
отрезка называются краевыми условиями. Будем задавать линейные краевые
условия вида:

                                                                                                 (2)

Решением краевой задачи называется
такое решение дифференциального уравнения, которое удовлетворяет заданным
краевым условиям.

Однородная краевая задача всегда
имеет решение: y≡0
(тривиальное решение).

п.2.2. Постановка краевой задачи

Рассмотрим дифференциальное уравнение
второго порядка: (3)

где
у — искомая функция; х — независимая переменная; f
— функция, определенная и непрерывная в некоторой замкнутой области D
изменения своих аргументов.

Общее решение такого
дифференциального уравнения содержит две произвольные постоянные. Если для их нахождения
задать при х=x₀ значения у(х₀) искомой функции
у(х) и ее производной у'(х₀), то придем к постановке
задачи Коши для дифференциального уравнения (3) с двумя начальными условиями.
Если же потребовать, чтобы искомое решение у(х) удовлетворяло также двум
условиям:

 (4),

но
в двух различных точках х=а и х=b,
то получим одну из возможных постановок краевой задачи, называемую двухточечной.
Соотношения вида (4) называют краевыми условиями данной задачи.
Геометрически постановка задачи с краевыми условиями (4) означает, что
требуется найти такую интегральную кривую у(х) дифференциального
уравнения (3), которая проходит через точки А(а,у_а) и В(b,у_b)
(рис. 3).

Рис.3

Возможно видоизменение постановки
краевой задачи: найти такое решение y=y(x) дифференциального уравнения
(3), чтобы в точках х=а и х=b были выполнены краевые условия для
производной функции у(х):

 (5)

где
 и  

Такая постановка краевой задачи с
геометрической точки зрения соответствует поиску интегральной кривой у(х)
дифференциального уравнения (1), пересекающей прямые х=а и х=b
под заданными углами  и  (рис.4),
где, согласно геометрическому смыслу производной функции у(х),  и .

Рис.4

Условия (4) и (5) принято называть
краевыми условиями первого и второго рода соответственно. Очевидно, имеет смысл
и постановка смешанной двухточечной краевой задачи, когда в точках х=а и
х=b заданы краевые условия
разного рода.

Необходимо отметить, что в отличие от
задачи Коши, для которой теорема Коши гарантирует при выполнении определенных
условий существование и единственность решения дифференциального уравнения,
краевая задача для того же дифференциального уравнения может не иметь решения
или иметь несколько решений (в том числе и бесконечное множество решений).

§3. Линейная краевая задача. Сведение
ее к задаче Коши

Рассмотрим линейное неоднородное
обыкновенное дифференциальное уравнение второго порядка:

 (6)

Функции p(x),
q(x),
f(x)
предполагаем непрерывными на отрезке [a,b].
Требуется найти на этом отрезке решение y(x)
дифференциального уравнения (6), удовлетворяющее
краевым условиям:

  (7)

где
, В – постоянные, причем  такой вариант краевых условий является
линейной комбинацией краевых условий первого и второго рода,  его называют краевыми
условиями третьего рода. В частном случае  и  соотношения (7) переходят в краевые
условия (4) первого рода, а при ,  — в краевые условия (5) второго рода.

Постановка двухточечной краевой
задачи в виде (6), (7) включает линейное дифференциальное уравнение второго
порядка и линейные относительно значений искомой функции и ее производных
краевые условия. В таком случае говорят о линейной двухточечной краевой задаче.
Ее называют однородной, если f(x)=0 и А=В=0, и неоднородной — в
противном случае.

Однородная краевая задача всегда
имеет тривиальное решение у(х)≡0. Однако в прикладных исследованиях
часто для однородной задачи представляют интерес решения у(х)0. В этом случае в дифференциальных
уравнениях или краевые условия (7) вводят параметр, изменяя который можно
добиться, чтобы при некоторых его значениях однородная краевая задача помимо
тривиального имела решение, отличное от тождественно нулевого. В некоторых
случаях такой параметр уже присутствует в исходной формулировке краевой задачи
и имеет вполне определенный физический, механический или геометрический смысл.
Эти исключительные значения параметра, при которых однородная краевая задача
имеет решение, отличное от тривиального, называют собственными значениями, а
отвечающие им решения — собственными функциями этой задачи.

Нахождение собственных значений и
собственных функций составляет содержание так называемой задачи на собственные
значения, или задачи Штурма — Лиувилля.

Краевую задачу (6), (7) можно свести
к задачам Коши для того же дифференциального уравнения (6) второго порядка и
соответствующего ему однородного дифференциального уравнения:

 (8)

Для этого решение краевой задачи
будем искать в виде

 (9)

где u=u(x)
— нетривиальное решение однородного дифференциального уравнения (8), a v(x)
— решение неоднородного дифференциального уравнения (6). Ясно, что (9) как
линейная комбинация решений неоднородного дифференциального уравнения и соответствующего
ему однородного уравнения также является решением дифференциального уравнения (6).

Потребуем, чтобы первое из краевых
условий (7) было выполнено для у(х) при любом значении μ. Подставив (9) в
это краевое условие, запишем

 

Это равенство будет выполнено при
любом значении μ, если приравнять нулю коэффициент при μ, что приведет к двум
равенствам

для выполнения которых достаточно,
например, положить:

 (10)

 (11)

В случае a₀=0
вместо (11) положим

v(a)=0,
 (12)

Таким образом, u(х)
есть решение задачи Коши для однородного дифференциального уравнения (8),
удовлетворяющее начальным условиям (10), а v(x)- решение задачи Коши для
неоднородного дифференциального уравнения (6), удовлетворяющее начальным
условиям (11) или (12). При этом для любого μ функция у(х)=μu(x) + v(x)
удовлетворяет первому из краевых условий (7) (при х=а). Постоянную μ
выбирают так, чтобы функция у(х) удовлетворяла второму из краевых
условий (7) (при х=b),
т.е.

 (13)

Если выполнено неравенство

 (14)

то из (13) находим

 (15)

Следовательно, краевая задача (6),
(7) сведена к двум задачам Коши относительно функций u(х)
и v(x) для однородного (8) и неоднородного (6) дифференциальных
уравнений соответственно. Эти дифференциальные уравнения удовлетворяют всем
условиям теоремы Коши о существовании и единственности решения задачи Коши,
т.е. существует единственное решение u(х)
дифференциального уравнения (8), удовлетворяющее начальным условиям (10), и
единственное решение v(x) дифференциального уравнения (6), удовлетворяющее
начальным условиям (11) или (12). Поэтому при выполнении неравенства (14) существует
решение рассматриваемой линейной краевой задачи (7), (8).

Отметим, что если исходное
дифференциальное уравнение (6) будет однородным, т.е. f(x)=0, и в (7) А=0,
то в силу начальных условий (11) или (12) имеем v(a)=0 и v'(a)=0,
и поэтому v(x)=0. Тогда при выполнении неравенства (14) получим где u(х)-
решение дифференциального уравнения (8),
удовлетворяющее начальным условиям (10).

Сведение задачи с краевыми условиями
к задаче Коши рассмотрим на примере 7, главы 2, §2.

§4. Функция Грина

Определение: Функцией Грина называется
функция G(x,s),
определенная при и при каждом фиксированном  обладающая свойствами:

1.
при функция G(x,s)
удовлетворяет уравнению:

                                                                                                             (16)

2. при x=a и x=b
функция G(x,s)
удовлетворяет краевым условиям (2);

3. при x=s функция G(x,s)
непрерывна по x,
а ее производная по x
терпит разрыв первого рода со скачком, равным 1/а(s),
т.е. G(s+0,s)=G(s-0,s),
 (17)

Чтобы найти функцию Грина краевой
задачи (16) с краевыми условиями (2), необходимо найти два решения y₁(x)
и y₂(х),
отличные от y(x)≡0,
уравнение (16), удовлетворяет соответственно первому и второму из краевых
условий (2).

Если
y₁(x)
не удовлетворяет одновременно обоим краевым условиям, то функция Грина G(x,s)
существует и ее можно представить в виде:

                                                                 (18)

где
функции  и  подбираются
так, чтобы функция (18) удовлетворяла условиям (17), т.е. чтобы  

Если найдена функция Грина G(x,s),
то решение краевой задачи (16), с краевыми условиями
(2) выражается формулой:

Замечание: Из
определения функции Грина еще не следует ее существование для каждой краевой
задачи.

Глава 2. Применение краевых задач на
практике

Краевые задачи на практике
применяются:

ü  
в изучении течения жидкостей в каналах;

ü  
уравнение колебаний струны;

ü  
рассеяние волн областью с неровной
поверхностью

ü  
и т.д.

В данной главе мы рассмотрим, как
можно физическую задачу свести к математической задаче.

А так же рассмотрим примеры решения
уравнений для обыкновенных дифференциальных уравнений второго порядка.

§1. Краевая задача для
дифференциального уравнения второго порядка в частных производных

п.1. Дифференциальные уравнения в
частных производных

В главе 1 данной курсовой работы были
рассмотрены дифференциальные уравнения, в которых участвовали искомые функции от
одной независимой переменной, вместе с их производными. Эти уравнения носят
названия обыкновенные дифференциальные уравнения.

Однако, в различных технических
вопросах наиболее часто встречается искомой функция, u,
от двух независимых переменных, x и t:

причем условия поставленного вопроса
дают для ее определения некоторое соотношение, связывающее не только величины x,
t,
y,
но и частные производные:

т.е. соотношение вида:

. (1)

Такое соотношение называется дифференциальным
уравнением в частных производных; порядок его определяется порядком
наивысшей встречающейся в нем производной. Число независимых переменных может
оказаться более двух. Для техники наибольшую важность представляют линейные
уравнения в частных производных второго или высшего порядка.

Уравнение (1) называется линейным,
если оно первой степени относительно искомой функции и всех производных и
не содержит их произведений, т.е. это уравнение может быть записано в виде

Причем коэффициенты A,
B,
C,
a,
b,
c
зависят только от x
и y.

Если эти коэффициенты не зависят от x
и y,
то уравнение (2) представляет собой линейное дифференциальное уравнение с
постоянными коэффициентами.

Пусть D =
B²-4AC
– дискриминант уравнения. В зависимости от значения D
уравнение (2) относится к одному из следующих типов:

 D
> 0 – эллиптический тип;

 D =
0 – параболический тип;

 D <
0  — гиперболический тип;

D
не сохраняет постоянного знака – смешанный тип.

Дифференциальное уравнение с частными
производными имеет  в общем случае бесчисленное множество решений. Для
конкретного решения уравнения нужны дополнительные условия – начальные или краевые
условия. Начальные условия характеризуют процесс в начальный момент
времени. Краевые условия описывают состояние физического процесса в граничных
(краевых) областях (точках).

Краевые задачи ставятся следующим
образом: найти функция u,
которая удовлетворяет уравнению Лапласа:

Во всех внутренних точках области S,
а на границе области  — некоторому условию. В
зависимости от вида условия различают следующие краевые задачи:

 —
задача Дирихле;

 —
задача Неймана.

В следующем пункте представлена
краевая задача для  дифференциального уравнения второго порядка в частных
производных, на примере уравнения колебания струны. 

п.2. Вывод уравнения колебаний
струны. Понятие о граничных и начальных условиях

Рассмотрим натянутую струны, т.е.
тонкую гибкую упругую нить, расположенную в плоскости Oxu,
которая в результате известного возмущения была
выведена из положения равновесия Ox.
Изучим поперечные колебания струны, полагая, что при
таком колебании струны ее  точки движутся перпендикулярно оси Ox.

Обозначим через u=u(x,t)
– смещение точки струны с абсциссой х в момент
времени t относительно оси Ох
(рис.5).

Тогда функцией u(x,t)
при  опишется процесс колебаний струны: для
любого фиксированного момента времени t=t₁
выражением u=u(x,t₁)
определяется мгновенной профиль струны.

Сделаем следующие допущения:

1.          
Предположим, что струна совершает малые
колебания, т.е. ее форма в процессе колебаний незначительно отличается от
прямой u=0.
Будем предполагать, что наклон касательной к графику функции u(x,t),
t=const,
т.е. , есть малая по модулю величина по
сравнению с единицей. Отсюда получаем, что  и

2.          
К концам участка струны
приложены направленные по касательной упругие силы натяжения (рис.5), модули
которых равны:  и являются практически
постоянными, т.е. Т₀  не зависит от х и t.

3.          
На струну действуют непрерывно
распределенные внешние силы, перпендикулярные оси Ox,
с плотностью (нагрузкой) p(x,t),
рассчитанной на единицу длины.

Вырежем из струны бесконечно малый
элемент , абсциссами которого являются х и х+dx.
Воздействие отброшенной левой и правой частей струны заменим соответствующими
силами натяжения. Тогда элемент  можно рассматривать,
как свободную материальную точку, находящуюся под действием упругих сил  и внешней силы  —
орт оси Оu.

Пусть  —
линейная плотность струны в точке х. Так в положении равновесия масса
элемента равна , то в силу сохранения массы,
элемент   имеет ту же массу. Обозначим через  и  углы,
образованные с осью Ох касательными к профилю струны в момент времени t в точках М  и  соответственно.
Проектируя на ось Ou
силы, приложенные к элементу , в силу закона Ньютона
и предположения 2) получим:

 (1)

Согласно предположению 1) углы  и  малы,
поэтому:

 (2)

и

 (2*).

Для подсчета (2*) используем
следующую формулу: , справедливую с точностью до
бесконечно малых высших порядков.

Получаем:

 (3)

Подставляя выражение (2) и (3) в
формулу (1), получим:

 (4)

Мы получили искомое уравнение малых
вынужденных поперечных колебаний струны.

В случае постоянной плотности () это уравнение принимает вид:

.
(5),

где , а  — плотность силы, отнесенная к единице
массы.

При отсутствии внешней силы (P(x,t)=0)
мы получаем уравнение малых свободных колебаний струны:

 (6)

Уравнение (4), как показано выше,
имеет бесчисленное множество решений. Поэтому для однозначной характеристики
процесса колебаний необходимо к уравнению присоединить некоторые дополнительные
условия, вытекающие их физического смысла данной задачи. Эти условия могут быть
весьма разнообразными. В простейшем случае, как и в динамике точки, задается
положение и скорость точек струны в начальный момент времени:

 (7)

Эти условия, которым должно
удовлетворять решение u(x,t)
при t=0,
 называются начальными условиями.

Если струна ограничена, то необходимо
задать условия на ее концах. В частности, для струны, концы которой x=0
и x=l закреплены,

 (8)

при всяком .
Условия (8) – граничные (краевые) условия.

Таким образом, физическая задача о
колебаниях струны, закрепленной на концах, свелась к следующей математической
задаче: найти решение u(x,t)
уравнения (4), удовлетворяющее начальным условиям (7) и граничным условиям (8).
Такая задача называется смешанной краевой задачей для уравнения колебания. К
ней также можно прийти при изучении одномерных колебаний идеального газа или
одномерных продольных колебаний стержня.

§2. Решение обыкновенных
дифференциальных уравнений второго порядка с заданными краевыми условиями

Пример 1.
Найти решение уравнения , удовлетворяющее
краевым условиям y(0)=3,
 

Решение:

Все решения данного дифференциального
уравнения выражаются формулой , где C₁,
C₂
– произвольные постоянные. Подберем C₁
и C₂
так, чтобы удовлетворялись заданные краевые условия, т.е. определим постоянные C₁
и C₂
из уравнений C₁
+C₂=3,
C₁
+C₂e
— C₂e=1.
Отсюда С₁=1, С₂=2. Таким образом, решением краевой задачи
является функция

Пример 2.
Найти решение уравнения  удовлетворяющее
краевым условиям  

Решение: Общее решение данного
дифференциального уравнения имеет вид  Условие
y(0)=0
удовлетворяется при С₁=0, при этом y=C₂sinx.
Если , где n
– целое число, то из второго граничного условия находим: , .

Следовательно, в этом случае
существует единственное решение данной краевой задачи:

.

Если , то из
второго краевого условия имеет бесконечное множество решений: , где С₂ может принимать любые
значения.

В случае, если , а  указанным
краевым условиям не удовлетворяет ни одно решение данного дифференциального
уравнения, т.е. краевая задача решений не имеет.

Пример 3: Решить
краевую задачу:

Решение: Общее решение данного
уравнения имеет вид:

Подставим общее решение в заданные
краевые условия, получим систему уравнений относительно постоянных C₁
и C₂:

Отсюда находим: C₁=-2,
C₂=1.

Следовательно,  

Пример 4:
Решить краевую задачу

Решение: Общее решение данного
уравнения имеет вид:

Так как  то из
общего решения следует, что  Из краевого условия  следует, что

В результате получаем:

Пример 5:
Построить функцию Грина для краевой задачи

Решение: Общее решение уравнения  есть  Условию
y(-1)=0
удовлетворяет, например, решение , а второму краевому
условию – решение

Функцию Грина для указанной краевой
задачи ищем в виде:

где функции  и
 определяются из условий  Отсюда

Таким образом, искомая функция Грина
имеет вид:

Построив функцию Грина G(x,s),
запишем решение данной краевой задачи:

Пример 6:
Решить краевую задачу  ограничена при

Решение: Построим функцию Грина для
этой задачи. Общее решение уравнения  есть  Решение  удовлетворяет
первому краевому условию, а решение  удовлетворяет второму
краевому условию, поэтому функцию Грина ищем в виде:

Функции  и  определяем из условий

, т.е.
 Отсюда получаем:

Искомое решение имеет вид:

Пример 7:
Решить краевую задачу

На примере этой краевой задачи
проиллюстрируем метод приведения краевых задач к задачам Коши. В данном случае
такое приведение не эффективно, но во многих случаях, особенно в связи с
методами численного решения, этот прием оказывается полезным. Найдем решение
указанной краевой задачи в виде:

 где  соответственно решения таких задач Коши:  Решив каждую из этих задач Коши, находим:

 Подберем
в выражении

коэффициенты a
и b так, чтобы это выражение удовлетворяло
краевым условиям. Подставляя в  краевые условия,
получаем уравнения для определения a и b:
a=b,
6a+b=7.

Отсюда a=b=1.
Таким образом, искомое решение имеет вид:

Заключение

Теория дифференциальных уравнений
является одним из самых больших разделов современной математики. Чтобы
охарактеризовать ее место в современной математической науке, прежде всего
необходимо подчеркнуть основные особенности теории дифференциальных уравнений,
состоящей из двух обширных областей математики: теории обыкновенных
дифференциальных уравнений и теории уравнений с частными производными.

Важная особенность — это
непосредственная связь теории дифференциальных уравнений с приложениями.
Характеризуя математику как метод проникновения в тайны природы, можно сказать,
что основным путем применения этого метода является формирование и изучение
математических моделей реального мира. Изучая какие-либо физические явления,
исследователь прежде всего создает его математическую идеализацию или, другими
словами, математическую модель, то есть, пренебрегая второстепенными
характеристиками явления, он записывает основные законы, управляющие этим
явлением, в математической форме. Очень часто эти законы можно выразить в виде
дифференциальных уравнений. Такими оказываются модели различных явлений
механики сплошной среды, химических реакций, электрических и магнитных явлений
и др.

В данной курсовой работе мы
познакомились с понятиями дифференциального уравнения, краевых условий;
рассмотрели применение дифференциальных уравнений второго порядка к практике.

Список литературы

1.          
Агафонов С.А., Герман А.Д., Муратова Т.В.
Диффенциальные уравнения. Математика в техническом университете. Выпуск 8.
Изд-во МГТУ им.Н.Э.Баумана. 2003 – 348.

2.          
Демидович Б.П., Моденов В.П.
Дифференциальные уравнения: Учебное пособие. 3-е изд.,стер. – Спб.:
Издательство «Лань», 2008. – 288 с.

3.          
Егоров А.И. Обыкновенные дифференциальные
уравнения с приложениями. – М.: Физматлит, 2005. – 384 с.

4.          
Камке Э. Справочник по обыкновенным
дифференциальным уравнения. М., 1965. – 704 с.

5.          
Кисилев А.И., Краснов М.Л., Макаренко Г.И.
Сборник задач по обыкновенным уравнениям.  – М.: Изд-во «Высшая школа», 1965. –
235 с.

6.          
Филиппов А.Ф. Сборник задач по
дифференциальным уравнениям. – Ижевск: НИЦ «Регулярная и хаотическая динамика»,
2000. – 176 с.

7.          
Фихтенгольц Г.М. Математика для инженеров,
часть вторая, выпуск второй. Государственное технико-теоретическое издательство
Ленинград, Москва 1933 г.