Определение 14. Пусть дан многочлен
и пусть
– квадратная матрица, тогда значением
многочлена
от матрицы
называется матрица
,
где
– единичная матрица,
– матрица, получающаяся при умножении
матрицы
на себя
раз.
№ 827 (П).
Найти значение многочлена
от матрицы
.
Р е ш е н и е.
Найдем
.

;
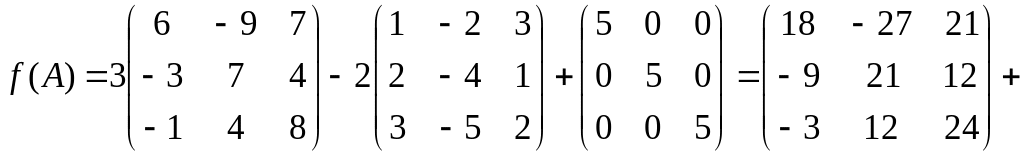
.
Ответ:
.
-
Обратная матрица
Определение 15. Матрица
называется обратной к квадратной
матрице
,
если
.
Определение 16. Квадратная матрица
называется невырожденной, если
она имеет единственную обратную матрицу
.
В противном случае
– вырожденная матрица.
Утверждение. Квадратная матрица
порядка
является невырож-денной в том и только
том случае, если определитель этой
матрицы отличен от нуля.
Для отыскания обратной матрицы
существуют два способа.
-
Припишем
к матрицесправа единичную матрицу и, применяя
метод Гаусса (см. §5), преобразуем
расширенную матрицу так, чтобы слева
стояла единичная матрица, тогда справа
будет находиться обратная матрица
:
.
.
Обоснование этого способа состоит в
следующем.
Пусть нам дана невырожденная квадратная
матрица. Задачу нахождения обратной
матрицы можно рассматривать как задачу
решения матричного уравнения
,
которое эквивалентно системе
уравнений с
неизвестными.
Эта система является объединением
систем уравнений, каждая из которых
содержит
неизвестных. Умножая поочередно строки
матрицы
на 1-й столбец матрицы
и приравнивая к 1-му столбцу матрицы
,
получим систему уравнений, матричная
форма записи которой имеет вид
(1.2.1)
С помощью элементарных операций над
строками матрицы систему уравнений
можно привести к виду
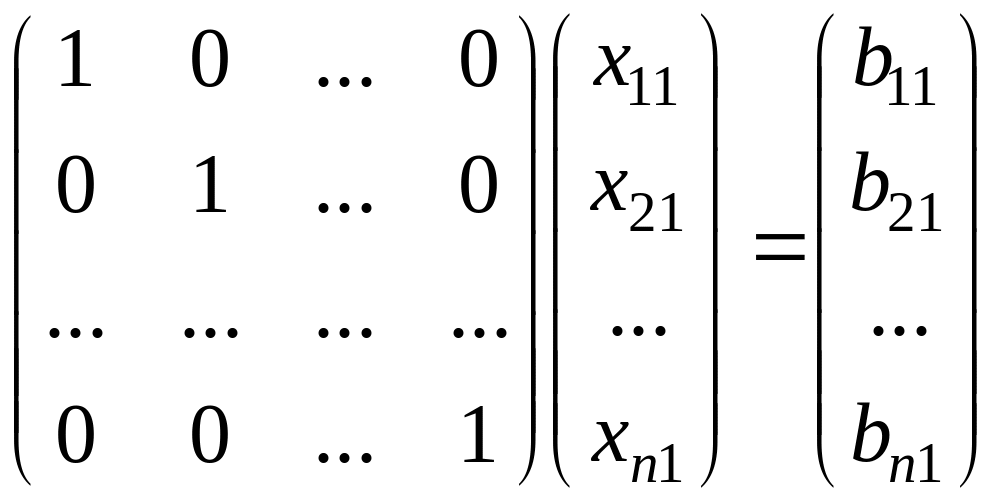
Умножая
поочередно строки матрицы
на второй столбец матрицы
и приравняв ко второму столбцу матрицы
,
получим систему уравнений
.
(1.2.2)
С помощью тех же элементарных операций,
что применялись для решения системы
(1.2.1), мы приведем систему (1.2.2) к виду
и т.д.
Поэтому
для нахождения обратной матрицы и был
предложен описанный выше способ.
-
,
где
– алгебраические дополнения к элементу
,
– определитель матрицы
(см. §2).
№ 840 (П).
Найти обратную матрицу для матрицы
.
Р е ш е н и е.
I
способ.


.
Ответ:
.
II
способ.

;
;
;
;
;
;
;
;
;
.
Таким образом,
.
Ответ:
.
№ 861 (П).
Решить матричное уравнение
.
Р е ш е н и е.
1 вариант.
Пусть
,
тогда
.
.
Ответ:
.
2 вариант.
Очевидно, что
.
Найдем матрицу, обратную к матрице
.
I
способ:
.
II
способ:
.
Таким образом,
.
Ответ:
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Многочлены от матриц
Напомним определение многочлена от матрицы. Пусть заданы многочлен (степени ) переменной
(7.40)
где — квадратная матрица n-го порядка. Выражение вида
(7.41)
называется многочленом от матрицы .
При больших значениях и
вычисление выражения (7.41) затруднительно из-за операции возведения матрицы в натуральную степень. Поэтому требуется найти другие, эквивалентные определению (7.41), формы записи и алгоритмы эффективного вычисления многочлена от матрицы. Для упрощения (7.41) имеются две возможности. Во-первых, можно упростить матрицу
так, чтобы многочлен (7.40) от упрощенной матрицы уже вычислялся сравнительно просто. Например, выражение (7.41) легко вычисляется, если матрица
диагональная. Во-вторых, можно понизить степень
многочлена, тогда самая трудоемкая операция — возведение матрицы в степень — упрощается.
Использование жордановой формы для нахождения многочлена от матрицы
Использование жордановой формы матрицы для нахождения многочлена от матрицы основано на трех свойствах.
1. Многочлены от подобных матриц подобны.
Действительно, пусть при помощи преобразования подобия матрица приведена к жордановой форме
. Подставим
в правую часть (7.41):
Учитывая, что для любого натурального
, получаем
Таким образом, многочлены и
подобны (с той же самой преобразующей матрицей
):
2. Многочлен от блочно-диагоналъной матрицы является блочно-диагоналъной матрицей.
Пусть , где
и
— квадратные матрицы, а
— нулевые матрицы соответствующих размеров. Для блочно-диагональных матриц справедливы равенства (они следуют из операций над блочными матрицами):
где
Поэтому .Для большего числа блоков доказательство V. о 1Аг)) аналогичное.
3. Многочлен (7.41) от жордановой клетки имеет вид
(7.42)
Это верхняя треугольная матрица r-го порядка, на главной диагонали которой стоят значения функции в точке
, над диагональю — значения первой производной в этой же точке и т.д., т.е. коэффициенты ряда Тейлора для функции
.
Действительно, разложим многочлен (7.40) по формуле Тейлора в окрестности точки
Остаточный член в данном случае равен нулю, так как все производные более высокого порядка, чем , тождественно равны нулю. При вычислении
линейный двучлен
заменяется матрицей
у которой элементы над главной диагональю равны единице, а остальные элементы равны нулю, т.е. , где
— i-й столбец единичной матрицы r-го порядка.
Можно показать, что при возведении в степень единичные элементы матрицы смещаются вверх:
и т.д.
причем — нулевая матрица при
. Подставляя эти матрицы в формулу Тейлора, получаем
Складывая матрицы в правой части, получаем квадратную матрицу r-го порядка, у которой элементы главной диагонали равны , элементы над главной диагональю равны —
и т.д., т.е. матрицу вида (7.42).
Пример 7.16. Найти многочлен от матриц
Решение. а) Матрица — это жорданова клетка 3-го порядка, соответствующая собственному значению 2:
. Находим значения функции и ее производных в точке
. Составляем матрицу вида (7.42), учитывая, что
Матрица имеет жорданову форму
, т.е. является блочно-диагональной. По свойству 2 многочлен от матрицы
является блочно-диагональной матрицей. Записываем многочлен
от каждой жордановой клетки по формуле (7.42):
Здесь число 7 рассматривается как квадратная матрица 1-го порядка. Составляем из этих квадратных матриц искомую блочно-диагональную матрицу
Матрица имеет жорданову форму
, т.е. является блочно-диагональной. Записываем многочлен
от каждой жордановой клетки по формуле (7.42):
Составляем из этих квадратных матриц искомую блочно-диагональную матрицу
Первый способ нахождения многочлена от матрицы
1. Привести матрицу к жордановой форме
, т.е. определить жорданову форму
и преобразующую матрицу
.
2. Составить блочно-диагональную матрицу , размещая на ее диагонали многочлены от жордановых клеток (7.42).
3. Найти многочлен от матрицы А по формуле .
Пример 7.17. Найти многочлен (при
) от матриц:
Решение. Матрица . 1. Жорданова форма
и преобразующая матрица
были найдены в примере 7.15:
2. Жорданова форма состоит из одной жордановой клетки
2-го порядка, соответствующей собственному значению
. Найдем значения функции
и ее производной
при
. Запишем многочлен от жордановой формы (блочно-диагональную матрицу с одним блоком):
.
3. Найдем многочлен от матрицы
Матрица В. 1. Жорданова форма и преобразующая матрица
были найдены в примере 7.15:
2. Жорданова форма состоит из одной жордановой клетки
3-го порядка, соответствующей собственному значению
. Найдем значения функции
и ее производных
при
. Запишем многочлен от жордановой формы
3. Найдем многочлен от матрицы
Матрица . 1. Жорданова форма
и преобразующая матрица
были найдены в примере 7.15:
2. Жорданова форма состоит из трех жордановых клеток 1-го порядка
, соответствующих собственным значениям
и
. Найдем значения функции
при
и
. Запишем многочлен от жордановой формы:
3. Найдем многочлен от матрицы
Результат совпадает с найденным в примерах 7.10, 7.12.
Матрица . 1. Жорданова форма
и преобразующая матрица
были найдены в примере 7.15:
2. Жорданова форма состоит из двух жордановых клеток 2-го и 1-го порядков
. соответствующих собственным значениям
и
. Найдем значения функции
и производной
(так как
). Запишем многочлен от жордановой формы
3. Найдем многочлен от матрицы
Использование аннулирующих многочленов
Для понижения степени многочлена (7.41) можно использовать аннулирующие многочлены матрицы , например, ее характеристический
или минимальный
многочлены.
Обозначим через степень минимального многочлена
Заметим, что не превосходит порядка
матрицы
(или, что то же самое, степени
характеристического многочлена
), т.е.
. Разделим заданный многочлен (7.40) на минимальный:
(7.43)
Здесь — частное, а
— остаток, степень которого меньше
(7.44)
Подставив в (7.43) вместо переменной матрицу
, получим:
(7.45)
поскольку минимальный многочлен является аннулирующим .
Таким образом, вместо вычисления многочлена (7.41) степени можно вычислить многочлен (7.44), степень которого меньше
. Коэффициенты
многочлена (7.44) находятся следующим образом.
Если все корни минимального многочлена простые, то, подставляя корень в (7.43), получаем
, так как
, т.е.
Если — корень минимального многочлена кратности
, учитывая, что
из (7.43), последовательно дифференцируя, получаем
(7.46)
Записывая равенства (7.46) для каждого корня минимального многочлена, получим совместную систему линейных уравнений с
неизвестными
.
Второй способ нахождения многочлена от матрицы
1. Найти минимальный многочлен матрицы
одним из способов, рассмотренных в разд.7.2.4. Определить его степень
и записать многочлен (7.44) с неопределенными коэффициентами
2. Для каждого корня (кратности
) минимального многочлена по формулам (7.46) составить
уравнений. Все уравнения объединить в одну систему.
3. Решить составленную систему, т.е. найти коэффициенты многочлена
.
4. По формуле (7.45) найти многочлен от матрицы:
Замечания 7.8.
1. Вместо минимального многочлена можно использовать характеристический многочлен матрицы, который также является аннулирующим (см. теорему Гамильтона-Кэли). При этом в пунктах 1,2 алгоритма минимальный многочлен заменяется характеристическим, степень которого равна .
2. В первом способе нахождения многочлена от матрицы используются все инвариантные множители, так как нужно получить жорданову форму. Во втором способе требуется только один последний инвариантный множитель, который совпадает с минимальным многочленом. Можно сказать, что жорданова форма матрицы излишне информативна для решения поставленной задачи.
Пример 7.18. Найти (вторым способом) многочлен (при
) от матриц:
Решение. Матрица . 1. Для матрицы
в примере 7.15 были найдены инвариантные множители. Минимальный многочлен совпадает с последним инвариантным множителем. Поэтому
. Степень
минимального многочлена равна двум. Значит, многочлен (7.44) линейный:
.
2. Для двойного корня составляем уравнения (7.46):
3. Решая систему, получаем и
.
4. Находим многочлен от матрицы
Матрица . 1. Инвариантные множители характеристической матрицы
найдены в примере 7.15. Минимальный многочлен равен последнему инвариантному множителю:
. Степень
минимального многочлена равна 3. Значит, многочлен (7.44) — это квадратный трехчлен:
.
2. Для тройного корня составляем уравнения (7.46):
3. Решая систему, получаем и
4. Вычисляя , записываем искомый многочлен:
Матрица . 1. Минимальный многочлен найден в примере7.15:
. Степень
многочлена равна 2. Следовательно, многочлен (7.44) имеет первую степень:
.
2. Для каждого простого корня и
записываем пер вое равенство из (7.46):
3. Решая систему, получаем и
.
4. Находим многочлен от матрицы
Найдем , используя характеристический многочлен вместо минимального. Согласно пункту 1 замечаний 7.8, выполняем все действия второго способа, заменяя минимальный многочлен характеристическим.
1. Найдем характеристический многочлен матрицы (см. при мер 7.11):
. Это многочлен 3-й степени. Поэтому многочлен (7.44) будет 2-ой степени:
.
2. Для двойного корня записываем два уравнения из (7.46), а для простого корня
одно:
3. Решая систему, получаем и
.
4. Вычисляя , записываем искомый многочлен:
Поскольку степень характеристического многочлена больше степени минимального многочлена , его применение менее эффективно.
Матрица . 1. Инвариантные множители характеристической матрицы
найдены в примере 7.15. Минимальный многочлен равен последнему инвариантному множителю:
. Степень
минимального многочлена равна 3. Значит, многочлен (7.44) — это квадратный трехчлен:
.
2. Для двойного корня записываем первые два равенства (7.46), а для простого корня
— первое равенство из (7.46). Получаем систему трех уравнений относительно коэффициентов квадратного трехчлена
3. Решая систему, получаем и
.
4. Находим многочлен от матрицы
Эта формула справедлива при , так как при
или
в системе для нахождения коэффициентов многочлена
появляются неопределенные выражения
. Впрочем, для этих показателей степени
многочлен
легко находится по определению
.
Все результаты совпадают с полученными в примере 7.17.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
|
01:26 Многочлен от матрицы |
||
|
Тема: Линейная алгебра.Калькулятор для вычисления многочлена от матрицы. Пример. Найти многочлен f(x)= x^2-5x+3 от матрицы Пусть дан многочлен Определение. Многочленом Пример 12. а) Найти значение многочлена Решение. Многочлен
б) Найти значение многочлена Тема: Линейная алгебра.Калькулятор для вычисления многочлена от матрицы. $CUT$ Пример. Найти многочлен f(x)= x^2-5x+3 от матрицы |
||
Категория: Линейная алгебра | Просмотров: 58621 | | Теги: Многочлен от матрицы, Возведение матрицы в степень | Рейтинг: 3.3/14 |
| Всего комментариев: 1 | |
|
Порядок вывода комментариев: |
|
From Wikipedia, the free encyclopedia
In mathematics, a matrix polynomial is a polynomial with square matrices as variables. Given an ordinary, scalar-valued polynomial
this polynomial evaluated at a matrix A is
where I is the identity matrix.[1]
A matrix polynomial equation is an equality between two matrix polynomials, which holds for the specific matrices in question. A matrix polynomial identity is a matrix polynomial equation which holds for all matrices A in a specified matrix ring Mn(R).
Characteristic and minimal polynomial[edit]
The characteristic polynomial of a matrix A is a scalar-valued polynomial, defined by 

There is a unique monic polynomial of minimal degree which annihilates A; this polynomial is the minimal polynomial. Any polynomial which annihilates A (such as the characteristic polynomial) is a multiple of the minimal polynomial.[2]
It follows that given two polynomials P and Q, we have 
where 


Matrix geometrical series[edit]
Matrix polynomials can be used to sum a matrix geometrical series as one would an ordinary geometric series,
If I − A is nonsingular one can evaluate the expression for the sum S.
See also[edit]
- Latimer–MacDuffee theorem
- Matrix exponential
- Matrix function
Notes[edit]
- ^ Horn & Johnson 1990, p. 36.
- ^ Horn & Johnson 1990, Thm 3.3.1.
- ^ Higham 2000, Thm 1.3.
References[edit]
- Gohberg, Israel; Lancaster, Peter; Rodman, Leiba (2009) [1982]. Matrix Polynomials. Classics in Applied Mathematics. Vol. 58. Lancaster, PA: Society for Industrial and Applied Mathematics. ISBN 978-0-898716-81-8. Zbl 1170.15300.
- Higham, Nicholas J. (2000). Functions of Matrices: Theory and Computation. SIAM. ISBN 089-871-777-9..
- Horn, Roger A.; Johnson, Charles R. (1990). Matrix Analysis. Cambridge University Press. ISBN 978-0-521-38632-6..
Многочлен и матрица как аргумент
| Исходный полином f(x) (его коэффициенты) |
| Аргумент является квадратной матрицей с элементами |
| Многочлен |
| Переменная x= |
| Результат вычислений |
Расссмотрим в данном материале одну из трудоёмких задач в высшей математике, которая звучит так: Найти чему задан многочлен
если аргумент есть квадратная матрица, то есть
И если сам принцип вычисления понятен, особенно если вы в совершенстве поняли как умножать матрицы, то непосредственное вычисление, для меня лично считается рутиной, которую по возможности нужно избежать.
Сразу хотелось бы сказать, где этот калькулятор пригодится. Для учителей, преподавателей, для создателей учебников, для тех, кому необходимо создавать оригинальные задачи по данной теме.
Также пригодится для студентов или аспирантов которые пишут рефераты, курсовые, дипломы.
Для всех остальных, это легкий способ проверить ошибку в заданном примере, решить, без долгих промежуточных вычислений, поставленную задачу.
Когда калькулятор был написан, оказалось что сайты, которые были посвещенны этой теме, содержали ошибки в промежуточных вычислениях и как как результат были неверные.
Данный калькулятор, я надеюсь избавлен от ошибок и Вы сможете безопасно решать любые примеры.
Как и подавляющее большинство калькуляторов на этом сайте, значениями как коэффициентов полинома, так и элементов матрицы, могут быть комплексные значения.
Такого на конец 2017 года, больше нигде не найдете, не считая конечно специальных созданных математических программ.
Приступим к примерам?
Найти значение полинома =2x^2-3x+4)
Еще один пример
Чему равен полином =ix^5+(2-i)x^2-11x)
Найти значение многочлена =x^4-x-1)
Удачный расчетов !










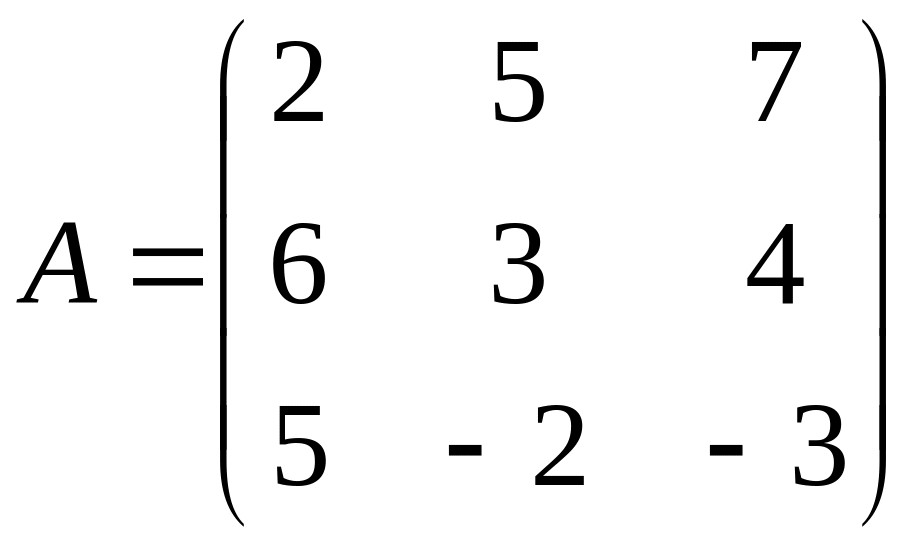





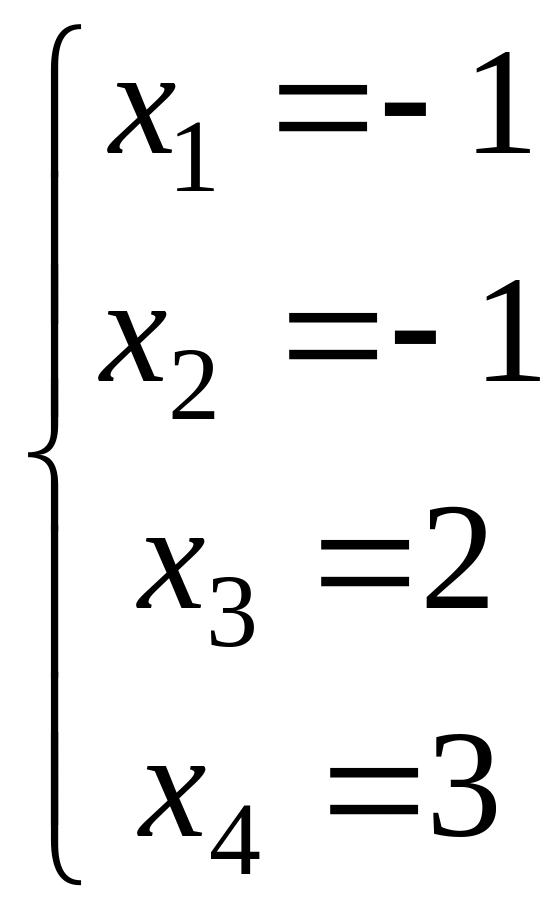














=a_0x^{n}+a_1x^{n-1}+a_2x^{n-2}+.....+a_{n-1}x+a_n)



