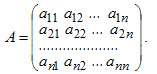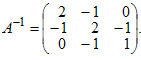Перед тем как перейти к решению систем линейных уравнений методом обратной матрицы вспомним, что такое обратная матрица, какие способы ее нахождения существуют, что такое матричные уравнения и как они решаются.
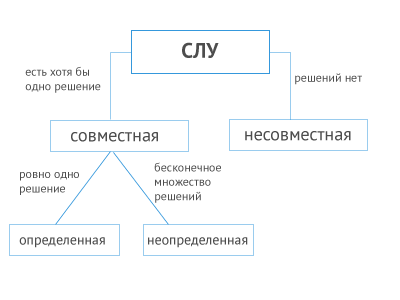
Система линейных уравнений (СЛУ)
Под системой линейных уравнений (СЛУ) будем понимать систему {a11x1+a12x2+a13x3+…+a1nxn=b1,a21x1+a22x2+a23x3+…+a2nxn=b2,………………………………….am1x1+am2x2+am3x3+…+amnxn=bm.begin{cases}a_{11}x_{1}+a_{12}x_{2}+a_{13}x_{3}+ldots+a_{1n}x_{n}=b_{1},\a_{21}x_{1}+a_{22}x_{2}+a_{23}x_{3}+ldots+a_{2n}x_{n}=b_{2},\ldotsldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots ldots.\a_{m1}x_{1}+a_{m2}x_{2}+a_{m3}x_{3}+ldots+a_{mn}x_{n}=b_{m}.end{cases},
содержащую mm уравнений и nn неизвестных.Линейность означает, что все неизвестные в уравнении содержатся в первой степени.
Рассмотрим на схеме основные понятия, связанные с понятием системы линейных уравнений.
Матричная форма записи СЛУ
С каждой системой линейных уравнений
{a11x1+a12x2+a13x3+…+a1nxn=b1,a21x1+a22x2+a23x3+…+a2nxn=b2,………………………………….am1x1+am2x2+am3x3+…+amnxn=bm.begin{cases}a_{11}x_{1}+a_{12}x_{2}+a_{13}x_{3}+ldots+a_{1n}x_{n}=b_{1},\a_{21}x_{1}+a_{22}x_{2}+a_{23}x_{3}+ldots+a_{2n}x_{n}=b_{2},\ldotsldotsldotsldotsldotsldotsldotsldotsldotsldotsldotsldotsldots.\a_{m1}x_{1}+a_{m2}x_{2}+a_{m3}x_{3}+ldots+a_{mn}x_{n}=b_{m}.end{cases} можно связать несколько матриц.
-
Матрица системы, состоящая из коэффициентов заданной системы линейных уравнений: A=(a11a12a13…a1na21a22a23…a2n……………am1am2am3…amn)A=begin{pmatrix}a_{11}&a_{12}&a_{13}&ldots&a_{1n}\a_{21}&a_{22}&a_{23}&ldots&a_{2n}\ldots&ldots&ldots&ldots&ldots\a_{m1}&a_{m2}&a_{m3}&ldots&a_{mn}end{pmatrix}.
-
Матрица неизвестных, состоящая из столбца, который содержит неизвестные x1,x2,…,xn:x_{1}, x_{2}, … , x_{n}:
X=(x1x2…xn)X=begin{pmatrix}x_{1}\x_{2}\…\x_{n}end{pmatrix}.
- Матрица свободных членов, состоящая из столбца, который содержит свободные члены b1,b2,…,bm:b_{1}, b_{2}, … , b_{m}:
B=(b1b2…bm)B=begin{pmatrix}b_{1}\b_{2}\ … \b_{m}end{pmatrix}.
Используя введенные обозначения (AA — матрица системы, XX — матрица неизвестных, BB — матрица свободных членов) СЛУ можно записать в виде матричного уравнения A⋅X=BAcdot X=B, поэтому метод обратной матрицы, по существу, является частным случаем матричного уравнения.
Метод обратной матрицы может применяться только для тех систем линейных уравнений, у которых определитель матрицы системы отличен от нуля, а именно ∣A∣≠0begin{vmatrix}Aend{vmatrix}neq0. Если же ∣A∣=0begin{vmatrix}Aend{vmatrix}=0, то решить СЛУ матричным методом невозможно (в таком случае СЛУ может быть решена методом Гаусса).
Алгоритм решения СЛУ методом обратной матрицы
- Записать систему линейных уравнений в матричной форме: A⋅X=BAcdot X=B, где
A=(a11a12a13…a1na21a22a23…a2n……………am1am2am3…amn)A=begin{pmatrix}a_{11}&a_{12}&a_{13}&ldots&a_{1n}\a_{21}&a_{22}&a_{23}&ldots&a_{2n}\ ldots&ldots&ldots&ldots&ldots\a_{m1}&a_{m2}&a_{m3}&ldots&a_{mn}end{pmatrix} — матрица системы,
X=(x1x2…xn)X=begin{pmatrix}x_{1}\x_{2}\…\x_{n}end{pmatrix} — матрица неизвестных,
B=(b1b2…bm)B=begin{pmatrix}b_{1}\b_{2}\…\b_{m}end{pmatrix} — матрица свободных членов.
- Решить матричное уравнение A⋅X=BAcdot X=B:
2.1 Найти обратную матрицу A−1A^{-1} одним из способов.
2.2 Найти XX, используя равенство X=(x1x2…xn)=A−1⋅BX=begin{pmatrix}x_{1}\x_{2}\…\x_{n}end{pmatrix}=A^{-1}cdot B.
Рассмотрим примеры решения СЛУ методом обратной матрицы.
Пример 1
Решить систему {x1−2×2+x3=1,2×1−x2+x3=2,3×1+2×2+2×3=−2.begin{cases}x_{1}-2x_{2}+x_{3}=1,\2x_{1}-x_{2}+x_{3}=2,\3x_{1}+2x_{2}+2x_{3}=-2.end{cases} с помощью обратной матрицы.
Запишем систему в матричной форме A⋅X=BAcdot X=B, где
A=(1−212−11322)A=begin{pmatrix}1&-2&1\2&-1&1\3&2&2end{pmatrix},
X=(x1x2x3)X=begin{pmatrix}x_{1}\x_{2}\x_{3}end{pmatrix},
B=(12−2):B=begin{pmatrix}1\2\-2end{pmatrix}:
(1−212−11322)⋅(x1x2x3)=(12−2)begin{pmatrix}1&-2&1\2&-1&1\3&2&2end{pmatrix}cdot begin{pmatrix}x_{1}\x_{2}\x_{3}end{pmatrix}=begin{pmatrix}1\2\-2end{pmatrix}.
∣1−212−11322∣=5≠0begin{vmatrix}1&-2&1\2&-1&1\3&2&2end{vmatrix}=5neq0, значит, уравнение можно решить методом обратной матрицы.
Найдем обратную матрицу A−1A^{-1} методом элементарных преобразований.
Составим расширенную матрицу:
(1−212−11322∣100010001)begin{pmatrix}left.begin{matrix}1&-2&1\2&-1&1\3&2&2end{matrix}right|begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}end{pmatrix}.
Прибавим к строке №2 строку №1, умноженную на -2:
(1−212−11322∣100010001)∼(1−2103−1322∣100−210001)begin{pmatrix}left.begin{matrix}1&-2&1\2&-1&1\3&2&2end{matrix}right|begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&-2&1\0&3&-1\3&2&2end{matrix}right|begin{matrix}1&0&0\-2&1&0\0&0&1end{matrix}end{pmatrix}.
Прибавим к строке №3 строку №1, умноженную на -3:
(1−2103−1322∣100−210001)∼(1−2103−108−1∣100−210−301)begin{pmatrix}left.begin{matrix}1&-2&1\0&3&-1\3&2&2end{matrix}right|begin{matrix}1&0&0\-2&1&0\0&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&-2&1\0&3&-1\0&8&-1end{matrix}right|begin{matrix}1&0&0\-2&1&0\-3&0&1end{matrix}end{pmatrix}.
Прибавим к строке №2 строку №3, умноженную на -1:
(1−2103−108−1∣100−210−301)∼(1−210−5008−1∣10011−1−301)begin{pmatrix}left.begin{matrix}1&-2&1\0&3&-1\0&8&-1end{matrix}right|begin{matrix}1&0&0\-2&1&0\-3&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&-2&1\0&-5&0\0&8&-1end{matrix}right|begin{matrix}1&0&0\1&1&-1\-3&0&1end{matrix}end{pmatrix}.
Умножим строку №2 на −15-frac{1}{5}:
(1−210−5008−1∣10011−1−301)∼(1−2101008−1∣100−15−1515−301)begin{pmatrix}left.begin{matrix}1&-2&1\0&-5&0\0&8&-1end{matrix}right|begin{matrix}1&0&0\1&1&-1\-3&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&-2&1\0&1&0\0&8&-1end{matrix}right|begin{matrix}1&0&0\-frac{1}{5}&-frac{1}{5}&frac{1}{5}\-3&0&1end{matrix}end{pmatrix}.
Прибавим к строке №3 строку №2, умноженную на -8:
(1−2101008−1∣100−15−1515−301)∼(1−2101000−1∣100−15−1515−7585−35)begin{pmatrix}left.begin{matrix}1&-2&1\0&1&0\0&8&-1end{matrix}right|begin{matrix}1&0&0\-frac{1}{5}&-frac{1}{5}&frac{1}{5}\-3&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&-2&1\0&1&0\0&0&-1end{matrix}right|begin{matrix}1&0&0\-frac{1}{5}&-frac{1}{5}&frac{1}{5}\-frac{7}{5}&frac{8}{5}&-frac{3}{5}end{matrix}end{pmatrix}.
Умножим строку №3 на -1:
(1−2101000−1∣100−15−1515−7585−35)∼(1−21010001∣100−15−151575−8535)begin{pmatrix}left.begin{matrix}1&-2&1\0&1&0\0&0&-1end{matrix}right|begin{matrix}1&0&0\-frac{1}{5}&-frac{1}{5}&frac{1}{5}\-frac{7}{5}&frac{8}{5}&-frac{3}{5}end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&-2&1\0&1&0\0&0&1end{matrix}right|begin{matrix}1&0&0\-frac{1}{5}&-frac{1}{5}&frac{1}{5}\frac{7}{5}&-frac{8}{5}&frac{3}{5}end{matrix}end{pmatrix}.
Прибавим к строке №1 строку №3, умноженную на -1:
(1−21010001∣100−15−151575−8535)∼(1−20010001∣−2585−35−15−151575−8535)begin{pmatrix}left.begin{matrix}1&-2&1\0&1&0\0&0&1end{matrix}right|begin{matrix}1&0&0\-frac{1}{5}&-frac{1}{5}&frac{1}{5}\frac{7}{5}&-frac{8}{5}&frac{3}{5}end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&-2&0\0&1&0\0&0&1end{matrix}right|begin{matrix}-frac{2}{5}&frac{8}{5}&-frac{3}{5}\-frac{1}{5}&-frac{1}{5}&frac{1}{5}\frac{7}{5}&-frac{8}{5}&frac{3}{5}end{matrix}end{pmatrix}.
Прибавим к строке №1 строку №2, умноженную на 2:
(1−20010001∣−2585−35−15−151575−8535)∼(100010001∣−4565−15−15−151575−8535)begin{pmatrix}left.begin{matrix}1&-2&0\0&1&0\0&0&1end{matrix}right|begin{matrix}-frac{2}{5}&frac{8}{5}&-frac{3}{5}\-frac{1}{5}&-frac{1}{5}&frac{1}{5}\frac{7}{5}&-frac{8}{5}&frac{3}{5}end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}right|begin{matrix}-frac{4}{5}&frac{6}{5}&-frac{1}{5}\-frac{1}{5}&-frac{1}{5}&frac{1}{5}\frac{7}{5}&-frac{8}{5}&frac{3}{5}end{matrix}end{pmatrix}.
A−1=(−4565−15−15−151575−8535)=15(−46−1−1−117−83)A^{-1}=begin{pmatrix}-frac{4}{5}&frac{6}{5}&-frac{1}{5}\-frac{1}{5}&-frac{1}{5}&frac{1}{5}\frac{7}{5}&-frac{8}{5}&frac{3}{5}end{pmatrix}=frac{1}{5}begin{pmatrix}-4&6&-1\-1&-1&1\7&-8&3end{pmatrix}.
Подставим матрицы в равенство X=A−1⋅BX=A^{-1}cdot B:
(x1x2x3)=15(−46−1−1−117−83)⋅(12−2)=15(10−5−15)=(2−1−3)begin{pmatrix}x_{1}\x_{2}\x_{3}end{pmatrix}=frac{1}{5}begin{pmatrix}-4&6&-1\-1&-1&1\7&-8&3end{pmatrix}cdot begin{pmatrix}1\2\-2end{pmatrix}=frac{1}{5}begin{pmatrix}10\-5\-15end{pmatrix}=begin{pmatrix}2\-1\-3end{pmatrix}.
Получили равенство (x1x2x3)=(2−1−3)begin{pmatrix}x_{1}\x_{2}\x_{3}end{pmatrix}=begin{pmatrix}2\-1\-3end{pmatrix}. Исходя из этого, имеем: x1=2,x2=−1,x3=−3x_{1}=2, x_{2}=-1, x_{3}=-3.
Ответ: x1=2,x2=−1,x3=−3x_{1}=2, x_{2}=-1, x_{3}=-3.
Пример 2
Решить систему {3×1+2×2+x3=5,2×1+3×2+x3=1,2×1+x2+3×3=11.begin{cases}3x_{1}+2x_{2}+x_{3}=5,\2x_{1}+3x_{2}+x_{3}=1,\2x_{1}+x_{2}+3x_{3}=11.end{cases} с помощью обратной матрицы.
Запишем систему в матричной форме A⋅X=BAcdot X=B,
где A=(321231213)A=begin{pmatrix}3&2&1\2&3&1\2&1&3end{pmatrix},
X=(x1x2x3)X=begin{pmatrix}x_{1}\x_{2}\x_{3}end{pmatrix},
B=(5111):B=begin{pmatrix}5\1\11end{pmatrix}:
(321231213)⋅(x1x2x3)=(5111)begin{pmatrix}3&2&1\2&3&1\2&1&3end{pmatrix}cdot begin{pmatrix}x_{1}\x_{2}\x_{3}end{pmatrix}=begin{pmatrix}5\1\11end{pmatrix}.
∣321231213∣=12≠0begin{vmatrix}3&2&1\2&3&1\2&1&3end{vmatrix}=12neq0, значит, уравнение можно решить методом обратной матрицы.
Найдем обратную матрицу A−1A^{-1} по формуле A−1=1∣A∣⋅A∗TA^{-1}=frac{1}{|A|}cdot A_{*}^{T}, где A∗TA_{*}^{T} — транспонированная матрица алгебраических дополнений.
A∗T=(a11a21a31a12a22a32a13a23a33)A_{*}^{T}=begin{pmatrix}a_{11}&a_{21}&a_{31}\a_{12}&a_{22}&a_{32}\a_{13}&a_{23}&a_{33}end{pmatrix}, aija_{ij} — алгебраические дополнения матрицы AA.
A∗T=(8−5−1−47−1−415)A_{*}^{T}=begin{pmatrix}8&-5&-1\-4&7&-1\-4&1&5end{pmatrix}.
A−1=112⋅(8−5−1−47−1−415)A^{-1}=frac{1}{12}cdot begin{pmatrix}8&-5&-1\-4&7&-1\-4&1&5end{pmatrix}.
Подставим матрицы в равенство X=A−1⋅BX=A^{-1}cdot B:
(x1x2x3)=112(8−5−1−47−1−415)⋅(5111)=112(24−2436)=(2−23)begin{pmatrix}x_{1}\x_{2}\x_{3}end{pmatrix}=frac{1}{12}begin{pmatrix}8&-5&-1\-4&7&-1\-4&1&5end{pmatrix}cdot begin{pmatrix}5\1\11end{pmatrix}=frac{1}{12}begin{pmatrix}24\-24\36end{pmatrix}=begin{pmatrix}2\-2\3end{pmatrix}.
Получили равенство (x1x2x3)=(2−23)begin{pmatrix}x_{1}\x_{2}\x_{3}end{pmatrix}=begin{pmatrix}2\-2\3end{pmatrix}.
Исходя из этого, имеем: x1=2,x2=−2,x3=3x_{1}=2, x_{2}=-2, x_{3}=3.
Ответ: x1=2,x2=−2,x3=3x_{1}=2, x_{2}=-2, x_{3}=3.
Возникают трудности с решением уравнений с помощью обратной матрицы? Советуем вам заказать решение задачи у наших экспертов!
Тест по теме “Линейные уравнения и и метод обратной матрицы”
Решение систем линейных алгебраических уравнений с помощью обратной матрицы.
Решение систем линейных алгебраических уравнений (СЛАУ) с помощью обратной матрицы (иногда этот способ именуют ещё матричным методом или методом обратной матрицы) требует предварительного ознакомления с таким понятием как матричная форма записи СЛАУ. Метод обратной матрицы предназначен для решения тех систем линейных алгебраических уравнений, у которых определитель матрицы системы отличен от нуля. Естественно, при этом подразумевается, что матрица системы квадратна (понятие определителя существует только для квадратных матриц). Суть метода обратной матрицы можно выразить в трёх пунктах:
- Записать три матрицы: матрицу системы $A$, матрицу неизвестных $X$, матрицу свободных членов $B$.
- Найти обратную матрицу $A^{-1}$.
- Используя равенство $X=A^{-1}cdot B$ получить решение заданной СЛАУ.
Почему $X=A^{-1}cdot B$? показатьскрыть
Перед переходом к чтению примеров рекомендую ознакомиться с методами вычисления обратных матриц, изложенными здесь.
Пример №1
Решить СЛАУ $
left { begin{aligned}
& -5x_1+7x_2=29;\
& 9x_1+8x_2=-11.
end{aligned} right.$ с помощью обратной матрицы.
Решение
Запишем матрицу системы $A$, матрицу свободных членов $B$ и матрицу неизвестных $X$.
$$
A=left(begin{array} {cc} -5 & 7\ 9 & 8 end{array}right);;
B=left(begin{array} {c} 29\ -11 end{array}right);;
X=left(begin{array} {c} x_1\ x_2 end{array}right).
$$
Найдём обратную матрицу к матрице системы, т.е. вычислим $A^{-1}$. В примере №2 на странице, посвящённой нахождению обратных матриц, обратная матрица была уже найдена. Воспользуемся готовым результатом и запишем $A^{-1}$:
$$
A^{-1}=-frac{1}{103}cdotleft(begin{array}{cc} 8 & -7\ -9 & -5end{array}right).
$$
Теперь подставим все три матрицы ($X$, $A^{-1}$, $B$) в равенство $X=A^{-1}cdot B$. Затем выполним умножение матриц в правой части данного равенства.
$$
left(begin{array} {c} x_1\ x_2 end{array}right)=
-frac{1}{103}cdotleft(begin{array}{cc} 8 & -7\ -9 & -5end{array}right)cdot
left(begin{array} {c} 29\ -11 end{array}right)=\
=-frac{1}{103}cdot left(begin{array} {c} 8cdot 29+(-7)cdot (-11)\ -9cdot 29+(-5)cdot (-11) end{array}right)=
-frac{1}{103}cdot left(begin{array} {c} 309\ -206 end{array}right)=left(begin{array} {c} -3\ 2end{array}right).
$$
Итак, мы получили равенство $left(begin{array} {c} x_1\ x_2 end{array}right)=left(begin{array} {c} -3\ 2end{array}right)$. Из этого равенства имеем: $x_1=-3$, $x_2=2$.
Ответ: $x_1=-3$, $x_2=2$.
Пример №2
Решить СЛАУ $
left{begin{aligned}
& x_1+7x_2+3x_3=-1;\
& -4x_1+9x_2+4x_3=0;\
& 3x_2+2x_3=6.
end{aligned}right.$ методом обратной матрицы.
Решение
Запишем матрицу системы $A$, матрицу свободных членов $B$ и матрицу неизвестных $X$.
$$
A=left(begin{array} {ccc} 1 & 7 & 3\ -4 & 9 & 4 \0 & 3 & 2end{array}right);;
B=left(begin{array} {c} -1\0\6end{array}right);;
X=left(begin{array} {c} x_1\ x_2 \ x_3 end{array}right).
$$
Теперь настал черёд найти обратную матрицу к матрице системы, т.е. найти $A^{-1}$. В примере №3 на странице, посвящённой нахождению обратных матриц, обратная матрица была уже найдена. Воспользуемся готовым результатом и запишем $A^{-1}$:
$$
A^{-1}=frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right).
$$
Теперь подставим все три матрицы ($X$, $A^{-1}$, $B$) в равенство $X=A^{-1}cdot B$, после чего выполним умножение матриц в правой части данного равенства.
$$
left(begin{array} {c} x_1\ x_2 \ x_3 end{array}right)=
frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)cdot
left(begin{array} {c} -1\0\6end{array}right)=\
=frac{1}{26}cdot left(begin{array} {c} 6cdot(-1)+(-5)cdot 0+1cdot 6 \ 8cdot (-1)+2cdot 0+(-16)cdot 6 \ -12cdot (-1)+(-3)cdot 0+37cdot 6 end{array}right)=frac{1}{26}cdot left(begin{array} {c} 0\-104\234end{array}right)=left(begin{array} {c} 0\-4\9end{array}right)
$$
Итак, мы получили равенство $left(begin{array} {c} x_1\ x_2 \ x_3 end{array}right)=left(begin{array} {c} 0\-4\9end{array}right)$. Из этого равенства имеем: $x_1=0$, $x_2=-4$, $x_3=9$.
Ответ: $x_1=0$, $x_2=-4$, $x_3=9$.
Естественно, что решение систем линейных уравнений с помощью обратной матрицы без применения специальных программ вроде Mathcad возможно лишь при сравнительно небольшом количестве переменных. Если СЛАУ содержит четыре и более переменных, то гораздо удобнее в таком случае применить метод Гаусса или метод Гаусса-Жордана.
Метод обратной матрицы (матричный способ)
Пусть задана система линейных алгебраических уравнений $$begin{cases} a_{11}x_1 + a_{12}x_2 + a_{13}x_3 = b_1 \ a_{21}x_1 + a_{22}x_2 + a_{23}x_3 = b_2 \ a_{31}x_1 + a_{32}x_2 + a_{33}x_3 = b_3 end{cases}.$$
Метод обратной матрицы подходит для решения систем линейных алгебраических уравнений в которых число строк совпадает с числом неизвестных переменных. Формула матричного метода выглядит следующим образом $$X = A^{-1} cdot B$$
Здесь $A^{-1}$ — это обратная матрица к матрице $A$, составленной из коэфициентов $a_{ij}$ в системе уравнений. $B$ — это вектор свободных членов, взятых из системы $$begin{pmatrix} x_1\x_2\x_3 end{pmatrix} = A^{-1} cdot begin{pmatrix} b_1 \ b_2 \ b_3 end{pmatrix}.$$
Важное замечание!
Для данного метода определитель матрицы $A$ не должен равняться нулю $det A neq 0$, так как это условие для существования обратной матрицы $A^{-1}$.
| Пример 1 |
| Решить систему уравнений методом обратной матрицы $$begin{cases} x_1+2x_2-x_3=2 \ 2x_1-3x_2 + 2x_3 = 2 \ 3x_1 + x_2 + x_3 = 8 end{cases}.$$ |
| Решение |
|
Составляем матрицу $$A = begin{pmatrix} 1&2&-1 \ 2&-3&2 \ 3&1&1 end{pmatrix}.$$ Прежде чем искать обратную матрицу, необходимо вычислить определитель и проверить то, что он неравен нулю. $$det A = begin{vmatrix} 1&2&-1 \ 2&-3&2 \ 3&1&1 end{vmatrix} = -3+12-2-9-2-4=-8 neq 0$$ Найдем обратную матрицу $A^{-1}$ с помощью единичной матрицы. Добавляем её к основной матрице сбоку. $$begin{pmatrix} 1&2&-1&|&1&0&0 \ 2&-3&2&|&0&1&0 \ 3&1&1&|&0&0&1 end{pmatrix}$$ Выполняем элементарные преобразования со строками приводим матрицу $A$ слева к единичной, а справа получаем обратную матрицу. Из второй строки вычитаем первую строчку, умноженную на 2. Из третьей строки вычитаем первую, умноженную на 3. $$begin{pmatrix} 1&2&-1&|&1&0&0 \ 2&-3&2&|&0&1&0 \ 3&1&1&|&0&0&1 end{pmatrix} sim begin{pmatrix} 1&2&-1&|&1&0&0 \ 0&-7&4&|&-2&1&0 \ 0&-5&4&|&-3&0&1 end{pmatrix}$$ Умножаем третью строку на 7 и вычитаем из неё вторую строчку, умноженную на 5. $$begin{pmatrix} 1&2&-1&|&1&0&0 \ 0&-7&4&|&-2&1&0 \ 0&0&8&|&-11&-5&7 end{pmatrix}$$ Теперь запускаем обратный ход. Умножаем вторую строку на 2 и вычитаем из неё третью. Умножаем первую строку на 8 и прибавляем к ней третью. $$begin{pmatrix} 8&16&0&|&-3&-5&7 \ 0&-14&0&|&7&7&-7 \ 0&0&8&|&-11&-5&7 end{pmatrix}$$ Умножаем первую строчку на 14 и прибавляем к ней вторую строчку, умноженную на 16. $$begin{pmatrix} 112&0&0&|&70&42&-14 \ 0&-14&0&|&7&7&-7 \ 0&0&8&|&-11&-5&7 end{pmatrix}$$ Теперь делим кажду строку на элемент стоящий на главной диагонали левой матрицы, чтобы получилась единичная. Первую строку делим на 112, вторую на (-14) и третью на 8. $$begin{pmatrix} 1&0&0&|&frac{70}{112}&frac{42}{112}&frac{-14}{112} \ 0&1&0&|&-frac{7}{14}&-frac{7}{14}&frac{7}{14} \ 0&0&1&|&-frac{11}{8}&-frac{5}{8}&frac{7}{8} end{pmatrix}$$ Итак, слева получилась обратная матрица $$A^{-1} = begin{pmatrix} frac{70}{112}&frac{42}{112}&frac{-14}{112} \ -frac{7}{14}&-frac{7}{14}&frac{7}{14} \ -frac{11}{8}&-frac{5}{8}&frac{7}{8} end{pmatrix}.$$ Теперь воспользуемся формулой $X = A^{-1} cdot B$, чтобы найти $x_1,x_2,x_3$ и тем самым решить поставленную задачу. Производим умножение обратной матрицы на столбец свободных членов $$begin{pmatrix} x_1\x_2\x_3 end{pmatrix} = begin{pmatrix} frac{70}{112}&frac{42}{112}&frac{-14}{70} \ -frac{7}{14}&-frac{7}{14}&frac{7}{14} \ -frac{11}{8}&-frac{5}{8}&frac{7}{8} end{pmatrix} cdot begin{pmatrix} 2\2\8 end{pmatrix} =$$ Произведение ищем по правилу умножения двух матриц. Напоминаем, находим сумму произведения элементов строк на столбец. $$=begin{pmatrix} frac{2cdot70}{112} + frac{2cdot42}{112} -frac{8cdot14}{112} \ -frac{2cdot7}{14} — frac{2cdot7}{14} + frac{8cdot7}{14} \ -frac{2cdot11}{8} -frac{2cdot5}{8} + frac{8cdot7}{8} end{pmatrix} = begin{pmatrix} 1\2\3 end{pmatrix}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$x_1 = 1, x_2=2, x_3=3$$ |
| Пример 2 |
| Решить систему уравнений матричным методом $$begin{cases} x_1+2x_2=10 \ 3x_1+2x_2+x_3=23 \ x_2+2x_3=13 end{cases}.$$ |
| Решение |
|
Составляем матрицу из коэффициентов $$A = begin{pmatrix} 1&2&0 \ 3&2&1 \ 0&1&2 end{pmatrix}$$ Находим обратную матрицу с помощью единичной матрицы. $$begin{pmatrix} 1&2&0 &|& 1&0&0 \ 3&2&1 &|& 0&1&0 \ 0&1&2 &|& 0&0&1 end{pmatrix}$$ Из второй строки вычитаем первую, умноженную на 3. $$begin{pmatrix} 1&2&0 &|& 1&0&0 \ 0&-4&1 &|& -3&1&0 \ 0&1&2 &|& 0&0&1 end{pmatrix}$$ Умножаем третью строчку на 4 и прибавляем к ней вторую. $$begin{pmatrix} 1&2&0 &|& 1&0&0 \ 0&-4&1 &|& -3&1&0 \ 0&0&9 &|& -3&1&4 end{pmatrix}$$ Начинаем обратный ход элементарных преобразований. Умножаем вторую строку на 9 и вычитаем третью. $$begin{pmatrix} 1&2&0 &|& 1&0&0 \ 0&-36&0 &|& -24&8&-4 \ 0&0&9 &|& -3&1&4 end{pmatrix}$$ Умножаем первую строку на 18 и прибавляем к ней вторую. $$begin{pmatrix} 18&0&0 &|& -6&8&-4 \ 0&-36&0 &|& -24&8&-4 \ 0&0&9 &|& -3&1&4 end{pmatrix}$$ Остаётся получить единицы на главной диагонали. Для этого делим первую строку на 18, вторую на (-36) и третью 9. $$begin{pmatrix} 1&0&0 &|& -frac{6}{18}&frac{8}{18}&-frac{4}{18} \ 0&1&0 &|& frac{24}{36}&-frac{8}{36}&frac{4}{36} \ 0&0&1 &|& -frac{3}{9}&frac{1}{9}&frac{4}{9} end{pmatrix}$$ Итак, выписываем полученную обратную матрицу $$A^{-1} = begin{pmatrix} -frac{6}{18}&frac{8}{18}&-frac{4}{18} \ frac{24}{36}&-frac{8}{36}&frac{4}{36} \ -frac{3}{9}&frac{1}{9}&frac{4}{9} end{pmatrix}.$$ Теперь пользуйся формулой $X = A^{-1} cdot B$ вычисляем $$begin{pmatrix} x_1\x_2\x_3 end{pmatrix} = begin{pmatrix} -frac{6}{18}&frac{8}{18}&-frac{4}{18} \ frac{24}{36}&-frac{8}{36}&frac{4}{36} \ -frac{3}{9}&frac{1}{9}&frac{4}{9} end{pmatrix} cdot begin{pmatrix} 10\23\13 end{pmatrix} = $$ Умножение производится по правилу произведения двух матриц: сумма произведений элементов строк первой матрицы на элементы второй матрицы. $$ = begin{pmatrix} -frac{6cdot10}{18}+frac{8cdot23}{18}-frac{4cdot13}{18} \ frac{24cdot10}{36}-frac{8cdot23}{36}+frac{4cdot13}{36} \ -frac{3cdot10}{9}+frac{23}{9}+frac{4cdot13}{9} end{pmatrix} = begin{pmatrix} 4\3\5 end{pmatrix}$$ Вот таким вот образом матричный метод помогает решать системы линейных алгебраических уравнений. Главное не забывать что данный способ работает, если определитель матрицы $A$ не равен нулю и число переменных в системе совпадает с числом уравнений. |
| Ответ |
| $$x_1 = 4, x_2 = 3, x_3 = 5$$ |
Метод обратной матрицы
(Матричный метод) решения систем линейных
алгебраических уравнений с ненулевым
определителем основной матрицы состоит
в поиске матрицы, обратной к основной
матрице, и умножению ее на матрицу
свободных членов.
Обратная матрица
Пусть имеется
квадратная матрица n-го порядка
Матрица
А-1 называется обратной матрицей по
отношению к матрице А, если А*А-1 = Е, где
Е — единичная матрица n-го порядка.
Единичная матрица —
такая квадратная матрица, у которой все
элементы по главной диагонали, проходящей
от левого верхнего угла к правому нижнему
углу, — единицы, а остальные — нули,
например:
Обратная матрица
может существовать только для квадратных
матриц т.е. для тех матриц, у которых
число строк и столбцов совпадают.
Теорема
условия существования обратной матрицы
Для того чтобы матрица
имела обратную матрицу необходимо и
достаточно, чтобы она была невырожденной.
Матрица А = (А1, А2,…Аn)
называется невырожденной, если
векторы-столбцы являются линейно
независимыми. Число линейно независимых
векторов-столбцов матрицы называется
рангом матрицы . Поэтому можно сказать,
что для того, чтобы существовала обратная
матрица, необходимо и достаточно, чтобы
ранг матрицы равнялся ее размерности,
т.е. r = n.
Алгоритм нахождения
обратной матрицы
Записать в таблицу
для решения систем уравнений методом
Гаусса матрицу А и справа (на место
правых частей уравнений) приписать к
ней матрицу Е.
Используя преобразования
Жордана, привести матрицу А к матрице,
состоящей из единичных столбцов; при
этом необходимо одновременно преобразовать
матрицу Е.
Если необходимо, то
переставить строки (уравнения) последней
таблицы так, чтобы под матрицей А исходной
таблицы получилась единичная матрица
Е.
Записать обратную
матрицу А-1, которая находится в последней
таблице под матрицей Е исходной таблицы.
Пример 1
Для матрицы А найти
обратную матрицу А-1
Решение: Записываем
матрицу А и справа приписываем единичную
матрицу Е. Используя преобразования
Жордана, приводим матрицу А к единичной
матрице Е. Вычисления приведены в таблице
31.1.
Проверим
правильность вычислений умножением
исходной матрицы А и обратной матрицы
А-1.
В результате умножения
матриц получилась единичная матрица.
Следовательно, вычисления произведены
правильно.
Ответ:
Решение матричных
уравнений
Матричные уравнения
могут иметь вид:
АХ = В, ХА = В, АХВ = С,
где А,В,С — задаваемые
матрицы, Х- искомая матрица.
Матричные
уравнения решаются с помощью умножения
уравнения на обратные матрицы.
Например, чтобы найти
матрицу из уравнения , необходимо
умножить это уравнение на слева.
Тогда:
Следовательно, чтобы
найти решение уравнения , нужно найти
обратную матрицу и умножить ее на матрицу
, стоящие в правой части уравнения.
Аналогично решаются
другие уравнения.
Пример
2
Решить уравнение АХ
= В, если
Решение: Так как
обратная матрица равняется (см. пример
1)
24. Решение слау методом гаусса
Ме́тод
Га́усса[1] — классический метод решения
системы линейных алгебраических
уравнений (СЛАУ). Это метод последовательного
исключения переменных, когда с помощью
элементарных преобразований система
уравнений приводится к равносильной
системе ступенчатого (или треугольного)
вида, из которой последовательно, начиная
с последних (по номеру) переменных,
находятся все остальные переменные.
Описание метода
Пусть исходная система
выглядит следующим образом
Матрица
A называется основной матрицей системы,
b — столбцом свободных членов.
Тогда согласно
свойству элементарных преобразований
над строками основную матрицу этой
системы можно привести к ступенчатому
виду(эти же преобразования нужно
применять к столбцу свободных членов):
При этом
будем считать, что базисный минор
(ненулевой минор максимального порядка)
основной матрицы находится в верхнем
левом углу, то есть в него входят только
коэффициенты при переменных
.
Тогда
переменные
называются главными переменными. Все
остальные называются свободными.
Если хотя
бы одно число, где i > r, то рассматриваемая система
несовместна.
Пусть
для любых i > r.
Перенесём свободные
переменные за знаки равенств и поделим
каждое из уравнений системы на свой
коэффициент при самом левом (, где —
номер строки):
,
где
Если свободным
переменным системы (2) придавать все
возможные значения и решать новую
систему относительно главных неизвестных
снизу вверх (то есть от нижнего уравнения
к верхнему), то мы получим все решения
этой СЛАУ. Так как эта система получена
путём элементарных преобразований над
исходной системой (1), то по теореме об
эквивалентности при элементарных
преобразованиях системы (1) и (2)
эквивалентны, то есть множества их
решений совпадают.
Следствия:
1: Если в
совместной системе все переменные
главные, то такая система является
определённой.
2: Если количество
переменных в системе превосходит число
уравнений, то такая система является
либо неопределённой, либо несовместной.
Условие совместности
Упомянутое
выше условие
для всех
может быть сформулировано в качестве
необходимого и достаточного условия
совместности:
Напомним, что рангом
совместной системы называется ранг её
основной матрицы (либо расширенной, так
как они равны).
Теорема Кронекера-Капелли.
Система
совместна тогда и только тогда, когда
ранг её основной матрицы равен рангу
её расширенной матрицы.
Следствия:
Количество главных
переменных равно рангу системы и не
зависит от её решения.
Если ранг
совместной системы равен числу переменных
данной системы, то она определена.
Алгоритм
Описание
Алгоритм решения
СЛАУ методом Гаусса подразделяется на
два этапа.
На первом этапе
осуществляется так называемый прямой
ход, когда путём элементарных преобразований
над строками систему приводят к
ступенчатой или треугольной форме, либо
устанавливают, что система несовместна.
А именно, среди элементов первого столбца
матрицы выбирают ненулевой, перемещают
его на крайнее верхнее положение
перестановкой строк и вычитают
получившуюся после перестановки первую
строку из остальных строк, домножив её
на величину, равную отношению первого
элемента каждой из этих строк к первому
элементу первой строки, обнуляя тем
самым столбец под ним. После того, как
указанные преобразования были совершены,
первую строку и первый столбец мысленно
вычёркивают и продолжают пока не
останется матрица нулевого размера.
Если на какой-то из итераций среди
элементов первого столбца не нашёлся
ненулевой, то переходят к следующему
столбцу и проделывают аналогичную
операцию.
На втором
этапе осуществляется так называемый
обратный ход, суть которого заключается
в том, чтобы выразить все получившиеся
базисные переменные через небазисные
и построить фундаментальную систему
решений, либо, если все переменные
являются базисными, то выразить в
численном виде единственное решение
системы линейных уравнений. Эта процедура
начинается с последнего уравнения, из
которого выражают соответствующую
базисную переменную (а она там всего
одна) и подставляют в предыдущие
уравнения, и так далее, поднимаясь по
«ступенькам» наверх. Каждой строчке
соответствует ровно одна базисная
переменная, поэтому на каждом шаге,
кроме последнего (самого верхнего),
ситуация в точности повторяет случай
последней строки.
Метод Гаусса требует
порядка O(n3) действий.
Этот метод опирается
на: Теорема (о приведении матриц к
ступенчатому виду).
Любую матрицу путём
элементарных преобразований только
над строками можно привести к ступенчатому
виду.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Матричный способ решения систем линейных уравнений
Рассмотрим систему линейных уравнений следующего вида:
$left{begin{array}{c} {a_{11} x_{1} +a_{12} x_{2} +…+a_{1n} x_{n} =b_{1} } \ {a_{21} x_{1} +a_{22} x_{2} +…+a_{2n} x_{n} =b_{2} } \ {…} \ {a_{n1} x_{1} +a_{n2} x_{2} +…+a_{nn} x_{n} =b_{n} } end{array}right. .$
Числа $a_{ij} (i=1..n,j=1..n)$ — коэффициенты системы, числа $b_{i} (i=1..n)$ — свободные члены.
Определение 1
В случае, когда все свободные члены равны нулю, система называется однородной, в противном случае — неоднородной.
Каждой СЛАУ можно поставить в соответствие несколько матриц и записать систему в так называемом матричном виде.
Определение 2
Матрица коэффициентов системы называется матрицей системы и обозначается, как правило, буквой $A$.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Столбец свободных членов образует вектор-столбец, который, как правило, обозначается буквой $B$ и называется матрицей свободных членов.
Неизвестные переменные образуют вектор-столбец, который, как правило, обозначается буквой $X$ и называется матрицей неизвестных.
Описанные выше матрицы имеют вид:
$A=left(begin{array}{cccc} {a_{11} } & {a_{12} } & {…} & {a_{1n} } \ {a_{21} } & {a_{22} } & {…} & {a_{2n} } \ {…} & {…} & {…} & {…} \ {a_{n1} } & {a_{n2} } & {…} & {a_{nn} } end{array}right),B=left(begin{array}{c} {b_{1} } \ {b_{2} } \ {…} \ {b_{n} } end{array}right),X=left(begin{array}{c} {x_{1} } \ {x_{2} } \ {…} \ {x_{n} } end{array}right).$
Используя матрицы, СЛАУ можно переписать в виде $Acdot X=B$. Такую запись часто называют матричным уравнением.
Вообще говоря, в матричном виде записать можно любую СЛАУ.
Примеры решения системы с помощью обратной матрицы
Пример 1
Дана СЛАУ: $left{begin{array}{c} {3x_{1} -2x_{2} +x_{3} -x_{4} =3} \ {x_{1} -12x_{2} -x_{3} -x_{4} =7} \ {2x_{1} -3x_{2} +x_{3} -3x_{4} =5} end{array}right. $. Записать систему в матричном виде.
Решение:
$A=left(begin{array}{cccc} {3} & {-2} & {1} & {-1} \ {1} & {-12} & {-1} & {-1} \ {2} & {-3} & {1} & {-3} end{array}right),B=left(begin{array}{c} {3} \ {7} \ {5} end{array}right),X=left(begin{array}{c} {x_{1} } \ {x_{2} } \ {x_{3} } end{array}right).$
$left(begin{array}{cccc} {3} & {-2} & {1} & {-1} \ {1} & {-12} & {-1} & {-1} \ {2} & {-3} & {1} & {-3} end{array}right)cdot left(begin{array}{c} {x_{1} } \ {x_{2} } \ {x_{3} } end{array}right)=left(begin{array}{c} {3} \ {7} \ {5} end{array}right)$
В случае, когда матрица системы является квадратной, СЛАУ можно решить уравнения матричным способом.
Имея матричное уравнение $Acdot X=B$, можно выразить из него $X$ следующим способом:
$A^{-1} cdot Acdot X=A^{-1} cdot B$
$A^{-1} cdot A=E$ (свойство произведения матриц)
$Ecdot X=A^{-1} cdot B$
$Ecdot X=X$ (свойство произведения матриц)
$X=A^{-1} cdot B$
Алгоритм решения системы алгебраических уравнений с помощью обратной матрицы:
- записать систему в матричном виде;
- вычислить определитель матрицы системы;
- если определитель матрицы системы отличен от нуля, то находим обратную матрицу;
- решение системы вычисляем по формуле $X=A^{-1} cdot B$.
«Решение систем линейных уравнений матричным методом» 👇
Если матрица системы имеет определитель, не равный нулю, то данная система имеет единственное решение, которое можно найти матричным способом.
Если матрица системы имеет определитель, равный нулю, то данную систему нельзя решить матричным способом.
Пример 2
Дана СЛАУ: $left{begin{array}{c} {x_{1} +3x_{3} =26} \ {-x_{1} +2x_{2} +x_{3} =52} \ {3x_{1} +2x_{2} =52} end{array}right. $. Решить СЛАУ методом обратной матрицы, если это возможно.
Решение:
$A=left(begin{array}{ccc} {1} & {0} & {3} \ {-1} & {2} & {1} \ {3} & {2} & {0} end{array}right),B=left(begin{array}{c} {26} \ {52} \ {52} end{array}right),X=left(begin{array}{c} {x_{1} } \ {x_{2} } \ {x_{3} } end{array}right). $
Нахождение определителя матрицы системы:
$begin{array}{l} {det A=left|begin{array}{ccc} {1} & {0} & {3} \ {-1} & {2} & {1} \ {3} & {2} & {0} end{array}right|=1cdot 2cdot 0+0cdot 1cdot 3+2cdot (-1)cdot 3-3cdot 2cdot 3-2cdot 1cdot 1-0cdot (-1)cdot 0=0+0-6-18-2-0=-26ne 0} end{array}$ Так как определитель не равен нулю, то матрица системы имеет обратную матрицу и, следовательно, система уравнений может быть решена методом обратной матрицы. Полученное решение будет единственным.
Решим систему уравнений с помощью обратной матрицы:
$A_{11} =(-1)^{1+1} cdot left|begin{array}{cc} {2} & {1} \ {2} & {0} end{array}right|=0-2=-2; A_{12} =(-1)^{1+2} cdot left|begin{array}{cc} {-1} & {1} \ {3} & {0} end{array}right|=-(0-3)=3;$
$A_{13} =(-1)^{1+3} cdot left|begin{array}{cc} {-1} & {2} \ {3} & {2} end{array}right|=-2-6=-8; A_{21} =(-1)^{2+1} cdot left|begin{array}{cc} {0} & {3} \ {2} & {0} end{array}right|=-(0-6)=6; $
$A_{22} =(-1)^{2+2} cdot left|begin{array}{cc} {1} & {3} \ {3} & {0} end{array}right|=0-9=-9; A_{23} =(-1)^{2+3} cdot left|begin{array}{cc} {1} & {0} \ {3} & {2} end{array}right|=-(2-0)=-2;$
$A_{31} =(-1)^{3+1} cdot left|begin{array}{cc} {0} & {3} \ {2} & {1} end{array}right|=0-6=-6; A_{32} =(-1)^{3+2} cdot left|begin{array}{cc} {1} & {3} \ {-1} & {1} end{array}right|=-(1+3)=-4;$
$A_{33} =(-1)^{3+3} cdot left|begin{array}{cc} {1} & {0} \ {-1} & {2} end{array}right|=2-0=2$
Искомая обратная матрица:
$A^{-1} =frac{1}{-26} cdot left(begin{array}{ccc} {-2} & {6} & {-6} \ {3} & {-9} & {-4} \ {-8} & {-2} & {2} end{array}right)=frac{1}{26} cdot left(begin{array}{ccc} {2} & {-6} & {6} \ {-3} & {9} & {4} \ {8} & {2} & {-2} end{array}right)=left(begin{array}{ccc} {frac{2}{26} } & {frac{-6}{26} } & {frac{6}{26} } \ {frac{-3}{26} } & {frac{9}{26} } & {frac{4}{26} } \ {frac{8}{26} } & {frac{2}{26} } & {frac{-2}{26} } end{array}right)=left(begin{array}{ccc} {frac{1}{13} } & {-frac{3}{13} } & {frac{3}{13} } \ {-frac{3}{26} } & {frac{9}{26} } & {frac{2}{13} } \ {frac{4}{13} } & {frac{1}{13} } & {-frac{1}{13} } end{array}right).$
Найдем решение системы:
$X=left(begin{array}{ccc} {frac{1}{13} } & {-frac{3}{13} } & {frac{3}{13} } \ {-frac{3}{26} } & {frac{9}{26} } & {frac{2}{13} } \ {frac{4}{13} } & {frac{1}{13} } & {-frac{1}{13} } end{array}right)cdot left(begin{array}{c} {26} \ {52} \ {52} end{array}right)=left(begin{array}{c} {frac{1}{13} cdot 26-frac{3}{13} cdot 52+frac{3}{13} cdot 52} \ {-frac{3}{26} cdot 26+frac{9}{26} cdot 52+frac{2}{13} cdot 52} \ {frac{4}{13} cdot 26+frac{1}{13} cdot 52-frac{1}{13} cdot 52} end{array}right)=left(begin{array}{c} {2-12+12} \ {-3+18+8} \ {8+4-4} end{array}right)=left(begin{array}{c} {2} \ {23} \ {8} end{array}right)$
$X=left(begin{array}{c} {2} \ {23} \ {8} end{array}right)$ — искомое решение системы уравнений.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме