Как найти решение уравнения с помощью графика

Решение уравнений с помощью графиков

Решение линейных уравнений

Как ты уже знаешь, графиком линейного уравнения является прямая линия, отсюда и название данного вида.

Линейные уравнения достаточно легко решать алгебраическим путем – все неизвестные переносим в одну сторону уравнения, все, что нам известно – в другую и вуаля! Мы нашли корень.

Сейчас же я покажу тебе, как это сделать графическим способом.

Итак, у тебя есть уравнение: ( displaystyle 2{x} -10=2)

Как его решить?

Вариант 1, и самый распространенный – перенести неизвестные в одну сторону, а известные в другую, получаем:

Иными словами, у нас будет:

Как ты думаешь, что является корнем нашего уравнения? Правильно, координата ( displaystyle x) точки пересечения графиков:

Наш ответ: ( displaystyle x=6)

Вот и вся премудрость графического решения. Как ты с легкостью можешь проверить, корнем нашего уравнения является число ( displaystyle 6)!

Вариант 1. Напрямую

Просто строим параболу по данному уравнению: ( displaystyle {{x}^{2}}+2{x} -8=0)

Чтобы сделать это быстро, дам тебе одну маленькую подсказку: удобно начать построение с определения вершины параболы. Определить координаты вершины параболы помогут следующие формулы:

Посчитал? Какие координаты вершины параболы у тебя получились? Давай разбираться вместе:

И вот мы знаем уже координаты вершины, а для построения параболы нам нужно еще … точек. Как ты думаешь, сколько минимум точек нам необходимо? Правильно, ( displaystyle 3).

Ты знаешь, что парабола симметрична относительно своей вершины, например:

Соответственно, нам необходимо еще две точки по левой или правой ветви параболы, а в дальнейшем мы эти точки симметрично отразим на противоположную сторону:

Возвращаемся к нашей параболе.

Для нашего случая точка ( displaystyle Aleft( -1;-9 right)). Нам необходимо еще две точки, соответственно, ( displaystyle x) можно взять положительные, а можно взять отрицательные? Какие точки тебе удобней?

Мне удобней работать с положительными, поэтому я рассчитаю при ( displaystyle x=0) и ( displaystyle x=2).

Как ты думаешь, что является решением уравнения?

Правильно, точки, в которых ( displaystyle y=0), то есть ( displaystyle x=2) и ( displaystyle x=-4). Потому что ( displaystyle {{x}^{2}}+2{x} -8=0).

И если мы говорим, что ( displaystyle y={{x}^{2}}+2{x} -8), то значит, что ( displaystyle y) тоже должен быть равен ( displaystyle 0), или ( displaystyle y={{x}^{2}}+2{x} -8=0).

Просто? Это мы закончили с тобой решение уравнения сложным графическим способом, то ли еще будет!

Конечно, ты можешь проверить наш ответ алгебраическим путем – посчитаешь корни через теорему Виета или Дискриминант.

Что у тебя получилось? То же самое?

Вот видишь! Теперь посмотрим совсем простое графическое решение, уверена, оно тебе очень понравится!

Решение смешанных неравенств

Теперь перейдем к более сложным неравенствам!

Как тебе такое:

Первое, с чего мы начнем, – это с построения двух графиков:

Расписал? Теперь строй два графика.

Сравним наши рисунки?

У тебя так же? Отлично!

Теперь расставим точки пересечения и цветом определим, какой график у нас по идее должен быть больше, то есть ( displaystyle {{y}_{2}}={{x}^{3}}).

Смотри, что получилось в итоге:

А теперь просто смотрим, в каком месте у нас выделенный график находится выше, чем график ( displaystyle {{y}_{1}}=4x)? Смело бери карандаш и закрашивай данную область! Она и будет решением нашего сложного неравенства!

На каких промежутках по оси ( displaystyle Ox) у нас ( displaystyle {{y}_{2}}={{x}^{3}}) находится выше, чем ( displaystyle {{y}_{1}}=4x)? Верно, ( displaystyle xin left( -2;0 right)cup left( 2;+infty right)).

Это и есть ответ!

Ну вот, теперь тебе по плечу и любое уравнение, и любая система, и уж тем более любое неравенство!

(y =b) (график — прямая, параллельная оси (x));

(y = kx) (график — прямая, которая проходит через начало координат);

(y = kx + m) (график — прямая);

Этот приём полезен при решении уравнений. Продемонстрируем это на примерах.

    

2. В одной системе координат начертить графики этих функций.

3. Определить точки пересечения полученных графиков.

4. Взять из них значения абсцисс.

  

Методика организации решения уравнений графическим способом как средство формирования графических умений у учащихся

Разделы: Математика

Графический метод обладает рядом преимуществ:

• он часто проще аналитического;
• обладает наглядностью. Особенно когда нет решений или требуется установить количество корней.
• он красив и доставляет эстетическое наслаждение. Выполнять графики нужно в цвете. Это помогает в выборе ответа.

Умение строить графики функций не является самоцелью. Часто построение графиков связано с исследованием поведения функций. Однако необходимость построения графиков облегчают нахождение решений уравнений и неравенств, сокращая или упрощая аналитические выкладки и часто при этом являются единственным методом решения таких задач. Графический метод решения способствует лучшему усвоению ряда понятий: функции, корней уравнения и неравенства, систем уравнений. При этом целесообразно при графическом решении уравнений устанавливать связи с такими свойствами функций как возрастание и убывание, знакопостоянство, обращение функции в ноль и т.д., что помогает глубже понять функциональную зависимость между величинами. Изучение поведения функций и построение их графиков является важным разделом математики. Свободное владение техникой построения графиков часто помогает решать многие задачи и порой является единственным средством их решения. Кроме того, умение строить график представляет большой самостоятельный интерес. Материал, связанный с построением графиков функций, в средней школе изучается недостаточно полно с точки зрения требований, предъявляемых на экзаменах. Поэтому задачи на построение графиков нередко вызывают затруднения у учащихся.

Для того, чтобы по графикам можно было получать достаточно приемлемые числовые ответы, графики должны быть особенно тщательно построены. Решается задача организации работы таким образом, чтобы выработать навыки быстрого построения графиков элементарных функций и их преобразований. Работа над формированием графических умений начинается с 5-го класса.

Изящно выполненная работа способствует развитию чувства красоты, удовлетворения от проделанной работы.

Изучение поведения функций и построение их графиков являются важным разделом школьного курса. Свободное владение техникой построения графиков часто помогает решать сложные задачи, а порой является единственным средством их решения. Кроме того, умение строить графики функций представляет большой интерес для самих учащихся. Однако на базе основной школы материал, связанный с этим вопросом, представлен несколько хаотично, изучается недостаточно полно, многие важные моменты не входят в программу.

Цель – прояснить и дополнить школьный материал, связанный с функциями и построение их графиков, применением их к решению уравнений, их систем.

В требованиях к уровню подготовки выпускников по разделу «Функции и графики» прописано:

• решать уравнения, системы уравнений, используя свойства функций и их графические представления;
• находить приближённые решения уравнений и их систем, используя графический метод.

В преподавание алгебры по учебнику под редакцией А.С.Теляковского. Линейная функция и функции у=х 2 , у=х 3 изучаются в 7 классе. Практически не вырабатываются навыки в применении графиков этих функций. Единственное упражнение: найти координаты точек пересечения графиков функций у=8,5х и у=0,5х-19,5. графики линейных функций только иллюстрируют решение систем линейных уравнений.

Автор вводит некоторые упражнения, необходимые в дальнейшем при решении уравнений и их систем:

— постройте в одной и той же координатной плоскости а) у=х 2 ; у=4; б) у=х 2 ; у=2х.

— изобразите схематически графики функций у = -0,9х + 4; у = 2,3х; у = х/10 . Но упражнения вводятся как дополнительные. И в «Задачах повышенной трудности» (в конце учебника) есть уравнения, которые тоже можно решать графическим способом: |х -3| = 7; |х+2| = 9; |4 — х| = 1,5.

В 8 классе изучаются функции у = к/х; у =. Представлены функции у = 4/|х|, у = -6/|х|.

— Могут ли графики функций у=к/х и у = ах +в пересекаться

а) в одной точке;

б) в двух точках;

в) в трёх точках.

— Могут ли графики функций у = к/х и у = ах +в пересекаться в двух точках, лежащих

а) в одной четверти;

б) в первой и второй четвертях;

в) в первой и третьей четвертях.

Опять же эти упражнения в дополнительных.

В 8 классе обучающихся знакомят с графическим способом решения уравнений (8/х = -х+6; (8/х = х 2 ). Появляются уравнения третьей степени, которые не решаются аналитическим способом. (х 3 — х + 1 = 0; х 3 + 2х — 4=0) На изучение этой темы отводится 1 час.

В 9 классе подробно изучается квадратичная функция и её график. Получены обучающимися представления о преобразовании графического объекта относительно осей координат. Именно в это время отрабатываются навыки в построении параболы. Но данные преобразования почти не переносятся на преобразования других графических объектов. Хотя есть два упражнения, которые соотносятся с заданиями, встречающимися в материалах ЕГЭ.

На рисунке изображён график одной их функций . Какой именно?

— Какой из трёх графиков, изображённых на рисунке, является графиком функции у = |х -2|

Сделаны попытки преобразования графических объектов.

— Какие преобразования надо выполнить, чтобы

а) из графика функции у=х 3 получить графики функций у = — х 3 ; у = (х-3) 3 ; у = х 3 + 4.

б) из графика функции у = получить графики функций у = — ;

— Постройте в одной координатной плоскости графики функций у = | х|; у =|х -4| ; у = |х -4|-3.

В учебнике 9 класса в главе «Целое уравнение и его корни» упоминается графический способ уравнений третьей и более высокой степени как один из способов наряду с разложением на множители.

Поэтому: уже в 7 классе строим графики функций у = | х| — 3, у = 4 — | х|; у =|х +4|; у = | х — 3|.

При построении параболы вводим первые преобразования:

— построить графики функций у = х 2 +3; у=х 2 -5, где смещение по оси ординат. А затем у = (х+2) 2 ; у = (х-1) 2 . Конечно, не все ученики усваивают, впрочем, как и всё содержание материала. Для успешных учеников это не сложно. Тем более это только пропедевтика.

В 8-м классе: Урок-практикум.

Тема: «График функции у = . Графический способ решения иррациональных уравнений»

Цель: отработать навыки в преобразовании графика функции у = , закрепить умения графически решать иррациональные уравнения.

I. Фронтально

1). Схематически в одной системе координат изобразить графики функций

2). Решить уравнения

II. Построить графики функций

III. Решение уравнений

X 2 -3 =

В 8 классе строим преобразования гиперболы и графика функции у = .

Упражнения взяты из «Сборника задач по алгебре 8-9 класса» М.Л.Галицкого, А.И.Звавича. Уже на факультативных занятиях или занятиях кружка решаем уравнения с параметром |х 2 -2х-3| = а. Определить, при каком а уравнение имеет три корня. Строим графики функций у = |х 2 -2х-3|; у = а. Получаем ответ а = 4.

В 9 классе больше занимаемся исследованием квадратного трёхчлена. Формулы функций усложняю. Рассматриваем графики вида у = (х 2 -2) 2 — (х 2 -1) 2 ;

Необычность конструкций, разрыв графиков, удаление точек вызывает некоторую удивлённость. Тем самым преодолевается стандартность мышления, развивается воображение, повышается интерес: а что ещё может получиться? В каких случаях?

Уравнения, решаемые графическим способом.

I. Решение уравнений Р(х) = 0, где Р(х) – многочлен степени большей 2.

Графический метод. Описание, примеры решения уравнений

Эта статья посвящена одному из направлений функционально-графического метода решения уравнений, а именно, графическому методу. Сначала дано описание графического метода: раскрыта его суть, сказано, на чем базируется метод, приведено его обоснование, обговорены особенности метода, связанные с точностью. Дальше идет практическая часть: записан алгоритм решения уравнений графическим методом и показаны решения характерных примеров.

В чем состоит метод и на чем он базируется

Графический метод решения уравнений состоит в использовании графиков функций, отвечающих частям уравнения, для нахождения с их помощью решения уравнения. Базируется он на следующем утверждении:

Решение уравнения f(x)=g(x) есть множество абсцисс точек пересечения графиков функций y=f(x) и y=g(x) .

Обоснованием этого утверждения займемся в следующем пункте. А сейчас выудим из него полезные сведения.

Основное из них таково: по количеству точек пересечения графиков функций y=f(x) и y=g(x) можно судить о количестве корней уравнения f(x)=g(x) , а по абсциссам точек пересечения можно судить о корнях этого уравнения. Проиллюстрируем сказанное.

Взглянем на чертеж, на котором изображены графики функций и .

Очевидно, в видимой области графики изображенных функций не имеют точек пересечения. За пределами видимой области графики тоже не имеют точек пересечения. Это мы можем утверждать в силу известного нам поведения графиков степенных функций и линейных функций. Отсутствие точек пересечения позволяет нам сделать вывод, что уравнение не имеет решений.

Другой пример. На следующем рисунке изображены графики функций и .

Сколько точек пересечения мы видим? Две. Известное поведение графиков показательных функций и линейных функций позволяет утверждать, что за пределами видимой области точек пересечения нет. Значит, графики функций и пересекаются в двух точках, следовательно, уравнение имеет два корня. А каковы значения этих корней? Для ответа на этот вопрос определяем абсциссы точек пересечения графиков. По рисунку находим, что абсциссы точек пересечения есть −2 и 1 . Через проверку подстановкой убеждаемся, что это действительно корни уравнения :

Здесь стоит заметить, что к проверке подстановкой мы обратились не случайно. Дело в том, что найденные по графикам значения корней можно считать лишь приближенными до проведения проверки. Подробнее об этом мы поговорим в одном из следующих пунктов этой статьи, раскрывающем особенности графического метода.

Обоснование метода

Докажем, что множество решений уравнения f(x)=g(x) есть множество абсцисс точек пересечения графиков функций y=f(x) и y=g(x) . Для этого достаточно показать, во-первых, что если x₀ – корень уравнения f(x)=g(x) , то x₀ – это абсцисса одной из точек пересечения графиков функций y=f(x) и y=g(x) , и, во-вторых, если x₀ – абсцисса одной из точек пересечения графиков функций y=f(x) и y=g(x) , то x₀ – корень уравнения f(x)=g(x) . Приступаем к доказательству.

Пусть x₀ – корень уравнения f(x)=g(x) . Тогда f(x₀)=g(x₀) – верное числовое равенство. Это равенство можно трактовать так: значения функции y=f(x) и y=g(x) в точке x₀ совпадают. А из этого следует, что x₀ – абсцисса одной из точек пересечения графиков функций y=f(x) и y=g(x) .

Первая часть доказана. Переходим к доказательству второй части.

Пусть x₀ – абсцисса одной из точек пересечения графиков функций y=f(x) и y=g(x) . Это означает, что значения функций y=f(x) и y=g(x) в точке x₀ равны, значит, f(x₀)=g(x₀) . А из этого равенства следует, что x₀ – корень уравнения f(x)=g(x) .

Так доказана вторая часть.

Особенности метода

Графический метод предполагает использование графиков функций. В общем случае построение графиков функций – дело непростое. Поэтому, графический метод решения уравнения обычно применяется лишь тогда, когда функции, отвечающие частям уравнения, довольно простые в плане построения графиков, и при этом не видно другого аналитического метода решения. Это одна из особенностей графического метода решения уравнений.

Другая особенность касается получаемых по графикам результатов. Полученные по графикам результаты можно считать лишь приближенными. Дело здесь в том, что сами по себе графики функций — вещь не совсем точная (но при этом очень наглядная и во многих отношениях удобная), особенно если говорить о графиках, построенных от руки. Это следует из принципов, которыми мы руководствуемся при построении графиков функций. Что мы делаем для построения графика функции в общем случае? Проводим исследование функции, чтобы получить ряд «опорных» точек, таких как граничные точки области определения, максимумы-минимумы, точки перегиба, и понять поведение функции на всех интервалах ее области определения. После этого определяем несколько контрольных точек. Дальше переносим все определенные в ходе исследования точки на координатную плоскость и, сейчас внимание, соединяем их плавной линией в соответствии с выясненным в ходе исследования поведением функции. Эта «плавная линия» и есть график функции. О какой точности можно здесь говорить? Понятно, что она определяется точностью нашего построения.

С приближенными, найденными по графикам, значениями корней уравнения можно так или иначе работать. В некоторых случаях определенные по графикам значения корней оказываются точными значениями, в чем позволяет убедиться проверка подстановкой. В других случаях есть возможность уточнить значения корней до требуемой степени точности, для этого существуют специальные методы уточнения значений корней. А вот если по графикам нет возможности определить количество корней, не говоря уже об их значении, то, почти наверняка, стоит отказываться от графического метода решения уравнения. Добавим наглядности сказанному.

Давайте посмотрим на изображенные в одной прямоугольной системе координат графики функций и y=−x 2 +6·x−5 .

По этому чертежу сложно судить даже о количестве корней уравнения , не говоря уже про их значения с приемлемой степенью точности. Здесь можно лишь грубо сказать, что если корни есть, то их значения находятся на промежутке от нуля до трех. Такую прикидку мы даем по той причине, что графики функций в обозначенном промежутке очень близки, почти совпадают. Если есть возможность построить графики более точно в обозначенном промежутке, то это немного проясняет картину:

Сейчас мы видим три точки пересечения, даже можем приближенно указать их абсциссы: 1 , 2 и 2,7 . Но опять же, это не более чем приближенные результаты, нуждающиеся в проверке и строгом обосновании.

Учитывая оговоренные особенности графического метода решения уравнения, для себя можно принять следующее: к графическому методу стоит обращаться лишь тогда, когда функции, отвечающие частям уравнения, довольно простые в плане построения графиков, когда по построенным графикам можно с уверенностью указать точное количество точек их пересечения, и когда не просматривается альтернативный метод решения.

Алгоритм решения уравнений графическим методом

Анализ приведенной выше информации позволяет записать алгоритм решения уравнений графическим методом. Чтобы решить уравнение графически, надо:

• Построить в одной прямоугольной системе координат графики функций, отвечающие левой и правой частям уравнения.
• По чертежу определить все точки пересечения графиков:
  • если точек пересечения нет, то решаемое уравнение не имеет корней,
  • если точки пересечения имеются, то переходим к следующему шагу алгоритма.
• По чертежу определить абсциссы всех точек пересечения графиков – это приближенные значения всех корней исходного уравнения.
• Если есть основания полагать, что некоторые или все определенные на предыдущем шаге значения являются точными значениями корней решаемого уравнения, то осуществить их проверку, например, подстановкой.

Дадим краткий комментарий к последнему шага алгоритма. Иногда определенные по чертежу приближенные значения корней оказываются точными. Обычно это касается целых значений. Но, опять же, прежде чем утверждать, что найденные значения является точными корнями уравнения, сначала нужно осуществить проверку этих значений, например, проверку подстановкой.

Решение примеров

Графический метод решения уравнений начинает входить в арсенал изучающих математику в 7 классе сразу же после знакомства с координатной плоскостью и самой первой функцией – линейной функцией y=k·x+b . Именно тогда мы сталкиваемся с заданиями, наподобие следующего: с помощью графика линейной функции y=2·x−6 определить, при каком значении x будет y=0 [1, с. 50-51]. Для ответа на поставленный вопрос мы строим график указанной линейной функции y=2·x−6 .

По чертежу находим точку пересечения графика с осью Ox (ось Ox отвечает графику функции y=0 ), и определяем абсциссу точки пересечения: x=3 . По сути, мы решаем уравнение 2·x−6=0 графическим методом.

Чуть позже в 7 классе изучается функция y=x 2 . После этого опять заходит разговор о графическом методе решения уравнений, но уже более детальный, где метод уже называется своим именем и дается его алгоритм [1, с. 149-151; 2, с. 109]. Там с его помощью решаются уравнения, одной части которых отвечает функция y=x 2 , а другой – линейная функция y=k·x+b . Например, уравнение x 2 =x+1 . Для его решения строятся в одной системе координат соответствующие графики функций y=x 2 и y=x+1 :

Графики, очевидно, пересекаются в двух точках. Можно определить приближенные значения их абсцисс: .

В 8 классе изучаются новые виды функций: y=k/x , квадратичная функция y=a·x 2 +b·x+c , . И, естественно, рассматривается графический метод решения соответствующих уравнений. Особенно тщательно разбирается графическое решение квадратных уравнений. В учебнике Мордковича А. Г. приведены аж пять способов графического решения уравнения x 2 −2·x−3=0 [2, с. 127-131].

И так далее: изучаются функции , степенные функции, тригонометрические, показательные, логарифмические, …, — рассматривается решение соответствующих уравнений графическим методом. Так к концу школьного курса математики мы начинаем воспринимать графический метод решения уравнений как общий метод, позволяющий решать уравнения не только определенных видов, но и уравнения, в которых уживаются самые разнообразные функции: показательные с корнями, тригонометрические с логарифмическими и т.д. Покажем решение такого уравнения.

Решите уравнение

В заключение вспомним, что в этой статье при разговоре об особенностях графического метода решения уравнений мы обращались к иррациональному уравнению . В качестве «благодарности» этому уравнению за помощь в обретении знаний приведем ссылку на его решение графическим методом.

Графический метод в задачах с параметром

Данный метод используется не только в задачах с параметром, но и для решения обыкновенных уравнений, систем уравнений или неравенств. Он входит в стандартный курс школьной программы и наверняка вы с ним сталкивались, но в несколько упрощенном варианте. Сначала я кратко напомню, в чем заключается этот метод. Затем разберем, как его применять для решения задач с параметром, и рассмотрим несколько типовых примеров.

Для начала рассмотрим уравнение с одной переменной (f(x)=0). Для того, чтобы решить его графическим методом, нужно построить график функции (y=f(x)). Точки пересечения графика с осью абсцисс (ось (х)) и будут решениями нашего уравнения.

Или рассмотрим уравнение (f(x)=g(x)). Точно так же строим на одной координатной плоскости графики функций (y=f(x)) и (y=g(x)), абсциссы точек их пересечения будут решениями уравнения.

Стоит отдельно отметить, что для решения графическим методом необходимо выполнять очень качественный и точный рисунок.

Решить графическим методом уравнение (x^2+3x=5x+3).

Решение: Построим на одной координатной плоскости графики функций (y=x^2+3x) и (y=5x+3). См. рис.1.

(y=5x+3) – красный график; (y=x^2+3x) – синий график.

Из Рис.1 видно, что графики пересекаются в точках ((-1;2)) и ((3;18)). Таким образом, решением нашего уравнения будут: (_<1>=-1; _<2>=3).

Теперь рассмотрим уравнение с двумя переменными (f(x,y)=0). Решением этого уравнения будет множество пар точек ((x,y)), которые можно изобразить в виде графика на координатной плоскости ((xOy)). Если решать это уравнение аналитически, то, как правило, мы выражаем одну переменную через другую ((x,y=f(x))) или ((x=f(y),y)).

В качестве примера рассмотрим обыкновенное линейное уравнение (2x-5y=10). (1) Выражаем (x=frac<10+5y><2>) – это называется общим решением уравнения. Изобразим его на координатной плоскости, построив график (Рис. 2):

Здравствуйте. В данной статье я попытаюсь показать вам возможные способы решения квадратных уравнений с помощью графиков.

Допустим, надо решить уравнение х² ‒ 2х ‒ 3 = 0. На этом примере мы рассмотрим варианты решения квадратного уравнения графически.

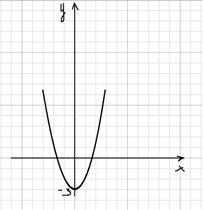
1) Можно представить наше уравнение в виде х² = 2х + 3. Далее построим в одной системе координат графики функций у = х² и у = 2х + 3. График у = х² представлен на рисунке 1, а оба графика на рисунке 2. 

Рисунок 1                                 Рисунок 2

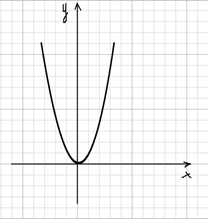
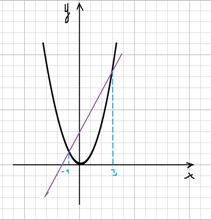
Графики пересекаются в двух точках, наше уравнение имеет решение х = – 1 и х = 3.

2) А ведь можно представить уравнение и по — другому, например х² ‒ 2х = 3 и построить в одной системе координат графики функций  у = х² ‒ 2х и у =3. Вы их можете увидеть на рисунках 3 и 4. На рисунке 3 изображен график у = х² ‒ 2х, а на рисунке 4 оба графика у = х² ‒ 2х и у =3.

Рисунок 3                                         Рисунок 4

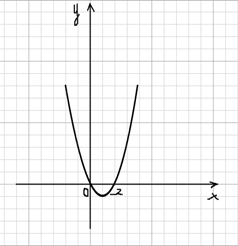
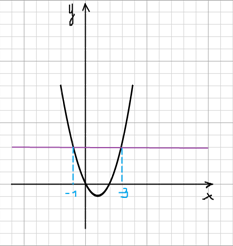
Как мы видим, эти два графика так же пересекаются в двух точках, где х = -1 и х = 3. Значит ответ: — 1; 3.

3) Есть и другой вариант представления этого уравнения х² ‒ 3 = 2х. И снова строим графики функций у = х² ‒ 3 и у = 2х в одной системе координат. Первый у = х² ‒ 3 на рисунке 5 и оба графика на рисунке 6.

Рисунок 5                                 Рисунок 6

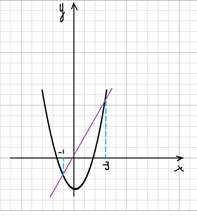
Они также пересекаются в двух точках, в которых х = -1 , х = 3.

Ответ: — 1; 3.

4) Можно построить параболу у = х² ‒ 2х ‒ 3.

Вершина параболы  х₀ = — b/2а = 2/2=1, у₀ = 1² ‒ 2·1 ‒ 3 = 1 – 2 – 3 = ‒ 4. Это точка (1; ‒ 4). Тогда наша парабола симметрична относительно прямой х =1. Если взять две точки симметричные относительно прямой х = 1 например: х = — 2 и х = 4, то мы получим две точки через которые проходят ветви графика.

Если х = -2, то у =(- 2)² ‒ 2( -2) ‒ 3 = 4 + 4 – 3 = 5.

Аналогично х =4, у = 4² ‒ 2 · 4 ‒ 3= 16 – 8 – 3 = 5. Полученные точки ( -2; 5); (1; 4) и (4; 5) отмечаем в на плоскости и проводим параболу рисунок 7.

Рисунок 7

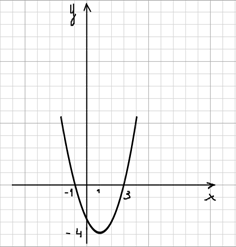
Парабола пересекает ось абсцисс в точках – 1 и 3. Это и есть корни уравнения х² ‒ 2х ‒ 3 = 0.

Ответ: – 1 и 3.

5) А можно выделить квадрат двучлена:

х² ‒ 2х ‒ 3= 0

(х² ‒ 2х + 1) ‒1 ‒ 3= 0

(х -1)² — 4 = 0

(х — 1)² = 4

Затем построить в одной системе координат графики функций у = (х — 1)² и у = 4. Первый график у = (х — 1)² на рисунке 8, а оба графика у = (х — 1)² и у = 4 на рисунке 9.

Рисунок 8                                     Рисунок 9

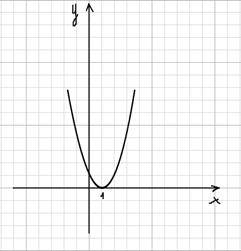
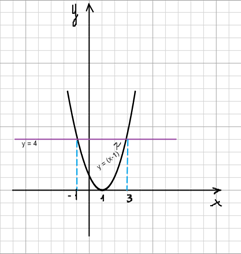
Они также пересекаются в двух точках, в которых х = -1 , х = 3.

Ответ: — 1; 3.

6) Так как х = 0 не является корнем уравнения х² ‒ 2х ‒ 3 = 0 (иначе выполнялось бы равенство 0² – 2· 0 –3 = 0), то можно все члены уравнения разделить на х. В результате мы получим уравнение х – 2 – 3/х = 0. Перенесем 3/х вправо и получаем уравнение х – 2 = 3/х Тогда можно построить в одной системе координат графики функций у = 3/х и у = х – 2.

На рисунке 10 изображен график функции у = 3/х, а на рисунке 11 оба графика функций у = 3/х и у = х – 2.

Рисунок 10                           Рисунок 11

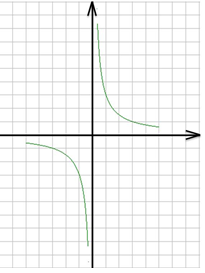
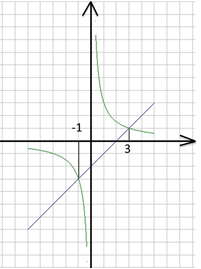
Они также пересекаются в двух точках, в которых х = -1 , х = 3.

Ответ: — 1; 3.

Если вы были внимательны, то обратили внимание, что каким бы образом вы не представили бы уравнение в виде двух функций, у вас всегда будет один и тот же ответ (разуметься, что вы не допустите ошибок при переносе выражений из одной части уравнения в другую и при построении графиков). Поэтому, решая графически уравнение, выбирайте способ представления функций графики которых вам легче построить. И еще одно замечание если корни уравнения не целые числа, то ответ получится не точным.

Репетитор Валентина Галиневская.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Решение системы линейных уравнений графическим способом

Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может: 

а) иметь единственное решение; 

б) не иметь решений; 

в) иметь бесконечное множество решений.

2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.

Пример 3

Графическое решение системы 

Пример 4

Выражаем у через х из каждого уравнения системы 2), а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.

Прямую y=2x+9 проводим через точки (0; 9) и (-3; 3). Прямую y=-1,5x+2 проводим через точки (0; 2) и (2; -1).

Наши прямые пересеклись в точке В(-2; 5).

Ответ: (-2; 5).

ОБЯЗАТЕЛЬНО: Познакомимся с видео, где нам объяснят как решаются системы линейных уравнений графическим способом. РАССКАЖУТ, КАК РЕШАТЬ СИСТЕМЫ ГРАФИЧЕСКИ.

ДОМАШНЯЯ РАБОТА: ВЫПОЛНЯТЬ ВСЕ ШАГИ ПОСТРОЕНИЯ, КАК ПОКАЗАНО В ВИДЕО РАЗБОРАХ И ПРИМЕРАХ. В УЧЕБНИКЕ ТЕОРИЯ НА СТРАНИЦАХ СТР 195-199. ВСЕ ИЗУЧИТЬ, ТЕМА ОЧЕНЬ ВАЖНАЯ.