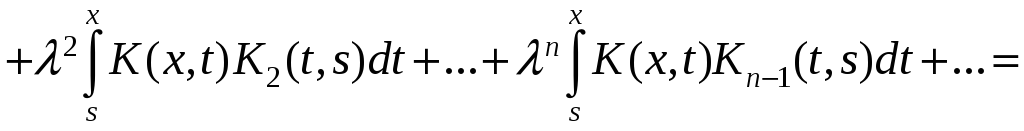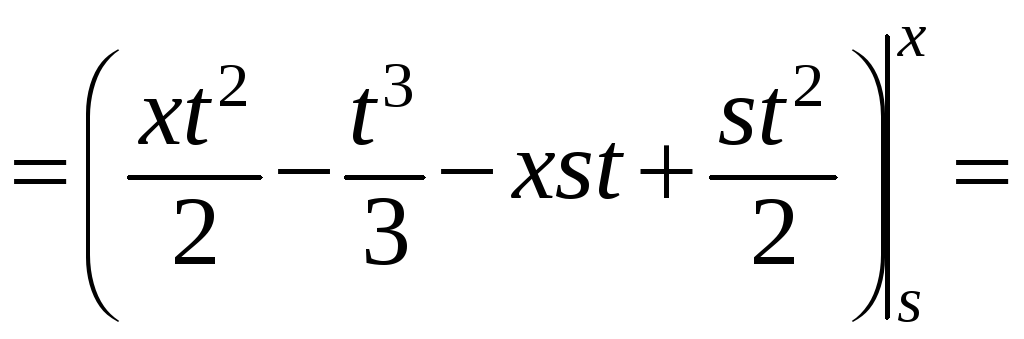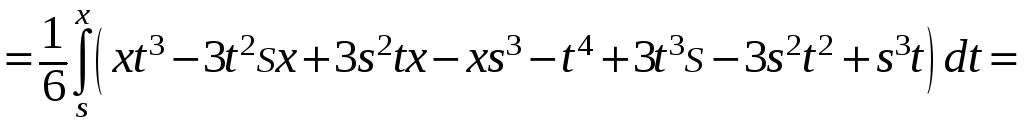Как найти резольвенты для ядра - Исправление недочетов и поиск решений вместе с Examum.ru

В
полученных выражениях (8.3) коэффициентов
ряда Неймана

последовательно произведем подстановку

в,
затем

в

и так далее, сменив обозначения переменных

В кратных
интегралах изменим порядок интегрирования
в соответствии с ниже изображенной
областью интегрирования

S=t

Как
и для интегральных уравнений Фредгольма,
приняв за первое итерированное ядро
данное ядро, за второе итерированное
ядро примем

тогда

Аналогично
найдем

где

………………………………………………………………………..

(9.1)

где

(9.2)

…………………………………… .

Подставим
полученные выражения коэффициентов
,
в соответствии с полученными формулами
(9.1), в ряд (8.2) и, в силу равномерной и
абсолютной сходимости этого ряда, можем
просуммировать интегралы

Выражение в
квадратных скобках назовем резольвентой
интегрального уравнения Вольтерра
второго рода и для нее введем обозначение

(9.3)

Если
итерированные ядра найдены, а следовательно
и резольвента, то решение интегрального
уравнения Вольтерра (8.1) определится по
формуле

.
(9.4)

Аналогично,
группируя интегралы попарно в формулах
(9.1) для коэффициентов

начиная с последней пары, для итерированных
ядер получим другую формулу

n=2,3,…
. (9.5)

В
формулу резольвенты (9.3) подставив
выражения итерированных ядер (9.2)

получим
интегральное уравнение резольвенты

(9.6)

Если
в формулу резольвенты (9.3) подставить
выражения итерированных ядер (9.5), то
получим другое интегральное уравнение
резольвенты

.
(9.7)

Пример
10. Построить
резольвенту ядра K(x,t)
= x
– t
.

Решение.
По формулам
(9.2) находим итерированные ядра

…………..,

и по индукции
выписываем

………….
.

Затем
по формуле (9.3) находим резольвенту

Пример
11. Вычислив
итерирование ядра и резольвенту, найти
решение уравнения

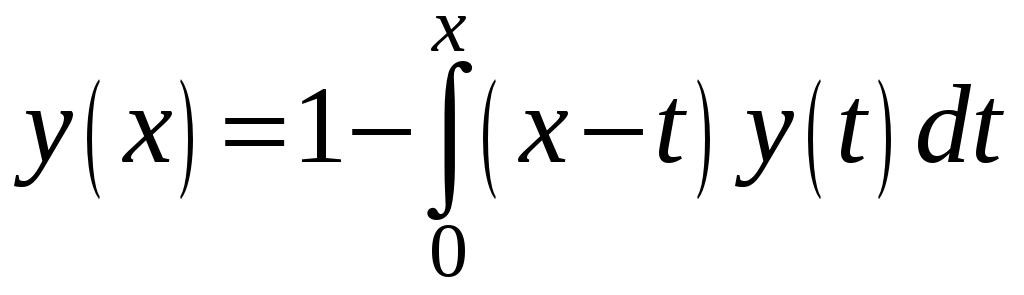
Решение.
Положив
,
выпишем ядро

Далее по формулам
(9.2) найдём

……………………………………………………………………..
.

По
индукции выпишем n-ое
итерированное ядро

и по формуле (9.3 )
найдём резольвенту

Решение
интегрального уравнения получим по
формуле (9.4)

Ответ:

Нетрудно проверить
что найденная функция является решением
исходного уравнения

!!!§10. Решение уравнений Вольтерра с разностными ядрами с помощью преобразования Лапласа

Преобразование
Лапласа
для произвольной (комплекснозначной)
функции
действительного переменного
определяется следующим образом:

(10.1)

где

– комплексная переменная.

Функция

называется оригиналом, а –изображением
(образом) функции .

Преобразование
Лапласа существует для непрерывных и
кусочно-непрерывных функций, удовлетворяющих
условию ,
где
— некоторые
числа. Далее считаем, что в указанной
оценке взято наименьшее из возможных
чисел ,
которое называется
показателем
роста
функции
f(x).

Для всякого
оригинала f(x)
функция

определена в полуплоскости
и является в этой полуплоскости
аналитической функцией.

Формулу (10.1) кратко
будем записывать так:

По
известному изображению
оригинал находится с помощью обратного
преобразования Лапласа

(10.2)

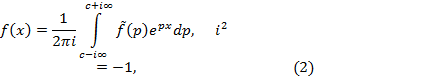
где путь интегрирования
расположен параллельно мнимой оси
комплексной плоскости справа от всех
особых точек функции f(p),что
соответствует .

Интеграл в (10.2)
понимается в смысле главного значения

Формула
(10.2) справедлива для непрерывных функций.
В отрицательной области формула (10.2)
даёт .

Если в точке ,
функция
f(x)имеет
конечный разрыв первого рода, то правая
часть формулы (10.2) в этой точке дает
значение
(при
первый член в квадратных скобках должен
быть опущен).!!!

Формулу обращения
преобразования Лапласа (10.2) кратко будем
записывать так:

Сверткой
(по Лапласу)
двух функций f(x)
и

называется выражение

!!!

Справедлива
теорема о свертке:

которая часто
используется при решении уравнений
Вольтерра с разностным ядром [2]. [20],
[33].

Уравнения Вольтерра
второго рода с ядром, зависящим от
разности аргументов, имеют вид

(10.3)

Применяя
преобразование Лапласа £ к уравнению
(10.3) и учитывая, что интеграл с ядром,
зависящим от разности аргументов, по
теореме о свертке преобразуется в
произведение
приходим к уравнению для образа искомой
величины

(10.4)

Решение уравнения
(10.4) определяется формулой

(10.5)

которую можно
записать в эквивалентном виде

(10.6)

Применяя к (10.6)
обратное преобразование Лапласа, получим
решение уравнения (10.3) в виде

(5)

(10.7)

где

При использовании
формулы (10.7) могут возникнуть технические
трудности:

1°. При получении
изображения
для конкретного ядра

2°. При нахождении
оригинала резольвенты (10.7), изображение
которого
находится по формуле (10.6).

Для вычисления
соответствующих интегралов применяют
таблицы прямых и обратных преобразований
Лапласа, причем во многих случаях для
обратного преобразования используют
методы теории функций комплексного
переменного, включая теорему о вычетах.

Замечание.
Если нижний предел в интеграле уравнения
Вольтерра с ядром, зависящим от разности
аргументов, равен ,
то его можно свести к уравнению вида
(10.3) с помощью замены

На
рисунке приведена принципиальная схема
решения интегральных уравнений Вольтерра
второго рода с разностным ядром с помощью
интегрального преобразования Лапласа.

Схема решения
интегральных уравнений Вольтерра
второго рода с разностным ядром с помощью
интегрального преобразования Лапласа,
–оригинал
функции

Преобразование
Лапласа можно применить для решения
систем интегральных уравнений Вольтерра
вида

Подействуем на
систему преобразованием Лапласа. Тогда
будем иметь

Решая эту
систему линейных алгебраических
уравнений, определим ,
и решение рассматриваемой системы
примет вид [2], [20]

Пример 12.
Рассмотрим
уравнение

которое
является частным случаем уравнения
(10.3)

Сначала, используя
таблицы преобразований Лапласа, получим
образ ядра интегрального уравнения
в виде

Затем по формуле
(10.6) найдем образ резольвенты

Используя далее
таблицы обратных преобразований Лапласа,
получим оригинал резольвенты

Заметим,
что в частном случае при
получаем
Подставляя эти выражения в формулу
(10.7), находим решение интегрального
уравнения. В частности, при
это решение имеет вид [20]

Пример 13.
Решить интегральное уравнение:

Решение.
Известно,
что

Пусть.
Применяя преобразование Лапласа к обеим
частям уравнения и учитывая при этом
теорему умножения (изображения свертки),
получим

Отсюда

или

Следовательно,
решение данного интегрального уравнения
есть

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Решения интегральных уравнений онлайн

В этом разделе мы рассмотрим типовые задачи по интегральным уравнениям с решениями. Интегральное уравнение содержит неизвестную функцию под знаком интеграла (по аналогии как дифференциальное — функцию под знаком дифференциала:)).

Выделяют два основных класса интегральных уравнений: уравнения Фредгольма I и II рода:

$$
(I) quad int_a^b K(x,s)u(s)ds = f(x),\
(II) quad u(x)=int_a^b K(x,s)u(s)ds + f(x). $$

В случае переменного верхнего предела интегрирования получаем соответственно уравнение Вольтерра I и II рода:

$$
(I) quad int_a^x K(x,s)u(s)ds = f(x),\
(II) quad u(x)=int_a^x K(x,s)u(s)ds + f(x). $$

Это линейные неоднородные уравнения (при $f(x)=0$ — однородные), иногда рассматриваются более общий случай с параметром $lambda$ перед интегралом.

Ниже вы найдете примеры нахождения решений интегральных уравнений, собственных значений и функций, исследования ядра, применения интегральных уравнений для решения других задач.

Примеры решений интегральных уравнений

Задача 1. Пользуясь теоремой Гильберта-Шмидта, исследовать и решить интегральное уравнение 2-го рода $(E+lambda A)x=y$ в гильбертовом пространстве $X$.

$$
X=L_2[0,pi], quad Ax(t)=int_0^pi K(t,s)x(s), quad K(t,s)=sum_{k=1}^{infty}frac{cos kt cos ks}{k^5}, yin X.
$$

Задача 2. Найти собственные значения и собственные функции уравнения:

$$
y(x)=lambda int_0^1 (cos 2pi x +2x sin 2pi t +t sin pi x)y(t)dt.
$$

Задача 3. Решить уравнение Вольтерры, сведя его к обыкновенному дифференциальному уравнению.

$$
y(x) = int_1^x frac{x}{t^2}y(t)dx+x^2.
$$

Задача 4. Решить или установить неразрешимость уравнений с вырожденным ядром.

$$
y(x)=2-3int_0^{pi/2} sin (x-2t) y(t)dt.
$$

Полезная страница? Сохрани или расскажи друзьям

Задача 5. Решить интегральное уравнение, сведя его предварительно к обыкновенному дифференциальному уравнению.

$$
y(x)=x+int_0^x(4 sin(x-t)-x+t)y(t)dt.
$$

Задача 6. Найти резольвенту для интегрального уравнения Вольтерры со следующим ядром $K(x,t)=x^{1/3}t^{2/3}$.

Задача 7. Исследовать решения уравнения с вырожденным ядром при различных значениях параметра $lambda$ (ограничиться случаем вещественных характеристических чисел).

$$
y(x)-lambda int_0^1 x y(t)dt = sin 2pi x.
$$

Задача 8. Для симметричного ядра
$$K(x,t) = frac{1}{2} sin |x-t| quad (0 le, x,t le pi)$$
найти характеристические числа и соответствующие им собственные функции, сводя интегральное уравнение к однородной краевой задаче для обыкновенного дифференциального уравнения.

Задача 9. Решить краевую задачу, используя функцию Грина

$$
y»+9y=x-pi/6, , y(0)=0, y(pi/6)=0.
$$

См. также: Примеры по уравнениям математической физики

Задача 10. Применяя преобразование Лапласа, решить интегральное уравнение

$$
y(x)=e^{-x}sin x +int_0^x e^{x-t}y(t)dt.
$$

См. также: Примеры по операционному исчислению

Помощь с интегральными уравнениями

Если вам нужна помощь с решением задач и контрольных по интегральным уравнениям (и другим разделам математического и функционального анализа), обращайтесь в МатБюро. Стоимость подробной консультации от 200 рублей, оформление производится в Word, срок от 1 дня.

Поможем с решением задач и уравнений

Дополнительная информация

Функциональный анализ: примеры решений
Вариационное исчисление: примеры решений
Почему МатБюро?

Полезные ссылки

Интегральные уравнения Краткая теория, примеры задач и задания для самостоятельного решения
Методы математической физики. Интегральные уравнения Кратко теория, типовые примеры, задания
Интегральные уравнения и вариационное исчисление Учебное пособие
Интегральные уравнения Курс лекций

Источник

Решения интегральных уравнений онлайн

Выделяют два основных класса интегральных уравнений: уравнения Фредгольма I и II рода:

$$ (I) quad int_a^b K(x,s)u(s)ds = f(x),\ (II) quad u(x)=int_a^b K(x,s)u(s)ds + f(x). $$

$$ (I) quad int_a^x K(x,s)u(s)ds = f(x),\ (II) quad u(x)=int_a^x K(x,s)u(s)ds + f(x). $$

Примеры решений интегральных уравнений

Задача 2. Найти собственные значения и собственные функции уравнения:

$$ y(x)=lambda int_0^1 (cos 2pi x +2x sin 2pi t +t sin pi x)y(t)dt. $$

Задача 3. Решить уравнение Вольтерры, сведя его к обыкновенному дифференциальному уравнению.

Задача 4. Решить или установить неразрешимость уравнений с вырожденным ядром.

Задача 6. Найти резольвенту для интегрального уравнения Вольтерры со следующим ядром $K(x,t)=x^<1/3>t^<2/3>$.

$$ y(x)-lambda int_0^1 x y(t)dt = sin 2pi x. $$

Задача 8. Для симметричного ядра $$K(x,t) = frac<1> <2>sin |x-t| quad (0 le, x,t le pi)$$ найти характеристические числа и соответствующие им собственные функции, сводя интегральное уравнение к однородной краевой задаче для обыкновенного дифференциального уравнения.

Задача 9. Решить краевую задачу, используя функцию Грина

Задача 10. Применяя преобразование Лапласа, решить интегральное уравнение

Помощь с интегральными уравнениями

Если вам нужна помощь с решением задач и контрольных по интегральным уравнениям (и другим разделам математического и функционального анализа), обращайтесь в МатБюро. Стоимость подробной консультации от 200 рублей , оформление производится в Word, срок от 1 дня.

Методы решения интегральных уравнений: Справочник — Манжиров А.В., Полянин А.Д.

Название: Методы решения интегральных уравнений: Справочник

Автор: Манжиров А.В., Полянин А.Д.

В книге излагаются точные, приближенные аналитические и численные методы решения линейных и нелинейных интегральных уравнений. Помимо классических методов описаны также некоторые новые методы. Для лучшего понимания рассмотренных методов во всех разделах книги даны примеры решения конкретных уравнений. Приведены некоторые точные и асимптотические решения интегральных уравнений, встречающихся в приложениях (в механике и физике).

Справочник предназначен для широкого круга научных работников, преподавателей вузов, аспирантов и студентов, специализирующихся в различных областях прикладной математики, механики, физики, теории управления и инженерных наук.

Оглавление
Предисловие 9
1. Основные определения и формулы. Интегральные преобразования 10
1.1. Предварительные замечания 10
1.1-1. Некоторые определения 10
1.1-2. Структура решений линейных интегральных уравнений 11
1.1-3. Интегральные преобразования 12
1.1-4. Вычеты. Формулы для вычислений 12
1.1-5. Лемма Жордана 13
1.2. Преобразование Лапласа 14
1.2-1. Определение. Формула обращения 14
1.2-2. Обращение рациональных функций 15
1.2-3. Теорема о свертке для преобразования Лапласа 15
1.2-4. Предельные теоремы 15
1.2-5. Основные свойства преобразования Лапласа 16
1.2-6. Формула Поста-Уиддера 16
1.3. Преобразование Меллина 17
1.3-1. Определение. Формула обращения 17
1.3-2. Основные свойства преобразования Меллина 17
1.3-3. Связь преобразований Меллина, Лапласа и Фурье 18
1.4. Преобразование Фурье 18
1.4-1. Определение. Формула обращения 18
1.4-2. Несимметричная форма преобразования 19
1.4-3. Альтернативное преобразование Фурье 19
1.4-4. Теорема о свертке для преобразования Фурье 20
1.5. Синус- и косинус-преобразования Фурье 20
1.5-1. Косинус-преобразование Фурье 20
1.5-2. Синус-преобразование Фурье 21
1.6. Другие интегральные преобразования 21
1.6-1. Преобразование Ханкеля 21
1.6-2. Преобразование Мейера 22
1.6-3. Преобразование Конторовича-Лебедева 22
1.6-4. У-преобразование и другие преобразования 22
2. Методы решения линейных уравнений вида ∫f£ K(x,t)y(t)dt = f(x) . 25
2.1. Уравнения Вольтерра первого рода 25
2.1-1. Структура уравнений. Классы функций и ядер 25
2.1-2. Существование и единственность решения 26
2.2. Уравнения с вырожденным ядром: K(x,t) = g1(x)h1(t) + • • • 4- 9n(x)^n(^) 26
2.2-1. Уравнения с ядром K(x,t) = g1(x)h1(t) 4- #2(Ж)^2М 26
2.2-2. Уравнения с вырожденным ядром общего вида 27
2.3. Сведение уравнений Вольтерра первого рода к уравнениям Вольтерра второго рода 28
2.3-1. Первый способ 28
2.3-2. Второй способ 28
2.4. Уравнения с разностным ядром: К(х, t) = К(х — t) 29
2.4-1. Метод решения, основанный на преобразовании Лапласа 29
2.4-2. Случай рационального образа решения 30
2.4-3. Представление решения в виде композиции 30
2.4-4. Использование вспомогательного уравнения 31
2.4-5. Сведение к обыкновенным дифференциальным уравнениям 32
2.4-6. Связь уравнений Вольтерра и Винера-Хопфа 33
2.5. Метод дробного дифференцирования 33
2.5-1. Определение дробных интегралов 33
2.5-2. Определение дробных производных 34
2.5-3. Основные свойства 35
2.5-4. Решение обобщенного уравнения Абеля 35
2.6. Уравнения с ядрами, имеющими слабую особенность 36
2.6-1. Метод преобразования ядра 36
2.6-2. Ядро с логарифмической особенностью 37
2.7. Метод квадратур 38
2.7-1. Квадратурные формулы 38
2.7-2. Общая схема метода 39
2.7-3. Алгоритм на основе формулы трапеций 40
2.7-4. Алгоритм для уравнения с вырожденным ядром 40
2.8. Уравнения с бесконечным пределом интегрирования 41
2.8-1. Уравнение с переменным нижним пределом интегрирования 41
2.8-2. Приведение к уравнению Винера-Хопфа первого рода 42
3. Методы решения линейных уравнений вида у(х) — J^ K(x, t)y(t) dt= f (х) 43
3.1. Интегральные уравнения Вольтерра второго рода 43
3.1-1. Предварительные замечания. Уравнения для резольвенты 43
3.1-2. Связь между решениями интегральных уравнений 44
3.2. Уравнения с вырожденным ядром: К(х, t) = g1(x)h1(t) + 4- 9n(x)^n(^) 44
3.2-1. Уравнения с ядром К(х, t) = ip(x) 4- ip(x)(x — t) 44
3.2-2. Уравнения с ядром К(х, t) = (p(t) 4- ip(t)(t — х) 45
3.2-3. Уравнения с ядром K(x,t) = J2m=i ^Рт(х)(х

£)m_1 46
3.2-4. Уравнения с ядром К(х, t) = E™=i

3.2-5. Уравнения с вырожденным ядром общего вида 47
3.3. Уравнения с разностным ядром: К(х, t) = К(х — t) 48
3.3-1. Метод решения, основанный на преобразовании Лапласа 48
3.3-2. Метод, основанный на решении вспомогательного уравнения 50
3.3-3. Сведение к обыкновенным дифференциальным уравнениям 50
3.3-4. Приведение к уравнению Винера-Хопфа второго рода 51
3.3-5. Метод дробного интегрирования для уравнения Абеля 51
3.3-6. Системы интегральных уравнений Вольтерра 53
3.4. Операторные методы решения линейных интегральных уравнений 53
3.4-1. Использование решения «укороченного» уравнения 53
3.4-2. Использование вспомогательного уравнения второго рода 54
3.4-3. Метод решения «квадратных» операторных уравнений 56
3.4-4. Решение операторных уравнений полиномиального вида 57
3.4-5. Некоторые обобщения 58
3.5. Построение решений уравнений со специальной правой частью 58
3.5-1. Общая схема 58
3.5-2. Порождающая функция экспоненциального вида 59
3.5-3. Порождающая функция степенного вида 61
3.5-4. Порождающая функция, содержащая синусы или косинусы 62
3.6. Метод модельных решений 63
3.6-1. Предварительные замечания 63
3.6-2. Описание метода 64
3.6-3. Модельное решение для экспоненциальной правой части 64
3.6-4. Модельное решение для степенной правой части 66
3.6-5. Модельное решение для синусоидальной правой части 67
3.6-6. Модельное решение для косинусоидальной правой части 67
3.6-7. Некоторые обобщения 67
3.7. Метод дифференцирования интегральных уравнений 68
3.7-1. Ядро содержит сумму экспонент 68
3.7-2. Ядро содержит сумму гиперболических функций 69
3.7-3. Ядро содержит сумму тригонометрических функций 70
3.7-4. Ядро содержит комбинации различных функций 71
3.8. Сведение уравнений Вольтерра второго рода к уравнениям Вольтерра первого рода 71
3.8-1. Первый способ 72
3.8-2. Второй способ 72
3.9. Метод последовательных приближений 72
3.9-1. Общая схема 72
3.9-2. Формула для резольвенты 73
3.10. Метод квадратур 74
3.10-1. Общая схема метода 74
3.10-2. Применение формулы трапеций 75
3.10-3. Случай вырожденного ядра 75
3.11. Уравнения с бесконечным пределом интегрирования 75
3.11-1. Случай переменного нижнего предела интегрирования 76
3.11-2. Приведение к уравнению Винера-Хопфа второго рода 77
4. Методы решения линейных уравнений вида Ja К(ж, t)y(t) dt = f (ж) . 78
4.1. Предварительные замечания 78
4.1-1. Интегральные уравнения Фредгольма первого рода 78
4.1-2. Интегральные уравнения первого рода со слабой особенностью 78
4.1-3. Интегральные уравнения типа свертки 79
4.1-4. Парные интегральные уравнения первого рода 80
4.2. Метод Крейна 80
4.2-1. Основное и вспомогательное уравнения 80
4.2-2. Решение основного уравнения 81
4.3. Метод интегральных преобразований 82
4.3-1. Уравнение с разностным ядром на всей оси 82
4.3-2. Уравнения с ядром K(x,t) = K(x/t) на полуоси 82
4.3-3. Уравнение с ядром K(x,t) = K(xt) и его обобщения 82
4.4. Задача Римана для действительной оси 83
4.4-1. Связь интеграла Фурье с интегралом типа Коши 84
4.4-2. Односторонние интегралы Фурье 85
4.4-3. Теорема об аналитическом продолжении и теорема Лиувилля 86
4.4-4. Краевая задача Римана 87
4.4-5. Задача Римана с рациональными коэффициентами 93
4.4-6. Исключительные случаи. Однородная задача 94
4.4-7. Исключительные случаи. Неоднородная задача 96
4.5. Метод Карлемана для уравнений типа свертки первого рода 99
4.5-1. Уравнение Винера-Хопфа первого рода 99
4.5-2. Интегральные уравнения с двумя ядрами первого рода 99
4.6. Парные интегральные уравнения первого рода 102
4.6-1. Метод Карлемана для уравнения с разностными ядрами 102
4.6-2. Точные решения некоторых парных уравнений первого рода 104
4.6-3. Приведение парных уравнений к уравнению Фредгольма 105
4.7. Асимптотические методы решения уравнений с логарифмической особенностью 109
4.7-1. Предварительные замечания 109
4.7-2. Решение при больших значениях характерного параметра 109
4.7-3. Решение при малых значениях характерного параметра ПО
4.7-4. Интегральные уравнения теории упругости 112
4.8. Методы регуляризации 112
4.8-1. Метод регуляризации Лаврентьева 112
4.8-2. Метод регуляризации Тихонова 113
5. Методы решения линейных уравнений вида у(х) —Ja K(x, t)y(t) dt= f(x) 114
5.1. Предварительные замечания 114
5.1-1. Уравнения Фредгольма и уравнения со слабой особенностью 114
5.1-2. Структура решений 115
5.1-3. Интегральные уравнения типа свертки второго рода 115
5.1-4. Парные интегральные уравнения второго рода 115
5.2. Уравнения Фредгольма второго рода с вырожденным ядром 116
5.2-1. Простейшее вырожденное ядро 116
5.2-2. Вырожденное ядро в общем случае 117
5.3. Решение в виде ряда по степеням параметра. Метод последовательных приближений 120
5.3-1. Итерированные ядра 120
5.3-2. Метод последовательных приближений 120
5.3-3. Построение резольвенты 121
5.3-4. Ортогональные ядра 122
5.4. Метод определителей Фредгольма 123
5.4-1. Формула для резольвенты 123
5.4-2. Рекуррентные соотношения 124
5.5. Теоремы и альтернатива Фредгольма 125
5.5-1. Теоремы Фредгольма 125
5.5-2. Альтернатива Фредгольма 125
5.6. Интегральные уравнения Фредгольма второго рода с симметричными ядрами . 125
5.6-1. Характеристические числа и собственные функции 125
5.6-2. Билинейный ряд 127
5.6-3. Теорема Гильберта-Шмидта 128
5.6-4. Билинейные ряды итерированных ядер 128
5.6-5. Решение неоднородного уравнения 129
5.6-6. Альтернатива Фредгольма для симметричных уравнений 130
5.6-7. Резольвента симметричного ядра 130
5.6-8. Экстремальные свойства характеристических чисел 131
5.6-9. Интегральные уравнения, приводимые к симметричным 131
5.6-10. Кососимметричное интегральное уравнение 132
5.7. Операторный метод решения интегральных уравнений второго рода 132
5.7-1. Простейшая схема 132
5.7-2. Решение уравнений второго рода на полуоси 132
5.8. Метод интегральных преобразований и метод модельных решений 133
5.8-1. Уравнение с разностным ядром на всей оси 133
5.8-2. Уравнение с ядром K(x,t) = t

1Q(x/t) на полуоси 135
5.8-3. Уравнение с ядром K(x,t) = tf3Q(xt) на полуоси 136
5.8-4. Метод модельных решений для уравнений на всей оси 137
5.9. Метод Карлемана для интегральных уравнений типа свертки второго рода . 137
5.9-1. Уравнение Винера-Хопфа второго рода 137
5.9-2. Интегральное уравнение второго рода с двумя ядрами 141
5.9-3. Уравнения типа свертки с переменным пределом интегрирования 146
5.9-4. Парное уравнение типа свертки второго рода 148
5.10. Метод Винера-Хопфа 149
5.10-1. Некоторые замечания 149
5.10-2. Однородное уравнение Винера-Хопфа второго рода 151
5.10-3. Общая схема метода. Проблема факторизации 154
5.10-4. Неоднородное уравнение Винера-Хопфа второго рода 156
5.10-5. Исключительный случай уравнения Винера-Хопфа второго рода 157
5.11. Метод Крейна для уравнения Винера-Хопфа 158
5.11-1. Некоторые замечания. Проблема факторизации 158
5.11-2. Решение уравнения Винера-Хопфа второго рода 159
5.11-3. Формула Хопфа-Фока 161
5.12. Методы решения уравнений с разностным ядром на конечном отрезке 162
5.12-1. Метод Крейна 162
5.12-2. Ядра с рациональными преобразованиями Фурье 163
5.12-3. Сведение к обыкновенным дифференциальным уравнениям 164
5.13. Метод замены ядра вырожденным 166
5.13-1. Аппроксимация ядра 166
5.13-2. Приближенное решение 167
5.14. Метод Бейтмена 168
5.14-1. Общая схема метода 168
5.14-2. Некоторые частные случаи 169
5.15. Метод коллокации 171
5.15-1. Общие замечания 171
5.15-2. Приближенное решение 172
5.15-3. Собственные функции уравнения 173
5.16. Метод наименьших квадратов 174
5.16-1. Описание метода 174
5.16-2. Построение собственных функций 175
5.17. Метод Бубнова-Галеркина 176
5.17-1. Описание метода 176
5.17-2. Характеристические числа уравнения 176
5.18. Метод квадратур 178
5.18-1. Общая схема для уравнений Фредгольма второго рода 178
5.18-2. Построение собственных функций 179
5.18-3. Особенности применения квадратурных формул 179
5.19. Системы интегральных уравнений Фредгольма второго рода 180
5.19-1. Некоторые замечания 180
5.19-2. Метод преобразования системы уравнений в одно уравнение 181
5.20. Метод регуляризации для некоторых уравнений второго рода 181
5.20-1. Основное уравнение и теоремы Нетера 181
5.20-2. Регуляризующие операторы 182
5.20-3. Метод регуляризации 183
6. Методы решения сингулярных интегральных уравнений первого рода . 185
6.1. Предварительные замечания 185
6.1-1. Интегральные уравнения первого рода с ядром Коши 185
6.1-2. Интегральные уравнения первого рода с ядром Гильберта 185
6.2. Интеграл типа Коши 186
6.2-1. Определение интеграла типа Коши 186
6.2-2. Условие Гёльдера 187
6.2-3. Главное значение сингулярного интеграла 187
6.2-4. Многозначные функции 189
6.2-5. Главное значение сингулярного криволинейного интеграла 190
6.2-6. Формула перестановки Пуанкаре-Бертрана 192
6.3. Краевая задача Римана 192
6.3-1. Теорема об аналитическом продолжении и теорема Лиувилля 192
6.3-2. Интерполяционный полином Эрмита 194
6.3-3. Понятие индекса 194
6.3-4. Постановка задачи Римана 196
6.3-5. Решение однородной задачи 198
6.3-6. Решение неоднородной задачи 199
6.3-7. Задача Римана с рациональными коэффициентами 201
6.3-8. Задача Римана для действительной оси 204
6.3-9. Исключительные случаи задачи Римана 206
6.3-10. Задача Римана для многосвязной области 210
6.3-11. Случаи разрывных коэффициентов и разомкнутых контуров 213
6.3-12. Краевая задача Гильберта 213
6.4. Сингулярные интегральные уравнения первого рода 214
6.4-1. Простейшее уравнение с ядром Коши 214
6.4-2. Уравнение с ядром Коши на действительной оси 214
6.4-3. Уравнение первого рода на конечном отрезке 215
6.4-4. Общее уравнение первого рода с ядром Коши 216
6.4-5. Уравнения первого рода с ядром Гильберта 217
6.5. Метод Мультоппа-Каландия 218
6.5-1. Решение, не ограниченное на концах отрезка 218
6.5-2. Решение, ограниченное на одном конце отрезка 220
6.5-3. Решение, ограниченное на обоих концах отрезка 221
7. Методы решения полных сингулярных интегральных уравнений 222
7.1. Некоторые замечания 222
7.1-1. Интегральные уравнения с ядром Коши 222
7.1-2. Интегральные уравнения с ядром Гильберта 223
7.1-3. Об уравнениях Фредгольма второго рода на контуре 224
7.2. Метод Карлемана для характеристических уравнений 226
7.2-1. Характеристическое уравнение с ядром Коши 226
7.2-2. Уравнение, союзное с характеристическим 229
7.2-3. Характеристическое уравнение на действительной оси 230
7.2-4. Исключительный случай характеристического уравнения 232
7.2-5. Характеристическое уравнение с ядром Гильберта 234
7.2-6. Уравнение Трикоми 234
7.3. Полные сингулярные интегральные уравнения, разрешаемые в замкнутой форме 235
7.3-1. Замкнутое решение при постоянных коэффициентах 235
7.3-2. Замкнутое решение в общем случае 236
7.4. Метод регуляризации для полных сингулярных интегральных уравнений . 238
7.4-1. Некоторые свойства сингулярных операторов 238
7.4-2. Регуляризующий оператор 240
7.4-3. Способы регуляризации слева и справа 241
7.4-4. Проблема равносильной регуляризации 242
7.4-5. Теоремы Нётера 243
7.4-6. Способ регуляризации Карлемана-Векуа 244
7.4-7. Регуляризация в исключительных случаях 246
7.4-8. Полное уравнение с ядром Гильберта 246
8. Методы решения нелинейных интегральных уравнений 250
8.1. Некоторые определения и замечания 250
8.1-1. Нелинейные интегральные уравнения Вольтерра 250
8.1-2. Нелинейные уравнения с постоянными пределами интегрирования . 251
8.2. Нелинейные интегральные уравнения Вольтерра 252
8.2-1. Метод интегральных преобразований 252
8.2-2. Метод дифференцирования интегральных уравнений 253
8.2-3. Метод последовательных приближений 254
8.2-4. Метод Ньютона-Канторовича 256
8.2-5. Метод коллокации 258
8.2-6. Метод квадратур 258
8.3. Уравнения с постоянными пределами интегрирования 260
8.3-1. Нелинейные уравнения с вырожденными ядрами 260
8.3-2. Метод интегральных преобразований 262
8.3-3. Метод дифференцирования интегральных уравнений 263
8.3-4. Метод последовательных приближений 264
8.3-5. Метод Ньютона-Канторовича 264
8.3-6. Метод квадратур 267
8.3-7. Метод регуляризации Тихонова 267
Список литературы 269

Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу Методы решения интегральных уравнений: Справочник — Манжиров А.В., Полянин А.Д. — fileskachat.com, быстрое и бесплатное скачивание.

Скачать djvu
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России. Купить эту книгу

источники:

http://obuchalka.org/2011022753598/metodi-resheniya-integralnih-uravnenii-spravochnik-manjirov-a-v-polyanin-a-d.html

Источник