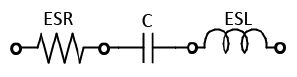Полное
сопротивление конденсатора
– это сопротивление конденсатора
переменному синусоидальному току
определенной частоты, обусловленное
наличием у реального конденсатора
наряду с емкостью также активного
сопротивления и индуктивности.
Полное сопротивление
конденсатора Z
при представлении его в качестве
последовательно соединенных собственной
емкости C,
индуктивности секции и выводов L,
активного сопротивления выводов,
контактного узла и сопротивления
обкладок r,
на частоте f
определяется по формуле

Самая низкая
частота, при которой полное сопротивление
конденсатора будет минимальным и чисто
активным, называется резонансной
частотой
конденсатора.
На частоте ниже
резонансной полное сопротивление
конденсатора носит емкостной характер,
на частотах выше резонансной – индуктивный
(рис. 2.2).
Ориентировочные значения резонансных
частот и собственных индуктивностей
различных типов конденсаторов представлены
в табл. 2.8.
Таблица 2.8
|
Группа |
Собственная |
Резонансная |
|
Керамические, |
0,25-15 |
1-5000 |
|
Бумажные, пленочные |
6-20 |
1,5-15 |
|
Бумажные, пленочные |
10-100 |
0,1-2,5 |
|
С оксидным |
3-40 |
2.3.8 Реактивная мощность
Произведение
напряжения
определенной частоты
,
приложенного к конденсатору, на силу
тока
,
проходящего через него, и на синус угла
сдвига фаз
между ними определяет значение реактивной
мощности
конденсатора. В большинстве случаев
угол сдвига фаз близок к 900,
поэтому
и
.
Понятие реактивной
мощности введено для высокочастотных
и особенно высоковольтных конденсаторов
и используется при установлении
допустимых электрических режимов
эксплуатации. При этом в области низких
частот ограничения определяются
допустимой амплитудой напряжения
переменного тока, а на высоких частотах
– допустимой реактивной мощностью
конденсатора. Таким образом, реактивная
мощность характеризует нагрузочную
способность конденсатора при наличии
на нем больших напряжений высокой
частоты.
При умножении
реактивной мощности на коэффициент
получим
активную мощность, обусловленную
наличием потерь в конденсаторе и
вызывающую его нагрев.
2.4 Специфические электрические параметры и характеристики подстроечных и переменных конденсаторов
Подстроечные и
переменные конденсаторы наряду с
основными параметрами, приведенными
выше, имеют дополнительные, учитывающие
особенности их функционального назначения
и конструктивное исполнение.
Вместо параметра
номинальная емкость используются
параметры максимальная и минимальная
емкости. Это максимальное и минимальное
значение емкости конденсатора, которое
может быть получено перемещением его
подвижной системы.
Специфичными
параметрами подстроечных и переменных
конденсаторов являются момент вращения,
скорость перестройки емкости и
износоустойчивость.
Момент вращения
– минимальный момент, необходимый для
непрерывного перемещения подвижной
системы конденсатора.
Скорость перестройки
емкости влияет на надежность и прочность
конденсатора. В нормативной документации
ограничивается скорость перестройки
емкости для керамических конденсаторов
– не более 10-15 циклов в минуту для
вакуумных 5-30. Под циклом перестройки
емкости понимается перестройка емкости
от минимальной до максимальной и обратно.
Количество допустимых циклов перестройки
емкости определяет износоустойчивость
конденсатора.
Под износоустойчивостью
понимают способность конденсатора
сохранять свои параметры (противостоять
изнашиванию) при многократных вращениях
подвижной системы.
Износоустойчивость
конденсаторов и скорость перестройки
емкости зависят от конструкции
конденсаторов, свойств примененных
материалов и технологии их изготовления.
Для вакуумных
конденсаторов наиболее важным параметром
является электрическая прочность. Этот
термин не следует отождествлять с
определением электрической прочности
диэлектрика, принятым в теории
диэлектриков. Для конденсаторов термин
электрическая прочность следует понимать
условно, как способность конденсаторов
выдерживать определенное время (обычно
небольшое, до нескольких минут) приложенное
к нему напряжение выше номинального
без изменения его эксплуатационных
характеристик и пробоя диэлектрика.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Введение
Частотные характеристики конденсаторов являются важными параметрами, которые необходимы для разработки схем. Понимание частотных характеристик конденсатора позволит вам определить, например, какие шумы может подавлять конденсатор или какие флуктуации напряжения цепи питания он может контролировать. Эта статья описывает два типа частотных характеристик: |Z| (импеданс или полное сопротивление) и ESR (эквивалентное последовательное сопротивление конденсатора).
Частотные характеристики конденсаторов
Импеданс Z идеального конденсатора определяется формулой 1, где ω — угловая частота, а C — емкость конденсатора.
Рисунок 1. Идеальный конденсатор
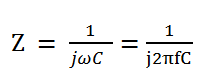
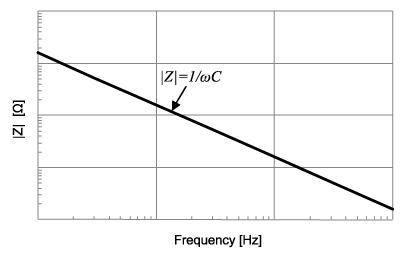
Из формулы 1 видно, что с увеличением частоты импеданс конденсатора уменьшается. Это показано на рисунке 1. В идеальном конденсаторе нет потерь и эквивалентное последовательное сопротивление (ESR) равно нулю.
Рисунок 2. Частотная характеристика идеального конденсатора
В реальном конденсаторе (рис. 3) существует некоторое сопротивление (ESR), вызванное диэлектрическими потерями, потерями на сопротивлении обкладок конденсатора и потерями связанные с сопротивлением утечки, а также паразитная индуктивность (ESL) выводов и обкладок конденсатора. В результате частотная характеристика импеданса принимает V образную форму (или U образную в зависимости от типа конденсатора), как показано на рисунке 4.Также на рисунке показана частотная характеристика ESR.
Рисунок 3. Реальный конденсатор
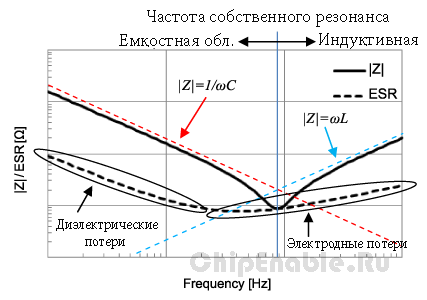
Рисунок 4. Пример частотной характеристики реального конденсатора
Причина, по которой графики |Z| и ESR имеют такой вид как на рисунке 4, можно объяснить следующим образом.
Низкочастотная область
|Z| в этой области уменьшается обратно пропорционально частоте, как и в идеальном конденсаторе. Значение ESR определяется диэлектрическими потерями в конденсаторе.
Область резонанса
При повышении частоты ESR, в результате паразитной индуктивности, сопротивления электродов и других факторов, вызывает отклонение |Z| от идеальной характеристики (красная пунктирная линия) и достигает минимального значения. Частота, на которой |Z| достигает минимума, называется собственной резонансной частотой и на этой частоте |Z| = ESR. После превышения собственной частоты резонанса, характеристика элемента меняется с емкостной на индуктивную и |Z| начинает повышаться. Область ниже собственной резонансной частоты называется емкостной областью, а область выше — индуктивной.
В области резонанса к диэлектрическим потерям добавляются потери на электродах.
Высокочастотная область
При дальнейшем увеличении частоты характеристика |Z| определяется паразитной индуктивностью конденсатора. В высокочастотной области |Z| увеличивается пропорционально частоте, согласно формуле 2. Что касается ESR, в этой области начинают проявляться скин-эффект , эффект близости и другие.
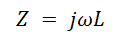
Итак, мы рассмотрели частотную характеристику реального конденсатора. Здесь важно запомнить, что c повышением частоты ESR и ESL уже нельзя игнорировать. Поскольку существуют большое количество приложений, в которых конденсаторы используются на высоких частотах, ESR и ESL становятся важными параметрами, характеризующими конденсатор помимо значения его емкости.
Частотные характеристики конденсаторов различных типов
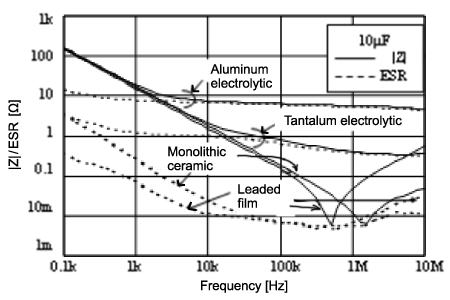
Паразитные составляющие реальных конденсаторов имеют различное значение в зависимости от их типа. Давайте посмотрим на частотные характеристики разных конденсаторов. На рисунке 5 показаны графики |Z| и ESR для конденсаторов емкостью 10 мкФ. Все конденсаторы, кроме пленочных, планарные (SMD).
Рисунок 5. Частотные характеристики конденсаторов разных типов.
Для всех типов конденсаторов |Z| ведет себя одинаково до частоты 1 кГц. После 1 кГц импеданс увеличивается сильнее в алюминиевых и танталовых электролитических конденсаторах, чем в монолитных керамических и пленочных конденсаторах.
Это происходит из-за того, что алюминиевые и танталовые конденсаторы имеют высокое удельное сопротивление электролита и большое ESR. В пленочных и монолитных керамических конденсаторах используются металлические материалы для электродов и, следовательно, они обладают очень маленьким ESR.
Монолитные керамические конденсаторы и пленочные показывают примерно одинаковые характеристики до точки собственного резонанса, но у монолитных керамических конденсаторов резонансная частота выше, а |Z| в индуктивной области ниже.
Эти результаты показывают, что импеданс монолитных керамических конденсаторов SMD типа в широком диапазоне частот имеет небольшое значение. Это делает их наиболее подходящими для высокочастотных приложений.
Частотные характеристики монолитных керамических конденсаторов
Существует также несколько типов монолитных керамических конденсаторов, изготовленных из различных материалов и имеющих различную форму. Давайте посмотрим, как эти факторы влияют на частотные характеристики.
ESR
ESR в емкостной области зависит от диэлектрических потерь, вызванных материалом диэлектрика. 2-й класс диэлектрических материалов на основе сегнетоэлектриков имеет высокую диэлектрическую постоянную и, как правило, высокое ESR. 1-ый класс материалов — температурно-компенсированные материалы на основе параэлектриков — имеют низкие диэлектрические потери и низкое ESR.
На высоких частотах в области резонанса и индуктивной области, в дополнение к сопротивлению материала электродов, их форме и количеству слоев, ESR зависит от скин-эффекта и эффекта близости. Электроды часто делают из Ni, но для дешевых конденсаторов иногда применяют Cu, который тоже имеет низкое сопротивление.
ESL
ESL монолитных керамических конденсаторов сильно зависит от внутренней структуры электродов. Если размеры внутренних электродов задаются длиной, шириной и толщиной, то индуктивность ESL может быть определена математически. Значение ESL уменьшается, когда электроды конденсатора короче, шире и тоньше.
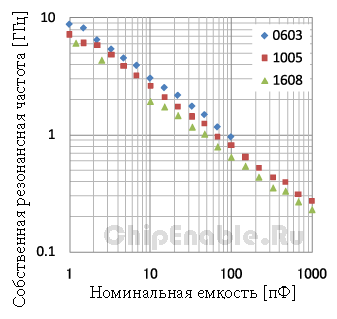
На рисунке 6 показана связь между номинальной емкостью и резонансной частотой различных типов монолитных керамических конденсаторов. Вы можете видеть, что при уменьшении размеров конденсатора собственная резонансная частота увеличивается, а ESL уменьшается для одинаковых значений емкости. Это означает, что небольшие конденсаторы короткой длины лучше подходят для высокочастотных приложений.
Рисунок 6.
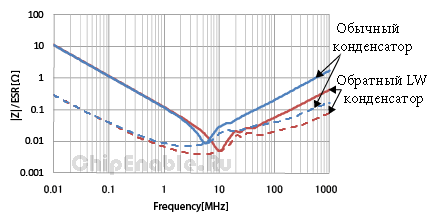
На рисунке 7 показан обратный LW конденсатор с короткой длиной L и большой шириной W. Из частотных характеристик, показанных на рисунке 8, можно увидеть, что LW конденсатор имеет меньший импеданс и лучшие характеристики, чем обычный конденсатор такой же емкости. С помощью LW конденсаторов можно достичь тех же характеристик, как у обычных конденсаторов, но меньшим числом компонентов. Уменьшение числа компонентов, позволяет сократить расходы и уменьшить монтажное пространство.
Рисунок 7. Внешний вид обратного LW конденсатора.
Рисунок 8. |Z| и ESR обратного LW конденсатора и конденсатора общего назначения
По материалам фирмы Murata.
Вольный перевод ChipEnable.Ru
Резонансная частота.
Параллельный колебательный контур (рисунок 1) или последовательный колебательный контур (рисунок 2) могут использоваться в генераторах синусоидальных колебаний. Если в одной из этих схем зарядить конденсатор то он будет разряжаться заряжая катушку индуктивности, катушка разряжаясь будет заряжать конденсатор, этот процесс будет повторяться с определённым периодом T. Период это время одного колебания. Частота колебаний это величина обратная периоду. Разделив единицу на численное значение периода получим численное значение частоты.
Рисунок 1 — Параллельный колебательный контур
Рисунок 2 — Последовательный колебательный контур
Частота возникших колебаний называется собственной частотой колебаний контура для контуров изображённых на рисунках выше эта частота равна резонансной частоте этих контуров. Резонансная частота контура зависит от индуктивности L и ёмкости C её элементов, для колебательного контура (последовательного или параллельного) её можно найти по формуле:
Где L-индуктивность катушки контура, C-ёмкость конденсатора контура.
Если на параллельный или последовательный колебательный контур подавать переменное синусоидальное напряжение и изменять его частоту то будут меняться реактивные сопротивления элементов контура, если частота увеличивается то сопротивление конденсатора уменьшается а сопротивление катушки увеличивается и наоборот: если частота уменьшается то сопротивление конденсатора увеличивается а сопротивление катушки уменьшается, очевидно что есть такая частота при которой сопротивление катушки и конденсатора равны эта частота и есть резонансная. Сопротивление параллельного колебательного контура при этой частоте будет наибольшим (по сравнению с сопротивлениями этого контура при других частотах) а сопротивление последовательного колебательного контура при такой частоте будет наименьшим. Эти свойства контуров используют для построения фильтров например в полосно-пропускающем фильтре последовательно с нагрузкой ставиться последовательный контур и при подаче на это соединение (нагрузки и контура) переменного напряжения с резонансной частотой ток в нагрузке будет максимальным при других частотах ток будет меньше. Резонанс в параллельном контуре называют — резонансом токов, резонанс в последовательном контуре — резонансом напряжений. Можно простым способом определить каким будет сопротивление контура при резонансной частоте: например допустим что на параллельный колебательный контур подаётся постоянный ток, постоянный ток можно считать частным случаем переменного короче говоря постоянный ток это переменный с наименьшей возможной частотой, известно что при постоянном токе катушка действует как перемычка следовательно сопротивление контура будет равно нулю если резонансная частота не бесконечно мала (т.е. не постоянный ток) и сопротивление есть то оно больше нуля (т.е. сопротивления при постоянном токе) следовательно сопротивление параллельного колебательного контура на резонансной частоте максимальное а у последовательного контура наоборот. Зная то что конденсатор постоянный ток не пропускает, можно аналогично определить каким д.б. сопротивление последовательного контура на резонансной частоте. Выведем формулу для расчёта резонансной частоты зная то что при резонансе реактивные сопротивления элементов (катушки и конденсатора) контура равны:
Для расчёта резонансной частоты и периода колебаний колебательного контура с катушкой и конденсатором можно воспользоваться программой:
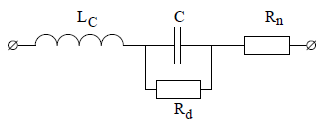
Схема замещения не идеального (реального) конденсатора:
При изменении частоты изменяются диэлектрическая проницаемость диэлектрика и степень влияния паразитных параметров — собственной индуктивности и сопротивления потерь. На высоких частотах любой конденсатор можно рассматривать как последовательный колебательный контур, образуемый емкостью C, собственной индуктивностью LC и сопротивлением потерь Rп.
Сопротивление потерь — эквивалентное последовательное сопротивление (ЭПС (англ. ESR), внутреннее сопротивление), обусловлено, главным образом, электрическим сопротивлением материала обкладок и выводов конденсатора и контактов между ними, а также учитывает потери в диэлектрике. Обычно ЭПС возрастает с увеличением частоты тока, протекающего через конденсатор, вследствие поверхностного эффекта (скин-эффекта). Подробнее о поверхностном эффекте можно прочитать [гиперссылка]здесь[/гиперссылка].
В большинстве практических случаев этим параметром можно пренебречь, но, иногда (например, в случае использования электролитических конденсаторов в фильтрах импульсных блоков питания), достаточно малое его значение существенно для надежности и устойчивости работы устройства. В электролитических конденсаторах, где один из электродов является электролитом, этот параметр при эксплуатации со временем деградирует, вследствие испарения растворителя из жидкого электролита и изменения его химического состава, вызванного взаимодействием с металлическими обкладками, что происходит относительно быстро в низкокачественных изделиях.
Некоторые схемы (например, стабилизаторы напряжения) критичны к диапазону изменения ЭПС конденсаторов в своих цепях. Это связано с тем, что при проектировании таких устройств инженеры учитывают этот параметр в фазочастотной характеристике (ФЧХ) обратной связи стабилизатора. Существенное изменение со временем ЭПС примененных конденсаторов изменяет ФЧХ, что может привести к снижению запаса устойчивости контуров авторегулирования, и, даже, к самовозбуждению.
Существуют специальные приборы (англ. ESR-метр) для измерения этого достаточно важного параметра конденсатора, по которому можно часто определить пригодность его дальнейшего использования в определенных целях. Этот параметр, кроме собственно емкости — часто имеет решающее значение в исследовании состояния старого конденсатора и принятия решения, стоит ли использовать его в определенной схеме, или он прогнозируемо выйдет за пределы допустимых отклонений.
Собственная индуктивность — эквивалентная последовательная индуктивность (ЭПИ (англ. ESL)), обусловлена, в основном, собственной индуктивностью обкладок и выводов конденсатора. Результатом этой распределенной паразитной индуктивности является превращение конденсатора в колебательный контур с характерной собственной частотой резонанса. Эта частота может быть измерена и обычно указывается в параметрах конденсатора либо в явном виде, либо в виде рекомендованной максимальной рабочей частоты.
Резонансная частота конденсатора:
При f > fр конденсатор в цепи переменного тока ведет себя как катушка индуктивности. Следовательно, конденсатор целесообразно использовать лишь на частотах f < fp, на которых его сопротивление носит емкостный характер. Обычно максимальная рабочая частота конденсатора примерно в 2—3 раза ниже резонансной.
Энергия заряженного конденсатора:
где:
U — напряжение (разность потенциалов) на обкладках конденсатора;
q – величина накопленного электрического заряда;
С – емкость конденсатора.
Несколько явлений, напрямую связанных с физикой диэлектриков:
Спойлер
Тангенс угла диэлектрических потерь:
Так как реальные среды анизотропные и неоднородные, диэлектрическая проницаемость будет иметь комплексный вид:
Тангенс угла диэлектрических потерь выражается отношением мнимой и вещественной части комплексной диэлектрической проницаемости:
где:
γ – проводимость среды;
ω – частота колебаний;
εа – абсолютная диэлектрическая проницаемость.
Очевидно, что у идеального диэлектрика проводимость γ→0, следовательно, тангенс угла потерь показывает степень отличия реального диэлектрика от идеального.
Электрическое сопротивление изоляции диэлектрика конденсатора Rd, ток утечки и саморазряд:
Сопротивление изоляции — это сопротивление конденсатора постоянному току, определяемое соотношением , где: U — напряжение, приложенное к конденсатору, Ileak. — ток утечки.
Из-за тока утечки, протекающего через слой диэлектрика между обкладками и по поверхности диэлектрика, предварительно заряженный конденсатор с течением времени теряет заряд (саморазряд конденсатора). Часто, в спецификациях на конденсаторы, сопротивление утечки определяют через постоянную времени τ саморазряда конденсатора, которая численно равна произведению емкости на сопротивление утечки:
τ — это время, за которое начальное напряжение на конденсаторе, неподключенном к внешней цепи уменьшится в e раз.
Хорошие конденсаторы с полимерными и керамическими диэлектриками имеют постоянные времени саморазряда достигающие многих сотен тысяч часов.
Диэлектрическая абсорбция:
Если заряженный конденсатор быстро разрядить до нулевого напряжения путем подключения низкоомной нагрузки, а затем снять нагрузку и наблюдать за напряжением на выводах конденсатора, то можно увидеть, что напряжение на обкладках снова появится, как если бы конденсатор разрядили не до нуля. Это явление получило название диэлектрическая абсорбция (диэлектрическое поглощение). Конденсатор ведет себя так, словно параллельно ему подключено множество последовательных RC-цепочек с различной постоянной времени. Интенсивность проявления этого эффекта зависит в основном от свойств диэлектрика конденсатора.
Подобный эффект можно наблюдать практически на всех типах диэлектриков. В электролитических конденсаторах он особенно ярок и является следствием химических реакций между электролитом и обкладками. У конденсаторов с твердым диэлектриком (например, керамических и слюдяных) эффект связан с остаточной поляризацией диэлектрика. Наименьшим диэлектрическим поглощением обладают конденсаторы с неполярными диэлектриками: тефлон (фторопласт), полистирол, полипропилен и т. п.
Эффект зависит от времени зарядки конденсатора, времени закорочения, иногда от температуры. Количественное значение абсорбции принято характеризовать коэффициентом абсорбции, который определяется в стандартных условиях.
Паразитный пьезоэффект:
Многие керамические материалы, используемые в качестве диэлектрика в конденсаторах (например, титанат бария, обладающий очень высокой диэлектрической проницаемостью в не слишком сильных электрических полях) проявляют пьезоэффект — способность генерировать напряжение на обкладках при механических деформациях. Это характерно для конденсаторов с пьезоэлектрическими диэлектриками. Пьезоэффект ведет к возникновению электрических помех, в устройствах, где использованы такие конденсаторы при воздействии акустического шума или вибрации на конденсатор. Это нежелательное явление иногда называют («микрофонным эффектом»).
Также, подобные диэлектрики проявляют и обратный пьезоэффект — при работе в цепи переменного напряжения происходит знакопеременная деформация диэлектрика, генерирующая акустические колебания, порождающие дополнительные электрические потери в конденсаторе.
Самовосстановление:
Конденсаторы с металлизированным электродом (бумажный и пленочный диэлектрик) обладают важным свойством самовосстановления (англ. self-healing, cleaning) электрической прочности после пробоя диэлектрика. Механизм самовосстановления заключается в отгорании металлизации электрода после локального пробоя диэлектрика посредством микродугового электрического разряда.
Электрическая цепь, состоящая из соединеных в контур конденсатора емкостью С и катушки индуктивностью L,
обладающая сопротивлением R(сопротивление активных потерь в катушке), называется электрическим колебательным контуром.
В контуре возникает колебательный процесс ввиду перехода энергии электрического поля в энергию магнитного и наоборот.
Реактивные сопротивления индуктивности и емкости зависят от частоты переменного тока.
При увеличении частоты реактивное сопротивление индуктивности растет, а емкости падает.
При уменьшении частоты, наоборот, индуктивное сопротивление падает, а емкостное — растет.
При некоторой частоте ƒ0, емкостное сопротивление конденсатора и индуктивное сопротивление катушки
становятся численно равными: Xc = XL.
При этом токи индуктивной и емкостной ветвей также равны, что приводит к возрастанию амплитуды вынужденных колебаний.
Режим, возникающий в цепи, состоящей из генератора и параллельно включенных катушки и конденсатора, при равенстве
емкостного и индуктивного сопротивлений, называют режимом резонанса токов.
Явление резонанса токов используется в полосовых фильтрах для выделения определенной частоты.
Такая схема необходима для работы телевизора, радиоприемника, ёмкостного генератора и т.п.
Расчет частоты резонанса параллельного LC-контура описывается формулами:
XL
— индуктивное реактивное сопротивление, Ом;
XС
— ёмкостное реактивное сопротивление, Ом;
ƒ0
— резонансная частота, Гц;
Расчет частоты резонанса LC-контура
Введите значения индуктивности и ёмкости конденсатора, чтобы узнать резонансную частоту контура,
или введите резонансную частоту генератора, чтобы рассчитать необходимые значения индуктивности и емкости.
XL =
XC =
ƒ0 =
φ = °
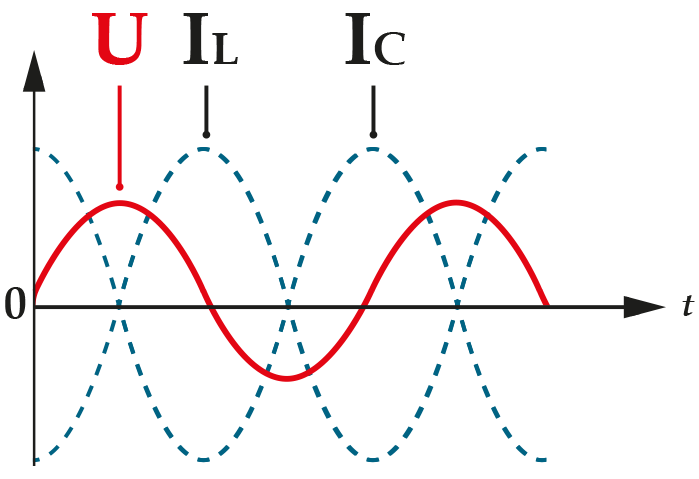
XL
>
XC
Цепь имеет емкостной характер,ее емкостное реактивное сопротивление меньше индуктивного.
Угол фазового сдвига между напряжением генератора и током в контуре приближается к 90°
Чем больше частота генератора отличается от собственной (резонансной) частоты контура, тем больше различаются токи IL и Іс,
тем больше реактивный ток в общей части цепи и меньше реактивное сопротивление контура.
Внимание! Производители объединяют элементы в серии или ряды: E6, E12, E24…
Для подбора компонентов будет использована серия E12.
Подбор конденсатора на сайте
Подбор катушки индуктивности на сайте
Обнаружили ошибку или неточность в работе калькулятора? Сообщите нам об этом.
Соблюдайте технику безопасности во время работы с электронными компонентами!