Как найти результат интерференции двух волн - Исправление недочетов и поиск решений вместе с Examum.ru

Интерференция волн.

Сложение колебаний.
Когерентные источники.
Условие максимума и минимума.
Интерференционная картина.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: интерференция света.

В предыдущем листке, посвящённом принципу Гюйгенса, мы говорили о том, что общая картина волнового процесса создаётся наложением вторичных волн. Но что это значит — «наложением»? В чём состоит конкретный физический смысл наложения волн? Что вообще происходит, когда в пространстве одновременно распространяются несколько волн? Этим вопросам и посвящён данный листок.

к оглавлению ▴

Сложение колебаний.

Сейчас мы будем рассматривать взаимодействие двух волн. Природа волновых процессов роли не играет — это могут быть механические волны в упругой среде или электромагнитные волны (в частности, свет) в прозрачной среде или в вакууме.

Опыт показывает, что волны складываются друг с другом в следующем смысле.

Принцип суперпозиции. Если две волны накладываются друг на друга в определённой области пространства, то они порождают новый волновой процесс. При этом значение колеблющейся величины в любой точке данной области равно сумме соответствующих колеблющихся величин в каждой из волн по отдельности.

Например, при наложении двух механических волн перемещение частицы упругой среды равно сумме перемещений, создаваемых в отдельности каждой волной. При наложении двух электромагнитных волн напряжённость электрического поля в данной точке равна сумме напряжённостей в каждой волне (и то же самое для индукции магнитного поля).

Разумеется, принцип суперпозиции справедлив не только для двух, но и вообще для любого количества накладывающихся волн. Результирующее колебание в данной точке всегда равно сумме колебаний, создаваемых каждой волной по отдельности.

Мы ограничимся рассмотрением наложения двух волн одинаковой амплитуды и частоты. Этот случай наиболее часто встречается в физике и, в частности, в оптике.

Оказывается, на амплитуду результирующего колебания сильно влияет разность фаз складывающихся колебаний. В зависимости от разности фаз в данной точке пространства две волны могут как усиливать друг друга, так и полностью гасить!

Предположим, например, что в некоторой точке фазы колебаний в накладывающихся волнах совпадают (рис. 1).

Рис. 1. Волны в фазе: усиление колебаний

Мы видим, что максимумы красной волны приходятся в точности на максимумы синей волны, минимумы красной волны — на минимумы синей (левая часть рис. 1). Складываясь в фазе, красная и синяя волны усиливают друг друга, порождая колебания удвоенной амплитуды (справа на рис. 1).

Теперь сдвинем синюю синусоиду относительно красной на половину длины волны. Тогда максимумы синей волны будут совпадать с минимумами красной и наоборот — минимумы синей волны совпадут с максимумами красной (рис. 2, слева).

Рис. 2. Волны в противофазе: гашение колебаний

Колебания, создаваемые этими волнами, будут происходить, как говорят, в противофазе — разность фаз колебаний станет равна . Результирующее колебание окажется равным нулю, т. е. красная и синяя волны попросту уничтожат друг друга (рис. 2, справа).

к оглавлению ▴

Когерентные источники.

Пусть имеются два точечных источника, создающие волны в окружающем пространстве. Мы полагаем, что эти источники согласованы друг с другом в следующем смысле.

Когерентность. Два источника называются когерентными, если они имеют одинаковую частоту и постоянную, не зависящую от времени разность фаз. Волны, возбуждаемые такими источниками, также называются когерентными.

Итак, рассматриваем два когерентных источника $S_{1}$ и $S_{2}$ . Для простоты считаем, что источники излучают волны одинаковой амплитуды, а разность фаз между источниками равна нулю. В общем, эти источники являются «точными копиями» друг друга (в оптике, например, источник $S_{2}$ служит изображением источника $S_{1}$ в какой-либо оптической системе).

Наложение волн, излучённых данными источниками, наблюдается в некоторой точке . Вообще говоря, амплитуды этих волн в точке не будут равны друг другу — ведь, как мы помним, амплитуда сферической волны обратно пропорциональна расстоянию до источника, и при разных расстояниях $S_{1}P$ и $S_{2}P$ амплитуды пришедших волн окажутся различными. Но во многих случаях точка расположена достаточно далеко от источников — на расстоянии гораздо большем, чем расстояние между самими источниками. В такой ситуации различие в расстояниях $S_{1}P$ и $S_{2}P$ не приводит к существенному отличию в амплитудах приходящих волн. Следовательно, мы можем считать, что амплитуды волн в точке также совпадают.

к оглавлению ▴

Условие максимума и минимума.

Однако величина $d=|S_{1}P-S_{2}P|$ , называемая разностью хода, имеет важнейшее значение. От неё самым решительным образом зависит то, какой результат сложения приходящих волн мы увидим в точке .

Рис. 3. Усиление колебаний в точке P

В ситуации на рис. 3 разность хода равна длине волны . Действительно, на отрезке $S_{1}P$ укладываются три полных волны, а на отрезке $S_{2}P$ — четыре (это, конечно, лишь иллюстрация; в оптике, например, длина таких отрезков составляет порядка миллиона длин волн). Легко видеть, что волны в точке складываются в фазе и создают колебания удвоенной амплитуды — наблюдается, как говорят, интерференционный максимум.

Ясно, что аналогичная ситуация возникнет при разности хода, равной не только длине волны, но и любому целому числу длин волн.

Условие максимума. При наложении когерентных волн колебания в данной точке будут иметь максимальную амплитуду, если разность хода равна целому числу длин волн:

(1)

Теперь посмотрим на рис. 4. На отрезке $S_{1}P$ укладываются две с половиной волны, а на отрезке $S_{2}P$ -три волны. Разность хода составляет половину длины волны (d=lambda /2[/math]).

Рис. 4. Гашение колебаний в точке P

Теперь нетрудно видеть, что волны в точке складываются в противофазе и гасят друг друга — наблюдается интерференционный минимум. То же самое будет, если разность хода окажется равна половине длины волны плюс любое целое число длин волн.

Условие минимума.
Когерентные волны, складываясь, гасят друг друга, если разность хода равна полуцелому числу длин волн:

$d=nlambda+frac{displaystyle lambda }{displaystyle 2}.$ (2)

Равенство (2) можно переписать следующим образом:

$d=(2n+1)frac{displaystyle lambda }{displaystyle 2}$ .

Поэтому условие минимума формулируют ещё так: разность хода должна быть равна нечётному числу длин полуволн.

к оглавлению ▴

Интерференционная картина.

А что, если разность хода принимает какое-то иное значение, не равное целому или полуцелому числу длин волн? Тогда волны, приходящие в данную точку, создают в ней колебания с некоторой промежуточной амплитудой, расположенной между нулём и удвоенным значением 2A амплитуды одной волны. Эта промежуточная амплитуда может принимать все значения от 0 до 2A по мере того, как разность хода меняется от полуцелого до целого числа длин волн.

Таким образом, в той области пространства, где происходит наложение волн когерентных источников $S_{1}$ и $S_{2}$ , наблюдается устойчивая интерференционная картина — фиксированное не зависящее от времени распределение амплитуд колебаний. А именно, в каждой точке $S_{1}P$ данной области амплитуда колебаний принимает своё значение, определяемое разностью хода $d=|S_{1}P-S_{2}P|$ приходящих сюда волн, и это значение амплитуды не меняется со временем.

Такая стационарность интерференционной картины обеспечивается когерентностью источников. Если, например, разность фаз источников будет постоянно меняться, то никакой устойчивой интерференционной картины уже не возникнет.

Теперь, наконец, мы можем сказать, что такое интерференция.

Интерференция — это взаимодействие волн, в результате которого возникает устойчивая интерференционная картина, то есть не зависящее от времени распределение амплитуд результирующих колебаний в точках области, где волны накладываются друг на друга.

Если волны, перекрываясь, образуют устойчивую интерференционную картину, то говорят попросту, что волны интерферируют. Как мы выяснили выше, интерферировать могут только когерентные волны. Когда, например, разговаривают два человека, то мы не замечаем вокруг них чередований максимумов и минимумов громкости; интерференции нет, поскольку в данном случае источники некогерентны.

На первый взгляд может показаться, явление интерференции противоречит закону сохранения энергии — например, куда девается энергия, когда волны полностью гасят друг друга? Но никакого нарушения закона сохранения энергии, конечно же, нет: энергия просто перераспределяется между различными участками интерференционной картины. Наибольшее количество энергии концентрируется в интерференционных максимумах, а в точки интерференционных минимумов энергия не поступает совсем.

На рис. 5 показана интерференционная картина, созданная наложением волн двух точечных источников $S_{1}$ и $S_{2}$ . Картина построена в предположении, что область наблюдения интерференции находится достаточно далеко от источников. Пунктиром отмечена ось симметрии интерференционной картины.

Рис. 5. Интерференция волн двух точечных источников

Цвета точек интерференционной картины на этом рисунке меняются от чёрного до белого через промежуточные оттенки серого. Чёрный цвет — интерференционные минимумы, белый цвет — интерференционные максимумы; серый цвет — промежуточное значение амплитуды, и чем больше амплитуда в данной точке, тем светлее сама точка.

Обратите внимание на прямую белую полосу, которая идёт вдоль оси симметрии картины. Здесь расположены так называемые центральные максимумы. Действительно, любая точка данной оси равноудалена от источников (разность хода равна нулю), так что в этой точке будет наблюдаться является интерференционный максимум.

Остальные белые полосы и все чёрные полосы слегка искривлены; можно показать, что они являются ветвями гипербол. Однако в области, расположенной на большом расстоянии от источников, кривизна белых и чёрных полос мало заметна, и выглядят эти полосы почти прямыми.

к оглавлению ▴

Интерференционный опыт, изображённый на рис. 5, вместе с соответствующим методом расчёта интерференционной картины называется схемой Юнга. Эта схема лежит в основе знаменитного
опыта Юнга (речь о котором пойдёт в теме Дифракция света). Многие эксперименты по интерференции света так или иначе сводятся к схеме Юнга.

В оптике интерференционную картину обычно наблюдают на экране. Давайте ещё раз посмотрим на рис. 5 и представим себе экран, поставленный перпендикулярно пунктирной оси.
На этом экране мы увидим чередование светлых и тёмных интерференционных полос.

На рис. 6 синусоида показывает распределение освещённости вдоль экрана. В точке O, расположенной на оси симметрии, находится центральный максимум. Первый максимум в верхней части экрана, соседний с центральным, находится в точке A. Выше идут второй, третий (и такдалее) максимумы.

Рис. 6. Интерференционная картина на экране

Расстояние , равное расстоянию между любыми двумя соседними максимумами или минимумами, называется шириной интерференционной полосы. Сейчас мы займёмся нахождением этой величины.

Пусть источники находятся на расстоянии друг от друга, а экран расположен на расстоянии от источников (рис. 7 ). Экран заменён осью ; начало отсчёта , как и выше, отвечает центральному максимуму.

Рис. 7. Вычисление координат максимумов

Точки $N_{1}$ и $N_{2}$ служат проекциями точек $S_{1}$ и $S_{2}$ на ось и расположены симметрично относительно точки . Имеем: $ON_{1}=ON_{2}=a/2$ .

Точка наблюдения может находиться на оси (на экране) где угодно. Координату точки
мы обозначим . Нас интересует, при каких значениях в точке будет наблюдаться интерференционный максимум.

Волна, излучённая источником $S_{1}$ , проходит расстояние:

$S_{1}P=sqrt{displaystyle S_{displaystyle 1}N_{displaystyle 1}^{displaystyle 2}+PN_{displaystyle 1}^{displaystyle 2}}=sqrt{L^{2}+(x-frac{displaystyle a}{displaystyle 2})^{displaystyle 2}}=Lsqrt{1+(frac{displaystyle 2x-a}{displaystyle 2L})^{displaystyle 2}}$ . (3)

Теперь вспомним, что расстояние между источниками много меньше расстояния от источников до экрана: aleq L . Кроме того, в подобных интерференционных опытах координата точки наблюдения также гораздо меньше . Это означает, что второе слагаемое под корнем в выражении (3) много меньше единицы:

$(frac{displaystyle 2x-a}{displaystyle 2L})^{displaystyle 2}leq 1$ .

Раз так, можно использовать приближённую формулу:

$sqrt{1+alpha }=1+frac{displaystyle alpha }{displaystyle 2}, alpha leq 1$ (4)

Применяя её к выражению (4), получим:

$S_{1}P=L(1+frac{1}{2}(frac{displaystyle 2x-a}{displaystyle 2L})^{displaystyle 2})=L+frac{(displaystyle 2x-a)^{displaystyle 2}}{displaystyle 8L}$ (5)

Точно так же вычисляем расстояние, которое проходит волна от источника $S_{2}$ до точки наблюдения:

$S_{2}P=sqrt{displaystyle S_{displaystyle 1}N_{displaystyle 2}^{displaystyle 2}+PN_{displaystyle 2}^{displaystyle 2}}=sqrt{L^{2}+(x+frac{displaystyle a}{displaystyle 2})^{displaystyle 2}}=Lsqrt{1+(frac{displaystyle 2x+a}{displaystyle 2L})^{displaystyle 2}}$ . (6)

Применяя к выражению (6) приближённую формулу (4), получаем:

$S_{2}P=L(1+frac{1}{2}(frac{displaystyle 2x+a}{displaystyle 2L})^{displaystyle 2})=L+frac{(displaystyle 2x+a)^{displaystyle 2}}{displaystyle 8L}$ . (7)

Вычитая выражения (7) и (5), находим разность хода:

$d=S_{2}P-S_{1}P=frac{(displaystyle 2x+a)^{displaystyle 2}-(displaystyle 2x-a)^{displaystyle 2}}{displaystyle 8L}=frac{displaystyle ax}{displaystyle L}$ . (8)

Пусть lambda — длина волны, излучаемой источниками. Согласно условию (1), в точке будет наблюдаться интерференционный максимум, если разность хода равна целому числу длин волн:

$d=frac{displaystyle ax}{displaystyle L}=nlambda (n=0,1,2,3,...).$

Отсюда получаем координаты максимумов в верхней части экрана (в нижней части максимумы идут симметрично):

$displaystyle x_{displaystyle n}=frac{displaystyle nlambda L}{displaystyle a} (n=0,1,2,3,...).$

При n=0 получаем, разумеется, $displaystyle x_{displaystyle n}=0$ (центральный максимум). Первый максимум рядом с центральным соответствует значению n=1 и имеет координату $displaystyle x_{displaystyle 1}=lambda L/a$ .Такой же будет и ширина интерференционной полосы:

$Delta x=displaystyle x_{displaystyle n+1}-displaystyle x_{displaystyle n}=frac{(displaystyle n+displaystyle 1)lambda L}{displaystyle a}-frac{displaystyle nlambda L}{displaystyle a}=frac{displaystyle lambda L}{displaystyle a}$ .

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Интерференция волн.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
07.05.2023

Источник

Интерференция света – явление ослабления или усиления интенсивности света в зависимости от соотношения фаз складываемых световых когерентных волн, линейно поляризованных в одной плоскости. Для уровня школьной физики данное определение является излишним. По умолчанию, световые волны являются когерентными и линейно поляризованными.

Таким образом, для нас в задачах на интерференцию важно наличие нескольких (чаще всего двух) волн и разности фаз (разности хода) между ними.

В школьных задачах на интерференцию основным вопросом является результат интерференции в наблюдаемой точке (усиление или ослабление света).

Для математического описания явления интерференции вводят оптическую длину пути ( displaystyle nr ) — произведение показателя преломления среды, по которой проходит свет, на геометрическую длину пути, которую прошёл луч. Тогда для двух лучей (рис. 1):

$displaystyle delta ={{n}_{1}}{{r}_{1}}-{{n}_{2}}{{r}_{2}}$ (1)

где

Рис. 1. Интерференция

Пусть от точечного источника системой зеркал два луча развели по двум областям с различными показателями преломления ( $displaystyle {{n}_{2}}$ и $displaystyle {{r}_{1}}$ ). Пути лучей в этих системах $displaystyle {{r}_{2}}$ и соответственно. Затем, вышедшие из областей, лучи обратно свели в точку displaystyle S' . За счёт того, что в средах с различным показателем преломления луч от одного и того же источника движется с разной скоростью, к одной и той же точке они приходят с ненулевой разностью хода (1).

Тогда результат интерференции (усиление или ослабление света) диктуется соотношениями:

максимум интерференции (максимальное усиление):

displaystyle delta =mlambda (2)

где
минимум интерференции (максимальное ослабление):

$displaystyle delta =(2m-1)frac{lambda }{2}$ (3)

где

Тогда для ответа на вопрос об усилении и ослаблении света можно анализировать приведённое уравнение (2):

$displaystyle m=frac{delta }{lambda }$ (4)

Тогда, если полученное целое или ближе к целому, то в точке наблюдается усиление света, в случае, если полуцелое или близко к полуцелому, в точке displaystyle S' — темнота.

Вывод: фактически задачи на интерференцию сводятся к анализу уравнения (4) и поиску оптической длины пути для (1).

Пример: Оптическая разность хода волн от двух когерентных источников в некоторой точке пространства $displaystyle {{lambda }_{1}}=671,$ мкм. Каков будет результат интерференции в этой точке, если длина волны будет: $displaystyle {{lambda }_{2}}=406,$ нм, $displaystyle {{lambda }_{2}}=406,$ нм.

Исходя из аналитической формулы (4):

$displaystyle {{m}_{1}}=frac{delta }{{{lambda }_{1}}}=frac{8,723*{{10}^{-6}}}{671*{{10}^{-9}}}=13,00$ (5)

$displaystyle {{m}_{2}}=frac{delta }{{{lambda }_{2}}}=frac{8,723*{{10}^{-6}}}{405*{{10}^{-9}}}approx 21,54$ (6)

Таким образом, получившийся параметр $displaystyle {{m}_{2}}$ получился целым числом, это говорит о том, что при данных параметрах в точке соединения лучей будет наблюдаться усиление света. Параметр $displaystyle {{m}_{2}}$ оказался ближе к полуцелому, таким образом, в исследуемой точке будет наблюдаться ослабление света.

Источник

В нашей традиционной рубрике «Физика для чайников» сегодня решение задач. Тема – интерференция света. Разберем несколько типовых задач и ответим на вопросы.

Хотите читать не только о скучных задачах, но и получать актуальные студенческие новости? Подпишитесь на наш телеграм! А за скидками на услуги и акциями для клиентов добро пожаловать на наш второй канал.

Интерференция света: решение задач

Чтобы решать задачи, сначала нужно изучить теорию. Также мы собрали вместе формулы, которые пригодятся для решения задач по интерференции света, и не только. А тем, кто еще не знает, как вообще подступиться к физическим задачам, рекомендуем почитать общую памятку. А теперь, примеры решения задач по интерференции.

Задача №1 на интерференцию света

Условие

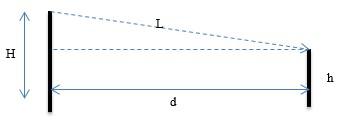
Высота радиомаяка над уровнем моря H = 200 м, расстояние до корабля d = 5,5 км. Определить оптимальную высоту мачты корабля для приема сигналов с длиной волны равной 1,5 м.

Решение

В данном случае волна, исходящая от радиомаяка, интерферирует с волной, отражённой от поверхности воды. Условие m-го максимума:

ym=2m-1dλ4H

Для нахождения оптимальной высоты мачты примем m=1:

y=dλ4H=5500·1,54·200=10,3м

Ответ: 10,3 м.

Задача №2 на интерференцию света

Условие

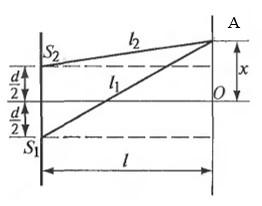
Источник света S с длиной волны 400 нм создает в схеме Юнга два когерентных источника, помещенных в бензол (n = 1,5). В точку А на экране луч от первого источника дошел за t1 =2,0000*10-10 c, а от второго за t2 =2,0002*10-10 c. Определить разность фаз колебаний в точке А и порядок интерференции k.

Решение

Найдем расстояния l1, пройденное лучом:

l1=v·t1=cn·t1l1=3·1081,5·2,0000·10-10=4 см

Найдем расстояние l2:

l2=v·t2=cn·t2l2=3·1081.5·2,0002·10-10=4,0004 см

Таким образом, разность хода составляет:

∆х=0,0004 см=4·10-6 м

Найдем разность фаз:

∆φ=2π∆хλ∆φ=2π·4·10-64·10-7=62,8

Условие максимума для интерференции:

∆φ=±2πk2πk=62,8

В данной точке порядок интерференции k=10.

Ответ: ∆φ=62,8 ; k=10.

Задача №3 на интерференцию света

Условие

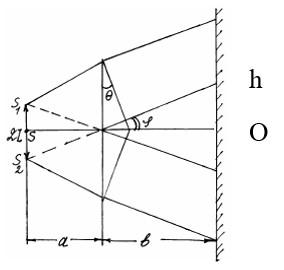
Найти расстояние от точки 0 на экране P в установке бипризмы Френеля до m-ой светлой полосы, если показатель преломления бипризмы n = 1,5, длина волны 500 нм, преломляющий угол альфа = 3 мин.26сек. (m = 6, а = 0,2 м, в = 1 м).

Решение

Условие максимума в данном случае:

∆=mλ

Из рисунка можно получить, что:

h=∆a+b2l=mλa+b2l

где 2l – расстояние между источниками, m-порядковый номер максимума.

Из рисунка:

2l=2a·sinφ=2aφ

Последнее предполоежение сделано вследстиве малости угла.

Тогда получаем:

h=mλa+b2aφ

Связь между преломляющим углом бипризмы Θ и φ определяется известной формулой:

n-1θ=φ

В итоге:

h=mλa+b2an-1θ

Подставляя численные значения получаем:

h=6·5·10-7·0,2+12·0,21,5-1·9,99·10-4=1,8·10-2 м

Ответ: 1,8 см.

Задача №4 на интерференцию света

Условие

На стеклянный клин нормально к поверхности падает пучок света (λ = 582 нм). Угол клина равен 20″. Какое число интерференционных полос приходится на единицу длины клина? Показатель преломления стекла равен 1,5.

Решение

Ширина интерференционных полос при интерференции на прозрачном клине равна:

B=λ2nα=585·10-9·3600·1802·1,5·20·3,14=2·10-3 м

Найдем число интерференционных полос, приходящихся на один сантиметр клина:

N=10-22·10-3=5 см-1

Ответ: 5 полос на сантиметр

Задача №5 на интерференцию света

Условие

Найти радиус кривизны стеклянной плоско-выпуклой линзы, примененной для получения колец Ньютона, если радиус третьего светлого кольца равен 1,4 мм; длина волны 589 нм. Кольца наблюдаются в отраженном свете.

Решение

В отраженном монохроматическом свете радиусы светлых колец равны:

r=2m+1Rλ2

Радиус кривизны линзы R найдем из этой формулы:

R=4r22m+1λ=4·1,4·10-322·3+1·589·10-9=1,9 м

Ответ: 1,9 м.

Нужно больше задач по оптике? У нас есть!

Вопросы на интерференцию света

Вопрос 1. Что такое интерференция?

Ответ. Интерференцией называется постоянное во времени явление взаимного ослабления и усиления колебаний в разных точках среды в следствии наложения когерентных волн.

Вопрос 2. Когда можно наблюдать интерференцию?

Ответ. Это явление наблюдается при наложении двух или нескольких световых пучков. Интенсивность света в области перекрытия пучков имеет характер чередующихся темных и светлых полос, причем в максимумах интенсивность больше, а в минимумах меньше суммы интенсивностей пучков.

Вопрос 3. Приведите примеры интерференции, с которыми мы часто сталкиваемся в жизни.

Ответ. Проявление интерференции света:

цвета масляных пятен и мыльных пузырей на асфальте;
окраска замерзающих оконных стекол;
цветные рисунки на крыльях некоторых жуков и бабочек.

Вопрос 4. Что влияет на интенсивность света в конкретной точке интерференционной картины?

Ответ. Интенсивность света в данной точке пространства определяется разностью фаз колебаний световых волн.

Вопрос 5. Проявлением какой природы света является интерференция: волновой или корпускулярной?

Ответ. Интерференция – проявление исключительно волновой природы.

Проблемы с решением задач? Обращайтесь в профессиональный сервис помощи учащимся в любое время суток!

Источник

«Interference pattern» redirects here. For Moiré patterns, see Moiré pattern.

The interference of two waves. When in phase, the two lower waves create constructive interference (left), resulting in a wave of added amplitude. When 180° out of phase, they create destructive interference (right), resulting in a wave of zero amplitude.

In physics, interference is a phenomenon in which two coherent waves are combined by adding their intensities or displacements with due consideration for their phase difference. The resultant wave may have greater intensity (constructive interference) or lower amplitude (destructive interference) if the two waves are in phase or out of phase, respectively.
Interference effects can be observed with all types of waves, for example, light, radio, acoustic, surface water waves, gravity waves, or matter waves as well as in loudspeakers as electrical waves.

Etymology[edit]

The word interference is derived from the Latin words inter which means «between» and fere which means «hit or strike», and was coined by Thomas Young in 1801.^[1]^[2]^[3]

Mechanisms[edit]

Interference of right traveling (green) and left traveling (blue) waves in Two-dimensional space, resulting in final (red) wave

Interference of waves from two point sources.

Cropped tomography scan animation of laser light interference passing through two pinholes (side edges).

The principle of superposition of waves states that when two or more propagating waves of the same type are incident on the same point, the resultant amplitude at that point is equal to the vector sum of the amplitudes of the individual waves.^[4] If a crest of a wave meets a crest of another wave of the same frequency at the same point, then the amplitude is the sum of the individual amplitudes—this is constructive interference. If a crest of one wave meets a trough of another wave, then the amplitude is equal to the difference in the individual amplitudes—this is known as destructive interference. In ideal mediums (water, air are almost ideal) energy is always conserved, at points of destructive interference energy is stored in the elasticity of the medium. For example when we drop 2 pebbles in a pond we see a pattern but eventually waves continue and only when they reach the shore is energy absorbed away from the medium.

A magnified image of a coloured interference pattern in a soap film. The «black holes» are areas of almost total destructive interference (antiphase).

Constructive interference occurs when the phase difference between the waves is an even multiple of π (180°), whereas destructive interference occurs when the difference is an odd multiple of π. If the difference between the phases is intermediate between these two extremes, then the magnitude of the displacement of the summed waves lies between the minimum and maximum values.

Consider, for example, what happens when two identical stones are dropped into a still pool of water at different locations. Each stone generates a circular wave propagating outwards from the point where the stone was dropped. When the two waves overlap, the net displacement at a particular point is the sum of the displacements of the individual waves. At some points, these will be in phase, and will produce a maximum displacement. In other places, the waves will be in anti-phase, and there will be no net displacement at these points. Thus, parts of the surface will be stationary—these are seen in the figure above and to the right as stationary blue-green lines radiating from the centre.

Interference of light is a unique phenomenon in that we can never observe superposition of the EM field directly as we can for example in water. Superposition in the EM field is an assumed and necessary requirement, fundamentally 2 light beam pass through each other and continue on their respective paths. Light can be explained classically by the superposition of waves, however a deeper understanding of light interference requires knowledge of wave-particle duality of light which is due to quantum mechanics. Prime examples of light interference are the famous double-slit experiment, laser speckle, anti-reflective coatings and interferometers. Traditionally the classical wave model is taught as a basis for understanding optical interference, based on the Huygens–Fresnel principle however an explanation based on the Feynman path integral exists which takes into account quantum mechanical considerations.

Derivation[edit]

The above can be demonstrated in one dimension by deriving the formula for the sum of two waves. The equation for the amplitude of a sinusoidal wave traveling to the right along the x-axis is

${displaystyle W_{1}(x,t)=Acos(kx-omega t)}$

where is the peak amplitude, is the wavenumber and is the angular frequency of the wave. Suppose a second wave of the same frequency and amplitude but with a different phase is also traveling to the right

${displaystyle W_{2}(x,t)=Acos(kx-omega t+varphi )}$

where varphi is the phase difference between the waves in radians. The two waves will superpose and add: the sum of the two waves is

${displaystyle W_{1}+W_{2}=A[cos(kx-omega t)+cos(kx-omega t+varphi )].}$

Using the trigonometric identity for the sum of two cosines: this can be written

${displaystyle W_{1}+W_{2}=2Acos left({varphi over 2}right)cos left(kx-omega t+{varphi over 2}right).}$

This represents a wave at the original frequency, traveling to the right like its components, whose amplitude is proportional to the cosine of .

Between two plane waves[edit]

Geometrical arrangement for two plane wave interference

Interference fringes in overlapping plane waves

A simple form of interference pattern is obtained if two plane waves of the same frequency intersect at an angle.
Interference is essentially an energy redistribution process. The energy which is lost at the destructive interference is regained at the constructive interference.
One wave is travelling horizontally, and the other is travelling downwards at an angle θ to the first wave. Assuming that the two waves are in phase at the point B, then the relative phase changes along the x-axis. The phase difference at the point A is given by

${displaystyle Delta varphi ={frac {2pi d}{lambda }}={frac {2pi xsin theta }{lambda }}.}$

It can be seen that the two waves are in phase when

${displaystyle {frac {xsin theta }{lambda }}=0,pm 1,pm 2,ldots ,}$

and are half a cycle out of phase when

${displaystyle {frac {xsin theta }{lambda }}=pm {frac {1}{2}},pm {frac {3}{2}},ldots }$

Constructive interference occurs when the waves are in phase, and destructive interference when they are half a cycle out of phase. Thus, an interference fringe pattern is produced, where the separation of the maxima is

${displaystyle d_{f}={frac {lambda }{sin theta }}}$

and d_f is known as the fringe spacing. The fringe spacing increases with increase in wavelength, and with decreasing angle θ.

The fringes are observed wherever the two waves overlap and the fringe spacing is uniform throughout.

Between two spherical waves[edit]

Optical interference between two point sources that have different wavelengths and separations of sources.

A point source produces a spherical wave. If the light from two point sources overlaps, the interference pattern maps out the way in which the phase difference between the two waves varies in space. This depends on the wavelength and on the separation of the point sources. The figure to the right shows interference between two spherical waves. The wavelength increases from top to bottom, and the distance between the sources increases from left to right.

When the plane of observation is far enough away, the fringe pattern will be a series of almost straight lines, since the waves will then be almost planar.

Multiple beams[edit]

Interference occurs when several waves are added together provided that the phase differences between them remain constant over the observation time.

It is sometimes desirable for several waves of the same frequency and amplitude to sum to zero (that is, interfere destructively, cancel). This is the principle behind, for example, 3-phase power and the diffraction grating. In both of these cases, the result is achieved by uniform spacing of the phases.

It is easy to see that a set of waves will cancel if they have the same amplitude and their phases are spaced equally in angle. Using phasors, each wave can be represented as $A e^{i varphi_n}$ for waves from n=0 to n = N-1 , where

${displaystyle varphi _{n}-varphi _{n-1}={frac {2pi }{N}}.}$

To show that

${displaystyle sum _{n=0}^{N-1}Ae^{ivarphi _{n}}=0}$

one merely assumes the converse, then multiplies both sides by ${displaystyle e^{i{frac {2pi }{N}}}.}$

The Fabry–Pérot interferometer uses interference between multiple reflections.

A diffraction grating can be considered to be a multiple-beam interferometer; since the peaks which it produces are generated by interference between the light transmitted by each of the elements in the grating; see interference vs. diffraction for further discussion.

Optical interference[edit]

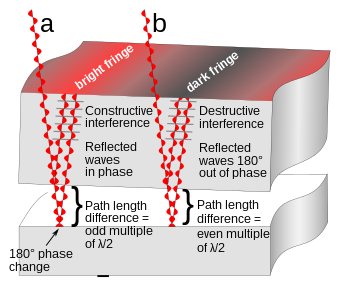
Creation of interference fringes by an optical flat on a reflective surface. Light rays from a monochromatic source pass through the glass and reflect off both the bottom surface of the flat and the supporting surface. The tiny gap between the surfaces means the two reflected rays have different path lengths. In addition the ray reflected from the bottom plate undergoes a 180° phase reversal. As a result, at locations (a) where the path difference is an odd multiple of λ/2, the waves reinforce. At locations (b) where the path difference is an even multiple of λ/2 the waves cancel. Since the gap between the surfaces varies slightly in width at different points, a series of alternating bright and dark bands, interference fringes, are seen.

Because the frequency of light waves (~10¹⁴ Hz) is too high for currently available detectors to detect the variation of the electric field of the light, it is possible to observe only the intensity of an optical interference pattern. The intensity of the light at a given point is proportional to the square of the average amplitude of the wave. This can be expressed mathematically as follows. The displacement of the two waves at a point r is:

${displaystyle U_{1}(mathbf {r} ,t)=A_{1}(mathbf {r} )e^{i[varphi _{1}(mathbf {r} )-omega t]}}$

${displaystyle U_{2}(mathbf {r} ,t)=A_{2}(mathbf {r} )e^{i[varphi _{2}(mathbf {r} )-omega t]}}$

where A represents the magnitude of the displacement, φ represents the phase and ω represents the angular frequency.

The displacement of the summed waves is

${displaystyle U(mathbf {r} ,t)=A_{1}(mathbf {r} )e^{i[varphi _{1}(mathbf {r} )-omega t]}+A_{2}(mathbf {r} )e^{i[varphi _{2}(mathbf {r} )-omega t]}.}$

The intensity of the light at r is given by

${displaystyle I(mathbf {r} )=int U(mathbf {r} ,t)U^{*}(mathbf {r} ,t),dtpropto A_{1}^{2}(mathbf {r} )+A_{2}^{2}(mathbf {r} )+2A_{1}(mathbf {r} )A_{2}(mathbf {r} )cos[varphi _{1}(mathbf {r} )-varphi _{2}(mathbf {r} )].}$

This can be expressed in terms of the intensities of the individual waves as

${displaystyle I(mathbf {r} )=I_{1}(mathbf {r} )+I_{2}(mathbf {r} )+2{sqrt {I_{1}(mathbf {r} )I_{2}(mathbf {r} )}}cos[varphi _{1}(mathbf {r} )-varphi _{2}(mathbf {r} )].}$

Thus, the interference pattern maps out the difference in phase between the two waves, with maxima occurring when the phase difference is a multiple of 2π. If the two beams are of equal intensity, the maxima are four times as bright as the individual beams, and the minima have zero intensity.

Classically the two waves must have the same polarization to give rise to interference fringes since it is not possible for waves of different polarizations to cancel one another out or add together. Instead, when waves of different polarization are added together, they give rise to a wave of a different polarization state.

Quantum mechanically the theories of Paul Dirac and Richard Feynman offer a more modern approach. Dirac showed that every quanta or photon of light acts on its own which he famously stated as «every photon interferes with itself». Richard Feynman showed that by evaluating a path integral where all possible paths are considered, that a number of higher probability paths will emerge. In thin films for example, film thickness which is not a multiple of light wavelength will not allow the quanta to traverse, only reflection is possible.

Light source requirements[edit]

The discussion above assumes that the waves which interfere with one another are monochromatic, i.e. have a single frequency—this requires that they are infinite in time. This is not, however, either practical or necessary. Two identical waves of finite duration whose frequency is fixed over that period will give rise to an interference pattern while they overlap. Two identical waves which consist of a narrow spectrum of frequency waves of finite duration (but shorter than their coherence time), will give a series of fringe patterns of slightly differing spacings, and provided the spread of spacings is significantly less than the average fringe spacing, a fringe pattern will again be observed during the time when the two waves overlap.

Conventional light sources emit waves of differing frequencies and at different times from different points in the source. If the light is split into two waves and then re-combined, each individual light wave may generate an interference pattern with its other half, but the individual fringe patterns generated will have different phases and spacings, and normally no overall fringe pattern will be observable. However, single-element light sources, such as sodium- or mercury-vapor lamps have emission lines with quite narrow frequency spectra. When these are spatially and colour filtered, and then split into two waves, they can be superimposed to generate interference fringes.^[5] All interferometry prior to the invention of the laser was done using such sources and had a wide range of successful applications.

A laser beam generally approximates much more closely to a monochromatic source, and thus it is much more straightforward to generate interference fringes using a laser. The ease with which interference fringes can be observed with a laser beam can sometimes cause problems in that stray reflections may give spurious interference fringes which can result in errors.

Normally, a single laser beam is used in interferometry, though interference has been observed using two independent lasers whose frequencies were sufficiently matched to satisfy the phase requirements.^[6]
This has also been observed for widefield interference between two incoherent laser sources.^[7]

It is also possible to observe interference fringes using white light. A white light fringe pattern can be considered to be made up of a ‘spectrum’ of fringe patterns each of slightly different spacing. If all the fringe patterns are in phase in the centre, then the fringes will increase in size as the wavelength decreases and the summed intensity will show three to four fringes of varying colour. Young describes this very elegantly in his discussion of two slit interference. Since white light fringes are obtained only when the two waves have travelled equal distances from the light source, they can be very useful in interferometry, as they allow the zero path difference fringe to be identified.^[8]

Optical arrangements[edit]

To generate interference fringes, light from the source has to be divided into two waves which then have to be re-combined. Traditionally, interferometers have been classified as either amplitude-division or wavefront-division systems.

In an amplitude-division system, a beam splitter is used to divide the light into two beams travelling in different directions, which are then superimposed to produce the interference pattern. The Michelson interferometer and the Mach–Zehnder interferometer are examples of amplitude-division systems.

In wavefront-division systems, the wave is divided in space—examples are Young’s double slit interferometer and Lloyd’s mirror.

Interference can also be seen in everyday phenomena such as iridescence and structural coloration. For example, the colours seen in a soap bubble arise from interference of light reflecting off the front and back surfaces of the thin soap film. Depending on the thickness of the film, different colours interfere constructively and destructively.

Applications[edit]

Beat[edit]

In acoustics, a beat is an interference pattern between two sounds of slightly different frequencies, perceived as a periodic variation in volume whose rate is the difference of the two frequencies.

With tuning instruments that can produce sustained tones, beats can be readily recognized. Tuning two tones to a unison will present a peculiar effect: when the two tones are close in pitch but not identical, the difference in frequency generates the beating. The volume varies like in a tremolo as the sounds alternately interfere constructively and destructively. As the two tones gradually approach unison, the beating slows down and may become so slow as to be imperceptible. As the two tones get further apart, their beat frequency starts to approach the range of human pitch perception,^[9] the beating starts to sound like a note, and a combination tone is produced. This combination tone can also be referred to as a missing fundamental, as the beat frequency of any two tones is equivalent to the frequency of their implied fundamental frequency.

Optical interferometry[edit]

Interferometry has played an important role in the advancement of physics, and also has a wide range of applications in physical and engineering measurement.

Thomas Young’s double slit interferometer in 1803 demonstrated interference fringes when two small holes were illuminated by light from another small hole which was illuminated by sunlight. Young was able to estimate the wavelength of different colours in the spectrum from the spacing of the fringes. The experiment played a major role in the general acceptance of the wave theory of light.^[8]
In quantum mechanics, this experiment is considered to demonstrate the inseparability of the wave and particle natures of light and other quantum particles (wave–particle duality). Richard Feynman was fond of saying that all of quantum mechanics can be gleaned from carefully thinking through the implications of this single experiment.^[10]

The results of the Michelson–Morley experiment are generally considered to be the first strong evidence against the theory of a luminiferous aether and in favor of special relativity.

Interferometry has been used in defining and calibrating length standards. When the metre was defined as the distance between two marks on a platinum-iridium bar, Michelson and Benoît used interferometry to measure the wavelength of the red cadmium line in the new standard, and also showed that it could be used as a length standard. Sixty years later, in 1960, the metre in the new SI system was defined to be equal to 1,650,763.73 wavelengths of the orange-red emission line in the electromagnetic spectrum of the krypton-86 atom in a vacuum. This definition was replaced in 1983 by defining the metre as the distance travelled by light in vacuum during a specific time interval. Interferometry is still fundamental in establishing the calibration chain in length measurement.

Interferometry is used in the calibration of slip gauges (called gauge blocks in the US) and in coordinate-measuring machines. It is also used in the testing of optical components.^[11]

Radio interferometry[edit]

In 1946, a technique called astronomical interferometry was developed. Astronomical radio interferometers usually consist either of arrays of parabolic dishes or two-dimensional arrays of omni-directional antennas. All of the telescopes in the array are widely separated and are usually connected together using coaxial cable, waveguide, optical fiber, or other type of transmission line. Interferometry increases the total signal collected, but its primary purpose is to vastly increase the resolution through a process called Aperture synthesis. This technique works by superposing (interfering) the signal waves from the different telescopes on the principle that waves that coincide with the same phase will add to each other while two waves that have opposite phases will cancel each other out. This creates a combined telescope that is equivalent in resolution (though not in sensitivity) to a single antenna whose diameter is equal to the spacing of the antennas farthest apart in the array.

Acoustic interferometry[edit]

An acoustic interferometer is an instrument for measuring the physical characteristics of sound waves in a gas or liquid, such velocity, wavelength, absorption, or impedance. A vibrating crystal creates ultrasonic waves that are radiated into the medium. The waves strike a reflector placed parallel to the crystal, reflected back to the source and measured.

Quantum interference[edit]

Quantum interference is quite different from the classical wave interference described above. Below, an enumeration of the important differences is provided. Quantum interference is, however, similar to optical interference.

Let be a wavefunction solution of the Schrödinger equation for a quantum mechanical object. Then the probability P(x) of observing the object at position is ${displaystyle P(x)=|Psi (x,t)|^{2}=Psi ^{*}(x,t)Psi (x,t)}$ where * indicates complex conjugation. Quantum interference concerns the issue of this probability when the wavefunction is expressed as a sum or linear superposition of two terms ${displaystyle Psi (x,t)=Psi _{A}(x,t)+Psi _{B}(x,t)}$ :

${displaystyle P(x)=|Psi (x,t)|^{2}=|Psi _{A}(x,t)|^{2}+|Psi _{B}(x,t)|^{2}+(Psi _{A}^{*}(x,t)Psi _{B}(x,t)+Psi _{A}(x,t)Psi _{B}^{*}(x,t))}$

Usually, ${displaystyle Psi _{A}(x,t)}$ and ${displaystyle Psi _{B}(x,t)}$ correspond to distinct situations A and B. When this is the case, the equation ${displaystyle Psi (x,t)=Psi _{A}(x,t)+Psi _{B}(x,t)}$ indicates that the object can be in situation A or situation B. The above equation can then be interpreted as: The probability of finding the object at is the probability of finding the object at when it is in situation A plus the probability of finding the object at when it is in situation B plus an extra term. This extra term, which is called the quantum interference term, is ${displaystyle Psi _{A}^{*}(x,t)Psi _{B}(x,t)+Psi _{A}(x,t)Psi _{B}^{*}(x,t)}$ in the above equation. As in the classical wave case above, the quantum interference term can add (constructive interference) or subtract (destructive interference) from ${displaystyle |Psi _{A}(x,t)|^{2}+|Psi _{B}(x,t)|^{2}}$ in the above equation depending on whether the quantum interference term is positive or negative. If this term is absent for all , then there is no quantum mechanical interference associated with situations A and B.

The best known example of quantum interference is the double-slit experiment. In this experiment, electrons, atoms or other quantum mechanical objects approach a barrier with two slits in it. If the quantum object succeeds in passing through the slits, its position is measured with a detection screen a certain distance beyond and behind the barrier. For this system, one lets ${displaystyle Psi _{A}(x,t)}$ be that part of the wavefunction that passes through one of the slits and lets ${displaystyle Psi _{B}(x,t)}$ be that part of the wavefunction that passes through the other slit. When the object almost reaches the screen, the probability of where it is located is given by the above equation. In this context, the equation says that the probability of finding the object at some point just before it hits the screen is the probability that would be obtained if it went through the first slit plus the probability that would be obtained if it went through the second slit plus the quantum interference term, which has no counterpart in classical physics. The quantum interference term can significantly change the pattern observed on the detection screen.

The separation of ${displaystyle Psi _{A}(x,t)+Psi _{B}(x,t)}$ is particularly clear in the path integral formulation of quantum mechanics in the context of the double-slit experiment. ${displaystyle Psi _{A}(x,t)}$ consists of the path integral contributions in which the paths pass through the first slit; ${displaystyle Psi _{B}(x,t)}$ consists of the path integral contributions in which they pass through the second slit.

Here is a list of some of the differences between classical wave interference and quantum interference:

In classical interference, two different waves interfere; In quantum interference, the wavefunction interferes with itself.
Classical interference is obtained simply by adding the displacements from equilibrium (or amplitudes) of the two waves; In quantum interference, the effect occurs for the probability function associated with the wavefunction and therefore the modulus of the wavefunction squared.
The interference involves different types of mathematical functions: A classical wave is a real function representing the displacement from an equilibrium position; a quantum wavefunction is a complex function. A classical wave at any point can be positive or negative; the quantum probability function is non-negative.
In classical optical interference the energy conservation principle is violated as it requires quanta to cancel. In quantum interference energy conservation is not violated, the quanta merely assume paths per the path integral. All quanta for example terminate in bright areas of the pattern.

References[edit]

^ On the mechanism of the eye / by Thomas Young.; Young, Thomas; University College, London Library Services (1801). Young, Thomas, 1773-1829. University College London (UCL) UCL Library Services. London : printed by W. Bulmer and Co., Cleveland Row, St. James’s.
^ Jones, Peter Ward (2001). Oxford University Press. Oxford Music Online. Oxford University Press. doi:10.1093/gmo/9781561592630.article.20622.
^ Kipnis, Nahum (1991). History of the Principle of Interference of Light. doi:10.1007/978-3-0348-8652-9. ISBN 978-3-0348-9717-4.
^ Ockenga, Wymke. Phase contrast. Leika Science Lab, 09 June 2011. «If two waves interfere, the amplitude of the resulting light wave will be equal to the vector sum of the amplitudes of the two interfering waves.»
^ Steel, W. H. (1986). Interferometry. Cambridge: Cambridge University Press. ISBN 0-521-31162-4.
^ Pfleegor, R. L.; Mandel, L. (1967). «Interference of independent photon beams». Phys. Rev. 159 (5): 1084–1088. Bibcode:1967PhRv..159.1084P. doi:10.1103/physrev.159.1084.
^ Patel, R.; Achamfuo-Yeboah, S.; Light R.; Clark M. (2014). «Widefield two laser interferometry». Optics Express. 22 (22): 27094–27101. Bibcode:2014OExpr..2227094P. doi:10.1364/OE.22.027094. PMID 25401860.
^ ^a ^b Born, Max; Wolf, Emil (1999). Principles of Optics. Cambridge: Cambridge University Press. ISBN 0-521-64222-1.
^ Levitin, Daniel J. (2006). This is Your Brain on Music: The Science of a Human Obsession. Dutton. p. 22. ISBN 978-0525949695.
^ Greene, Brian (1999). The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory. New York: W.W. Norton. pp. 97–109. ISBN 978-0-393-04688-5.
^ RS Longhurst, Geometrical and Physical Optics, 1968, Longmans, London.

External links[edit]

Easy JavaScript Simulation Model of One Dimensional Wave Interference
Expressions of position and fringe spacing
Java simulation of interference of water waves 1
Java simulation of interference of water waves 2
Flash animations demonstrating interference

Источник

Интерференция

Подробности: Категория: Оптика

Необходимы более веские доказательства того, что свет при распространении ведет себя как волна. Любому волновому движению присущи явления интерференции и дифракции. Для того чтобы быть уверенным в том, что свет имеет волновую природу, необходимо найти экспериментальные доказательства интерференции и дифракции света.

Интерференция — достаточно сложное явление . Чтобы лучше понять его суть, мы вначале остановимся на интерференции механических волн.

Сложение волн. Очень часто в среде одновременно распространяется несколько различных волн. Например, когда в комнате беседуют несколько человек, то звуковые волны накладываются друг на друга. Что при этом происходит?

Проще всего проследить за наложением механических волн, наблюдая волны на поверхности воды. Если мы бросим в воду два камня, создав этим две кольцевые волны, то нетрудно заметить, что каждая волна проходит сквозь другую и ведет себя в дальнейшем так, как будто бы другой волны совсем не существовало. Точно так же любое число звуковых волн может одновременно распространяться в воздухе, ничуть не мешая друг другу. Множество музыкальных инструментов в оркестре или голосов в хоре создают звуковые волны, одновременно улавливаемые нашим ухом. Причем ухо в состоянии отличить один звук от другого.

Теперь посмотрим более внимательно, что происходит в местах, где волны накладываются друг на друга. Наблюдая волны на поверхности воды от двух брошенных в воду камней, можно заметить, что некоторые участки поверхности не возмущены, в других же местах возмущение усилилось. Если две волны встречаются в одном месте гребнями, то в этом месте возмущение поверхности воды усиливается.

Если же, напротив, гребень одной волны встречается с впадиной другой, то поверхность воды не будет возмущена.

Вообще же в каждой точке среды колебания, вызванные двумя волнами, просто складываются. Результирующее смещение любой частицы среды представляет собой алгебраическую (т. е. с учетом их знаков) сумму смещений, которые происходили бы при распространении одной из волн в отсутствие другой.

Интерференция. Сложение в пространстве волн, при котором образуется постоянное во времени распределение амплитуд результирующих колебаний, называется интерференцией.

Выясним, при каких условиях имеет место интерференция волн. Для этого рассмотрим более подробно сложение волн, образуемых на поверхности воды.

Можно одновременно возбудить две круговые волны в ванне с помощью двух шариков, укрепленных на стержне, который совершает гармонические колебания (рис. 118). В любой точке М на поверхности воды (рис. 119) будут складываться колебания, вызванные двумя волнами (от источников O₁ и О₂). Амплитуды колебаний, вызванных в точке М обеими волнами, будут, вообще говоря, отличаться, так как волны проходят различные пути d₁ и d₂. Но если расстояние l между источниками много меньше этих путей (l « d₁ и l « d₂ ) , то обе амплитуды
можно считать практически одинаковыми.

Результат сложения волн, приходящих в точку M, зависит от разности фаз между ними. Пройдя различные расстояния d₁ и d₂, волны имеют разность хода Δd = d₂—d₁. Если разность хода равна длине волны λ, то вторая волна запаздывает по сравнению с первой ровно на один период (как раз за период волна проходит путь, равный длине волны). Следовательно, в этом случае гребни (как и впадины) обеих волн совпадают.

Условие максимумов. На рисунке 120 изображена зависимость от времени смещений X₁ и X₂ , вызванных двумя волнами при Δd= λ. Разность фаз колебаний равна нулю (или, что то же самое, 2л, так как период синуса равен 2п). В результате сложения этих колебаний возникает результирующее колебание с удвоенной амплитудой. Колебания результирующего смещения на рисунке показаны цветом (пунктир). То же самое будет происходить, если на отрезке Δd укладывается не одна, а любое целое число длин волн.

Амплитуда колебаний среды в данной точке максимальна, если разность хода двух волн, возбуждающих колебания в этой точке, равна целому числу длин волн:

Δd=κλ

где к=0,1,2,….

Условие минимумов. Пусть теперь на отрезке Δd укладывается половина длины волны. Очевидно, что при этом вторая волна отстает от первой на половину периода. Разность фаз оказывается равной п, т. е. колебания будут происходить в противофазе. В результате сложения этих колебаний амплитуда результирующего колебания равна нулю, т. е. в рассматриваемой точке колебаний нет (рис. 121). То же самое произойдет, если на отрезке укладывается любое нечетное число полуволн.

Амплитуда колебаний среды в данной точке минимальна, если разность хода двух волн, возбуждающих колебания в этой точке, равна нечетному числу полуволн:

Δd=(2к+1)λ/2

Если разность хода d₂ — d₁ принимает промежуточное значение
между λ и λ/2 , то и амплитуда результирующего колебания принимает некоторое промежуточное значение между удвоенной амплитудой и нулем. Но наиболее важно то, что Амплитуда колебаний в любой точке he меняется с течением времени. На поверхности воды возникает определенное, неизменное во времени распределение амплитуд колебаний, которое называют интерференционной картиной. На рисунке 122 показан рисунок с фотографии интерференционной картины двух круговых волн от двух источников (черные кружки). Белые участки в средней части фотографии соответствуют максимумам колебаний, а темные — минимумам.

Когерентные волны. Для образования устойчивой интерференционной картины необходимо, чтобы источники волн имели одинаковую частоту и разность фаз их колебаний была постоянной.

Источники, удовлетворяющие этим условиям, называются когерентными. Когерентными называют и созданные ими волны. Только при сложении когерентных волн образуется устойчивая интерференционная картина.

Если же разность фаз колебаний источников не остается постоянной, то в любой точке среды разность фаз колебаний, возбуждаемых двумя волнами, будет меняться. Поэтому амплитуда результирующих колебаний с течением времени изменяется. В результате максимумы и минимумы перемещаются в пространстве и интерференционная картина размывается.

Распределение энергии при интерференции. Волны несут энергию. Что же с этой энергией происходит при гашении волн друг другом? Может быть, она превращается в другие формы и в минимумах интерференционной картины выделяется тепло? Ничего подобного. Наличие минимума в данной точке интерференционной картины означает, что энергия сюда не поступает совсем. Вследствие интерференции происходит перераспределение энергии в пространстве. Она не распределяется равномерно по всем частицам среды, а концентрируется в максимумах за счет того, что в минимумы не поступает совсем.

ИНТЕРФЕРЕНЦИЯ СВЕТОВЫХ ВОЛН

Если свет представляет собой поток волн, то должно наблюдаться явление интерференции света. Однако получить интерференционную картину (чередование максимумов и минимумов освещенности) с помощью двух независимых источников света, например двух электрических лампочек, невозможно. Включение еще одной лампочки лишь увеличивает освещенность поверхности, но не создает чередования минимумов и максимумов освещенности.

Выясним, в чем причина этого и при каких условиях можно наблюдать интерференцию света.

Условие когерентности световых волн. Причина состоит в том, что световые волны, излучаемые различными источниками, не согласованы друг с другом. Для получения же устойчивой интерференционной картины нужны согласованные волны. Они должны иметь одинаковые длины волн и постоянную разность фаз в любой точке пространства. Напомним, что такие согласованные волны с одинаковыми длинами волн и постоянной разностью фаз называются когерентными.

Почти точного равенства длин волн от двух источников добиться нетрудно. Для этого достаточно использовать хорошие светофильтры, пропускающие свет в очень узком интервале длин волн. Но невозможно осуществить Постоянство разности фаз от двух независимых источников. Атомы источников излучают свет независимо друг от друга отдельными «обрывками» (цугами) синусоидальных волн, имеющими длину около метра. И такие цуги волн от обоих источников налагаются друг на друга. В результате амплитуда колебаний в любой точке пространства хаотически меняется со временем в зависимости от того, как в данный момент времени цуги волн от различных источников сдвинуты друг относительно друга по фазе. Волны от различных источников света некогерентны из-за того, что разность фаз волн не остается постоянной. Никакой устойчивой картины с определенным распределением максимумов и минимумов освещенности в пространстве не наблюдается.

Интерференция в тонких пленках. Тем не менее интерференцию света удается наблюдать. Курьез состоит в том, что ее наблюдали очень давно, но только не отдавали себе в этом отчета.

Вы тоже много раз видели интерференционную картину, когда в детстве развлекались пусканием мыльных пузырей или наблюдали за радужным переливом цветов тонкой пленки керосина или нефти на поверхности воды. «Мыльный пузырь, витая в воздухе… зажигается всеми оттенками цветов, присущими окружающим предметам. Мыльный пузырь, пожалуй, самое изысканное чудо природы» (Марк Твен). Именно интерференция света делает мыльный пузырь столь достойным восхищения.

Английский ученый Томас Юнг первым пришел к гениальной мысли о возможности объяснения цветов тонких пленок сложением волн 1 и 2 (рис. 123), одна из которых (1) отражается от наружной поверхности пленки, а вторая (2) —от внутренней. При этом происходит интерференция световых волн — сложение двух волн, вследствие которого наблюдается устойчивая во времени картина усиления или ослабления результирующих световых колебаний в различных точках пространства. Результат интерференции (усиление или ослабление результирующих колебаний) зависит от угла падения света на пленку, ее толщины и длины волны. Усиление света произойдет в том случае, если преломленная волна 2 отстанет от отраженной волны 1 на целое число длин волн. Если же вторая волна отстанет от первой на половину длины волны или на нечетное число полуволн, то произойдет ослабление света.

Когерентность волн, отраженных от наружной и внутренней поверхностей пленки, обеспечивается тем, что они являются частями одного и того же светового пучка. Цуг волн от каждого излучающего атома разделяется пленкой на два, а затем эти части сводятся вместе и интерферируют.

Юнг также понял, что различие в цвете связано с различием в длине волны (или частоте световых волн). Световым пучкам различного цвета соответствуют волны различной длины. Для взаимного усиления волн, отличающихся друг от друга длиной (углы падения предполагаются одинаковыми), требуется различная толщина пленки. Следовательно, если пленка имеет неодинаковую толщину, то при освещении ее белым светом должны появиться различные цвета.

Кольца Ньютона. Простая интерференционная картина возникает в тонкой прослойке воздуха между стеклянной пластиной и положенной на нее плоско-выпуклой линзой, сферическая поверхность которой имеет большой радиус кривизны. Эта интерференционная картина имеет вид концентрических колец, получивших название кольца Ньютона.

Возьмите плоско-выпуклую линзу с малой кривизной сферической поверхности и положите ее на стеклянную пластину. Внимательно разглядывая плоскую поверхность линзы (лучше через лупу), вы обнаружите в месте соприкосновения линзы и пластины темное пятно и вокруг него совокупность маленьких радужных колец. Расстояния между соседними кольцами быстро убывают с увеличением их радиуса (рис.111). Это и есть кольца Ньютона. Ньютон наблюдал и исследовал их не только в белом свете, но и при освещении линзы одноцветным (монохроматическим) пучком. Оказалось, что радиусы колец одного и того же порядкового номера увеличиваются при переходе от фиолетового конца спектра к красному; красные кольца имеют максимальный радиус . Все это вы можете проверить с помощью самостоятельных наблюдений.

Удовлетворительно объяснить, почему возникают кольца, Ньютон не смог. Удалось это Юнгу. Проследим за ходом его рассуждений. В их основе лежит предположение о том, что свет — это волны. Рассмотрим случай, когда волна определенной длины падает почти перпендикулярно на плоско-выпуклую линзу (рис. 124). Волна 1 появляется в результате отражения от выпуклой поверхности линзы на границе стекло — воздух, а волна 2 — в результате отражения от пластины на границе воздух — стекло. Эти волны когерентны: они имеют одинаковую длину и постоянную разность фаз, которая возникает из-за того, что волна 2 проходит больший путь, чем волна 1. Если вторая волна отстает от первой на целое число длин волн, то, складываясь, волны усиливают друг друга. Вызываемые ими колебания происходят в одной фазе.

Напротив, если вторая волна отстает от первой на нечетное число полуволн, то колебания, вызванные ими, будут происходить в противоположных фазах и волны гасят друг друга.

Если известен радиус кривизны R поверхности линзы, то можно вычислить, на каких расстояниях от точки соприкосновения линзы со стеклянной пластиной разности хода таковы, что волны определенной длины λ гасят друг друга. Эти расстояния и являются радиусами темных колец Ньютона. Ведь линии постоянной толщины воздушной прослойки представляют собой окружности. Измерив радиусы колец, можно вычислить длины волн.

Длина световой волны. Для красного света измерения дают λ_кр = 8•10^-7 м, а для фиолетового — λ_ф = 4•10^-7 м. Длины волн, соответствующие другим цветам спектра, принимают промежуточные значения. Для любого цвета длина световой волны очень мала. Представьте себе среднюю морскую волну длиной в несколько метров, которая увеличилась настолько, что заняла весь Атлантический океан от берегов Америки до Европы. Длина световой волны в том же увеличении лишь ненамного превысила бы ширину этой страницы.

Явление интерференции не только доказывает наличие у света волновых свойств, но и позволяет измерить длину волны. Подобно тому как высота звука определяется его частотой, цвет света определяется частотой колебаний или длиной волны.

Вне нас в природе нет никаких красок, есть лишь волны разной длины. Глаз — сложный физический прибор, способный обнаруживать различие в цвете, которому соответствует весьма незначительная (около 10^-6 см) разница в длине световых волн. Интересно, что большинство животных неспособны различать цвета. Они всегда видят чернобелую картину. Не различают цвета также дальтоники — люди, страдающие цветовой слепотой.

При переходе света из одной среды в другую длина волны изменяется. Это можно обнаружить так. Заполним водой или другой прозрачной жидкостью с показателем преломления п воздушную прослойку между линзой и пластиной. Радиусы интерференционных колец уменьшатся.

Почему это происходит? Мы знаем, что при переходе света из вакуума в какую-нибудь среду скорость света уменьшается в n раз. Так как v = λv, то при этом должна уменьшиться в n раз либо частота, либо длина волны. Но радиусы колец зависят от длины волны. Следовательно, когда свет входит в среду, изменяется в n раз именно длина волны, а не частота.

Интерференция электромагнитных волн. На опытах с генератором СВЧ можно наблюдать интерференцию электромагнитных (радио) волн.

Генератор и приемник располагают друг против друга (рис. 125). Затем подводят снизу металлическую пластину в горизонтальном положении. Постепенно поднимая пластину, обнаруживают поочередное ослабление и усиление звука.

Явление объясняется следующим образом. Часть волны из рупора генератора непосредственно попадает в приемный рупор. Другая же ее часть отражается от металлической пластины. Меняя расположение пластины, мы изменяем разность хода прямой и отраженной волн. Вследствие этого волны либо усиливают, либо ослабляют друг друга в зависимости от того, равна ли разность хода целому числу длин волн или нечетному числу полуволн.

Наблюдение интерференции света доказывает, что свет при распространении обнаруживает волновые свойства. Интерференционные опыты позволяют измерить длину световой волны: она очень мала—от 4•10^-7 до 8•10^-7 м.

Интерференция двух волн. Бипризма Френеля — 1

Интерференция двух волн. Бипризма Френеля — 2

Интерферометр Маха-Цандера: его устройство

Интерферометр Маха-Цандера. Поворот стеклянной пластинки

Интерферометр Маха-Цандера. «Деформация» основания»

Стоячие трехсантиметровые волны

Трехсантиметровые волны: стоячие волны в резонаторе

Дециметровая стоячая волна

«Стоячая волна» на экране осциллографа

Поперечные стоячие волны на линейке со свободным концом

Поперечные стоячие волны на резиновом шнуре

Поперечные стоячие волны на проводе с переменным током

Настройщик фортепиано и другие

Поющая Труба

Источник

Интерференция волн.

Сложение колебаний.

Когерентные источники.

Условие максимума и минимума.

Интерференционная картина.

Интерференция света: решение задач

Задача №1 на интерференцию света

Задача №2 на интерференцию света

Задача №3 на интерференцию света

Задача №4 на интерференцию света

Задача №5 на интерференцию света

Вопросы на интерференцию света

Etymology[edit]

Mechanisms[edit]

Derivation[edit]

Between two plane waves[edit]

Between two spherical waves[edit]

Multiple beams[edit]

Optical interference[edit]

Light source requirements[edit]

Optical arrangements[edit]

Applications[edit]

Beat[edit]

Optical interferometry[edit]

Radio interferometry[edit]

Acoustic interferometry[edit]

Quantum interference[edit]

See also[edit]

References[edit]

External links[edit]

Интерференция

ИНТЕРФЕРЕНЦИЯ СВЕТОВЫХ ВОЛН