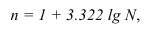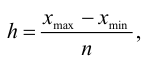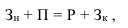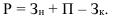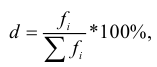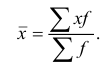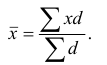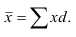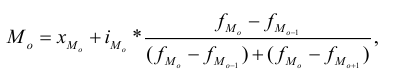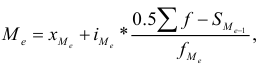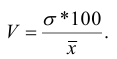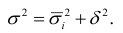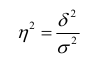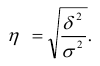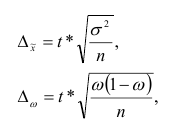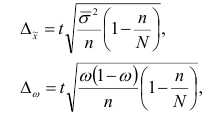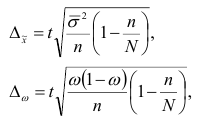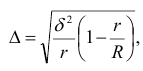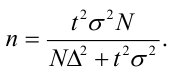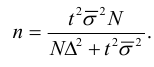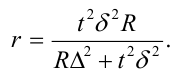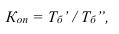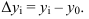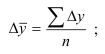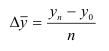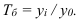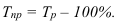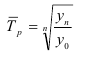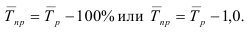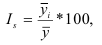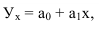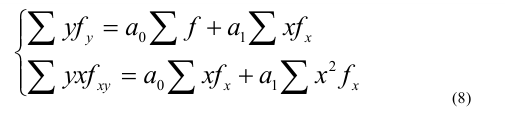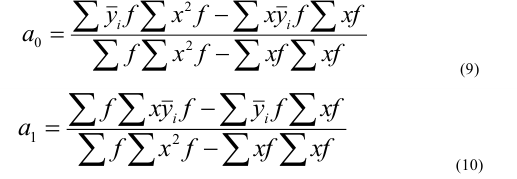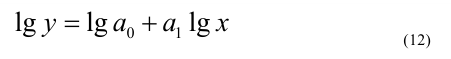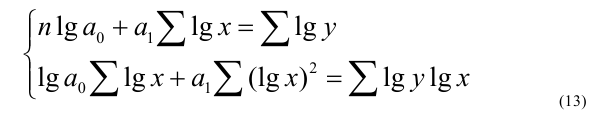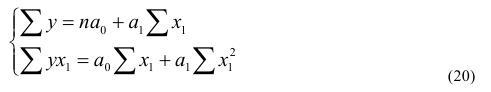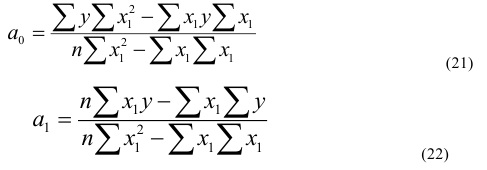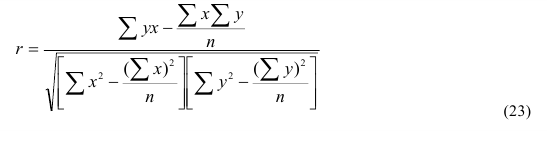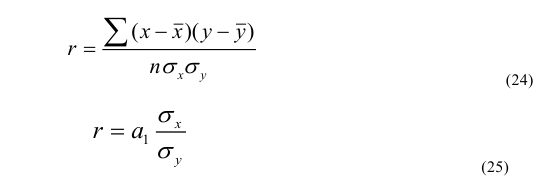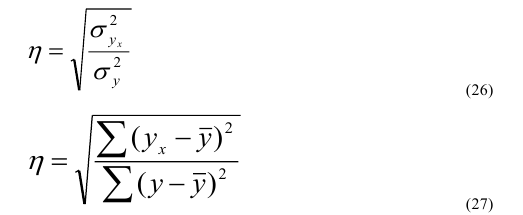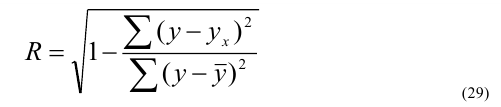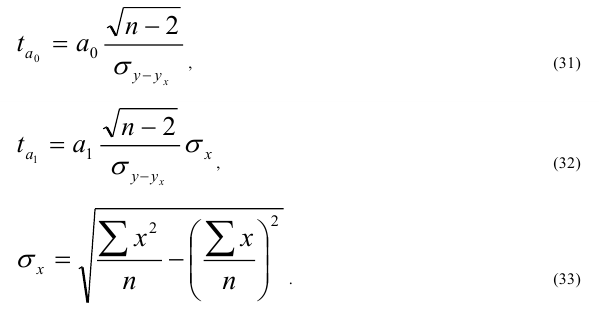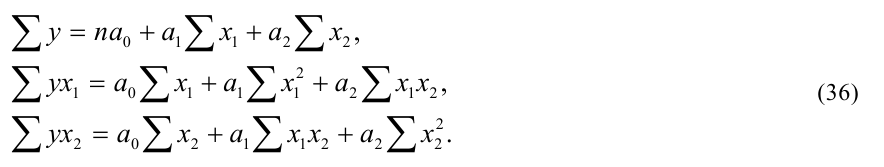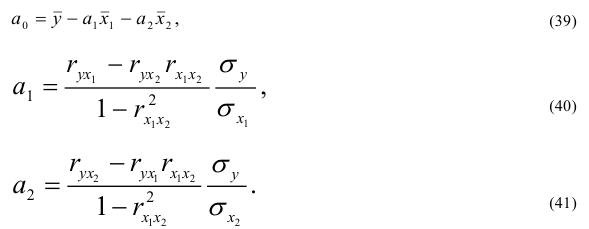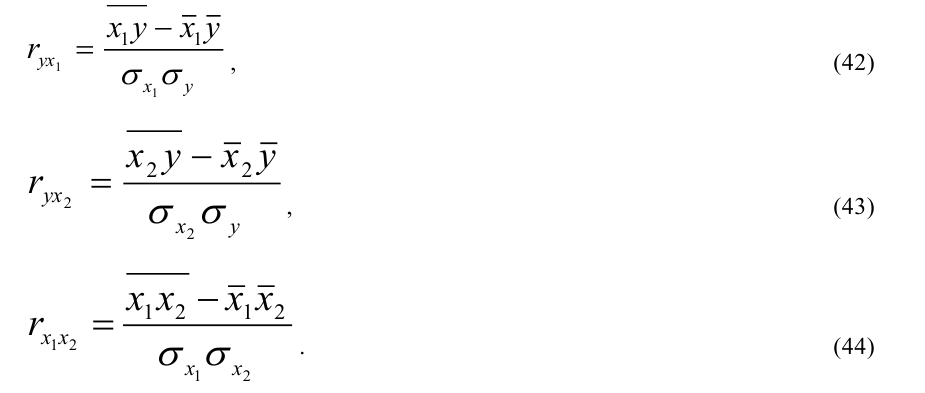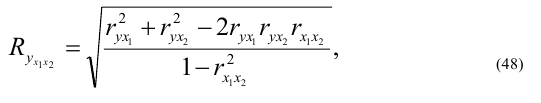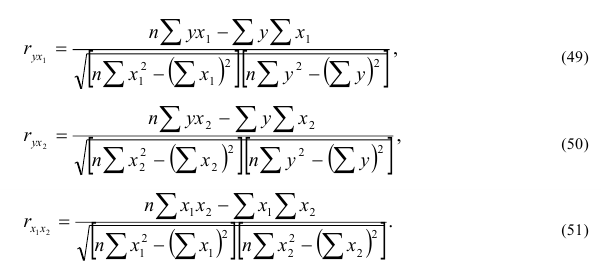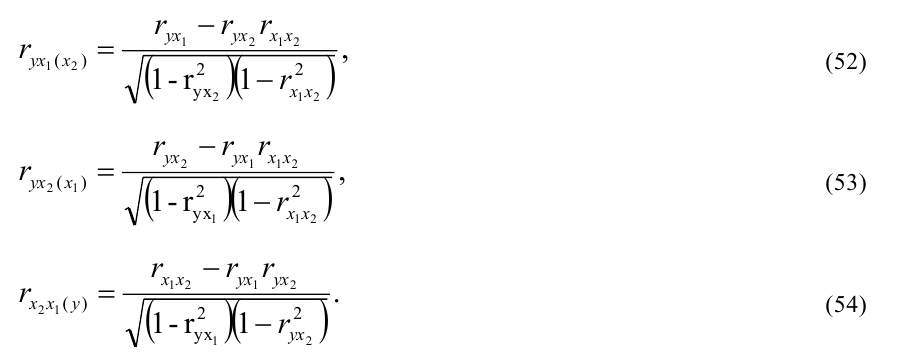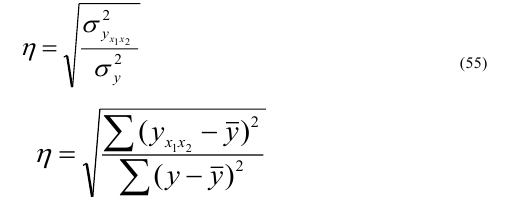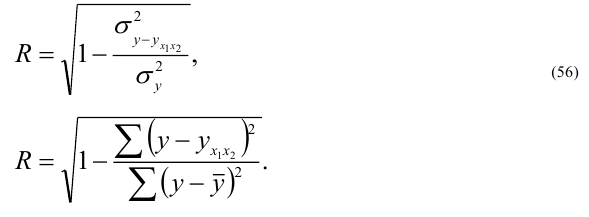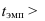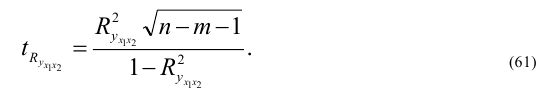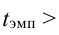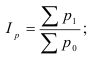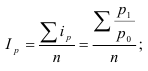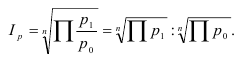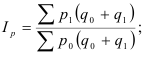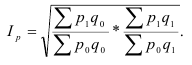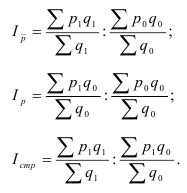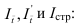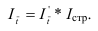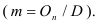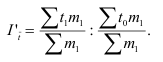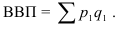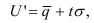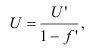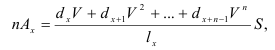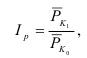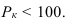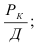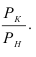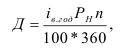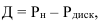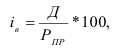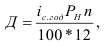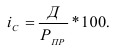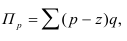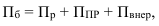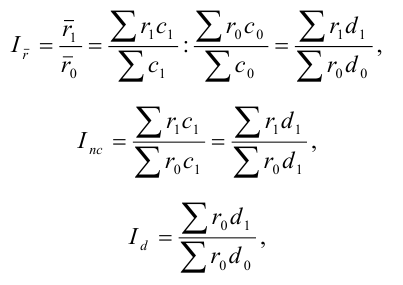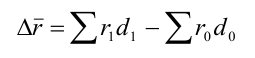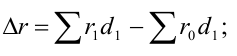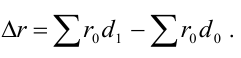Математически
результативный признак (зависимая
переменная величина) обозначены через
Y,
а факторы-аргументы (независимые
переменные) через X.
Определяем
среднеарифметическое значение
результативного признака и фактора-аргумента
по исходным данным для расчета:
Таблица 1.
|
Вариант № |
Модель машины |
Доверительная |
|||||
|
Обозначение и |
Р= |
||||||
|
Исходные данные |
|||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
Xi |
|||||||
|
Yi |
,
;
(1)
где, Xi
— значение фактора-аргумента;
Yi
— значение результативного признака;
n
– число исходных данных (пар Xi;
Yi).
3. Выбор формы связи (аппроксимация связей между параметрами)
От правильности
выбора аппроксимирующей функции зависит,
насколько полученная связь будет
адекватна реально существующей связи
между параметрами и будет ли она
отображать эту связь с заданной степенью
точности.
Выбор формы связи
начинают с предварительного аналитического
или графического анализа исходной
информации построением поля корреляции
и прочерчиванием приблизительной
кривой. Для этого, откладывая в
прямоугольной системе координат по оси
абсцисс (X)
факторный признак, а по оси ординат (Y)
– результативный и заполняя первый
квадрат точками с координатами X
и Y,
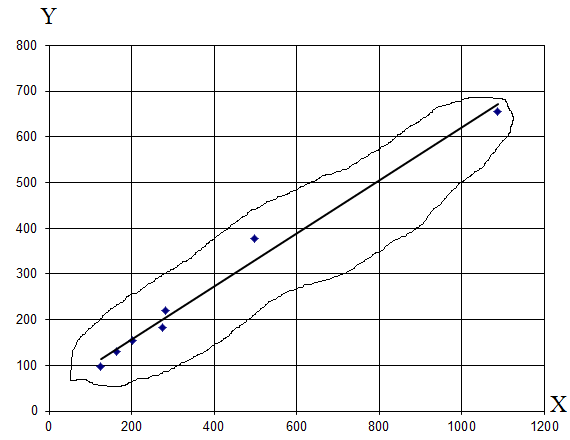
получают корреляционное поле (рис. 1).
Чем больше
разбросанность точек по всему полю, тем
слабее зависимость, и наоборот.
Разбросанность точек в определенном
направлении говорит о прямой или обратной
связи. Те точки, которые резко выпадают
из общей картины наблюдения, рекомендуется
исключить из дальнейшего рассмотрения.
Сопоставляя каждому
значению одной величины, например, X,
среднее из соответствующих значений
другой величины, например, Y,
мы получим функцию регрессии Y
на X.
Функция регрессии изображается графически
линией регрессии (Рис. 1).
Рис. 1 Поле
корреляции и линии регрессии зависимости
Y=
f
(X).
Если анализ
показывает, что величина результативного
признака Y
изменяется приблизительно равномерно
в соответствии с изменением величины
влияющего фактора X,
то, следовательно, существует прямая
линейная связь; если неравномерно, то
– криволинейная.
Корреляционные
связи, применяемые в исследованиях,
имеют следующий вид:
Линейная
(прямая)
y
=a0
+a1x,
(2)
обычно применяется
в простейших случаях, когда экспериментальные
данные возрастают или убывают с постоянной
скоростью.
Полиномиальная
y =
a0+a1x+a2x2+…+anxn,
(3)
где до шестого
порядка включительно (n≤6), ai–
константы. Используется для описания
экспериментальных данных, попеременно
возрастающих и убывающих. Степень
полинома определяется количеством
экстремумов (максимумов или минимумов)
кривой. Полином второй степени можно
описать только один максимум или минимум,
полином третьей степени может иметь
один или два экстремума, четвертой
степени – не более трех экстремумов и
т.д.
Логарифмическая
y
= a·lnx+b,
(4)
где
a и b – константы, ln – функция натурального
логарифма. Функция применяется для
описания экспериментальных данных,
которые вначале быстро растут или
убывают, а затем постепенно стабилизируются.
Экспоненциальная
y
= b·eax,
(5)
где a и b – константы,
e – основание натурального логарифма.
Применяется для описания экспериментальных
данных, которые быстро растут или
убывают, а затем постепенно стабилизируются.
Часто ее использование вытекает из
теоретических соображений.
Степенная
(факториальная)
y
= b·xa,
(6)
где a и b – константы.
Аппроксимация степенной функцией
используется для экспериментальных
данных с постоянно увеличивающейся
(или убывающей) скоростью роста. Данные
не должны иметь нулевых или отрицательных
значений.
Выбираем линейную
форму связи: y
=a0
+a1x,
т.к. на практике она получила большее
распространение:
— линейные модели
просты и требуют относительно меньшего
объема вычислений;
— именно линейным
формам связи свойственно нормальное
распределение, которое встречается
наиболее часто.
Криволинейную
зависимость часто можно заменить
прямолинейной, потому что при сравнительно
больших диапазонах изменений показателей
любую кривую в первом приближении всегда
можно с некоторой погрешностью представить
в виде набора прямых отрезков.
Степень близости
аппроксимации экспериментальных данных
выбранной функцией оценивается
коэффициентом детерминации (R2).
Таким образом,
если есть несколько подходящих вариантов
типов аппроксимирующих функций, можно
выбрать функцию с большим коэффициентом
детерминации (стремящимся к 1).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Построение линейной модели регрессии по данным эксперимента
- Результативные и факторные признаки
- Линейная модель парной регрессии
- Метод наименьших квадратов, вывод системы нормальных уравнений
- Оценка тесноты связи
п.1. Результативные и факторные признаки
Совокупность информации, которая характеризует исследуемый процесс или объект, называют набором признаков.
Если признаки связаны между собой причинно-следственными связями, то их разделяют на два класса:
1) факторные (независимые) признаки – те, что влияют на изменение других признаков;
2) результативные (зависимые) признаки – те, что меняются под действием факторных признаков.
Например:
Факторный (независимый) признак
Результативный (зависимый) признак
Инвестиции в проект
Прибыльность проекта
Затраты на рекламу
Объем продаж
По характеру зависимости признаков различают:
- Функциональную зависимость, когда каждому определенному значению факторного признака x соответствует одно и только одно значение результативного признака (y=f(x)).
- Статистическую зависимость, когда каждому определенному значению факторного признака x соответствует некоторое распределение (F_Y(y|x)) вероятностей значений результативного признака.
Например:
Функциональные зависимости: (y(x)=x^2+3, S(R)=pi R^2, V(a)=a^3)
Статистические зависимости: средний балл успеваемости в зависимости от потраченного на учебу времени, рост в зависимости от возраста, количество осадков в зависимости от времени года и т.п.
Линейная модель парной регрессии
Статистическая модель – это результат обобщения результатов экспериментального исследования на основе их статистической обработки.
Например:
Прогноз погоды, автоматическая диагностика заболевания по результатам обследования, распознавание отпечатка на сканере и т.п.
В принципе, все сегодняшние компьютерные «чудеса» по поиску, обучению и распознаванию основаны на статистических моделях.
Рассмотрим саму простую модель: построение прямой (Y=aX+b) на основе полученных данных. Такая модель называется линейной моделью парной регрессии.
Пусть Y — случайная величина, значения которой требуется определить в зависимости от факторной переменной X.
Пусть в результате измерений двух случайных величин X и Y был получен набор точек (left{(x_i;y_i)right}, x_iin X, y_iin Y).
Пусть (y*=y*(x)) — оценка значений величины Y на данном наборе (x_i). Тогда для каждого значения x случайной величиной является ошибка оценки: $$ varepsilon (x)=y*(x)-Y $$ Например, если полученный набор точек при размещении на графике имеет вид:
тогда разумно будет выдвинуть гипотезу, что для генеральной совокупности (Y=aX+b).
А для нашей выборки: (y_i=ax_i+b+varepsilon_i, i=overline{1,k})
т.к., каждая точка выборки может немного отклоняться от прямой.
Наша задача: на данном наборе точек (left{(x_i;y_i)right}) найти параметры прямой a и b и построить эту прямую так, чтобы отклонения (varepsilon_i) были как можно меньше.
п.3. Метод наименьших квадратов, вывод системы нормальных уравнений
Идея метода наименьших квадратов (МНК) состоит в том, чтобы найти такие значения a и b, для которых сумма квадратов всех отклонений (sum varepsilon_i^2rightarrow min) будет минимальной.
Т.к. (y_i=ax_i+b+varepsilon_i), сумма квадратов отклонений: $$ sum_{i=1}^k varepsilon_i^2=sum_{i=1}^k (y_i-ax_i-b)^2rightarrow min $$ Изучая производные, мы уже решали задачи на поиск экстремума (см. §50 данного справочника).
В данном случае нас интересует «двойной» экстремум, по двум переменным: $$ S(a,b)=sum_{i=1}^k (y_i-ax_i-b)^2 $$ Сначала берем производную по a, считая b постоянной, и приравниваем её к 0: begin{gather*} frac{partial S(a,b)}{partial a}=frac{partial}{partial a}sum_{i=1}^k (y_i-ax_i-b)^2=sum_{i=1}^k frac{partial}{partial a}(y_i-ax_i-b)^2=\ =sum_{i=1}^k 2(y_i-ax_i-b)cdot (-x_i)=-2sum_{i=1}^k x_i(y_i-ax_i-b)=0 end{gather*} Теперь то же самое делаем для b: begin{gather*} frac{partial S(a,b)}{partial b}=frac{partial}{partial b}sum_{i=1}^k (y_i-ax_i-b)^2=sum_{i=1}^k frac{partial}{partial b}(y_i-ax_i-b)^2=\ =sum_{i=1}^k 2(y_i-ax_i-b)cdot (-1)=-2sum_{i=1}^k (y_i-ax_i-b)=0 end{gather*} Получаем систему: begin{gather*} begin{cases} sum_{i=1}^k x_i(y_i-ax_i-b)=0\ sum_{i=1}^k (y_i-ax_i-b)=0 end{cases} \ begin{cases} sum_{i=1}^k x_iy_i-asum_{i=1}^k x_i^2-bsum_{i=1}^k x_i=0\ sum_{i=1}^k y_i-asum_{i=1}^k x_i-bsum_{i=1}^k 1=0 end{cases} end{gather*} Переставим уравнения местами и запишем в удобном для решения виде.
Система нормальных уравнений для параметров парной линейной регрессии $$ begin{cases} asum_{i=1}^k x_i+bk=sum_{i=1}^k y_i\ asum_{i=1}^k x_i^2+bsum_{i=1}^k x_i=sum_{i=1}^k x_iy_i end{cases} $$
Наши неизвестные – это a и b. И получена нами система двух линейных уравнений с двумя неизвестными, которую мы решаем методом Крамера (см. §48 справочника для 7 класса). begin{gather*} triangle = begin{vmatrix} sum_{i=1}^k x_i & k\ sum_{i=1}^k x_i^2 & sum_{i=1}^k x_i end{vmatrix}, triangle_a = begin{vmatrix} sum_{i=1}^k y_i & k\ sum_{i=1}^k x_iy_i & sum_{i=1}^k x_i end{vmatrix}, triangle_b = begin{vmatrix} sum_{i=1}^k x_i & sum_{i=1}^k y_i\ sum_{i=1}^k x_i^2 & sum_{i=1}^k x_iy_i end{vmatrix} \ a=frac{triangle_a}{triangle}, b=frac{triangle_b}{triangle} end{gather*}
Например:
Найдем и построим прямую регрессии для набора точек, представленных на графике выше. Общее число точек k=10.
Расчетная таблица:
| (i) | (x_i) | (y_i) | (x_i^2) | (x_iy_i) |
| 1 | 0 | 3,86 | 0 | 0 |
| 2 | 0,5 | 3,25 | 0,25 | 1,625 |
| 3 | 1 | 4,14 | 1 | 4,14 |
| 4 | 1,5 | 4,93 | 2,25 | 7,395 |
| 5 | 2 | 5,22 | 4 | 10,44 |
| 6 | 2,5 | 7,01 | 6,25 | 17,525 |
| 7 | 3 | 6,8 | 9 | 20,4 |
| 8 | 3,5 | 7,79 | 12,25 | 27,265 |
| 9 | 4 | 9,18 | 16 | 36,72 |
| 10 | 4,5 | 9,77 | 20,25 | 43,965 |
| ∑ | 22,5 | 61,95 | 71,25 | 169,475 |
Получаем: begin{gather*} sum_{i=1}^k x_i=22,2; sum_{i=1}^k x_i^2=71,25; sum_{i=1}^k x_iy_i=169,475; sum_{i=1}^k y_i=61,95\ triangle = begin{vmatrix} 22,2 & 10\ 71,25 & 22,2 end{vmatrix}=22,2^2-10cdot 71,25=-206,25\ triangle_a = begin{vmatrix} 61,95 & 10\ 169,475 & 22,2 end{vmatrix}=61,95cdot 22,2-10cdot 169,475=-300,875\ triangle_b = begin{vmatrix} 22,2 & 61,95\ 71,25 & 169,475 end{vmatrix}=22,2cdot 169,475-61,95cdot 71,25=-600,75 \ a=frac{triangle_a}{triangle}=frac{-300,875}{-206,25}approx 1,46, b=frac{triangle_b}{triangle}=frac{-600,75}{-206,25}approx 2,91 end{gather*}
Уравнение прямой регрессии: $$ Y=1,46cdot X+2,91 $$
п.4. Оценка тесноты связи
Найденное уравнение регрессии всегда дополняют расчетом показателя тесноты связи.
Введем следующие средние величины: $$ overline{x}=frac1ksum_{i=1}^k x_i, overline{y}=frac1ksum_{i=1}^k y_i, overline{x^2}=frac1ksum_{i=1}^k x_i^2, overline{y^2}=frac1ksum_{i=1}^k y_i^2, overline{xy}=frac1ksum_{i=1}^k x_iy_i $$ Дисперсия каждой из случайных величин x и y: $$ D_x=overline{x^2}-(overline{x})^2, D_y=overline{y^2}-(overline{y})^2 $$ СКО каждой из случайных величин: $$ sigma_x=sqrt{overline{x^2}-(overline{x})^2}, sigma_y=sqrt{overline{y^2}-(overline{y})^2}, $$
Линейный коэффициент корреляции (r_{xy}) является показателем тесноты линейной связи между факторной переменной x и результативной переменной y и рассчитывается по формуле: $$ r_{xy}=frac{overline{xy}-overline{x}cdot overline{y}}{sigma_x sigma_y} $$
Значения линейного коэффициента корреляции находится в интервале $$ -1leq r_{xy}leq 1 $$ Чем ближе (|r_{xy}|) к единице, тем сильнее линейная связь между x и y.
Отрицательные значения (|r_{xy}|) соответствуют обратной связи: убывающей прямой с отрицательным угловым коэффициентом.
Для оценки тесноты связи на практике пользуются шкалой Чеддока:
Значение (|r_{xy}|)
Теснота линейной связи
(left.left[0; 0,3right.right))
Очень слабая
(left.left[0,3; 0,5right.right))
Слабая
(left.left[0,5; 0,7right.right))
Средняя
(left.left[0,7; 0,9right.right))
Высокая
([0,9; 1])
Очень высокая
Например:
Для построенной выше прямой регрессии получаем: begin{gather*} overline{x}=frac1ksum_{i=1}^k x_i=frac{22,2}{10}=2,22\ overline{y}=frac1ksum_{i=1}^k y_i=frac{61,95}{10}=6,195\ overline{x^2}=frac1ksum_{i=1}^k x_i^2=frac{71,25}{10}=7,125\ overline{y^2}=frac1ksum_{i=1}^k y_i^2approx frac{429,94}{10}=42,994\ overline{xy}=frac1ksum_{i=1}^k x_i y_i= frac{169,475}{10}approx 16,948\ overline{xy}-overline{x}cdot overline{y}=16,948-2,22cdot 6,195approx 3,009\ D_x=overline{x^2}-(overline{x})^2=7,125-(2,22)^2approx 2,063\ D_y=overline{y^2}-(overline{y})^2=42,994-(6,195)^2approx 4,616\ r_{xy}=frac{overline{xy}-overline{x}cdot overline{y}}{sqrt{D_xcdot D_y}}approx frac{3,009}{sqrt{2,063cdot 4,616}}approx 0,975 end{gather*}
По шкале Чеддока полученное значение коэффициента (r_{xy}) указывает на очень высокую прямую линейную связь.
ОБЩАЯ ТЕОРИЯ СТАТИСТИКИ
Тема 3. СВОДКА И ГРУППИРОВКА СТАТИСТИЧЕСКИХ
ДАННЫХ
Целью следующего этапа статистического исследования является
систематизация первичных данных и получение на этой основе сводной
характеристики всего объекта при помощи обобщающих статистических показателей.
Сводка представляет собой комплекс
последовательных операций по обобщению конкретных единичных фактов, образующих
совокупность, для выявления типичных черт и закономерностей, присущих
изучаемому явлению в целом.
В процессе сводки материалы упорядочиваются и делятся на группы по
существенным признакам. Это достигается с помощью группировки.
Группировка – разделение единиц совокупности
на группы по существенному варьирующему признаку.
Группировка лежит в основе всей дальнейшей работы собирания информации.
На основе группировки рассчитывают показатели по группам. Появляется
возможность их сравнения, анализа причин различия между группами, изучение
взаимосвязи между группами.
Таким образом, значение группировки состоит в том, что
это метод обеспечивает обобщение данных, представление их в компактном виде и
создаёт основу для последовательного анализа.
Для проведения группировки необходимо определить группировочный признак
или основание группировки.
Основанием группировки может служить атрибутивный или количественный
признак.
Атрибутивный (качественный) – свойством
данного признака является его наименование.
Количественный признак имеет цифровое
выражение.
Количественный признак может быть дискретным
(прерывным) и интервальным (непрерывным).
Количественные признаки могут выражаться дискретными или непрерывными
величинами, соответственно, и вариационный ряд будет либо дискретным, либо
интервальным (непрерывным в пределах интервала). Так, количество детей в семье
может выражаться только целыми числами, а вес человека может отличаться от веса
другого на сколь угодно малую величину, определяемую точностью измерения.
Дискретный признак изменяется через определённый шаг. Если в основу
группировки положен количественный признак, необходимо решить два вопроса:
1) об интервалах группировки;
2) о числе групп.
1) Интервал – это значение варьирующего признака лежащего в
определённых границах.
Величина интервала – разность между верхней и
нижней границей.
Интервалы группировки могут быть равными и неравными.
Если мы применяем равные интервалы, то можно рассчитать его величину:
,
где i –величина интервала,
n – число выделяемых групп,
Xmax и Xmin – соответственно максимальное и
минимальное значение единиц совокупности.
Первый и последний интервал могут быть открытыми. Открытый интервал
не имеет одну из границ.
Когда одна и та же величина встречается дважды (как верхняя граница
одного интервала и нижняя граница другого интервала), единица обладающая этим
значением, обычно относится к той группе, где эта величина выступает в роли
верхней границы.
При построении вариационного ряда непрерывного признака невозможно
указать абсолютно точное значение варианта, поэтому совокупность распределяется
по интервалам его значений. Интервалы можно брать как равные, так и неравные.
Для каждого из них указывается частота или частость, т.е. абсолютное или
относительное число единиц, у которых значение признака находится внутри
данного интервала.
Первый и последний интервалы рядов чаще всего берутся открытыми.
Использование открытых интервалов удобно, когда в совокупностях встречается
незначительное число единиц с очень малыми или очень большими значениями
вариантов, резко отличающимися от всех остальных значений.
Если построен ряд с равными интервалами, то частоты дают представление
о том, как заполнен единицами совокупности тот или иной интервал. При сравнении
частот ряда с неравными интервалами для характеристики их заполненности
рассчитывают плотность распределения. Средняя плотность в интервале — это
частное от деления частоты или частости на величину интервала: в первом случае
получается абсолютная, во втором — относительная плотность распределения.
Средняя плотность показывает, сколько единиц (или сколько процентов единиц)
совокупности приходится на единицу изменения варианта.
2)
Существует зависимость между числом групп и числом
совокупности (формула Стэрджеса):
n = 1+3,322·lgN,
где n – число групп,
N – число единиц совокупности
Виды группировок.
С помощью группировок можно выделить технологические группы
совокупности, изучить структуру совокупности, выявить взаимосвязи между
признаками.
Эти задачи решаются с помощью соответственных группировок:
типологической, структурной, аналитической.
ТИПОЛОГИЧЕСКАЯ группировка служит для
определения социально-экономических типов. Этот вид группировок в значительной
степени определяет представления экспертов о том, какие типы могут быть
встречены в изучаемой совокупности.
Чтобы построить группировку необходимо назвать тип явления, выбрать
группировочный признак, установить границы интервалов. Для типологической
группировки характерны не равные и открытые интервалы.
СТРУКТУРНАЯ группировка характеризует состав,
структуру совокупности по группировочному признаку.
Для структурной группировки характерны закрытые и равные интервалы.
При анализе структурной группировки выделяются наибольшее и наименьшее
значение показателя по группам.
АНАЛИТИЧЕСКАЯ группировка строится для
выделения взаимосвязи между признаками. Необходимо определить какой признак
является результативным, а какой факторным.
Результативный признак – зависимый признак
Факторный признак – влияющий на результаты и
независимый.
В основу аналитической группировки кладётся факторный признак. По
каждой группе факторного признака определяется сумма результативного признака и
определяется значение результативного признака на единицу совокупности (или
среднее значение результативного признака).
Если с увеличением факторного признака происходит увеличение
результативного признака, то между ними существует прямая связь. Если с
увеличением факторного признака происходит уменьшение результативного признака,
то — обратная связь.
В зависимости от числа положенных в основание группировки признаков
различают простые и многомерные группировки.
Простой
называется группировка, выполненная по одному признаку. Среди простых
группировок особо выделяются ряды распределения.
Ряд распределения – это группировка, в которой для характеристики групп
(упорядоченно расположенных по значению признака) применяется один показатель –
численность группы. Ряды, построенные по атрибутивному признаку, называются
атрибутивными рядами распределения. Ряды распределения, построенные по
количественному признаку, называются вариационными рядами.
Многомерная группировка
производится по двум и более признакам. Частным случаем многомерной группировки
является комбинационная группировка, базирующаяся на двух и более признаках,
взятых во взаимосвязи, в комбинации.
По отношениям между признаками выделяют:
—
иерархические группировки, выполняемые по двум и
более
признакам, при этом значения второго признака определяются
областью значении первого (например, классификация отраслей
промышленности по подотраслям);
—
неиерархические группировки, которые строятся,
когда
строгой зависимости значений второго признака от первого не
существует.
По очередности обработки информации группировки бывают первичные (составленные на основе
первичных данных) и вторичные,
являющиеся результатом перегруппировки ранее уже сгруппированного материала.
Тема
4. СРЕДНИЕ ВЕЛИЧИНЫ
4.1.
Средние показатели
Средняя величина есть обобщающая количественная характеристика
совокупности однотипных явлений по одному варьирующему признаку.
Она отражает определённый уровень достигнутый в процессе развития
явления к определённому периоду или моменту времени.
Средняя величина – абстрактная величина. Поэтому анализ проводимый при
ней всегда дополняется показом индивидуальных величин.
Среднее может быть вычислено только для какой-то однородной
совокупности.
Расчёт средней необходимо сочетать с группировкой.
В статистике рассчитывают индивидуальные и общие средние.
Общее среднее затушёвывает существенные (существующие) отличия между
явлениями таким образом во многих случаях они становятся фиктивными.
Признак по которым находится среднее
называется усредняемое (Х). Величина усредняемого признака у каждой единицы
совокупности называется индивидуальное значение.
Значение признака, которое встречается у
крупных единиц или отдельных единиц и не повторяется называется вариантами
признака (Х1, Х2, …).
Средняя арифметическая.
Средняя
арифметическая простая (рассчитывается по несгруппированным данным):
. 
где x1 ,x2, …, xn-значение признака (варианты), n— число вариантов.
Средняя арифметическая взвешенная (рассчитывается
по сгруппированным данным):
,
где f1, f2, …, fn — веса
(частоты) значений признака.
f— частота повторения соответствующих вариантов в статистике называется
весом.
Пример: 1) Вычислить средний возраст выпуска, возраст
которого: 24,22,25,24,25,24,22,22,24,26 лет.
Расчёт по средней арифметической простой:
3)
Расчёт по средней
арифметической взвешенной.
|
Возраст (х) |
Число выпускников (f) |
Сумма возрастов (хf) |
|
22 24 25 26 |
3 4 2 1 |
66 96 50 26 |
|
Сумма |
10 |
238 |
.
Свойства средней арифметической:
1)
Сумма отклонений
значений признака от средней арифметической равно 0.

2)
Если от каждого
варианта вычесть или к каждому варианту прибавить какое-либо постоянное число,
то среднее увеличится или уменьшится на то же самое число.
3)
Если каждый вариант
умножить или разделить на какое-либо число, то среднее уменьшится или
увеличится во столько же раз.
4)
Если веса или частоты
разделить или умножить на какое-либо число, то величина средней не изменится.
Это свойство даёт возможность частоты заменять их удельными весами
,
где р – удельный вес, выраженный в процентах.
Если удельный вес выражается в доле, то
.
Средняя гармоническая.
Рассчитывается, когда 1) среднее арифметическое по
имеющимся данным рассчитать невозможно, 2) расчет средней гармонической более
удобен.
Средняя гармоническая простая: 
Средняя гармоническая взвешенная: 
Пример: требуется вычислить
производительность труда рабочей силы, если первому рабочему требуется для
изготовления единицы продукции 0,25 часа, второму – 1/3 часа, третьему – 1/2
часа.

Средняя геометрическая.
Средняя геометрическая простая:
.
Средняя геометрическая взвешенная:
.
Наиболее широкое применение этот вид средней получил в анализе динамики
для определения среднего темпа роста.
Средняя квадратическая.
Средняя квадратическая простая:

Средняя квадратическая взвешенная:

Пример: Оценка за ответ на первый вопрос – 2, на
второй вопрос – 5.
4.2.
Структурные средние
Для того чтобы определить среднее в некоторых случаях нет необходимости,
или возможности прибегать к расчёту степенных средних в этих случаях появляется
возможность или необходимость расчёта структурной средней.
Если величина средней (ср. арифметической) зависит от всех значений
признака, встречаемых в данном распределении, то значение структурной средней
определяется структурой распределения, местом распределения. Отсюда их
названия.
Медиана – значение признака, приходящееся на
середину ранжированной (упорядоченной) совокупности. Медиана делит совокупность
на две равные части.
Медиана в интервальном ряду рассчитывается следующим образом:
Для определения медианы прежде всего исчисляют её порядковый номер по
формуле
или
(для интервальных
рядов) и строят ряд накопленных частот. Накопленной частоте, которая равна
порядковому номеру медианы или первая его превышает, в дискретном вариационном
ряду соответствует вариант, являющийся медианой, а в интервальном вариационном
ряду – медианный интервал.
где Х0 – нижняя граница медианного
интервала,
d – величина медианного интервала,
fi – частота i-го интервала,
Sме-1
– сумма накопленных весов по интервалу
предшествующему медианному,
fMe
– частота медианного интервала.
Пример: Имеются
данные о з/п рабочих:
|
Месячная з/п (руб) х |
Количество рабочих, fi |
Накопленные частоты, Si |
|
До 800 |
1 |
1 |
|
800- 1000 |
2 |
3 |
|
1000- 1200 |
4 |
7 |
|
1200- 1400 |
1 |
8 |
|
1400 и более |
2 |
10 |
|
Итого |
10 |
,

Мода – значение признака, которое чаще других
встречается в данном ряду распределения.
Мода для дискретного ряда определяется как варианта, имеющая
наибольшую частоту.
Для интервального ряда:
,
где Х0 –нижняя граница модального
интервала,
d – величина модального интервала,
fMo-1 – частота (вес) интервала,
предшествующего модальному,
fMo – частота (вес) модального интервала,
fMo+1 – частота (вес) интервала, следующего за модальным.
Пример: (См. предыдущую задачу)
.
Квартили – значения признака, делящие
ранжированную совокупность на четыре равновеликие части.
Рассчитывают 1-й и 3-й квартили.

XQ1 – нижняя граница интервала, содержащего
нижний квартиль (интервал определяется по накопленной частоте, первой
превышающей 25%),
d – величина интервала,
fQ1 – частота квартильного интервала,
SQ1-1 – сумма накопленных частот в интервале, предшествующего квартильному.
Q2=Мe.

обозначения
аналогичны 1-му квартилю с изменением на верхний.
Децили – варианты, делящие ранжированный ряд
на десять равных частей.
Вычисляются они по той же схеме, что и медиана, и квартили. Обычно
рассчитывают только первый и девятый децили:


Значения признака, делящие ряд на сто частей, называются перцентилями.
Расчёт средних всегда производится одновременно с
количественным анализом, изучаемых совокупностей, средние величины
рассчитываются не всегда, когда на лицо количественная вариация признаков.
Средняя величина должна быть рассчитываема для количественно-однородной
совокупности.
Это требование состоит в том, что среднее нельзя применить к таким
совокупностям, отдельные части которых подчинены различным законам развития
относительных величин признака.
Тема 5. ПОКАЗАТЕЛИ
ВАРИАЦИИ
5.1.
Меры вариации
Колеблемость, многообразие, изменяемость величины признака у единиц
совокупности называются вариацией.
Вариация существует в пространстве и во времени.
Вариация в пространстве – колеблемость значений
признака по отдельным территориям.
Вариация во времени – изменение значений признака в
различные периоды (или моменты) времени.
Для измерения вариации используются такие показатели,
как размах вариации, среднее линейное отклонение, дисперсия, среднее
квадратическое отклонение, коэффициент вариации.
Простейший показатель – размах вариации.
R=Xmax – Xmin.
Из приведённой формы видно, что величина этого показателя целиком
зависит от случайности расположения крайних членов ряда.
Его недостаток в том, что варьирование значения признака из основной
массы членов ряда не находит отражения в этом показателе. В то же время
колеблимость признака складывается из всех его значений.
Среднее линейное отклонение:
– простая,

Показывает в среднем отклонение вариантов признака от их средней
величины.
Дисперсия:
простая,
взвешенная.

Это средняя величина квадратов отклонений.
Среднее квадратическое отклонение:

Это обобщающая характеристика размеров вариации признака в
совокупности. Оно выражается в тех же единицах измерения, что и признак.
Для расчёта дисперсии в дискретном рядах используется следующая
формула.
,
где 

Пример: Распределение коров колхозной фермы по
годовому удою молока и расчёт абсолютных показателей вариации.
|
Годовой удой молока от коровы тыс.кг. (Хi) |
Число коров, fi |
Средняя величина признака, сер. интерв. |
Хifi |
Хi–Х |
|Xi–X|fi |
(Xi–X)2 |
(Xi–X)2fi |
|
До-2 |
4 |
1,5 |
6 |
-1,3 |
5,2 |
1,69 |
6,76 |
|
2-3 |
2 |
2,5 |
5 |
-0,3 |
0,6 |
0,09 |
0,18 |
|
3-4 |
2 |
3,5 |
7 |
+0,7 |
1,4 |
0,49 |
0,98 |
|
4-5 |
1 |
4,5 |
4,5 |
+1,7 |
1,7 |
2,89 |
2,89 |
|
5 и более |
1 |
5,5 |
5,6 |
+2,1 |
2,7 |
7,29 |
7,29 |
|
Итого |
10 |
28 |
11,6 |
18,1 |
1) Находим среднюю арифметическую
2) Среднее линейное отклонение:

2)
Дисперсия

4) Среднее квадратическое отклонение:
тыс.кг.
Дисперсия обладает рядом свойств, некоторые из которых позволяют
упростить её вычисление.
1. Дисперсия постоянной величины равна 0
2. Если все варианты значений признака уменьшить на одно число то
дисперсия не изменится.
3. Если все варианты значений признака уменьшить (увеличить) в одно и тоже
число раз (в К раз), то дисперсия уменьшится (увеличится) в К2
раз.
Дисперсия и среднее квадратическое отклонение – наиболее широко
применяемые показатели вариации, т.к. они входят в большинство теорем теории
вероятности, которая служит фундаментом математической статистики.
Коэффициент вариации.
Он используется не только для сравнения оценки вариации, но и для
характеристики однородной совокупности.
Совокупность считается однородной если коэффициент вариации <=0,33.
В статистике наряду с показателем вариации количественного признака
определяется показатель вариации качественного или альтернативного
признака.
Альтернативными признаками являются признаки, которым
обладают одни единицы совокупности и не обладают другие.
При статистическом выражении колеблимости признака, наличие изучаемого
признака обозначается «1», а его отсутствие «0».
Доля вариантов обладающих изучаемым признаком обозначается р, а
доля вариантов не обладающих изучаемым признаком обозначается q.
Найдём среднее:
.
Дисперсия альтернативного признака:
.
Пример: имеется совокупность новорождённых –
205 человек, девочки – 100.
Доля девочек р=100/205=0,488
Доля мальчиков q =105/205=0,512
Дисперсия альт. призн.= 0,488·0,512= 0,2498
p+q не может быть >1
p·q не может быть >0.25
5.2. Виды дисперсий
Общая дисперсия измеряет вариацию признака во всей совокупности под
влиянием всех факторов, обусловивших эту вариацию.
Межгрупповая дисперсия отражает вариацию
изучаемого признака, которая возникает под влиянием признака фактора,
положенного в основу группировки. Она характеризует колеблимость групповых
(частных) средних около общей средней

где – среднее по определённой группе; ni
– численность отдельных групп.
Внутригрупповая дисперсия отражает случайную
вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и
не зависящую от признака-фактора, положенного в основание группировки.

Средняя из внутригрупповых дисперсий:

Правило сложения дисперсий:
.
Можно рассчитать относительные показатели.
1.
Эмпирический коэффициент детерминации
Он показывает долю (удельный вес) общей вариации изучаемого признака,
обусловленную вариацией группировочного признака.
2. Эмпирическое корреляционное отношение
Оно характеризует влияние признака, положенного в
основание группировки, на вариацию результативного признака. Чем больше это
число, тем больше зависимость результативного признака от факторов положенных
в основу группировки.
Пример:
|
Тип хозяйства |
Посевная площадь тысяч гект. |
Средняя урожайность |
Среднее |
|
1 |
300 |
20 |
2 |
|
2 |
100 |
10 |
2,5 |
1)
Находим среднюю урожайности по двум типах хозяйств
2)
Средняя из групп дисперсий
(22ּ300+2,52ּ100)/400=4,5625
3)
Определяем межгрупповую дисперсию
4)
Определяем общую дисперсию
5)
Эти данные свидетельствуют о том, что фактор положенный в основу группировки
оказывает существенное влияние на среднюю урожайность.
Выбор знака: если вариация факторного и результативного признака идёт в
одном направлении, то берётся знак «+», а если нет, то «–», сам по себе знак не
характеризует тесноту связи. Помимо расчета общей дисперсии и её составных
частей по абсолютным данным можно производить расчёт дисперсии доли.
5.3.
Теоретическое распределение в анализе вариационных рядов
При анализе изучаемых явлений в совокупности с другими, аналогичными по
своей сущности, часто удается обнаружить закономерность, связанную с их
возникновением. Наиболее часто закономерности описывают с помощью нормального
распределения:

Чем больше случайных величин действует вместе, тем точнее подчиненность
закону нормального распределения.
Примеры нормального распределения: 1) распределение отклонений в
производственном процессе при нормальном уровне организации и технологии, 2)
распределение населения определенного возраста по размеру обуви и т.д.
Соответствие эмпирического распределения нормальному можно оценивать с
помощью особых статистических показателей – критериев согласия.
Критерий согласия Пирсона (хи-квадрат)

где fэ и fт – эмпирические и теоретические частоты
соответственно.
Затем с помощью «хи-квадрат» и числа степеней свободы (n-1) находят по специальным таблицам вероятность .
При Р>0,5 считается, что эмпирическое и теоретическое распределения
близки, при 0,2<P<0,5 – удовлетворительное, в
остальных случаях – недостаточное.
Критерий Романовского (С)

где γ – число степеней свободы (число групп минус три).
При С<3 различие несущественно, эмпирическое распределение близкое к
нормальному.
Критерий Колмогорова (λ)

где D – максимальное значение разности между
накопленными эмпирическими и теоретическими частотами,
fi – эмпирические частоты.
Далее по таблицам вероятностей определяем . Чем
ближе к 1, тем лучше.
Тема 6. ИЗУЧЕНИЕ ДИНАМИКИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ
ЯВЛЕНИЙ
6.1. Понятие рядов динамики
Изучение изменения различных явлений во времени – одна из важнейших
задач статистики. Решается эта задача путем составления и анализа так
называемых рядов динамики (иногда их также называют временными или
хронологическими рядами).
Динамика – процесс развития, движения
социально-экономических явлений во времени.
Ряды динамики – ряды изменяющихся во времени
значений статистического показателя, расположенных в хронологическом порядке.
Составными элементами ряда динамики являются показатели уровней ряда и
периоды времени (годы, кварталы, месяцы, сутки) или моменты (даты) времени.
Обозначения:
y – уровни ряда,
t – моменты или периоды времени, к которым относятся уровни.
Ряды динамики, как правило, представляют в виде таблицы или графически.
При графическом изображении ряда динамики на оси абсцисс строится шкала времени
t, а на оси ординат – шкала уровней ряда у (арифметическая или иногда
логарифмическая).
Одна из первых задач изучения рядов динамики – выявить основную
тенденцию (закономерность) в изменении уровней ряда, именуемую трендом.
Закономерность в изменении уровней ряда в одних случаях проявляется довольно
наглядно, в других – может затушевываться колебаниями, вызванными случайными и
неслучайными причинами.
Виды рядов динамики.
В одних рядах уровни могут быть выражены абсолютными показателями, в
других – средними или относительными. В зависимости от вида показателей уровней
ряда ряды динамики также подразделяют на ряды абсолютных, относительных и
средних величин (показателей).
На основе рядов абсолютных величин образуются ряды динамики
относительных и средних величин, поэтому ряды абсолютных величин рассматривают
как исходные, а ряды относительных и средних величин — как производные.
Ряды относительных величин могут характеризовать: темпы роста (или
снижения) определенного показателя; изменение удельного веса того или иного
показателя в совокупности (например, удельного веса (доли) городского населения
или доли приватизированных предприятий в той или иной отрасли); изменение показателей
интенсивности отдельных явлений (например, производство продукции на душу
населения, уровень рождаемости и смертности на 1000 человек населения) и др.
Примерами рядов динамики средних величин служат данные о среднегодовой
численности занятых в экономике (или безработных), о средней заработной плате в
отдельных отраслях, о среднем размере пенсий, о средней урожайности отдельных
сельскохозяйственных культур и др.
Кроме того, уровни рядов динамики могут относиться к определенным
моментам времени (датам) или же периодам (интервалам). В соответствии с этим в
статистике различают моментные и интервальные ряды динамики
Моментным называется ряд, уровни которого
характеризуют значение показателя (явления) по состоянию на определенные
моменты времени (дату).
Интервальным называется ряд, уровни которого
характеризуют значение показателя, достигнутое за определенный период (интервал).
Отметим отличительную особенность интервальных рядов абсолютных
величин: их уровни можно дробить и складывать (суммировать). Так, зная добычу
угля по годам, можно разделить каждый уровень на 12 и получить новые данные – о
среднемесячной добыче угля за указанный период. Или же, суммируя данные о
численности родившихся по месяцам, можно получить численность родившихся за
год. Подобные действия с уровнями моментного ряда лишены смысла.
Суммируя уровни интервальных рядов абсолютных величин, можно строить
ряды с нарастающим итогом.
6.2.
Показатели изменения уровней ряда динамики
Анализ рядов динамики начинается с определения того, как именно
изменяются уровни ряда (увеличиваются, уменьшаются или остаются неизменными) в
абсолютном и относительном выражении.
Анализ скорости и интенсивности развития явления во времени
осуществляется с помощью статистических показателей, которые получаются в
результате сравнения уровней между собой. При этом сравниваемый уровень
называют отчетным, а уровень, с которым производят сравнение, – базисным.
Чтобы проследить за направлением и размером изменений уровней во
времени, для рядов динамики рассчитывают такие показатели, как:
—
абсолютные приросты (изменения) уровней;
—
темпы роста;
—
темпы прироста (снижения) уровней.
Абсолютный прирост (Δy) характеризует размер
изменения уровня ряда за определенный промежуток времени. Он рассчитывается как
разность между двумя уровнями ряда. Абсолютный прирост показывает, на сколько
(в единицах измерения показателей ряда) уровень одного периода больше или
меньше уровня какого-либо предшествующего периода, и, следовательно, может
иметь знак «+» (при увеличении уровней) или «–» (при уменьшении уровней).
Δyi=yi – yi-1, i=1..n.
В зависимости от базы сравнения абсолютные приросты могут
рассчитываться как цепные и как базисные.
Вычитая из каждого уровня предыдущий
Δу
= yi – yi-1,
получаем
абсолютные изменения уровней ряда за отдельные периоды как цепные.
Вычитая
из каждого уровня начальный
Δу
= yi – y0,
получаем
накопленные итоги прироста (изменения) показателя с начала изучаемого периода,
т.е. абсолютные изменения рассчитываются как базисные.
Если значения цепных абсолютных изменений постоянны, то уровни ряда
изменяются равномерно. Если же абсолютные приросты от периода к периоду
возрастают (или убывают), то уровни изменяются ускоренно (или замедленно). В
этом случае рассчитывается показатель ускорения как разность между двумя
смежными цепными абсолютными приростами.
Абсолютное ускорение (Δ′) – показывает,
насколько данная скорость больше (меньше) предыдущей.
Δ′=Δyi–Δyi-1
Наряду с абсолютными изменениями уровней ряда важно измерить также их
относительное изменение.
Темп роста (Тр) – показатель интенсивности
изменения уровня ряда, относительный показатель, рассчитываемый как отношение
двух уровней ряда.
В зависимости от базы сравнения темпы роста могут рассчитываться как
цепные, когда каждый уровень сопоставляется с уровнем предыдущего периода, и
как базисные, когда все уровни сопоставляются с уровнем одного какого-то
периода, принятого за базу сравнения (часто это начальный уровень ряда). Соответственно,
цепные темпы роста характеризуют интенсивность изменения в каждом отдельном
периоде, а базисные – за отрезок времени, отделяющий данный уровень от
базисного.
Базисный темп роста:
.
Цепной темп роста:
Темпы роста как относительные величины могут выражаться в виде
коэффициентов, т.е. простого кратного отношения (если база сравнения
принимается за единицу), и в процентах (если база сравнения принимается за 100
единиц). Говоря о темпах, чаще всего имеют в виду отношение уровней в
процентах.
Выраженные в коэффициентах темпы роста показывают, во сколько раз
уровень данного периода больше уровня базы сравнения или какую часть его
составляет. При процентном выражении темп роста показывает, сколько процентов
составляет уровень данного периода по сравнению с уровнем базы сравнения.
Между цепными и базисными коэффициентами роста существует связь,
позволяющая при необходимости переходить от цепных к базисным и наоборот.
В частности:
—
произведение цепных коэффициентов роста равно
базисному;
—
результат деления двух базисных коэффициентов равен
цепному
Темп прироста (Тпр) характеризует
относительную скорость изменения уровня ряда в единицу времени, это относительный
показатель, показывающий, на сколько процентов данный уровень больше (или
меньше) другого, принимаемого за базу сравнения. Показатель Тпр
можно рассчитать двояко:
—
путем вычитания 100% из темпа роста (снижения),
—
как процентное отношение абсолютного прироста к
тому уровню, по сравнению с которым рассчитан абсолютный прирост.
Абсолютное значение одного процента прироста
Абсолютное значение 1% прироста равно одной сотой предыдущего уровня
Для базисных абсолютных приростов и темпов прироста расчет не имеет
смысла, так как при сравнении всех накопленных приростов с одним и тем же
первоначальным уровнем для всех периодов будет получаться одно и то же значение
1% прироста.
Каждый ряд динамики можно рассматривать как некую совокупность изменяющихся
во времени показателей, которые можно обобщать в виде средних величин. Такие
обобщенные (средние) показатели особенно необходимы при сравнении изменений
того или иного показателя в разные периоды, в разных странах и т. д.
Средний уровень
ряда динамики. Для разных видов
рядов динамики средний уровень рассчитывается различным образом.
Для моментного равноотстоящего ряда динамики по средней хронологической:

Для моментного ряда динамики с неравноотстоящими уровнями:

где ti – длительность интервала времени
между уровнями.
Для интервального ряда с равноотстоящими уровнями:
Для интервального ряда с неравноотстоящими уровнями:
Средний абсолютный прирост
Средний темп роста
Средний темп прироста
При анализе динамики социально-экономических явлений необходимо
параллельно использовать показатели скорости и интенсивности изменения уровней.
6.3. Анализ основной тенденции в рядах динамики
Описание тенденции в ряду динамики производится с
помощью методов сглаживания. Методы сглаживания разделяются на две основные
группы:
1)
сглаживание или
механическое выравнивание отдельных членов ряда динамики с использованием фактических
значений соседних уровней;
2)
выравнивание с применением
кривой, проведенной между конкретными уровнями таким образом, чтобы она
отображала тенденцию, присущую ряду, и освободила его от незначительных
колебаний.
Метод усреднения по левой и правой половине. Ряд динамики разделяют на две части, находят
для каждой из них среднее арифметическое значение и проводят через полученные
точки линию тренда на графике.
Метод укрупнения интервалов. Производится укрупнение периодов времени, к которым
относятся уровни ряда. Например, ряд ежесуточного выпуска продукции заменяется
рядом месячного выпуска продукции.
Метод скользящей средней. Вычисляется средний уровень из определенного числа
первых по порядку уровней ряда, затем – начиная со второго, далее – с третьего
и т.д.
Алгоритм расчета скользящей средней:
1.
Определяем интервал
сглаживания, т.е. число входящих в него уровней m (m<n).
2.
Вычислить среднее значение
уровней, образующих интервал сглаживания, по формуле

где m – число уровней, входящих в интервал
сглаживания,
i – порядковый номер уровня в интервале сглаживания,
p – при нечетном m равно: p=(m-1)/2.
При четном m проводят центрирование:
находят среднюю из двух смежных скользящих средних для отнесения полученного
уровня к определенной дате.
3. Сдвинуть интервал сглаживания на одну точку вправо, затем вычислить все
последующие сглаженные значения, производя одновременно сдвиги.
Пример:
|
Год |
Центнеров с 1 га |
Скользящие трехлетние суммы |
Трехлетние скользящие средние |
|
1982 1983 1984 1985 1986 1987 1988 1989 |
9,5 13,7 12,1 14,0 13,2 15,6 15,4 14,0 |
— — 35,3 39,8 39,3 42,8 44,2 45 |
— 11,77 13,27 13,1 14,27 14,73 15 — |
Тема
7. ИНДЕКСНЫЕ МЕТОДЫ
7.1. Понятие индексов
В статистике под индексами понимаются относительные
величины, выражающие изменение сложных экономических явлений во времени,
пространстве и по сравнению с планом. В связи с этим различают динамические
индексы, характеризующие изменения явлений во времени; индексы выполнения
плана и территориальные индексы.
Индексы относятся либо к элементам сложного экономического явления,
либо ко всему явлению в целом. Показатели характеризующие изменение более или
менее однородных объектов входящих в состав сложных явлений называются
индивидуальные индексы
Принятые обозначения:
Q, q – физический объём;
p – цена единицы товара;
z – себестоимость единицы продукции;
pq – стоимость продукции или товарооборот;
zq – издержки производства.
7.2. Индивидуальные и общие индексы
Индивидуальные индексы (i) – это обычные относительные величины.
Индивидуальный индекс объёма:
=
,
q0 – базисный период (пояснить);
q1 – текущий период (пояснить).
Индивидуальный индекс цены:
.
Индивидуальный индекс товарооборота:
Индекс как индивидуальный так и общий получает название по названию
индексированной величины. Индексы как индивидуальные так и общие обозначаются
либо в виде коэффициента, либо в виде процентов.
Явления общественные и социальные, изучаемые в экономике состоят из
несопоставимых элементов. Таким образом, основным вопросом построения индексов,
общих и сводных состоит в том, чтобы обеспечить эту сопоставимость
Самый лёгкий способ сопоставления – сложные явления разбиваются на
простые элементы которые в известной мере являются однородными.
Общий индекс обозначается – I. Различают агрегатные и средневзвешенные индексы.
Основной формой сводного индекса является агрегатный индекс. Для
того, чтобы его построить необходимо свести различные элементы сложного явления
к такому виду, который делает их соизмеримыми.

продукции(Ласпейреса).

продукции(Пааше).




производства.
Та часть индекса, которая не изменяется, называется весом.
Веса свободного индекса в агрегатной форме выбираются исходя из
следующих данных:
Если индексируемая величина – суть количественный
показатель, то вес выбирается на уровне базисного периода.
В том случае если индексируется величина – качественный признак вес
принимается на уровне текущего периода. Такой подход к выбору весов даёт нам
возможность записать следующее равенство индексов
Итак, в целом по совокупности, состоящей из элементов, непосредственно
несоизмеримых (различные виды продукции, товарные группы и т.д.), изменение
физического объема реализации и цен характеризуется с помощью агрегатных
индексов, формулы построения которых сведены в табл. 1.
Таблица 1
Агрегатные индексы
|
Формулы индексов |
Название индексов |
|
|
Индекс физического объема и других первичных признаков |
Индекс цен и других вторичных признаков |
|
|
По формуле Ласпейреса (по базисным весам) |
|
|
|
По формуле Пааше (по отчетным весам) |
|
|
|
Индекс Фишера |
|
|
Пример:
|
Товары |
Ед. измер |
Базисный период |
Текущий период |
Индивидуаль-ный индекс |
|||
|
P0 , (руб) |
Q0 (ед.) |
P1 |
Q1 |
|
|
||
|
Капуста |
Кг. |
17 |
350000 |
15 |
420000 |
0,882 |
1,2 |
|
Молоко |
Литры |
28 |
25400 |
35 |
23600 |
1,25 |
0,929 |
|
Яйца |
Десятки |
120 |
125 |
120 |
140 |
1 |
1,29 |
Индекс товарооборота:
Это значит товарооборот текущего периода по отношению к базисному вырос
на 7% этот показатель отражает изменение товарооборота под влиянием р и q.
Индекс физического объёма продукции (Ласпейраса):
Это значит товарооборот в текущем периоде возрос на 17% в связи с
изменением объёма реализации.
Индекс цены (Пааше):
Индекс цены показал нам, что стоимость продукции в текущем периоде по
сравнению с базисным сократился на 9% под влиянием изменения цен.
7.3.
Средние индексы
Агрегатная форма индекса – его основная форма, но не единственная в
ряде случаев для удобства расчётов в том случае если мы располагаем значениями
индивидуальных индексов на практике удобно использовать средние индексы.
Средний индекс – индекс, вычисленный как
средняя величина из индивидуальных индексов.
Средний гармонический индекс цены:
Средний арифметический индекс физического объема:
Цепные индексы – ряд индексов одного и того же
явления, вычисленных с меняющейся от индекса к индексу базой сравнения.
,
.
7.4. Индексы структурных сдвигов
При изучении динамики показателей приходится
определять изменение средней величины индексируемого показателя, которое
обусловлено взаимодействием двух факторов – изменением значения индексируемого
показателя у отдельных групп единиц и изменением структуры явления, т.е.
изменением доли отдельных групп единиц совокупности в общей их численности. Для
этого вычисляются три индекса: переменного состава, постоянного состава и
структурных сдвигов.
Индекс переменного состава – индекс,
выражающий соотношение средних уровней изучаемого явления, относящихся к разным
периодам времени. Он отражает изменение не только индексируемой величины, но и
структуры совокупности (весов).

Индекс постоянного (фиксированного) состава –
индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода,
и показывающий изменение только индексируемой величины. Это агрегатный индекс.

Индекс структурных сдвигов – индекс,
характеризующий влияние изменения структуры изучаемого явления на динамику
среднего уровня этого явления.

Существует взаимосвязь между этими индексами: .
Пример: по имеющимся данным о себестоимости
единицы продукции на трех предприятиях в текущем и базисном периодах получили
следующие индексы структурных сдвигов
средняя себестоимость по трем
предприятиям снизилась в текущем периоде по сравнению с базисным на 3,25%.
себестоимость в текущем периоде по
сравнению с базисным возросла в среднем на 2,1%.
изменение доли предприятий в общем объеме
произведенной продукции привело к снижению себестоимости на 5,24%.
Рекомендуемая литература
1.
Елисеева И.И., Юзбашев М.М. Общая теория
статистики: Учебник. – М.: ИНФРА-М, 1998.
2.
Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая
теория статистики: Учебник. Изд. 2-е, испр. и доп. – М.: ИНФРА-М, 2001. – 416
с. — (Серия «Высшее образование»).
3.
Практикум по теории статистики: Учеб. Пособие / Под
ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2001.- 416 с.: ил.
4.
Теория статистики: Учебник / Под ред. проф. Р.А.
Шмойловой. – 3-е изд., перераб. – М.: Финансы и статистика, 2001.- 506 с.: ил.
5.
Теория статистики: Учебно-практическое пособие для
системы дистанционного образования /Под ред. В.Г. Минашкина. – М.: МЭСИ, 1998.
Виктория
Николаевна Шайкина
общая теория статистики
Учебное
пособие
Под ред.
В.В. Лихолетова
Технический
редактор А.В. Миних
Издательство Южно-Уральского государственного университета
Подписано
в печать
Формат
60х84 1/16. Печать офсетная. Усл. печ. л. Уч.-изд. л.
Тираж 100 экз. Заказ . Цена р.
Отпечатано
в типографии Издательства ЮУрГУ. 454080,
г. Челябинск,
пр. им. В.И.Ленина, 76
.
Здравствуйте, на этой странице я собрала краткий курс лекций по предмету «Статистика».
Лекции подготовлены для студентов любых специальностей и охватывает курс предмета «Статистика».
В лекциях вы найдёте основные законы, теоремы, формулы и примеры с решением.
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Стати́стика — отрасль знаний, наука, в которой излагаются общие вопросы сбора, измерения, мониторинга, анализа массовых статистических (количественных или качественных) данных и их сравнение; изучение количественной стороны массовых общественных явлений в числовой форме. wikipedia.org/wiki/Статистика
Статистическое наблюдение, сводка и группировка
Статистическое наблюдение – это сбор данных (фактов, сведений) об изучаемых явлениях. При подготовке к проведению статистического наблюдения решаются программно-методологические и организационные вопросы.
Программно-методологические вопросы включают в себя формулировку задачи наблюдения, определение объекта и единиц наблюдения, а также составление программы наблюдения.
Объектом наблюдения называют явление или совокупность явлений, информацию о которых собирают в процессе наблюдения.
Единицы наблюдения – первичные элементы объекта, являющиеся носителями признаков, подлежащих регистрации.
Программа наблюдения – перечень вопросов, ответы на которые получают в процессе наблюдения.
Для решения организационных вопросов составляется организационный план статистического наблюдения, определяющий цель, вид, форму, способ наблюдения, место и сроки его проведения.
В результате статистического наблюдения получают первичные данные о единицах совокупности, которые на следующем этапе статистического исследования – этапе сводки – обобщаются в группы, систематизируются. Статистическая сводка – это приведение собранной информации к виду, удобному для проведения анализа. Простая сводка заключается в простом подсчете общих итогов, сложная – в группировке единичных данных по однородному признаку, подсчете итогов по ним и представлении результатов в виде статистических таблиц.
Статистические группировки в зависимости от решаемых задач подразделяются на типологические, структурные и аналитические.
Статистическая группировка позволяет дать характеристику размеров, структуры и взаимосвязи изучаемых явлений, выявить их закономерности.
Важным направлением в статистической сводке является построение рядов распределения, одно из назначений которых состоит в изучении структуры исследуемой совокупности, характера и закономерности распределения.
Ряд распределения – это простейшая группировка, представляющая собой распределение численности единиц совокупности по значению какого-либо признака.
Вариантами ряда распределения являются отдельные значения признака, а численности отдельных вариантов или групп ряда, показывающие, как часто встречаются те или иные варианты в ряду распределения, называют частотами.
Ряды распределения, в основе которых лежит качественный признак, называют атрибутивными. Если ряд построен по количественному признаку, его называют вариационным.
Различают дискретные (признак – целое число) и интервальные вариационные ряды (признак принимает разные значения в пределах интервала).
При построении вариационного ряда с равными интервалами определяют число групп 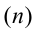
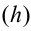
где N – число единиц совокупности.
Величина равного интервала рассчитывается по формуле:
где 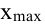
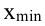
Для изучения связи между явлениями и их признаками строят корреляционную таблицу и аналитическую группировку.
Корреляционная таблица – это специальная комбинационная таблица, в которой представлена группировка по двум взаимосвязанным признакам: факторному и результативному.
Концентрация частот около диагоналей матрицы данных свидетельствует о наличии корреляционной связи между признаками.
Аналитическая группировка позволяет изучать взаимосвязь факторного и результативного признаков.
Основные этапы проведения аналитической группировки – обоснование и выбор факторного и результативного признаков, подсчет числа единиц в каждой из образованных групп, определение объема варьирующих признаков в пределах созданных групп, а также исчисление средних размеров результативного показателя. Результаты группировки оформляются в таблице.
Абсолютные и относительные показатели
Абсолютные и относительные величины являются обобщающими показателями, характеризующими количественную сторону общественных явлений. Различают два вида обобщающих показателей: абсолютные и относительные величины.
Абсолютные величины – именованные числа, имеющие определенную размерность и единицы измерения. Они характеризуют показатели на момент времени или за период. В зависимости от различных причин и целей анализа применяются натуральные, условнонатуральные, денежные и трудовые единицы измерения.
В практической деятельности при отсутствии необходимой информации абсолютные величины получают расчетным путем, например на основе балансовой увязки:
где 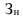
П – поступление за период;
Р – расход за период; 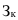
Отсюда:
Абсолютные статистические величины широко используют в анализе и прогнозировании состояния и развития явлений общественной жизни. На основе абсолютных величин исчисляют относительные величины.
Относительные величины характеризуют количественное соотношение сравниваемых абсолютных величин.
Числитель – сравниваемая величина, ее называют текущей или отчетной величиной; знаменатель называют базой сравнения или основанием сравнения. Как правило, базу сравнения принимают равной 1, 100, 1000, 10000. Если отношение равно 1, то относительная величина показывает, во сколько раз текущая величина больше базисной или какую долю от базисной она составляет, и выражается в коэффициентах. Если база сравнения равна 100, то относительная величина выражена а процентах (%), если база сравнения равна 1000 – в промилле (‰), 10000 – в продецимилле (‰0).
Различают следующие виды относительных показателей: планового задания и выполнения плана, динамики, структуры, интенсивности, координации, сравнения.
1. Относительные показатели планового задания (ОППЗ) – отношение уровня, запланированного на предстоящий период (П), уровню показателя, достигнутого в предыдущем периоде 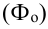
Относительные показатели выполнения плана (ОПВП) – отношение фактически достигнутого уровня в текущем периоде 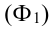
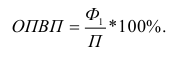
2. Относительные показатели динамики характеризуют изменение уровня развития какого-либо явления во времени. Показатели этого вида получаются делением уровня признака за определенный период или момент времени на уровень этого же показателя в предыдущий период или момент. Относительные величины динамики иначе называют темпами роста. Они могут быть выражены в коэффициентах или процентах и определяются с использованием переменной базы сравнения – цепные и постоянной базы сравнения – базисные.
3. Относительные показатели структуры характеризуют состав изучаемой совокупности, доли, удельные веса элементов совокупности в общем итоге и представляют собой отношение части единиц совокупности 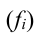
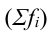
где d – удельный вес частей совокупности.
4. Относительные показатели интенсивности характеризуют степень насыщенности или развития данного явления в определенной среде, являются именованными показателями и могут выражаться в кратных отношениях, процентах, промилле и других формах.
5. Относительные показатели координации (ОПК) характеризуют отношения частей изучаемой совокупности к одной из них, принятой за базу сравнения. Они показывают, во сколько раз одна часть совокупности больше другой или сколько единиц одной части приходится на 1, 10, 100, 1000 единиц другой части. Эти относительные величины могут быть исчислены как по абсолютным показателям, так и по показателям структуры.
6. Относительные показатели сравнения (ОПС) характеризуют отношения одноименных абсолютных показателей, соответствующих одному и тому же периоду или моменту времени, но к различным объектам или территориям.
Средние величины и показатели вариации
Средняя является обобщающей характеристикой совокупности единиц по качественно однородному признаку. В статистике применяются различные виды средних: арифметическая, гармоническая, квадратическая, геометрическая и структурные средние – мода, медиана. Средние, кроме моды и медианы, исчисляются в двух формах: простой и взвешенной. Выбор формы средней зависит от исходных данных и содержания определяемого показателя. Наибольшее распространение получила средняя арифметическая, как простая, так и взвешенная.
Средняя арифметическая простая равна сумме значений признака, деленной на их число:
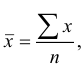
где х – значение признака (вариант);
n – число единиц признака.
Средняя арифметическая простая применяется в случаях, когда варианты представлены индивидуально в виде их перечня в любом порядке или ранжированного ряда.
Если данные представлены в виде дискретных или интервальных рядов распределения, в которых одинаковые значения признака (х) объединены в группы, имеющие различное число единиц (f), называемое частотой (весом), применяется средняя арифметическая взвешенная:
В качестве весов могут быть использованы относительные величины, выраженные в процентах (d). Метод расчета средней не изменяется:
Если проценты заменить коэффициентами 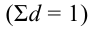
В статистике приходится вычислять средние по вариантам, которые являются групповыми (частными) средними. В таких случаях общая средняя определяется как средняя арифметическая взвешенная из групповых средних, в которой весами являются объемы единиц в группах.
Наряду со средней арифметической применяется средняя гармоническая, которая вычисляется из обратных значений осредняемого признака и по форме может быть простой и взвешенной.
Мода – значение признака, наиболее часто встречающееся в изучаемой совокупности. Для дискретных рядов распределения модой является вариант с наибольшей частотой. Для интервальных вариационных рядов распределения мода рассчитывается по формуле:
где 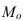
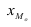
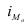
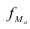
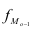
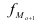
Медианой называется вариант, расположенный в середине упорядоченного вариационного ряда, делящий его на две равные части. Для интервальных вариационных рядов медиана рассчитывается по формуле:
где 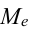
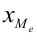
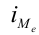
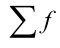
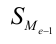
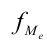
Показатели вариации. Для измерения степени колеблемости отдельных значений признака от средней исчисляются основные обобщающие показатели вариации: дисперсия, среднее квадратическое отклонение и коэффициент вариации.
Дисперсия 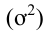
В зависимости от исходных данных дисперсия вычисляется по формуле средней арифметической простой или взвешенной:
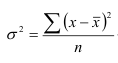
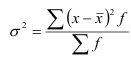
Среднее квадратическое отклонение 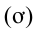
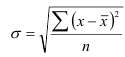
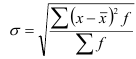
В отличие от дисперсии среднее квадратическое отклонение является абсолютной мерой вариации признака в совокупности и выражается в единицах измерения варьирующего признака (рублях, тоннах, процентах и т.д.).
Для сравнения размеров вариации различных признаков, а также для сравнения степени вариации одноименных признаков в нескольких совокупностях исчисляется относительный показатель вариации – коэффициент вариации (V), который представляет собой процентное отношение среднего квадратического отклонения к средней арифметической:
По величине коэффициента вариации можно судить о степени вариации признаков, а следовательно, об однородности состава совокупности. Чем больше его величина, тем больше разброс значений признака вокруг средней, тем менее однородна совокупность по составу.
Правило сложения дисперсий (вариаций). Для статистической совокупности, сгруппированной по изучаемому признаку, возможно вычисление трех видов дисперсий: общей 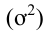
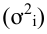
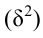
Если основанием группировки является факторный признак, то с помощью правила сложения дисперсий можно измерить силу его влияния на результативный признак, вычислив коэффициент детерминации и эмпирическое корреляционное отношение.
Коэффициент детерминации равен отношению межгрупповой дисперсии к общей:
и показывает долю общей вариации результативного признака, обусловленную вариацией группировочного признака.
Корень квадратный из коэффициента детерминации называется эмпирическим корреляционным отношением:
По абсолютной величине он может изменяться от 0 до 1. Если 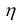
Возможно эта страница вам будет полезна:
Выборочное наблюдение
Целью выборочного наблюдения является определение характеристик генеральной совокупности – генеральной средней 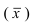
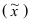
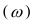
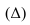
Собственно-случайная и механическая выборки. При случайном повторном отборе предельная ошибка выборки для средней 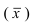
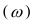
где 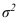
n – численность выборки;
t – коэффициент доверия, который определяется по таблице значений интегральной функции Лапласа при заданной вероятности (Р).
При бесповторном случайном и механическом отборе предельная ошибка выборки определяется по формулам:
где N – численность генеральной совокупности.
Типическая выборка. При типическом (районированном) отборе генеральная совокупность разбивается на однородные типические группы, районы. Отбор единиц наблюдения в выборочную совокупность производится различными методами. Рассмотрим типическую выборку с пропорциональным отбором внутри типических групп.
Объем выборки из типической группы при отборе, пропорциональном численности типических групп, определяется по формуле
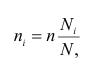
где 
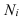
Предельная ошибка выборочной средней и доли при бесповторном случайном и механическом способе отбора внутри типических групп рассчитывается по формулам:
где 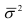
Серийная выборка. При серийном способе отбора генеральную совокупность делят на одинаковые по объему группы – серии. В выборочную совокупность отбираются серии. Внутри серий производится сплошное наблюдение единиц, попавших в серию.
При бесповторном отборе серий предельные ошибки выборочной средней и доли определяются по формуле
где 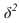
R – число серий в генеральной совокупности;
r – число отобранных серий.
В практике проектирования выборочного наблюдения возникает потребность в нахождении численности выборки, которая необходима для обеспечения определенной точности расчета генеральных характеристик – средней и доли.
Предельная ошибка выборки, вероятность ее появления и вариации признака предварительны известны.
При случайном повторном отборе численность выборки определяется по формуле:
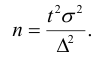
При случайном бесповторном и механическом отборе численность выборки вычисляется по формуле:
Для типической выборки
Для серийной выборки
Ряды динамики
Ряды динамики характеризуют изменение уровней показателя во времени. Ряды динамики подразделяют на ряды динамики абсолютных, средних и относительных величин. По признаку времени ряды динамики абсолютных величин подразделяют на моментные и интервальные ряды динамики. Каждый ряд динамики состоит из двух элементов: 1) периодов или моментов времени; 2) уровней.
Уровни ряда динамики должны сопоставимы по методологии расчета показателя, территории, продолжительности периодов, охватываемого объекта, единицам измерения и другим признакам.
В тех случаях, когда вначале имеются уровни ряда, исчисляемые по одной методологии или в одних границах, а затем уровни, исчисляемые по другой методологии или в других границах, уровни ряда динамики оказываются несопоставимы между собой. Чтобы привести уровни в ряду динамики к сопоставимому, годному для анализа виду, необходимо применить прием, который называют смыканием рядов динамики.
В статистике для сравнения базисных темпов роста изучаемых рядов динамики за анализируемый период принято исчислять коэффициент опережения 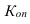
где 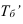
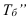
Для интервального ряда динамики средний уровень 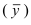
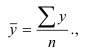
где у – уровни ряда.
Для моментного рядя динамики с равными интервалами средний уровень ряда исчисляется по формуле средней хронологической:
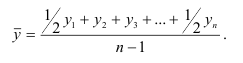
Для моментного ряда динамики с неравными интервалами средний уровень ряда исчисляется по формуле:
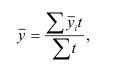
где 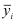
t – интервал времени (число месяцев между моментами времени).
Аналитические показатели ряда динамики
1. Абсолютный прирост (Δу) – это разность между последующим уровнем ряда и предыдущим (или базисным). цепной – 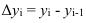
Средний абсолютный прирост исчисляется двумя способами: а) как средняя арифметическая простая годовых (цепных) приростов:
б) как отношение базисного прироста к числу периодов:
2. Темп роста 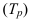
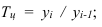
Между цепными и базисными темпами роста имеется взаимосвязь: произведение соответствующих цепных темпов роста равна базисному. Зная базисные темпы, можно исчислить цепные делением каждого последующего базисного темпа роста на каждый предыдущий.
3. Темп прироста 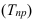
а) как отношение абсолютного прироста к предыдущему уровню:
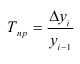
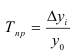
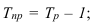
4. Абсолютное значение одного процента прироста (А1%) равно отношению абсолютного прироста цепного к темпу прироста цепному.
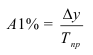
Этот показатель может быть исчислен иначе: как одна сотая часть предыдущего уровня.
Расчет среднего абсолютного значения одного процента прироста за несколько лет производится по формуле:
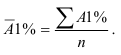
Среднегодовой темп роста исчисляется по формуле средней геометрической из цепных коэффициентов роста:
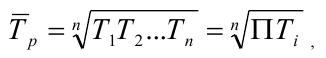
где n – число коэффициентов;
П — знак произведения.
Среднегодовой темп роста может быть исчислен из отношения конечного 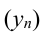
Среднегодовой темп прироста исчисляется следующим образом:
Выявление основной тенденции развития показателей может определяться следующими методами:
1) методом скользящей средней;
2) методом аналитического выравнивания.
2. Метод аналитического выравнивания ряда динамики по прямой. Уравнение прямой имеет вид
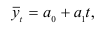
где 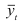
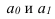
t – показатель времени (дни, месяцы, годы и т.д.).
Для нахождения параметров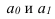
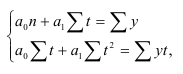
где у – фактические уровни ряда динамики;
n – число уровней.
После решения уравнения наносим на график фактические уровни и исчисленную прямую линию, характеризующую тенденцию динамического ряда.
Индексы сезонности.
Для исчисления индексов сезонности применяют различные методы, выбор которых зависит от характера общей тенденции ряда динамики. Если ряд динамики не содержит ярко выраженной тенденции развития, то индексы сезонности исчисляют непосредственно по эмпирическим данным без их предварительного выравнивания.
Для расчета индексов сезонности необходимо иметь помесячные данные минимум за три года. Для каждого месяца рассчитывается средний уровень 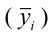
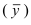
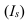
где 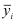
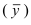
Когда уровни ряда динамики проявляют тенденцию к росту или снижению, то отклонения от постоянного среднего уровня могут исказить сезонные колебания. В таких случаях фактические данные сопоставляются с выравненными.
Для расчета индекса сезонности в таких рядах динамики применяется формула:
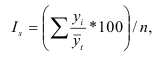
где 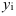
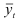
n – число лет.
Индексы
Индексы – обобщающие показатели сравнения во времени и в пространстве не только однотипных (одноименных) явлений, но и совокупностей, состоящих из несоизмеримых элементов.
Методики построения и расчета индексов как для временных, так и для пространственных сравнений одинаковы. Не различаются между собой и методы построения индексов различных явлений. Поэтому в данной главе формулы для расчета индексов приведены на примере индексируемых цен (р), объемов продаж (производства) (q), товарооборота (рq), изменяющихся во времени.
Динамика одноименных явлений изучается с помощью индивидуальных индексов (i), которые представляют собой известные относительные величины сравнения, динамики и выполнения плана (обязательств):
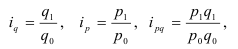
где подстрочное обозначение «0» соответствует уровню базисного периода (с которым сравнивают) или момент времени, «1» — уровню отчетного (сравниваемого) периода или момента времени.
Изменения совокупностей, состоящих из элементов, непосредственно не сопоставимых (например, различных видов продукции), изучают с помощью групповых, или общих, индексов (I). Последние по методам построения подразделяются на агрегатные индексы и средневзвешенные из индивидуальных индексов.
Формулы агрегатных индексов:
1) физического объема:
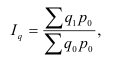
где q – индексируемая величина; 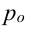
В случае индексов объемных показателей весами являются качественные показатели (цена, себестоимость и др.), зафиксированные на уровне базисного периода.
Разница между числителем и знаменателем индекса
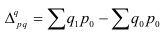
в данном случае означает абсолютное изменение товарооборота (прирост или снижение) за счет изменения физического объема;
2) цен и других качественных показателей:
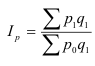
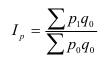
где q – объемы (количества) являются весами, взятыми на одинаковом уровне (отчетном или базисном).
Разница между числителем и знаменателем индексов
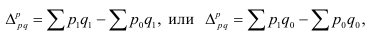
означает:
— в первом случае – абсолютный прирост товарооборота (выручки от продаж) в результате изменения цен или экономию (перерасход_ денежных средств населения в результате среднего снижения (повышения) цен;
— во втором случае – условный абсолютный прирост товарооборота, если бы объемы продаж в отчетном периоде совпали с объемами продаж в базисном периоде;
3) товарооборота (выручки от реализации или продаж):
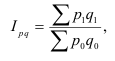
где pq – индексируемое сложное явление, в состав которого входят соизмеримые элементы совокупности. Разница между числителем и знаменателем индекса 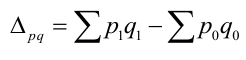
Формулы средних индексов из индивидуальных:
1) физического объема:
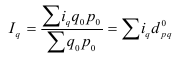
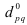
2) цен:
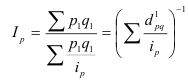
где 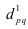
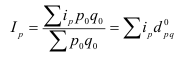
Если индексы качественных показателей построены на основе весов, взятых на уровне отчетного периода (например, по формуле Пааше), то рассмотренные выше агрегатные индексы, а также их элементы взаимосвязаны между собой: 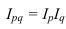
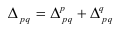
Участие каждого фактора в формировании общего прироста товарооборота в относительном выражении может быть определено так:
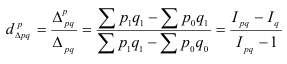
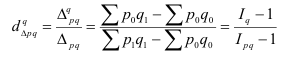
При этом 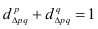
Если сравнивают друг с другом не два периода (момента), а более, то выделяют цепную и базисную системы индексов.
Цепные и базисные индивидуальные индексы взаимосвязаны между собой:
— произведение цепных индексов равно конечному базисному;
— частное от деления двух смежных базисных индексов равно промежуточному цепному.
Между цепными и базисными общими индексами, построенными на основе постоянных весов, существует взаимосвязь, аналогичная взаимосвязи между индивидуальными индексами.
Индексы, построенные на основе переменных весов, непосредственно перемножать и делить нельзя.
Индексный метод широко применяется также для изучения динамики средних величин и выявления факторов, влияющих на динамику средних. С этой целью исчисляется система взаимосвязанных индексов: переменного, постоянного состава и структурных сдвигов.
Индекс переменного состава представляет собой отношение двух взвешенных средних величин с переменными весами, характеризующее изменение индексируемого (осредняемого) показателя.
Индекс переменного состава для любых качественных показателей имеет следующий вид:
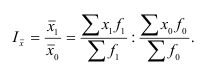
Величина этого индекса характеризует изменение средневзвешенной средней за счет влияния двух факторов: осредняемого показателя у отдельных единиц совокупности и структуры изучаемой совокупности.
Индекс постоянного (фиксированного) состава представляет собой отношение средних взвешенных с одними и теми же весами (при постоянной структуре). Индекс постоянного состава учитывает изменение только индексируемой величины и показывает средний размер изменения изучаемого показателя (х) у единиц совокупности. В общем виде он может быть записан следующим образом:
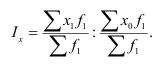
Для расчета индекса постоянного состава можно использовать агрегатную форму индекса:
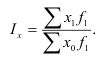
Индекс структурных сдвигов характеризует влияние изменения структуры изучаемого явления на динамику среднего уровня индексируемого показателя и рассчитывается по формуле:
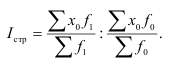
Под структурными изменениями понимается изменение доли отдельных групп единиц совокупности в общей их численности (d). Система взаимосвязанных индексов при анализе динамики среднего уровня качественного показателя имеет вид:
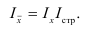
В индексах средних уровней в качестве весов могут быть взяты удельные веса единиц совокупности 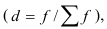
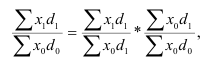
или

Аналогично приведенным формулам строятся индексы средних уровней: цен, себестоимости продукции, фондоотдачи, производительности труда, оплаты труда и др.
Возможно эта страница вам будет полезна:
Статистические методы изучения взаимосвязей
При статистическом исследовании корреляционных связей одной из основных задач является определение их формы, т.е. построение модели связи.
Построение регрессионной модели проходит несколько этапов: предварительный теоретический анализ, определение объекта, отбор факторов, сбор и подготовка информации, выбор модели связи, исчисление показателей тесноты корреляционной связи, оценка адекватности регрессионной модели.
Вычисление параметров корреляционных линейных уравнений по первичным данным. Если результативный признак с увеличением факторного признака равномерно возрастает или убывает, то такая зависимость является линейной и выражается уравнением прямой
(1)
где у — индивидуальные значения результативного признака;
х — индивидуальные значения факторного признака;
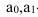
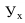
Параметры уравнения прямой 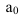
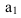
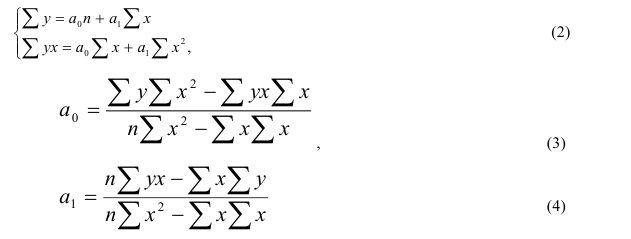
Что касается параметра уравнения регрессии в виде свободного члена, то возможен и такой подсчет:
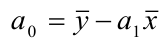
Ясно, что практически приемлемым является наименее трудоемкий вариант расчета (возможно производить расчеты на компьютере).
В уравнении прямой параметр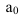
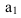

где 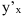
Средний коэффициент эластичности определяется для уравнения прямой по формуле
Коэффициент эластичности показывает, насколько процентов изменяется результативный признак при изменении факторного признака на 1%.
Определение параметров линейного однофакторного уравнения регрессии по сгруппированным данным. Если данные сгруппированы и представлены в виде корреляционной таблицы, то параметры линейного уравнения регрессии могут быть определены путем решения следующей системы нормальных уравнений:
или по формулам
где 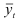
Параметр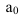
Расчет параметров степенной функции. Если значения факторного признака расположены в порядке геометрической прогрессии и соответствующие значения результативного признака также образуют геометрическую прогрессию, то связь между признаками может быть представлена степенной функцией вида
Для определения параметров степенной функции методом наименьших квадратов необходимо привести ее к линейному виду путем логарифмирования:
Система нормальных уравнений имеет вид
Параметры можно определить, решая систему нормальных уравнений или по формулам
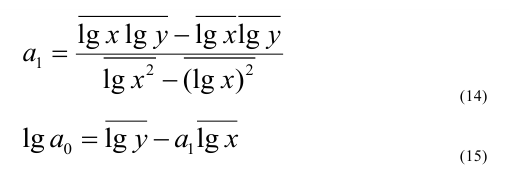
или
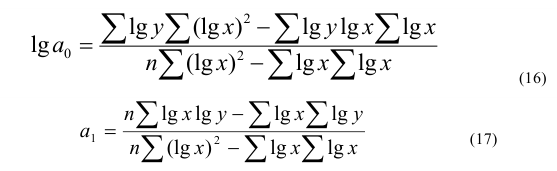
Параметр 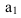
Расчет параметров уравнения гиперболы. Если результативный признак с увеличением факторного признака возрастает (или убывает) не бесконечно, а стремится к конечному пределу, то для анализа такого признака применяется уравнение гиперболы вида
Для определения параметров этого уравнения используется система нормальных уравнений
Чтобы определить параметры уравнения гиперболы методом наименьших квадратов, необходимо привести его к линейному виду. Для этого произведем замену переменных 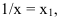
Параметры уравнения гиперболы можно вычислить по формулам
Статистические методы измерения тесноты корреляционной связи между двумя признаками. Одним из важнейших этапов исследования корреляционной связи является измерение ее тесноты. Для этого применяются: линейный коэффициент корреляции, теоретическое корреляционное отношение, индекс корреляции.
Линейный коэффициент корреляции вычисляется по формулам и применяется для измерения тесноты связи только при линейной форме связи:
Теоретическое корреляционное отношение и индекс корреляции применяются для измерения тесноты корреляционной связи между признаками при любой форме связи, как линейной, так и нелинейной.
Оба показателя можно вычислять только после того, как определена форма связи и исчислена теоретическая линия регрессии.
Теоретическое корреляционное отношение рассчитывается по формулам
где 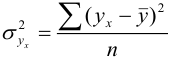
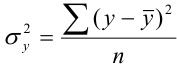
Теоретическое корреляционное отношение изменяется от 0 до 1: чем ближе корреляционное отношение к 1, тем теснее связь между признаками.
Для упрощения расчетов меры тесноты корреляционной связи часто применяется индекс корреляционной связи, который определяется по следующим формулам:
, где 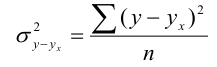
Проверка адекватности однофакторной регрессионной модели и значимости показателей тесноты корреляционной связи. Адекватность регрессионной модели при малой выборке можно оценить F-критерием Фишера:
, где m — число параметров модели;
n — число единиц наблюдения.
Эмпирическое значение критерия 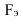
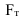
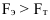
Значимость коэффициентов линейного уравнения регрессии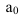
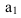
Эмпирическое значение t — критерия сравнивается с критическим (табличным) значением t — распределения Стьюдента с уровнем значимости 0,01 или 0,05 и числом степеней свободы (n — 2). Параметр признается значимым, если эмпирическое значение t больше табличного.
Аналогично проводится оценка коэффициента корреляции r с помощью t критерия, который определяется по формуле
где (n — 2) — число степеней свободы.
Если эмпирическое значение t оказывается больше табличного, то линейный коэффициент корреляции признается значимым.
Построение моделей связи в виде уравнения множественной регрессии. Изменение экономических явлений происходит под влиянием не одного, а большого числа самых разнообразных факторов. Связь между результативным признаком и двумя и более факторами принято выражать уравнением множественной регрессии.
Уравнения множественной регрессии могут быть линейные, криволинейные и комбинированные.
Наиболее простым видом уравнения множественной регрессии является линейное уравнение с двумя независимыми переменными:
Параметры уравнения множественной регрессии определяются методом наименьших квадратов путем решения системы нормальных уравнений:
Параметры уравнения множественной регрессии показывают изменение результативного признака при изменении факторного признака на единицу. Для оценки влияния факторных признаков на результативный рассчитываются частные коэффициенты эластичности и бета-коэффициенты.
Частный коэффициент эластичности (Э) вычисляется по формуле
где 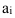
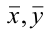
Частный коэффициент эластичности показывает, на сколько процентов изменяется результативный признак при изменении факторного признака на 1% при фиксированных значениях других факторов.
Бета-коэффициент (β) вычисляется по формуле
Бета-коэффициент показывает, на какую часть сигмы изменяется результативный признак при изменении факторного признака на величину его сигмы.
Сравнение бета-коэффициентов при различных факторах дает возможность оценить силу их воздействия на результативный признак.
Параметры уравнения регрессии можно определять по формулам через коэффициенты корреляции и средние квадратические отклонения:
Парные коэффициенты корреляции можно вычислить по следующим формулам:
Средние квадратические отклонения определяются по формулам
Статистические методы измерения тесноты корреляционной связи в многофакторных моделях. При проведении многофакторного корреляционного анализа возникает необходимость расчета множественных, парных и частных коэффициентов корреляции. Для измерения тесноты корреляционной связи между результативным признаком и несколькими факторными при линейной форме связи рассчитывается множественный коэффициент корреляции по формуле
где 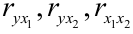
Множественный коэффициент корреляции изменяется от 0 до +1. Он показывает тесноту корреляционной связи между результативным признаком и факторными признаками, включенными в уравнение множественной регрессии.
Парные коэффициенты корреляции вычисляются по формулам
или по формулам (42), (43), (44).
Парные коэффициенты корреляции показывают тесноту корреляционной связи как между факторными и результативными признаками, так и между признаками-факторами.
Для исследования тесноты корреляционной связи между признаками при построении моделей множественной регрессии применяются частные (парные) коэффициенты корреляции, которые характеризуют тесноту корреляционной связи между факторным и результативным признаками, при элиминировании влияния учтенных факторов.
Возможно эта страница вам будет полезна:
Частные коэффициенты корреляции вычисляются по формулам
Теоретическое корреляционное отношение и совокупный индекс корреляции. Эти показатели имеют такой же экономический смысл, что и при парной регрессии, и определяются по формулам
Вместо теоретического корреляционного отношения может быть использован адекватный ему показатель — совокупный индекс корреляции:
Проверка адекватности многофакторной регрессионной модели. Построенное уравнение множественной регрессии необходимо содержательно интерпретировать и оценить его с точки зрения адекватности реальной действительности. Прежде всего следует установить, соответствуют ли полученные данные тем гипотетическим представлениям, которые сложились в результате анализа, и показывают ли они причинно-следственные связи, которые ожидались. Для оценки адекватности модели можно вычислить отклонение теоретических данных от эмпирических, остаточную дисперсию, также ошибку аппроксимации, которая определяется по формуле
Особое внимание необходимо обратить на интерпретацию и оценку параметров уравнения. Параметры уравнения регрессии следует проверить на их значимость.
Для оценки значимости параметров при малых выборках уравнения множественной регрессии используется t -критерий Стьюдента при (n — m- 1) степенях свободы:
Значения 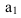
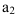
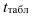
Адекватность уравнения регрессии оценивается с помощью F-критерия Фишера, который определяется по формуле
Если 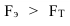
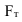
Существенность совокупного коэффициента корреляции также оценивается с помощью t-критерия Стьюдента:
Если 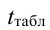
Статистика населения и трудовых ресурсов
Экономически активное население (рабочая сила) – часть населения, обеспечивающая предложение рабочей силы для производства товаров и услуг. Численность экономически активного населения включает занятых и безработных.
Коэффициент экономической активности населения определяется отношением численности экономически активного населения к общей численности населения:
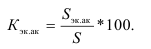
Коэффициент занятости населения определяется отношением численности занятого населения к численности экономически активного населения:
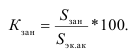
Коэффициент безработицы определяется отношением численности безработных к численности экономически активного населения:
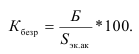
Численность трудовых ресурсов определяется как численность трудоспособного населения в трудоспособном возрасте и работающих лиц за пределами трудоспособного возраста (лица пенсионного возраста и подростки).
Статистика национального богатства
По определению, принятому в отечественной статистике, национальное богатство представляет собой совокупность ресурсов страны – экономических активов, создающих необходимые условия для производства товаров, оказания услуг и обеспечения жизни людей.
Экономические активы, включаемые в состав национального богатства, подразделяются на финансовые и нефинансовые.
Объем национального богатства определяется, как правило, в стоимостном выражении в текущих и постоянных ценах на начало и конец года.
Значительный удельный вес в составе накопленного богатства занимают основные производственные фонды. Статистика характеризует фонды системой показателей, среди которых показатели объема, состава фондов, коэффициенты состояния, движения основных фондов, показатели их использования, показатели динамики.
К коэффициентам состояния основных фондов относятся:
— коэффициент износа основных фондов;

— коэффициент годности основных фондов:
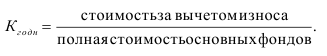
Эти коэффициенты являются моментными показателями, то есть характеризуют степень физического состояния фондов на определенную дату.
Расширенное воспроизводство основных фондов характеризуют коэффициенты выбытия и обновления за период.
Коэффициент выбытия рассчитывается как отношение стоимости фондов, выбывших за год, к стоимости фондов на начало года.
Коэффициент обновления представляет собой отношение стоимости введенных за год новых фондов к их полной стоимости на конец года.
Для характеристики простого и расширенного воспроизводства основных фондов составляют балансы основных фондов по полной стоимости и по стоимости за вычетом износа. В балансах основных фондов показывается их наличие на начало года, поступление по источникам, выбытие по направлениям, наличие на конец года. При составлении баланса основных фондов по стоимости за вычетом износа, кроме того. учитывают сумму амортизации, уменьшающей стоимость основных фондов.
Эффективность использования основных фондов характеризует показатель фондоотдачи, рассчитываемый как отношение объема выпуска продукции за год к среднегодовой полной стоимости основных фондов.
Статистика рассчитывает ряд показателей для характеристики оборотных фондов. Основными из них являются коэффициент оборачиваемости (количество оборотов) оборотных средств и продолжительность одного оборота.
Коэффициент оборачиваемости есть отношение объема реализации к оборотным средствам. Продолжительность одного оборота может быть рассчитана как отношение числа дней в периоде к числу оборотов.
При ускорении оборачиваемости оборотных средств часть их высвобождается из оборота. Эта высвобождающаяся в результате ускорения оборачиваемости часть может быть рассчитана по формуле
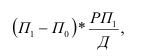
где 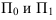
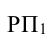
Д — продолжительность периода (месяц — 30 дней, квартал — 90 дней, год — 360 дней).
Возможно эта страница вам будет полезна:
Статистика макроэкономических показателей
Система показателей, характеризующих развитие экономики, включает результаты деятельности на всех уровнях производства. Оценка конечных результатов деятельности осуществляется на уровне отдельного предприятия, организации, учреждения и других хозяйствующих субъектов, а также в разрезе секторов отраслей и экономики в целом.
Система статистических показателей необходима для достоверной оценки результатов функционирования и прогнозирования дальнейшего развития экономики страны.
Показатели результатов функционирования экономики в целом на макроуровне принято называть макроэкономическими показателями. Они определяются на основе системы национальных счетов (СНС) и характеризуют различные стадии экономической деятельности: производство товаров и услуг, образование и распределение доходов и их конечное использование.
Стадия производства характеризуется следующими показателями: валовой выпуск (ВВ), промежуточное потребление (ПП), валовая добавленная стоимость (ВДС) и валовой внутренний продукт (ВВП).
Валовой выпуск — это суммарная стоимость всех произведенных товаров и услуг за год в экономике, имеющих рыночный и нерыночный характер.
Товары и услуги оцениваются по основным ценам, т.е. ценам, по которым они продаются, поэтому валовой выпуск в отраслевом разрезе исчисляется в основных ценах.
Промежуточное потребление определяется как стоимость товаров и рыночных услуг, которые трансформируются или полностью потребляются в течение данного периода с целью производства других товаров и услуг. Потребление основного капитала (амортизация) не входит в промежуточное потребление.
Валовая добавленная стоимость (ВДС) исчисляется на уровне отраслей экономики как разность между валовым выпуском товаров, услуг и промежуточным потреблением. Термин «валовая» означает то, что показатель включает потребленную в процессе производства стоимость основного капитала.
В системе национальных счетов валовая добавленная стоимость оценивается в основных ценах, т.е. в ценах, включающих субсидии на продукты, но не включающих налоги на продукты.
Налоги на продукты включают платежи, размер которых прямо зависит от стоимости произведенной продукции и оказанных услуг: налог на добавленную стоимость, налог с продаж, акцизы и др. Налоги на импорт — это налоги на импортируемые товары и услуги.
Термин «чистые» налоги на продукты и импорт (ЧНП) и (ЧНИ) в данном случае означает, что налоги показаны за вычетом соответствующих субсидий.
Субсидии (С) — текущие некомпенсируемые выплаты из федерального бюджета предприятиям при условии производства ими определенного вида продукции или услуг.
ВДС (в основных ценах) = (ВВ — ПП) — косвенно измеряемые услуги финансового посредничества.
ВДС (в рыночных ценах) = ВДС (в основных ценах) + ЧНП + ЧНИ, ЧНП = НП — С, ЧНИ = НИ — С,
где ЧНП, ЧНИ — чистые налоги на продукты и импорт,
НП и НИ — налоги на продукты и импорт,
С — субсидии.
Валовой внутренний продукт (ВВП) является основным экономическим индикатором в зарубежной и отечественной статистике. ВВП — показатель стоимости товаров и услуг, созданной в результате производственной деятельности институциональных единиц на экономической территории данной страны, как правило, за год.
ВВП на стадии производства рассчитывается как сумма валовой добавленной стоимости всех отраслей и секторов экономики в рыночных ценах (включая налоги на продукты и импорт без НДС):
ВВП = Σ ВДС.
ВВП исчисляется также в рыночных ценах:
ВВП = Σ ВДС + ЧНП + ЧНИ.
Стадия образования доходов в СНС характеризуется следующими показателями:
• оплата труда наемных работников (ОТ);
• налоги на производство и импорт (включая налоги на продукты) (НП);
• другие налоги на производство (ДНП);
• субсидии на производство и импорт;
• валовая прибыль экономики (ВПЭ). Таким образом, ВВП на стадии образования доходов равен сумме:
ВВП = ОТ + ЧНП + ЧНИ + ДНП + ВПЭ.
Валовая прибыль экономики (ВПЭ) — макроэкономический показатель, характеризующий превышение доходов над расходами, которые предприятия имеют в результате производства до вычета явных или скрытых процентных издержек, арендной платы или других доходов от собственности.
Показатель ВПЭ рассчитывается балансовым путем и определяется как валовая добавленная стоимость (ВДС) за вычетом оплаты труда наемных работников (ОТ) и других чистых налогов на производство (ДЧНП):
ВПЭ = ВДС — ОТ — ДЧНП.
Чистая прибыль экономики (ЧПЭ) — это показатель макроэкономической прибыли в СНС, который рассчитывается путем вычитания потребления основного капитала (ПОК) из валовой прибыли экономики:
ЧПЭ = ВПЭ — ПОК.
На стадии использования ВВП рассчитывается как сумма конечного потребления продуктов и услуг (КП), валового накопления (ВН) и чистого экспорта товаров и услуг, который представляет разницу между экспортом и импортом (Э — И):
ВВП = КП + ВН + (Э — И).
Конечное потребление продуктов и услуг складывается из расходов на конечное потребление домашних хозяйств, государственных учреждений, некоммерческих организаций, обслуживающих домашние хозяйства. Валовое накопление рассчитывается как сумма валового накопления основного капитала, изменения запасов материальных оборотных средств и чистого приобретения ценностей. Прирост основного капитала приравнивается к общему объему капитальных вложений за счет всех источников финансирования.
Чистый экспорт товаров и услуг рассчитывается во внутренних ценах как разница между экспортом и импортом и включает в себя оборот российской торговли со странами как дальнего, так и ближнего зарубежья.
Для оценки качества расчетов, проводимых в СНС, используют специфический показатель — статистическое расхождение между произведенным и использованным ВВП. Он показывает расхождение между объемами ВВП, рассчитанными различными способами: на стадии производства и на стадии использования. Расхождение может возникнуть из-за многих объективных и субъективных причин. К основным причинам возникновения статистического расхождения относятся: недостаток необходимой информации, определенные методологические неточности, связанные с переходным характером современной российской экономики и общей незавершенностью системы национальных счетов. В международной практике принято считать допустимым уровнем погрешности статистическое расхождение, составляющее не более 5% ВВП.
Индекс-дефлятор ВВП — отношение ВВП измеренного в текущих ценах к объему ВВП, исчисленного в постоянных ценах базисного периода. Индекс-дефлятор ВВП рассчитывается по структуре веса отчетного периода, характеризует среднее изменение цен на добавленную стоимость, созданную во всех отраслях экономики (включая рыночные и нерыночные услуги), и чистых налогов на продукты и импорт.
Для обобщающей характеристики экономики региона рассчитывается показатель валовой региональный продукт (ВРП). Расчеты ВРП осуществляются производственным методом как сумма валовой добавленной стоимости, произведенной на территории региона за определенный период.
Валовой национальный доход (ВИД) равен сумме ВВП в рыночных ценах плюс доходы от собственности, полученные от «остальною мира», минус соответствующие им потоки, переданные «остальному миру».
Чистый национальный доход (ЧНД) в рыночных ценах получается в результате вычитания потребления основного капитала (ПОК) из валового национального дохода:
ЧНД = ВНД — ПОК.
Потребление основного капитала представляет собой уменьшение стоимости основного капитала в течение отчетного периода в результате его физического и морального износа, случайных повреждений.
Располагаемый доход образуется в результате распределения и перераспределения доходов и предназначен для конечного потребления и сбережения.
Располагаемый национальный доход (РНД) в рыночных ценах представляет собой ЧНД плюс чистые текущие трансферты из-за границы (т.е. дарения, пожертвования, гуманитарная помощь, а также аналогичные перераспределительные поступления из-за границы за вычетом аналогичных трансфертов, переданных за границу).
Валовой располагаемый доход (ВРД) равен ВНД в рыночных ценах плюс (минус) текущие трансферты, полученные от «остального мира» и переданные «остальному миру».
Чистый располагаемый доход (ЧРД) представляет собой разность между ВРД и потреблением основного капитала (ПОК):
ЧРД = ВРД — ПОК.
Сбережение — часть ВРД, которая не входит в конечное потребление товаров и услуг. В экономическом смысле она соответствует сложившемуся в отечественной практике показателю «Накопление». Сбережение определяется как разность между суммой текущих доходов и расходов.
Валовое сбережение (ВС) — сбережение до вычета потребления основного капитала, равное сумме валовых сбережений всех секторов экономики.
Валовое накопление в целом по экономике включает валовое накопление основного капитала, изменение запасов материальных оборотных средств и чистое приобретение ценностей.
Социальная статистика
К основным социально-экономическим индикаторам уровня жизни населения относятся денежные доходы и расходы населения, их состав и использование; динамика реальных располагаемых доходов населения; показатели потребления товаров и услуг; показатели дифференциации доходов; уровень бедности и др.
Среднедушевые денежные доходы населения (или средние по домашним хозяйствам) исчисляются делением общей суммы денежного дохода за год на среднегодовую численность населения (или число домохозяйств).
Располагаемые доходы — это номинальные денежные доходы за вычетом обязательных платежей и взносов.
Среднемесячная начисленная заработная плата работников в отраслях экономики рассчитывается делением начисленного месячного фонда заработной платы на среднесписочную численность работающих (занятых в экономике) в расчете на месяц.
С целью устранения фактора изменений цен номинальные и располагаемые денежные доходы (расходы) населения рассчитываются в реальном выражении с корректировкой на индексы потребительских цен (сводный и субиндексы на отдельные товарные группы).
Расчет показателей в реальном выражении осуществляется делением соответствующих показателей текущего периода на индекс потребительских цен.
Индекс реальной заработной платы исчисляется по формуле
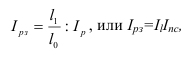
где 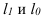
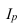
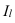
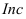
Реальные располагаемые денежные доходы определяются исходя из денежных доходов текущего года за минусом обязательных платежей и взносов, скорректированных на индекс потребительских цен.
Для оценки интенсивности изменения структуры доходов (расходов) населения, а также потребительских расходов домашних хозяйств по группам населения в одном из исследуемых периодов используют:
1) линейный коэффициент структурных различий (сдвигов)
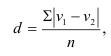
где 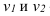
n — число структурных составляющих:
2) квадратический коэффициент структурных сдвигов (в том случае, если показатели измерены в процентах,
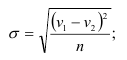
3) интегральный коэффициент К. Гатева
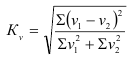
изменяется в пределах
4) индекс Салаи
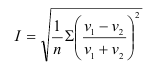
изменяется в пределах
Динамика общего объема потребления населением товаров и услуг, а также динамика потребления по отдельным товарным группам или услугам изучается индексным методом.
Стоимость реализованных населению товаров и услуг в фактических ценах пересчитывается в цены и тарифы базисного периода методом дефлятирования. При этом общий объем потребления населением товаров и услуг отчетного периода делят на средний индекс потребительских цен товаров и услуг:
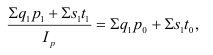
где 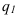
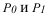
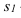
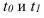
Расчет агрегатного индекса физического объема потребления осуществляется по формуле
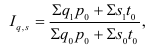
где 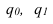
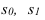
Для изучения динамики потребления отдельных групп товаров или услуг применяется средний гармонический индекс физического объема следующего вида:
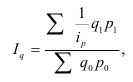
где 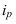
В социальной статистике на практике используется коэффициент эластичности потребления в зависимости от изменения доходов, который рассчитывается по формуле
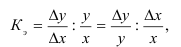
где х и у — начальные доход и потребление;
Δх и Δy — их приращения за некоторый период (или при переходе от одной группы к другой).
Он позволяет определить, на сколько процентов возрастает (или снижается) потребление товаров или услуг при росте дохода на 1%.
Если коэффициент эластичности отрицательный, то качество товара принято квалифицировать как низкое, т.е. потребление товара уменьшается с повышением доходов. Если 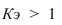
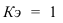
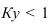
К основным характеристикам дифференциации доходов населения и уровня бедности относятся следующие показатели:
• модальный, медианный и средний доход;
• коэффициент фондов, децильный коэффициент дифференциации;
• коэффициент концентрации доходов Джини;
• уровень бедности, среднедушевой доход бедного населения, дефицит дохода.
Их исчисляют на основе распределения численности (или долей) населения по размеру среднедушевого (среднего на домохозяйство) денежного дохода, сгруппированного по интервалам с заданными (фиксированными) границами, децильным (10%-м) и другим интервалам.
Коэффициент фондов 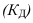
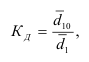
где 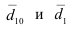
При расчете среднего дохода 10% населения в знаменателе показателей 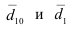
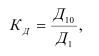
где 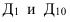
Децильные коэффициенты доходов и потребления населения 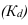
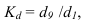
где 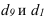
Коэффициент концентрации доходов Джини 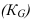
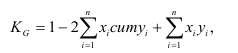
где 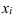
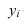
n — число социальных групп; 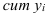
При равномерном распределении доходов коэффициент Джини стремится к нулю. Чем выше поляризация доходов в обществе, тем ближе этот коэффициент к единице.
Для графического изображения степени неравномерности в распределении доходов строится кривая Лоренца. При равномерном распределении доходов каждая 20%-я группа населения имела бы пятую часть доходов общества. На графике это изображается диагональю квадрата, что означает равномерное распределение. При неравномерном распределении «линия концентрации» представляет собой вогнутую вниз кривую. Чем больше отклонение кривой Лоренца от диагонали квадрата, тем выше поляризация доходов общества. Коэффициент Джини можно рассчитать но кривой Лоренца как отношение площади фигуры, образуемой кривой Лоренца и линией равномерного распределения 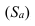
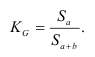
Уровень бедности — это удельный вес населения с доходами ниже прожиточного минимума в общей численности населения. Прожиточный минимум представляет собой стоимость минимальной продовольственной «корзины», а также расходы на непродовольственные товары и услуги, налоги и обязательные платежи, исходя из доли затрат на эти цели в бюджетах у 10% низкодоходных домашних хозяйств.
Показатель дефицита дохода равен суммарному доходу населения, недостающему до величины прожиточного минимума.
Возможно эта страница вам будет полезна:
Система национальных счетов
Система национальных счетов (СНС) — это современная информационная база, адекватная реальному хозяйственному механизму и используемая для описания и анализа процессов рыночной экономики на макроуровне. СНС представляет собой развернутую статистическую макроэкономическую модель экономики.
СНС — основа национального счетоводства. Для экономического анализа деятельности хозяйствующих субъектов и для макроэкономического анализа на национальном уровне экономические операции представляются в виде отдельных счетов. Счета используются для регистрации экономических операций, осуществляемых институциональными единицами, а именно предприятиями, учреждениями, организациями, домашними хозяйствами и др., которые являются резидентами данной страны. Отражаются также и операции между резидентами данной страны и нерезидентами.
Национальные счета — набор взаимосвязанных таблиц, имеющих вид балансовых построений. По методу построения национальные счета аналогичны бухгалтерским счетам. Каждый счет представляет собой баланс в виде двухсторонней таблицы, в которой каждая операция отражается дважды: один раз — в ресурсах, другой — в использовании. Итоги операций на каждой стороне счета балансируются или по определению, или с помощью балансирующей статьи, которая является ресурсной статьей следующего счета.
Балансирующая статья счета, обеспечивающая баланс (равенство) его правой и левой частей, рассчитывается как разность между объемами ресурсов и их использованием. Иначе говоря, балансирующая статья предыдущего счета, отраженная в разделе «Использование», является исходным показателем раздела «Ресурсы» последующего счета (табл. 12.1). Этим достигается увязка счетов между собой и образование системы национальных счетов. Таблица 12.1 — Балансирующие статьи счетов
Реализуемая в отечественной статистике Система национальных счетов основана на методологии, рекомендованной ООН, но категории и понятия СНС ООН приняты с учетом специфики организации и функционирования экономики страны. В ходе построения счетов использовались некоторые рекомендации новой версии Системы национальных счетов ООН, пересмотренной и принятой Статистической комиссией ООН в 1993 г. (СНС-93). Система национальных счетов, реализуемая в Российской Федерации, включает следующие счета:
Счета внутренней экономики:
• счет производства;
• счет образования доходов;
• счет распределения доходов:
а) счет распределения первичных доходов;
б) счет вторичного распределения доходов;
• счет использования располагаемого дохода;
• счет операций с капиталом;
• счет товаров и услуг.
Счета внешнеэкономических связей («остального мира»):
• счет текущих операций;
• счет капитальных затрат;
• финансовый счет.
Все счета являются консолидированными, т.е. построенными для экономики в целом, и отражают, с одной стороны, отношения между национальной экономикой и зарубежными странами, а с другой — взаимосвязь различных показателей системы счетов.
Для каждого сектора внутренней экономики предусматривается составление набора счетов — от счета производства до финансового счета. Счета разрабатываются также по секторам и регионам.
Статистика цен
Статистика уровня и структуры цен. Обобщающей характеристикой уровня цен на одноименный товар является его средняя цена. Наилучшая характеристика средней цены — средняя взвешенная:
• арифметическая, когда весами являются объемы продаж в натуральном выражении:
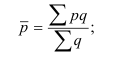
• гармоническая, когда весами служат объемы продаж в стоимостном выражении (выручка от продаж, или товарооборот):
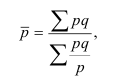
где р — индивидуальные значения цен на определенный момент времени (временные интервалы) регистрации или на конкурентных субрынках;
q — объемы продаж в натуральном выражении;
pq — выручка от продажи, или товарооборот.
Если данные об указанных весах недоступны, то в качестве весов могут использоваться другие показатели, например численность населения или число семей, проживающих на территориях, обслуживаемых субрынком. Здесь применяется средняя арифметическая взвешенная. Если, например, известно число дней непрерывной торговли при данном уровне цен, то используется средняя гармоническая взвешенная.
В тех случаях, когда сведения о весах отсутствуют вообще, допускается применение средних невзвешенных (простых) величин. Предпочтение при этом чаще всего отдается средней арифметической. Так, например, рассчитывается средняя цена конкретного товара, реализуемого различными торговыми точками за торговый день. Таким же образом определяют и среднюю цену товара на конкретном торговом месте за определенный период па основе данных о ежедневных значениях цен или одинаковых значениях цен в течение равных промежутков времени. Однако если цена резко возрастает в течение изучаемого периода, что вызывает заметное снижение объема продаж товара, то средняя арифметическая дает завышенное значение обобщающего показателя. Меньшее значение средней цены получается при использовании средней гармонической простой.
Средние цены в п. 2 и 3 совпали между собой. Они представляют собой наиболее точный уровень, истинное значение обобщающей характеристики цен торгового дня.
Остальные значения отличаются от найденного выше, поскольку были вычислены либо без взвешивания (п.1), либо с использованием не прямых, а косвенных показателей в качестве весов.
При этом завышение средней цены, найденной без взвешивания, объясняется отрицательной корреляцией между уровнями цен и объемами продаж — по более низким ценам продается больше товара, чем по более высокой цене.
Завышение цен, найденных в п. 4 и 5, вызвано неодинаковой структурой объема продаж товара и структурой населения, обслуживаемого различными субрынками. В данном случае доля населения, проживающего на территории субрынка I, выше, чем доля этого субрынка по количеству продаж. На данном субрынке цена самая высокая, что и приводит к завышению общей средней цены.
Средняя цена, вычисленная в п. 4, больше, чем в п. 5. Объясняется это различиями в структуре семейных образований между территориями. Здесь средний размер семьи на территории, обслуживаемой субрынком II, меньше, чем на территории субрынка I, a число семей больше. При этом цена товара на субрынке II ниже, что и занижает общую среднюю характеристику цены.
Структура цен изучается с помощью традиционных статистических методов на основе расчета и анализа во времени и в пространстве удельных весов или долей (относительных величин структуры) отдельных элементов общего уровня цен, выделяемых по различным признакам, исходя из целей исследования. Наиболее общую методику такого изучения см. в гл. 2.
Специфические особенности изучения структуры в статистике цен состоят в анализе числа и роли посреднических звеньев в формировании конечной (например, розничной) цены.
Определение числа посреднических звеньев связано с расчетом коэффициента звенности 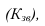
Роль звеньев-посредников в нарастании конечной цены товара характеризуется соотношением этой цены с оптовой ценой производителя товара.
Статистика вариации цен. Для изучения собственно вариации (дифференциации) цен используются традиционные методы анализа, основанные на вычислении таких показателей, как размах вариации, среднее линейное (арифметическое) отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации. Методику их расчета и решение типовой задачи см. в гл. 3.
Связанная (зависимая от факторов) вариация цен изучается с помощью дисперсионного анализа, проводимого на основе аналитической группировки с расчетом показателей тесноты взаимосвязи, например коэффициента детерминации и эмпирического корреляционного отношения.
Если наличие эмпирической зависимости между уровнем цен и влияющим на него фактором установлено, то анализ дополняется расчетом коэффициентов эластичности. Применяемый для фактических данных эмпирический коэффициент эластичности А. Маршала вычисляется по формуле
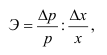
где Δх и Δр — абсолютные приросты факторного признака и цены; х и р — базовые значения факторного признака и цены соответственно.
Если, например, при изучении изменения цен в зависимости от уровня доходов населения по территориям коэффициент эластичности составил +1,1, то это означает, что прирост денежных доходов на один процент вызывает увеличение уровня цен на 1,1%.
Статистика динамики цен. Методику традиционного анализа динамических рядов любых явлений, включая цены, а также вычисления индексов с решением типовых задач см. в гл. 5 и 6.
Однако помимо традиционных методик для расчета индексов цен используются и другие.
Например, для однородных товаров (услуг) могут быть вычислены простейшие агрегатные индексы (субиндексы) по методикам:
Дюто —
Карли —
средней геометрической —
Для разноименных товаров (услуг) помимо общеизвестных также вычисляют индексы по методикам:
Эджворта — Маршалла —
Фишера (так называемая «идеальная» формула) —
Если при изучении динамики средней цены традиционная методика не дает положительных результатов оценки влияния структурного сдвига, то вычисления индексов цен переменного состава 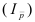
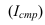
Статистика кредита
Статистика кредита использует различные показатели, изучающие объем, состав, структурные сдвиги, динамику, взаимосвязи и эффективность кредитный вложений.
Для характеристики объема кредитных вложений используются следующие показатели: остатки задолженности и размер выданных и погашенных ссуд (оборот по погашению и выдаче), средний размер ссуды, средний размер задолженности но кредиту, средний срок ссуды, средняя процентная ставка (доходность кредита) и др.
Состав кредитных вложений изучают по целевому назначению, формам собственности, территориям, категориям заемщиков, экономическим секторам, срокам погашения, видам остатков задолженности и другим признакам.
Большое внимание статистика уделяет изучению просроченных ссуд по их объему, составу и динамике.
Для анализа и прогноза кредитных вложений статистика кредита рассматривает тенденции их изменения, интенсивность изменений кредита во времени с использованием показателей анализа ряда динамики, а также трендовых и факторных динамических моделей.
Для выявления статистических закономерностей статистика изучает взаимосвязи кредитных вложений с показателями объема производства, капитальных вложений и т.д. при помощи однофакторного и многофакторного регрессионного анализа и индексного метода. Особое внимание уделяется эффективности кредитных вложений, т.е. анализу оборачиваемости кредитов, оценке влияния отдельных факторов на изменения оборачиваемости ссуд и др.
Структура, динамика, взаимосвязи кредитных вложений рассматриваются в гл. 2 «Абсолютные и относительные показатели», гл. 5 «Ряды динамики», гл. 6 «Индексы», гл. 7 «Статистические методы изучения взаимосвязей».
В данной главе изучаются объем и эффективность кредитных вложений.
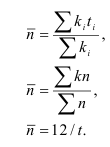
Для изучения влияния отдельных факторов на изменение средней длительности пользования кредитом строится система взаимосвязанных индексов
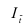
1) изменения длительности пользования кредитом в отраслях;
2) структурных сдвигов в однодневном обороте
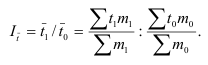
Абсолютное изменение средней длительности пользования кредитом за счет двух факторов:
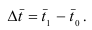
Далее, 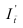
Абсолютное изменение средней длительности пользования кредитом за счет снижения длительности пользования кредитом в отраслях составит:
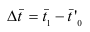
И, наконец, 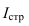
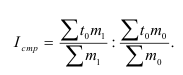
Абсолютное изменение средней длительности пользования кредитам за счет структурных сдвигов в однодневном обороте составит:
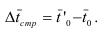
Общее изменение средней длительности пользования кредитом
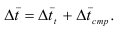
Индексы средней длительности пользования кредитом можно определить и по формулам
где 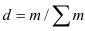
Возможно эта страница вам будет полезна:
Статистика денежного обращения
Система показателей статистики денежного обращения включает: денежный оборот, денежную массу, наличные деньги внебанковской системы, безналичные средства, скорость обращения, продолжительность оборота, купюрное строение денежной массы, индекс-дефлятор, покупательную способность рубля и др.
Денежная масса является важным количественным показателем движения денег, ее величина зависит от количества денег в обращении и от скорости их обращения.
Скорость обращения денег измеряется двумя показателями:
1) количеством оборотов (V) денег в обращении за рассматриваемый период, которое рассчитывается по формуле
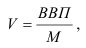
где ВВП — валовой внутренний продукт в текущих ценах;
М — общая масса денег, рассчитанная как остатки денег за изучаемый период.
Этот показатель характеризует скорость оборота денежной единицы. На практике в качестве универсального показателя денежной массы применяется денежный агрегат М2, который представляет собой объем наличных денег в обращении (вне банков) и остатков средств в национальной валюте на расчетных, текущих счетах и депозитах нефинансовых предприятий, организаций и физических лиц, являющихся резидентами Российской Федерации;
2) продолжительностью одного оборота денежной массы, которая рассчитывается по формуле
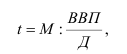
где Д — число календарных дней в периоде.
Рассмотренные показатели взаимосвязаны, поэтому если известна величина одного из них, то можно определить и другой показатель:
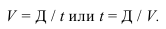
Скорость обращения денег зависит от величины валового внутреннего продукта, или совокупности созданных продуктов и услуг, и денежной массы.
Из известного уравнения денежного обмена MV = PQ, которое означает, что произведение денежной массы на скорость обращения денег равно произведению уровня цен на объем произведенных товаров и услуг (ВВП в текущих ценах), можно записать: MV = ВВП Тогда скорость обращения денег определяется по формуле
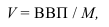
где
Этот показатель находится в прямой зависимости от объема ВВП и динамики цен на товары и услуги и обратно пропорционален денежной массе.
Изучение данных показателей в динамике позволяет установить их взаимосвязь:
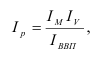
где 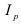
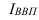
На практике индекс-дефлятор ВВП рассчитывается по формуле
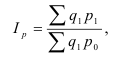
где 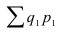
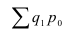
При увеличении числа оборотов скорость обращения денежной массы возрастает; при сокращении числа дней, необходимых для одного оборота денег, требуется меньшая денежная масса.
Для определения изменения скорости обращения денежной массы используется взаимосвязь следующих индексов:
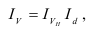
где 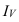
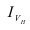
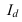
Абсолютное изменение скорости обращения денежной массы, определяемое индексным метолом, обусловлено влиянием следующих факторов:
1) изменением скорости обращения наличной денежной массы
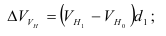
2) изменением доли наличности в общем объеме денежной массы
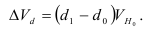
Таким образом, абсолютное изменение скорости обращения массы денег равно
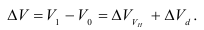
Для контроля за динамикой денежной массы и анализа объемов кредитных вложений коммерческих банков в экономику используется показатель, называемый денежным мультипликатором 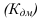
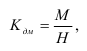
где М — денежная масса в обращении; Н — денежная база.
При этом денежная масса определяется по денежному агрегату М2, а показатель «денежная база» включает в себя наличные деньги н обращении (в том числе остатки средств в кассах коммерческих банков), остатки средств коммерческих банков на корреспондентских счетах в Банке России, фонд обязательных резервов коммерческих банков в Банке России. Денежный мультипликатор представляет собой коэффициент, характеризующий увеличение денежной массы в обороте в результате роста банковских резервов.
Для характеристики динамики купюрного строения денежной массы и выявления тенденции его изменения необходимы данные о величине средней купюры, которую можно рассчитать но формуле средней арифметической взвешенной:
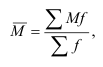
где М — достоинство купюр; f — число купюр.
В случае когда происходит переполнение каналов денежного обращения избыточной денежной массы при отсутствии увеличения произведенных товаров и услуг, возникает проблема опенки инфляции. Инфляция, как правило, измеряется с помощью индекса-дефлятора ВВП и индекса потребительских цен. На практике чаще всего для измерения инсоляции применяется индекс потребительских цен или индекс покупательной способности денежной единицы, определяемый как величина, обратная индексу потребительских цен:
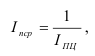
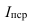
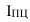
Индекс покупательной способности рубля показывает, во сколько раз обесценились деньги, т.е. характеризует инфляцию, и может исчисляться по отношению к денежной единице текущего и базисного периодов. Если индекс цен за анализируемый период повысится, то индекс покупательной способности рубля снизится, и наоборот, если индекс цен за рассматриваемый период понизится, то индекс покупательной способности рубля возрастет. Относительные показатели инсоляции рассчитывают как темпы роста или снижения покупательной способности рубля. Относительный показатель инфляции можно представить также как величину, обратную индексу потребительских цен.
При исчислении индекса изменения цен на товары и услуги необходимо учитывать также изменение курса рубля (по отношению к иностранным валютам, в частности к доллару США), соответственно должен корректироваться и индекс покупательной способности рубля. При этом корректировка номинального индекса покупательной способности должна осуществляться пропорционально доле денежного оборота в иностранной валюте в общем денежном обороте страны.
Обратная величина индекса курса рубля по отношению к доллару США и другим иностранным валютам, котирующимся в России, представляет собой индекс цен на покупку долларов в России.
Статистика страхования
Страховой рынок подразделяется на отрасли имущественного, личного страхования, страхования ответственности и социального страхования.
Объектами имущественного страхования являются основные и оборотные фонды предприятий, организаций, домашнее имущество граждан. К основным абсолютным показателям этой отрасли относятся: страховое поле 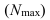
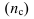
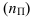
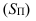
Нетто-ставка исчисляется по формуле
где 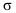
3. Брутто-ставка определяется по формуле
где f — доля нагрузки к нетто-ставке:
Важнейшей задачей статистики личного страхования является расчет единовременных тарифных ставок на дожитие, на случай смерти с различным сроком договора и выдачи платежей.
Единовременная нетто-ставка на дожитие определяется по формуле
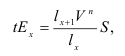
где 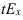
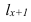
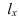
V — дисконтный множитель;
S — страховая сумма.
Единовременная ставка на случай смерти — временная, т.е. на определенный срок. Она равна
где 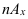
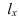
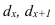
Расчет тарифных нетто-ставок производится с использованием таблиц смертности и средней продолжительности жизни.
Для практических расчетов разработаны специальные таблицы коммутационных чисел, в которых содержатся показатели, взятые из таблиц смертности, дисконтирующие множители и расчетные показатели (коммутационные числа). Таблицы составлены в двух видах: на дожитие и на случай смерти. Для удобства вычислений они могут быть объединены в одну показатели уровня травматизма:
1) частоту травматизма;
2) тяжесть травматизма;
3) коэффициент нетрудоспособности (количество человеко-дней нетрудоспособности на одного работающего).
Статистика ценных бумаг
Рынок ценных бумаг — часть финансового рынка, на котором обращаются средне- и долгосрочные бумаги. К ценным бумагам относятся акции, облигации, сертификаты, векселя, казначейские обязательства и др. Рынок ценных бумаг складывается из спроса и предложения и уравновешивающих их цен. Существуют различные виды ценных бумаг: с нефиксированным доходом, с фиксированным доходом. Смешанные формы.
Акции не имеют установленного срока обращения, их владельцы получают дивиденды в течение всего срока существования акционерного общества (АО).
В зависимости от длительности обращения ценных бумаг на рынке устанавливаются цены на акции: номинальная, эмиссионная, рыночная. На акции указывается номинальная стоимость, которая определяется путем деления величины уставного капитала на количество выпущенных акций:
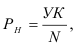
где 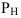
УК — величина уставного капитала;
N — количество выпущенных акций.
На основе номинальной стоимости устанавливается эмиссионная цена, по которой осуществляется первичное размещение акций. На рынке ценных бумаг акции реализуются по рыночной цене, зависящей от соотношения спроса и предложения.
Активность бирж базируется на биржевых индексах цен, характеризующих динамику цен и средний уровень цены на акции.
Индекс цены на акцию определенного наименования исчисляется по формуле
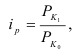
где 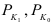
Индекс средних уровней
где 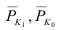
Доходность акции определяется двумя факторами: получением части распределяемой прибыли АО (дивидендом) и дополнительным доходом, который равен разнице между курсовой ценой и ценой приобретения (∆ = РК — РПР).
Годовая ставка дивиденда рассчитывается по формуле
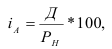
где
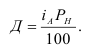
Д — абсолютный уровень дивиденда. Сумма годового дохода акции определяется по формуле
Для оценки дохода по акции, приобретенной по курсу, используют показатель рендит, который характеризует процент прибыли от цены приобретения акции:
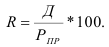
Совокупная доходность исчисляется отношением совокупного дохода (СД = Д + ∆д ) к цене приобретения:
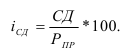
Доходность облигации определяется двумя факторами: купонными выплатами, которые производятся ежегодно (иногда раз в квартал или полугодие), и разницей между ценой погашения и приобретения бумаги:
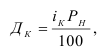
где 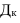
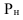
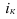
Разница между ценой погашения и приобретения бумаги определяет величину прироста или убытка капитала за весь срок займа. Если погашение производится по номиналу, а облигация куплена с дисконтом, инвестор имеет прирост капитала. При покупке облигации по цене с премией владелец, погашая бумагу, терпит убыток. Облигация с премией имеет доходность ниже указанной на купоне. Сумма купонных выплат и годового прироста (убытка) капитала определяет величину совокупного годового дохода по облигации. Совокупная годовая доходность облигации представляет собой отношение совокупного годового дохода к цене приобретения облигации:
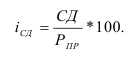
Текущая доходность облигации без выплаты процентов исчисляется по формуле
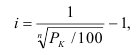
где 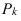
n — срок от момента приобретения до выкупа облигации.
При этом, если облигация приобретена с дисконтом, до ее выкупа
Доходность облигации с выплатой процентов в конце срока рассчитывается по формуле
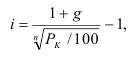
где g — объявленная годовая норма доходности по облигации.
Доходность облигации с периодической выплатой процентов, погашаемой в конце срока, определяется по формулам:
а) сложных процентов:
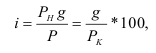
где g — норма доходности по купонам;
Р — рыночная цена;
б) простых процентов:
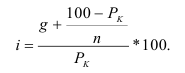
Текущая доходность облигаций с учетом налоговых льгот исчисляется по формуле
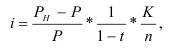
где t — ставка налоговых льгот;
n — срок от даты приобретения до погашения облигации;
К — количество дней в году.
Стоимость облигации без обязательного погашения с периодической выплатой процентов определяется по формулам:
а) современная стоимость:
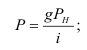
б) курсовая цена:
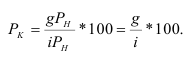
Для сравнительной оценки акций используются следующие показатели:
ценность акции =
коэффициент котировки =
Ожидаемая доходность акций рассчитывается по эффективной ставке процентов:
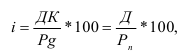
где Д — ожидаемый доход;
n — срок операций;
Р — ожидаемая цена акции.
При расчете доходности векселей необходимо учитывать следующее:
1) если владелец векселя держит документ до даты его погашения, причем вексель размещен по номинальной цене с доходом в виде процента, то векселедержатель сверх номинала получает сумму дохода, равную
где 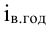
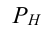
n — число дней от даты выставления векселя до даты погашения.
2) если вексель размещен с дисконтом, а погашение производится по номиналу, доход владельца составляет
где 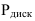
Доходность векселя
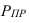
Абсолютный размер дохода по сертификату определяется по формуле
где 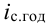
n — число месяцев, на которое выпущен сертификат.
Доходность сертификата исчисляется по формуле
Кстати тут дополнительная теория из учебников.
Статистика финансов предприятий и организаций
В условиях рыночной экономики, когда развитие предприятий и организаций осуществляется в основном за счет собственных средств, важное значение имеет устойчивое финансовое состояние, которое характеризуется системой показателей. Эта система содержит четыре группы показателей: ликвидность, оборачиваемость активов, привлечение средств, прибыльность.
Первая группа — показатели ликвидности: коэффициент ликвидности, который определяется как отношение быстрореализуемых активов (денежные средства, отгруженные товары, дебиторская задолженность) к краткосрочным обязательствам (краткосрочные ссуды, задолженность рабочим и служащим по заработной плате и социальным выплатам, кредиторская задолженность); коэффициент покрытия, который рассчитывается как отношение всех ликвидных активов к краткосрочным обязательствам.
Вторая группа — коэффициенты оборачиваемости активов (оборачиваемость всех активов основных средств, дебиторских счетов, средств в расчетах и запасов).
Третья группа — степень покрытия фиксированных платежей — определяется как отношение балансовой прибыли к сумме фиксированных платежей.
Четвертая группа — показатели прибыли и рентабельности.
Прибыль oт реализации продукции определяется как разница между выручкой, полученной от реализации продукции, и затратами на ее производство:
где р — цена единицы продукции;
z — затраты па производство единицы продукции:
q -объем продукции.
Балансовая прибыль предприятия
где 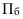
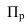
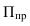
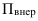
Чистая прибыль представляет собой разность между балансовой прибылью и суммой платежей в бюджет.
Прибыльность предприятия определяется показателями рентабельности.
Рассчитывают рентабельность продукции и предприятия.
Рентабельность продукции (r) исчисляют как отношение прибыли 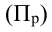
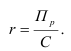
Рентабельность предприятия (R) определяется по формуле
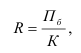
где К — величина капитала.
Анализируя показатели прибыли и рентабельности, статистика дает не только общую оценку их размера, но и характеризует их изменение под влиянием отдельных факторов.
Относительное изменение среднего уровня рентабельности продукции определяется системой индексов:
где 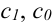
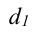
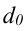
Абсолютное изменение среднего уровня рентабельности
обусловлено влиянием следующих факторов:
а) рентабельности:
б) структуры:
Оборачиваемость оборотных средств характеризуется двумя показателями: числом оборотов и продолжительностью одного оборота.
Количество (n) оборотов оборотных средств определяется отношением стоимости реализованной продукции (РП) к средним
остаткам оборотных средств 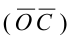
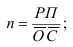
продолжительность (t) одного оборота оборотных средств равна
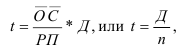
где Д — количество календарных дней.
Финансовые вычисления
Методы финансовых расчетов подразделяются на общие и специфические, применяемые при выполнении особого класса финансовых операций и сделок, требующих адаптации общих методов, их видоизменения применительно к сути финансовых операций и сделок, исполнения на основе документарных данных.
Ввиду очевидной специфики указанных методов примеры их применения приводятся отдельно в виде решения актуарных и инвестиционных задач, исчисления биржевых индексов, проведения приближенных расчетов и т.д.
К наиболее распространенным относятся методы исчисления простых и сложных процентов, математического и банковского дисконтирования, консолидированных и рентных расчетов.
Ниже представлены основные формулы, по которым производится подавляющее большинство расчетов в современной практике финансовых вычислений.
Здесь S — наращенная сумма (стоимость);
Р — первоначальная сумма;
n— число периодов;
i — процентная ставка:
m — число случаев начисления в периоде:
d — учетная ставка:
R — член ренты.
В зарубежной практике к этим широко применяемым формулам добавляются, как правило, следующие шесть дополнительных, предназначенных для определения различных норм эффективности.
1. Срок окупаемости
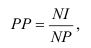
где NI — чистые инвестиции (приведенные затраты):
NP — чистая прибыль (годовая).
2. Норма эффективности (окупаемости инвестиций)
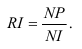
3. Чистая текущая (дисконтированная) стоимость
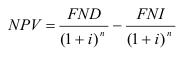
где FND — чистая сумма будущих доходов;
FNI — чистая сумма будущих расходов.
4. Внутренняя ставка доходности
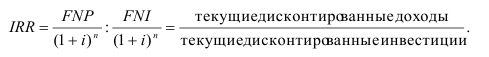
5. Ставка доходности дисконтированных денежных потоков
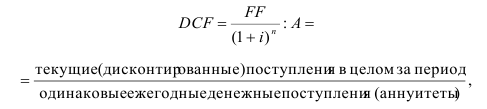
где FF — объем будущих поступлений;
А — аннуитеты.
6. Учетная ставка доходности