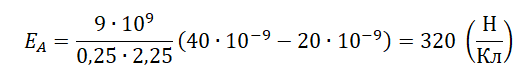ВУЗ. Найти напряженность поля и потенциал (30.10.2011)
Чертов А. Г., Воробьев А. А. Задачник по физике: Учебное пособие для вузов. 7 изд., 2001 г.
- версия для печати
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Комментарии
В центре треугольника напряженность равна геометрической сумме напряженностей, создаваемых зарядами 1, 2 и 3.
Заряды по модулю равны, поэтому:
E1 = E2 = E3 = 3k|q| / a 2 , так как a(√3) / 3 — расстояние от вершины треугольника до центра треугольника О.
Напряженность поля в точке О: E = E3 + E1 cos 60° + E2 cos 60° = 2E1 = 6k|q| / a 2 .
Потенциал в точке O равен алгебраической сумме потенциалов, создаваемых зарядами 1, 2 и 3:
В двух вершинах равностороннего треугольника со стороной
Задача. В двух вершинах равностороннего треугольника со стороной длиной см находятся два заряда, модули которых нКл. Определите потенциал поля в третьей вершине треугольника, если: a) оба заряда положительные; b) оба заряда отрицательные; c) заряды противоположных знаков.
Дано:
Решение
Думаем: источником электростатического поля в задаче являются точечные заряды, тогда для потенциала точечного заряда:
Т.к. зарядов несколько,, то для поиска общих параметров системы будем использовать принцип суперпозиции для потенциала (полный потенциал, создаваемый в точке равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в этой точке):
Решаем: для визуализации системы нарисуем её (рис. 1).
Рис. 1. Система зарядов для поиска потенциала
Точка А — точка, где по нашему условию нужно найти потенциал. Каждый из зарядов создаёт свой потенциал в искомой точке, который мы можем найти из (1):
Тогда, исходя из (2), получим общий потенциал в точке A:
А теперь адаптируем получившееся соотношение (5) под условия задачи. Разница в условиях задачи по пунктам состоит в том, что значения зарядов различные.
a) в случае 0″ title=»displaystyle <_<1>>=<
_<2>>>0″ data-lazy-src=»https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%7B%7Bq%7D_%7B1%7D%7D%3D%7B%7Bq%7D_%7B2%7D%7D%3E0&is-pending-load=1#038;bg=ffffff&fg=000000&s=0″ srcset=»data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7″>:
Считаем: вспоминаем константы Н*м /Кл , И не забываем перевести все параметры (расстояния) в единицы СИ.
Принцип суперпозиции сил и полей
теория по физике 🧲 электростатика
Принцип суперпозиции сил
Результирующая, или равнодействующая, сила равна векторной сумме всех сил, действующих на тело:
Fi— сила, с которой электрическое поле зарядом q действует на пробный заряд qi, помещенный в это поле на расстоянии riот этого заряда. Численно ее можно вычислить по формуле:
F i = k q i q r 2 i . .
Алгоритм решения задач на определение равнодействующей силы (точечный заряд находится в поле, созданном другими точечными зарядами):
- Сделать чертеж. Указать расположение всех зарядов и их знаки.
- Выделить заряд, для которого определяют равнодействующую.
- Пронумеровать остальные заряды.
- Определить расстояния от выделенного заряда до всех остальных.
- Построить все силы, действующие на интересующий нас заряд. При этом необходимо учитывать знаки зарядов, их модули и расстояния между зарядами.
- Найти геометрическую (векторную) сумму всех сил, действующих на выделенный заряд.
- Пользуясь формулами геометрии и законом Кулона, определить модуль равнодействующей.
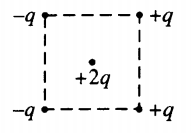
Пример №1. Как направлена (вправо, влево, вверх, вниз) кулоновская сила − F K , действующая на положительный точечный электрический заряд +2q, помещенный в центр квадрата, в вершинах которого находятся заряды +q, +q, –q, –q?
Известно, что одноименные заряды отталкиваются, а разноименные – притягиваются. Из рисунка видно, что заряд +2q, находящийся в центре квадрата, будет отталкиваться от зарядов +q, находящихся справа, и будет притягиваться к зарядам –q, находящимся слева.
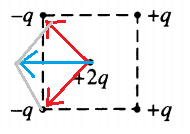
Сила Кулона обратно пропорциональна квадрату расстояния между зарядами, то есть с увеличением расстояния r убывает по квадратическому закону. Так как заряд +q находится точно в центре квадрата, то расстояния от зарядов +q, +q, -q, -q будут равны, следовательно, равна по модулю и сила Кулона, действующая на заряд +2q. Суперпозиция сил, действующих на заряд +2q:
Из рисунка видно, что кулоновская сила − F K , действующая на положительный точечный электрический заряд +2q, направлена влево.
Принцип суперпозиции полей
Если в некоторой точке пространства складываются электрические поля от нескольких зарядов, то результирующая напряженность находится как векторная сумма напряженностей отдельных полей:
− E i — напряженность, создаваемая зарядом q i в точке, находящейся на расстоянии r i :
− E i = k q i r 2 i . .
Векторное сложение напряженностей аналогично нахождению равнодействующей сил Кулона, только в интересующую нас точку пространства помещают положительный пробный заряд. Чтобы найти результирующий потенциал в точке, необходимо алгебраически сложить потенциалы всех полей. Нельзя забывать, что знак потенциала определяется знаком заряда, создающим электрическое поле:
φ i — потенциал электростатического поля, создаваемого зарядом q i на расстоянии r i от него. Численно он равен:
φ i = ± k q i r i . .
Для определения полной энергии надо сложить потенциальные энергии всех пар зарядов:
W i p — потенциальная энергия взаимодействия зарядов q i и q n , находящихся на расстоянии r i друг от друга. Численно она равна:
W i p = ± k q i q n r i . .
Примеры определения расстояний
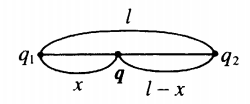 |
Два заряда лежат на одной прямой на расстоянии l друг от друга. Изучаемый заряд лежит между ними: |
r 1 = x ; r 2 = l − x
Изучаемый заряд лежит в вершине квадрата со стороной a:
r 1 = r 3 = a ; r 2 = a √ 2
Изучаемый заряд лежит в центре равностороннего треугольника со стороной a:
r 1 = r 2 = r 3 = a √ 3 . .
Изучаемый заряд лежит в вершине прямоугольника со сторонами a и b:
r 1 = b ; r 2 = √ a 2 + b 2 ; r 3 = a
Изучаемый заряд лежит в точке пересечения диагоналей ромба со стороной a. Угол при вершине ромба 120 о :
r 1 = r 3 = a √ 3 2 . . ; r 2 = r 4 = a 2 . .
Изучаемый заряд лежит в центре правильного шестиугольника со стороной a:
r 1 = r 2 = r 3 = r 4 = r 5 = r 6 = a
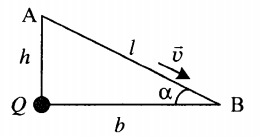
Пример №2. Маленький заряженный шарик массой m, имеющий заряд q, движется с высоты h по наклонной плоскости с углом наклона α. В вершине прямого угла, образованного высотой и горизонталью, находится неподвижный заряд Q. Какова скорость шарика у основания наклонной плоскости v, если его начальная скорость равна нулю? Трением пренебречь.
Применим закон сохранения энергии, согласно которому полная энергия шарика в точке А равна полной энергии шарика в точке В (трением пренебрегаем):
Полная энергия шарика с зарядом qв точке А равна сумме его механической потенциальной энергии и потенциальной энергии взаимодействия с зарядом Q:
E A = m g h + k q Q h . .
В точке В механическая потенциальная энергия шарика равна нулю, но в этой точке максимальная его кинетическая энергия. Полная энергия шарика в точке В равна:
E B = m v 2 2 . . + k q Q b . .
Расстояние между точкой В и местом, где находится заряд Q:
Приравняем правые части уравнений:
m g h + k q Q h . . = m v 2 2 . . + k q Q b . .
m g h + k q Q h . . = m v 2 2 . . + k q Q tan . α h . .
m v 2 2 . . = m g h + k q Q h . . − k q Q tan . α h . . = m g h + k q Q h . . ( 1 − tan . α )
v = . ⎷ 2 ( m g h + k q Q h . . ( 1 − tan . α ) ) m . . = √ 2 g h + 2 k Q m h . . ( 1 − tan . α )
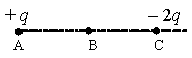
http://www.abitur.by/fizika/zadachi-po-fizike/potencial-elektrostaticheskogo-polya-zadachi/v-dvux-vershinax-ravnostoronnego-treugolnika-so-storonoj/
Решение.
Определим энергию взаимодействия зарядов.
[ begin{align}
& W={{W}_{12}}+{{W}_{23}}+{{W}_{13}}, {{W}_{12}}=frac{kcdot {{q}_{1}}cdot {{q}_{2}}}{a}, {{W}_{23}}=frac{kcdot {{q}_{2}}cdot {{q}_{3}}}{a}, {{W}_{13}}=frac{kcdot {{q}_{1}}cdot {{q}_{3}}}{a}, \
& {{q}_{1}}={{q}_{2}}={{q}_{3}},{{W}_{12}}={{W}_{23}}={{W}_{13}} , W=frac{3cdot kcdot {{q}^{2}}}{a}. \
end{align} ]
W = 6,75∙10-4 Дж.
Найдем потенциал поля φ в центре треугольника. Радиус описанной окружности около равностороннего треугольника определяется по формуле:
[ begin{align}
& r=frac{a}{sqrt{3}} (1). \
& varphi ={{varphi }_{1}}+{{varphi }_{2}}+{{varphi }_{3}}, {{varphi }_{1}}={{varphi }_{2}}={{varphi }_{3}}, varphi =3cdot {{varphi }_{1}} \
& {{varphi }_{1}}=frac{kcdot q}{r}, {{varphi }_{1}}=frac{kcdot qcdot sqrt{3}}{a}, varphi =frac{3cdot kcdot qcdot sqrt{3}}{a}. \
end{align} ]
φ = 2,33∙105 В.
Определим какой заряд q0 необходимо поместить в точку О, чтобы система зарядов находилась в равновесии. Система будет находится в равновесии когда равнодействующая сила которая действует на заряд который находится в вершине треугольника равна нулю. Покажем рисунок.
[ begin{align}
& {{{vec{F}}}_{12}}+{{{vec{F}}}_{13}}+{{{vec{F}}}_{10}}=0 (1). \
& {{{vec{F}}}_{12}}+{{{vec{F}}}_{13}}={{{vec{F}}}_{23}}. \
end{align} ]
Для нахождения равнодействующей силы F23 используем теорему косинусов:
[ begin{align}
& {{F}_{23}}^{2}=F_{12}^{2}+F_{13}^{2}+2cdot {{F}_{12}}cdot {{F}_{13}}cdot cos alpha , alpha =60{}^circ , \
& {{F}_{23}}=sqrt{F_{12}^{2}+F_{13}^{2}+2cdot {{F}_{12}}cdot {{F}_{13}}cdot frac{1}{2}} , \
& {{F}_{12}}=frac{kcdot left| {{q}_{1}} right|cdot left| {{q}_{2}} right|}{{{a}^{2}}}=frac{kcdot {{q}^{2}}}{{{a}^{2}}}, {{F}_{13}}=frac{kcdot left| {{q}_{1}} right|cdot left| {{q}_{3}} right|}{{{a}^{2}}}=frac{kcdot {{q}^{2}}}{{{a}^{2}}}, \
& {{F}_{23}}=frac{sqrt{3}cdot kcdot {{q}^{2}}}{{{a}^{2}}} (2). \
end{align} ]
[ {{F}_{23}}={{F}_{10}}, frac{sqrt{3}cdot kcdot {{q}^{2}}}{{{a}^{2}}}=frac{kcdot left| {{q}_{0}} right|cdot qcdot 3}{{{a}^{2}}}, {{q}_{0}}=-frac{q}{sqrt{3}}. ]
k = 9∙109 Н∙м2 / Кл2.
q0 = -2,89∙10-9 Кл.
Принцип суперпозиции сил
Определение
Результирующая, или равнодействующая, сила равна векторной сумме всех сил, действующих на тело:
−R=∑−Fi
Fi — сила, с которой электрическое поле зарядом q действует на пробный заряд qi, помещенный в это поле на расстоянии ri от этого заряда. Численно ее можно вычислить по формуле:
Fi=kqiqr2i
Алгоритм решения задач на определение равнодействующей силы (точечный заряд находится в поле, созданном другими точечными зарядами):
- Сделать чертеж. Указать расположение всех зарядов и их знаки.
- Выделить заряд, для которого определяют равнодействующую.
- Пронумеровать остальные заряды.
- Определить расстояния от выделенного заряда до всех остальных.
- Построить все силы, действующие на интересующий нас заряд. При этом необходимо учитывать знаки зарядов, их модули и расстояния между зарядами.
- Найти геометрическую (векторную) сумму всех сил, действующих на выделенный заряд.
- Пользуясь формулами геометрии и законом Кулона, определить модуль равнодействующей.
Пример №1. Как направлена (вправо, влево, вверх, вниз) кулоновская сила −FK, действующая на положительный точечный электрический заряд +2q, помещенный в центр квадрата, в вершинах которого находятся заряды +q, +q, –q, –q?
Известно, что одноименные заряды отталкиваются, а разноименные – притягиваются. Из рисунка видно, что заряд +2q, находящийся в центре квадрата, будет отталкиваться от зарядов +q, находящихся справа, и будет притягиваться к зарядам –q, находящимся слева.
Сила Кулона обратно пропорциональна квадрату расстояния между зарядами, то есть с увеличением расстояния r убывает по квадратическому закону. Так как заряд +q находится точно в центре квадрата, то расстояния от зарядов +q, +q, -q, -q будут равны, следовательно, равна по модулю и сила Кулона, действующая на заряд +2q. Суперпозиция сил, действующих на заряд +2q:
Из рисунка видно, что кулоновская сила −FK, действующая на положительный точечный электрический заряд +2q, направлена влево.
Принцип суперпозиции полей
Определение
Если в некоторой точке пространства складываются электрические поля от нескольких зарядов, то результирующая напряженность находится как векторная сумма напряженностей отдельных полей:
−E=∑−Ei
−Ei — напряженность, создаваемая зарядом qi в точке, находящейся на расстоянии ri:
−Ei=kqir2i
Векторное сложение напряженностей аналогично нахождению равнодействующей сил Кулона, только в интересующую нас точку пространства помещают положительный пробный заряд. Чтобы найти результирующий потенциал в точке, необходимо алгебраически сложить потенциалы всех полей. Нельзя забывать, что знак потенциала определяется знаком заряда, создающим электрическое поле:
φ=∑φi
φi — потенциал электростатического поля, создаваемого зарядом qi на расстоянии ri от него. Численно он равен:
φi=±kqiri
Для определения полной энергии надо сложить потенциальные энергии всех пар зарядов:
Wp=∑Wip
Wip — потенциальная энергия взаимодействия зарядов qi и qn, находящихся на расстоянии ri друг от друга. Численно она равна:
Wip=±kqiqnri
Примеры определения расстояний
 |
Два заряда лежат на одной прямой на расстоянии l друг от друга. Изучаемый заряд лежит между ними:
r1=x; r2=l−x |
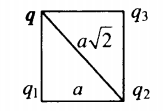 |
Изучаемый заряд лежит в вершине квадрата со стороной a:
r1=r3=a; r2=a√2 |
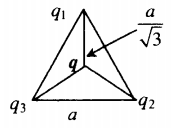 |
Изучаемый заряд лежит в центре равностороннего треугольника со стороной a:
r1=r2=r3=a√3 |
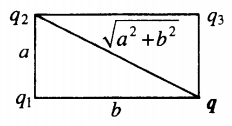 |
Изучаемый заряд лежит в вершине прямоугольника со сторонами a и b:
r1=b; r2=√a2+b2; r3=a |
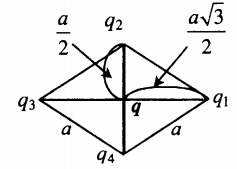 |
Изучаемый заряд лежит в точке пересечения диагоналей ромба со стороной a. Угол при вершине ромба 120о:
r1=r3=a√32; r2=r4=a2 |
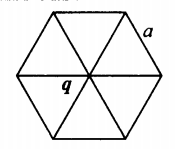 |
Изучаемый заряд лежит в центре правильного шестиугольника со стороной a:
r1=r2=r3=r4=r5=r6=a |
Пример №2. Маленький заряженный шарик массой m, имеющий заряд q, движется с высоты h по наклонной плоскости с углом наклона α. В вершине прямого угла, образованного высотой и горизонталью, находится неподвижный заряд Q. Какова скорость шарика у основания наклонной плоскости v, если его начальная скорость равна нулю? Трением пренебречь.
Построим чертеж:
Применим закон сохранения энергии, согласно которому полная энергия шарика в точке А равна полной энергии шарика в точке В (трением пренебрегаем):
EA=EB
Полная энергия шарика с зарядом qв точке А равна сумме его механической потенциальной энергии и потенциальной энергии взаимодействия с зарядом Q:
EA=mgh+kqQh
В точке В механическая потенциальная энергия шарика равна нулю, но в этой точке максимальная его кинетическая энергия. Полная энергия шарика в точке В равна:
EB=mv22+kqQb
Расстояние между точкой В и местом, где находится заряд Q:
b=htanα
Приравняем правые части уравнений:
mgh+kqQh=mv22+kqQb
mgh+kqQh=mv22+kqQtanαh
mv22=mgh+kqQh−kqQtanαh=mgh+kqQh(1−tanα)
v=⎷2(mgh+kqQh(1−tanα))m=√2gh+2kQmh(1−tanα)
Задание EF17563
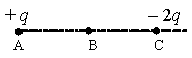
Ответ:
а) − 5q
б) − 4q
в) 4q
г) 5q
Алгоритм решения
1.Определить направление вектора напряженности для зарядов в точках А и С.
2.Определить напряженность поля в точке В, используя принцип суперпозиции.
3.Найти, какой заряд нужно поместить в точку С вместо имеющегося, чтобы напряженность электростатического поля в точке В увеличилась вдвое.
Решение
Вектор напряженности заряда в точке А направлен в направлении от этого заряда, так как он положительный. Это значит, что в точке В вектор напряженности EA направлен вправо. Вектор напряженности заряда в точке С направлен к этому заряду, так как он отрицательный. Поэтому в точке В вектор напряженности EC тоже направлен вправо. Следовательно, при векторном сложении модули напряженностей должны складываться:
E=EA+EC=k|q|r2+k|−2q|r2=3kqr2
Найдем, какой нужно поместить заряд в точку С, чтобы напряженность увеличилась вдвое:
k|q|r2+k|x|r2=2·3kqr2=6kqr2
Преобразуем выражение и получим:
|q|+|x|=6q
Отсюда:
|x|=5q
Этот заряд должен быть отрицательным, так как в этом случае линии напряженности поля, создаваемого зарядом в точке С, будут складываться с линиями напряженности поля, создаваемыми положительным зарядом в точке А. Следовательно, x = –5q.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17967
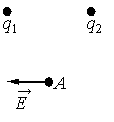
Ответ:
а) q1 > 0; q2 < 0
б) q1 < 0; q2 > 0
в) q1 > 0; q2 > 0
г) q1 < 0; q2 < 0
Алгоритм решения
1.Вспомнить, как направлены векторы напряженности полей, созданных положительным и отрицательным зарядами.
2.Построить параллелограмм, сторонами которого являются отрезки, равные длинам векторов напряженности полей, создаваемыми двумя точечными зарядами.
3.Определить, какое направление должны иметь векторы напряженности, чтобы результатом их вычитания/сложения был вектор −E.
4.Определить знаки зарядов с учетом направления векторов напряженности полей.
Решение
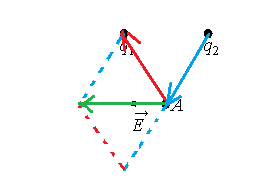
Векторы напряженности электростатического поля, создаваемого положительным точечным зарядом, направлены по радиусным линиям от заряда. Векторы напряженности электростатического поля, создаваемого отрицательным точечным зарядом, направлены по радиусным линиям к заряду.
Построим параллелограмм. Чтобы получить вектор −E, нужно вычесть из вектора −E1 вектор −E2. Причем первый должен быть направлен в сторону заряда, а второй — от заряда.
Следовательно, заряд q1 отрицательный (q1 < 0), а заряд q2 положительный (q2 > 0).
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18357
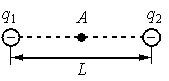
Ответ:
а) 160 Н/Кл
б) 320 Н/Кл
в) 125 Н/Кл
г) 640 Н/Кл
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Определить направление векторов напряженности в точке А.
3.Выполнить общее решение задачи, применив принцип суперпозиции полей.
4.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Величина первого заряда: q1 = –20 нКл.
• Величина второго заряда: q2 = –40 нКл.
• Расстояние между зарядами: L = 1,5 м.
–20 нКл = –20∙10–9 Кл
–40 нКл = –40∙10–9 Кл
Вектор напряженности поля, создаваемого первым зарядом в точке А, направлен влево (в сторону заряда), так как он отрицательный. Второй заряд тоже отрицательный, но он лежит по другую сторону от точки А. Поэтому в ней вектор напряженности поля, создаваемого вторым зарядом, будет направлен вправо. Так как модуль второго заряда больше модуля первого, результирующая напряженность будет направлена вправо. Напряженность в точке А в этом случае будет вычисляться как разность двух напряженности:
EA=E2−E1
Напряженность определяется формулой:
E=k|q|r2
Следовательно:
EA=k|q2|(0,5L)2−k|q1|(0,5L)2=k(0,5L)2(|q2|−|q1|)
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 3.3k
UCHEES.RU — помощь студентам и школьникам
В 7:27 поступил вопрос в раздел ЕГЭ (школьный), который вызвал затруднения у обучающегося.
Вопрос вызвавший трудности
Три заряда -q, +q и +q расположены в вершинах равностороннего треугольника со стороной а Определите результирующий потенциал
Ответ подготовленный экспертами Учись.Ru
Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике «ЕГЭ (школьный)». Ваш вопрос звучал следующим образом: Три заряда -q, +q и +q расположены в вершинах равностороннего треугольника со стороной а Определите результирующий потенциал
После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:
ответ к заданию по физике
НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:
Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.
Белоусова Анэля Протасьевна — автор студенческих работ, заработанная сумма за прошлый месяц 91 600 рублей. Её работа началась с того, что она просто откликнулась на эту вакансию
ПОМОГАЕМ УЧИТЬСЯ НА ОТЛИЧНО!
Выполняем ученические работы любой сложности на заказ. Гарантируем низкие цены и высокое качество.
Деятельность компании в цифрах:
Зачтено оказывает услуги помощи студентам с 1999 года. За все время деятельности мы выполнили более 400 тысяч работ. Написанные нами работы все были успешно защищены и сданы. К настоящему моменту наши офисы работают в 40 городах.
РАЗДЕЛЫ САЙТА
Ответы на вопросы — в этот раздел попадают вопросы, которые задают нам посетители нашего сайта. Рубрику ведут эксперты различных научных отраслей.
Полезные статьи — раздел наполняется студенческой информацией, которая может помочь в сдаче экзаменов и сессий, а так же при написании различных учебных работ.
Красивые высказывания — цитаты, афоризмы, статусы для социальных сетей. Мы собрали полный сборник высказываний всех народов мира и отсортировали его по соответствующим рубрикам. Вы можете свободно поделиться любой цитатой с нашего сайта в социальных сетях без предварительного уведомления администрации.
ЗАДАТЬ ВОПРОС
НОВЫЕ ОТВЕТЫ
- Абадзехская стоянка, Даховская пещера. ..
- По закону сохранения заряда каждый шарик после соприкасl..
- 2)прогудел первый мохнатый шмель 3) Зазвенела Прогудел 4) ..
- В мілкій траві ворушаться сліди веселих, сполоханих доще
..
ПОХОЖИЕ ВОПРОСЫ
- Два заряда +q и -q находятся в вершинах прямоугольного треугольника, катеты которого 9 и 12 м Определите результирующий
- Два разноимённых заряда +3q и -2q находятся на расстоянии 5 м друг от друга. Определите результирующий потенциал в точке А,
- Четыре заряда +q,—2q, +2q и +q расположены в вершинах и в середине ромба, составленного из двух равносторонних треугольников,
Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.
2020 — 2023 — UCHEES.RU
От нашего клиента с логином rWtiTYfs на электронную почту пришел вопрос: «Три заряда -q, +q и +q расположены в вершинах равностороннего треугольника со стороной а Определите результирующий потенциал» это здание мы отнесли к разделу ЕГЭ (школьный). Так как клиент является зарегистрированным пользователем нашего сайта, то мы бесплатно предоставим ответ.
ЕГЭ (школьный) — довольно сложный раздел, здесь действительно попадаются вопросы, которые даже у специалиста с законченным высшим образованием поставят в тупик при подготовке правильного ответа. Но мы известны тем, что сложности нас не останавливают, а наоборот развивают и расширяют наши знания.
Вы спрашивали Три заряда -q, +q и +q расположены в вершинах равностороннего треугольника со стороной а Определите результирующий потенциал? — отвечаем:
ответ к заданию по физике