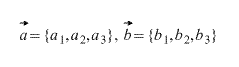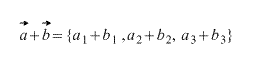В механике существуют два типа величин:
- скалярные величины, задающие некоторое числовое значение — время, температура, масса и т.д.
- векторные величины, которые вместе с некоторым числовым значением задают направление — скорость, сила и т.д..
Рассмотрим сначала алгебраический подход к сложению векторов.
Покоординатное сложение векторов.
Пусть даны два вектора, заданные покоординатно ( чтобы вычислить координаты вектора, нужно вычесть из соответствующих координат его конца соответствующие координаты его начала, т.е. из первой координаты — первую, из второй — вторую и т.д.):
Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:
В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.
Теперь перейдем к геометрическому смыслу сложения двух векторов:
При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:
- правило параллелограмма
- правило треугольника
- тригонометрический способ
Правило параллелограмма. Сложение векторов по правилу параллелограмма. |
|
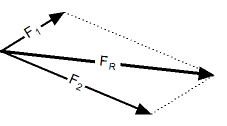 |
Процедура сложения векторов по правилу параллелограмма заключается в следующем:
|
Правило треугольника. Сложение векторов по правилу треугольника. |
|
 |
Сложение векторов по правилу треугольника заключается в следующем:
|
Тригонометрический способ. Сложение векторов тригонометрическим способом. |
|
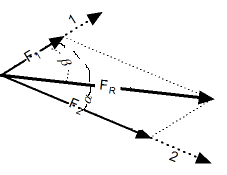 |
Результирующий вектор сложения двух компланарных векторов может быть вычислен с помощью теоремы косинусов:
Угол между результирующим вектором и одним из исходных векторов может быть вычислен по теореме синусов:
|
Пример — сложение векторов.
Сила 1 равна 5кН и воздействует на тело в направлении, на 80o отличающемся от направления действия второй силы, равной 8 кН.
Результирующая сила вычисляется следующим образом:
Fрез = [ (5 кН)2 + (8 кН)2 — 2 (5 кН)(8 kН) cos(180o — (80o)) ]1/2
= 10,14кН
Угол между результирующей силой и первой силой равен:
β= arcsin[ (8кН) sin(180o — (80o)) / (10,14кН) ]
= 51o
А угол между второй и результирующей силой можно посчитать следующим образом: as
α = arcsin [ (5 кН) sin(180o — (80o)) / (10,2 кН) ]
= 29o
Он-лайн калькулятор сложения векторов.
Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.

In mathematics, we often heard about the two terms scalar and vector. Scalar is a quantity which has only magnitude i.e. Scalar quantity describes the distance. On the other hand, Vector is a quantity which deals with both magnitude and direction. Vector quantity has both magnitude and direction.
Resultant vector formula gives the resultant value of two or more vectors. The result is obtained by computing the vectors with consideration of the direction of each vector with respect to others. This formula has various applications in Engineering & Physics. Based on the direction of a vector with respect to other vectors, the Resultant Vector formula is classified into three types.
Resultant vector 1st formula
If the vectors are in the same direction then the resultant of the vector can be calculated by adding the vectors which are in the same direction. Let “a” and “b” are the vectors with the same direction then the resultant vector “r” is given by-
r = a + b
Resultant vector 2nd formula
If the vectors are in different directions then the resultant of the vector can be calculated by subtracting the vectors from each other. Let “b” be a vector which is in opposite direction with respect to vector “a” then the resultant vector “r” is given by-
r = a – b
Resultant vector 3rd formula
If any vectors are inclined to each other at some angle then the resultant of these vectors can be calculated by this formula. Let “a”, and “b” are two vectors inclined to each other at an angle θ, then the resultant vector “r” is given by-
r = a2 + b2 + 2abcosθ
Here a2, b2 represents magnitude of the vector a, b.
Resultant vector representation
Sample Problems
Question 1: Find the resultant vector for the vectors i+2j+3k and 4i+8j+12k
Solution:
Given two vectors are a=i+2j+3k and b=4i+8j+12k
The direction ratios of the two vectors are in equal proportion. So two vectors are in the same direction.
The resultant vector formula for the given vectors is given by-
r = a + b
= (i+2j+3k) + (4i+8j+12k)
= 5i+10j+15k
The resultant vector from the given vectors is 5i+10j+15k
Question 2: Find the resultant vector for the vectors i-2j+5k and 2i-4j+10k
Solution:
Given two vectors are a=i-2j+5k and b=2i-4j+10k
The direction ratios of the two vectors are in equal proportion. So two vectors are in the same direction.
The resultant vector formula for the given vectors is given by-
r = a + b
= (i-2j+5k) + (2i-4j+10k)
= 3i-6j+15k
The resultant vector from the given vectors is 3i-6j+15k
Question 3: Find the resultant vector for the vectors 2i-2j+k and 2i+7j+3k
Solution:
Given two vectors are a=2i-2j+k and b=2i+7j+3k
The direction ratios of the two vectors are not in equal proportions. So two vectors are in opposite direction.
The resultant vector formula for the given vectors is given by-
r = a – b
= (2i-2j+k) – (2i+7j+3k)
= 0i-9j-2k
The resultant vector from the given vectors is 0i-9j-2k
Question 4: Find the resultant vector for the vectors 9i+2j-3k and i-3j+2k
Solution:
Given two vectors are a=9i+2j-3k and b=i-3j+2k
The direction ratios of the two vectors are not in equal proportions. So two vectors are in opposite direction.
The resultant vector formula for the given vectors is given by-
r = a – b
= (9i+2j-3k) – (i-3j+2k)
= 8i+5j-5k
The resultant vector from the given vectors is 8i+5j-5k
Question 5: Find the resultant of the vectors 2i+2j+2k and i+2j+3k which are inclined at an angle 30° to each other.
Solution:
Given two vectors are a=2i+2j+2k and b=i+2j+3k
Also given that given two vectors are inclined at an angle θ=30°
So the resultant vector formula for the given vectors is given by-
r = a2 + b2 + 2abcosθ
Magnitude of vector a (a2) = sqrt{2^2+2^2+2^2}
= sqrt{4+4+4}
=√12
a2=2√3
Magnitude of vector b (b2) = sqrt{1^2+2^2+3^2}
= sqrt{1+4+9}
=√14
b2=√14
r = a2 + b2 + 2abcosθ
= 2√3 + √14 + 2(2√3)(√14)cos30°
= 2√3 + √14 + 4(√3)(√14)(√3/2)
= 29.65
The resultant vector from the given vectors is 29.65
Question 6: Find the resultant of the vector having magnitude 2, 4 which is inclined at 45°.
Answer:
Given,
Magnitude of vector a (a2)=2
Magnitude of vector b (b2)=4
θ = 45°
So the resultant vector formula for the given vectors is given by-
r = a2 + b2 + 2abcosθ
= 2+4+2(2)(4)cos45°
= 6+16×(1/√2)
= 17.31
The resultant vector from the given vectors is 17.31
Last Updated :
10 Jun, 2022
Like Article
Save Article
Загрузить PDF
Загрузить PDF
Вектор — это математический объект, который характеризуется величиной и направлением (например, ускорение, перемещение), чем и отливается от скаляров, у которых направления нет (например, расстояние, энергия). Скаляры можно складывать, сложив их значения (например, 5 кДж работы плюс 6 кДж работы равно 11 кДж работы), а вот векторы складывать и вычитать не так просто.
-
1
Так как векторы имеют величину и направление, то их можно разложить на компоненты, основываясь на размерностях х, у и/или z. Они, как правило, обозначаются так же, как точки в системе координат (например, <х,у,z>). Если компоненты известны, то сложить/вычесть векторы так же просто, как сложить/вычесть координаты x, y, z.
- Обратите внимание, что векторы могут быть одномерными, двумерными или трехмерными. Таким образом, векторы могут иметь компонент «х», компоненты «х» и «у» или компоненты «х», «у», «z». Ниже рассмотрены трехмерные векторы, но процесс аналогичен для одномерных и двумерных векторов.
- Предположим, что вам даны два трехмерных вектора — вектор А и вектор B. Запишите эти векторы в векторной форме: А = <a1, b1, c1> и B = <a2, b2, c2>, где a1 и а2 — компоненты «х», b1 и b2 — компоненты «у», c1 и c2 — компоненты «z».
-
2
Для сложения двух векторов сложите их соответствующие компоненты. Другими словами, сложите компонент «х» первого вектора с компонентом «х» второго вектора (и так далее). В результате вы получите компоненты х, у, z результирующего вектора.
- A+B = <a1+a2,b1+b2,c1+c2>.
- Сложим векторы A и B. A = <5, 9, -10> и B = <17, -3, -2>. A + B = <5+17, 9+-3, -10+-2>, или <22, 6, -12>.
-
3
Для вычитания одного вектора из другого необходимо вычесть соответствующие компоненты. Как будет показано ниже, вычитание можно заменить сложением одного вектора и вектора, обратного другому. Если компоненты двух векторов известны, вычтите соответствующие компоненты одного вектора из компонентов другого.
- A-B = <a1-a2,b1-b2,c1-c2>
- Вычтем векторы A и B. A = <18, 5, 3> и B = <-10, 9, -10>. A — B = <18—10, 5-9, 3—10>, or <28, -4, 13>.
Реклама
-
1
Так как векторы имеют величину и направление, то у них есть начало и конец (начальная точка и конечная точка, расстояние между которыми равно значению вектора). При графическом отображении вектора он рисуется в виде стрелки, у которой наконечник — конец вектора, а противоположная точка — начало вектора.
- При графическом отображении векторов стройте все углы очень точно; в противном случае вы получите неправильный ответ.
-
2
Для сложения векторов нарисуйте их так, чтобы конец каждого предыдущего вектора соединялся с началом следующего вектора. Если вы складываете только два вектора, то это все, что вам нужно сделать, прежде чем найти результирующий вектор.
- Обратите внимание, что порядок соединения векторов не важен, то есть вектор А + вектор B = вектор B + вектор А.
-
3
Для вычитания вектора просто прибавьте обратный вектор, то есть измените направление вычитаемого вектора, а затем соедините его начало с концом другого вектора. Другими словами, чтобы вычесть вектор, поверните его на 180o (вокруг точки начала) и сложите его с другим вектором.
-
4
Если вы складываете или вычитаете насколько (больше двух) векторов, то последовательно соедините их концы и начала. Порядок, в котором вы соединяете векторы, не имеет значения. Этот метод можно использовать для любого числа векторов.
-
5
Нарисуйте новый вектор, начиная от начала первого вектора и заканчивая концом последнего вектора (при этом число складываемых векторов не важно). Вы получите результирующий вектор, равный сумме всех складываемых векторов. Обратите внимание, что этот вектор совпадает с вектором, полученным путем сложения компонентов «х», «у», «z» всех векторов.
- Если вы нарисовали длины векторов и углы между ними очень точно, то вы можете найти значение результирующего вектора, просто измерив его длину. Кроме того, вы можете измерить угол (между результирующим вектором и другим указанным вектором или горизонтальной/вертикальной прямыми), чтобы найти направление результирующего вектора.
- Если вы нарисовали длины векторов и углы между ними очень точно, то вы можете найти значение результирующего вектора при помощи тригонометрии, а именно теоремы синусов или теоремы косинусов. Если вы складываете несколько векторов (более двух), сначала сложите два вектора, затем сложите результирующий вектор и третий вектор и так далее. Смотрите следующий раздел для получения дополнительной информации.
-
6
Представьте результирующий вектор, обозначив его значение и направление. Как отмечалось выше, если вы нарисовали длины складываемых векторов и углы между ними очень точно, то значение результирующего вектора равно его длине, а направление — это угол между ним и вертикальной или горизонтальной прямой. К значению вектора не забудьте приписать единицы измерения, в которых даны складываемые/вычитаемые вектора.
- Например, если вы складываете векторы скорости, измеряемые в м/с, то и к значению результирующего вектора припишите «м/с», а также укажите угол результирующего вектора в формате «o к горизонтальной прямой».
Реклама
-
1
Чтобы найти значения компонентов векторов необходимо знать значения самих векторов и их направление (угол относительно горизонтальной или вертикальной прямой). Рассмотрим двумерный вектор. Сделайте его гипотенузой прямоугольного треугольника, тогда катетами (параллельными осям Х и Y) этого треугольника будут компоненты вектора. Эти компоненты можно рассматривать как соединенные два вектора, которые при сложении дают исходный вектор.
- Длины (значения) двух компонентов (компонентов «х» и «у») исходного вектора можно вычислить при помощи тригонометрии. Если «х» — это значение (модуль) исходного вектора, то компонент вектора, прилежащий к углу исходного вектора, равен xcosθ, а компонент вектора, противолежащий углу исходного вектора, равен xsinθ.
- Важно отметить направление компонентов. Если компонент направлен противоположно направлению одной из осей, то его значение будет отрицательным, например, если на двумерной плоскости координат компонент направлен влево или вниз.
- Например, дан вектор с модулем (значением) 3 и направлением 135o (по отношению к горизонтали). Тогда компонент «х» равен 3cos 135 = -2,12, а компонент «у» равен 3sin135 = 2,12.
-
2
После того, как вы нашли компоненты всех складываемых векторов, просто сложите их значения и найдете значения компонентов результирующего вектора. Сначала сложите значения всех горизонтальных компонентов (то есть компонентов, параллельных оси Х). Затем сложите значения всех вертикальных компонентов (то есть компонентов, параллельных оси Y). Если значение компонента отрицательное, то оно вычитается, а не прибавляется.
- Например, сложим вектор <-2,12, 2,12> и вектор <5,78, -9>. Результирующий вектор будет таким <-2,12 + 5,78, 2,12-9> или <3,66, -6,88>.
-
3
Вычислите длину (значение) результирующего вектора, используя теорему Пифагора: c2=a2+b2 (так как треугольник, образованный исходным вектором и его компонентами является прямоугольным). В этом случае катетами являются компоненты «х» и «у» результирующего вектора, а гипотенузой — сам результирующий вектор.
- Чтобы найти значение результирующего вектора, компоненты <3,66, -6,88> которого вы нашли в предыдущем шаге, используйте теорему Пифагора.
- c2=(3,66)2+(-6,88)2
- c2=13,40+47,33
- c=√60,73 = 7,79
- Чтобы найти значение результирующего вектора, компоненты <3,66, -6,88> которого вы нашли в предыдущем шаге, используйте теорему Пифагора.
-
4
Чтобы найти направление результирующего вектора, используйте формулу θ=tan-1(b/a), где θ — угол между вектором и горизонтальной осью, b — значение компонента «у», а — значение компонента «х».
- Найдите направление результирующего вектора из нашего примера.
- θ=tan-1(-6,88/3,66)
- θ=tan-1(-1,88)
- θ=-61,99o
- Найдите направление результирующего вектора из нашего примера.
-
5
Представьте результирующий вектор, обозначив его значение и направление. К значению вектора не забудьте приписать единицы измерения, в которых даны складываемые/вычитаемые вектора.
- Например, если в нашем примере вы складывали силу, измеряемую в Ньютонах, то ответ запишите так: 7,79 Н под углом -61,99o (к горизонтальной оси).
Реклама
Советы
- Не путайте векторы с их модулями (значениями).
- Векторы, у которых одно направление, можно складывать или вычитать, просто сложив или отняв их значения. Если складываются два противоположно направленных вектора, то их значения вычитаются, а не складываются.
- Векторы, которые представлены в виде xi + yj + zk можно сложить или вычесть, просто сложив или вычтя соответствующие коэффициенты. Ответ также запишите в виде i,j,k.
- Значение вектора в трехмерном пространстве можно найти с помощью формулы a2=b2+c2+d2, где a — значение вектора, b, c, и d — компоненты вектора.
- Векторы-столбцы можно складывать/вычитать, сложив/вычтя соответствующие значения в каждой строке.
Реклама
Об этой статье
Эту страницу просматривали 183 256 раз.
Была ли эта статья полезной?
Содержание
- Примеры
- Геометрические методы сложения двух векторов
- Метод параллелограмма
- Упражнения
- -Упражнение 1
- Решение
- Упражнение 2.
- Решение
- Вычисление декартовых компонент результирующего вектора
- Величина и направление результирующего вектора
- Ссылки
В результирующий вектор — это результат, полученный с помощью операции с векторами, результатом которой также является вектор. Обычно эта операция представляет собой сумму двух или более векторов, с помощью которой получается вектор с эквивалентным эффектом.
Таким образом получаются такие векторы, как результирующая скорость, ускорение или сила. Например, когда на тело действует несколько сил. F1, F2, F3,…. векторная сумма всех этих сил равна чистой силе (равнодействующей), которая математически выражается следующим образом:
F1 + F2 + F3 +… = Fр или FN
Результирующий вектор, будь то силы или любая другая величина вектора, находится с применением правил сложения векторов. Поскольку векторы имеют направление и смысл, а также числовое значение, недостаточно добавить модули, чтобы получить результирующий вектор.
Это верно только в том случае, если задействованные векторы направлены в одном направлении (см. Примеры). В противном случае необходимо использовать методы векторной суммы, которые в зависимости от случая могут быть геометрическими или аналитическими.
Примеры
Геометрическими методами нахождения результирующего вектора являются метод траверса и метод параллелограмма.
Что касается аналитических методов, существует метод компонентов, с помощью которого можно найти вектор, полученный из любой системы векторов, при условии, что у нас есть его декартовы компоненты.
Геометрические методы сложения двух векторов
Предположим, что векторы или Y v (Мы обозначили их жирным шрифтом, чтобы отличить их от скаляров). На рисунке 2а) они расположены на плоскости. На рисунке 2 б) он переведен в вектор v таким образом, что его начало совпадает с концом или. Результирующий вектор идет от начала координат первого (или) до кончика последнего (v):
Результирующая фигура в этом случае представляет собой треугольник (треугольник — это 3-сторонний многоугольник). Если у нас есть два вектора в одном направлении, процедура такая же: поместите один из векторов за другим и нарисуйте тот, который идет от начала или хвоста первого до конца или конца последнего.
Обратите внимание, что порядок, в котором выполняется эта процедура, не имеет значения, поскольку сумма векторов коммутативна.
Также обратите внимание, что в этом случае модуль (длина или размер) результирующего вектора — это сумма модулей добавленных векторов, в отличие от предыдущего случая, когда модуль результирующего вектора меньше суммы модулей участников.
Метод параллелограмма
Этот метод очень подходит, когда вам нужно добавить два вектора, исходные точки которых совпадают, скажем, с началом системы координат x-y. Предположим, что это так для наших векторов или Y v (рисунок 3а):
На рисунке 3b) параллелограмм построен с помощью пунктирных линий, параллельных или уже v. Результирующий вектор имеет начало в точке O и конец в точке пересечения пунктирных линий. Эта процедура полностью эквивалентна описанной в предыдущем разделе.
Упражнения
-Упражнение 1
Учитывая следующие векторы, найдите результирующий вектор с помощью метода обхода.
Решение
Метод траверса — первый из известных. Помните, что сумма векторов коммутативна (порядок слагаемых не влияет на сумму), поэтому вы можете начать с любого из векторов, например или (рисунок 5а) или р (рисунок 5b):
Полученная фигура представляет собой многоугольник, а результирующий вектор (синий) называется р. Если вы начнете с другого вектора, сформированная форма может быть другой, как показано в примере, но результирующий вектор будет таким же.
Упражнение 2.
На следующем рисунке известно, что модули векторов или Y v соответственно они равны u = 3 условных единицы и v = 1,8 условных единиц. Угол, который или форма с положительной осью абсцисс составляет 45º, а v образует 60º с осью Y, как показано на рисунке. Найдите результирующий вектор, величину и направление.
Решение
В предыдущем разделе результирующий вектор был найден методом параллелограмма (на рисунке выделен бирюзовым цветом).
Простой способ найти результирующий вектор аналитически — выразить слагаемые векторы через их декартовы компоненты, что легко, когда известны модуль и угол, например векторы в этом примере:
илиИкс = u. cos 45º = 3 x cos 45º = 2,12; илиY = u. грех 45º = 3x грех 45º = 2,12
vИкс = v. sin 60º = 1,8 x sin 60º = 1,56; vY = -v. cos 60º = -1,8 x cos 60º = — 0,9
Векторы или Y v это векторы, принадлежащие плоскости, поэтому каждый из них имеет по две компоненты. Вектор u находится в первом квадранте, а его компоненты положительны, а вектор v — в четвертом квадранте; его компонент x положительный, но его проекция на вертикальную ось падает на отрицательную ось y.
Вычисление декартовых компонент результирующего вектора
Результирующий вектор находится путем алгебраического сложения соответствующих компонентов x и y, чтобы получить их декартовы компоненты:
рИкс = 2.12 + 1.56 = 3.68
рY = 2.12 + (-0.9) = 1.22
Как только декартовы компоненты указаны, вектор становится полностью известным. Полученный вектор можно записать в квадратных скобках (подтяжки):
R = <3,68; 1,22> условные единицы
Обозначение в квадратных скобках используется для отличия вектора от точки на плоскости (или в пространстве). Другой способ выразить полученный вектор аналитически — использовать единичные векторы я и j в плоскости (я, j Y k в пространстве):
р = 3.68 я + 1.22 j условные единицы
Поскольку обе компоненты результирующего вектора положительны, вектор р принадлежит к первому квадранту, который ранее уже был замечен графически.
Величина и направление результирующего вектора
Зная декартовы компоненты, величина R вычисляется по теореме Пифагора, так как полученный вектор рвместе со своими компонентами RИкс и RY образуют прямоугольный треугольник:
Величина или модуль: R = (3.682 + 1.222)½ = 3.88
Направление q, взяв за основу положительную ось x: q = arctan (RY / РИкс) = arctg (1,22 / 3,68) = 18,3 º
Ссылки
- Добавление векторов и правил. Получено с: newt.phys.unsw.edu.au
- Фигероа, Д. Серия: Физика для науки и техники. Том 1. Кинематика. 31-68.
- Физический. Модуль 8: Векторы. Получено с: frtl.utn.edu.ar
- Хиббелер, Р. 2006. Механика для инженеров. Статический. 6-е издание. Континенталь Издательская Компания. 15-53.
- Калькулятор сложения векторов. Получено с: www.1728.org
Вектор – это направленный прямолинейный отрезок, то есть отрезок, имеющий
определенную длину и определенное направление. Пусть точка А – начало вектора, а точка B – его конец, тогда вектор обозначается символом 


вектору 
обозначен 
Сформулируем ряд базовых определений.
Длиной
или модулем
вектора 
длина отрезка и обозначается 

не имеет. Вектор 
направление которого совпадает с направлением вектора 

Векторы
называются коллинеарными, если они лежат на одной прямой или на
параллельных прямых, записывают
противоположные направления. Нулевой вектор считают коллинеарным любому
вектору.
Векторы
называются равными 
одинаковые длины.
Три вектора в пространстве называются компланарными,
если они лежат в одной плоскости или на параллельных плоскостях. Если среди
трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы
компланарны.
Рассмотрим в
пространстве прямоугольную систему координат 0xyz. Выделим на осях координат 0x, 0y, 0z единичные векторы (орты) и
обозначим их через 
Выберем произвольный вектор
пространства и совместим его начало с началом
координат. Спроектируем вектор
на координатные
оси и обозначим проекции через ax, ay, az
соответственно. Тогда нетрудно показать, что

Эта
формула является основной в векторном исчислении и называется разложением
вектора по ортам координатных осей. Числа ax, ay, az называются координатами вектора 
проекциями на оси координат. Векторное равенство (2.25) часто записывают в
виде

скобках, чтобы визуально легче различать координаты вектора и координаты точки.
С использованием формулы длины отрезка, известной из школьной геометрии, можно
найти выражение для вычисления модуля вектора
:

то
есть модуль вектора равен корню квадратному из суммы квадратов его координат.
Обозначим углы между вектором
и осями
координат через α, β, γ соответственно. Косинусы этих углов называются
для вектора 

свойства проекции вектора на ось, которое будет рассмотрено в нижеследующем
пункте 4.
Пусть в трехмерном пространстве заданы векторы 
координатами. Имеют место следующие
операции над ними: линейные (сложение, вычитание, умножение на число и
проектирование вектора на ось или другой вектор); не линейные – различные
произведения векторов (скалярное, векторное, смешанное).
1. Сложение двух векторов производится покоординатно, то
есть если

Данная
формула имеет место для произвольного конечного числа слагаемых.
Геометрически
два вектора складываются по двум правилам:
а) правило треугольника –
результирующий вектор суммы двух векторов соединяет начало первого из них с
концом второго при условии, что начало второго совпадает с концом первого
вектора; для суммы векторов –
результирующий вектор суммы соединяет начало первого из них с концом последнего
вектора-слагаемого при условии, что начало последующего слагаемого совпадает с
концом предыдущего;
б)
правило
параллелограмма (для двух
векторов) – параллелограмм строится на векторах-слагаемых как на сторонах,
приведенных к одному началу; диагональ параллелограмма исходящая из их общего начала, является суммой
векторов.
2. Вычитание двух векторов производится
покоординатно, аналогично сложению, то есть если 

Геометрически два
вектора складываются по уже упомянутому правилу параллелограмма с учетом того, что разностью векторов
является диагональ, соединяющая концы векторов, причем результирующий вектор
направлен из конца вычитаемого в конец уменьшаемого вектора.
Важным следствием
вычитания векторов является тот факт, что если известны координаты начала и
конца вектора, то для вычисления координат вектора необходимо из координат его конца
вычесть координаты его начала. Действительно, любой вектор пространства 
представлен в виде разности двух векторов, исходящих из начала координат: 


координатами точек А и В, так как начало координат О(0;0;0). Таким образом, по правилу
вычитания векторов следует произвести вычитание координат точки А из координат точки В.
3. Умножение вектора на число λ покоординатно:
При λ>0
– вектор





4. Пусть в пространстве задана
направленная прямая (ось l), вектор 
координатами конца и начала. Обозначим проекции точек A и B на ось l
соответственно через A’ и B’.
Проекцией 


знаком «+», если вектор 
знаком «–», если 
Если
в качестве оси l взять некоторый другой вектор 


Рассмотрим некоторые
основные свойства проекций:
1) проекция вектора 
вектора 
между вектором и осью, то есть 
2.) проекция вектора на ось
положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и
равна нулю, если этот угол – прямой;
3) проекция суммы нескольких
векторов на одну и ту же ось равна сумме проекций на эту ось.
Сформулируем определения и
теоремы о произведениях векторов, представляющих нелинейные операции над
векторами.
5. Скалярным произведением 


число (скаляр), равное произведению длин этих векторов на косинус угла φ между
ними, то есть

Очевидно, что скалярный квадрат любого ненулевого вектора равен квадрату его длины, так как в этом случае угол 
Теорема 2.2. Необходимым и достаточным условием
перпендикулярности двух векторов является равенство нулю их скалярного
произведения
Следствие. Попарные скалярные произведения единичных орт равны нулю, то есть
Теорема 2.3. Скалярное произведение двух векторов 
заданных своими координатами, равно сумме произведений их одноименных координат, то есть

С помощью скалярного произведения векторов можно
вычислить угол между ними.
Если заданы два ненулевых вектора
своими координатами 

Отсюда
следует условие перпендикулярности ненулевых векторов



Нахождение проекции вектора 
заданное вектором 

С помощью скалярного произведения векторов находят
работу постоянной силы 
прямолинейном участке пути.
Предположим, что под действием постоянной силы 
положения А в положение B. Вектор силы 



равна 
Следовательно, работа постоянной силы
при прямолинейном перемещении точки ее приложения равна скалярному произведению
вектора силы на вектор перемещения.
Пример
2.9. С
помощью скалярного произведения векторов найти угол при вершине A параллелограмма ABCD, построенного на векторах
Решение. Вычислим модули векторов и их скалярное произведение
по теореме (2.3):
Отсюда согласно формуле (2.29) получим косинус
искомого угла
Пример 2.10. Затраты сырьевых и материальных ресурсов, используемых
на производство одной тонны творога, заданы в таблице 2.2 (руб.).
Какова общая цена этих ресурсов, затрачиваемых на изготовление одной
тонны творога?
Таблица 2.2
Решение. Введем в рассмотрение два вектора: вектор затрат
ресурсов на тонну продукции 
соответствующего ресурса 
Тогда 
ресурсов 
векторов 
Таким образом, общая цена затрат на производство одной
тонны творога составляет 279 541,5 рублей
Примечание. Действия с векторами, осуществленные в примере 2.10,
можно выполнить на персональном компьютере. Для нахождения скалярного
произведения векторов в MS Excel используют функцию СУММПРОИЗВ( ), где в качестве
аргументов указываются адреса диапазонов элементов матриц, сумму произведений
которых необходимо найти. В MathCAD
скалярное произведение двух векторов выполняется при помощи соответствующего
оператора панели инструментов Matrix
Пример 2.11. Вычислить работу, произведенную силой 
из положения A(2;4;6) в положение A(4;2;7). Под каким углом к AB направлена сила 
Решение. Находим вектор перемещения, вычитая из координат его конца координаты
начала


Угол φ между 

формуле (2.29), то есть
6. Три некомпланарных вектора 
тройку, если при наблюдении из конца третьего вектора 
поворот от первого вектора 
вектору 
если по часовой стрелке.
Векторным
произведением 


вектор 
– 


– имеет длину, равную 


– векторы 
тройку (рис. 2.15).

условием коллинеарности двух векторов является равенство нулю их векторного
произведения 
Теорема 2.5. Векторное произведение векторов 
третьего порядка вида

Примечание. Определитель (2.25)
раскладывается по свойству 7 определителей
Следствие 1. Необходимым и достаточным условием коллинеарности двух
векторов является пропорциональность их соответствующих координат
Следствие 2. Векторные произведения единичных орт равны
Следствие 3. Векторный квадрат любого вектора равен нулю
Геометрическая
интерпретация векторного произведения состоит в том, что длина результирующего
вектора численно равна площади S
параллелограмма, построенного на векторах–сомножителях как на сторонах,
приведенных к одному началу. Действительно, согласно определению, модуль
векторного произведения векторов равен 
построенного на векторах 


. Следовательно,

Также с помощью векторного произведения можно
определить момент силы относительно точки и линейную скорость вращения.
Пусть в точке A приложена
сила 
некоторая точка пространства (рис. 2.16). Из курса физики известно, что моментом
силы 
точки O называется вектор 
— перпендикулярен плоскости, проходящей через точки O, A, B;
— его модуль численно равен произведению силы на плечо 
— 


Следовательно,
момент силы 
точки O представляет собой векторное произведение


Линейная скорость 
угловой скоростью 
неподвижной оси, определяется формулой Эйлера 
точка оси (рис. 2.17).
Пример 2.12. С помощью
векторного произведения найти площадь треугольника ABC, построенного на векторах

Решение. Найдем векторное произведение заданных векторов по
формуле (2.32).

произведения двух неколлинеарных векторов численно равен площади
параллелограмма, построенного на данных векторах как на сторонах, приведенных к
общему началу, то есть 

. Следовательно, искомая площадь равна 
площади)
7. Рассмотрим произведение трех векторов 

результирующий вектор – скалярно на третий. Такое произведение 
произведением трех векторов
(векторно–скалярным произведением).
Теорема 2.6. Необходимым и достаточным условием компланарности
трех векторов является равенство нулю их смешанного произведения
Теорема 2.7. Если три вектора 
произведение представляет собой определитель третьего порядка, составленный из
координат векторов- сомножителей соответственно, то есть

Нетрудно показать, что объем параллелепипеда,
построенного на векторах 
сторонах, приведенных к общему началу, численно равен модулю смешенного
произведения этих векторов 
Объем треугольной пирамиды, построенной на этих же
векторах, равен

Пример 2.13. Вершинами пирамиды служат точки 
Решение. Найдем
координаты векторов

По формуле (2.36) объем пирамиды, построенной на
векторах 


Рассмотрим очень важный вопрос о
разложении вектора по базису. Приведем
следующие определения.
Система векторов 
линейно зависимой, если существуют такие числа 
место равенство

Отсюда всегда можно один из линейно
зависимых векторов выразить через линейную комбинацию остальных. Действительно,
допустим для определенности, что 
получим выражение вектора 
остальные векторы
Линейно независимыми называют векторы, если равенство
(2.37) выполняется только тогда, когда
все


независимых векторов равняется рангу матрицы, которая составлена из координат
этих векторов (смотри раздел I.5).
Базисом n – мерного
пространства En называют любую совокупность линейно независимых векторов n – мерного пространства.
Произвольный вектор 
– мерного пространства можно представить
в виде линейной комбинации векторов базиса
таким образом:
Числа

вектора 
векторов 
Линейное пространство называется
конечномерным и имеет размерность n, если в этом
пространстве существует система из n линейно независимых векторов (базис) такая,
что каждое ее расширение приводит к линейной зависимости системы.
Например, в трехмерном пространстве
существует базис единичных орт 
линейно независимых векторов, то есть каждый вектор 
пространства, приводит к линейной зависимости векторов (является линейной
комбинацией орт 

по ортам 

пространстве.
Вопросы для самопроверки