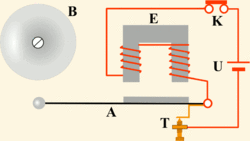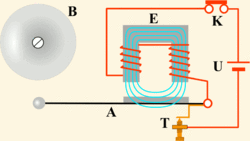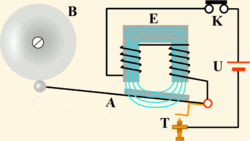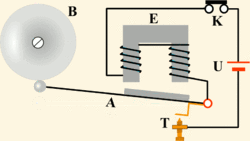
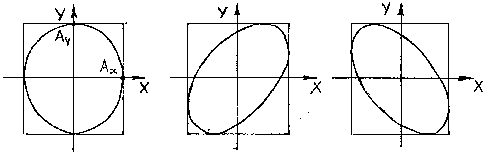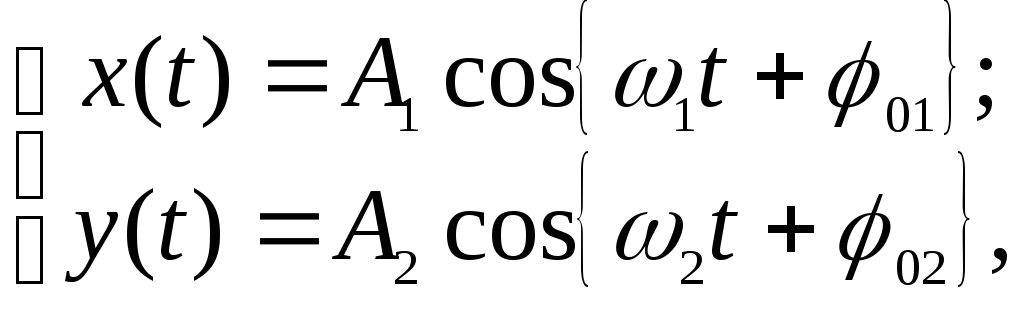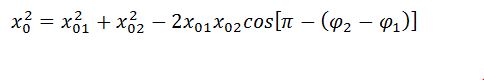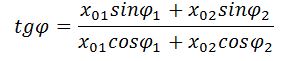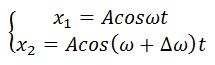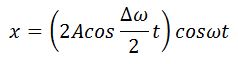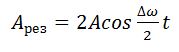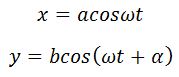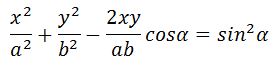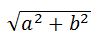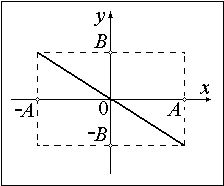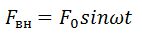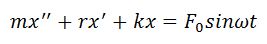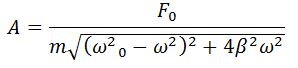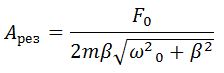2.1. Сложение гармонических колебаний одного направления
2.2. Сложение взаимно перпендикулярных колебаний
Одно и то же тело может одновременно участвовать в двух и более движениях. Простым примером является движение шарика, брошенного под углом к горизонту. Можно считать, что шарик участвует в двух независимых взаимно перпендикулярных движениях: равномерном по горизонтали и равнопеременном по вертикали. Одно и то же тело (материальная точка) может участвовать в двух (и более) движениях колебательного типа.
Под сложением колебаний понимают определение закона результирующего колебания, если колебательная система одновременно участвует в нескольких колебательных процессах. Различают два предельных случая – сложение колебаний одного направления и сложение взаимно перпендикулярных колебаний.
2.1. Сложение гармонических колебаний одного направления
1. Сложение двух колебаний одного направления (сонаправленных колебаний)
можно провести с помощью метода векторных диаграмм (Рисунок 9) вместо сложения двух уравнений.
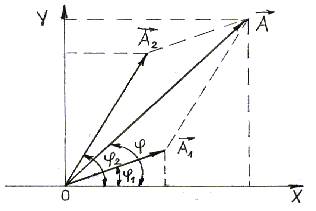
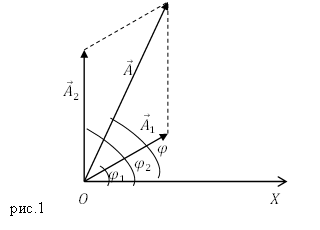
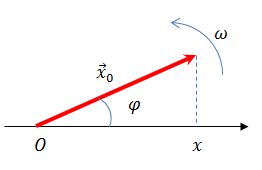
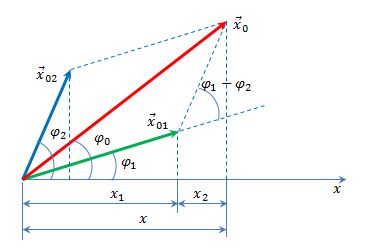
На Рисунке 2.1 показаны векторы амплитуд А1(t) и А2(t) складываемых колебаний в произвольный момент времени t, когда фазы этих колебаний соответственно равны и
. Сложение колебаний сводится к определению
. Воспользуемся тем фактом, что на векторной диаграмме сумма проекций складываемых векторов равна проекции векторной суммы этих векторов.
Результирующему колебанию соответствует на векторной диаграмме вектор амплитуды
и фаза
.
Рисунок 2.1 – Сложение сонаправленных колебаний.
Величина вектора А(t) может быть найдена по теореме косинусов:
.
Фаза результирующего колебания задается формулой:
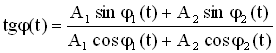
Если частоты складываемых колебаний ω1 и ω2 не равны, то и фаза φ(t), и амплитуда А(t) результирующего колебания будут изменяться с течением времени. Складываемые колебания называются некогерентными в этом случае.
2. Два гармонических колебания x1 и x2 называются когерентными, если разность их фаз не зависит от времени:
.
Но так как , то для выполнения условия когерентности двух этих колебаний должны быть равны их циклические частоты
.
Амплитуда результирующего колебания, полученного при сложении сонаправленных колебаний с равными частотами (когерентных колебаний) равна:
.
Начальную фазу результирующего колебания легко найти, если спроектировать векторы А1 и А2 на координатные оси ОХ и ОУ (см. Рисунок 9):
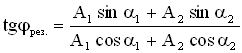
Итак, результирующее колебание, полученное при сложении двух гармонических сонаправленных колебаний с равными частотами, также является гармоническим колебанием .
3. Исследуем зависимость амплитуды результирующего колебания от разности начальных фаз складываемых колебаний.
Если , где n – любое целое неотрицательное число
(n = 0, 1, 2…), то , т.е. результирующая амплитуда будет минимальной. Складываемые колебания в момент сложения находились в противофазе. При
результирующая амплитуда равна нулю
.
Если , то
, т.е. результирующая амплитуда будет максимальной. В момент сложения складываемые колебания находились в одной фазе, т.е. были синфазны. Если амплитуды складываемых колебаний одинаковы
, то
.
4. Сложение сонаправленных колебаний с неравными, но близкими частотами.
Частоты складываемых колебаний не равны , но разность частот
много меньше и ω1, и ω2. Условие близости складываемых частот записывается соотношениями
.
Примером сложения сонаправленных колебаний с близкими частотами является движение горизонтального пружинного маятника, жесткость пружин которого немного различна k1 и k2.
Пусть амплитуды складываемых колебаний одинаковы, а начальные фазы равны нулю
. Тогда уравнения складываемых колебаний имеют вид:
,
.
Результирующее колебание описывается уравнением:
.
Получившееся уравнение колебаний зависит от произведения двух гармонических функций: одна – с частотой , другая – с частотой
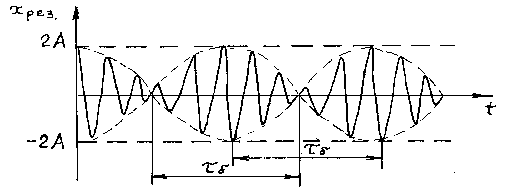
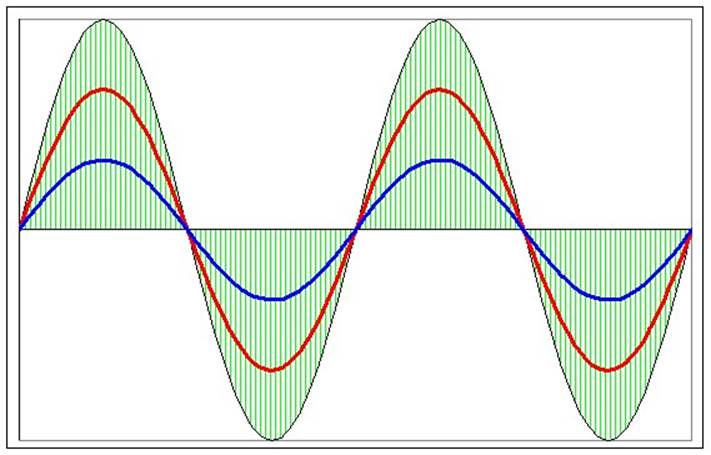
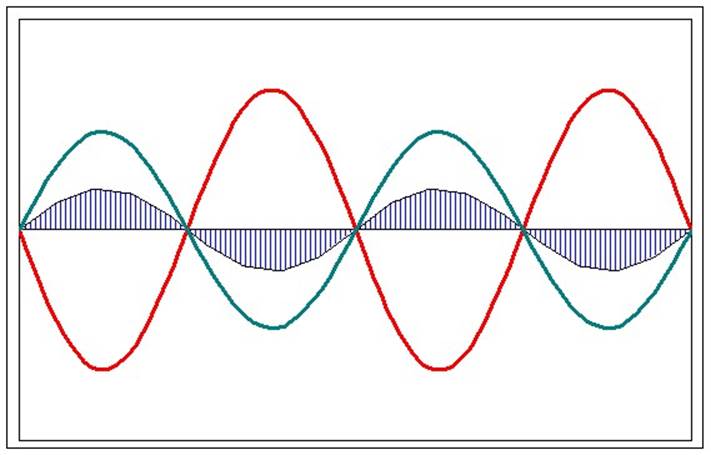
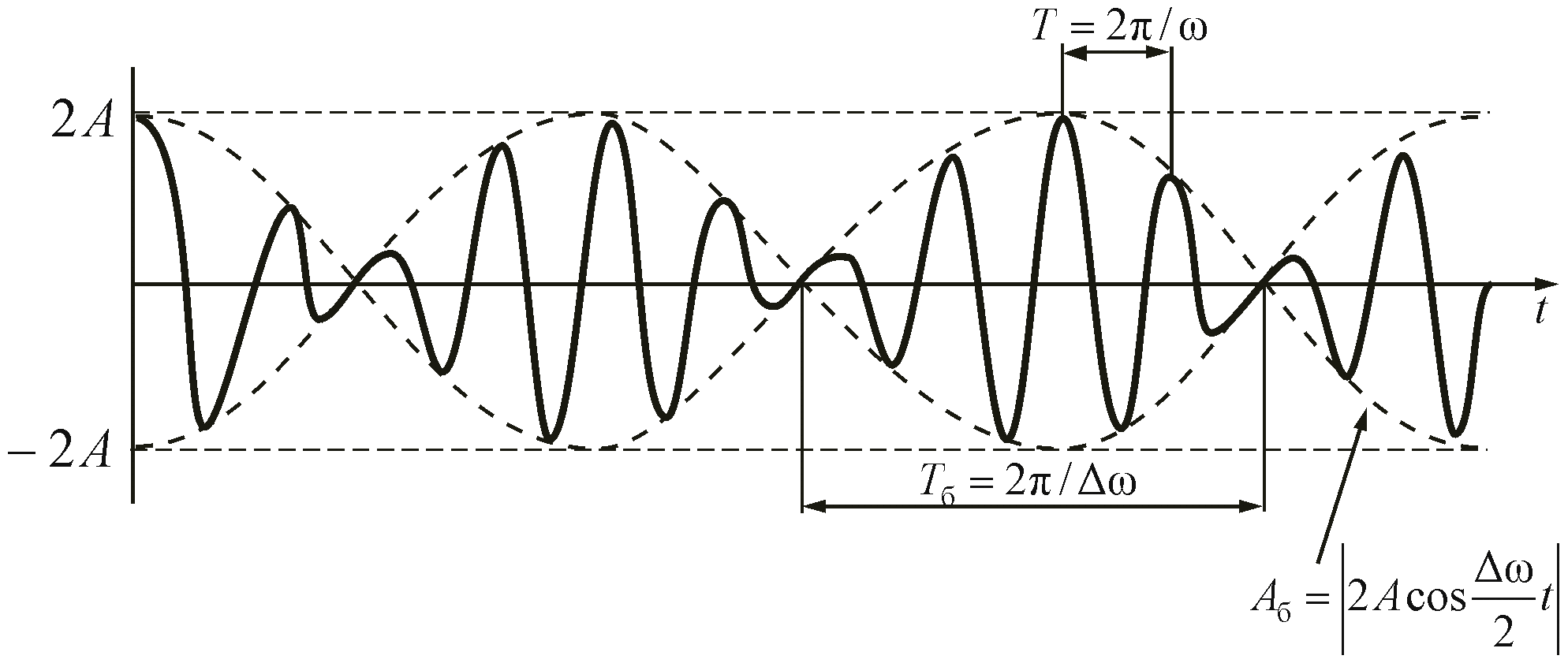
, где ω близка к частотам складываемых колебаний (ω1 или ω2). Результирующее колебание можно рассматривать как гармоническое колебание с изменяющейся по гармоническому закону амплитудой. Такой колебательный процесс называется биениями. Строго говоря, результирующее колебание в общем случае не является гармоническим колебанием.
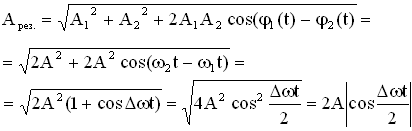
Рисунок 2.2 – Зависимость смещения от времени при биениях.
Амплитуда биений медленно меняется с частотой . Абсолютное значение косинуса повторяется, если его аргумент изменяется на π, значит и значение результирующей амплитуды повторится через промежуток времени τб, называемый периодом биений (см. Рисунок 12). Величину периода биений можно определить из следующего соотношения:
.
Величина — период биений.
Величина 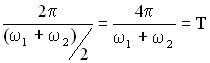
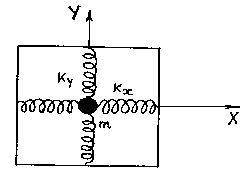
1. Модель, на которой можно продемонстрировать сложение взаимно перпендикулярных колебаний, представлена на Рисунке 2.3. Маятник (материальная точка массой m) может совершать колебания по осям ОХ и ОУ под действием двух сил упругости, направленных взаимно перпендикулярно.
Рисунок 2.3
Складываемые колебания имеют вид:
.
Частоты колебаний определяются как 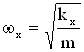
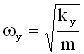
,
-коэффициенты жесткости пружин.
2. Рассмотрим случай сложения двух взаимно перпендикулярных колебаний с одинаковыми частотами , что соответствует условию
(одинаковые пружины). Тогда уравнения складываемых колебаний примут вид:
Когда точка участвует одновременно в двух движениях, ее траектория может быть различной и достаточно сложной. Уравнение траектории результирующего колебаний на плоскости ОХУ при сложении двух взаимно перпендикулярных с равными частотами можно определить, исключив из исходных уравнений для х и y время t:
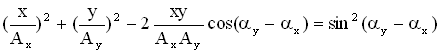
Вид траектории определяется разностью начальных фаз складываемых колебаний, которые зависят от начальных условий (см. § 1.1.2). Рассмотрим возможные варианты.
а) Если , где n = 0, 1, 2…, т.е. складываемые колебания синфазные, то уравнение траектории примет вид:
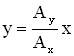
|
|
|
|
Рисунок 2.3.а |
Рисунок 2.3 б |
б) Если (n = 0, 1, 2 …), т.е. складываемые колебаний находятся в противофазе, то уравнение траектории записывается так:
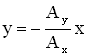
В обоих случаях ( а, б) результирующее движение точки будет колебание по прямой, проходящей через точку О. Частота результирующего колебания равна частоте складываемых колебаний ω0, амплитуда определяется соотношением:
.
Угол, который прямая (траектория) составляет с осью ОХ, можно найти из уравнения:
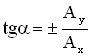
Результатом сложения взаимно перпендикулярных колебаний (случай а и б) является колебание, которое называется линейно поляризованным.
в) Если (n = 0, 1, 2 …), то уравнение траектории результирующего движения примет вид:
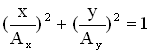
Это уравнение эллипса, его оси совпадают с осями координат ОХ и ОУ, а размеры его полуосей равны и
(Рисунок 2.4 ).
Рисунок 2.4
Точка в результате участия в двух взаимно перпендикулярных колебаниях описывает эллипс за время, равное периоду складываемых колебаний .
3. Сложение взаимно перпендикулярных колебаний с кратными частотами.
Складываются взаимно перпендикулярные колебания, частоты которых не равны , но
,
, где a и b – целые числа.
Периоды колебаний вдоль осей ОХ и ОУ соответственно равны и
. Отношение периодов
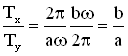
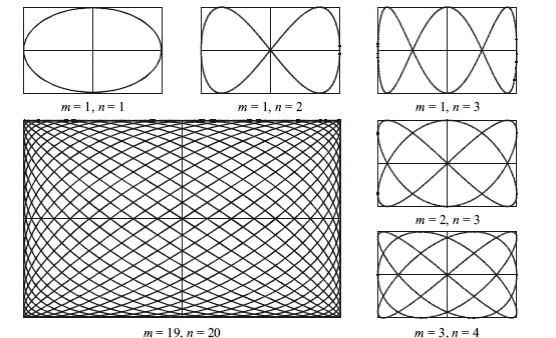
Траектория точки, участвующей во взаимно перпендикулярных колебаниях с кратными частотами, — замкнутая кривая, форма которой зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний. Такие замкнутые траектории называются фигурами Лиссажу.
4.1. Основные формулы и обозначения
П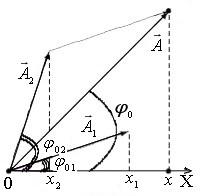
сложении гармонических колебаний одного
направления и одинаковой частоты,
например, колебаний
и
удобно использовать метод векторных
диаграмм. Каждое колебание изображается
вектором на плоскости (например,и
).
Длина этого вектора равна амплитуде
соответствующего колебания. Угол между
вектором и Рис. 5
горизонтальной осью равен фазе
соответствующего колебания в данный
момент времени. Векторописывающий результирующее колебание,
строится по правилам сложения векторов.
Частота результирующего колебаниятакже равна
Амплитуда и начальная фаза результирующего
колебания определяются по диаграмме
для начального момента времени (рис. 5)
и вычисляются соответственно по формулам:
(70)
(71)
При сложении
гармонических взаимно перпендикулярных
колебаний,
совершаемых точкой в плоскости
,
например, колебаний
(72)
уравнение траектории
движения содержит только переменные
и
но не содержит времени
Следовательно, уравнение траектории
можно найти, если каким-либо образом
исключить из формул (72) время, например,
выразитьчерез
или
.
Если при этом
отношение частот (периодов)
является рациональной дробью (отношением
целых чисел), то траектория оказывается
замкнутой, а движение – периодическим.
4.2. Примеры решения задач
З а д а ч а 10.
Построить векторную диаграмму в начальный
момент времени при сложении двух
гармонических колебаний одинаковой
частоты и одного направления. Найти
графически и аналитически амплитуду и
начальную фазу результирующего колебания.
Записать закон результирующего колебания.
Законы складываемых колебаний имеют
вид:
где
см;
см;
с-1;
|
Дано:
Найти: |
Решение.
Чтобы найти
|
где
.
(74)
Тогда
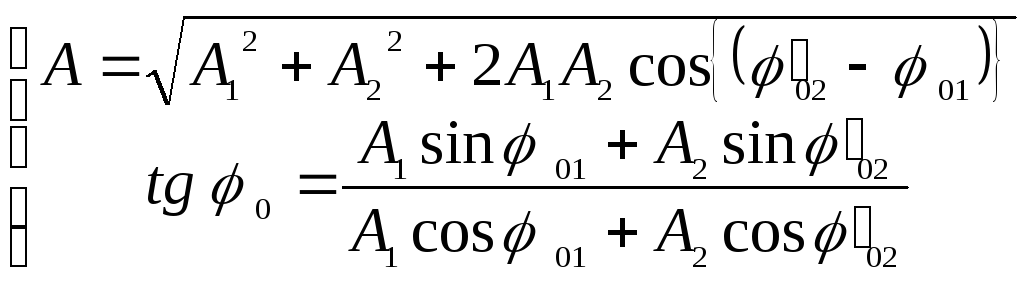
(75)
Подставляя в
равенства (75) численные данные и учитывая
формулу (74), получим:
см;
Отсюда
°
рад.
Следовательно, закон результирующего
колебания имеет вид:где
см;
с-1;
рад.
Начертим векторную
диаграмму сложения колебаний в начальный
момент времени (рис. 6). Для этого в
соответствии с правилами построения,
изложенными в подразделе 4.1, сопоставим
колебанию
вектор
длиной
,
который направим под угломк горизонтальной оси
,
т. е. вертикально вверх; колебаниюсопоставим вектор
длиной
,
который направим под угломк горизонтальной оси
,
т. е. отложим его в направлении оси (см.
рис. 6). Результирующее колебание будет
описываться векторомдлиной
полученным по правилу параллелограмма
сложением векторови
Угол, образованный вектором
и осью
равен начальной фазе результирующего
колебания
О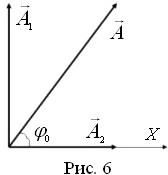
где
см;
с-1;
Рис. 6
рад.
З а д а ч а 11.
Получить уравнение траектории частицы
и построить траекторию в плоскости
,
если частица одновременно участвует в
двух взаимно перпендикулярных колебаниях:где
см,
см.
|
Дано:
Найти: |
Решение.
Чтобы найти |
;
(76)
(77)
исключить время.
Для этого из уравнения (76) выразим
:
. (78)
Отсюда
. (79)
Преобразовав и
возведя в квадрат уравнение (77), а затем,
последовательно применив формулы
приведения и двойного аргумента к
тригонометрическим функциям, получим:
. (80)
Используя соотношения
(78) и (79), из выражения (80) можно исключить
время и получить уравнение траектории:
Для построения
траектории в плоскости
выберем наиболее удобные точки. Это
точки, имеющие равную нулю, наибольшую
и наименьшую из возможных ординату ()
или абсциссу ().
|
Таблица |
|
|
|
|
|
|
|
|
|
|
Используя уравнение
траектории (81), найдем вторые координаты
этих точек Рис. 7
(см. Табл. 2).
Траектория,
построенная по этим точкам, показана
на рис. 7. Координата
достигает максимума по модулю четырежды,
а– дважды. Это объясняется соответствующим
отношением частот: за время одного
колебания вдоль оситочка совершает два колебания вдоль
оси
Ответ:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
09.04.2015619.52 Кб161.doc
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сложение колебаний, теория и онлайн калькуляторы
Сложение колебаний
Тело, совершающее колебания, способно принимать участие в нескольких колебательных процессах одновременно. В таком случае
возникает необходимость выяснить, каким будет результирующее колебание.
Сложение колебаний направленных по одной прямой
Рассмотрим сложение двух гармонических колебаний одинакового направления и равной частоты. Тогда смещение ($x$) совершающего колебания тела будет равно сумме смещений $x_1$ и $x_2$, которые представим в виде уравнений:
[x_1=A_1{cos left({omega }_0t+{varphi }_1right) }left(1right),]
[x_2=A_2{cos left({omega }_0t+{varphi }_2right) }left(2right).]
Колебания (1) и (2) представим на векторной диаграмме в виде векторов ${overline{A}}_1$ и ${overline{A}}_2$ (рис.1).
Результирующее колебание отображает вектор $overline{A}$, который вращается с той же скоростью (${omega }_0$),
что векторы его составляющие. Сложением колебание векторов ${overline{A}}_1$+${overline{A}}_2$=$overline{A}$ является гармоническим колебанием:
[x=A{cos {(omega }_0t+varphi ) (3) }.]
Из рис.1 видно, что амплитуду результирующего колебания можно найти как:
[A=sqrt{A^2_1+A^2_2+2A_1A_2{cos left({varphi }_2-{varphi }_1right) }left(4right),}]
где $A_1$; $A_2$ — амплитуды сложенных колебаний; ${varphi }_2;;{varphi }_1$ — начальные фазы суммирующихся колебаний. При этом начальную фазу полученного колебания ($varphi $) вычисляют, применяя формулу:
[tg varphi =frac{A_1{sin {varphi }_1+A_2{sin {varphi }_2 } }}{A_1{cos {varphi }_1+A_2{cos {varphi }_2 } }}left(5right).]
Из выражения (4) видно, что если ${varphi }_2-{varphi }_1=0$, тогда получим колебание, амплитуда которого равна:
[A=A_1+A_2left(6right).]
При разности фаз равной ${varphi }_2-{varphi }_1=pm pi $, что означает, что колебания находятся в противофазе, амплитуда сложенных колебания составляет:
[A=left|A_1-A_2right|left(7right).]
Если частоты сложенных гармонических колебаний не равны, то есть векторы ${overline{A}}_1$и ${overline{A}}_2$ вращаются с разной скоростью, результирующее колебание гармоническим не будет. Вектор $overline{A}$ будет пульсировать по величине, и вращаться с переменной скоростью.
Суперпозиция взаимно перпендикулярных колебаний
Пусть у нас происходят два взаимно перпендикулярные гармонические колебания с одной частотой ${omega }_0$. Колебания происходят вдоль осей X и Y. Пусть начало отсчета времени было таким, что начальная фаза первого колебания равнялась нулю. При этом уравнения колебаний предстанут в виде:
[x=A_1{cos left({omega }_0t{+varphi }_1right) }left(8right),]
[y=A_2{cos left({omega }_0t+{varphi }_2right) }left(9right),]
Уравнения (8) и (9) вместе представляют уравнение траектории движения точки в параметрическом виде. Исключаем время из уравнений, получаем уравнение траектории:
Уравнение траектории точки, которая принимает участие в перпендикулярных колебаниях с амплитудами $A_1$и $A_2$ и начальными фазами ${varphi }_2и{varphi }_1$:
[frac{x^2}{A^2_1}+frac{y^2}{A^2_2}-frac{2xy}{A_1A_2}{cos left({varphi }_2-{varphi }_1right) }={sin}^2left({varphi }_2-{varphi }_1right)left(10right).]
Уравнение (10) — это уравнение эллипса.
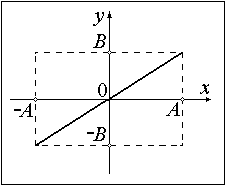
В случае равенства начальных фаз составляющих колебаний уравнение траектории преобразуется к виду:
[y=frac{A_2}{A_1}x или y=-frac{A_2}{A_1}x left(11right),]
что говорит о движении точки по прямой линии. Точка, совершающая гармонические колебания движется по этой прямой, расстояние от начала координат до точки равно:
[r=sqrt{x^2+y^2}.]
Если $Delta varphi ={varphi }_2-{varphi }_1=frac{pi }{2},$ уравнением траектории становится выражение:
[frac{x^2}{A^2_1}+frac{y^2}{A^2_2}=1left(12right),]
что означает, траектория движения эллипс.
Если частоты нормальных друг другу колебаний отличны на очень небольшую величину $Delta omega $, то их рассматривают как колебания с равными частотами, но переменной разностью фаз. При этом суммарное движение проходит по медленно изменяющей вид кривой.
Траектории движений суперпозиций взаимно нормальных колебаний с разными частотами представляют собой сложные кривые, которые называют фигурами Лиссажу.
Примеры задач на сложение колебаний
Пример 1
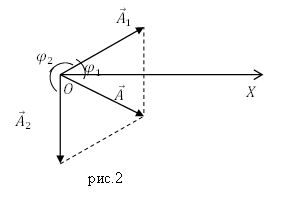
Задание. Какова разность фаз суммируемых колебаний, если складывались два колебания, направленных по одной прямой, обладающих одинаковыми амплитудами и периодами? Сложились они в колебание той же амплитуды.
Решение. В качестве основы для решения задачи используем выражение для вычисления амплитуды складывающихся колебаний, если они направлены вдоль одной прямой:
[A^2=A^2_1+A^2_2+2A_1A_2{cos left({varphi }_2-{varphi }_1right) }(1.1)]
Учитывая условия задачи выражение (1.1) преобразуем к виду:
[A^2=A^2+A^2+2AA{cos left(Delta varphi right) }left(1.2right)]
Выразим из (1.2) искомую разность фаз:
[-frac{1}{2}={cos left(Delta varphi right) }to Delta varphi =frac{4pi }{3}]
Изобразим векторную диаграмму колебаний (рис.2).
Ответ. $Delta varphi =frac{4pi }{3}илиfrac{2pi }{3}$
Пример 2
Задание. Материальная точка совершает одновременно два взаимно перпендикулярных колебания: $x=A{cos left({omega }_0tright) },y=B{cos left({omega }_0tright) },$ каким будет уравнение траектории движения точки?
Решение. Из уравнения:
[x=A{cos left({omega }_0tright) } (2.1)]
выразим ${cos left({omega }_0tright) }$, получим:
[{cos left({omega }_0tright) }=frac{x}{A}left(2.2right).]
Подставим правую часть выражения (2.2) вместо ${cos left({omega }_0tright) }$ в формулу:
[y=B{cos left({omega }_0tright) }left(2.3right),]
имеем:
[y=frac{B}{A}x.]
Уравнением движения точки будет прямая линия.
Ответ. $y=frac{A_2}{A_1}x$
Читать дальше: тело, брошенное горизонтально.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Сложение нескольких гармонических колебаний становится наглядней, если изображать колебания в виде векторов на плоскости. Полученная таким образом схема называется векторной диаграммой.
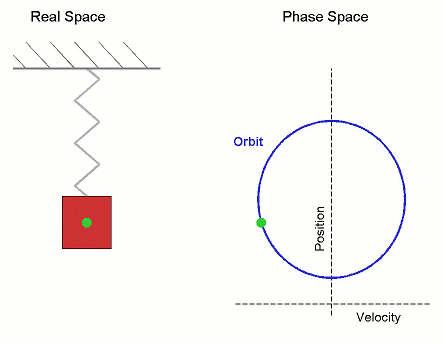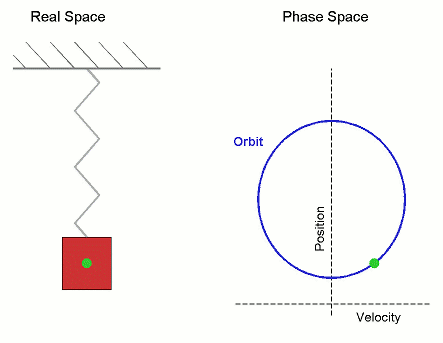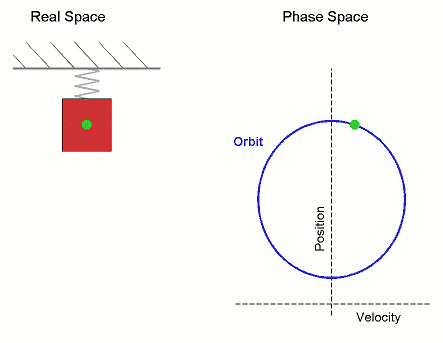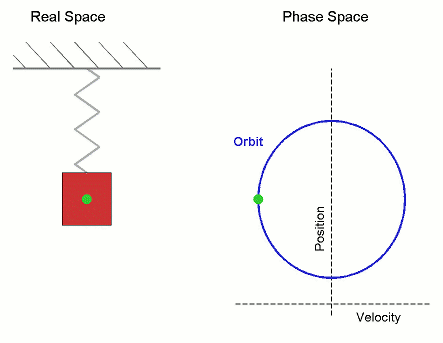
Тогда координата проекции вектора изменяется со временем по закону
Гармоническое колебание может быть задано с помощью вектора, длина которого равна амплитуде колебаний, направление вектора образует с осью х угол, равный начальной фазе колебаний, а угловая скорость вращения вектора равна его циклической частоте.
Сложение двух гармонических колебаний одинакового направления и одинаковой частоты
Смещение х колеблющегося тела будет равно сумме смещений х1 и х2:
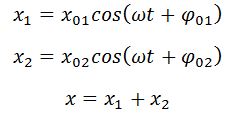
Вектор х0 представляет собой результирующую амплитуду колебаний. Он вращается с той же угловой скоростью ω и начальной фазой φ0.
Рассмотрим частные случаи.
- Если разность фаз φ1 — φ2 колебаний равна 0 (отличается на 2π), то амплитуда результирующего колебания равна сумме амплитуд: х = х1 + х2.
- Если оба колебания находятся в противофазе (разность фаз равна ±π), то результирующая амплитуда х = |х1 — х2|.
- Если частоты неодинаковы, то векторы будут вращаться с различной скоростью. Результирующий вектор пульсирует по величине и вращается с непостоянной скоростью.
Биения
Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биением.
Пусть два колебания мало отличаются по частоте. Тогда амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω намного меньше ω. Начало отсчета выберем так, чтобы начальные фазы обоих колебаний были равны нулю:
Тогда результирующее колебание можно представить в виде:
Амплитуда результирующего колебания меняется со временем по закону
Сложение взаимно перпендикулярных колебаний
Допустим, что материальная точка может совершать колебания как вдоль оси х, так и вдоль перпендикулярной к ней оси у. Если возбудить оба колебания, материальная точка будет двигаться по некоторой, вообще говоря, криволинейной траектории, форма которой зависит от разности фаз обоих колебаний.
Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнения колебаний запишутся следующим образом:
где α — разность фаз обоих колебаний.
После преобразования получим уравнение траектории, которое представляет собой параметрическое уравнение эллипса, оси которого повернуты относительно осей х и у.
Рассмотрим частные случаи.
1. Разность фаз равна нулю. В этом случае получается уравнение прямой.
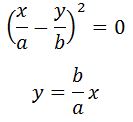
Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой ω и амплитудой
2. Разность фаз равна ±π. Уравнение имеет вид прямой.
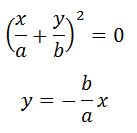
3. При α = ±π/2 получается уравнение эллипса, приведенного к координатным осям. При равенстве амплитуд эллипс превращается в окружность.
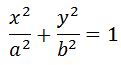
При сложении взаимно перпендикулярных колебаний разных частот получаются различные траектории материальной точки, названные фигурами Лиссажу. Чем ближе отношение частот к единице, тем сложнее получается фигура Лиссажу.
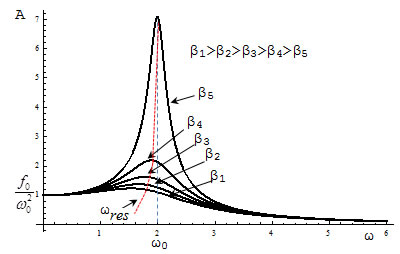
Резонанс
Резонанс — явление резкого возрастания амплитуды вынужденных колебаний при совпадении частот вынуждающей силы и собственных колебаний маятника. Вынужденные колебания происходят, если внешняя сила изменяется периодически:
Дифференциальное уравнение вынужденных колебаний
где Fтр = — rx’
Амплитуда колебания определяется формулой
где коэффициент затухания β = r/2m.
Для определения резонансной частоты надо найти минимум знаменателя. Резонансная амплитуда
Автоколебания
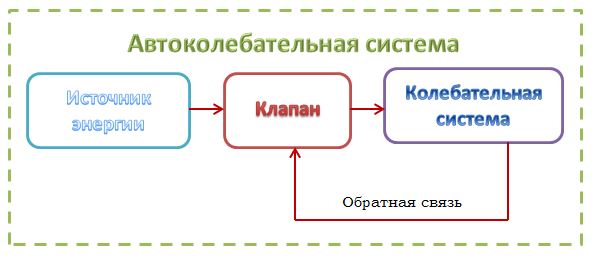
При затухающих колебаниях энергия системы расходуется на преодоление сил сопротивления. Если восполнять эти потери, то колебания станут незатухающими. Если система сама управляет воздействием внешних сил, то такое колебательное движение называется автоколебанием.
В автоколебательной системе обязательно присутствуют элементы:
- сама колебательная ситема, ее параметры определяют частоту автоколебаний;
- источник энергии, поддерживающий автоколебания;
- клапан, регулирующий поступление энергии;
- механизм обратной связи, посредством которой система управляет клапаном так, чтобы поступающая энергия компенсировала потери за счет трения и сопротивления среды.
Примеры автоколебательных систем
|
Маятниковые часы |
Электрический звонок
|
Биологические системы (сердце, легкие) |

Сложение гармонических колебаний
Если колебательная система одновременно участвует в двух (или более) независимых колебательных движениях, возникает задача — найти результирующее колебание. В случае однонаправленных колебаний под этим понимается нахождение уравнения результирующего колебания; в случае взаимно перпендикулярных колебаний — нахождение траектории результирующего колебания.
Метод векторных диаграмм
Рассмотрим вращающийся против часовой стрелки с постоянной угловой скоростью w вектор А. Очевидно, что угол j = w t + j0 где j0 — начальный угол.
Проекции вектора А на оси координат запишутся:
Видно, что проекции вращающегося вектора на оси координат по форме совпадают с уравнением гармонических колебаний, если угловой скорости вектора сопоставить угловую частоту колебаний, а начальному углу — начальную фазу.
Проводя аналогию дальше, можно сказать, что результат сложения двух однонаправленных колебаний можно получить следующим путем: необходимо сложить два вектора, а проекции суммарного вектора на оси координат будут являться уравнениями результирующего колебания. Рассмотрим этот метод на примере сложения двух колебаний с произвольными частотами. Пусть наше тело участвует в двух совпадающих по направлению колебаниях:
Сопоставим этим колебаниям два вектора А1 и А2, вращающихся с соответствующими угловыми скоростями.
Сопоставляем колебаниям проекции векторов на ось y. Задача сложения колебаний сводится к нахождению проекции вектора А на ось y (амплитуда результирующего колебания) и угла f (фаза результирующего колебания).
Из очевидных геометрических соображений находим:
Отметим, что в общем случае сложения колебаний с разными частотами амплитуда результирующего колебания будет зависеть от времени. Если же частоты одинаковы, то , то есть зависимость от времени исчезает. На языке векторной диаграммы это означает, что складываемые векторы при своем вращении не меняют своего относительного положения. В этом случае формулы для амплитуды и фазы результирующего колебания запишутся так:
Рассмотрим сложение двух однонаправленных колебаний с неравными, но близкими частотами, то есть , и пусть для определенности . Для простоты пусть начальные фазы и амплитуды этих колебаний равны. В результате сложения двух колебаний
получим уравнение суммарного колебания:
Полученное результирующее колебание не является гармоническим (сравни с уравнением (1)); такого вида колебания носят название биений, название понятно, если посмотреть на график колебаний.
Величина, стоящая перед синусом, меняется со временем относительно медленно, так как разность частот мала. Эту величину условно называют амплитудой биений, а разность складываемых частот — частотой биений (циклической).
При сложении взаимно перпендикулярных колебаний необходимо найти уравнение траектории тела, то есть из уравнений колебаний типа x = x(t), y = y(t) исключить t и получить зависимость типа y(x).
например, сложим два колебания с одинаковыми частотами:
исключив время, получим:
В общем случае это — уравнение эллипса. При A1=A2 — окружность, при (m — целое) — отрезок прямой.
Вид траектории при сложении взаимно перпендикулярных колебаний зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний. Получающиеся кривые носят название фигур Лиссажу.
Вращающийся вектор амплитуды
4.2. Вращающийся вектор амплитуды
Если одна и та же материальная точка участвует в нескольких колебательных процессах одновременно, то ее смещение в любой момент времени можно найти геометрически методом вращающегося вектора амплитуды (методом векторных диаграмм).
Изобразим на координатной плоскости XOY вектор А с началом в точке О (рис. 24).
Рис. 24. Проекции вектора А на координатные оси совершают гармонические колебания с частотой О)
Длина вектора А равна амплитуде колебаний. Угол, образуемый вектором А с осью ОХ, равен начальной фазе колебания ф0. Если привести вектор А во вращение вокруг начала координат О с частотой, равной циклической частоте колебания (о, то его проекции на координатные оси ОХ и OY будут изменяться по гармоническому закону:
Рассмотрим некоторые частные случаи сложения гармонических колебаний методом векторных диаграмм.
Сложение гармонических колебаний одного направления
Пусть два гармонических колебания происходят в одном направлении ОХ, имеют одинаковые частоты C0j = (о2 = со, но различные начальные фазы ф, ф ф2. Запишем уравнения этих колебаний:
Результирующее смещение точки равно:
Амплитуду и начальную фазу (А,ф) результирующего колебания найдем методом векторных диаграмм (методом вращающегося вектора амплитуды). Изобразим на координатной плоскости два вращающихся вектора амплитуд А, и А, (рис. 25).
Рис. 25. Сложение гармонических колебаний одного направления и одинаковой частоты графическим методом
Углы, образуемые этими векторами с осью ОХ в начальный момент времени ф1 иф., равны начальным фазам колебаний. Так как вектора
А, и А, вращаются вокруг начала координат с одинаковой угловой скоростью со, равной круговой частоте колебаний, то угол между ними не меняется со временем и равен ср = ф] — (р2 •
Как следует из рис. 3, амплитуда результирующего колебания (длина вектора А) равна
а начальная фаза определяется соотношением:
Если разность фаз колебаний равна четному числу полуоборотов, или другими словами четному числу ж радиан, то есть:
то амплитуда результирующего колебания будет максимальной:
Если разность фаз колебаний равна нечетному числу полуоборотов, или другими словами нечетному числу ж радиан, то есть:
то амплитуда результирующего колебания будет минимальной:
Сложение гармонических колебаний
Вы будете перенаправлены на Автор24
Сложением колебаний называют применение закона, описывающего состояние колебательной системы, если она принимает участие одномоментно в нескольких колебательных процессах.
При этом выделяют два предельных случая:
- суммирование колебаний, имеющих одинаковые направления;
- сложение взаимно нормальных колебаний.
К первому варианту сложения колебаний можно отнести случай, когда груз ($a$) совершает колебания на пружине 1 относительно другого колеблющегося груза ($b$) и совместно с ним на пружине 2 (рис.1).
Рисунок 1. Суммирование колебаний, имеющих одинаковые направления. Автор24 — интернет-биржа студенческих работ
Такой случай реализуется при наложении колебаний скалярных физических параметров, характеризующих систему колебаний, например:
- давления;
- температуры;
- плотности;
- силы тока;
- заряда и т.д.
Суммирование однонаправленных гармонических колебаний
Сложение пары гармонических колебаний вида:
$s_1=A_1 sin (omega_1 t+varphi_1) (1)$ и $ s_2=A_2 sin (omega_2 t+varphi_2) (2)$
можно выполнить, если воспользоваться методом векторных диаграмм.
Рисунок 2. Метод векторных диаграмм. Автор24 — интернет-биржа студенческих работ
Рисунок 2 показывает векторы $vec A_1(t)$ и $vec A_2(t)$ амплитуд соответствующих колебаний в момент времени $t$. Фазы этих колебаний в обозначенный момент времени равны:
$Ф_1=omega_1 t+varphi_1 (3)$ и $Ф_2=omega_2 t+varphi_2 (4)$.
Готовые работы на аналогичную тему
Суммарному колебанию $s=s_1+s_2$ соответствует вектор:
проекция вектора $s$ на ось $Y$ равна:
Используя теорему косинусов, получим:
Когерентные и некогерентные гармонические колебания
Пару колебательных процесса называют когерентными в том случае, если их течение согласовано во времени, при этом разность их фаз не изменяется:
Из выражения (8) следует, что гармонические колебания будут когерентными, если
их круговые частоты будут одинаковыми:
в каждый момент времени разность фаз когерентных колебаний равна разности фаз их начальных колебаний:
Сложение двух гармонических однонаправленных когерентных колебаний дают колебание с той же круговой частотой $omega$, что исходные колебания, при этом имеем:
где $A^2=A_1^2+A_2^2+2A_1A_2cos (varphi_2-varphi_1)$;
Амплитуда суммарных колебаний изменяется в зависимости от разности начальных фаз:
от $A=|A_1-A_2|$ при $varphi_2-varphi_1=pm (2n+1)pi$
до $A=A_1+A_2$ при $varphi_2-varphi_1=pm 2npi$,
где $n=0,1,2. $ — целое положительное число или ноль.
При $varphi_2-varphi_1=pm 2npi$ колебания происходят в одной фазе (колебания называют софазными).
Если $varphi_2-varphi_1=pm (2n+1)pi$ колебания происходя в противофазе.
Если складываются гармонические колебания с разными циклическими частотами (некогерентные колебания), получаются негармонические колебания. Векторы амплитуд $A_1$ и $A_2$ вращаются с разными угловыми скоростями, построенный на них параллелограмм постоянно искажается, его диагональ изменяет длину и совершает вращения с изменяющейся угловой скоростью.
Пару гармонических колебаний, имеющих разные круговые частоты можно приближенно считать когерентными только на малом отрезке времени, в течение которого разность фаз колебаний изменяется на малую величину.
Сумму двух гармонических колебаний с разными, но близкими по величине круговыми частотами называют биениями.
Биения – это негармоническое колебание.
Суммирование взаимно перпендикулярных гармонических колебаний
Точка $N$ совершает одновременно два колебания. Они имеют одинаковые круговые частоты. Одно из них происходит вдоль оси $X$, другое вдоль оси $Y$. Их законы запишем как:
$x=A_1sin (omega t+varphi_1) (10)$ и
$y=A_2sin (omega t+varphi_2) (11),$
где $x$ и $y$ — декартовы координаты точки N.
Уравнение траектории движения точки N при этом:
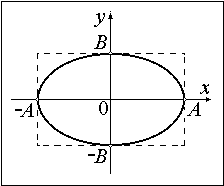
Траектория движения точки имеет форму эллипса. Точка $M$ описывает данный эллипс за период суммируемых колебаний. Такие движения точки называют эллиптически поляризованными колебаниями.
Ориентация этого эллипса в плоскости $XOY$ и его размеры зависят от амплитуд складываемых колебаний $A_1$ и $A_2$ и разности начальных фаз $varphi_2-varphi_1$.
При $varphi_2-varphi_1=(2n+1)frac<pi><2>$, где $n=0,pm 1, pm 2. $ оси эллипса будут совпадать с осями $OX$ и $OY$, при этом величины его полуосей равны $A_1$ и $A_2$:
Если помимо прочего, $A_1=A_2$, то траекторией точки $N$ является окружность. При этом движение точки $N$ называют поляризованными циркулярно колебаниями (колебаниями которые поляризованы по кругу).
При $varphi_2-varphi_1=npi$ где $n=0,pm 1, pm 2. $, эллипс вырожден в отрезок прямой, при этом:
где знак плюс в выражении (14) при четных значениях $n$, то есть если складываются синфазные колебания; минус ставят при нечетных значения $n$, то есть если складываются колебания в противофазе. Такие колебания точки $N$ называют линейно поляризованными.
При линейно поляризованных колебаниях точка $N$ совершает гармонические колебания с частотой суммируемых колебаний и амплитудой, равной:
вдоль прямой линии, которая составляет с осью $OX$ угол:
Пусть взаимно нормальные колебания, имеющие циклические частоты $pomega$ и $qomega$, где $p$ и $q$ — целые числа:
$x=A_1sin (pomega t+varphi_1)$ и $y=A_2sin (qomega t+varphi_2) (16).$
Координаты $x$ и $y$ точки $N$, которая совершает колебания, одновременно повторяется спустя одинаковые отрезки времени $T_0$, равные общему минимальному кратному:
$T_1=frac<2pi>$ и $T_2=frac<2pi>$ периодов вдоль осей $OX$ и $OY$. Следовательно, траекторией точки $N$ является замкнутая кривая. Форма этой кривой связана с соотношением между:
- амплитудами,
- частотами,
- начальными фазами
суммируемых колебаний. Эти траектории точки $N$, выполняющей гармонические колебания в двух взаимно нормальных плоскостях одновременно, называют фигурами Лиссажу.
Фигуры Лиссажу можно вписать в прямоугольник:
- с центром, совпадающим с началом координат;
- сторонами параллельными осям координат ($OX$ и $OY$) и находящимися по обе стороны от них на расстояниях равных $A_1$ $A_2$;
- отношение частот суммируемых колебаний определяет количество касаний соответствующей им фигуры Лиссажу со стороной прямоугольника, параллельной оси $OY$ и со стороной, параллельной оси $OX$.
http://studref.com/696344/matematika_himiya_fizik/vraschayuschiysya_vektor_amplitudy
http://spravochnick.ru/fizika/garmonicheskie_kolebaniya/slozhenie_garmonicheskih_kolebaniy/