Как найти rобщ в последовательной цепи

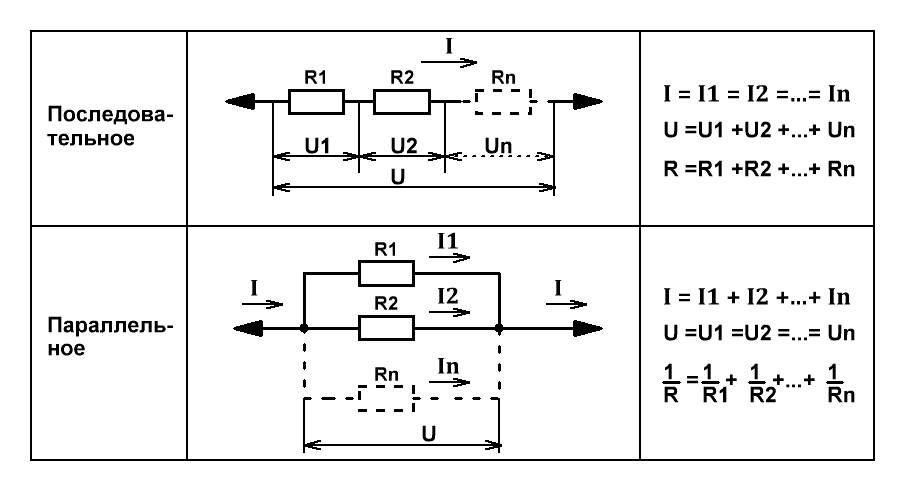
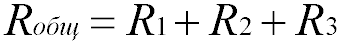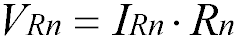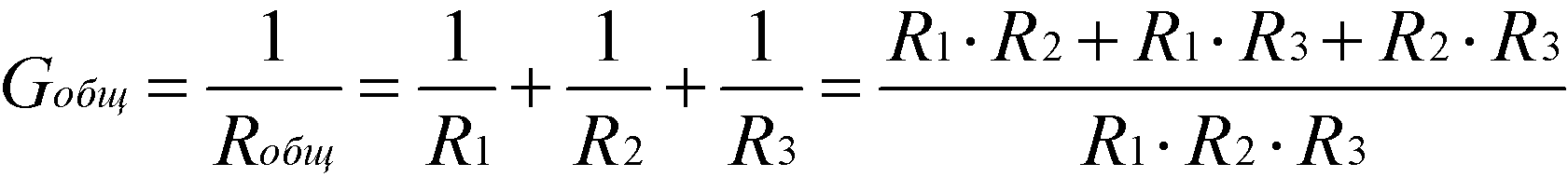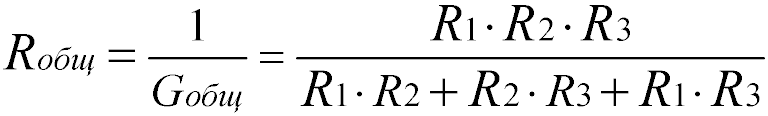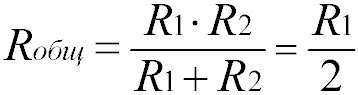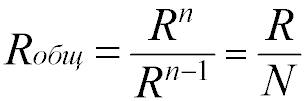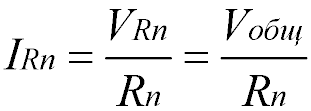Последовательное и параллельное соединение резисторов

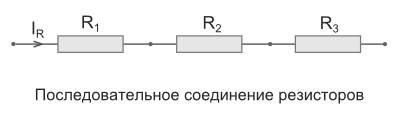
Последовательное соединение резисторов

Последовательное соединение – это соединение двух или более резисторов в форме цепи,
в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.

Общее сопротивление R_общ

При таком соединении, через все резисторы проходит один и тот же электрический ток.
Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него.
Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается,
и оно равно сумме всех сопротивлений.

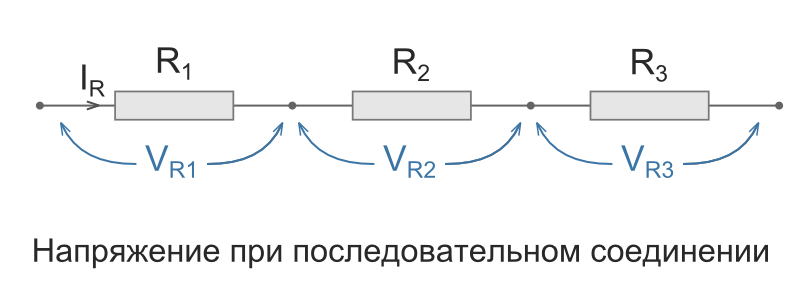
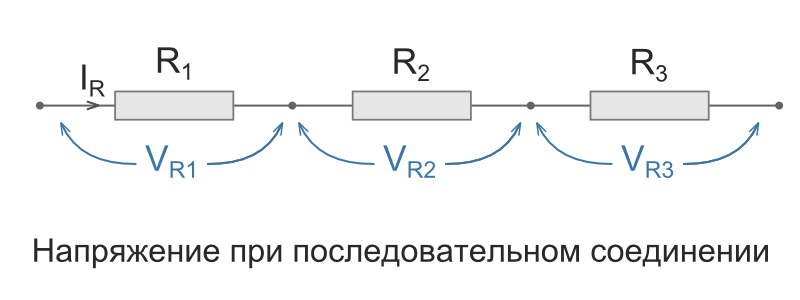
Напряжение при последовательном соединении

Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:

Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.

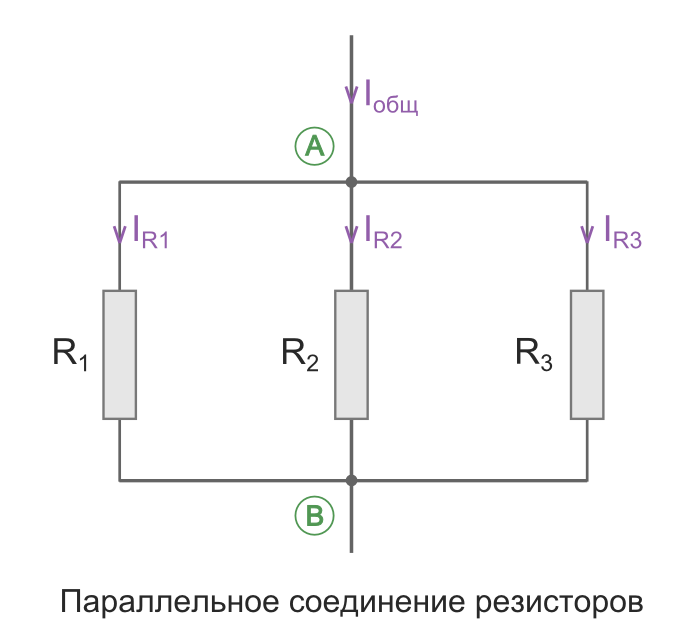
Параллельное соединение резисторов

Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами.
В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.

Общее сопротивление R_общ

При таком соединении, через каждый резистор потечет отдельный ток.
Сила данного тока будет обратно пропорциональна сопротивлению резистора.
В результате общая проводимость такого участка электрической цепи увеличивается,
а общее сопротивление в свою очередь уменьшается.

Таким образом, при параллельном подсоединении резисторов с разным сопротивлением,
общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.

Формула общей проводимости при параллельном соединении резисторов:

Формула эквивалентного общего сопротивления при параллельном соединении резисторов:

Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:

Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.

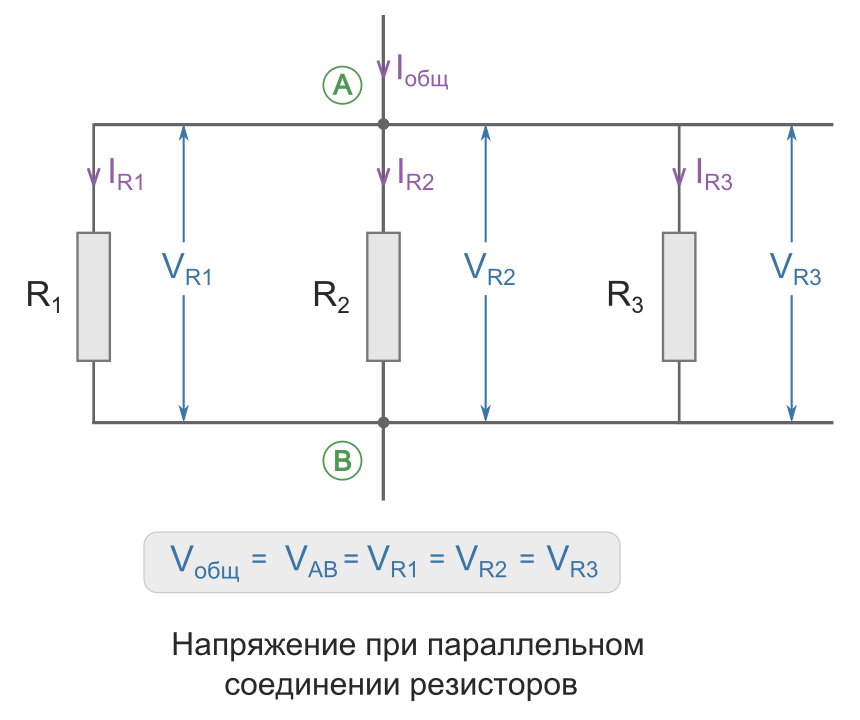
Напряжение при параллельном соединении

Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности.
Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.

Электрический ток при параллельном соединении

Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора.
Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:

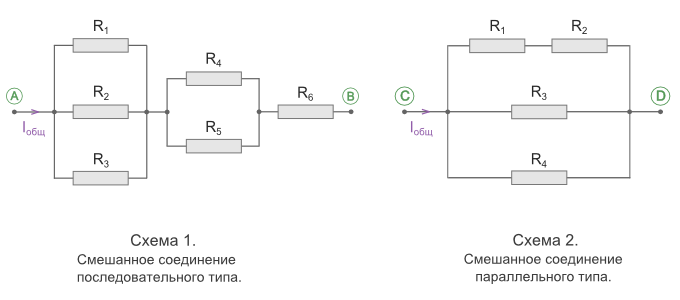
Смешанное соединение резисторов

Смешанным соединением называют участок цепи, где часть резисторов
соединяются между собой последовательно, а часть параллельно.
В свою очередь, смешанное соединение бывает последовательного и параллельного типов.

Общее сопротивление R_общ

Для того чтобы посчитать общее сопротивление смешанного соединения:

• Цепь разбивают на участки с только пареллельным или только последовательным соединением.
• Вычисляют общее сопротивление для каждого отдельного участка.
• Вычисляют общее сопротивление для всей цепи смешанного соединения.

Так это будет выглядеть для схемы 1:

Также существует более быстрый способ расчета общего сопротивления для смешанного соединения.
Можно, в соответствии схеме, сразу записывать формулу следующим образом:

• Если резисторы соединяются последоватеьно — складывать.
• Если резисторы соединяются параллельно — использовать условное обозначение «||».
• Подставлять формулу для параллельного соединения где стоит символ «||».

Так это будет выглядеть для схемы 1:

После подстановки формулы параллельного соединения вместо «||»:

Была ли эта статья полезной?

Как я и обещал в статье про переменные резисторы (ссылка), сегодня речь пойдет о возможных способах соединения, в частности о последовательном соединении резисторов и о параллельном.

Последовательное соединение резисторов.

Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях, будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:

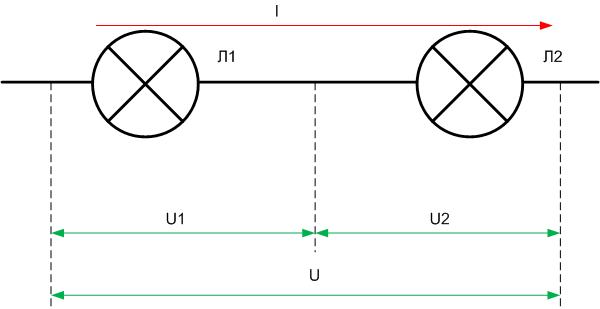
Здесь у нас классический случай последовательного соединения — два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:

А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:

В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:

Тогда для вычисления общего напряжения можно использовать следующее выражение:

U = U_1 + U_2 = IR_2 + IR_2 = I(R_1 + R_2)

Но для общего напряжения также справедлив закон Ома:

Здесь R_0 — это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:

Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников.

Например, для следующей цепи:

Общее сопротивление будет равно:

R_0 = R_1 + R_2 + R_3 + R_4 + R_5 + R_6 + R_7 + R_8 + R_9 + R_{10}

Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление, будет работать в любом случае. А если при последовательном  соединении все сопротивления равны (R_1 = R_2 = … = R), то общее сопротивление цепи составит:

В данной формуле n равно количеству элементов. С последовательным соединением резисторов разобрались, логичным образом переходим к параллельному.

Параллельное соединение резисторов.

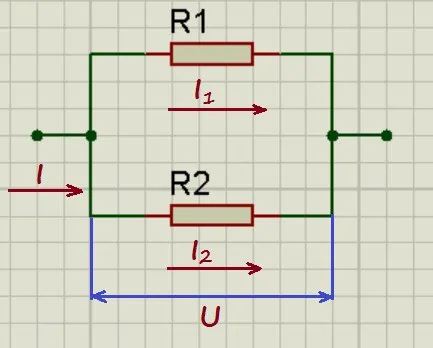
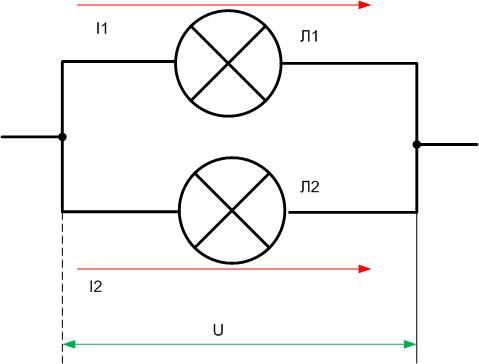
При параллельном соединении напряжения на проводниках равны:

А для токов справедливо следующее выражение:

То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:

I_1 = frac{U_1}{R_1} = frac{U}{R_1}

I_2 = frac{U_2}{R_2} = frac{U}{R_2}

Подставим эти выражения в формулу общего тока:

I = frac{U}{R_1} + frac{U}{R_2} = Umedspace (frac{1}{R1} + frac{1}{R2})

А по закону Ома:

Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:

frac{1}{R_0} = frac{1}{R_1} + frac{1}{R_2}

Данную формулу можно записать и несколько иначе:

R_0 = frac{R_1R_2}{R_1 + R_2}

Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Аналогичная ситуация будет наблюдаться и при большем количестве проводников, соединенных параллельно:

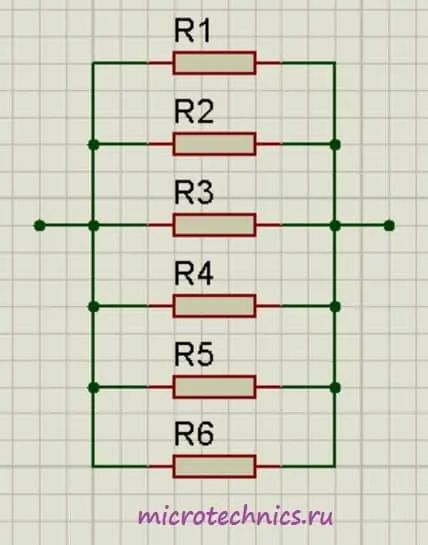
frac{1}{R_0} = frac{1}{R_1} + frac{1}{R_2} + frac{1}{R_3} + frac{1}{R_4} + frac{1}{R_5} + frac{1}{R_6}

Смешанное соединение резисторов.

Помимо параллельного и последовательного соединений резисторов существует еще смешанное соединение. Из названия уже понятно, что при таком соединении в цепи присутствуют резисторы, соединенные как параллельно, так и последовательно. Вот пример такой цепи:

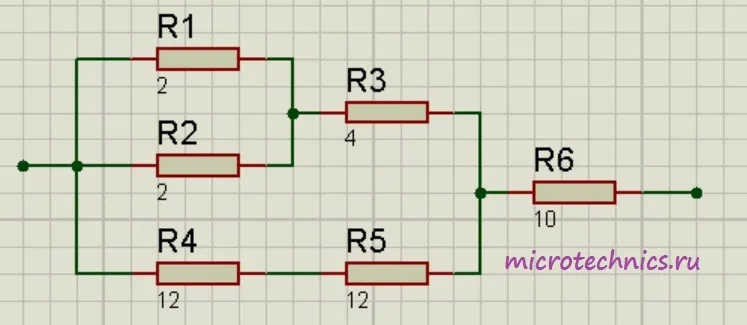
Давайте рассчитаем общее сопротивление. Начнем с резисторов R_1 и R_2 — они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором R_{1-2}:

R_{1-2} = frac{R1cdot R2}{R1 + R2} = 1

Теперь у нас образовались две группы последовательно соединенных резисторов:

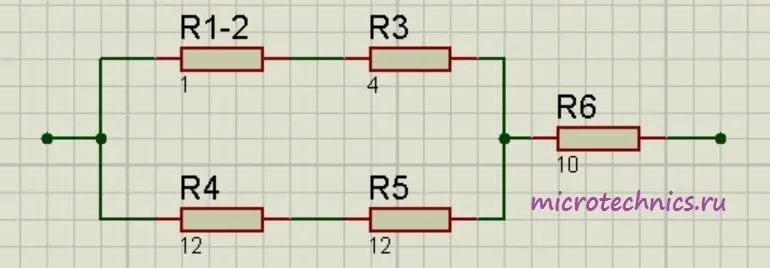
• R_{1-2} и R_3
• R_4 и R_5

Заменим эти две группы двумя резисторами, сопротивление которых равно:

R_{1-2-3} = R_{1-2} + R_3 = 5

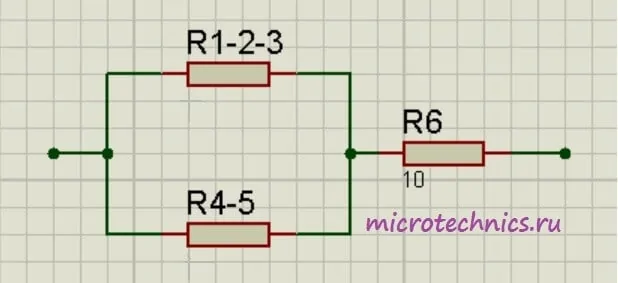
Как видите, схема стала уже совсем простой. Заменим группу параллельно соединенных резисторов R_{1-2-3} и R_{4-5}  одним резистором R_{1-2-3-4-5}:

R_{1-2-3-4-5}enspace = frac{R_{1-2-3}medspacecdot R_{4-5}}{R_{1-2-3} + R_{4-5}} = frac{5cdot24}{5 + 24} = 4.14

И в итоге у нас на схеме осталось только два резистора соединенных последовательно:

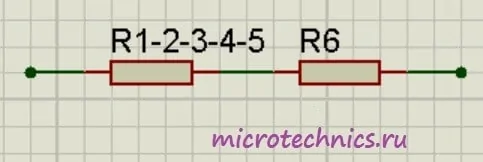
Общее сопротивление цепи получилось равным:

R_0 = R_{1-2-3-4-5}medspace +medspace R_6 = 4.14 + 10 = 14.14

Таким вот образом достаточно большая схема свелась к банальнейшему последовательному соединению двух резисторов. Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление — для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях. А сегодняшняя статья на этом подошла к концу, до скорых встреч на нашем сайте 🤝

Большое разнообразие схем основано на двух видах соединений – последовательное параллельное. Для каждого типа существуют свои собственные законы и принципы. Именно это и позволяет создавать устройства с самыми различными техническими параметрами, в том числе и резисторы. Что же такое резистор?

Резистор – радиодеталь, созданная для контроля напряжения и тока в цепи, увеличивая либо понижая его. Резисторы могут быть двух видов – постоянные и переменные. Так, например, светодиоды требуют для себя совсем небольшого тока. Для этого в электрическую цепочку перед светодиодом устанавливается резистор, который обеспечивает необходимое напряжение для работы последнего.

В статье подробны рассмотрены все аспекты последовательного и параллельного подключения резисторов. Бонусом к статье являются видеоролик и детальная информационная статья на рассматриваемую тему.

Последовательное подключение

Начнем с последовательного соединения. По этой схеме каждый резистор подключается с другим только в одной точке, их может быть в цепи 2, 3 и больше. Обозначим сопротивления: R1, R2, R3 и напряжение источника в цепи Uц. При подключении источника питания в ней начнет протекать ток Iц. В цепи с последовательным соединением ток протекает по всем резисторам один за другим.

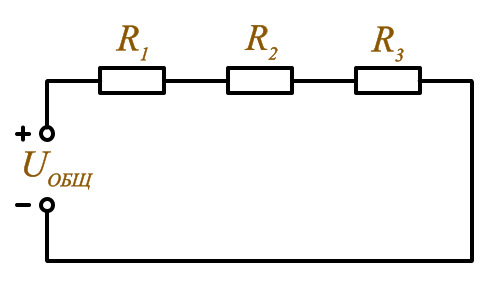
Поскольку ток течет через все резисторы их сопротивления и ток суммируется, Iц = I1+I2+I3, Rц = R1 +R2 + R3, чем больше отдельно взятое сопротивление, тем тяжелее электронам преодолевать участок цепи. Мощность резисторов при последовательном и параллельном соединении рассчитывается по разным формулам. В последовательных цепях — складываем, в параллельных — это обратно пропорциональная величина.

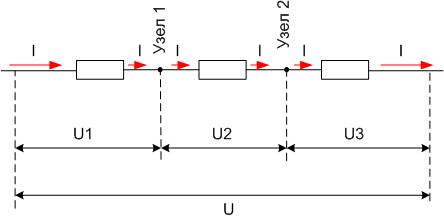
Последовательное соединение характеризуется тем, что элементы идут друг за другом. Конец одного подключается к началу другого. При подключении полученной цепочки к источнику тока получается кольцо.

Теоретическая часть

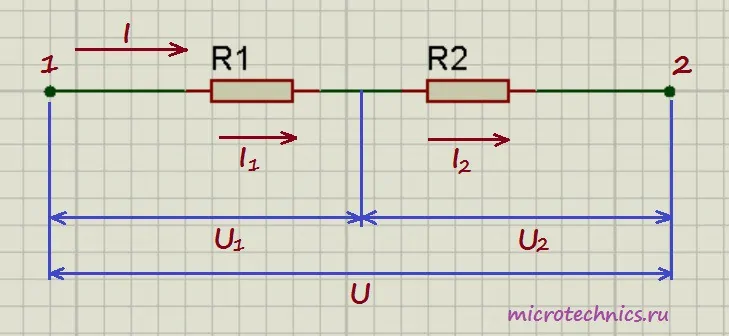
Последовательное соединение характерно тем, что через все элементы протекает ток одинаковой силы. То есть, если цепочка состоит из двух резисторов R1 и R2 (как на рисунке ниже), то ток протекающий через каждое из них и любую другую часть цепи будет одинаковой (I = I1 = I2). Суммарное сопротивление всей цепи последовательно соединенных резисторов считается как сумма сопротивлений всех ее элементов. То есть, номиналы складывают. R = R1 + R2 — это и есть формула расчета сопротивления при последовательном соединении резисторов. Если элементов больше двух, будет просто больше слагаемых. Еще одно свойство последовательного соединения — на каждом элементе напряжение отличается. Ток в цепи одинаковый, а напряжение на резисторе зависит от его номинала.

Примеры расчета

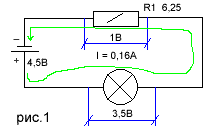
Давайте рассмотрим пример. Цепь представлена на рисунке выше. Есть источник тока и два сопротивления. Пусть R1=1,2 кОм, R2= 800 Ом, а ток в цепи 2 А. По закону Ома U = I * R. Подставляем наши значения:

• U1 = R1 * I = 1200 Ом * 2 А = 2400 В;
• U2 = R2 * I = 800 Ом * 2А = 1600 В.

Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В. Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток.   R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом.

Если подставить в формулу напряжения при последовательном соединении сопротивлений, получаем: U = R * I = 2000 Ом * 2  А = 4000 В. Получаем, что общее напряжение данной цепи 4000 В.

А теперь посмотрите на схему. На первом вольтметре (возле резистора R1) показания будут 2400 В, на втором  — 1600 В.  При этом напряжение источника питания — 4000 В. Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.

Материал по теме: Как проверить варистор мультиметром.

Общее сопротивление R_общ

При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.

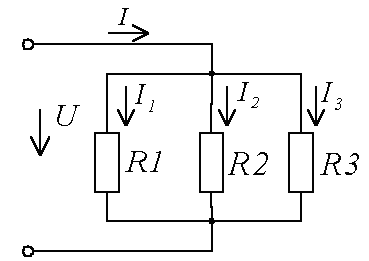
Параллельное соединение резисторов

Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.

Общее сопротивление R_общ

При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается. Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора. Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение.

То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение U = U1 = U2 = U3. Получается, что ток разделяется на несколько «ручейков». То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи. В случае с параллельным соединением резисторов — от их номинала.

Предлагаем также почитать интересный материал про малоизвестные факты о двигателях постоянного тока в другой нашей статье.

Схема параллельного соединения

Общее сопротивление участка цепи при таком соединении становится ниже. Его высчитывают по формуле: 1/R = 1/R1 + 1/R + 1/R3+. Такая форма хоть и понятна, но неудобна. Формула расчета сопротивления параллельно подключенных резисторов получается тем сложнее, чем больше элементов соединены параллельно. Но больше двух-трех редко кто объединяет, так что на практике достаточно знать только две формулы приведенные ниже.

Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала. Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.

Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом. Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом. Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.

Как высчитывать сопротивление составных резисторов

Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом. При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее.

Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом. Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом. Получим результирующее сопротивление 4,61 Ом. Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.

Параллельное соединение резисторов

Параллельное соединение резисторов это соединение, в котором начала всех резисторов соединены в одну общую точку (А), а концы в другую общую точку. При этом по каждому резистору течет свой ток. При параллельном соединении при протекании тока из точки А в точку Б, он имеет несколько путей. Таким образом, увеличение числа параллельно соединенных резисторов ведет к увеличению путей протекания тока, то есть к уменьшению противодействия протеканию тока. А это значит, чем большее количество резисторов соединить параллельно, тем меньше станет значение общего сопротивления такого участка цепи. Общее сопротивление параллельно соединенных резисторов определяется следующим отношением: 1/Rобщ= 1/R1+1/R2+1/R3+…+1/Rn.

Следует отметить, что здесь действует правило «меньше – меньшего». Это означает, что общее сопротивление всегда будет меньше сопротивления любого параллельно включенного резистора. Общее сопротивление для двух параллельно соединенных резисторов рассчитывается по следующей формуле: Rобщ= R1*R2/R1+R2.

Если имеет место два параллельно соединенных резистора с одинаковыми сопротивлениями, то их общее сопротивление будет равно половине сопротивления одного из них. Параллельное соединение резисторов. При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви.

[stextbox id=’info’]Заменяя лампы резисторами с сопротивлениями R1, R2, R3, При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома: I₁=U/R₁; I₂=U/R₂; I₃=U/R₃.[/stextbox]

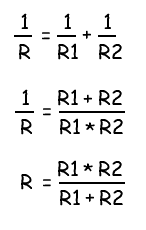
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I₁+I₂+I₃, или I = U / R₁ + U / R₂ + U / R₃ = U (1/R₁ + 1/R₂ + 1/R₃) = U / R_эк . Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой 1/R_эк = 1/R₁ + 1/R₂ + 1/R_3. Вводя в формулу (24) вместо значений 1/R_эк, 1/R₁, 1/R₂ и 1/R₃ соответствующие проводимости G_эк, G₁, G₂ и G₃, получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов:

G_эк = G₁+ G₂ +G₃ (25)

Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается. Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях I₁ : I₂ : I₃ = 1/R₁ : 1/R₂ : 1/R₃ = G₁ + G₂ + G_3.

В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам. Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи – R_эк=R₁R₂/(R₁+R₂) при трех параллельно включенных резисторах R_эк=R₁R₂R₃/(R₁R₂+R₂R₃+R₁R₃).

При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.

R_эк = R1 / n.

Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока: I1 = I / n. При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными.

[stextbox id=’info’]Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.[/stextbox]

На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.

Более подробную информацию можно узнать, прочитав файл по данной теме “Расчет мощности резисторов”.  Всю новую информацию по этой и многим другим темам, вы сможете найти в группе. Подписывайтесь на нашу группу в социальной сети «Вконтакте».

Для этого вам необходимо будет перейти по следующей ссылке https://vk.com/electroinfonet. Также в группе можно задавать вопросы и получать на них подробные ответы от профи. В завершение объемной статьи хочу выразить благодарность источникам, откуда мы черпали информацию:

www.elektroznatok.ru

www.themechanic.ru

www.electrono.ru

www.hightolow.ru

www.sxemotehnika.ru

Предыдущая

РезисторыКак рассчитать резистор для светодиода?

Следующая

РезисторыЧто такое фоторезистор?

При разработке электрических цепей применяется последовательное и параллельное соединение проводников. Умение анализировать (как количественно, так и качественно) и рассчитывать такие схемы является базовым принципом знаний электротехники.

Виды соединений электрических проводников

Основными схемами подключения являются параллельное и последовательное соединение. Также существуют комбинации из этих двух включений.

Последовательное

При последовательном (в зарубежной терминологии serial) соединении выводы элементов соединяются так, чтобы получилась цепочка. Один вывод устройства подключается к одному соседнему звену, а второй – к другому, с противоположной стороны.

Параллельное

При параллельном (parallel) включении одноименные выводы элементов цепи соединяются между собой. Практический пример – лампы в многорожковой люстре или повторители светового сигнала поворота в автомобиле.

Смешанное

В одной цепи схема подключения может быть комбинированной – serial+parallel. Часть элементов подключена в параллель, образуя звенья. Эти звенья могут быть включены в последовательную цепочку. Или наоборот – последовательные цепи включаются параллельно.

Как вычисляются напряжение, сила тока и электрическая мощность в зависимости от подключения

Параметры электрической цепи рассчитываются по-разному в зависимости от типа подключения. Чтобы разобраться, какова будет сила тока, проходящего через каждое сопротивление, можно воспользоваться первым законом Кирхгофа. Одна из его формулировок гласит, что алгебраическая сумма токов, втекающих в узел, равна сумме токов, вытекающих из узла. Остальные зависимости будут вытекать из данного рассуждения.

При параллельном соединении

Если рассмотреть параллельное соединение, например, трех резисторов, то можно отметить, что втекающий ток I в узле 1 распадается на три ветви I₁, I₂, I₃, причем Кирхгоф утверждает, что их сумма I₁+ I₂+ I₃ = I. В узле 2 все токи стекаются в один ток, и снова I= I₁+ I₂+ I₃.

Очевидно, что напряжение на каждом резисторе одинаково и равно U, следовательно, по закону Ома:

• I₁=U/R₁;
• I₂=U/R₂;
• I₃=U/R₃;
• I=U/R_общ.

Отсюда U/R_общ= U/R₁+ U/R₂+ U/R₃, после сокращения обеих частей на U получается формула для нахождения общего сопротивления при параллельном соединении резисторов:

1/R_общ= 1/R₁+ 1/R₂+ 1/R_3.

Отсюда следует, что при параллельном соединении общее сопротивление будет меньше наименьшего сопротивления в наборе. При соединении двух резисторов формула принимает вид R_общ=R₁* R₂/(R₁+ R₂).

Также из равенства I=U/R₁+U/R₂+U/R₃ следует, что токи через параллельно включенные резисторы распределяются обратно пропорционально значениям их сопротивлений – чем выше сопротивление, тем ниже ток, и наоборот. Если все резисторы имеют одинаковый номинал, то ток, текущий через каждый из них, находится делением общего тока на количество сопротивлений. Если элементов в сборке три, то через каждый течет треть общего тока, а если параллельно включены n одинаковых резисторов, то через каждый протекает I/n.

Так как электрическая мощность равна P=U*I, а напряжение на каждом резисторе равно, то мощность, выделяемая на каждом элементе, распределяется пропорционально току и обратно пропорционально сопротивлению резистора. Если все элементы одинаковы, то и мощность на них будет рассеиваться одинаковая.

Для наглядности видео.

При последовательном соединении

Если рассматривать последовательную цепь из трех элементов, можно заметить, что ток, втекающий в узел 1 будет равен вытекающему. В узле 2 выполняется то же самое соотношение и так до бесконечности.

Отсюда сила тока в последовательном соединении будет одинакова для любого элемента и равна I. Напряжение, приложенное к цепи и равное I*R, распределится между резисторами:

U=U₁+U₂+U₃=I*R₁+I*R₂+I*R₃ = I* R_общ

После сокращения на I можно найти общее сопротивление цепи. Оно равно сумме составляющих, и общее значение сопротивления будет выше сопротивления любого элемента:

R_общ=R₁+R₂+R₃

Очевидно, что падение напряжения в последовательной цепи прямо пропорционально сопротивлению каждого элемента – чем выше сопротивление, тем выше на нем напряжение. Точно так же, эти соотношения выполняются для цепи из n элементов.

Примеры расчетов

В качестве практических примеров можно рассмотреть несколько вариантов расчетов параметров цепи в разных схемах соединения.

Для резисторов

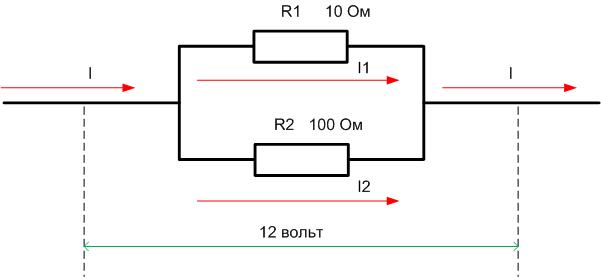
Самым простым примером расчета будет цепь из двух сопротивлений – 10 Ом и 100 Ом, соединенных в цепочку. К цепи приложено 12 вольт.

Сначала надо найти R_общ, оно равно сумме R₁ и R₂. R_общ=100+10=110 Ом. Отсюда ток в цепи I=U/R=12/110=0,109 ампер. Падение на каждом элементе можно вычислить исходя из равенств U₁=I*R₁ и U₂=I*R₂. Отсюда U₁=1,1 В, а U₂=10,9 В. Очевидно, что U₁/U₂=R₁/R₂. На первом элементе будет рассеиваться мощность P₁=U₁*I=1,1*0,109=0,12 ватт (для практики подойдет стандартный компонент на 0,125 ватт), а на втором – P₂=U₂*I=10,9*0,109=1,19 ватт (для практической реализации понадобится двухваттник).

Если соединить эти же два резистора параллельно и подать то же самое напряжение, то параметры распределятся по-другому.

Сначала надо определить R_общ=R₁*R₂/(R₁+R₂)=110*10/(110+10)=1100/120=9,17 Ом (меньше наименьшего значения в 10 Ом). Общий ток составит I=U/Rобщ=12/9,17=1,31 ампер. Через первый элемент потечет I₁=U/R₁=12/10=1,2 ампер, через второй I₂=U/R₂=12/100=0,12. Очевидно, что I₁+I₂=I (с учетом погрешностей округления). Мощности потребуются такие:

• P₁=I₁*U=1,2*12=14,2 ватт;
• P₂=I₂*U=0,12*12=1,42 ватт.

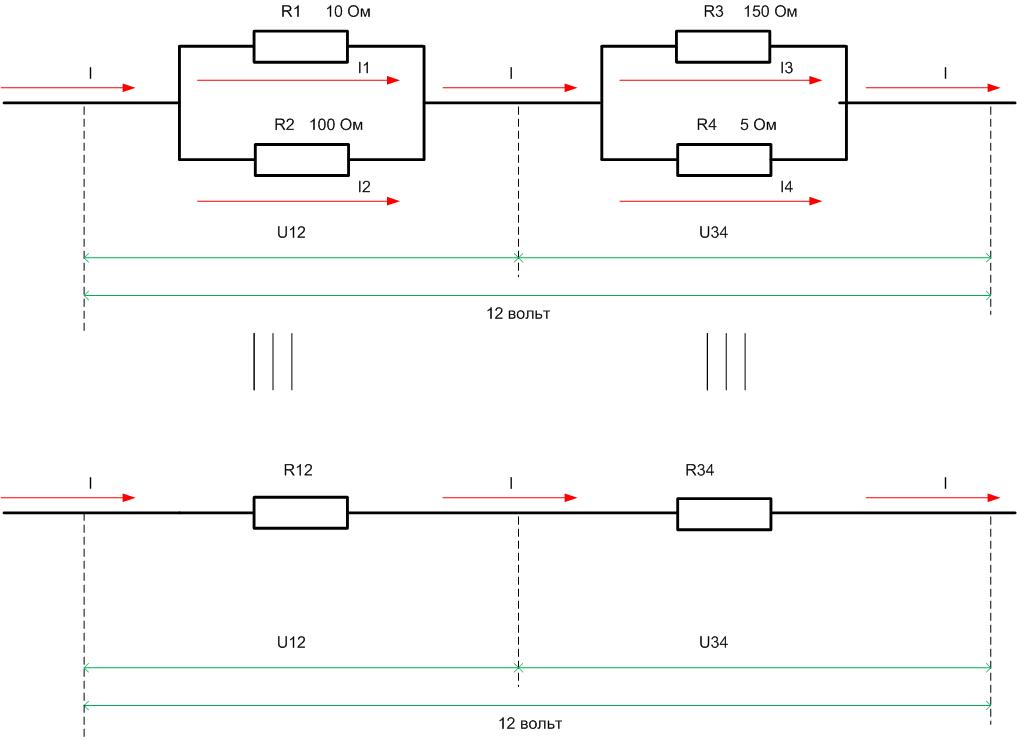
Если имеется смешанное соединение элементов, надо сначала преобразовать схему к однотипному виду – параллельному или последовательному. Пусть имеется схема следующего вида.

В данном случае удобно заменить параллельную сборку R₁ и R₂ на резистор с эквивалентным сопротивлением R₁₂, а R₃ и R₄ – на R₃₄. Сначала находится R₁₂=R₁*R₂/(R₁+R₂)=9,17 Ом. Тем же способом рассчитывается R₃₄=150*5/(150+5)=4,8 Ом. Тогда общее сопротивление эквивалентной цепи будет равно R₁₂+R₃₄=9,17+4,8=13,97 Ом.

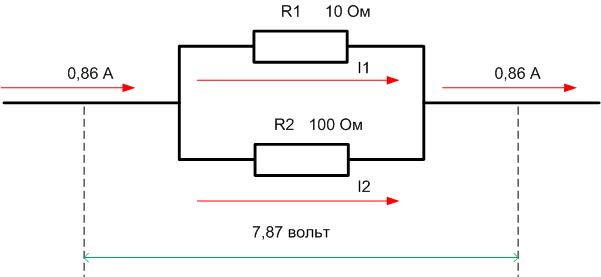
Отсюда I=U/R=12/13,97=0,86 ампер. На “гирлянде» R₁R₂ падает U₁₂=I*R₁₂=0,86*9,17=7,87 вольт, а на R₃R₄ падение составит U₃₄= I*R₃₄=0,86*4,8=4,13 вольт. Дальше надо вернуться к исходной схеме и рассмотреть отдельно участок схемы R₁R₂ с найденными параметрами.

Отсюда I₁=U/R₁=7,87/10=0,787 ампер, I₂=U/R₂=7,87/100=0,0787 ампер. По мощностям – P₁=U*I₁=7,87*0,787=6,2 ватт, P₂= U*I₂=7,87*0,0787=0,62 ватт.

Аналогично рассчитывается и участок, содержащий элементы R₃R₄.

Для лампочек

Точно такими же способами можно рассчитать параметры цепи, состоящей из двух или более лампочек накаливания – на практике с такой ситуацией можно столкнуться чаще. Но есть две проблемы. Первая из них – на лампочках и в технических данных на них не указывается сопротивление нити. Его придется пересчитывать исходя из номинального напряжения и мощности. Так как P=U*I, а I=U*R, то P=U²/R, а R=U²/P. Так, для 10-ваттной лампочки на 12 вольт сопротивление нити будет равно 12²/10=144/10=14,4 Ом. Можно рассчитать характеристики цепи для двух последовательно и параллельно соединенных лампочек.

В первом случае ток, текущий через каждую лампу будет общим, и равным I=U/Rобщ=12/(14,4+14,4)=12/28,8=0,42 А. На каждой лампе упадет U/2=6 вольт. А электрическая мощность каждого элемента составит 0,42*6=2,5 Вт, что составляет ¼ от номинала лампочки. Такое уменьшение произошло из-за двукратного снижения тока и двукратного снижения напряжения. Естественно, лампочки будут светиться далеко не в полный накал. Чтобы довести яркость свечения до нормальной, придется вдвое увеличивать напряжение, что одновременно вдвое увеличит ток.

Если лампочки соединить в параллель, то на каждой из них упадет номинальный уровень в 12 вольт. Через каждый элемент потечет I=U/R= 12/14,4=0,83 А, а мощность на каждой лампочке будет равна P=U*I=12*0,83=10 ватт, то есть, номинал. И каждая нить будет светить в полный накал. Но вся цепь будет потреблять 20 ватт и через нее потечет 0,83*2=1,66 А, что вдвое больше значения для одной лампы.

Есть и вторая проблема. В общем случае сопротивление зависит от тока и приложенного напряжения, но у ламп накаливания эта зависимость выражена ярко. Нить в холодном состоянии имеет низкое сопротивление, а номинального значения достигает при прогреве в номинальном режиме. Поэтому данные выше расчеты верны лишь для штатного напряжения 12 вольт. В других условиях характеристики лампы будут другими, и, по большому счету, расчет для параллельного случая неточен – сопротивление нити будет меньше 14,4 Ом. Зато это свойство позволяет применять лампу в качестве стабилизатора тока – при увеличении его значения нить нагреется, сопротивление вырастет, ток упадет примерно до прежнего уровня. При его уменьшении произойдет обратный процесс со снижением уровня накала нити лампочки.

Рекомендуем посмотреть видео урок «Просто физика»

Для светодиодов

Еще сложнее ситуация со светодиодами. В отличие от лампочек они стабилизируют напряжение, причем не всегда, а только после открывания. Иными словами, сначала при росте напряжения на последовательной цепочке (LED+резистор), она ведет себя согласно закону Ома. После того, как светодиод открылся (и начал светиться), увеличение падения на нем прекратилось, и рост напряжения на цепочке ведет к росту тока и увеличению U на резисторе. На полупроводниковом приборе напряжение остается стабильным (в зависимости от технологии изготовления – от 1,2 до 3 вольт или выше), хотя ток через него также растет.

По мере освоения приемов расчета можно научиться анализировать все более сложные схемы, содержащие как параллельное, так и последовательное подключение элементов. Потом можно переходить к следующему этапу – анализ и расчет устройств, содержащих реактивные (а впоследствии – и нелинейные) компоненты.