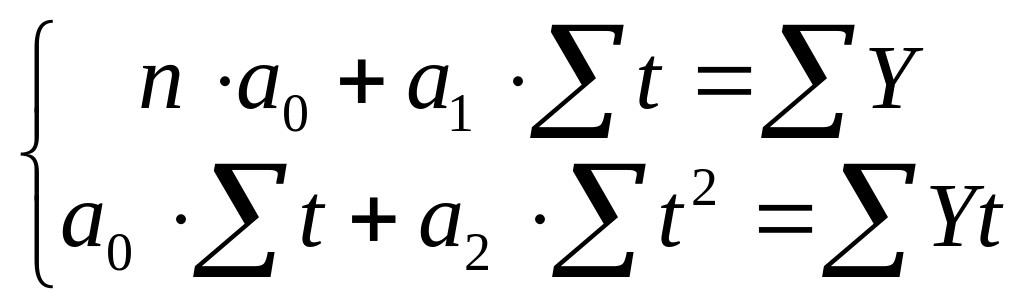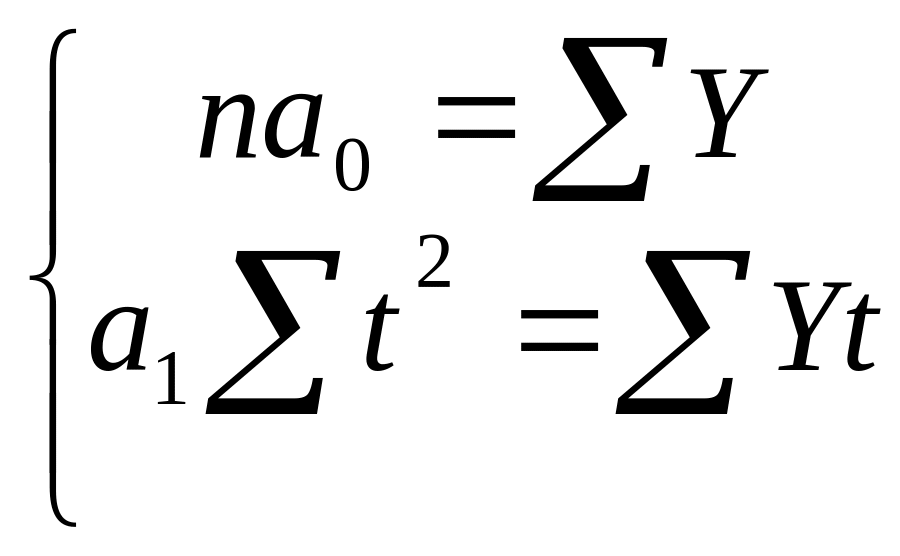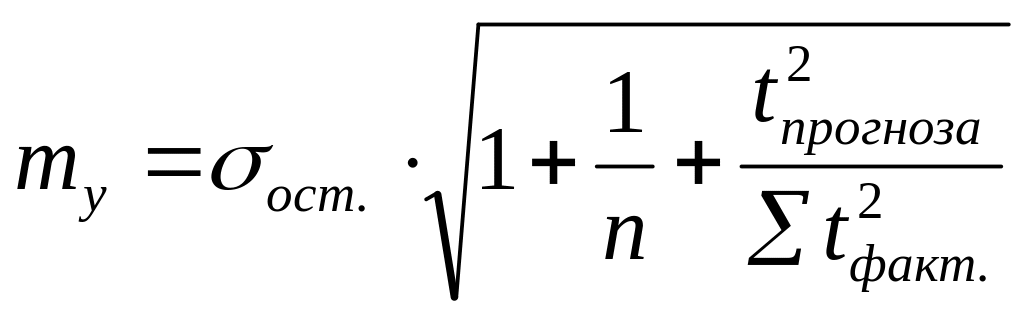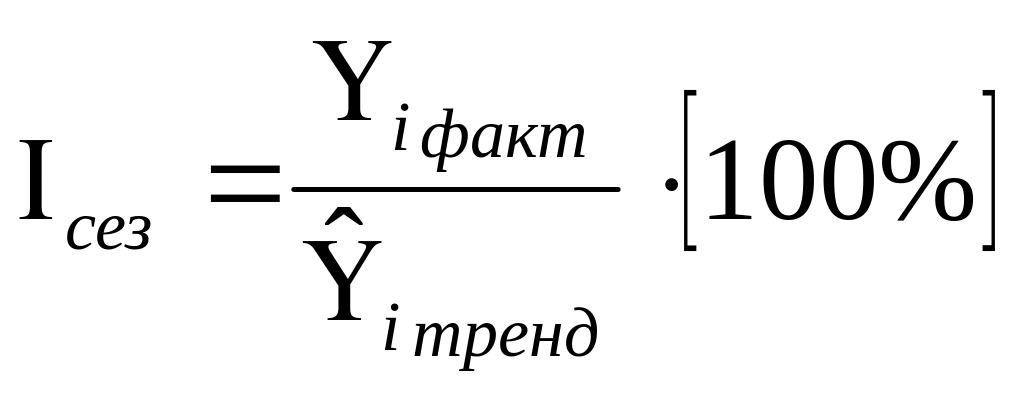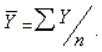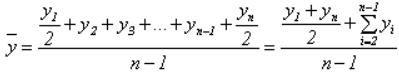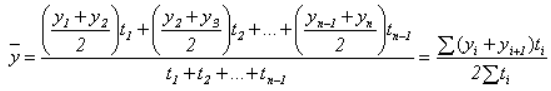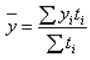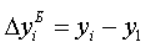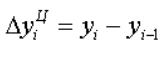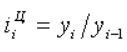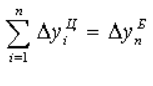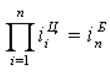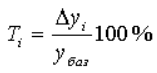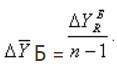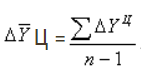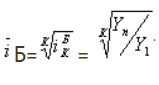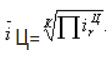Формулы для расчета показателей ряда динамики.
Подстрочные
символы “ц” и “б” отражают цепной и
базисный способы расчета показателей
ряда динамики.
Абсолютный
прирост
показывает, на сколько больше или меньше
значение уровня ряда с тем значением,
с которым проводится сравнение (соседним
или выбранным за базу сравнения).
или
(7.1)
Коэффициент
роста (темп роста) показывает,
во сколько раз больше или меньше значение
уровня ряда с тем значением, с которым
проводится сравнение (соседним или
выбранным за базу сравнения). Коэффициент
роста может быть выражен в процентах.
или
(7.2)
Темп
прироста характеризует
относительную скорость изменения уровня
ряда в единицу времени. Темп прироста
показывает, на какую долю (или процент)
уровень ряда рассматриваемого периода
больше или меньше базового (выбранного
для сравнения).
или
Тц,б=Кц,б–1
или Тц,б=Кц,б%–100%;
(7.3)
Предыдущий
показатель не отражает «вес» каждого
процента прироста. Например, в двух
бригадах урожайность зерновых выросла
по сравнению с предыдущим годом на 1,2%.
Но это не значит, что в натуральном
выражении это будет составлять одинаковое
количество центнеров. Оценить каждый
процент изменения позволяет следующий
показатель.
Абсолютное
значение 1% прироста
показывает натуральную величину
показателя, приходящегося на 1% изменения
относительно базисного (взятого за
основу сравнения) значения.
(7.4)
Формулы для расчета средних значений показателей ряда динамики:
1)
Средний уровень ряда может быть вычислен
по одной из формул (7.5 – для интервальных
радов; 7.6 – для моментных рядов)
или
(7.5)
(7.6)
2)
Средний абсолютный прирост:
или
(7.7)
где
(n
–1) – число периодов.
-
Средний
темп роста:
,
(7.8)
где
n
– количество цепных темпов роста уровня
ряда
,
(7.9)
где
n
– число уровней ряда
4)
Средний темп прироста:
или
(7.10)
Средний
уровень ряда рассчитаем по формуле
средней арифметической простой У=1145,057
Средний
темп роста вычислим по любой из формул
8.8 или 8.9 и получим один и тот же результат
К= 0,9913= 99,13%. Это значение отражает среднее
ежегодное снижение численности населения
по сравнению с предыдущим периодом.
Средний темп
прироста (снижения) Т=-0,0087=–0,87%, т.е.
ежегодно на 0,87% уменьшалась численность
населения РБ.
Абсолютное среднее
ежегодное уменьшение численности
населения будут равно Δ =–9,97 тыс. чел.
Все
эти значения показывают ухудшающуюся
демографическую ситуацию в РБ.
Например:
Таблица
7.5. Численность сельского населения РБ
на начало года, тыс. чел.
|
Годы |
Y |
Δ |
К |
Т |
А |
|||
|
ц |
б |
ц |
б |
ц |
б |
ц |
||
|
1 |
1173,9 |
— |
— |
— |
— |
— |
— |
— |
|
2 |
1166,2 |
-7,7 |
-7,7 |
0,993441 |
0,993441 |
-0,006559 |
-0,006559 |
1173,9 |
|
3 |
1156,5 |
-9,7 |
-17,4 |
0,991682 |
0,985178 |
-0,008318 |
-0,014822 |
1166,2 |
|
4 |
1146,1 |
-10,4 |
-27,8 |
0,991007 |
0,976318 |
-0,008993 |
-0,023682 |
1156,5 |
|
5 |
1135,1 |
-1,1 |
2309 |
0,990402 |
0,966948 |
-0,009598 |
-0,033052 |
1146,1 |
|
6 |
1123,5 |
-11,6 |
-50,4 |
0,989781 |
0,957066 |
-0,010219 |
-0,042934 |
1135,1 |
|
7 |
1114,1 |
-9,4 |
-59,8 |
0,991633 |
0,949059 |
-0,008367 |
-0,050941 |
1123,5 |
В
3. Приемы
выравнивания рядов динамики.
Часто
в рядах динамики сложно определить
общую тенденцию развития. Второй задачей
рядов динамики является выявление таких
периодов развития, которые достаточно
однородны по своим условиям и
взаимодействиям связей между показателями.
Под
тенденцией
понимается общее направление к росту,
снижению или стабилизации уровня явления
с течением времени.
Тенденция
по периодам может не совпадать с общей
тенденцией. Иногда вообще сложно
определить общую тенденцию. В этом
случае прибегают к различным методам
выравнивания ряда для определения его
тенденции:
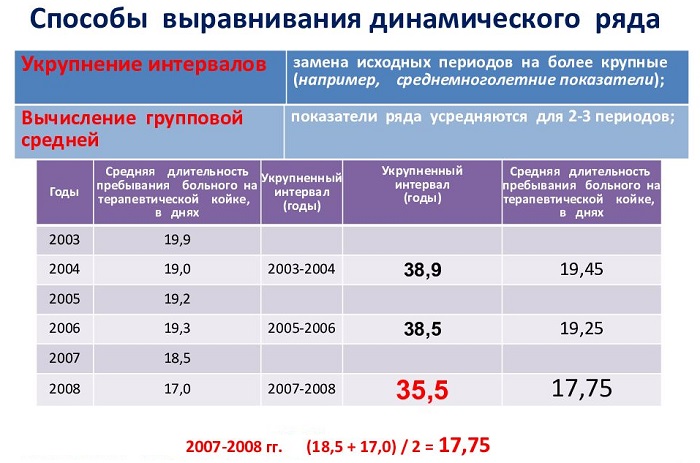
1) способу укрупнения
интервалов;
2) сглаживанию ряда
с помощью скользящей средней;
3)
производят аналитическое выравнивание
и получают уравнение тренда.
Первый
способ
заключается в переходе от меньших
временных интервалов к большим и расчете
усредненных уровней ряда за укрупненный
интервал. Временной промежуток для
укрупнения интервала производят с
учетом общей длины анализируемого ряда
и величины исходных интервалов. Так,
например, если исходный ряд содержит
информацию за каждый месяц, то можно
перейти к укрупненному интервалу
величиной в квартал. Если представлена
информация по годам, то «укрупнение»
можно произвести за 2,3,4,5 лет в зависимости
от длины исходного ряда.
График
этого ряда изображен на рисунке 7.2, где
видно, что имеются периоды спада
производства продукции и периоды
подъема. Если рассмотреть только часть
графика, начиная с 1998 года по 2005, то
сложно установить общую тенденцию
производства продукции данного вида.
Поэтому более четко общая тенденция
будет просматриваться, если произвести
выравнивание ряда одним из методов.
Так, использование метода укрупнения
интервалов дает результаты, представленные
в таблице 7.6 и 7.7.
Например:
Таблица
7.6. Производство цельномолочной продукции
в пересчете на молоко, тыс. тонн.
|
Годы |
Цельномолочная |
Годы |
Цельномолочная |
|
1995 |
801 |
2001 |
963 |
|
1996 |
744 |
2002 |
906 |
|
1997 |
813 |
2003 |
927 |
|
1998 |
952 |
2004 |
992 |
|
1999 |
1032 |
2005 |
1122 |
|
2000 |
954 |
2006 |
1284 |
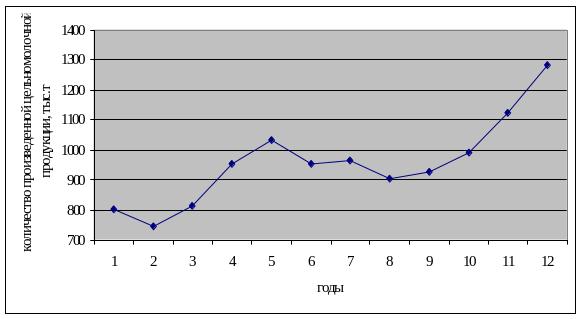
Рисунок
7.2. График динамики производства
цельномолочной продукции в РБ
Таблица
7.7. Расчет производства цельномолочной
продукции по укрупненным периодам
(трехлетиям).
|
Укрупненные |
Сумма цельномолочной |
Среднегодовое |
|
1995-1997 |
2358 |
786,0 |
|
1998-2000 |
2938 |
979,3 |
|
2001-2003 |
2796 |
932,0 |
|
2004-2006 |
3398 |
1132,7 |
Алгоритм
расчета:
801+744+813
= 2358; 2358/3=786,0
952+1032+954=2938;
2938/3=979,3 и т.д.
Из
последнего столбика таблицы 7.7 и рисунка
7.3 более четко видна тенденция к росту
производства цельномолочной продукции.
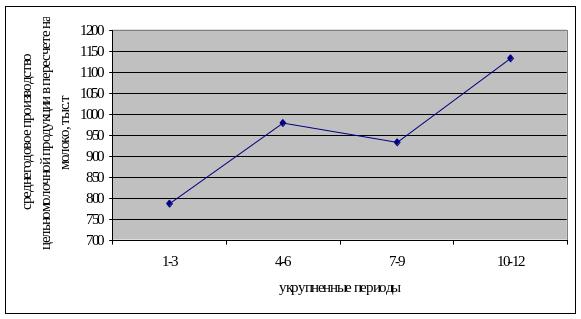
Рисунок
7.3. График ряда, выровненного по укрупненным
интервалам
Второй
способ
заключается в последовательном расчете
средних уровней за выбранный лаг времени,
передвигая этот лаг
на
1 интервал по времени t.
Величину лага L
выбирают произвольно в зависимости от
длины анализируемого ряда: L
= 2, 3, 4, …, n
. Например, мы выберем трехлетний лаг.
И тогда выровненный ряд можно представить
в следующей таблице (7.8).
Алгоритм расчета:
801+744+813=2358; 2358/3=786,0
744+813+952=2509; 2509/3=836,3
813+952+1032=2797;
2797/3=932,3 и т.д.
В настоящее время
в основном используют третий метод,
который рассмотрим в следующем вопросе.
Таблица
7.8 – Расчет трехлетней скользящей
средней.
|
Годы |
Цельномолочная |
Сумма цельномолочной |
Трехлетняя |
|
1995 |
801 |
— |
– |
|
1996 |
744 |
— |
– |
|
1997 |
813 |
2358 |
786,0 |
|
1998 |
952 |
2509 |
836,3 |
|
1999 |
1032 |
2797 |
932,3 |
|
2000 |
954 |
2938 |
979,3 |
|
2001 |
963 |
2949 |
983,0 |
|
2002 |
906 |
2823 |
941,0 |
|
2003 |
927 |
2796 |
932,0 |
|
2004 |
992 |
2825 |
941,7 |
|
2005 |
1122 |
3041 |
1013,7 |
|
2006 |
1284 |
3398 |
1132,7 |
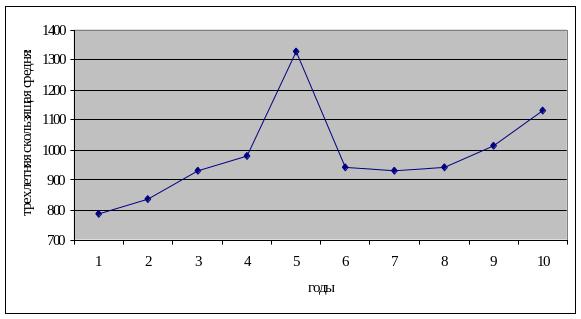
Рисунок
7.4. График ряда, выровненного по скользящей
средней
В
4. Тренд.
Аналитическое выравнивание ряда.
Прогнозы по тренду.
Самые
точные результаты выравнивания ряда
динамики дает аналитическое выравнивание,
с помощью которого строят математическое
уравнение, наилучшим образом описывающее
тенденцию изменения показателя.
Понятие
об уравнении тенденции динамики ввел
в 1902 году английский ученый Р.Гукер. Он
предложил называть такое уравнение
трендом (the
trend).
Под
трендом
понимают уравнение линии во времени,
вдоль которой расположена ломаная ряда
динамики.
Этапы построения
тренда:
1.
Выявляют этапы развития явления (спады,
подъемы, однородные участки и т.д.).
2.
Анализируют показатели ряда динамики
на этих этапах и выбирают вид уравнения
(вид тренда).
3.
Вычисляют параметры тренда, используя
метод наименьших квадратов.
4.
Оценивают адекватность уравнения
развитию анализируемого показателя,
оценивая колеблемость фактических
уровней ряда вокруг теоретических, т.е.
вычисленных по тренду.
Рассмотрим
3-ий этап на простейшем примере, когда
трендом является уравнение прямой
линии. Будем искать уравнение в виде:
(7.11)
где
t
– параметр времени; Yt
– соответствующие времени уровни ряда,
Ŷt–
выровненные уровни ряда, т.е. вычисленные
по тренду.
Исходную
информацию и расчетные показатели
представим в виде таблицы 7.9.
Используя
метод наименьших квадратов, построим
систему уравнений:
(7.12)
Таблица
7.9. Схема таблицы для расчета параметров
тренда
|
t |
Yi |
t2 |
Y∙t |
Ŷ |
|
1 2 3 … n |
Y1 Y2 Y3 … Yn |
Ŷ Ŷ |
||
|
t |
Y |
t2 |
(Y∙t) |
ΣŶ |
Решение
этой системы позволит найти значения
параметров уравнения. Если уравнение
построено качественно, то Yi
= Σ Ŷt
.
Эти
расчеты можно упростить, если иначе
производить номерацию параметра t.
Ее нужно произвести следующим образом:
начало отсчета должно находиться в
середине анализируемого ряда. Если
количество точек нечетное, то в середине
ряда t
ставим 0; если количество точек четное,
то нуль выбрасывается. К началу ряда
счет идет со знаком «–», к концу – со
знаком «+», тогда t
становиться равной 0 (т.е. t=0).
Таблица
7.10. Схема номерации уровней ряда от
середины ряда
|
t для |
t для четного |
|
–к |
–к |
|
… |
… |
|
–2 |
… |
|
–1 |
–2 |
|
0 |
–1 |
|
+1 |
+1 |
|
+2 |
+2 |
|
… |
… |
|
+к |
+к |
|
кi=0 |
кi=0 |
Тогда
в системе нормальных уравнений (7.12)
исчезнут слагаемые, в которые входит
сумма t
(Σt=0),
т.е. мы получим упрощенную систему
(7.13)
где
n
– количество точек анализируемого
ряда.
Отсюда:
(7.14)
(7.15)
Параметр
а1
соответствует абсолютному приросту за
единицу периода времени.
Тенденции
или тренды могут быть выражены в виде
кривых. Это могут быть: парабола, ветка
гиперболы, экспонента или показательная
кривая, логарифмическая линия и т.д.
Виды трендов в виде кривых и их построение
рассмотрим ниже.
Прогноз
по тренду.
Используя уравнение можно построить
точечный прогноз на последующие периоды
времени, подставляя в уравнение тренда
(7.11) номера t,
следующие за последним фактическим
номером, используемым при построении
тренда. Например:
Таблица
7.11. Схема расчета прогноза при различной
номерации показателей ряда динамики
|
Номерация t |
Номерация t |
|
1 |
-6 |
|
2 |
… |
|
… |
-1 |
|
11 |
+1 |
|
прогноз 12 |
+2 |
|
прогноз 13 |
… |
|
прогноз 14 |
+6 |
|
прогноз 15 |
прогноз 7 |
|
и т.д. |
прогноз 8 |
Параметры
а0
и а1
в уравнении тренда, построенных различным
способом нумерации t, будут отличаться,
а прогнозы будут совпадать.
Оценка
точности тренда.
В экономическом анализе необходимо
оценить силу разброса фактических точек
вокруг расчетных (трендовых). Это
оценивается по величине остаточного
среднеквадратического отклонения и
коэффициенту вариации:
(7.16)
где
n
– число уровней ряда; m
– число параметров в уравнении тренда
(например, для прямой m=2,
для параболы m=3).
(7.17)
г
де
Yi
– средний
уровень ряда.
Чем
меньше значения σост.
и V,
тем лучше тренд отражает тенденцию
изменения показателя.
Имея оценку качества
тренда, производят оценку качества
прогноза на перспективу.
Для
точечного прогноза по тренду, также как
и для выборочного наблюдения, необходимо
оценить среднюю ошибку прогноза.
Для
линейного тренда средняя ошибка прогноза
рассчитывается:
(7.18)
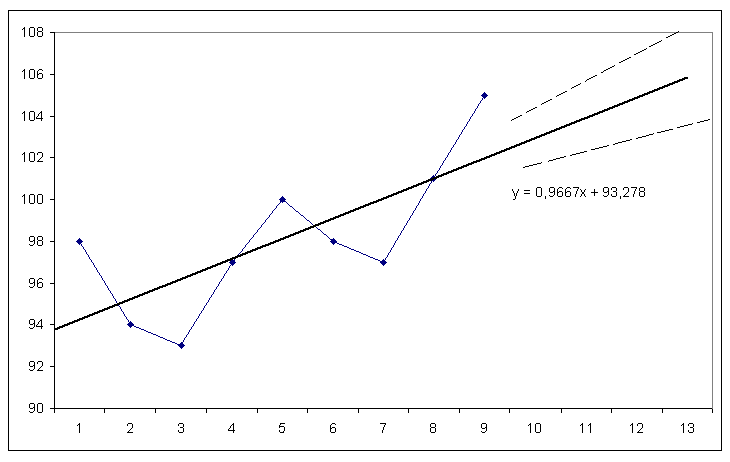
Рисунок
7.5. Точечное и интервальное прогнозирование
Доверительный
интервал или предельная ошибка прогноза
равна средней ошибке умноженной на
коэффициент доверия t-Стьюдента,
при доверительных вероятностях p=0,90;
0,95; 0,99. Строчку в таблицах находим по
числу степеней свободы тренда n
– m
.
В
5. Сезонные колебания в рядах динамики
Если
ряд динамики насчитывает достаточное
количество уровней, например 100, то можно
обнаружить колебания, которые повторяются,
т.е. наличие регулярных спадов и подъёмов.
Такие макроэкономические колебания
называются циклическими.
Такого вида колебания рассматриваются
в курсе макроэкономики, когда оценивают
динамику экономического развития
отдельных государств.
Внутри
годичные колебания, имеющие регулярный
характер, т.е. повторяющиеся из года в
год, называются сезонными
.
Сезонные
подъёмы и спады в производстве снижают
равномерность, устойчивость технологического
процесса и реализации продукции и должны
учитываться при планировании производства.
Сезонные
колебания показателя могут накладываться
на тенденцию роста или спада фактора,
а могут наблюдаться при постоянной
случайной колеблемости. В зависимости
от этого графики могут иметь следующий
вид:
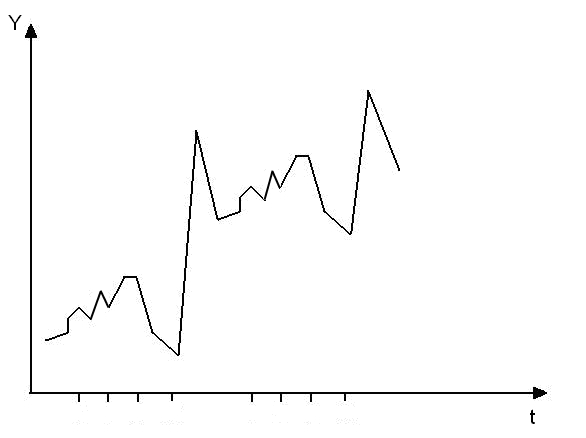
Рисунок
7.6. Наличие тенденции, случайных и
сезонных колебаний
На
рисунке хорошо видны спады в четвертом
квартале и подъемы в первом. В остальные
периоды наблюдается случайная колеблемость
при наличии тенденции к росту показателя.
На
рисунке 7.7. видно, что изменение показателя
не имеет тенденции ни к росту, ни к
снижению. Однако видна четко выраженная
сезонная колеблемость показателя, т.е.
есть периоды «впадин» и «подъемов».
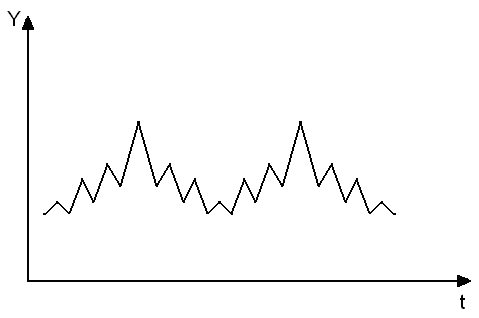
Рисунок
7.7. Наличие сезонных и случайных колебаний
Чаще
всего степень сезонных колебаний
определяют по величине индекса сезонности.
Различают индивидуальные индексы
сезонности и средние, с учётом тренда
и без его наличия.
Если
тренд отсутствует, то индивидуальный
индекс сезонности может быть вычислен
как отношение величины месячного
(квартального) уровня к среднегодовому:
(7.19)
Средний
индекс сезонности равен сумме
индивидуальных индексов сезонности,
делённой на количество сезонов n.
Так как анализ может проводиться за
несколько полных лет и один (последний)
неполный год, то число n
будет различным для той части времени,
где учитываются только полные годы и
для той, где есть дополнительно значения
ряда за неполный год.
(7.20)
В
сельском хозяйстве анализ сезонных
колебаний на основе данных поквартального
учёта несколько ухудшает показатель
сезонности, потому что времена года
(сезоны) не совпадают с календарными
периодами. Поэтому исследование наличия
сенных колебаний лучше
проводить на основании данных помесячного
учета.
Если
анализируемый показатель имеет не
только сезонные колебания, но и достоверную
тенденцию (тренд), то в знаменателе
берётся показатель ряда, взятый по
тренду:
(7.21)
Оценка
индекса сезонности осуществляется по
среднему линейному или среднеквадратическому
отклонению для каждого года. Если
коэффициенты сезонности (линейный и
среднеквадратический) увеличиваются,
то это свидетельствует об усилении
сезонных колебаний; если уменьшаются,
то наоборот.
Среднее
линейное отклонение коэффициента
сезонности рассчитывают по формуле:
=
(7.22)
Среднеквадратическое
отклонение коэффициента сезонности
рассчитывают по формуле:
=
(7.23)
где
n – число сезонов.
Чем
меньше значения этих показателей, тем
меньше сезонная колеблемость и выше
стабильность показателя.
В
6. Модели рядов с учетом тенденции и
сезонности.
Тенденцию
ряда и наличие сезонности можно
представить в виде двух различных
моделей:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Показатели ряда динамики
Примеры решения задач
Задача 1
По АО
«Керамик» имеются данные о производстве кирпича за год. Рассчитайте все
недостающие в таблице уровни ряда и цепные показатели анализа динамики.
Рассчитайте средний уровень ряда, средние абсолютный прирост и темп роста.
| Месяцы |
Произведено кирпича, тыс.р. |
Цепные показатели | |||
| абсолютный | темп роста, % | темп прироста, % |
абсолютное значение 1% прироста |
||
| Январь | 450 | ||||
| Февраль | 100 | ||||
| Март | 80 | ||||
| Апрель | -30 | ||||
| Май | 250 | ||||
| Июнь | -30 | ||||
| Июль | |||||
| Август | 300 | 5,0 | |||
| Сентябрь | 150 | ||||
| Октябрь | 80 | ||||
| Ноябрь | -60 | ||||
| Декабрь | 300 |
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Формулы цепных показателей динамики
Абсолютный цепной прирост можно
найти по формуле:
-уровень ряда;
-предыдущий
уровень ряда
Цепной темп роста:
Темп прироста:
Абсолютное
содержание 1% прироста:
Расчет недостающих уровней ряда динамики
Исходя из формул, заполним
недостающие показатели:
Февраль:
Март:
Апрель:
Май:
Июнь:
Июль:
Август:
Сентябрь:
Октябрь:
Ноябрь:
Декабрь:
Вычисление цепных показателей динамики
|
Абсолютные приросты цепные: |
Темпы роста цепные: |
|
Темпы прироста цепные: |
Абсолютное содержание 1% прироста: |
Показатели динамики производства кирпича
| Месяцы |
Произведено кирпича, тыс.р. |
Цепные показатели |
|||
| абсолютный |
темп роста, % |
темп прироста, % |
абсолютное значение 1% прироста |
||
| Январь | 450 | —- | 100 | —- | —— |
| Февраль | 900 | 450 | 200 | 100 | 4.5 |
| Март | 720 | -180 | 80.0 | -20.0 | 9,0 |
| Апрель | 690 | -30 | 95.8 | -4.2 | 7.2 |
| Май | 1725 | 1035 | 250.0 | 150.0 | 6.9 |
| Июнь | 1208 | -517 | 70.0 | -30.0 | 17.25 |
| Июль | 500 | -708 | 41.4 | -58.6 | 12.08 |
| Август | 800 | 300 | 160.0 | 60.0 | 5,0 |
| Сентябрь | 1200 | 400 | 150.0 | 50.0 | 8,0 |
| Октябрь | 2160 | 960 | 180.0 | 80.0 | 12,0 |
| Ноябрь | 2100 | -60 | 97.2 | -2.8 | 21.6 |
| Декабрь | 6300 | 4200 | 300 | 200 | 21,0 |
Расчет средних уровней ряда динамики
Средний
уровень исследуемого динамического ряда найдем по формуле средней
арифметической:
Среднегодовой
абсолютный прирост:
Среднегодовой
темп роста:
Среднегодовой
темп прироста:
Вывод к задаче
Среднемесячный
показатель производства составил 1562,8 тыс.р. В среднем за месяц показатель
увеличивался на 531,8 тыс.р. или на 27,1% в относительном выражении.
Задача 2
Для
изучения динамики товаропотока рассчитайте:
- Абсолютные и относительные показатели динамики по годам периода (абсолютные
приросты – базисные и цепные; темпы роста – базисные и цепные). - Динамические средние за период в целом – среднегодовой уровень ряда,
среднегодовой абсолютный прирост, среднегодовой темп роста. Объясните их смысл. - Выполните прогнозы уровня ряда на следующий год, используя среднегодовой
абсолютный прирост и среднегодовой темп роста. Сделайте выводы о развитии
изучаемого процесса. - Постройте график динамики изучаемого процесса.
Динамика
экспорта РФ в Португалию, млрд. долл. США
| Годы | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| Экспорт | 0.62 | 1.14 | 1.38 | 1.25 | 0.21 | 0.13 | 0.20 |
Решение
1)
|
Абсолютные приросты цепные: |
Абсолютные приросты базисные: |
|
Темпы роста цепные: |
Темпы роста базисные: |
|
Темпы прироста цепные: |
Темпы прироста базисные: |
Показатели динамики экспорта 2004-2010 гг.
| Годы |
Экспорт, млрд.долл |
Абсолютные приросты, млрд.долл |
Темпы роста, % |
Темпы прироста, % |
|||
| цепные | базисные | цепные | базисные | цепные | базисные | ||
| 2004 | 0.62 | —— | —— | 100.0 | 100.0 | —— | —— |
| 2005 | 1.14 | 0.52 | 0.52 | 183.9 | 183.9 | 83.9 | 83.9 |
| 2006 | 1.38 | 0.24 | 0.76 | 121.1 | 222.6 | 21.1 | 122.6 |
| 2007 | 1.25 | -0.13 | 0.63 | 90.6 | 201.6 | -9.4 | 101.6 |
| 2008 | 0.21 | -1.04 | -0.41 | 16.8 | 33.9 | -83.2 | -66.1 |
| 2009 | 0.13 | -0.08 | -0.49 | 61.9 | 21.0 | -38.1 | -79.0 |
| 2010 | 0.20 | 0.07 | -0.42 | 153.8 | 32.3 | 53.8 | -67.7 |
2)
Средний уровень исследуемого динамического ряда найдем по формуле средней
арифметической:
Среднегодовой
абсолютный прирост:
Среднегодовой
темп роста:
Среднегодовой
темп прироста:
Таким
образом в среднем за исследуемый период экспорт
составлял 0,704 млрд. долл. в год. В среднем показатель уменьшался на 0,07 млрд.долл. в год или на 17,2% в
относительном выражении.
3)
Прогноз на 2011 год с помощью среднего абсолютного прироста:
Прогноз
на 2011 год с помощью среднегодового темпа роста:
На
2011 год показатель, прогнозируемый с помощью среднего
абсолютного прироста составил 0,13 млрд. долл., а с помощью
среднегодового темпа роста – 0,166 млрд. долл.
4)
График динамики экспорта 2004-2010 гг.
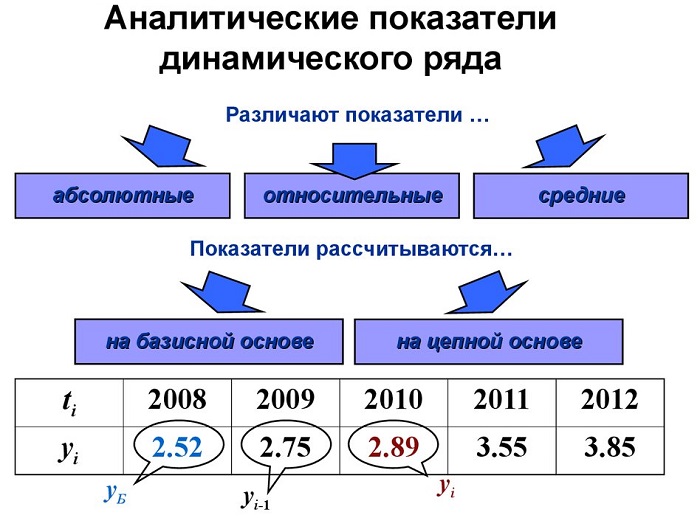
Что такое ряд динамики в статистике, и какие они бывают, мы рассмотрели в первой части этой темы. Теперь поговорим об анализе рядов динамики. Как уже отмечалось, ряды динамики характеризуют развитие явление во времени, а это развитие подлежит изучению. Ведь статистику интересует, как это явление развивается, какие есть тенденции (тренды) в развитии явления. Или наоборот тенденций нет.
Именно для целей изучения динамики или скорости изменений во временных периодах и используются показатели анализа рядов динамики.
Но прежде чем мы перейдем к самим показателям и формулам их расчета необходимо уточнить важнейший момент.
Анализ рядов динамики
Дело в том что сам анализ может проводиться двумя способами, в зависимости от того как и с чем мы будем проводить сравнение уровней ряда. Если мы хотим сравнить с каким-то одним данным это один способ, а если с непосредственно предшествующим, то это уже другой способ расчета.
Как правило, расчет проводится сразу и тем и другим способом, если мы говорим о полноценном исследовании.
- Расчет показателей анализа рядов динамики С ПОСТОЯННОЙ БАЗОЙ СРАВНЕНИЯ (БАЗИСНЫЕ показатели) – каждый уровень рядя сравнивается с одним и тем же уровнем выбранным за базу сравнения.
Например: база сравнение 2005 год, а уровни, начиная с 2006 по 2009, тогда получаем следующую последовательность расчетов уровень 2006 года с уровнем 2005 года, 2007 – с 2005, 2008 – с 2005 и 2009 – с 2005.
- Расчет показателей анализа рядов динамики С ПЕРЕМЕННОЙ БАЗОЙ СРАВНЕНИЯ (ЦЕПНЫЕ показатели) – в данном случае каждый уровень ряда сравнивается с тем который стоит перед ним, получается такое цепное сравнение или цепь расчетов взаимно перетекающих друг в друга, поэтому и второе название способа ЦЕПНЫЕ показатели анализа рядов динамики.
Например: имеем уровни начиная с 2005 по 2009 годы, тогда получаем следующую последовательность расчетов уровень 2006 года с уровнем 2005 года, 2007 – с 2006, 2008 – с 2007 и 2009 – с 2008.
Вот такие нехитрые расчеты. А теперь можем перейти к самим показателям анализа. Следует сказать, что эти показатели условно можно разделить на две группы:
— простые показатели анализа рядов динамики рассчитываются по каждому уровню ряда;
— обобщающие или средние показатели анализа рядов динамики они рассчитываются для всего ряда в целом, собственно как и любые средние величины.
А вот самих показателей всего пять.
- Абсолютный прирост – рассчитывается путем вычитания из текущего уровня базисного или предшествующего уровня, то есть простое математическое вычитание. В отличие от всех других показателей абсолютный прирост имеет те же единицы измерения, что и исходный уровень ряда. Может получиться отрицательным.
- Коэффициент роста – рассчитывается делением текущего уровня на базисный или предшествующий уровень. Показывает во сколько раз данный уровень больше или меньше базисного. Поскольку это относительная величина, то наименование у коэффициента роста нет.
- Темп роста – рассчитывается умножением коэффициента роста на 100%. Показывает, сколько процентов данный уровень составляет по отношению к базисному. Выражается в процентах.
- Темп прироста – рассчитывается вычитанием из темпа роста 100%. Показывает на сколько процентов данный уровень больше или меньше базисного. Выражается в процентах. Может получиться отрицательным.
- Абсолютное значение одного процента прироста – рассчитывается из имеющихся уже абсолютного прироста и темпа прироста путем деления первого на второй. Получаем как раз размер 1 % прироста, но в абсолютно выражении. Следует сказать, что данный показатель носит больше статистический характер и в широкой практике используется нечасто.
Формулы для анализа рядов динамики
Ниже в сводной таблице представим все формулы простых показателей анализа рядов динамики с постоянной и переменной базой сравнения.
Обобщающие показатели анализа рядов динамики имеют практически похожие названия, и выполняют роль средневзвешенных показателей, для упрощения анализа. Их также пять:
- Средний абсолютный прирост.
- Средний коэффициент роста – рассчитывается по формуле средней геометрической.
- Средний темп роста.
- Средний темп прироста.
- Среднее значение одного процента прироста.
Формулы для расчета вышеуказанных показателей сведем в общую таблицу. Также для полноты картины приведем и формулы расчета средних уровней, которые были разобраны в первой части.

| Год | Выпуск продукции, млн. руб. |
| 2010 | 219,7 |
| 2011 | 221,4 |
| 2012 | 234,2 |
| 2013 | 254,1 |
| 2014 | 241,8 |
| Итого | 1171,2 |
А для простоты можно воспользоваться вот такой таблицей для занесения итоговых расчетов.
| Год | y | Δ | К | Тр | Тпр | α | |||||
| Б | Ц | Б | Ц | Б | Ц | Б | Ц | Б | Ц | ||
| 2010 | 219,7 | — | — | — | — | — | — | — | — | — | — |
| 2011 | 221,4 | ||||||||||
| 2012 | 234,2 | ||||||||||
| 2013 | 254,1 | ||||||||||
| 2014 | 241,8 |
Если вам что-то не понятно, вы всегда можете спросить в комментариях или написать в нашу группу вконтакте! А также вы можете выслать туда решение, чтобы мы проверили его!
Может еще поучимся? Загляни сюда!
Пример решения задачи. Ряд динамики
Условие задачи
Определить
вид ряда динамики. Для полученного ряда рассчитать: цепные и базисные
абсолютные приросты, темпы
роста, темпы прироста, средний уровень ряда, средний темп роста, средний
темп прироста. Проверить взаимосвязь абсолютных приростов и темпов роста. По
расчетам сделать выводы. Графически изобразить полученный ряд динамики.
| Годы |
Объем производства, млн.р. |
| 2011 | 12 |
| 2012 | 10 |
| 2013 | 11 |
| 2014 | 10 |
| 2015 | 9 |
Решение задачи
Данный
ряд динамики – интервальный, так как значение показателя заданы за определенный
интервал времени.
Определяем цепные и базисные показатели ряда динамики
|
Абсолютные приросты цепные: |
Абсолютные приросты базисные: |
|
Темпы роста цепные: |
Темпы роста базисные: |
|
Темпы прироста цепные: |
Темпы прироста базисные: |
Показатели динамики объема производства 2011-2015 гг
| Годы |
Объем производства, млн.р. |
Абсолютные приросты, млн.р. | Темпы роста, % | Темпы прироста, % | |||
| цепные | базисные | цепные | базисные | цепные | базисные | ||
| 2011 | 12 | —— | —— | 100.0 | 100.0 | —— | —— |
| 2012 | 10 | -2 | -2 | 83.3 | 83.3 | -16.7 | -16.7 |
| 2013 | 11 | 1 | -1 | 110.0 | 91.7 | 10.0 | -8.3 |
| 2014 | 10 | -1 | -2 | 90.9 | 83.3 | -9.1 | -16.7 |
| 2015 | 9 | -1 | -3 | 90.0 | 75.0 | -10.0 | -25.0 |
Определяем средние показатели ряда динамики
Средний
уровень исследуемого динамического ряда найдем по формуле средней
арифметической:
Среднегодовой
абсолютный прирост:
Среднегодовой
темп роста:
Среднегодовой
темп прироста:
Строим график
График динамики объема производства 2011-2015 гг
Таким образом на протяжении всего исследуемого
периода за исключением 2013 года объем производства продукции на предприятиях
снижался. В среднем предприятия производили продукции на 10,4 млн.р. в год. В
среднем показатель снижался на 0,75 млн.р. в год или на 6,9% в относительном
выражении.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная оплата переводом на карту СберБанка.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Ряды динамики в статистике помогают отслеживать и анализировать изменение каких-либо собранных показателей с течением временем.
Форма представления может отличаться, но принципы обработки остаются неизменными.
Понятие ряда динамики в статистике
Подразумевается совокупность чисел, описывающая состояние интересующего фактора. При этом должна соблюдаться хронологическая последовательность с образованием временного ряда.
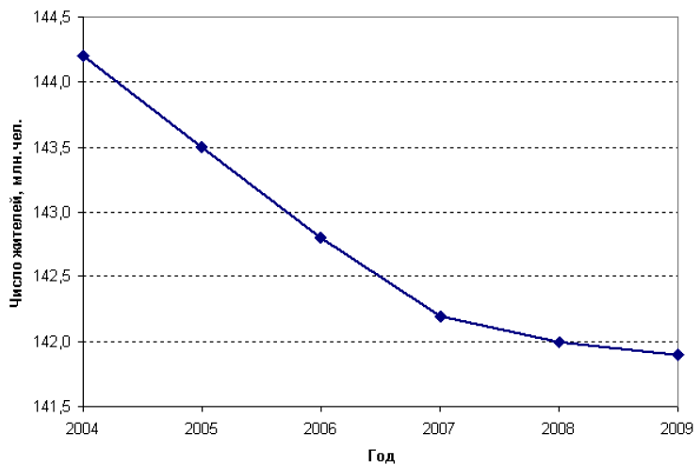
Ряд может быть подан в виде таблицы. Например, ниже указано население в миллионах человек по годам на 1-е февраля.
Представляется более наглядной и динамической графическая интерпретация, показанная на рисунке ниже:
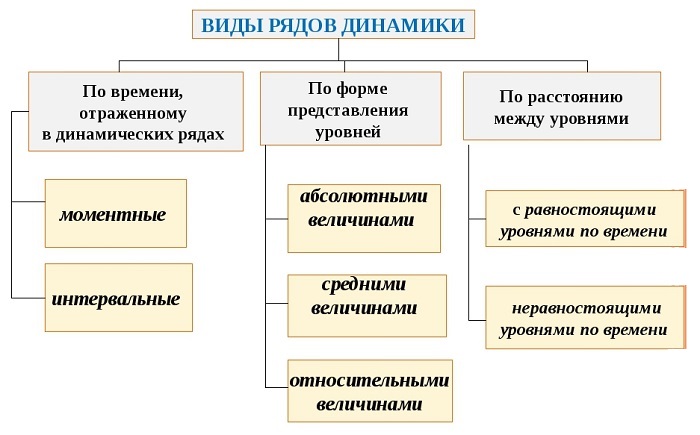
Виды рядов динамики в статистике
Разделяют последовательности по временным показателям и по представлению чисел:
-
Отсечка производится по конкретному отрезку времени (моментный ряд) или суммируется за какой-то промежуток (интервальный ряд). В приведенном примере – первый случай. Показано состояние на определенную дату. Попытка что-то просуммировать даст бессмысленное число. Второй способ актуален, если, например, характеризуется выпуск товаров за неделю, месяц, квартал.
-
С постоянным или изменяющимся временным отрезком. В нашем случае отображаются регулярные годовые замеры.
-
Показаны абсолютные, средние или относительные безразмерные числа. У нас иллюстрируется количество живущих в государстве людей без каких-либо алгебраических вмешательств.
-
По сути показателей. Может сопоставляться курс валюты (одномерный критерий), а может состоять из объемов закупки разных валют (многомерный). В примере фигурирует только одна величина.
Уровни рядов динамики
Понятие «уровень» относится к интересующим замеренным числам. В расчетной документации в большинстве случаев зашифровываются латинской литерой «y».
Базисный или первый уровень подразумевает начальное число в таблице, конечный – последнее. Все, что связано со временем фиксации факта, скрывается под «t».
Расчеты среднего уровня в рядах динамики
Существуют случаи, когда требуются какие-то резюмирующие значения. Среднее – из таких. При этом методики его определения для разных видов рядов отличаются.
Интервальный ряд динамики
В этом случае требуется просто поиск среднего арифметического. Таким образом можно показать какие-то сезонные колебания производства, продаж.
Рассчитать можно по формуле:
где Y – уровни;
n – их количество.
В нашем случае подобная цифирь полезной нагрузки не несет, только для наглядности:
(144,2 + … + 141,9) / 6 = 866,6 / 6 = 142,77.
Таково среднее население за 5 лет.
Моментный ряд динамики
Если разрыв в датах неизменен, то можно записать последовательность в средних значениях. Получим (n – 1) чисел такого вида
После нехитрых выкладок обнаруживаем, что
y(1), y(n) – базисный и конечный уровни;
y(i) – внутренние.
Считаем:
((141.2 + 141,9) / 2 + 143,5 + … + 142) / 5 = (143,05 + 570,5) / 2 = 142,71.
Мы получили среднее хронологическое.
Но это для равных отрезков. Когда они меняются, необходимо учитывать временной фактор. Если уровни меняются с течением времени, то выводится такое:
Выражение несколько упрощается, если уровни постоянны до следующей отсечки.
t(i) – длительность периода, когда уровень i зафиксирован.
Показатели анализа рядов динамики
Методы анализа сводятся к видоизменению полученных данных к виду, облегчающему отслеживание динамики и выявляющему ее направленность. Так или иначе придется сопоставлять уровни для понимания темпов роста / убыли.
Для оценки применяются абсолютные (вычитание уровней) и относительные (отношение уровней ряда) величины.
Базисные показатели можно получить, если сравнивать с первым элементом. Цепные показатели – с соседними.
Это базисная и цепная абсолютные разницы соответственно.
То же в относительном выражении. В таком виде мы получим характеристику в виде коэффициента. Для более наглядного представления следует умножить на «100» и получить %%.
Надо заметить, что цепные критерии имеют свойства накапливаться и переходить в базисные:
И самые важные для оценки параметров динамики понятия — темпы:
Опять же в абсолютном и относительных видах. Если речь идет об анализе плавной кривой, то отношение заменит производная, указывающая на тангенс угла наклона касательной прямой.
Об усредненных величинах мы уже говорили. Стоит немного вернуться и рассмотреть их в связи с темпами:
Так выглядят базисный и цепной средние темпы прироста:
А вот так в относительных единицах.
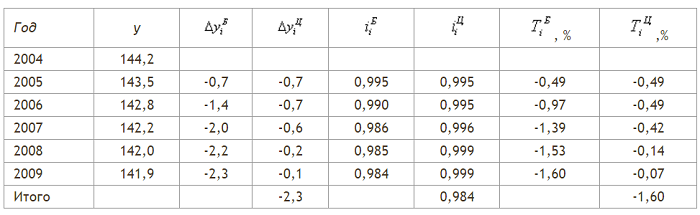
Теперь на основании изложенного дополним нашу исходную таблицу и сделаем напрашивающиеся выводы.
Вполне очевидно, что отрицательные значения абсолютных величин и менее 1 относительные указывают на падение населения. При этом темпы роста ниже 0, и это указывает на сохранение неблагоприятной тенденции.
Методы выравнивания рядов динамики
Выравнивание используется для определения общего направления динамики процессов. Кратковременные случайные всплески роста / падения иногда нарушают целостность восприятия картины.
Ещё можно заметить, что:
-
Увеличение периодов позволяет построить данные таким образом, чтобы изменения явно демонстрировали основную линию. Выравниваются средние значения.
-
Плавающая средняя означает, что она подсчитывается из определенного числа соседних уровней. По новым правилам построения организуется новый ряд из средних. Метод оптимален, если графическая интерпретация близка к прямой. В противном случае искажение динамики может оказаться чрезмерным.
-
Аналитический метод сводится к аппроксимации параметров математическим уравнением с высокой корреляцией. Дальнейшая работа базируется на нем. Так легче выявить тенденцию, можно позволить какие-то прогнозы. Облегчается использование численных методов.
Заключение
Ряды динамики позволяют понятными способами анализировать полученные данные. Наглядными становятся происходящие изменения.
Ситуация становится еще более ясной на графиках с представлением средних, различий, темпов роста / падения.