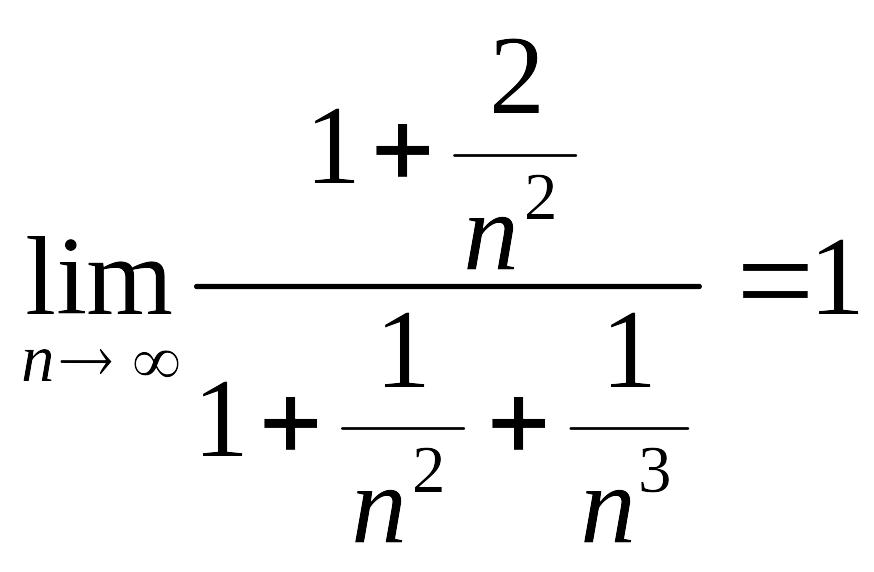Как найти ряд для сравнения - Исправление недочетов и поиск решений вместе с Examum.ru

Признаки сравнения числовых рядов. Первая часть.

Перед началом работы с этой темой советую посмотреть раздел с терминологией для числовых рядов. Особенно стоит обратить внимание на понятие общего члена ряда и свойства числовых рядов (в частности, нам понадобятся свойства №3 и №4). Если у вас есть сомнения в правильности выбора признака сходимости, советую глянуть тему «Выбор признака сходимости числовых рядов».

Признаки сравнения применяются для исследования числовых рядов, члены которых неотрицательны, т.е. больше или равны нулю. Такие ряды называются положительными (в части литературы – неотрицательными или знакоположительными). Именно такие ряды мы и станем рассматривать в данной теме.

Первый признак сравнения (или первая теорема сравнения) формулируется следующим образом:

Первый признак сравнения

Пусть заданы два положительных ряда $sumlimits_{n=1}^{infty}u_n$ и $sumlimits_{n=1}^{infty}v_n$. Если начиная с некоторого номера $n_0$ выполнено неравенство $u_n≤ v_n$, то:

если ряд $sumlimits_{n=1}^{infty}u_n$ расходится, то ряд $sumlimits_{n=1}^{infty}v_n$ будет расходящимся.
если ряд $sumlimits_{n=1}^{infty}v_n$ сходится, то ряд $sumlimits_{n=1}^{infty}u_n$ будет сходящимся.

Упрощённо говоря, если ряд с меньшими членами не имеет суммы (расходится), то и ряд с бо́льшими членами тоже будет расходиться. И это логично, ибо если исходная сумма была бесконечно большой, то после увеличения слагаемых она такой и останется.

Ну, и если ряд с бо́льшими членами имеет сумму (сходится), то и ряд с меньшими членами тоже будет сходиться.

Признак сравнения можно сформулировать также и в иной форме. Обычно говорят, что это второй признак сравнения (или вторая теорема сравнения). Иногда его называют предельным признаком сравнения или признаком сравнения в предельной форме. Формулировка его такова:

Второй признак сравнения

Пусть заданы два положительных ряда $sumlimits_{n=1}^{infty}u_n$ и $sumlimits_{n=1}^{infty}v_n$. Если при условии $v_nneq 0$ существует предел
$$lim_{ntoinfty}frac{u_n}{v_n}=K,$$
где $0 < K < infty$, то ряды $sumlimits_{n=1}^{infty}u_n$ и $sumlimits_{n=1}^{infty}v_n$ сходятся либо расходятся одновременно.

Заметьте, что для применения признаков сравнения нам нужно иметь некий ряд, сходимость которого известна заранее. Чаще всего в роли ряда для сравнения выступает обобщённый гармонический ряд

$$
begin{equation}
sumlimits_{n=1}^{infty}frac{1}{n^alpha}
end{equation}
$$

Если $alpha > 1$, то ряд $sumlimits_{n=1}^{infty}frac{1}{n^alpha}$ сходится, а если $alpha ≤ 1$, то ряд $sumlimits_{n=1}^{infty}frac{1}{n^alpha}$ расходится. Например, ряд $sumlimits_{n=1}^{infty}frac{1}{n^5}$ сходится, так как $5 > 1$, а ряд $sumlimits_{n=1}^{infty}frac{1}{sqrt[7]{n^4}}=sumlimits_{n=1}^{infty}frac{1}{n^{frac{4}{7}}}$ расходится, так как $frac{4}{7}≤ 1$.

Особо стоит обратить внимание на случай $alpha=1$, т.е. ряд $sumlimits_{n=1}^{infty}frac{1}{n^1}=sumlimits_{n=1}^{infty}frac{1}{n}$. Ряд $sumlimits_{n=1}^{infty}frac{1}{n}$ называют гармоническим рядом. Гармонический ряд расходится.

Кроме того, частенько для сравнения используется ряд такого вида:

$$
begin{equation}
sumlimits_{n=1}^{infty}aq^n
end{equation}
$$

Этот ряд представляет собой сумму членов геометрической прогрессии с первым членом $b_1=a$ и знаменателем $q$. Этот ряд сходится если $|q| < 1$ и расходится если $|q|≥ 1$. Например, ряд $sumlimits_{n=1}^{infty}frac{4cdot 3^n}{5^n}=sumlimits_{n=1}^{infty}left(4cdotleft(frac{3}{5}right)^nright)$ подпадает под вид ряда (2). Этот ряд сходится, так как $left| frac{3}{5}right|=frac{3}{5} < 1$.

Чаще всего в стандартных примерах признаки сравнения применяются, если общий член ряда представлен дробью, числитель и знаменатель которой есть некие многочлены. Например, $u_n=frac{9n+7}{2n^3+5n^2-4}$ (см. пример №1). Или же вместо многочленов (или вместе с ними) могут присутствовать корни от многочленов (см. пример №3). Для рядов такого вида приходится выбирать между необходимым признаком сходимости и признаками сравнения. Иногда общий член ряда может содержать не только многочлен, а и некий «отвлекающий элемент», который не влияет на сходимость (см. вторую часть этой темы). Иногда, чтобы увидеть ряд для сравнения, приходится использовать эквивалентные бесконечно малые функции (см. примеры в третьей части).

Для вычисления пределов будем использовать методы, изложенные в теме «Пределы с иррациональностями», а также «Предел отношения двух многочленов».

Пример №1

Исследовать сходимость ряда $sumlimits_{n=1}^{infty}frac{9n+7}{2n^3+5n^2-4}$.

Решение

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=frac{9n+7}{2n^3+5n^2-4}$. Так как при $n≥ 1$ имеем $9n+7 > 0$ и $2n^3+5n^2-4 > 0$, то $u_n > 0$. Следовательно, наш ряд является положительным. Кстати сказать, для положительного ряда достаточно выполнения условия $u_n≥ 0$. Однако для нашего ряда мы можем записать более точно: $u_n > 0$.

Для начала неплохо бы проверить выполнение необходимого условия сходимости, т.е. найти $lim_{ntoinfty}u_n$. Вдруг нам повезёт и окажется, что $lim_{ntoinfty}u_nneq 0$? Тогда ряд будет расходиться, и решение на этом закончится. При нахождении предела будем использовать метод, описанный в теме «Предел отношения двух многочленов». В процессе решения разделим числитель и знаменатель на $n^3$:

$$
lim_{ntoinfty}u_n=lim_{ntoinfty}frac{9n+7}{2n^3+5n^2-4}=left|frac{infty}{infty} right|=lim_{ntoinfty}frac{frac{9}{n^2}+frac{7}{n^3}}{2+frac{5}{n}-frac{4}{n^3}}=frac{0+0}{2+0-0}=0.
$$

Так как $lim_{ntoinfty}u_n=0$, то никакого вывода про сходимость нашего ряда мы сделать не в состоянии. Ряд может как сходиться, так и расходиться. Попробуем применить признаки сравнения.

Для того, чтобы эти признаки использовать, нам понадобится ряд, с которым станем сравнивать. Чтобы выбрать ряд для сравнения, поисследуем поведение общего члена заданного нам ряда при $ntoinfty$. Это можно сделать с помощью несколько неформальных рассуждений. Так как эти рассуждения, возможно, будут интересны не всем читателям, то я скрою их под примечание.

Как выбрать ряд для сравнения? показатьскрыть

Рассмотрим, как решить нашу задачу с помощью как первого, так и второго признаков сравнения.

Решение с помощью первого признака сравнения

Итак, общий член ряда таков: $u_n=frac{9n+7}{2n^3+5n^2-4}$. Неформальными рассуждениями (скрытыми выше под примечание) мы пришли к выводу, что наш ряд сходится. Для этого случая применяется второй пункт первого признака сравнения. Нам нужно показать, что общий член нашего ряда удовлетворяет неравенству $frac{9n+7}{2n^3+5n^2-4}≤ v_n$, при этом ряд $sumlimits_{n=1}^{infty}v_n$ сходится. Тогда и заданный нам ряд будет сходиться.

Станем увеличивать дробь $frac{9n+7}{2n^3+5n^2-4}$. Наша цель: привести данную дробь к виду $frac{1}{n^2}$. Почему именно к этому виду? Для ответа на данный вопрос прошу раскрыть примечание выше.

Чтобы увеличить некую дробь, есть два пути: увеличить числитель или уменьшить знаменатель. Согласитесь, что так как $n≥ 1$, то $9n+7 ≥ 9n+7n=16n$. Следовательно, если мы в числителе вместо $9n+7$ разместим выражение $16n$, то увеличим рассматриваемую дробь:

$$
frac{9n+7}{2n^3+5n^2-4}≤frac{16n}{2n^3+5n^2-4}.
$$

Пойдём далее и поработаем со знаменателем. Чтобы увеличить дробь, знаменатель нужно уменьшить. Например, можно рассудить так: мы знаем, что $n≥ 1$. Тогда $5n^2-4 > 0$. Значит, если мы отбросим в знаменателе выражение $5n^2-4$, то знаменатель уменьшится. Следовательно, наша дробь увеличится. Продолжим предыдущее неравенство:

$$
frac{9n+7}{2n^3+5n^2-4}≤frac{16n}{2n^3+5n^2-4} < frac{16n}{2n^3}=8cdotfrac{1}{n^2}.
$$

Так как ряд $sumlimits_{n=1}^{infty}frac{1}{n^2}$ сходится, то будет сходиться и ряд $sumlimits_{n=1}^{infty}left(8cdotfrac{1}{n^2}right)$ (см. пункт №4 в разделе про свойства числовых рядов). Так как ряд $sumlimits_{n=1}^{infty}left(8cdotfrac{1}{n^2}right)$ сходится и $frac{9n+7}{2n^3+5n^2-4} < 8cdotfrac{1}{n^2}$, то согласно первому признаку сравнения (пункт №2) ряд $sumlimits_{n=1}^{infty}frac{9n+7}{2n^3+5n^2-4}$ сходится.

Решение с помощью второго признака сравнения

Если в предыдущем пункте мы занимались самодеятельностью, выбирая и отбрасывая некие «куски» в формуле общего члена ряда, то решение с помощью предельного признака сравнения полностью алгоритмично. В примечании выше мы уже выяснили, что сравнивать наш ряд нужно с сходящимся рядом $sumlimits_{n=1}^{infty}frac{1}{n^2}$. Итак, общий член нашего ряда $u_n=frac{9n+7}{2n^3+5n^2-4}$. Общий член ряда, с которым мы сравниваем: $v_n=frac{1}{n^2}$. Второй признак сравнения работает с пределом $lim_{ntoinfty}frac{u_n}{v_n}$. Кстати сказать, нам совершенно всё равно, какой общий член располагать в числителе, а какой – в знаменателе. Главное, чтобы выражение в знаменателе не равнялось нулю. Например, так как $v_nneq 0$, то этот общий член вполне можно расположить в знаменателе:

$$
lim_{ntoinfty}frac{frac{9n+7}{2n^3+5n^2-4}}{frac{1}{n^2}}=lim_{ntoinfty}frac{n^2cdot(9n+7)}{2n^3+5n^2-4}=lim_{ntoinfty}frac{9n^3+7n^2}{2n^3+5n^2-4}=left|frac{infty}{infty} right|=\
=lim_{ntoinfty}frac{frac{9n^3}{n^3}+frac{7n^2}{n^3}}{frac{2n^3}{n^3}+frac{5n^2}{n^3}-frac{4}{n^3}}=lim_{ntoinfty}frac{9+frac{7}{n}}{2+frac{5}{n}-frac{4}{n^3}}=frac{9+0}{2+0-0}=frac{9}{2}.
$$

Так как $0<frac{9}{2}<infty$, то ряды $sumlimits_{n=1}^{infty}frac{9n+7}{2n^3+5n^2-4}$ и $sumlimits_{n=1}^{infty}frac{1}{n^2}$ сходятся либо расходятся одновременно. Так как ряд $sumlimits_{n=1}^{infty}frac{1}{n^2}$ сходится, то одновременно с ним будет сходиться и ряд $sumlimits_{n=1}^{infty}frac{9n+7}{2n^3+5n^2-4}$.

В общем случае, конечно, выбирают один признак сравнения, а не оба сразу При решении примеров на этой странице я буду использовать оба способа – для наглядности.

Ответ: ряд сходится.

Пример №2

Исследовать сходимость ряда $sumlimits_{n=1}^{infty}frac{4n^3+2n+9}{n^2(3n+5)^2}$.

Решение

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=frac{4n^3+2n+9}{n^2(3n+5)^2}$. Общий член $u_n > 0$, т.е. наш ряд является положительным.

Как и в предыдущем примере, попробуем проверить выполнение необходимого условия сходимости, т.е. найдём $lim_{ntoinfty}u_n$. При нахождении предела будем использовать метод, описанный в теме «Предел отношения двух многочленов». В ходе решения разделим и числитель и знаменатель на $n^4$:

$$
lim_{ntoinfty}u_n=lim_{ntoinfty}frac{4n^3+2n+9}{n^2(3n+5)^2}=left|frac{infty}{infty}right|=lim_{ntoinfty}frac{frac{4}{n}+frac{2}{n^3}+frac{9}{n^4}}{left(3+frac{5}{n}right)^2}=frac{0+0+0}{(3+0)^2}=0.
$$

Выясним, с каким же рядом нужно сравнивать заданный в условии ряд. Попробуем отбросить «лишние» элементы числителя и знаменателя точно так же, как это было сделано в примере №1. Останется у нас такая дробь: $frac{4n^3}{n^2cdot (3n)^2}=frac{4}{9}cdotfrac{1}{n}$. Вот с гармоническим рядом $sumlimits_{n=1}^{infty}frac{1}{n}$ мы и станем сравнивать заданный ряд. Гармонический ряд расходится, поэтому и наш ряд будет расходиться. Нам осталось лишь показать это формально с помощью признаков сравнения.

Решение с помощью первого признака сравнения

Неформальными рассуждениями, проведенными выше, мы пришли к выводу, что наш ряд расходится. Для этого случая применяется первый пункт первого признака сравнения. Нам нужно показать, что общий член нашего ряда удовлетворяет неравенству $v_n≤ frac{4n^3+2n+9}{n^2(3n+5)^2}$, при этом ряд $sumlimits_{n=1}^{infty}v_n$ расходится. Тогда и заданный нам ряд будет расходиться.

Станем уменьшать дробь $frac{4n^3+2n+9}{n^2(3n+5)^2}$. Наша цель: привести данную дробь к виду $frac{1}{n}$.

Чтобы уменьшить некую дробь, есть два пути: уменьшить числитель или увеличить знаменатель. Так как $n≥ 1$, то $2n+9 > 0$. Поэтому если мы отбросим в числителе $2n+9$, то уменьшим числитель, тем самым уменьшив рассматриваемую дробь:

$$
frac{4n^3+2n+9}{n^2(3n+5)^2} > frac{4n^3}{n^2(3n+5)^2}
$$

Поработаем с знаменателем. Если мы его увеличим, то дробь уменьшится. Так как $n≥ 1$, то $3n+5≤ 3n+5n=8n$. Итак, если мы вместо $3n+5$ запишем $8n$, то знаменатель увеличится:

$$
frac{4n^3+2n+9}{n^2(3n+5)^2} > frac{4n^3}{n^2(3n+5)^2}≥ frac{4n^3}{n^2(8n)^2}=frac{4n^3}{64n^4}=frac{1}{16}cdotfrac{1}{n}.
$$

Дальнейшие рассуждения стандартны: так как ряд $sumlimits_{n=1}^{infty}frac{1}{n}$ расходится, то будет расходиться и ряд $sumlimits_{n=1}^{infty}left( frac{1}{16}cdotfrac{1}{n}right)$. Так как ряд $sumlimits_{n=1}^{infty}left( frac{1}{16}cdotfrac{1}{n}right)$ расходится и $frac{4n^3+2n+9}{n^2(3n+5)^2} > frac{1}{16}cdotfrac{1}{n}$, то согласно первому признаку сравнения (пункт №1) ряд $sumlimits_{n=1}^{infty}frac{4n^3+2n+9}{n^2(3n+5)^2}$ будет расходиться.

Решение с помощью второго признака сравнения

Ранее мы уже выяснили, что сравнивать заданный ряд нужно с расходящимся рядом $sumlimits_{n=1}^{infty}frac{1}{n}$. Сравним заданный ряд $sumlimits_{n=1}^{infty}frac{4n^3+2n+9}{n^2(3n+5)^2}$ с рядом $sumlimits_{n=1}^{infty}frac{1}{n}$, используя второй признак сравнения . Данный признак работает с пределом $lim_{ntoinfty}frac{u_n}{v_n}$. Оба общих члена сравниваемых рядов не равны нулю, поэтому в знаменателе можем размещать общий член любого ряда:

$$
lim_{ntoinfty}frac{frac{4n^3+2n+9}{n^2(3n+5)^2}}{frac{1}{n}}=lim_{ntoinfty}frac{nleft(4n^3+2n+9right)}{n^2(3n+5)^2}=lim_{ntoinfty}frac{4n^3+2n+9}{n(3n+5)^2}=left|frac{infty}{infty}right|=\
=lim_{ntoinfty}frac{frac{4n^3}{n^3}+frac{2n}{n^3}+frac{9}{n^3}}{frac{n(3n+5)^2}{n^3}}=lim_{ntoinfty}frac{4+frac{2}{n^2}+frac{9}{n^3}}{left(3+frac{5}{n}right)^2}=frac{4+0+0}{(3+0)^2}=frac{4}{9}.
$$

Так как $0<frac{4}{9}<infty$, то ряды $sumlimits_{n=1}^{infty}frac{4n^3+2n+9}{n^2(3n+5)^2}$ и $sumlimits_{n=1}^{infty}frac{1}{n}$ сходятся либо расходятся одновременно. Так как ряд $sumlimits_{n=1}^{infty}frac{1}{n}$ расходится, то одновременно с ним будет расходиться и ряд $sumlimits_{n=1}^{infty}frac{4n^3+2n+9}{n^2(3n+5)^2}$.

Ответ: ряд расходится.

Пример №3

Исследовать ряд $sumlimits_{n=1}^{infty}frac{5n^2-3}{sqrt[3]{7n^{10}+2n^3-4}}$ на сходимость.

Решение

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=frac{5n^2-3}{sqrt[3]{7n^{10}+2n^3-4}}$. Сразу обращаем внимание, что $u_n > 0$, т.е. наш ряд положительный. Точно так же, как и в предыдущих примерах, можно проверить выполнение необходимого условия сходимости, однако эта проверка лишь покажет, что $lim_{ntoinfty}u_n=0$. Т.е. ничего определённого про сходимость ряда сказать нельзя и нужно использовать иные критерии.

Для проверки сходимости заданного ряда с помощью признаков сравнения для начала составим ряд, с которым станем сравнивать. Попробуем отбросить «лишние» элементы числителя и знаменателя точно так же, как это было сделано в примерах №1 и №2. Останется у нас такая дробь:

$$frac{5n^2}{sqrt[3]{7n^{10}}}=frac{5}{sqrt[3]{7}}cdotfrac{n^2}{n^{frac{10}{3}}}=frac{5}{sqrt[3]{7}}cdotfrac{1}{n^{frac{10}{3}-2}}=
frac{5}{sqrt[3]{7}}cdotfrac{1}{n^{frac{4}{3}}}.$$

Вот с рядом $sumlimits_{n=1}^{infty}frac{1}{n^{frac{4}{3}}}$ мы и станем сравнивать заданный ряд. Так как $frac{4}{3} > 1$, то ряд $sumlimits_{n=1}^{infty}frac{1}{n^{frac{4}{3}}}$ сходится. Следовательно, и наш ряд будет сходиться, нам осталось лишь показать это формально с помощью признаков сравнения.

Решение с помощью первого признака сравнения

Неформальными рассуждениями выше мы пришли к выводу, что наш ряд сходится. Для этого случая применяется второй пункт первого признака сравнения. Нам нужно показать, что общий член нашего ряда удовлетворяет неравенству $frac{5n^2-3}{sqrt[3]{7n^{10}+2n^3-4}}≤ v_n$ и ряд $sumlimits_{n=1}^{infty}v_n$ сходится. Тогда и заданный нам ряд будет сходиться.

Станем увеличивать дробь $frac{5n^2-3}{sqrt[3]{7n^{10}+2n^3-4}}$. Наша цель: привести данную дробь к виду $frac{1}{n^{frac{4}{3}}}$.

Чтобы увеличить данную дробь, для начала увеличим числитель. Если мы отбросим число (-3), то числитель станет больше. А значит и сама дробь увеличится:

$$
frac{5n^2-3}{sqrt[3]{7n^{10}+2n^3-4}}< frac{5n^2}{sqrt[3]{7n^{10}+2n^3-4}}
$$

Поработаем с знаменателем. Если мы его уменьшим, то дробь увеличится. Так как $n≥ 1$, то $7n^{10}-4≥ 7n^{10}-4n^{10}=3n^{10}$. Итак, если мы вместо $7n^{10}-4$ запишем $3n^{10}$, то знаменатель уменьшится, а дробь увеличится:

$$
frac{5n^2-3}{sqrt[3]{7n^{10}+2n^3-4}}< frac{5n^2}{sqrt[3]{7n^{10}+2n^3-4}}≤ frac{5n^2}{sqrt[3]{3n^{10}+2n^3}}
$$

Теперь сделаем так: выкинем из знаменателя слагаемое $2n^3$. Тем самым мы уменьшим знаменатель, а саму дробь увеличим:

$$
frac{5n^2-3}{sqrt[3]{7n^{10}+2n^3-4}}< frac{5n^2}{sqrt[3]{7n^{10}+2n^3-4}}≤ frac{5n^2}{sqrt[3]{3n^{10}+2n^3}} < frac{5n^2}{sqrt[3]{3n^{10}}}=
frac{5}{sqrt[3]{3}}cdotfrac{1}{n^{frac{4}{3}}}.
$$

Так как ряд $sumlimits_{n=1}^{infty}frac{1}{n^{frac{4}{3}}}$ сходится, то будет сходиться и ряд $sumlimits_{n=1}^{infty}left(frac{5}{sqrt[3]{3}}cdotfrac{1}{n^{frac{4}{3}}}right)$. Так как ряд $sumlimits_{n=1}^{infty}left(frac{5}{sqrt[3]{3}}cdotfrac{1}{n^{frac{4}{3}}}right)$ сходится и $frac{5n^2-3}{sqrt[3]{7n^{10}+2n^3-4}}<frac{5}{sqrt[3]{3}}cdotfrac{1}{n^{frac{4}{3}}}$, то согласно первому признаку сравнения (пункт №2) ряд $sumlimits_{n=1}^{infty}frac{5n^2-3}{sqrt[3]{7n^{10}+2n^3-4}}$ будет сходиться.

Решение с помощью второго признака сравнения

Мы уже выяснили, что сравнивать заданный ряд нужно с сходящимся рядом $sumlimits_{n=1}^{infty}frac{1}{n^{frac{4}{3}}}$. Сравним заданный ряд $sumlimits_{n=1}^{infty}frac{5n^2-3}{sqrt[3]{7n^{10}+2n^3-4}}$ с рядом $sumlimits_{n=1}^{infty}frac{1}{n^{frac{4}{3}}}$, используя второй признак сравнения . Данный признак работает с пределом $lim_{ntoinfty}frac{u_n}{v_n}$. Оба общих члена сравниваемых рядов не равны нулю, поэтому в знаменателе можем размещать общий член любого ряда:

$$
lim_{ntoinfty}frac{frac{5n^2-3}{sqrt[3]{7n^{10}+2n^3-4}}}{frac{1}{n^{frac{4}{3}}}}=lim_{ntoinfty}frac{5n^{frac{10}{3}}-3n^{frac{4}{3}}}{sqrt[3]{7n^{10}+2n^3-4}}=left|frac{infty}{infty}right|=left|text{делим числитель и знаменатель на }n^{frac{10}{3}}right|=\

=lim_{ntoinfty}frac{frac{5n^{frac{10}{3}}}{n^{frac{10}{3}}}-frac{3n^{frac{4}{3}}}{n^{frac{10}{3}}}}{sqrt[3]{frac{7n^{10}}{n^{10}}+frac{2n^3}{n^{10}}-frac{4}{n^{10}}}}=lim_{ntoinfty}frac{5-frac{3}{n^2}}{sqrt[3]{7+frac{2}{n^7}-frac{4}{n^{10}}}}=
frac{5-0}{sqrt[3]{7+0-0}}=frac{5}{sqrt[3]{7}}.

Для вычисления предела был использован метод, изложенный в теме «Пределы с иррациональностями». Так как $0<frac{5}{sqrt[3]{7}}<infty$, то ряды $sumlimits_{n=1}^{infty}frac{5n^2-3}{sqrt[3]{7n^{10}+2n^3-4}}$ и $sumlimits_{n=1}^{infty}frac{1}{n^{frac{4}{3}}}$ сходятся либо расходятся одновременно. Так как ряд $sumlimits_{n=1}^{infty}frac{1}{n^{frac{4}{3}}}$ сходится, то одновременно с ним будет сходиться и ряд $sumlimits_{n=1}^{infty}frac{5n^2-3}{sqrt[3]{7n^{10}+2n^3-4}}$.

Ответ: ряд сходится.

Пример №4

Исследовать сходимость ряда $sumlimits_{n=1}^{infty}left(sqrt{2n+3}-sqrt{2n-1}right)$.

Решение

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=sqrt{2n+3}-sqrt{2n-1}$. Здесь сразу можно заметить, что так как $sqrt{2n+3}> sqrt{2n-1}$, то $u_n > 0$, т.е. наш ряд положительный. Можно при желании проверить выполнение необходимого условия сходимости, однако эта проверка ничего не даст (предел $lim_{ntoinfty}u_n$ вычисляется по аналогии с примером №8 на этой странице), так как $lim_{ntoinfty}u_n=0$. Перейдём к применению признаков сравнения.

Перед тем, как применять некие признаки сравнения, выражение общего члена ряда лучше немного преобразовать. Тут поможет домножение на сопряжённое выражение, т.е. на $sqrt{2n+3}+sqrt{2n-1}$. Естественно, что если мы домножаем на некое выражение, то на него же обязаны и разделить. При упрощении нам поможет формула $(a-b)(a+b)=a^2-b^2$. Итак:

$$
u_n=sqrt{2n+3}-sqrt{2n-1}=frac{left(sqrt{2n+3}-sqrt{2n-1}right)cdot left(sqrt{2n+3}+sqrt{2n-1}right)}{sqrt{2n+3}+sqrt{2n-1}}=\
=frac{left(sqrt{2n+3}right)^2-left(sqrt{2n-1}right)^2}{sqrt{2n+3}+sqrt{2n-1}}=frac{2n+3-(2n-1)}{sqrt{2n+3}+sqrt{2n-1}}=
frac{4}{sqrt{2n+3}+sqrt{2n-1}}.
$$

Теперь наш ряд имеет вид $sumlimits_{n=1}^{infty}frac{4}{sqrt{2n+3}+sqrt{2n-1}}$. Применяя рассуждения, аналогичные проведённым в предыдущих примерах, получим, что сравнивать наш ряд надо с рядом $sumlimits_{n=1}^{infty}frac{1}{sqrt{n}}$. Ряд $sumlimits_{n=1}^{infty}frac{1}{sqrt{n}}=sumlimits_{n=1}^{infty}frac{1}{n^{frac{1}{2}}}$ расходится, так как степень $frac{1}{2}≤ 1$. Значит, будет расходиться и наш ряд, осталось лишь показать это формально.

Решение с помощью первого признака сравнения

Неформальными рассуждениями выше мы пришли к выводу, что наш ряд расходится. Станем уменьшать дробь $frac{4}{sqrt{2n+3}+sqrt{2n-1}}$. Так как $sqrt{2n+3}> sqrt{2n-1}$, то записав выражение $sqrt{2n+3}$ вместо $sqrt{2n-1}$ мы увеличим знаменатель, тем самым уменьшив дробь:

$$
frac{4}{sqrt{2n+3}+sqrt{2n-1}} > frac{4}{sqrt{2n+3}+sqrt{2n+3}}=frac{4}{2sqrt{2n+3}}=frac{2}{sqrt{2n+3}}.
$$

Увеличим знаменатель ещё раз. Так как $2n+3 < 2n+7n=9n$, то заменяя выражение в знаменателе на $sqrt{9n}$ мы увеличим знаменатель, тем самым уменьшив дробь:

$$
frac{4}{sqrt{2n+3}+sqrt{2n-1}} >frac{2}{sqrt{2n+3}} > frac{2}{sqrt{9n}}=frac{2}{3}cdotfrac{1}{sqrt{n}}.
$$

Так как ряд $sumlimits_{n=1}^{infty}frac{1}{sqrt{n}}$ расходится, то будет расходиться и ряд $sumlimits_{n=1}^{infty}left(frac{2}{3}cdotfrac{1}{sqrt{n}}right)$. Так как ряд $sumlimits_{n=1}^{infty}left(frac{2}{3}cdotfrac{1}{sqrt{n}}right)$ расходится и $frac{4}{sqrt{2n+3}+sqrt{2n-1}} >frac{2}{3}cdotfrac{1}{sqrt{n}}$, то согласно первому признаку сравнения (пункт №1) ряд $sumlimits_{n=1}^{infty}frac{4}{sqrt{2n+3}+sqrt{2n-1}}$ будет расходиться.

Решение с помощью второго признака сравнения

Мы уже выяснили, что сравнивать заданный ряд нужно с расходящимся рядом $sumlimits_{n=1}^{infty}frac{1}{sqrt{n}}$. Сравним заданный ряд $sumlimits_{n=1}^{infty}frac{4}{sqrt{2n+3}+sqrt{2n-1}}$ с рядом $sumlimits_{n=1}^{infty}frac{1}{sqrt{n}}$, используя второй признак сравнения. Оба общих члена сравниваемых рядов не равны нулю, поэтому в знаменателе можем размещать общий член любого ряда:

$$
lim_{ntoinfty}frac{frac{4}{sqrt{2n+3}+sqrt{2n-1}}}{frac{1}{sqrt{n}}}=lim_{ntoinfty}frac{4sqrt{n}}{sqrt{2n+3}+sqrt{2n-1}}=left|frac{infty}{infty} right|=left|text{делим числитель и знаменатель на }sqrt{n}right|=\

=lim_{ntoinfty}frac{4}{sqrt{2+frac{3}{n}}+sqrt{2-frac{1}{n}}}=frac{4}{sqrt{2+0}+sqrt{2-0}}=frac{2}{sqrt{2}}=sqrt{2}.

Так как $0<sqrt{2}<infty$, то ряды $sumlimits_{n=1}^{infty}frac{4}{sqrt{2n+3}+sqrt{2n-1}}$ и $sumlimits_{n=1}^{infty}frac{1}{sqrt{n}}$ сходятся либо расходятся одновременно. Так как ряд $sumlimits_{n=1}^{infty}frac{1}{sqrt{n}}$ расходится, то одновременно с ним будет расходиться и ряд $sumlimits_{n=1}^{infty}frac{4}{sqrt{2n+3}+sqrt{2n-1}}$.

Ответ: ряд расходится.

Продолжение темы исследования сходимости рядов с помощью признаков сравнения рассмотрим во второй и третьей частях.

Источник

Исследовать на сходимость числовой ряд

Числовой ряд в общем виде задаётся следующей формулой: $$sum_{n=1}^infty a_n.$$ Разберем из чего состоит ряд. $a_n$ — это общий член ряда. $n$ — это переменная суммирования, которая может начинаться с нуля или любого натурального числа. Таким образом ряд расписывается следующим образом: $$sum_{n=1}^infty a_n = a_1+a_2+a_3+…$$ Слагаемые $a_1,a_2,a_3,…$ называются членами ряда. Если они неотрицательные, то ряд называется положительными числовым рядом.

Ряд расходится, если сумма его членов равна бесконечности: $$sum_{n=1}^infty n^2+1 = 2+5+10+…$$Ряд сходится, если сумма его членов равна конечному числу. Например, бесконечно убывающая геометрическая прогрессия: $$sum_{n=0}^infty frac{1}{2^n} = 1+frac{1}{2} + frac{1}{4}+frac{1}{8}+…$$ Её сумма вычисляется по следующей формуле $S = frac{A}{1-q}$, где $A$ — первый член прогрессии, а $q$ — основание. В данном случае сумма равна $S = frac{1}{1 — frac{1}{2}} = 2$.

Стоит заметить, что вычислить сумму ряда в большинстве случаев просто так не получится. Поэтому используют признаки сходимости, выполнение которых достаточно для установления сходимости ряда. Например, признаки Коши и Даламбера. Зависит это от общего члена ряда.

Необходимый признак сходимости ряда

Необходимый признак сходимости ряда нужно применять мысленно перед тем, как использовать достаточные признаки. Именно благодаря ему, можно заранее установить, что ряд расходится и не тратить время на проверку достаточными признаками. Для этого, нужно найти предел общего члена ряда и в зависимости от его значения сделать вывод.

Если ряд сходится, то $limlimits_{nto infty} a_n = 0$
Если $limlimits_{nto infty} a_n neq 0$ или не существует, то ряд расходится

ЗАМЕЧАНИЕ ! Первый пункт не работает в обратную сторону и нужно использовать достаточный признак сходимости. То есть, если предел общего члена ряда равен нулю, то это ещё не значит, что ряд сходится! Требуется использовать один из достаточных признаков сходимости.

Пример 1

Проверить сходимость числового ряда $sum_{nto 1}^infty n^2 + 1$

Решение

Применяем необходимый признак сходимости ряда $$lim_{ntoinfty} n^2+1 = infty$$Так как получили бесконечность, то значит ряд расходится и на этом исследование заканчивается. Если бы предел равнялся нулю, то действовали бы дальше применяя достаточные признаки.

Ответ

Ряд расходится

Пример 2

Проверить сходимость $sum_{nto 1}^infty frac{1}{n^2+1}$

Решение

Ищем предел общего члена ряда $$lim_{xtoinfty} frac{1}{n^2+1} = 0$$Так как предел получился равным нулю, то нельзя сказать сходится или расходится ряд. Нужно применить один из достаточных признаков сходимости.

Ответ

Требуется дополнительное исследование

Признаки сравнения

Обобщенный гармонический ряд записывается следующим образом $ sum_{n=1} ^infty frac{1}{n^p} $.

Если $ p = 1 $, то ряд $ sum_{n=1} ^infty frac{1}{n} $ расходится
Если $ p leqslant 1 $, то ряд расходится. Пример,$ sum_{n=1} ^infty frac{1}{sqrt{n}} $, в котором $ p = frac{1}{2} $
Если $ p > 1 $, то ряд сходится. Пример, $ sum_{n=1} ^infty frac{1}{sqrt{n^3}} $, в котором $ p = frac{3}{2} > 1 $

Этот ряд пригодится нам при использовании признаков сравнения, о которых пойдет речь дальше.

Признак сравнения

Пусть даны два знакоположительных числовых ряда $sum_{n=1}^infty a_n$ и $sum_{n=1}^infty b_n$, причем второй ряд сходящийся. Тогда, если начиная с некоторого номера $n$ выполнено неравенство $a_n le b_n$, то ряд $sum_{n=1}^infty a_n$ сходится вместе с $sum_{n=1}^infty b_n$.

Предельный признак сравнения

Если предел отношения общих членов двух рядов $sum_{n=1}^infty a_n$ и $sum_{n=1}^infty b_n$ равен конечному числу и отличается от нуля $$lim_{ntoinfty} frac{a_n}{b_n} = A,$$то оба ряда сходятся или расходятся одновременно.

ЗАМЕЧАНИЕ. Предельный признак удобно применять когда хотя бы один из общих членов ряда представляет собой многочлен.

Пример 3

Исследовать сходимость ряда с помощью признака сравнения $$sum_{n=1}^infty frac{1}{n^3+n^2+1}$$

Решение

Проверяем ряд на необходимый признак сходимости и убеждаемся в его выполнении $$lim_{ntoinfty} frac{1}{n^3+n^2+1} = 0.$$

Теперь данный ряд нужно сравнить с одним из гармонических рядов. В данном случае видим, что в знаменателе старшая степень $n^3$, значит подойдет гармонический ряд $frac{1}{n^3}$, а он как известно сходится. Но нужно дополнительно мысленно проверить, что выполняется неравенство $n^3 le n^3+n^2+1$. Убедившись в этом получаем, что $$frac{1}{n^3+n^2+1} le frac{1}{n^3}.$$Это означает, что $sum_{n=1}^infty frac{1}{n^3+n^2+1}$ сходится.

Ответ

Ряд сходится

Пример 4

Исследовать сходимость ряда с помощью признака сравнения $$sum_{n=1}^infty frac{1}{n^2-2n}$$

Решение

Воспользуемся предельным признаком сравнения. Сравним данный ряд со сходящимся рядом $sum_{n=1}^infty frac{1}{n^2}$. Найти предел отношения общих членов двух рядов $$lim_{ntoinfty} frac{frac{1}{n^2}}{frac{1}{n^2-2n}} = lim_{ntoinfty} frac{n^2-2n}{n^2} =$$Выносим за скобку $n^2$ и сокращаем на него числитель и знаменатель $$lim_{ntoinfty} frac{n^2(1-frac{2}{n})}{n^2} = lim_{ntoinfty} (1-frac{2}{n}) = 1.$$ Итак, получили конечное число отличное от нуля, значит оба ряда сходятся одновременно.

Ответ

Ряд сходится

Признак Даламбера

Признак рекомендуется использовать, если в общем члене ряда есть:

Число в степени. Например, $2^n, 3^{n+1}$
Присутствует факториал. Например, $(n+1)!,(2n-3)!$

Для исследования сходимости ряда по признаку Даламбера нужно найти предел отношения двух членов ряда: $$lim_{ntoinfty} frac{a_{n+1}}{a_n} = L$$

В зависимости от значения предела делается вывод о сходимости или расходимости ряда:

При $0 le L le 1$ ряд сходится
При $L > 1$ или $L = infty$ ряд расходится
При $L = 1$ признак не даёт ответа и нужно пробовать другой

Пример 5

Исследовать ряд на сходимость по признаку Даламбера $$sum_{n=1}^infty frac{2^{n+1}}{n!}$$

Решение

Общий член ряда $a_n = frac{2^{n+1}}{n!}$, тогда следующий член ряда будет $$a_{n+1} = frac{2^{(n+1)+1}}{(n+1)!} = frac{2^{n+2}}{(n+1)!}$$

Теперь находим предел предыдущего и последующего членов ряда $$L=lim_{ntoinfty} frac{a_{n+1}}{a_n} = lim_{ntoinfty} frac{frac{2^{n+2}}{(n+1)!}}{frac{2^{n+1}}{n!}} = lim_{ntoinfty} frac{2^{n+2} n!}{(n+1)! 2^{n+1}}$$ Выполняем сокращение на $2^{n+1}$ и $n!$ и находим значение предела $$L=lim_{ntoinfty} frac{2}{n+1} = 0$$ Так как предел равен нулю ($L=0$), то ряд сходится по признаку Даламбера.

Ответ

Числовой ряд сходится

Пример 6

Исследовать сходимость ряда по признаку Даламбера $$sum_{n=1}^infty frac{3^{n+1}}{sqrt{2n+5}}$$

Решение

Начинаем с того, что выписываем общий член ряда $$a_n = frac{3^{n+1}}{sqrt{2n+5}}.$$

Подставляем в него $n = n + 1$ и раскрываем скобки $$a_{n+1} = frac{3^{(n+1)+1}}{sqrt{2(n+1)+5}} = frac{3^{n+2}}{sqrt{2n+7}}.$$

Находим отношение следующего общего члена к предыдущему и упрощаем $$frac{a_{n+1}}{a_n} = frac{frac{3^{n+2}}{sqrt{2n+7}}}{frac{3^{n+1}}{sqrt{2n+5}}} = frac{(3^{n+2})sqrt{2n+5}}{sqrt{2n+7}(3^{n+1})} = frac{3sqrt{2n+5}}{sqrt{2n+7}}$$

Теперь вычисляем предел последней дроби, чтобы проверить признаком Даламбера сходимость. Для этого сократим числитель и знаменатель на $n$ $$L = limlimits_{ntoinfty} frac{3sqrt{2n+5}}{sqrt{2n+7}} = 3limlimits_{ntoinfty} frac{sqrt{2+frac{5}{n}}}{sqrt{2+frac{7}{n}}} = 3frac{sqrt{2}}{sqrt{2}} = 3.$$

Так как получился $L > 0$, то по признаку Даламбера представленный ряд расходится.

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

Ряд расходится

Радикальный признак Коши

Для установления сходимости ряда по радикальному признаку Коши нужно вычислить предел корня $n$ степени из общего члена ряда $$L = limlimits_{ntoinfty} sqrt[n]{a_n}.$$

Если $L<1$, то ряд сходится,
если $L>1$, то ряд расходится,
если $L=1$, то признак не даёт ответа о сходимости.

Применяется данный признак в случаях, когда общий член ряда находится в степени содержащей $n$.

Пример 7

Исследовать ряд на сходимость $$sum_{n=1}^infty bigg(frac{3n+1}{2n+7}bigg)^{3n}.$$

Решение

Так как у общего члена есть тепень, в составе которой, присутствует $n$, то есть смысл попробовать применить радикальный признак сходимости Коши. Для этого, извлекаем корень $n$ степени из общего члена. $$sqrt[n]{bigg(frac{3n+1}{2n+7}bigg)^{3n}} = bigg(frac{3n+1}{2n+7}bigg)^3.$$

Теперь вычисляем предел полученного выражения. $$L = limlimits_{ntoinfty} bigg(frac{3n+1}{2n+7}bigg)^3 = limlimits_{ntoinfty}frac{(3n+1)^3}{(2n+7)^3}$$

Осталось вынести за скобки $n^3$ одновременно в числетеле и знаменателе. $$L=limlimits_{ntoinfty} frac{n^3(3+frac{1}{n})^3}{n^3(2+frac{7}{n})^3} = limlimits_{ntoinfty} frac{(3+frac{1}{n})^3}{2+frac{7}{n}} = frac{3}{2}.$$

Делаем вывод: так как $L > 1$, то представленный ряд расходится.

Ответ

Ряд расходится

Пример 8

Исследовать сходимость ряда $$sum_{n=1}^infty frac{1}{3^n} bigg(frac{n}{n+1}bigg)^n.$$

Решение

Выписываем общий член ряда и извлекаем из него корень $n$ степени. $$sqrt[n]{frac{1}{3^n} bigg(frac{n}{n+1}bigg)^n} = frac{1}{3}frac{n}{n+1}$$

Вычисляем предел $$L = limlimits_{ntoinfty} frac{1}{3}frac{n}{n+1} = frac{1}{3} cdot 1 = frac{1}{3}.$$

Так как предел меньше единицы $L = frac{1}{3} < 1$, то данный ряд сходится.

Ответ

Ряд сходится

Источник

Определение
.
Числовой ряд называется знакоположительным,
если u_n>0
при всех n=1,2,3…
.

Нахождение
суммы ряда S=

часто
связано с большими техническими
трудностями. В таких случаях сумму
находят приближённо: S≈S_n.
Последнее равенство тем точнее, чем
больше n,
при условии, что ряд сходится. Сходимость
или расходимость ряда во многих случаях
можно установить с помощью достаточных
признаков сходимости числовых рядов.
В этом параграфе будем рассматривать
знакоположительные числовые ряды. Для
таких рядов частичные суммы S₁,
S₂,
…,S_n,…
образуют возрастающую числовую
последовательность S₁<S₂<…<S_n<…
.

Возможны
два случая:

1) последовательность
частичных сумм неограничена; в этом
случае

=∞
и ряд расходится;

2) последовательность
частичных сумм ограничена, то есть
существует такое число С>0,
что S_n<C
при
любых n=1,2,…
. В этом случае существует конечный
предел

,
следовательно, ряд сходится.

Таким
образом, для доказательства сходимости
знакоположительного числового ряда
достаточно доказать ограниченность
последовательности его частичных сумм.

Теорема.
(Признак
сравнения)

Пусть
даны два знакоположительных числовых
ряда

(7)

(8)

причём
u_n≤v_n
при любых n=1,2,…
.

Тогда: 1.
Если ряд (8) сходится, то сходится и ряд
(7);

2.
Если ряд (7) расходится, то расходится и
ряд (8).

Доказательство.
Обозначим n-е
частичные суммы рядов (7) и (8) через S_n
и s_n
соответственно. Пусть ряд (8) сходится.
Это значит, что существует конечный

=s.
По условию теоремы 0< u_n≤v_n,
поэтому S_n<s_n<s
при всех n=1,2,…
, то есть последовательность {S_n}
ограничена, следовательно, ряд (7)
сходится. Пусть теперь ряд (7) расходится,
то есть

=∞.
Тогда из неравенства S_n<s_n
следует, что и

=∞,
следовательно, ряд (8) расходится. Теорема
доказана.

Замечания.
1. В
силу теоремы 1 признак сравнения
справедлив и в случае, если u_n≤v_n
начиная с некоторого номера к,
то есть при n≥k.

2. Для
использования признака сравнения нужно
иметь для сравнения ряды, про которые
заранее известно, сходятся они или
расходятся. В качестве таких рядов можно
использовать сходящуюся бесконечно
убывающую геометрическую прогрессию,
а также обобщённые гармонические ряды

где к
– действительное
число. Несколько позже будет доказано,
что при к≤1
такие ряды расходятся, а при k>1
сходятся. При к=1
получаем уже упоминавшийся расходящийся
гармонический ряд.

Пример

Исследовать
на сходимость ряд

.Рассмотрим
расходящийся ряд

Он
расходится, так как получен из
гармонического ряда отбрасыванием
u₁=1.
Так как ln(n+1)<n+1
при любом n=1,2,…,
то

поэтому
данный ряд расходится по признаку
сравнения.

Теорема

(Предельный признак сравнения)

Пусть
даны два знакоположительных числовых
ряда (7) и (8). Если существует конечный
предел

≠0,
то ряды (7) и (8) сходятся или расходятся
одновременно.

Доказательство.
По условию теоремы существует конечный
предел

.
Это означает, что для любого положительного
числа Е
существует такой номер N,
что для всех номеров n≥N
выполняется условие

Последнее неравенство равносильно
двойному неравенству –E<

—A<E
или A—E<

<A+E
или

(9)

Неравенство
(9) верно при любом E>0.
Выберем поэтому Е
так, чтобы выполнялось А-Е>0.
Если ряд (8) сходится, то сходится и ряд

по теореме 2. Но тогда по признаку
сравнения, учитывая (9), сходится и ряд
(7). Если ряд (7) сходится, то по признаку
сравнения, учитывая (9), сходится ряд

и по теореме 2 сходится ряд (8). Аналогично
доказывается, учитывая (9), что из
расходимости одного из рядов следует
расходимость другого ряда. Докажите
эту часть самостоятельно.

Замечание.
Предельный признак сравнения рекомендуется
применять в тех случаях, когда общий
член ряда представляет собой отношение
степенных функций. Для сравнения
выбирается обобщённый гармонический
ряд, общий член которого равен отношению
старших степеней числителя и знаменателя
общего члена данного ряда.

Пример.

Исследовать
на сходимость ряд

Здесь u_n=

Возьмём
для сравнения ряд с общим членом v_n=

то
есть расходящийся гармонический ряд

Применим предельный признак сравнения.

¹0,
следовательно,
данный ряд расходится по предельному
признаку сравнения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Необходимый признак сходимости как первый из специальных признаков, вообще говоря, не даст возможности судить о том, сходится данный ряд или нет. В этом мы убедились, рассматривая в лекции 32 ряд 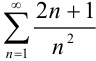(пример 32.6.). Необходимый признак для него выполняется, но исследование сходимости требует дополнительной проработки. В решении вопросов исследования сходимости данного ряда и других рядов хорошим аппаратом являются так называемые достаточные признаки сходимости. К ним относятся признаки сравнения, Даламбера, радикальный и интегральный Коши.

Рассмотрим их для положительных числовых рядов. Числовой ряд с неотрицательными членами называется положительным (знакоположительным). Заметим, что исследование сходимости отрицательных рядов (рядов с не положительными членами) осуществляется с помощью тех же достаточных признаков. Это связано с тем, что отрицательный ряд переходит в положительный путем умножения его на (-1), что в силу известного свойства (свойство 2 лекции 32), не влияет на сходимость ряда.

Признак сравнения позволяет исследовать положительный ряд на сходимость путем сравнения его с другим («эталонным») рядом, о котором известно, сходится он или нет.

Сформулируем признак без доказательства.

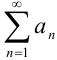
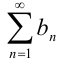
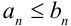
Признак сравнения: Пусть даны два положительных ряда и . Если, начиная с некоторого номера, выполняется неравенство , то

Другими словами,

если общий член исследуемого ряда меньше общего члена сходящегося ряда, то исследуемый ряд сходится;
если общий член исследуемого ряда больше общего члена расходящегося ряда, то исследуемый ряд расходится.

Обратимся к примерам использования признака сравнения для исследования сходимости положительных рядов.

Пример №33.1.

Исследуйте ряд 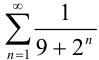на сходимость, применяя признак сравнения.

Решение:

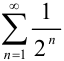
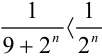
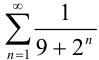
Сравним данный ряд с рядом геометрической прогрессии , сходимость которого мы установили в примере 32.3. лекции 32. Имеем: . Таким образом, общий член нашего ряда меньше общего члена сходящегося ряда. Следовательно, по признаку сравнения, ряд сходится.

Ответ: 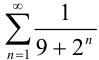сходится.

Пример №33.2.

Исследуйте ряд 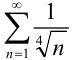на сходимость, применяя признак сравнения.

Решение:

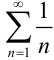
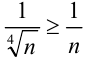
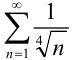
Сравним данный ряд с гармоническим рядом , который расходится (лекция 32). Имеем: . Таким образом, общий член нашего ряда больше общего члена расходящегося ряда. Следовательно, по признаку сравнения, ряд расходится.

Ответ: 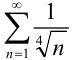расходится.

Признак сравнения позволяет исследовать сходимость положительных рядов, если удастся сравнить их с «эталонными» рядами, поведение которых в смысле сходимости известно.

В качестве «эталонных» обычно используют следующие ряды:

1. — расходящийся гармонический ряд;

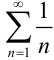
2. , если — расходящийся обобщенный гармонический ряд,

, если — сходящийся обобщенный гармонический ряд;

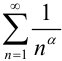
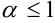
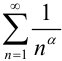
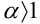
3. , если — расходящийся ряд геометрической прогрессии,

, если — сходящийся ряд геометрической прогрессии.

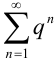
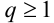
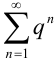
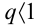
Пример №33.3.

Исследуйте ряд 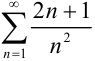на сходимость.

Решение:

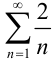
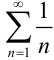
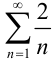
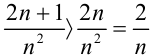
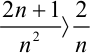
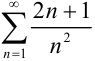
Рассмотрим ряд . Поскольку он получается из расходящегося гармонического ряда умножением на 2, то, согласно свойству 2 числовых рядов (лекция 32), он расходится. Сравним исследуемый ряд с рядом . Имеем: , т.е. . Таким образом, общий член исследуемого ряда больше общего члена расходящегося ряда. Следовательно, по признаку сравнения, ряд расходится.

Ответ: 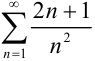расходится.

Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:

Предмет высшая математика

Другие лекции по высшей математике, возможно вам пригодятся:

Источник

Сходимость ряда и признаки сходимости числовых рядов

Определение сходимости ряда. Сумма ряда
Признаки сходимости и расходимости числовых рядов

Необходимый признак сходимости и критерий Коши
Признак сравнения
Предельный признак сравнения
Признак Даламбера
Признак Коши
Интегральный признак Коши

Определение сходимости ряда. Сумма ряда

Числовой ряд

называется сходящимся, если его частичная сумма

имеет предел при

. Величина

называется при этом суммой ряда, а число

остатком ряда.

Если предел

не существует, то ряд называется расходящимся.

Пример 1

Исследовать на сходимость
ряд, рассматривая последовательность его частичных сумм. В случае сходимости
найти сумму ряда.

Решение

Преобразуем выражение под
знаком суммы:

Данный ряд — сумма
геометрических прогрессий со знаменателями

ряд сходится

Признаки сходимости и расходимости числовых рядов

Необходимый признак сходимости и критерий Коши

Если ряд сходится, то

Обратное утверждение неверно

Критерий Коши

Для сходимости ряда необходимо и достаточно, чтобы для всякого
положительного числа

можно подобрать такое

,
чтобы при

и любом положительном

выполнялось неравенство

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Сходимость или расходимость ряда не нарушится, если прибавить или
отбросить конечное число его членов.

Пример 2

Исследовать на сходимость
ряд:

Решение

Воспользуемся
необходимым признаком сходимости:

Необходимый
признак сходимости не выполняется — ряд расходится.

Признак сравнения

Если

,
начиная с некоторого

,
и ряд

сходится, то ряд

также сходится. Если ряд (**) расходится,
то расходится и ряд (*).

В качестве рядов для сравнения удобно, в частности, выбирать
геометрическую прогрессию:

которая сходится при

и расходится при

,
и гармонический ряд

являющийся рядом расходящимся.

Пример 3

Решение

Этот ряд сходится, так как

Причем геометрическая прогрессия

знаменатель которой

,
сходится

Предельный признак сравнения

Если существует конечный и отличный от нуля предел

(в частности, если

,
то ряды

сходятся или расходятся одновременно.

Пример 4

Ряд

Решение

Сравним заданный ряд с расходящимся гармоническим рядом

Таким образом ряды одновременно
расходятся, так как найденный предел конечный и отличный от нуля.

Признак Даламбера

Пусть

(начиная с некоторого

)
и существует предел

Тогда ряд

сходится, если

,
и расходится, если

.
Если

,
то вопрос о сходимости ряда остается открытым.

Пример 5

Решение

Воспользуемся признаком
Даламбера

Ряд
сходится

Признак Коши

Пусть

(начиная с некоторого

)
и существует предел

Тогда ряд

сходится, если

,
и расходится, если

.
Если

,
то вопрос о сходимости ряда остается открытым.

Пример 6

Решение

Воспользуемся признаком
Коши:

Ряд расходится

Интегральный признак Коши

Если

,
где функция

положительна, монотонно убывает и непрерывна
при

,
то ряд

и интеграл

сходится или расходится одновременно.

С помощью интегрального признака доказывается, что ряд Дирихле

сходится, если

,
и расходится, если

.
Сходимость многих рядов можно исследовать при помощи сравнения с
соответствующим рядом Дирихле.

Пример 7

Исследовать на сходимость
числовой ряд:

Решение

Используем интегральный признак Коши.

Соответствующий интеграл:

расходится, следовательно, расходится исходный ряд

Источник