Random converter
Перевести единицы: микрофарад [мкФ] в фарад [Ф]
1 микрофарад [мкФ] = 1E-06 фарад [Ф]
Подробнее об электрической емкости
Сенсорный экран этого планшета выполнен с использованием проекционно-емкостной технологии.
Общие сведения
Использование емкости
Конденсаторы — устройства для накопления заряда в электронном оборудовании
Историческая справка
Маркировка конденсаторов
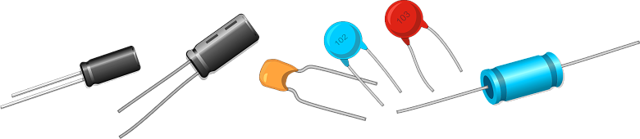
Примеры конденсаторов
Ионисторы
Емкостные сенсорные экраны
Поверхностно-емкостные экраны
Проекционно-емкостные экраны
Общие сведения
Измерение емкости конденсатора номинальной емкостью 10 мкФ с помощью осциллографа-мультиметра
Электрическая емкость — это величина, характеризующая способность проводника накапливать заряд, равная отношению электрического заряда к разности потенциалов между проводниками:
C = Q/∆φ
Здесь Q — электрический заряд, измеряется в кулонах (Кл), — разность потенциалов, измеряется в вольтах (В).
В системе СИ электроемкость измеряется в фарадах (Ф). Данная единица измерения названа в честь английского физика Майкла Фарадея.
Фарад является очень большой емкостью для изолированного проводника. Так, металлический уединенный шар радиусом в 13 радиусов Солнца имел бы емкость равную 1 фарад. А емкость металлического шара размером с Землю была бы примерно 710 микрофарад (мкФ).
Так как 1 фарад — очень большая емкость, поэтому используются меньшие значения, такие как: микрофарад (мкФ), равный одной миллионной фарада; нанофарад (нФ), равный одной миллиардной; пикофарад (пФ), равный одной триллионной фарада.
В системе СГСЭ основной единицей емкости является сантиметр (см). 1 сантиметр емкости — это электрическая емкость шара с радиусом 1 сантиметр, помещенного в вакуум. СГСЭ — это расширенная система СГС для электродинамики, то есть, система единиц в которой сантиметр, грам, и секунда приняты за базовые единицы для вычисления длины, массы и времени соответственно. В расширенных СГС, включая СГСЭ, некоторые физические константы приняты за единицу, чтобы упростить формулы и облегчить вычисления.
Использование емкости
Конденсаторы — устройства для накопления заряда в электронном оборудовании
Условные обозначения конденсаторов на принципиальных схемах
Понятие электрической емкости относится не только к проводнику, но и к конденсатору.
Конденсатор — система двух проводников, разделенных диэлектриком или вакуумом. В простейшем варианте конструкция конденсатора состоит из двух электродов в виде пластин (обкладок). Конденсатор (от лат. condensare — «уплотнять», «сгущать») — двухэлектродный прибор для накопления заряда и энергии электромагнитного поля, в простейшем случае представляет собой два проводника, разделённые каким-либо изолятором. Например, иногда радиолюбители при отсутствии готовых деталей изготавливают подстроечные конденсаторы для своих схем из отрезков проводов разного диаметра, изолированных лаковым покрытием, при этом более тонкий провод наматывается на более толстый. Регулируя число витков, радиолюбители точно настраивают контура аппаратуры на нужную частоту. Примеры изображения конденсаторов на электрических схемах приведены на рисунке.
Параллельная RLC-цепь, состоящая из резистора, конденсатора и катушки индуктивности
Историческая справка
Еще 275 лет назад были известны принципы создания конденсаторов. Так, в 1745 г. в Лейдене немецкий физик Эвальд Юрген фон Клейст и нидерландский физик Питер ван Мушенбрук создали первый конденсатор — «лейденскую банку» — в ней диэлектриком были стенки стеклянной банки, а обкладками служили вода в сосуде и ладонь экспериментатора, державшая сосуд. Такая «банка» позволяла накапливать заряд порядка микрокулона (мкКл). После того, как ее изобрели, с ней часто проводили эксперименты и публичные представления. Для этого банку сначала заряжали статическим электричеством, натирая ее. После этого один из участников прикасался к банке рукой, и получал небольшой удар током. Известно, что 700 парижских монахов, взявшись за руки, провели лейденский эксперимент. В тот момент, когда первый монах прикоснулся к головке банки, все 700 монахов, сведенные одной судорогой, с ужасом вскрикнули.
В Россию «лейденская банка» пришла благодаря русскому царю Петру I, который познакомился с Мушенбруком во время путешествий по Европе, и подробнее узнал об экспериментах с «лейденской банкой». Петр I учредил в России Академию наук, и заказал Мушенбруку разнообразные приборы для Академии наук.
В дальнейшем конденсаторы усовершенствовались и становились меньше, а их емкость — больше. Конденсаторы широко применяются в электронике. Например, конденсатор и катушка индуктивности образуют колебательный контур, который может быть использован для настройки приемника на нужную частоту.
Существует несколько типов конденсаторов, отличающихся постоянной или переменной емкостью и материалом диэлектрика.
Примеры конденсаторов
Оксидные конденсаторы в блоке питания сервера.
Промышленность выпускает большое количество типов конденсаторов различного назначения, но главными их характеристиками являются ёмкость и рабочее напряжение.
Типичные значение ёмкости конденсаторов изменяются от единиц пикофарад до сотен микрофарад, исключение составляют ионисторы, которые имеют несколько иной характер формирования ёмкости – за счёт двойного слоя у электродов – в этом они подобны электрохимическим аккумуляторам. Суперконденсаторы на основе нанотрубок имеют чрезвычайно развитую поверхность электродов. У этих типов конденсаторов типичные значения ёмкости составляют десятки фарад, и в некоторых случаях они способны заменить в качестве источников тока традиционные электрохимические аккумуляторы.
Вторым по важности параметром конденсаторов является его рабочее напряжение. Превышение этого параметра может привести к выходу конденсатора из строя, поэтому при построении реальных схем принято применять конденсаторы с удвоенным значением рабочего напряжения.
Для увеличения значений ёмкости или рабочего напряжения используют приём объединения конденсаторов в батареи. При последовательном соединении двух однотипных конденсаторов рабочее напряжение удваивается, а суммарная ёмкость уменьшается в два раза. При параллельном соединении двух однотипных конденсаторов рабочее напряжение остаётся прежним, а суммарная ёмкость увеличивается в два раза.
Третьим по важности параметром конденсаторов является температурный коэффициент изменения ёмкости (ТКЕ). Он даёт представление об изменении ёмкости в условиях изменения температур.
В зависимости от назначения использования, конденсаторы подразделяются на конденсаторы общего назначения, требования к параметрам которых некритичны, и на конденсаторы специального назначения (высоковольтные, прецизионные и с различными ТКЕ).
Маркировка конденсаторов
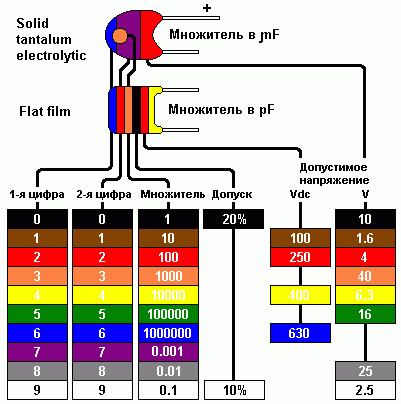
Подобно резисторам, в зависимости от габаритов изделия, может применяться полная маркировка с указанием номинальной ёмкости, класса отклонения от номинала и рабочего напряжения. Для малогабаритных исполнений конденсаторов применяют кодовую маркировку из трёх или четырёх цифр, смешанную цифро-буквенную маркировку и цветовую маркировку.
Соответствующие таблицы пересчёта маркировок по номиналу, рабочему напряжению и ТКЕ можно найти в Интернете, но самым действенным и практичным методом проверки номинала и исправности элемента реальной схемы остаётся непосредственное измерение параметров выпаянного конденсатора с помощью мультиметра.
Оксидный конденсатор собран из двух алюминиевых лент и бумажной прокладки с электролитом. Одна из алюминиевых лент покрыта слоем оксида алюминия и служит анодом. Катодом служит вторая алюминиевая лента и бумажная лента с электролитом. На алюминиевых лентах видны следы электрохимического травления, позволяющего увеличить их площадь поверхности, а значит и емкость конденсатора.
Предупреждение: поскольку конденсаторы могут накапливать большой заряд при весьма высоком напряжении, во избежание поражения электрическим током необходимо перед измерением параметров конденсатора разряжать его, закоротив его выводы проводом с высоким сопротивлением внешней изоляции. Лучше всего для этого подходят штатные провода измерительного прибора.
Оксидные конденсаторы: данный тип конденсатора обладает большой удельной емкостью, то есть, емкостью на единицу веса конденсатора. Одна обкладка таких конденсаторов представляет собой обычно алюминиевую ленту, покрытую слоем оксида алюминия. Второй обкладкой служит электролит. Так как оксидные конденсаторы имеют полярность, то принципиально важно включать такой конденсатор в схему строго в соответствии с полярностью напряжения.
Твердотельные конденсаторы: в них вместо традиционного электролита в качестве обкладки используется органический полимер, проводящий ток, или полупроводник.
Трехсекционный воздушный конденсатор переменной емкости
Переменные конденсаторы: емкость может меняться механическим способом, электрическим напряжением или с помощью температуры.
Пленочные конденсаторы: диапазон емкости данного типа конденсаторов составляет примерно от 5 пФ до 100 мкФ.
Имеются и другие типы конденсаторов.
Ионисторы
В наши дни популярность набирают ионисторы.
Ионистор (суперконденсатор) — это гибрид конденсатора и химического источника тока, заряд которого накапливается на границе раздела двух сред — электрода и электролита. Начало созданию ионисторов было положено в 1957 году, когда был запатентован конденсатор с двойным электрическим слоем на пористых угольных электродах. Двойной слой, а также пористый материал помогли увеличить емкость такого конденсатора за счет увеличения площади поверхности. В дальнейшем эта технология дополнялась и улучшалась. На рынок ионисторы вышли в начале восьмидесятых годов прошлого века.
С появлением ионисторов появилась возможность использовать их в электрических цепях в качестве источников напряжения. Такие суперконденсаторы имеют долгий срок службы, малый вес, высокие скорости зарядки-разрядки. В перспективе данный вид конденсаторов может заменить обычные аккумуляторы. Основными недостатками ионисторов является меньшая, чем у электрохимических аккумуляторов удельная энергия (энергия на единицу веса), низкое рабочее напряжение и значительный саморазряд.
Ионисторы применяются в автомобилях Формулы-1. В системах рекуперации энергии, при торможении вырабатывается электроэнергия, которая накапливается в маховике, аккумуляторах или ионисторах для дальнейшего использования.
Электромобиль А2В Университета Торонто. Общий вид
В бытовой электронике ионисторы применяются для стабилизации основного питания и в качестве резервного источника питания таких приборов как плееры, фонари, в автоматических коммунальных счетчиках и в других устройствах с батарейным питанием и изменяющейся нагрузкой, обеспечивая питание при повышенной нагрузке.
В общественном транспорте применение ионисторов особенно перспективно для троллейбусов, так как становится возможна реализация автономного хода и увеличения маневренности; также ионисторы используются в некоторых автобусах и электромобилях.
Электромобиль А2В Университета Торонто. Под капотом
Электрические автомобили в настоящем времени выпускают многие компании, например: General Motors, Nissan, Tesla Motors, Toronto Electric. Университет Торонто совместно с компанией Toronto Electric разработали полностью канадский электромобиль A2B. В нем используются ионисторы вместе с химическими источниками питания, так называемое гибридное электрическое хранение энергии. Двигатели данного автомобиля питаются от аккумуляторов весом 380 килограмм. Также для подзарядки используются солнечные батареи, установленные на крыше электромобиля.
Емкостные сенсорные экраны
В современных устройствах все чаще применяются сенсорные экраны, которые позволяют управлять устройствами путем прикосновения к панелям с индикаторами или экранам. Сенсорные экраны бывают разных типов: резистивные, емкостные и другие. Они могут реагировать на одно или несколько одновременных касаний. Принцип работы емкостных экранов основывается на том, что предмет большой емкости проводит переменный ток. В данном случае этим предметом является тело человека.
Поверхностно-емкостные экраны
Cенсорный экран iPhone выполнен по проекционно-емкостной технологии.
Таким образом, поверхностно-емкостный сенсорный экран представляет собой стеклянную панель, покрытую прозрачным резистивным материалом. В качестве резистивного материала обычно применяется имеющий высокую прозрачность и малое поверхностное сопротивление сплав оксида индия и оксида олова. Электроды, подающие на проводящий слой небольшое переменное напряжение, располагаются по углам экрана. При касании к такому экрану пальцем появляется утечка тока, которая регистрируется в четырех углах датчиками и передается в контроллер, который определяет координаты точки касания.
Преимущество таких экранов заключается в долговечности (около 6,5 лет нажатий с промежутком в одну секунду или порядка 200 млн. нажатий). Они обладают высокой прозрачностью (примерно 90%). Благодаря этим преимуществам, емкостные экраны уже с 2009 года активно начали вытеснять резистивные экраны.
Недостаток емкостных экранов заключается в том, что они плохо работают при отрицательных температурах, есть трудности с использованием таких экранов в перчатках. Если проводящее покрытие расположено на внешней поверхности, то экран является достаточно уязвимым, поэтому емкостные экраны применяются лишь в тех устройствах, которые защищены от непогоды.
Проекционно-емкостные экраны
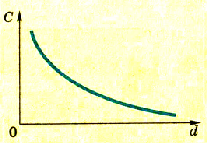
Помимо поверхностно-емкостных экранов, существуют проекционно-емкостные экраны. Их отличие заключается в том, что на внутренней стороне экрана нанесена сетка электродов. Электрод, к которому прикасаются, вместе с телом человека образует конденсатор. Благодаря сетке, можно получить точные координаты касания. Проекционно-емкостный экран реагирует на касания в тонких перчатках.
Проекционно-емкостные экраны также обладают высокой прозрачностью (около 90%). Они долговечны и достаточно прочные, поэтому их широко применяют не только в персональной электронике, но и в автоматах, в том числе установленных на улице.
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Электротехника
Электротехника — область технических наук, изучающая получение, распределение, преобразование и использование электрической энергии. Электротехника включает в себя такие области техники как электроэнергетику, электронику, системы управления, обработку сигналов и связь.
Электрическая емкость
Электрическая ёмкость — характеристика проводника, определяющая его способность накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками или величину емкости ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками.
Устройства для накопления заряда и энергии электрического поля, имеющие два вывода и обладающие высоким сопротивлением, используются в электротехнике и электронике и называются конденсаторами. Типичные значения емкости конденсаторов составляют от единиц пикофарад до десятков фарад (ионисторы). В связи с этим фарады часто используется с дольными десятичными приставками (микрофарады, пикофарады и нанофарады) и крайне редко — с кратными приставками. Для измерения емкости применяются мультиметры.
В Международной системе единиц (СИ) ёмкость измеряется в фарадах. В системе СГС в сантиметрах. 1 фарад равен ёмкости конденсатора, при которой заряд 1 кулон создаёт между его обкладками напряжение 1 вольт. 1 фарад — это очень большая емкость. Для сравнения можно сказать, что емкость Земли около 700 микрофарад. В то же время, современные ионисторы, называемые также суперконденсаторами или двухслойными электрохимическими конденсаторами, могут иметь емкость в несколько фарад при рабочем напряжении до десяти вольт.
Использование конвертера «Электрическая емкость»
На этих страницах размещены конвертеры единиц измерения, позволяющие быстро и точно перевести значения из одних единиц в другие, а также из одной системы единиц в другую. Конвертеры пригодятся инженерам, переводчикам и всем, кто работает с разными единицами измерения.
Пользуйтесь конвертером для преобразования нескольких сотен единиц в 76 категориях или несколько тысяч пар единиц, включая метрические, британские и американские единицы. Вы сможете перевести единицы измерения длины, площади, объема, ускорения, силы, массы, потока, плотности, удельного объема, мощности, давления, напряжения, температуры, времени, момента, скорости, вязкости, электромагнитные и другие.
Примечание. В связи с ограниченной точностью преобразования возможны ошибки округления. В этом конвертере целые числа считаются точными до 15 знаков, а максимальное количество цифр после десятичной запятой или точки равно 10.
Для представления очень больших и очень малых чисел в этом калькуляторе используется компьютерная экспоненциальная запись, являющаяся альтернативной формой нормализованной экспоненциальной (научной) записи, в которой числа записываются в форме a · 10x. Например: 1 103 000 = 1,103 · 106 = 1,103E+6. Здесь E (сокращение от exponent) — означает «· 10^», то есть «…умножить на десять в степени…». Компьютерная экспоненциальная запись широко используется в научных, математических и инженерных расчетах.
- Выберите единицу, с которой выполняется преобразование, из левого списка единиц измерения.
- Выберите единицу, в которую выполняется преобразование, из правого списка единиц измерения.
- Введите число (например, «15») в поле «Исходная величина».
- Результат сразу появится в поле «Результат» и в поле «Преобразованная величина».
- Можно также ввести число в правое поле «Преобразованная величина» и считать результат преобразования в полях «Исходная величина» и «Результат».
Мы работаем над обеспечением точности конвертеров и калькуляторов TranslatorsCafe.com, однако мы не можем гарантировать, что они не содержат ошибок и неточностей. Вся информация предоставляется «как есть», без каких-либо гарантий. Условия.
Если вы заметили неточность в расчётах или ошибку в тексте, или вам необходим другой конвертер для перевода из одной единицы измерения в другую, которого нет на нашем сайте — напишите нам!
Канал Конвертера единиц TranslatorsCafe.com на YouTube
Содержание:
Электроемкость:
Сообщая телу определенный заряд, мы изменяем его потенциал. Это изменение непосредственно связано со значением заряда, сообщаемого телу.
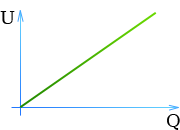
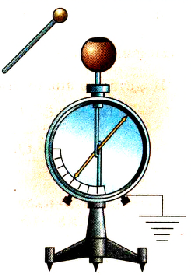
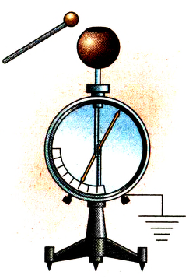
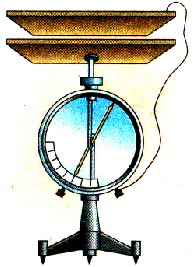
Для исследования зависимости потенциала тела от его заряда проведем опыт с электрометром, корпус которого соединен с поверхностью Земли. ‘Гикая система может измерять потенциал тела относительно Земли. Укрепим на стержне этого электрометра пустотелый металлический шар и будем сообщать ему заряд с помощью маленького металлического шарика на изоляционной ручке. Если коснуться заряженным шариком внутренней поверхности металлического шара, то весь его заряд перейдет на шар, а стрелка электрометра покажет увеличение потенциала шара. Последовательно повторяя опыт с переносом заряда на большой шар, заметим, что каждый раз его потенциал увеличивается (рис. 1.28).
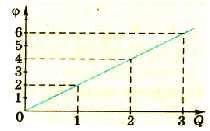
Применяя более точные способы измерения заряда и потенциала, можно установить, что потенциал возрастает пропорционально возрастанию заряда. Потенциал пропорционален заряду шара. Результаты одного из таких опытов отражены на графике (рис 1.29).
Если ни стержне электрометра укрепим шар большего (меньшего) диаметра и продолжим опыты (рис. 1.31), то увидим, что скорость зарядки изменилась, соответственно уменьшилась (увеличилась).
Процесс электризации шара большего диаметра отображен графиком на рисунке 1.32.
Сопоставив графики, которые иллюстрируют процессы зарядки шаров различных диаметров (рис. 1.30 и 1.32), увидим, что графики имеют различный наклон относительно горизонтальной оси. Это свидетельствует о том, что при одинаковых значениях заряда шары разных диаметров будут иметь разные потенциалы. Оказывается, что на князь между зарядом и потенциалом шара существенно влияют геометрические размеры шаров.
Рис. 130. Электризация шара большего диаметра
Потенциал металлического шара пропорционален его заряду; коэффициент пропорциональности для различных шаров разный.
Анализируя результаты опытов и соответствующие графики, можно сделать выводы:
- потенциал каждого шара пропорционален его заряду:
- для тел различных размеров коэффициент пропорциональности разный.
Установлено, что этот коэффициент для каждого тела имеет вполне определенное значение, что отражает способность тела накапливать электрический заряд. Физическая величина, равная отношению электрического заряда, сообщенного телу, к его потенциалу, называется электроемкостью тела.
где C — электроемкость проводника; Q — заряд; φ — потенциал.
Для измерения электроемкости в физике применяют единицу, которую называют фарад (Ф).
Тело имеет электроемкость в 1 фарад, если при изменении его заряда на 1 кулон потенциал изменяется па 1 вольт:
Электроемкость 1 фарад имеют тела, у которых при изменении заряда на 1 кулон потенциал изменяется на 1 вольт.
- 1Ф — довольно большое значение электроемкости. Например, электроемкость Земли, имеющей радиус 6400 км, составляет всего 7 ∙ 104 Ф. Поэтому на практике используют единицу электроемкости, кратную фараду:
- 1 микрофарад = 1 мкФ = 10-5 Ф.
- 1 пикофарад = 1 пФ = 10-12 Ф.
Пример:
Два шара, электроемкости которых 50 мкф и 80 мкФ, а потенциалы 120 В и 50 В соответственно, соединяют проводом. Найти потенциал шаров после соединения.
|
Дано: |
Решение |
| φ-? |
После соединения шаров произойдет перераспределение зарядов между ними так, что их потенциалы станут одинаковыми. Согласно закону сохранения электрических зарядов
Отсюда
или
Подставив значения физических величин и произведя расчеты, получим:
Ответ: после соединения шары будут иметь потенциал 77 В.
Конденсатор
Чтобы экспериментально определить электроемкость проводника, как и его потенциал, нужно создать условия, исключающие влияние всех окружающих тел, которые, влияя па тело, изменяют его потенциал и электроемкость.
Это утверждение можно проверить опытом.
Укрепим на стержне электрометра металлический шар и сообщим ему определенный заряд. Стрелка прибора отклонится от положения равновесия и покажет определенное значение потенциала относительно земли.
Поднесем к шару металлическую пластину, соединенную проводником с землей (рис. 1.32).
Pиc. 132. Заземленная металлическая пластина влияет на электроемкость шара
Показания стрелки электрометра уменьшатся. Поскольку заряд шара в опыте не изменялся, то уменьшение потенциала свидетельствует об увеличении электроемкости шара. Изменение потенциала и соответственно электроемкости шара будет наблюдаться и в случае изменения расстояния между шаром и пластиной.
Таким образом, определяя электроемкость тела, необходимо учитывать также наличие окружающих тел. Поскольку на практике это сделать трудно, то применяют систему из двух или более проводников произвольной формы, разделенных диэлектриком. В этом случае электрические свойства такой системы проводников и диэлектрика не зависят от окружающих тел. Такую систему называют конденсатором. Простейшим для изучения и расчетов является конденсатор из двух металлических пластин, разделенных диэлектриком.
Электроемкость конденсатора, в отличие от обособленного тела, определяется по разности потенциалов между пластинами:
где Q — заряд одной пластины; (φl— φ2) и ∆φ — разность потенциалов между пластинами.
Слово конденсатор обозначает накопитель. В электричестве понимают как «накопитель электрических зарядов».
Пример:
Какую электроемкость имеет конденсатор, если на его обкладках накапливается заряд 50 нКл при разности потенциалов 2,5 кВ?
|
Дано: |
Решение |
| С-? |
Подставим значения физических величин:
Ответ: электроемкость данного конденсатора 20 пФ.
Первый конденсатор был создан в 1745 г. голландским ученым Питером ван Мушенбруком, профессором Лейденского университета. Проводя опыты по электризации различных тел, он опустил проводник от кондуктора электрической машины в стеклянный графин с водой (рис. 1.33).
 |
Питер ван Мушенбрук (1692-1781) — голландский физик; работы посвящены электричеству, теплоте, оптике; изобрел первый конденсатор — лейденскую банку и провел опыты с ней. |
Pиc. 133. Из истории открытия простейшего конденсатора лейденской банки
Случайно коснувшись пальцем этого проводника, ученый ощутил сильный электрический удар. В дальнейшем жидкость заменили металлическими проводниками, укрепленными на внутренней и внешней поверхностях банки. Такой конденсатор назвали лейденской банкой. В таком первозданном виде она использовалась в лабораториях более 200 лет.
Более совершенные конденсаторы применяются в современной электротехнике и радиоэлектронике. Их можно найти в преобразователях напряжения (адаптерах), питающих постоянным электрическим током электронные приборы, в радиоприемниках и радиопередатчиках как поставные части колебательных контуров. Они применяются практически во всех функциональных узлах электронной аппаратуры. В фотовспышках конденсаторы накапливают большие заряды, необходимые для действия вспышки.
В электротехнике конденсаторы обеспечивают необходимый режим работы электродвигателей, автоматических и релейных приборов, линий электропередач и т. п.
Во многих широкодиапазонных радиоприемниках конденсаторы переменной емкости (рис. 1.34) позволяют плавно изменять собственную частоту колебательного контура н процессе поиска передачи определенной радиостанции.
Рис. 134. Конденсатор переменной емкости с воздушным диэлектриком
Весьма распространены конденсаторы варикапы, электроемкость которых можно изменять электрическим способом. Конструктивно они весьма схожи с полупроводниковыми диодами.
Конденсаторы могут быть плоскими, трубчатыми, дисковыми. В качестве диэлектрика в них используют парафинированную бумагу, слюду, воздух, пластмассы, керамику (рис. 1.35).
Рис. 1.35. Различные типы конденсаторов
Искусственно созданные диэлектрические материалы позволяют создавать конденсаторы больших емкостей при небольших размерах.
Электроемкость плоского конденсатора
Плоским конденсатором обычно называют систему плоских проводящих пластин — обкладок, разделенных диэлектриком. Благодаря простоте конструкции такого конденсатора легко рассчитывать его емкость и получать значения, подтверждаемые опытами. Для этого достаточно знать его геометрические параметры и электрические свойства диэлектрика между его пластинами. Зависимость электроемкости плоского конденсатора от указанных параметров можно исследовать в школьной лаборатории.
Создадим плоский конденсатор из двух плоских пластин. Для этого одну пластину укрепим на стержне электрометра, я другую — па изоляционной подставке, присоединив ее проводником к корпусу электрометра (рис. 1.36.). В такой системе электрометр будет измерять разность потенциалов между пластинами, образующими плоский конденсатор.
Pиc. 136. Плоский конденсатор, присоединенный к электрометру
Проводя исследования, нужно помнить, что при постоянном значении заряда на пластинах уменьшение разности потенциалов свидетельствует об увеличении электроемкости конденсатора, и наоборот.
При постоянном значении заряда на пластинах уменьшение разности потенциалов свидетельствует об увеличении электроемкости конденсатора, и наоборот.
Сообщим пластинам некоторый заряд и отметим показания стрелки прибора. Когда начнем сближать пластины, уменьшая расстояние между ними, показания стрелки начнут уменьшаться. Это будет свидетельством того, что при уменьшении расстояния между пластинами электроемкость конденсатора будет увеличиваться. При увеличении расстояния между пластинами показания стрелки будут увеличиваться, что свидетельствует об уменьшении электроемкости.
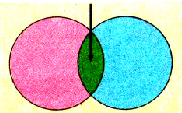
Электроемкость плоского конденсатора обратно пропорциональна расстоянию между его обкладками.
где d — расстояние между обкладками.
Эту, зависимость можно изобразить на графике как обратно пропорциональную зависимость (рис. 1.37).
Электроемкость плоского конденсатора обратно пропорциональна расстоянию между его обкладками.
Pиc. 137. График зависимости электроемкости и плоского конденсатора от расстояния между пластинами
Будем смещать одну пластину относительно другой в параллельных плоскостях, не изменяя расстояния между ними. При атом площадь перекрытия между пластинами будет изменяться (рис. 1.38). Изменение разности потенциалов, отмеченное электрометром, засвидетельствует изменение электроемкости.
Pиc. 138. При расчетах электроемкости плоского конденсатора учитывают площадь перекрытия пластин
Увеличение площади перекрытия приведет к увеличению электроемкости, при уменьшении — наоборот.
Электроемкость плоского конденсатора пропорциональна площади пластин, которые перекрываются.
где S — площадь пластин, которые перекрываются.
Электроемкость плоского конденсатора пропорциональна площади пластин, которые перекрываются.
Эту зависимость можно изобразить графиком прямой пропорциональной зависимости (рис. 1.39).
Pиc. 139. График зависимости электроемкости плоского конденсатора от площади его пластин
Возвратив пластины в первоначальное положение, внесем в пространство между обкладками пластину из диэлектрика. Электрометр отметит уменьшение разности потенциалов между пластинами, что свидетельствует об увеличении электроемкости. Если внести пластину из другого диэлектрика (другая диэлектрическая проницаемость), то изменение электроемкости будет другим.
Электроемкость плоского конденсатора зависит от диэлектрической проницаемости диэлектрика между обкладками.
где ε — диэлектрическая проницаемость диэлектрика.
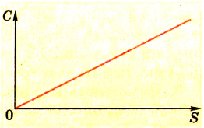
Эта зависимость изображена графиком на рисунке 1.40.
Рис. 1.40. График зависимости электроемкости плоского конденсатора от диэлектрической проницаемости диэлектрика
Результаты описанных выше исследований можно обобщить формулой электроемкости плоского конденсатора
где ε — относительная диэлектрическая проницаемость диэлектрика; ε0— электрическая постоянная; d — расстояние между пластинами; S — площадь пластины.
Электроемкость плоского конденсатора зависит от диэлектрической проницаемости диэлектрика.
Соединение конденсаторов в батареи
Для получения необходимых значений электроемкости конденсаторы соединяют в батареи. На практике встречается параллельное, последовательное и смешанное соединение конденсаторов.
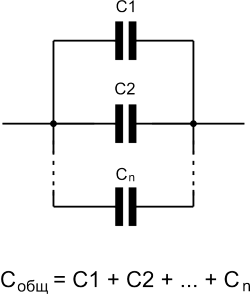
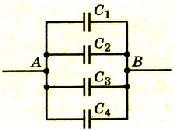
При параллельном соединении конденсаторов все обкладки соединяются в две группы, в каждую из которых входит по одной обкладке каждого конденсатора. На рисунке 1.41 приведена схема такого соединения. При таком соединении каждая группа обкладок имеет одинаковый потенциал.
Pиc 1.41. Схема параллельного соединения конденсаторов
Если батарею параллельно соединенных конденсаторов зарядить, то между обкладками каждого конденсатора будет одинаковая разность потенциалов. Общий заряд батареи будет равен сумме зарядов каждого из конденсаторов, входящих в батарею:
Если учесть, что 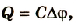
или
Электроемкость батареи параллельно соединенных конденсаторов равна сумме электроемкостей всех конденсаторов.
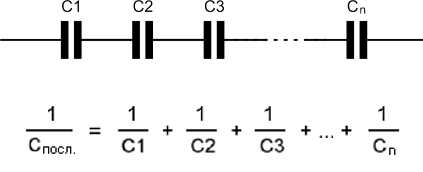
При последовательном соединении конденсаторов соединяются между собой только две пластины разных конденсаторов. Если в каждом конденсаторе пластины обозначить буквами А и В, то при последовательном соединении пластина B1 будет соединена с пластиной A2, пластина B2 -с пластиной А3 и т. д. (рис. 1.43).
Если цепочку последовательно соединенных конденсаторов присоединить к источнику тока, то об-
кладка A1 и обкладка B1 будут иметь одинаковые по значению заряды +Q и -Q. Благодаря этому все обкладки внутри цепочки будут иметь такие же, но попарно противоположные по знаку заряды:
Pиc. 1.42. Последовательное соединение конденсаторов
Вместе с тем общая разность потенциалов на концах цепочки будет равна сумме разностей потенциалов на каждом конденсаторе:
Учитывая, что 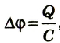
Разделим левую и правую части равенства на Q:
При последовательном соединении конденсаторов обратное значение электроемкости цепочки равно сумме обратных значений электроемкостей каждого из конденсаторов.
При последовательном соединении конденсаторов обратное значение электроемкости цепочки равно с
При последовательном соединении конденсаторов обратное значение электроемкости цепочки равно сумме обратных значений электроемкостей каждого из конденсаторов.
При последовательном соединении конденсаторов разной электроемкости C1, C2, C3, … Сn общая электроемкость С будет меньше электроемкости самого меньшего конденсатора.
Если C1 < C7 < C9 < … < Cn, то C < C1.
Электроемкость
То, что деньги хранят в банках, знает даже первоклассник. А вот где хранят заряды? И зачем вообще хранить заряды?
Что такое электроемкость
Электроемкость характеризует способность проводника или системы проводников накапливать электрический заряд. Различают электроемкость уединенного проводника и электроемкость системы проводников (например, конденсатора). Уединенным называют проводник, расположенный вдали от других тел так, что они не оказывают на этот проводник никакого влияния.
Электроемкость уединенного проводника (C) — физическая величина, характеризующая способность проводника накапливать заряд и равная отношению электрического заряда q проводника к его потенциалу М:
Единица электроемкости в Си — фарад: [C] = 1 Ф (названа в честь М. Фарадея).
1 Ф — это электроемкость такого проводника, потенциал которого равен 1 В при сообщении ему заряда 1 Кл;
1 Ф — очень большая единица емкости, поэтому используют дольные единицы:
Что такое конденсатор
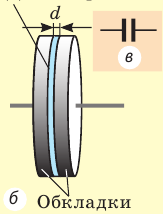
Конденсатор — устройство, представляющее собой систему из двух проводящих обкладок, разделенных тонким слоем диэлектрика (рис. 44.1).
Рис. 44.1. Школьный воздушный конденсатор: а — вид; б — устройство; в — обозначение на схемах
Обкладкам конденсатора передают одинаковые по модулю, но противоположные по знаку заряды, что способствует накоплению зарядов: разноименные заряды притягиваются, а значит, располагаются на внутренних поверхностях обкладок.
Обычно для зарядки конденсатора обе его обкладки соединяют с полюсами батареи аккумуляторов: на обкладках появляются равные по модулю, но противоположные по знаку заряды. Результат не изменится, если соединить с полюсом батареи только одну обкладку, заземлив вторую: вследствие электростатической индукции на заземленной обкладке тоже появится заряд, равный по модулю заряду на другой обкладке, но имеющий противоположный знак.
Зарядом конденсатора называют модуль заряда одной из обкладок. Отношение заряда q данного конденсатора к разности потенциалов (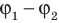
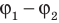
где U — напряжение между обкладками: 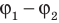
Как показывают исследования, емкость конденсатора увеличится, если увеличить площадь поверхности обкладок или приблизить обкладки друг к другу. На емкость конденсатора влияет также диэлектрик: чем больше его диэлектрическая проницаемость, тем большую емкость имеет конденсатор.
Конденсатор, состоящий из двух параллельных металлических пластин (обкладок), разделенных слоем диэлектрика, называют плоским (см. рис. 44.1). Электроемкость плоского конденсатора вычисляют по формуле:
где 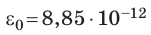
Поле между пластинами плоского конденсатора однородно, поэтому напряженность Е поля связана с напряжением U на конденсаторе формулой U=Ed.
Как рассчитывают электроемкость батареи конденсаторов
Конденсаторы характеризуются емкостью и максимальным рабочим напряжением Umax. Если напряжение, поданное на конденсатор, значительно превысит Umax, произойдет пробой — между обкладками возникнет искра, которая разрушит изоляцию.
Чтобы получить необходимую электроемкость при определенном рабочем напряжении, конденсаторы соединяют в батареи, применяя параллельное, последовательное и смешанное соединения. Рассмотрим батарею из трех конденсаторов электроемкостями
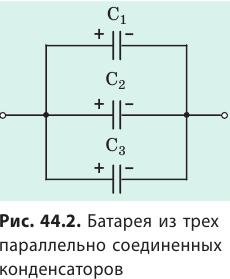
При параллельном соединении конденсаторов положительно заряженные обкладки всех конденсаторов соединяют в один узел, а отрицательно заряженные — в другой узел (рис. 44.2). В таком случае общий заряд q батареи конденсаторов равен алгебраической сумме зарядов отдельных конденсаторов:
Соединенные в один узел обкладки представляют собой один проводник, поэтому потенциалы обкладок, а следовательно, и разность потенциалов (напряжение) между обкладками всех конденсаторов одинаковы:
Таким образом, при параллельном соединении конденсаторов допустимое рабочее напряжение батареи определяется рабочим напряжением одного конденсатора.
Поскольку 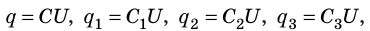
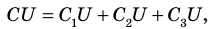
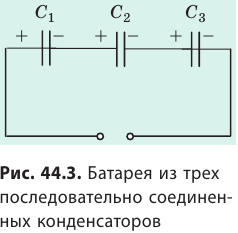
При последовательном соединении конденсаторы соединяют друг с другом разноименно заряженными обкладками (рис. 44.3). В этом случае заряды всех конденсаторов будут одинаковы и равны заряду батареи:
Напряжение на батарее последовательно соединенных конденсаторов равно сумме напряжений на отдельных конденсаторах:
Таким образом, допустимое рабочее напряжение батареи последовательно соединенных конденсаторов больше допустимого рабочего напряжения отдельного конденсатора. Электроемкость батареи последовательно соединенных конденсаторов вычисляют по формуле:
При последовательном соединении конденсаторов емкость батареи меньше, чем емкость конденсатора с минимальной емкостью.
Приведенные соотношения можно обобщить для любого количества конденсаторов.
Обратите внимание!
- Если батарея содержит n параллельно соединенных конденсаторов электроемкостью C′ каждый, то: C=nC′
- Если батарея содержит n последовательно соединенных конденсаторов электроемкостью C′ каждый, то:
Энергия заряженного конденсатора
Заряженный конденсатор, как и любая другая система заряженных тел, обладает энергией.
Убедимся в этом с помощью простого эксперимента. Присоединим к обкладкам заряженного конденсатора лампочку. Замкнем ключ — лампочка загорится. Теперь измерим напряжение на обкладках конденсатора — оно равно нулю, то есть конденсатор разрядился, а это означает, что заряженный конденсатор обладал энергией, которая частично превратилась в энергию света.
Вычислим энергию заряженного до напряжения 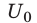
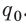
При разрядке конденсатора напряжение U на его обкладках изменяется прямо пропорционально заряду q конденсатора: 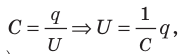
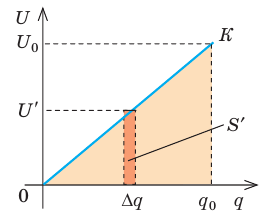
Рис. 44.4. К определению работы, которую совершает электрическое поле заряженного конденсатора при его разрядке
Мысленно разделим весь заряд конденсатора на маленькие «порции» Dq и будем считать, что при потере каждой такой «порции» напряжение на конденсаторе не изменяется. Таким образом получим ряд полос. Площадь S′ каждой полосы равна произведению двух ее сторон: 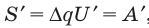
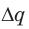
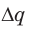
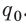
Следовательно,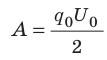
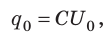
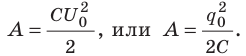
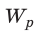
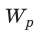
Для чего нужны конденсаторы
В современной технике сложно найти отрасль, где не применялись бы конденсаторы. Без них не обходятся радио и телеаппаратура (настройка колебательных контуров), радиолокационная и лазерная техника (получение мощных импульсов), телефония и телеграфия (разделение цепей переменного и постоянного токов, тушение искр в контактах), электроизмерительная техника (создание образцов емкости). И это далеко не полный перечень.
В современной электроэнергетике конденсаторы тоже имеют широкое применение: они присутствуют в конструкциях люминесцентных светильников, электросварочных аппаратов, устройств защиты от перенапряжений. Конденсаторы применяют и в других, не электротехнических, областях техники и промышленности (в медицине, фототехнике и т. д.).
Разнообразие областей применения обусловливает большое разнообразие конденсаторов. Наряду с миниатюрными конденсаторами, имеющими массу меньше грамма, а размеры порядка нескольких миллиметров, существуют конденсаторы массой несколько тонн и высотой больше человеческого роста. Емкость современных конденсаторов может составлять от долей, а рабочее напряжение может быть в пределах от нескольких вольт до нескольких сотен киловольт. Конденсаторы можно классифицировать по следующим признакам и свойствам:
- по назначению — постоянной и переменной емкости;
- по форме обкладок — плоские, сферические, цилиндрические и др.;
- по типу диэлектрика — воздушные, бумажные, слюдяные, керамические, электролитические и др.
Выводы:
- Энергию заряженного конденсатора можно вычислить по формулам:
- Конденсаторы классифицируют по назначению (постоянной и переменной емкости); по форме обкладок (плоские, сферические, цилиндрические и др.); по типу диэлектрика (воздушные, бумажные, слюдяные, керамические, электролитические и др.).
- Полупроводники
- Потенциал электрического поля
- Постоянный электрический ток
- Законы постоянного тока
- Принцип суперпозиции электрических полей
- Проводники в электрическом поле
- Диэлектрики в электрическом поле
- Закон Кулона
Расчёт ёмкости конденсатора
Содержание
- 1 Конденсатор
- 2 Емкость
- 3 Зависимость
- 4 Расчет
- 4.1 Плоский конденсатор
- 4.2 Электроемкость
- 4.3 Сферический конденсатор
- 4.4 Цилиндрический
- 5 Проверка
- 6 Заключение
- 7 Видео по теме
Конденсаторы нашли в наше время очень широкое применение в электронике и электротехнике, ведь они являются основными элементами большинства электрических цепей и схем. Постараемся подробно в данной статье рассказать — что такое электроемкость конденсатора. Так же будут приведены применяемые формулы расчета, описаны различные виды таких устройств и рассказано об их маркировке. Кроме того будет затронуто влияние различных факторов на емкость конденсатора.
Конденсатор
Прежде чем разобраться с тем, что такое емкость простейшего конденсатора, необходимо определиться, что из себя представляет этот электроэлемент. Конденсатором является радиоэлектронная деталь, которая может накапливать и отдавать определенную порцию электрического заряда. Состоит устройство из следующих элементов:
- Корпуса. Зачастую выполняется из алюминия. По форме он может быть плоским, сферическим и цилиндрическим.
- Обкладок (2 и более). Их делают из металлических пластинок или фольги.
- Диэлектрической прокладки. Устанавливается между обкладками и служит в качестве изолятора.
- Двух или более выводных контактов для подключения устройства в электроцепь.
Работает такой накопитель электрического заряда следующим образом.
- В момент подключения элемента к источнику электрического тока, он выступает в роли проводника. В этот момент электроток имеет максимальное значение, а напряжение — минимальное.
- На обкладках элемента начинают скапливаться положительные и отрицательные заряды (электроны и ионы). Таким образом происходит зарядка самого устройства. На момент заряда сила электротока постепенно уменьшается, а напряжение наоборот — увеличивается.
- После того как количество заряда в конденсаторе станет больше допустимого предела, он разряжается и процесс опять начинает повторяться циклически.
Основой работоспособности данного устройства является его емкость. Именно от этого параметра зависит время накопления заряда и общая «вместимость» устройства. О том, как на схемах обозначается простейший конденсатор, поможет понять следующий рисунок ниже.
Электрическая емкость, как и сами конденсаторы, нашли широкую область применения. Их используют в качестве:
- Частотных фильтров.
- Источника импульсов для различной фотоаппаратуры.
- Сглаживателей пульсирующих токов в выпрямителях.
- Фазосдвигающих элементов для электрических двигателей.
Применение конденсаторов в различных сферах основано именно на способности устройства накапливать электрический заряд. В более сложной электроаппаратуре эти устройства используются для бесперебойного поддержания определенного напряжения в разных накопителях данных.
Емкость
Емкостью конденсатора является физическая величина, которая определяет отношение между накопленным зарядом на обкладках и разностью потенциалов между ними.
В системе «СИ» емкость конденсатора и ее единица измерения — Фарад. В формулах для ее обозначения используется буква Ф (F). Однако емкость конденсатора редко измеряется в Фарадах, потому что это довольно большая величина. Чаще всего применяют ее кратные и дольные значения.
Значение электроемкости конденсатора всегда можно найти в маркировке устройства, которая нанесена на его корпус.
На схеме элемент обозначается буквой «С». Обозначение емкости является обязательным условием, ведь это позволит упростить процесс подбора необходимой электродетали для схемы.
Зависимость
Благодаря приведенному ранее описанию, мы узнали — что такое емкость. Далее попытаемся разобраться, от чего зависит эта характеристика. Емкость конденсатора зависит от расстояния между обкладками, их площади, а так же от самого материала диэлектрика. Благодаря этому можно сказать, от чего зависит емкость устройства: она прямопропорциональна площади пластины конденсатора и обратно пропорциональна расстоянию между пластинами.
Рассмотрим, как найти данную величину. Для плоского конденсатора формула расчета емкости выглядит следующим образом:
Зависимость способности устройства накапливать заряд от площади его обкладок и толщины диэлектрической прослойки так же указывает на то, что на данную величину оказывают влияние и общие размеры элемента.
Расчет
Расчет емкости конденсатора делается по довольно простой формуле:
В этой формуле:
- q — величина заряда, накопленного конденсатором.
- φ1−φ2 — разница потенциалов между его обкладками.
Данное выражение помогает довольно легко рассчитать емкость любого плоского конденсатора. Как и говорилось ранее в статье, этот величина электроёмкости конденсаторов всегда зависит от его геометрических размеров.
Плоский конденсатор
Отличительная особенность плоского конденсатора — наличие двух параллельно расположенных обкладок. Такие устройства могут иметь квадратную, круглую или прямоугольную форму.
Рассмотрим далее, как определить емкость данного вида конденсаторов. Найти емкость такого типа конденсаторов всегда поможет следующая формула:
Электроемкость
Зачастую применение конденсаторов подразумевает подключение в цепь сразу нескольких таких элементов. Благодаря этому можно увеличить общую емкость. Формула для определения электроемкости плоского конденсатора при параллельном подключении выглядит следующим образом:
Определение общей емкости для такой электроцепи делается следующим образом: C=C1+C2
Величина заряда и напряжение для такой схемы соединения определяется следующим образом:
qобщ=q1+q2
Uобщ=U1=U2
Определить емкость конденсатора для последовательного соединения элементов позволит формула:
То есть в этом случае общую электроемкость плоского конденсатора находят с помощью выражения:
1/Cобщ=1/C1+1/C1
Благодаря данным выражениям найдем общее напряжение и определим величину заряда для последовательного соединения элементов:
qобщ=q1=q2
Uобщ=U1+U2
Емкость конденсатора и применяемые формулы расчетов для различных вариантов соединения плоских устройств приведены на рисунке ниже. Можно сказать, что она очень наглядная и удобная для использования:
Сферический конденсатор
Сферическое устройство имеет две обкладки в форме концентрических сфер, между которыми расположен диэлектрик. Емкость сферического конденсатора можно определить следующим образом:
В данном выражении значение «4π» определяет коэффициент рассеивания зарядов на поверхности сферических плоскостей.
Расчет емкости сферического конденсатора можно сделать по формуле для плоского устройства в том случае, если зазор по сравнению с радиусом сферы имеет довольно маленькое значение.
Цилиндрический
Цилиндрическое устройство немного схоже с ранее описанным сферическим. В них применяются схожие по форме обкладки. Они имеют так же круглую форму, а значит на расчет емкости цилиндрического устройства так же будет влиять такой параметр, как радиус обкладок. Отличием заключается только в самой вытянутой форме пластин цилиндрического конденсатора. Емкость цилиндрического конденсатора определяется по формуле:
Сферические и цилиндрические типы элементов сильно зависимы от толщины слоя диэлектрика. Чем он толще, тем меньше будет объем заряда, а значит у него повысится устойчивость к воздействию пробивного напряжения.
Проверка
Как отмечалось ранее, емкость устройства проставляется на его корпусе. Проверить паспортную величину и имеющуюся емкость устройства можно при помощи тестера с режимом «СХ». Например, для этого подойдут популярные модели M890D, AM-1083, DT9205A, UT139C, другие. Далее надо будет:
- Выпаять и разрядить устройство. Разрядка проводится строго изолированным металлическим предметом.
- Вставить ножки конденсатора в пазы «СХ», соблюдая полярность.
- Прибор отобразит на табло результат измерений. Его нужно будет сравнить с тем, который прописан в маркировке на его корпусе. Если значения между собой сильно отличаются, то это говорит о том, что элемент неисправный и требует замены.
Если мультиметр показал наличие бесконечной емкости, то это говорит о коротком замыкании внутри корпуса устройства и оно так же признается неисправным, требующим замены. Кроме того неисправность всегда можно определить визуально по трещинам или вздутию корпуса.
Заключение
В статье было описано — что такое конденсатор, как определить его емкость, от чего зависит этот параметр и основные формулы для расчета емкости различных типов таких устройств. Устройства всегда имеют на корпусе специальную маркировку, поэтому довольно просто выбрать наиболее подходящий по значению накопитель электрозаряда. Кроме того был приведен способ проверки устройства, который позволяет определить возможные его неисправности.
Видео по теме
Основной параметр:ёмкостьЕдиница измерения:
Фарад
Обозначениеконденсатора
на схемах
Конденсатор — это пассивный электронный прибор, который способен накапливать электрический заряд (заряжаться). Основной характеристикой конденсаторов является емкость, которую измеряют в фарадах (Ф, F).
- Фарад — большая величина, на практике используются дольные единицы измерения емкости конденсаторов: микрофарады (мкФ, µF), нанофарады (нФ, nF), пикофарады (пФ, pF).
- 1 Ф = 1 000 000 мкФ
- 1 мкФ = 1 000 нФ = 1 000 000 пФ
- 1 нФ = 1 000 пФ
Обозначениеэлектролитическогоконденсатора
на схемах
Номинал конденсатора на схемах указывают рядом с его обозначением. При емкости менее 10000 пФ ставят число пикофарад без обозначения размерности, например, 22, 180, 6800. Для емкости 0,01 мкФ и более ставят число микрофарад. Зарубежные обозначения часто заменяют греческую букву µ (мю) на латинскую u («uF» вместо «µF»).
Конденсаторы используют для сглаживания тока в электрических цепях, в колебательных системах (колебательных контурах, генераторах импульсов, мультивибраторах).
Конденсаторы состоят из двух пластин (обкладок), разделенных слоем диэлектрика. По материалу диэлектрика конденсаторы разделяют на керамические, электролитические, бумажные, слюдяные и другие.

Керамические конденсаторы имеют емкость от единиц до тысяч пикофарад. Электролитические конденсаторы обладают большей емкостью, которая может достигать тысяч микрофарад. Большинство электролитических конденсаторов имеют положительный и отрицательный полюса, что требует включения их в схемы с соблюдением полярности.
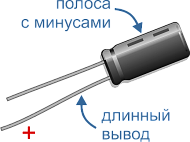
На корпусе электролитического конденсатора в большинстве случаев есть полоска, обозначающая отрицательный вывод. Кроме того, длина положительного вывода конденсатора немного больше, чем отрицательного.
Конденсаторы имеют рабочее напряжение, которое чаще всего указывают на корпусе. При подборе конденсатора следует выбирать конденсатор с напряжением равным или большим, указанному в схеме.
Цифровая кодировка конденсаторов
- При обозначении номинала на керамических конденсаторах используется цифровая кодировка, в которой последняя цифра обозначает количество нулей (емкость в пикофарадах).
- 681 — 680 пФ
- 102 — 1 000 пФ
- 103 — 10 000 пФ (0.01 мкФ)
- 104 — 100 000 пФ (0.1 мкФ)
- 154 — 150 000 пФ (0.15 мкФ)
- 224 — 220 000 пФ (0.22 мкФ)
При параллельном соединении конденсаторов их емкость складывается. А допустимое напряжение будет равно напряжению конденсатора с самым малым значением этого напряжения.
При последовательном соединении конденсаторов общую емкость можно рассчитать по приводимой формуле. Общее допустимое напряжение при этом будет равно сумме всех допустимых напряжений конденсаторов.
Переменный и подстроечный конденсатор
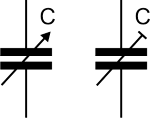
конденсатора на схемах
- Конденсаторы могут обладать не только постоянной емкостью, но и переменной емкостью, которую можно плавно менять в заданных пределах.
- Конденсаторы с переменной емкостью используют в колебательных контурах радиоприемников и ряде других устройств.
- Подстроечные конденсаторы применяются для настройки работы электронной схемы, когда в процессе работы устройства их емкость не меняется.
- Дополнение
Ещё примеры маркировки конденсаторов:
- Кодовая маркировка конденсаторов
Источник: https://myrobot.ru/wiki/index.php?n=Components.RCL
Преобразовать микрофарад в фарад (мкФ в Ф):
Прямая ссылка на этот калькулятор:https://www.preobrazovaniye-yedinits.info/preobrazovat+mikrofarad+v+farad.php
- Выберите нужную категорию из списка, в данном случае ‘Ёмкость’.
- Введите величину для перевода. Основные арифметические операции, такие как сложение (+), вычитание (-), умножение (*, x), деление (/, :, ÷), экспоненту (^), скобки и π (число пи), уже поддерживаются на настоящий момент.
- Из списка выберите единицу измерения переводимой величины, в данном случае ‘микрофарад [мкФ]’.
- И, наконец, выберите единицу измерения, в которую вы хотите перевести величину, в данном случае ‘фарад [Ф]’.
- После отображения результата операции и всякий раз, когда это уместно, появляется опция округления результата до определенного количества знаков после запятой.
С помощью этого калькулятора можно ввести значение для конвертации вместе с исходной единицей измерения, например, ‘134 микрофарад’. При этом можно использовать либо полное название единицы измерения, либо ее аббревиатуруНапример, ‘микрофарад’ или ‘мкФ’.
После ввода единицы измерения, которую требуется преобразовать, калькулятор определяет ее категорию, в данном случае ‘Ёмкость’. После этого он преобразует введенное значение во все соответствующие единицы измерения, которые ему известны. В списке результатов вы, несомненно, найдете нужное вам преобразованное значение.
Как вариант, преобразуемое значение можно ввести следующим образом: ’74 мкФ в Ф‘ или ’28 мкФ сколько Ф‘ или ’22 микрофарад -> фарад‘ или ’95 мкФ = Ф‘ или ’19 микрофарад в Ф‘ или ‘6 мкФ в фарад‘ или ‘5 микрофарад сколько фарад‘. В этом случае калькулятор также сразу поймет, в какую единицу измерения нужно преобразовать исходное значение. Независимо от того, какой из этих вариантов используется, исключается необходимость сложного поиска нужного значения в длинных списках выбора с бесчисленными категориями и бесчисленным количеством поддерживаемых единиц измерения. Все это за нас делает калькулятор, который справляется со своей задачей за доли секунды.
Кроме того, калькулятор позволяет использовать математические формулы. В результате, во внимание принимаются не только числа, такие как ‘(88 * 57) мкФ’. Можно даже использовать несколько единиц измерения непосредственно в поле конверсии.
Например, такое сочетание может выглядеть следующим образом: ‘134 микрофарад + 402 фарад’ или ’34mm x 6cm x 78dm = ? cm^3′.
Объединенные таким образом единицы измерения, естественно, должны соответствовать друг другу и иметь смысл в заданной комбинации.
Если поставить флажок рядом с опцией ‘Числа в научной записи’, то ответ будет представлен в виде экспоненциальной функции. Например, 9,999 999 909 ×1020. В этой форме представление числа разделяется на экспоненту, здесь 20, и фактическое число, здесь 9,999 999 909.
В устройствах, которые обладают ограниченными возможностями отображения чисел (например, карманные калькуляторы), также используется способ записи чисел 9,999 999 909 E+20. В частности, он упрощает просмотр очень больших и очень маленьких чисел.
Если в этой ячейке не установлен флажок, то результат отображается с использованием обычного способа записи чисел. В приведенном выше примере он будет выглядеть следующим образом: 999 999 990 900 000 000 000.
Независимо от представления результата, максимальная точность этого калькулятора равна 14 знакам после запятой. Такой точности должно хватить для большинства целей.
Сколько фарад в 1 микрофарад?
1 микрофарад [мкФ] = 0,000 001 фарад [Ф] — Калькулятор измерений, который, среди прочего, может использоваться для преобразования микрофарад в фарад.
Источник: https://www.preobrazovaniye-yedinits.info/preobrazovat+mikrofarad+v+farad.php
Фарад — это… Что такое Фарад?
Фара́д (обозначение: Ф, F; прежнее название — фара́да) — единица измерения электрической ёмкости в Международной системе единиц (СИ), названа в честь английского физика Майкла Фарадея.
1 фарад равен ёмкости конденсатора, при которой заряд 1 кулон создаёт между его обкладками напряжение 1 вольт:
1 Ф = 1 Кл/1 В = I·T/U.
Ф = А² · с4 · кг−1 · м−2 = Дж/В2 = Кл2/Дж = А · с / В = с/Ом.
Таким образом, конденсатор ёмкостью 1Ф, в идеале, может зарядиться до 1В при зарядке током 1А в течение 1 секунды. На практике же, ёмкость зависит от напряжения на обкладках конденсатора.
Фарад — очень большая ёмкость для уединённого проводника. Ёмкостью 1 Ф обладал бы уединённый металлический шар, радиус которого равен 13 радиусам Солнца. Ёмкость же Земли (точнее, шара размером с Землю, используемого как уединённый проводник) составляет около 710 микрофарад.
Ионистор со взаимной ёмкостью в 1 фарад.
Промышленные конденсаторы имеют номиналы, измеряемые в микро-, нано- и пикофарадах и выпускаются ёмкостью до десятков фарад; в звуковой аппаратуре используются гибридные конденсаторы ёмкостью до 40 фарад[1].
Область применения
Фарад измеряет электрическую ёмкость, то есть характеризует заряды, создаваемые электрическими полями. Например в фарадах (и производных единицах) измеряют ёмкость кабелей, конденсаторов, межэлектродные ёмкости различных приборов.
Не следует путать электрическую ёмкость и электрохимическую ёмкость батареек и аккумуляторов, которая имеет другую природу и измеряется в других единицах — ампер-часах, соразмерных электрическому заряду (1 ампер-час равен 3600 кулонам).
Кратные и дольные единицы
Образуют с помощью стандартных приставок СИ.
Кратные
10−1 Ф
10−2 Ф
10−3 Ф
10−6 Ф
10−9 Ф
10−12 Ф
10−15 Ф
10−18 Ф
10−21 Ф
10−24 Ф
| декафарад | даФ | daF | децифарад | дФ | dF |
| гектофарад | гФ | hF | сантифарад | сФ | cF |
| килофарад | кФ | kF | миллифарад | мФ | mF |
| мегафарад | МФ | MF | микрофарад | мкФ | µF |
| гигафарад | ГФ | GF | нанофарад | нФ | nF |
| терафарад | ТФ | TF | пикофарад | пФ | pF |
| петафарад | ПФ | PF | фемтофарад | фФ | fF |
| эксафарад | ЭФ | EF | аттофарад | аФ | aF |
| зеттафарад | ЗФ | ZF | зептофарад | зФ | zF |
| йоттафарад | ИФ | YF | йоктофарад | иФ | yF |
| применять не рекомендуется не применяются или редко применяются на практике |
Дольные
величина
название
обозначение
величина
название
обозначение
101 Ф
102 Ф
103 Ф
106 Ф
109 Ф
1012 Ф
1015 Ф
1018 Ф
1021 Ф
1024 Ф
- В советской практике использовались только две единицы — микрофарада и пикофарада. Ёмкость в 1-100 мФ и нФ выражалась в тысячах микрофарад и пикофарад соответственно. Ёмкость в 100-1000 мФ и нФ выражалась в десятых долях фарады и микрофарады соответственно. Никакие другие единицы использовать было не принято.
- Также на схемах электрических цепей и часто в маркировке ранних конденсаторов советского производства число без буквы обозначало величину в пикофарадах, а с буквой м либо m — в микрофарадах. Этот нюанс надо учитывать при чтении схем в старых чертежах журналах советского издания, поскольку обычно одиночная буква «м» обозначает «милли-».
- В текстах на языках, использующих латиницу, очень часто при обозначении микрофарад в тексте заменяют букву µ (мю) на латинскую u (uF вместо µF) из-за отсутствия в раскладке греческих букв.
Связь с единицами измерения в других системах
- Сантиметр (другое название — статфарад, статФ) — единица электрической ёмкости в СГСЭ и гауссовой системе, ёмкость шара радиусом 1 см в вакууме.
- 1 статФ ≈ 1,1126… пФ.
- 1 Ф = 8,9875517873681764×1011 статФ (точно). Коэффициент равен с2×10−5 Ф/см = 100/(4πε0).
- Абфарад — единица электрической ёмкости в СГСМ; очень большая единица, 1 абФ = 109 Ф = 1 ГФ.
См. также
Примечания
- ↑ Однако ёмкость т. н. ионисторов (супер-конденсаторов с двойным электрическим слоем) может достигать многих килофарад.
Источник: https://dic.academic.ru/dic.nsf/ruwiki/10505
Сокращённая запись численных величин
Радиоэлектроника для начинающих
- При сборке электронных схем волей неволей приходится пересчитывать величины сопротивлений резисторов, ёмкостей конденсаторов, индуктивность катушек.
- Так, например, возникает необходимость переводить микрофарады в пикофарады, килоомы в омы, миллигенри в микрогенри.
- Как не запутаться в расчётах?
- Если будет допущена ошибка и выбран элемент с неверным номиналом, то собранное устройство будет неправильно работать или иметь другие характеристики.
Такая ситуация на практике не редкость, так как иногда на корпусах радиоэлементов указывают величину ёмкости в нанофарадах (нФ), а на принципиальной схеме ёмкости конденсаторов, как правило, указаны в микрофарадах (мкФ) и пикофарадах (пФ). Это вводит многих начинающих радиолюбителей в заблуждение и как следствие тормозит сборку электронного устройства.
Чтобы данной ситуации не происходило нужно научиться простым расчётам.
Чтобы не запутаться в микрофарадах, нанофарадах, пикофарадах нужно ознакомиться с таблицей размерности. Уверен, она вам ещё не раз пригодиться.
Данная таблица включает в себя десятичные кратные и дробные (дольные) приставки. Международная система единиц, которая носит сокращённое название СИ, включает шесть кратных (дека, гекто, кило, мега, гига, тера) и восемь дольных приставок (деци, санти, милли, микро, нано, пико, фемто, атто). Многие из этих приставок давно используются в электронике.
| Множитель | Приставка | ||
| Наименование | Сокращённое обозначение | ||
| русское | международное | ||
| 1000 000 000 000 = 1012 | Тера | Т | T |
| 1000 000 000 = 109 | Гига | Г | G |
| 1000 000 = 106 | Мега | М | M |
| 1000 = 103 | кило | к | k |
| 100 = 102 | Гекто | г | h |
| 10 = 101 | дека | да | da |
| 0,1 = 10-1 | деци | д | d |
| 0,01 = 10-2 | санти | с | c |
| 0,001 = 10-3 | милли | м | m |
| 0,000 001 = 10-6 | микро | мк | μ |
| 0,000 000 001 = 10-9 | нано | н | n |
| 0,000 000 000 001 = 10-12 | пико | п | p |
| 0,000 000 000 000 001 = 10-15 | фемто | ф | f |
| 0,000 000 000 000 000 001 = 10-18 | атто | а | a |
Как пользоваться таблицей?
Как видим из таблицы, разница между многими приставками составляет ровно 1000. Так, например, такое правило действует между кратными величинами, начиная с приставки кило-.
- Кило — 1000
- Мега — 1 000 000
- Гига – 1 000 000 000
- Тера – 1 000 000 000 000
Так, если рядом с обозначением резистора написано 1 Мом (1 Мегаом), то его сопротивление составит – 1 000 000 (1 миллион) Ом. Если же имеется резистор с номинальным сопротивлением 1 кОм (1 килоом), то в Омах это будет 1000 (1 тысяча) Ом.
Для дольных или по-другому дробных величин ситуация похожа, только происходит не увеличение численного значения, а его уменьшение.
Чтобы не запутаться в микрофарадах, нанофарадах, пикофарадах, нужно запомнить одно простое правило. Нужно понимать, что милли, микро, нано и пико – все они отличаются ровно на 1000.
То есть если вам говорят 47 микрофарад, то это значит, что в нанофарадах это будет в 1000 раз больше – 47 000 нанофарад. В пикофарадах это уже будет ещё на 1000 раз больше – 47 000 000 пикофарад.
Как видим, разница между 1 микрофарадой и 1 пикофарадой составляет 1 000 000 раз.
Также на практике иногда требуется знать значение в микрофарадах, а значение ёмкости указано в нанофарадах. Так если ёмкость конденсатора 1 нанофарада, то в микрофарадах это будет 0,001 мкф. Если ёмкость 0,01 мкф., то в пикофарадах это будет 10 000 пФ, а в нанофарадах, соответственно, 10 нФ.
Приставки, обозначающие размерность величины служат для сокращённой записи. Согласитесь проще написать 1мА, чем 0,001 Ампер или, например, 400 мкГн, чем 0,0004 Генри.
В показанной ранее таблице также есть сокращённое обозначение приставки. Так, чтобы не писать Мега, пишут только букву М. За приставкой обычно следует сокращённое обозначение электрической величины.
Например, слово Ампер не пишут, а указывают только букву А. Также поступают при сокращении записи единицы измерения ёмкости Фарада. В этом случае пишется только буква Ф.
Наравне с сокращённой записью на русском языке, которая часто используется в старой радиоэлектронной литературе, существует и международная сокращённая запись приставок. Она также указана в таблице.
Главная » Радиоэлектроника для начинающих » Текущая страница
Также Вам будет интересно узнать:
Источник: https://go-radio.ru/cokrasheniya.html
Фарад
Фара́д (русское обозначение: Ф; международное обозначение: F; прежнее название — фара́да) — единица измерения электрической ёмкости в Международной системе единиц (СИ), названная в честь английского физика Майкла Фарадея[1]. 1 фарад равен ёмкости конденсатора, при которой заряд 1 кулон создаёт между его обкладками напряжение 1 вольт:
1 Ф = 1 Кл/1 В.
Через основные единицы системы СИ фарад выражается следующим образом:
Ф = А2·с4·кг−1·м−2.
В соответствии с правилами СИ, касающимися производных единиц, названных по имени учёных, наименование единицы «фарад» пишется со строчной буквы, а её обозначение — с заглавной (Ф).
Такое написание обозначения сохраняется и в обозначениях производных единиц, образованных с использованием фарада.
Например, обозначение единицы измерения абсолютной диэлектрической проницаемости «фарад на метр» записывается как Ф/м.
В Международную систему единиц фарад введён решением XI Генеральной конференции по мерам и весам в 1960 году, одновременно с принятием системы СИ в целом[2].
Фарад — очень большая ёмкость для уединённого проводника: ёмкостью 1 Ф обладал бы уединённый металлический шар, радиус которого равен 13 радиусам Солнца (ёмкость же шара размером с Землю, используемого как уединённый проводник, составляла бы около 710 микрофарад).
Ионистор со взаимной ёмкостью в 1 фарад.
В фарадах измеряют электрическую ёмкость проводников, то есть их способность накапливать электрический заряд. Например, в фарадах (и производных единицах) измеряют: ёмкость кабелей, конденсаторов, межэлектродные ёмкости различных приборов.
Промышленные конденсаторы имеют номиналы, измеряемые в микро-, нано- и пикофарадах и выпускаются ёмкостью до ста фарад; в звуковой аппаратуре используются гибридные конденсаторы ёмкостью до сорока фарад. Ёмкость т. н.
ионисторов (супер-конденсаторов с двойным электрическим слоем) может достигать многих килофарад.
Не следует путать электрическую ёмкость и электрохимическую ёмкость батареек и аккумуляторов, которая имеет другую природу и измеряется в других единицах: ампер-часах, соразмерных электрическому заряду (1 ампер-час равен 3600 кулонам).
- Фарад может быть выражен через основные единицы системы СИ как:
- с4⋅А2⋅м−2⋅кг−1.
- Таким образом, его значение равно:
Ф = Кл·В−1 = А·с·В−1 = Дж·В−2 = Вт·с·В−2 = Н·м·В−2 = Кл2·Дж−1 = Кл2·Н−1·м−1 = с2·Кл2·кг−1·м−2 = с4·А2·кг−1·м−2 = с·Ом−1 = Ом−1·Гц−1 = с2·Гн−1,
где Ф — фарад, А — ампер, В — вольт, Кл — кулон, Дж − джоуль, м — метр, Н — ньютон, с — секунда, Вт — ватт, кг — килограмм, Ом — ом, Гц — герц, Гн — генри.
Образуются с помощью стандартных приставок СИ.
Кратные
Дольные
название
обозначение
величина
название
обозначение
10−1 Ф
10−2 Ф
10−3 Ф
10−6 Ф
10−9 Ф
10−12 Ф
10−15 Ф
10−18 Ф
10−21 Ф
10−24 Ф
| декафарад | даФ | daF | децифарад | дФ | dF |
| гектофарад | гФ | hF | сантифарад | сФ | cF |
| килофарад | кФ | kF | миллифарад | мФ | mF |
| мегафарад | МФ | MF | микрофарад | мкФ | µF |
| гигафарад | ГФ | GF | нанофарад | нФ | nF |
| терафарад | ТФ | TF | пикофарад | пФ | pF |
| петафарад | ПФ | PF | фемтофарад | фФ | fF |
| эксафарад | ЭФ | EF | аттофарад | аФ | aF |
| зеттафарад | ЗФ | ZF | зептофарад | зФ | zF |
| иоттафарад | ИФ | YF | иоктофарад | иФ | yF |
| применять не рекомендуется не применяются или редко применяются на практике |
величина101 Ф102 Ф103 Ф106 Ф109 Ф1012 Ф1015 Ф1018 Ф1021 Ф1024 Ф
- Дольную единицу пикофарад до 1967 года называли микромикрофарада (русское обозначение: мкмкф; международное: µµF)[3].
- На схемах электрических цепей и (часто) в маркировке ранних конденсаторов советского производства целое число (например, «47») означало ёмкость в пикофарадах, а десятичная дробь (например, «10,0» или «0,1») — в микрофарадах; никакие буквенные обозначения единиц измерения ёмкости на схемах не применялись… Позже и до сегодняшних дней: любое число без указания единицы измерения — ёмкость в пикофарадах; с буквой н — в нанофарадах; а с буквами мк — в микрофарадах. Использование других единиц ёмкости на схемах не стандартизовано (как и обозначение номинала на конденсаторах). На малогабаритных конденсаторах используют различного рода сокращения: например, после двух значащих цифр ёмкости в пикофарадах указывают число следующих за ними нулей (таким образом, конденсатор с обозначением «270» имеет номинальную ёмкость 27 пикофарад, а «271» — 270 пикофарад)[источник не указан 2428 дней].
- В текстах на языках, использующих латиницу, очень часто при обозначении микрофарад в тексте заменяют букву µ (мю) на латинскую u («uF» вместо «µF») из-за отсутствия в раскладке клавиатуры греческих букв.
Источник: https://ruwikiorg.ru/wiki/Farad
Электрическая емкость
Если сообщать телу электрический заряд, то его потенциал относительно какой-либо точки (например, Земли) будет возрастать пропорционально заряду: U ~ Q.
Коэффициент пропорциональности между зарядом и потенциалом называется электрической емкостью тела.
Емкость характеризует способность тела накапливать заряды.
Электрическая емкость C есть отношение сообщенного заряда Q
к возникающему в результате этого потенциалу U.
Единица СИ электрической емкости:
[ [C] = frac{Кл}{В} = фарад enspace (Ф) ]
Если
| С | электрическая емкость тела, | фарад |
|---|---|---|
| Q | подведенный заряд, | Кулон |
| U | потенциал, | Вольт |
то
[ C = frac{Q}{U} ]
Соотношение между единицами электрической емкости
1 Ф = 106 микрофарад (мкФ) = 1012 пикофарад (пФ)
Вычислить найти электрическую емкость по формуле (2)
| Q (Кулон) | U (Вольт) |
Вычислить
нажмите кнопку для расчета
Электрическая емкость, подтемы
- Конденсатор
- Плоский конденсатор
- Емкость плоского конденсатора
- Сферический конденсатор
- Емкость сферического конденсатора
- Емкость шара
- Плоский конденсатор
- Соединение конденсаторов
- Параллельное соединение конденсаторов, Емкость параллельно соединенных конденсаторов
- Последовательное соединение конденсаторов, Емкость последовательно соединенных конденсаторов
Электрическая емкость |
стр. 630 |
|---|


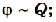
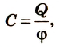
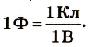
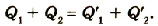
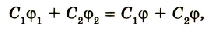
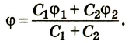
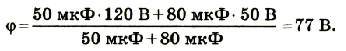

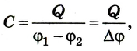
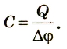
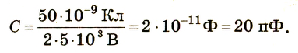



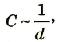
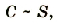
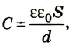
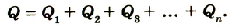
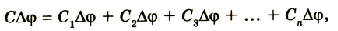
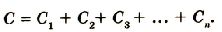
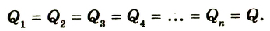
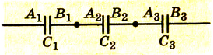
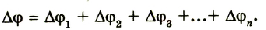
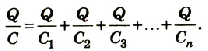
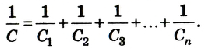
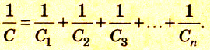
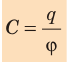
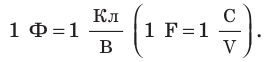
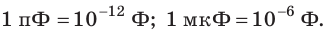

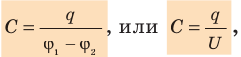
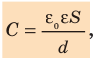
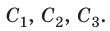
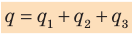
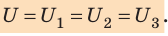
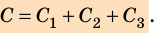
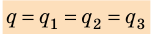
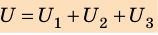
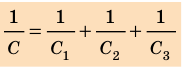
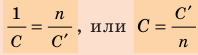
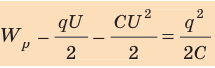

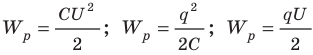















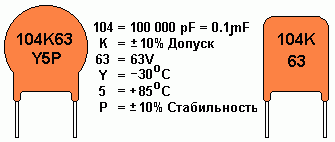 Цифровая кодировка конденсаторов
Цифровая кодировка конденсаторов