Матрица BB является обратной матрицей к квадратной матрице AA, если AB=BA=EAB = BA = E.
Из определения можно понять, что обратная матрица BB будет квадратной матрицей аналогичного порядка, какой имеет матрица AA (иначе какое-либо из произведений ABAB или BABA будет не определено).
Обратная матрица для исходной матрицы AA определяется так: A−1A^{-1}. Можно утверждать, что если A−1A^{-1} существует, то AA−1=A−1A=EAA^{-1} = A^{-1} A= E.
Также легко видеть, что (A−1)−1=A(A^{-1})^{-1} = A.
Если детерминант матрицы является нулем, то обратную к ней матрицу нельзя получить.
Онлайн-калькулятор
Квадратную матрицу AA можно назвать вырожденной матрицей тогда, когда определитель матрицы AA равен нулю, и невырожденной, если определитель не равен нулю.
В том случае, если обратная матрица может существовать, то она будет единственной.
Формула для вычисления обратной матрицы
Обратную матрицу A−1A^{-1} к матрице AA можно найти по формуле:
A−1=1detA⋅A∗A^{-1}=frac{1}{det A}cdot A^*
detAdet A — определитель матрицы A,A,
A∗A^* — транспонированая матрица алгебраических дополнений к матрице A.A.
Нужно найти обратную матрицу для следующей матрицы:
A=(1−20 342 −131)A = begin{pmatrix}
1& -2 & 0\
3 & 4 & 2\
-1& 3& 1 \
end{pmatrix}
Решение
Вычислим детерминант:
detA=∣1−20342−131∣=1∣4231∣−(−2)∣32−11∣+0∣34−13∣=8det A = begin{vmatrix}
1 & -2 & 0 \
3 & 4 & 2 \
-1 & 3 & 1 \
end{vmatrix} = 1 begin{vmatrix}
4 & 2 \
3 & 1 \
end{vmatrix} — (-2) begin{vmatrix}
3 & 2 \
-1 & 1 \
end{vmatrix} +0 begin{vmatrix}
3 & 4 \
-1 & 3 \
end{vmatrix} = 8
Так как detA≠0det A neq 0, то матрица – невырожденная, и обратная для нее существует.
Посчитаем алгебраические дополнение:
A11=(−1)1+1∣4231∣=−2,A_{11} = (-1)^{1+1} begin{vmatrix}
4 & 2 \
3 & 1 \
end{vmatrix} = -2,
A12=(−1)1+2∣32−11∣=−5,A_{12} = (-1)^{1+2} begin{vmatrix}
3 & 2 \
-1 & 1 \
end{vmatrix} = -5,
A13=(−1)1+3∣34−13∣=13A_{13} = (-1)^{1+3} begin{vmatrix}
3 & 4 \
-1 & 3 \
end{vmatrix} = 13,
A21=(−1)2+1∣−2031∣=2A_{21} = (-1)^{2+1} begin{vmatrix}
-2 & 0 \
3 & 1 \
end{vmatrix} = 2,
A22=(−1)2+2∣10−11∣=1A_{22} = (-1)^{2+2} begin{vmatrix}
1 & 0 \
-1 & 1 \
end{vmatrix} = 1,
A23=(−1)2+3∣1−2−13∣=−1A_{23} = (-1)^{2+3} begin{vmatrix}
1 & -2 \
-1 & 3 \
end{vmatrix} = -1,
A31=(−1)3+1∣−2042∣=−4A_{31} = (-1)^{3+1} begin{vmatrix}
-2 & 0 \
4 & 2 \
end{vmatrix} = -4,
A32=(−1)3+2∣1032∣=−2A_{32} = (-1)^{3+2} begin{vmatrix}
1 & 0 \
3 & 2 \
end{vmatrix} = -2,
A33=(−1)3+3∣1−234∣=10.A_{33} = (-1)^{3+3} begin{vmatrix}
1 & -2 \
3 & 4 \
end{vmatrix} = 10.
Обратная матрица:
A−1=18(−22−4−51−213−110)A^{-1} = frac{1}{8} begin{pmatrix}
-2 & 2 & -4 \
-5 & 1 & -2 \
13 & -1 & 10 \
end{pmatrix}
Чтобы избежать ошибок, необходимо сделать проверку: для этого нужно посчитать произведение первоначальной матрицы на конечную. Если в результате получится единичная матрица, то вы нашли обратную матрицу безошибочно.
Найдите обратную матрицу для матрицы:
A=(13−25)A = begin{pmatrix}
1 & 3\
-2 & 5 \
end{pmatrix}
Решение
detA=11≠0→A−1det A= 11 neq 0 rightarrow A^{-1} – существует.
A11=(−1)1+1⋅5=5A_{11} = (-1)^ {1+1} cdot 5 = 5,
A12=(−1)1+2⋅(−2)=2A_{12} = (-1)^ {1+2} cdot (-2) = 2,
A21=(−1)2+1⋅3=−3A_{21} = (-1)^ {2+1} cdot 3 = -3,
A22=(−1)2+2⋅1=1.A_{22} = (-1)^ {2+2} cdot 1 = 1.
Ответ:
A−1=111(5−321)A^{-1} = frac{1}{11} begin{pmatrix}
5 & -3 \
2 & 1 \
end{pmatrix}
Нами был рассмотрен способ нахождения матрицы с помощью алгебраических дополнений. Существует еще один способ, который называется методом элементарных преобразований.
Метод элементарных преобразований
Метод основан на элементарных преобразованиях матриц, под которыми будем понимать такие преобразования, в результате которых сохраняется эквивалентность матриц:
- перестановка местами любых двух рядов (строк или столбцов) матрицы;
- умножение любого ряда матрицы (строки или столбца) на некоторое число, отличное от нуля;
- прибавление к любому ряду (строке или столбцу) матрицы другого ряда (строки или столбца), умноженного на некоторое число, отличное от нуля.
Рассмотрим алгоритм нахождения обратной матрицы данным методом.
Алгоритм нахождения обратной матрицы методом элементарных преобразований
- Из исходной матрицы AA и единичной матрицы EE того же порядка составить расширенную матрицу, т.е. матрицу вида (A∣E)begin{pmatrix}A|Eend{pmatrix}.
- С помощью элементарных преобразований над строками расширенной матрицы получить единичную матрицу слева от черты: (E∣A−1)begin{pmatrix}E|A^{-1}end{pmatrix}.
- Выписать обратную матрицу, которая находится справа от черты.
Найти матрицу K−1K^{-1}, если K=(1301)K=begin{pmatrix}1&3\0&1end{pmatrix}.
Из матрицы KK второго порядка и единичной матрицы второго порядка составим расширенную матрицу:
(1301∣1001)begin{pmatrix}left.begin{matrix}1&3\0&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.
Произведем элементарные преобразования расширенной матрицы.
Прибавим к строке №1 строку №3, умноженную на -3:
(1301∣1001)∼(1001∣1−301)begin{pmatrix}left.begin{matrix}1&3\0&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}1&-3\0&1end{matrix}end{pmatrix}.
Слева получили единичную матрицу.
Выпишем обратную матрицу:
K−1=(1−301)K^{-1}=begin{pmatrix}1&-3\0&1end{pmatrix}.
Сделаем проверку, чтобы убедиться в том, что найденная матрица действительно является обратной.
K⋅K−1=(1301)⋅(1−301)=(1⋅1+3⋅01⋅(−3)+3⋅10⋅1+1⋅00⋅(−3)+1⋅1)=(1001)Kcdot K^{-1}=begin{pmatrix}1&3\0&1end{pmatrix}cdotbegin{pmatrix}1&-3\0&1end{pmatrix}=begin{pmatrix}1cdot1+3cdot0&1cdot(-3)+3cdot1\0cdot1+1cdot0&0cdot(-3)+1cdot1end{pmatrix}=begin{pmatrix}1&0\0&1end{pmatrix}.
Значит, обратная матрица найдена правильно.
Найти матрицу F−1F^{-1}, если F=(110010033)F=begin{pmatrix}1&1&0\0&1&0\0&3&3end{pmatrix}.
Из матрицы FF третьего порядка и единичной матрицы третьего порядка составим расширенную матрицу:
(110010033∣100010001)begin{pmatrix}left.begin{matrix}1&1&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}end{pmatrix}.
Произведем элементарные преобразования расширенной матрицы.
Прибавим к строке №1 строку №2, умноженную на -1:
(110010033∣100010001)∼(100010033∣1−10010001)begin{pmatrix}left.begin{matrix}1&1&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&0&1end{matrix}end{pmatrix}.
Прибавим к строке №3 строку №2, умноженную на -3:
(100010033∣1−10010001)∼(100010003∣1−100100−31)begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&3&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-3&1end{matrix}end{pmatrix}.
Умножим строку №3 на 13frac{1}{3}:
(100010003∣1−100100−31)∼(100010001∣1−100100−113)begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&3end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-3&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0&0\0&1&0\0&0&1end{matrix}right|begin{matrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{matrix}end{pmatrix}.
Слева получили единичную матрицу.
Выпишем обратную матрицу:
F−1=(1−100100−113)F^{-1}=begin{pmatrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{pmatrix}.
Сделаем проверку, чтобы убедиться в том, что найденная матрица действительно является обратной.
F⋅F−1=(110010033)⋅(1−100100−113)=(100010001)Fcdot F^{-1}=begin{pmatrix}1&1&0\0&1&0\0&3&3end{pmatrix}cdotbegin{pmatrix}1&-1&0\0&1&0\0&-1&frac{1}{3}end{pmatrix}=begin{pmatrix}1&0&0\0&1&0\0&0&1end{pmatrix}.
Значит, обратная матрица найдена правильно.
Выполнение контрольных работ на заказ недорого от профильных авторов на бирже Студворк!
Содержание:
- Матрицы: основные определения и понятия
- Умножение матрицы на число
- Сложение и вычитание матриц
- Умножение матриц
- Транспонирование матрицы
- Минор и алгебраическое дополнение
- Вычисление определителя
- Нахождение обратной матрицы
- Нахождение ранга матрицы
Матрицы широко применяются в математике для
компактной записи СЛАУ или систем дифференциальных уравнений. Тогда количество
строк матрицы соответствует количеству уравнений системы, а количество столбцов равно количеству неизвестных. Матричный
аппарат позволяет свести решение громоздких СЛАУ к компактным
операциям над матрицами.
На практике, они позволяют не делать лишних операций и сократить время выполнения задач.
Поэтому, будущим специалистам очень важно понять теорию матриц и научиться решать задачи с ними.
Перед изучением примеров решения задач советуем изучить теоретический материал по матрицам, прочитать
все определения и свойства. Список тем находится в правом меню.
Примеры по темам:
- Матрицы: основные определения и понятия
- Умножение матрицы на число
- Сложение и вычитание матриц
- Умножение матриц
- Транспонирование матрицы
- Минор и алгебраическое дополнение
- Вычисление определителя
- Нахождение обратной матрицы
- Нахождение ранга матрицы
Матрицы: основные определения и понятия
Теоретический материал по теме — основные определения и понятия матриц.
Пример
Задание. Чему равен элемент $ a_{23} $
матрицы $ A=left( begin{array}{rrr}{1} & {4} & {0} \ {-1} & {3} & {7}end{array}right) $ ?
Решение. Находим элемент, который стоит на пересечении второй строки и третьего столбца:
Таким образом, $a_{23}=7$.
Ответ. $a_{23}=7$
Умножение матрицы на число
Теоретический материал по теме — умножение матрицы на число.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Пусть $A=left( begin{array}{r}{3} \ {-1}end{array}right)$ .
Найти матрицу 2$A$.
Решение. $2 A=2 cdot left( begin{array}{r}{3} \ {-1}end{array}right)=left( begin{array}{c}{2 cdot 3} \ {2 cdot(-1)}end{array}right)=left( begin{array}{r}{6} \ {-2}end{array}right)$
Ответ. $2 A=left( begin{array}{r}{6} \ {-2}end{array}right)$
Сложение и вычитание матриц
Теоретический материал по теме — сложение и вычитание матриц.
Пример
Задание. Найти $A+B$, если
$A=left( begin{array}{rrr}{1} & {-2} & {4} \ {2} & {0} & {-1}end{array}right)$,
$B=left( begin{array}{lll}{5} & {2} & {3} \ {4} & {6} & {2}end{array}right)$
Решение. $C=A+B=left( begin{array}{rrr}{1} & {-2} & {4} \ {2} & {0} & {-1}end{array}right)+left( begin{array}{lll}{5} & {2} & {3} \ {4} & {6} & {2}end{array}right)=$
$=left( begin{array}{rrr}{1+5} & {-2+2} & {4+3} \ {2+4} & {0+6} & {-1+2}end{array}right)=left( begin{array}{lll}{6} & {0} & {7} \ {6} & {6} & {1}end{array}right)$
Ответ. $C=left( begin{array}{lll}{6} & {0} & {7} \ {6} & {6} & {1}end{array}right)$
Пример
Задание. Найти матрицу $C=A-3 B$,
если $A=left( begin{array}{rr}{1} & {2} \ {2} & {-1} \ {3} & {0}end{array}right), B=left( begin{array}{rr}{-1} & {1} \ {1} & {2} \ {0} & {0}end{array}right)$
Решение. $C=A-3 B=left( begin{array}{rr}{1} & {2} \ {2} & {-1} \ {3} & {0}end{array}right)-3 cdot left( begin{array}{rr}{-1} & {1} \ {1} & {2} \ {0} & {0}end{array}right)=$
$left( begin{array}{rr}{1} & {2} \ {2} & {-1} \ {3} & {0}end{array}right)-left( begin{array}{rr}{-3} & {3} \ {3} & {6} \ {0} & {0}end{array}right)=left( begin{array}{cc}{1-(-3)} & {2-3} \ {2-3} & {-1-6} \ {3-0} & {0-0}end{array}right)=left( begin{array}{rr}{4} & {-1} \ {-1} & {-7} \ {3} & {0}end{array}right)$
Ответ. $C=left( begin{array}{rr}{4} & {-1} \ {-1} & {-7} \ {3} & {0}end{array}right)$
Умножение матриц
Теоретический материал по теме — умножение матриц.
Пример
Задание. Вычислить $A B$ и $B A$,
если $A=left( begin{array}{rr}{1} & {-1} \ {2} & {0} \ {3} & {0}end{array}right), B=left( begin{array}{ll}{1} & {1} \ {2} & {0}end{array}right)$
Решение. Так как $A=A_{3 times 2}$ , а
$B=B_{2 times 2}$ , то произведение возможно и результатом операции умножения будет матрица
$C=C_{3 times 2}$ , а это матрица вида $C=left( begin{array}{cc}{c_{11}} & {c_{12}} \ {c_{21}} & {c_{22}} \ {c_{31}} & {c_{32}}end{array}right)$ .
Вычисли элементы матрицы $C$ :
$ c_{11}=a_{11} cdot b_{11}+a_{12} cdot b_{21}=1 cdot 1+(-1) cdot 2=-1 $
$ c_{12}=a_{11} cdot b_{12}+a_{12} cdot b_{22}=1 cdot 1+(-1) cdot 0=1 $
$ c_{21}=a_{21} cdot b_{11}+a_{22} cdot b_{21}=2 cdot 1+0 cdot 2=2 $
$ c_{22}=a_{21} cdot b_{12}+a_{22} cdot b_{22}=2 cdot 1+0 cdot 0=2 $
$ c_{31}=a_{31} cdot b_{11}+a_{32} cdot b_{21}=3 cdot 1+0 cdot 2=3 $
$ c_{31}=a_{31} cdot b_{12}+a_{32} cdot b_{22}=3 cdot 1+0 cdot 0=3 $
Итак, $C=A B=left( begin{array}{rl}{-1} & {1} \ {2} & {2} \ {3} & {3}end{array}right)$ .
Выполним произведения в более компактном виде:
$=left( begin{array}{rrr}{1 cdot 1+(-1) cdot 2} & {1 cdot 1+(-1) cdot 0} \ {2 cdot 1+0 cdot 2} & {2 cdot 1+0 cdot 0} \ {3 cdot 1+0 cdot 2} & {3 cdot 1+0 cdot 0}end{array}right)=left( begin{array}{rr}{-1} & {1} \ {2} & {2} \ {3} & {3}end{array}right)$
Найдем теперь произведение $D=B A=B_{2 times 2} cdot A_{3 times 2}$. Так как
количество столбцов матрицы $B$ (первый сомножитель) не совпадает с
количеством строк матрицы $A$ (второй сомножитель), то данное произведение
неопределенно. Умножить матрицы в данном порядке невозможно.
Ответ. $A B=left( begin{array}{rr}{-1} & {1} \ {2} & {2} \ {3} & {3}end{array}right)$ .
В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы
$B$ не совпадает с
количеством строк матрицы $A$ .
Транспонирование матрицы
Теоретический материал по теме — транспонирование матрицы.
Пример
Задание. Найти матрицу $A^{T}$, если
$A=left( begin{array}{rl}{1} & {0} \ {-2} & {3}end{array}right)$
Решение. $A^{T}=left( begin{array}{rr}{1} & {0} \ {-2} & {3}end{array}right)^{T}=left( begin{array}{rr}{1} & {-2} \ {0} & {3}end{array}right)$
Ответ. $A^{T}=left( begin{array}{rr}{1} & {-2} \ {0} & {3}end{array}right)$
Минор и алгебраическое дополнение
Теоретический материал по теме — минор и алгебраическое дополнение.
Пример
Задание. Найти минор
$M_{23}$ к элементу
$a_{23}$ определителя
$left| begin{array}{rrr}{1} & {2} & {-1} \ {1} & {0} & {3} \ {7} & {8} & {4}end{array}right|$ .
Решение. Вычеркиваем в заданном определителе вторую строку и третий столбец:
тогда $M_{23}=left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$
Ответ. $M_{23}=left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$
Пример
Задание. Найти алгебраическое дополнение
$A_{23}$ к элементу
$a_{23}$ определителя
$left| begin{array}{rrr}{1} & {2} & {-1} \ {1} & {0} & {3} \ {7} & {8} & {4}end{array}right|$ .
Решение. $A_{23}=(-1)^{2+3} cdot M_{23}=(-1)^{5} cdot left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|=-left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$
Ответ. $A_{23}=-left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$
Вычисление определителя
Теоретический материал по теме — методы вычисления определителей.
Пример
Задание. Вычислить определитель второго порядка
$left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|$
Решение. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=11 cdot 5-(-2) cdot 7=55+14=69$
Ответ. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=69$
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ методом треугольников.
Решение. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$
$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Пример
Задание. Вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. Выполним следующие преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному.
$left| begin{array}{ccc}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=left| begin{array}{cccc}{1} & {2} & {3} \ {4-4 cdot 1} & {5-4 cdot 2} & {6-4 cdot 3} \ {7-7 cdot 1} & {8-7 cdot 2} & {9-7 cdot 3}end{array}right|=$
$=left| begin{array}{rrr}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {-6} & {-12}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {2 cdot(-3)} & {2 cdot(-6)}end{array}right|=0$
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Пример
Задание. Вычислить определитель
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|$ приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {2} & {-5} & {3} & {0} \ {-1} & {4} & {2} & {-3}end{array}right|$
Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
$Delta=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {2} & {5} & {-1}end{array}right|$
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {3} & {-1} & {2} \ {0} & {2} & {5} & {-1}end{array}right|$
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:
$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {-10} & {-10} \ {0} & {0} & {-1} & {-9}end{array}right|$
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:
$Delta=-10 left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {-1} & {-9}end{array}right|=$
$=-10 cdot left| begin{array}{cccc}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {0} & {-8}end{array}right|=(-10) cdot 1 cdot(-1) cdot 1 cdot(-8)=-80$
Ответ. $Delta=-80$
Нахождение обратной матрицы
Теоретический материал по теме — нахождение обратной матрицы.
Пример
Задание. Для матрицы $A=left( begin{array}{ll}{7} & {4} \ {5} & {3}end{array}right)$
найти обратную методом присоединенной матрицы.
Решение. Приписываем к заданной матрице
$A$ справа единичную матрицу второго порядка:
$Aleft|E=left( begin{array}{ll|ll}{7} & {4} & {1} & {0} \ {5} & {3} & {0} & {1}end{array}right)right.$
От первой строки отнимаем вторую (для этого от элемента первой строки отнимаем соответствующий элемент второй строки):
$Aleft|E sim left( begin{array}{rr|rr}{2} & {1} & {1} & {-1} \ {5} & {3} & {0} & {1}end{array}right)right.$
От второй строки отнимаем две первых:
$Aleft|E sim left( begin{array}{rr|rr}{2} & {1} & {1} & {-1} \ {1} & {1} & {-2} & {3}end{array}right)right.$
Первую и вторую строки меняем местами:
$Aleft|E sim left( begin{array}{rr|r|rr}{1} & {1} & {-2} & {3} \ {2} & {1} & {1} & {-1}end{array}right)right.$
От второй строки отнимаем две первых:
$Aleft|E sim left( begin{array}{rr|rr}{1} & {1} & {-2} & {3} \ {0} & {-1} & {5} & {-7}end{array}right)right.$
Вторую строку умножаем на (-1), а к первой строке прибавляем вторую:
$Aleft|E sim left( begin{array}{rr|rr}{1} & {0} & {3} & {-4} \ {0} & {1} & {-5} & {7}end{array}right)right.$
Итак, слева получили единичную матрицу, а значит матрица, стоящая в
правой части (справа от вертикальной черты), является обратной к исходной.
Таким образом, получаем, что $A^{-1}=left( begin{array}{rr}{3} & {-4} \ {-5} & {7}end{array}right)$
Ответ. $A^{-1}=left( begin{array}{rr}{3} & {-4} \ {-5} & {7}end{array}right)$
Пример
Задание. Найти обратную матрицу для $A=left( begin{array}{ll}{1} & {1} \ {1} & {2}end{array}right)$
Решение. Шаг 1. Находим определитель: $Delta=left| begin{array}{ll}{1} & {1} \ {1} & {2}end{array}right|=2-1=1 neq 0$
Шаг 2. $A^{prime}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right)$
Шаг 3. $A^{-1}=frac{1}{Delta} cdot A^{prime}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right)$
Ответ. $A^{-1}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right)$
Пример
Задание. Найти обратную матрицу к матрице $A=left( begin{array}{rrr}{1} & {0} & {2} \ {2} & {-1} & {1} \ {1} & {3} & {-1}end{array}right)$
Решение. Вычисляем определитель матрицы:
$Delta=left| begin{array}{rrr}{1} & {0} & {2} \ {2} & {-1} & {1} \ {1} & {3} & {-1}end{array}right|=1 cdot(-1) cdot(-1)+2 cdot 3 cdot 2+0 cdot 1 cdot 1-$
$-1 cdot(-1) cdot 2-3 cdot 1 cdot 1-2 cdot 0 cdot(-1)=1+12+0+2-3+0=12 neq 0$
Так как определитель не равен нулю, то матрица имеет обратную.
Обратная матрица $A^{-1}$ к матрице
$A$ находится по формуле:
$A^{-1}=frac{1}{Delta} cdot widetilde{A}^{T}$
Найдем союзную матрицу $check{A}$ , для этого вычислим алгебраические
дополнения к элементам матрицы $A$ :
$A_{11}=(-1)^{1+1} left| begin{array}{rr}{-1} & {1} \ {3} & {-1}end{array}right|=(-1) cdot(-1)-3 cdot 1=1-3=-2$
$A_{12}=(-1)^{1+2} left| begin{array}{rr}{2} & {1} \ {1} & {-1}end{array}right|=-[2 cdot(-1)-1 cdot 1]=-(-2-1)=3$
$A_{13}=(-1)^{1+3} left| begin{array}{rr}{2} & {-1} \ {1} & {3}end{array}right|=2 cdot 3-1 cdot(-1)=6+1=7$
$A_{21}=(-1)^{2+1} left| begin{array}{rr}{0} & {2} \ {3} & {-1}end{array}right|=-[0 cdot(-1)-3 cdot 2]=-(0-6)=6$
$A_{22}=(-1)^{2+2} left| begin{array}{rr}{1} & {2} \ {1} & {-1}end{array}right|=1 cdot(-1)-1 cdot 2=-1-2=-3$
$A_{23}=(-1)^{2+3} left| begin{array}{cc}{1} & {0} \ {1} & {3}end{array}right|=-[1 cdot 3-1 cdot 0]=-(3-0)=-3$
$A_{31}=(-1)^{3+1} left| begin{array}{rr}{0} & {2} \ {-1} & {1}end{array}right|=0 cdot 1-(-1) cdot 2=0+2=2$
$A_{32}=(-1)^{3+2} left| begin{array}{cc}{1} & {2} \ {2} & {1}end{array}right|=-[1 cdot 1-2 cdot 2]=-(1-4)=3$
$A_{33}=(-1)^{3+3} left| begin{array}{rr}{1} & {0} \ {2} & {-1}end{array}right|=1 cdot(-1)-2 cdot 0=-1-0=-1$
Таким образом, $tilde{A}=left( begin{array}{rrr}{-2} & {3} & {7} \ {6} & {-3} & {-3} \ {2} & {3} & {-1}end{array}right)$
Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером):
$widetilde{A}^{T}=left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right)$
Итак, $A^{-1}=frac{1}{12} left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right)$
Ответ. $A^{-1}=frac{1}{12} left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right)$
Нахождение ранга матрицы
Теоретический материал по теме — нахождение ранга матрицы.
Пример
Задание. Найти ранг матрицы $A=left( begin{array}{cccc}{0} & {4} & {10} & {1} \ {4} & {8} & {18} & {7} \ {10} & {18} & {40} & {17} \ {1} & {7} & {17} & {3}end{array}right)$
Решение. С помощью элементарных преобразований над ее строками приведем матрицу $A$ к
ступенчатому виду. Для этого вначале от третьей строки отнимем две вторых:
$A sim left( begin{array}{cccc}{0} & {4} & {10} & {1} \ {4} & {8} & {18} & {7} \ {2} & {2} & {4} & {3} \ {1} & {7} & {17} & {3}end{array}right)$
От второй строки отнимаем четвертую строку, умноженную на 4; от третьей — две четвертых:
$A sim left( begin{array}{rrrr}{0} & {4} & {10} & {1} \ {0} & {-20} & {-50} & {-5} \ {0} & {-12} & {-30} & {-3} \ {1} & {7} & {17} & {3}end{array}right)$
Ко второй строке прибавим пять первых, к третьей — три третьих:
$A sim left( begin{array}{cccc}{0} & {4} & {10} & {1} \ {0} & {0} & {0} & {0} \ {0} & {0} & {0} & {0} \ {1} & {7} & {17} & {3}end{array}right)$
Меняем местами первую и вторую строчки:
$A sim left( begin{array}{cccc}{0} & {0} & {0} & {0} \ {0} & {4} & {10} & {1} \ {0} & {0} & {0} & {0} \ {1} & {7} & {17} & {3}end{array}right)$
Далее четвертую и первую строки:
$A sim left( begin{array}{cccc}{1} & {7} & {17} & {3} \ {0} & {4} & {10} & {1} \ {0} & {0} & {0} & {0} \ {0} & {0} & {0} & {0}end{array}right) Rightarrow r a n g A=2$
Ответ. $operatorname{rang} A=2$
Пример
Задание. Найти ранг матрицы $A=left( begin{array}{rrrr}{1} & {2} & {-1} & {-2} \ {2} & {4} & {3} & {0} \ {-1} & {-2} & {6} & {6}end{array}right)$ ,
используя метод окаймления миноров.
Решение. Минорами минимального порядка являются миноры первого порядка, которые равны элементам
матрицы $A$ . Рассмотрим, например, минор
$M_{1}=1 neq 0$ . расположенный в первой строке и первом
столбце. Окаймляем его с помощью второй строки и второго столбца, получаем минор
$M_{2}^{1}=left| begin{array}{ll}{1} & {2} \ {2} & {4}end{array}right|=0$ ; рассмотрим еще один минор второго
порядка, для этого минор $M_{1}$ окаймляем при
помощи второй строки и третьего столбца, тогда имеем минор $M_{2}^{2}=left| begin{array}{rr}{1} & {-1} \ {2} & {3}end{array}right|=5 neq 0$ ,
то есть ранг матрицы не меньше двух. Далее рассматриваем миноры третьего порядка, которые окаймляют минор
$M_{2}^{2}$ . Таких миноров два: комбинация
третьей строки со вторым столбцом или с четвертым столбцом. Вычисляем эти миноры:
$M_{3}^{1}=left| begin{array}{rrr}{1} & {2} & {-1} \ {2} & {4} & {3} \ {-1} & {-2} & {6}end{array}right|=0$
так как содержит два пропорциональных столбца (первый и второй); второй минор
$M_{3}^{2}=left| begin{array}{rrr}{1} & {-1} & {-2} \ {2} & {3} & {0} \ {-1} & {6} & {6}end{array}right|$
преобразуем следующим образом: к первой строке прибавим третью, а ко второй две третьих:
$M_{3}^{2}=left| begin{array}{rrr}{0} & {5} & {4} \ {0} & {15} & {12} \ {-1} & {6} & {6}end{array}right|=0$
И так как первая и вторая строки пропорциональны, то минор равен нулю.
Таким образом, все окаймляющие миноры третьего порядка равны нулю. А, значит, ранг матрицы $A$
равен двум: $operatorname{rang} A=2$
Ответ. $operatorname{rang} A=2$
Читать первую тему — основные определения и понятия матриц,
раздела матрицы.
Заказать задачи по любым предметам можно здесь от 10 минут
Как найти обратную матрицу
- Быстрый способ для матриц $2 times 2$
- Пример 1
- Пример 2
- Нахождение с помощью метода Гаусса
- Пример 3
- Пример 4
- Метод союзной матрицы(алгебраические дополнения)
- Пример 5
Обратная матрица обозначается $ A^{-1} $ и существует только для матриц, у которых определитель не равен нулю $ det A neq 0 $.
Быстрый способ для матриц $2 times 2$
Пусть задана матрица $A = begin{pmatrix} a&b\c&d end{pmatrix}$. Для быстрого способа нахождения обратной матрицы необходимо поменять местами элементы стоящие на главной диагонали, а для оставшихся элементов поменять знак на противоположный. Затем каждый элемент разделить матрицы разделить на определитель исходной матрицы. Математическая формула выглядит следующим образом $$A^{-1} = frac{1}{det A} begin{pmatrix} d&-b \ -c&a end{pmatrix} = frac{1}{ad-bc} begin{pmatrix} d&-b \ -c&a end{pmatrix}.$$
| Пример 1 |
| Найти обратную матрицу для $A = begin{pmatrix} 3&4 \ 5&9 end{pmatrix}$. |
| Решение |
|
Первым делом вычисляем определитель и убеждаемся, что он не равен нулю $$det A = begin{vmatrix} 3&4 \ 5&9 end{vmatrix} = 3cdot9 — 4cdot5 = 27 — 20 = 7.$$ Итак, определитель не равен нулю, значит, обратная матрица существует. Продолжаем наш алгоритм. Меняем элементы на главной диагонали местами, а у оставшихся элементов меняем знак на противоположный. $$A^{-1} = frac{1}{7} begin{pmatrix} 9&-4 \ -5&3 end{pmatrix} = begin{pmatrix} frac{9}{7}&frac{-4}{7} \ frac{-5}{7}&frac{3}{7} end{pmatrix}.$$ |
| Ответ |
| $$A^{-1} = begin{pmatrix} frac{9}{7}&frac{-4}{7} \ frac{-5}{7}&frac{3}{7} end{pmatrix}$$ |
| Пример 2 |
| Вычислить обратную матрицу для $A = begin{pmatrix} 2&-1 \ 4&-6 end{pmatrix}$. |
| Решение |
|
Находим определитель $$det A = begin{vmatrix} 2&-1 \ 4&-6 end{vmatrix} = 2cdot(-6) — 4cdot(-1) = -12 + 4 = -8.$$ Меняем местами элементы главной диагонали, а остальным меняем знак на противоположный. Не забываем затем каждый элемент разделить на определитель. $$A^{-1} = frac{1}{-8} begin{pmatrix} -6&1 \ -4&2 end{pmatrix} = begin{pmatrix} frac{-6}{-8}&frac{1}{-8} \ frac{-4}{-8}&frac{2}{-8} end{pmatrix} = begin{pmatrix} frac{3}{4}&-frac{1}{8} \ frac{1}{2}&-frac{1}{4} end{pmatrix}$$ |
| Ответ |
| $$A^{-1} = begin{pmatrix} frac{3}{4}&-frac{1}{8} \ frac{1}{2}&-frac{1}{4} end{pmatrix}$$ |
Нахождение с помощью метода Гаусса
На практике чаще всего метод Гаусса используется как способ нахождения обратной матрицы. Суть метода в том, что к основной матрице добавляется дополнительная единичная матрица с такой же размерностью.
$$ Bigg (begin{matrix} a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33} end{matrix} Bigg | begin{matrix} 1&0&0\0&1&0\0&0&1 end{matrix} Bigg ) $$
Далее нужно путем простейших элементарных преобразований привести левую матрицу к единичной, а одновременно с ней справа получится обратная матрица:
$$ Bigg (begin{matrix} 1&0&0\0&1&0\0&0&1 end{matrix} Bigg | begin{matrix} b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\b_{31}&b_{32}&b_{33} end{matrix} Bigg ) $$
$$A^{-1} = begin{pmatrix} b_{11}&b_{12}&b_{13}\b_{21}&b_{22}&b_{23}\b_{31}&b_{32}&b_{33} end{pmatrix}$$
| Пример 3 |
| Найти обратную матрицу элементарными преобразованиями $$A = begin{pmatrix} 2&-1&0 \ 0&2&-1 \ -1&-1&1 end{pmatrix}.$$ |
| Решение |
|
Вычисляем определитель матрицы, чтобы убедиться что он не равен нулю $$det A = begin{vmatrix} 2&-1&0 \ 0&2&-1 \ -1&-1&1 end{vmatrix} = 4-1+0-0-2-0=1 neq 0.$$ Выписываем основную матрицу и добавляем справа единичную матрицу. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ -1&-1&1 &|& 0&0&1 end{pmatrix}$$ Проводим элементарные преобразования над строками матриц таким образом, чтобы слева получилась единичная матрица. В то же время как справа получим обратную матрицу. Умножаем третью строку на 2 и прибавляем первую. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ 0&-3&2 &|& 1&0&2 end{pmatrix}$$ Умножаем третью строку на 2 и прибавляем к ней вторую строку, умноженную на 3. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&-1 &|& 0&1&0 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Теперь запускаем обратный ход преобразований снизу вверх. Ко второй строке прибавляем третью. $$begin{pmatrix} 2&-1&0 &|& 1&0&0 \ 0&2&0 &|& 2&4&4 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Умножаем первую строку на 2 и прибавляем к ней вторую строчку матрицы. $$begin{pmatrix} 4&0&0 &|& 4&4&4 \ 0&2&0 &|& 2&4&4 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Теперь, чтобы слева получилась единичная матрица нужно первую строку разделить на 4, вторую на 2. $$begin{pmatrix} 1&0&0 &|& 1&1&1 \ 0&1&0 &|& 1&2&2 \ 0&0&1 &|& 2&3&4 end{pmatrix}$$ Справа как видим получилась обратная матрица $$A^{-1} = begin{pmatrix} 1&1&1 \ 1&2&2 \ 2&3&4 end{pmatrix}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$A^{-1} = begin{pmatrix} 1&1&1 \ 1&2&2 \ 2&3&4 end{pmatrix}$$ |
| Пример 4 |
| Дана матрица, найти обратную $$A = begin{pmatrix} 3&2&1 \ 1&0&2 \ 4&1&3 end{pmatrix}.$$ |
| Решение |
|
Первым делом вычисляем определитель, чтобы убедиться в существовании обратной матрицы $$det A = begin{vmatrix} 3&2&1 \ 1&0&2 \ 4&1&3 end{vmatrix} = 0+16+1-0-6-6=5.$$ Теперь справа от матрицы дописываем единичную матрицу $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 1&0&2 &|& 0&1&0 \ 4&1&3 &|& 0&0&1 end{pmatrix}.$$ Теперь с помощью элементарных преобразований делаем так, чтобы слева стояла единичная матрица. А справа получим одновременно обратную матрицу. Умножаем вторую строку на 3 и вычитаем из неё первую. Умножаем третью строчку на 3 и вычитаем первую, умноженную на 4. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&-5&5 &|& -4&0&3 end{pmatrix}$$ Умножаем третью строку на 2 и вычитаем вторую, умноженную на 5. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&0&-15 &|& -3&-15&6 end{pmatrix}$$ Третью строку можно разделить на 3, чтобы уменьшить числа для дальнейшего удобства. Сделаем это. $$begin{pmatrix} 3&2&1 &|& 1&0&0 \ 0&-2&5 &|& -1&3&0 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ Начинаем проводить преобразования над строками теперь снизу вверх. Умножаем первую строку на 5 и прибавляем к ней третью. Ко второй строке просто прибавляем третью. $$begin{pmatrix} 15&10&0 &|& 4&-5&2 \ 0&-2&0 &|& -2&-2&2 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ К первой строке прибавляем вторую, умноженную на 5. $$begin{pmatrix} 15&0&0 &|& -6&-15&12 \ 0&-2&0 &|& -2&-2&2 \ 0&0&-5 &|& -1&-5&2 end{pmatrix}$$ Осталось разделить первую строку на 15, вторую на (-2), а третью на (-5). $$begin{pmatrix} 1&0&0 &|& -frac{2}{5}&-1&frac{4}{5} \ 0&1&0 &|& 1&1&-1 \ 0&0&1 &|& frac{1}{5}&1&-frac{2}{5} end{pmatrix}$$ |
| Ответ |
| $$begin{pmatrix} 1&0&0 &|& -frac{2}{5}&-1&frac{4}{5} \ 0&1&0 &|& 1&1&-1 \ 0&0&1 &|& frac{1}{5}&1&-frac{2}{5} end{pmatrix}$$ |
Метод союзной матрицы(алгебраические дополнения)
Формула нахождения обратной матрицы через алгебраические дополнения выглядит следующим образом
$$A^{-1} = frac{1}{|A|} (A^*)^T. $$
Матрица $A^*$ называется союзной (присоединенной) матрицей и представляет собой набор алгебраических дополнений матрицы $ A $:
$$ A^* = begin{pmatrix} A_{11}&A_{12}&A_{13}\A_{21}&A_{22}&A_{23}\A_{31}&A_{22}&A_{33} end{pmatrix}, text{ где } A_{ij}=(-1)^{i+j} M_{ij} $$
$M_{ij} $ называется минором матрицы, который получается путем вычеркивания $ i $-ой строки и $ j $-того столбца из матрицы.
| Пример 5 |
| Найти обратную матрицу методом алгебраических дополнений $$ A = begin{pmatrix} 3&1&2\-1&3&-2\0&-1&4 end{pmatrix} $$ |
| Решение |
|
Итак, пользуемся формулой $ A^{-1} = frac{1}{|A|} (A^*)^T $ Первым делом вычисляем определитель матрицы $ A $, так как необходимым условием существование обратной матрицы является неравенство его к нулю: $$ |A| = begin{vmatrix} 3&1&2\-1&3&-2\0&-1&4 end{vmatrix} = 36 + 0 + 2 — 0 — 6 + 4 = 36 neq 0 $$ Находим алгебраические дополнения матрицы $ A $. Для этого удаляем все элементы стоящие в i-ой строке и в j-ом столбце. Оставшиеся элементы матрицы переписываем в определитель и проводим его вычисление. Вычеркиваем первую строку и первый столбец: $$ A_{11} = (-1)^{1+1} cdot begin{vmatrix} 3&-2\-1&4 end{vmatrix} = 12 — 2 = 10 $$ Убираем первую строку и второй столбец: $$ A_{12} = (-1)^{1+2} cdot begin{vmatrix} -1&-2\0&4 end{vmatrix} = -(-4 — 0) = 4 $$ Оставшиеся алгебраические дополнения находим по аналогии с предыдущими двумя. $$ A_{13} = (-1)^{1+3} cdot begin{vmatrix} -1&3\0&-1 end{vmatrix} = 1 — 0 = 1 $$ $$ A_{21} = (-1)^{2+1} cdot begin{vmatrix} 1&2\-1&4 end{vmatrix} = -(4 + 2) = -6 $$ $$ A_{22} = (-1)^{2+2} cdot begin{vmatrix} 3&2\0&4 end{vmatrix} = 12 — 0 = 12 $$ $$ A_{23} = (-1)^{2+3} cdot begin{vmatrix} 3&1\0&-1 end{vmatrix} = -(-3 — 0) = 3 $$ $$ A_{31} = (-1)^{3+1} cdot begin{vmatrix} 1&2\3&-2 end{vmatrix} = -2 — 6 = -8 $$ $$ A_{32} = (-1)^{3+2} cdot begin{vmatrix} 3&2\-1&-2 end{vmatrix} = -(-6 + 2) = 4 $$ $$ A_{33} = (-1)^{3+3} cdot begin{vmatrix} 3&1\-1&3 end{vmatrix} = 9+1 = 10 $$ Составляем союзную (присоединенную) матрицу $ A^* $ из алгебраических дополнений: $$ A^* = begin{pmatrix} 10&4&1\-6&12&3\-8&4&10 end{pmatrix}. $$ Транспонируем её и обозначаем $ (A^*)^T $: $$ (A^*)^T = begin{pmatrix} 10&-6&-8\4&12&4\1&3&10 end{pmatrix} $$ В итоге находим обратную матрицу $ A^{-1} $: $$ A^{-1} = frac{1}{36} begin{pmatrix} 10&-6&-8\4&12&4\1&3&10 end{pmatrix} $$ Делим каждый элемент матрицы на 36 и получаем следующее: $$begin{pmatrix} frac{5}{18}&-frac{1}{6}&-frac{2}{9}\ frac{1}{9}&frac{1}{3}&frac{1}{9}\frac{1}{36}&frac{1}{12}&frac{5}{18} end{pmatrix}.$$ |
| Ответ |
| $$A^{-1} =begin{pmatrix} frac{5}{18}&-frac{1}{6}&-frac{2}{9}\ frac{1}{9}&frac{1}{3}&frac{1}{9}\frac{1}{36}&frac{1}{12}&frac{5}{18} end{pmatrix}$$ |
В статье расскажем, что такое обратная матрица и обоснуем её основные свойства. Также рассмотрим несколько примеров с подробным решением, при помощи которых вы научитесь строить обратную матрицу для заданной.
Понятие обратной матрицы
Обратная матрица действует только для квадратных матриц с определителями, которые отличны от нуля. Это невырожденные матрицы
Обратная матрица лучше всего рассматривается на примере квадратной матрицы третьего порядка, которую по аналогии можно будет обобщить для матриц произвольного порядка.
Пусть
Квадратная матрица называется обратной матрицей этой
, если выполняется равенство:
(1)
тогда произведение этих матриц равняется единичной матрице
Давайте рассмотрим теорему на основании вышеописанных определений:
Если матрица – неособенная
тогда это условие необходимое и достаточное для существования обратной матрицы
Докажем необходимость:
Пусть у матрицы есть обратная матрица
, то есть
Согласно теореме про определитель произведения двух матриц получается:
так как
(2)
Достаточность. Пусть определитель матрицы не равен нулю, то есть
Сокращённо обозначим
Покажем, как найти обратную матрицу.
Для каждого из элементов матрицы
найдём соответствующие им алгебраические дополнения
=
: тогда
, разместив их в виде новой матрицы
соответственно расположению элементов
в
Получим:
(3)
Транспонируем матрицу , заменяя строки столбцами, получим формулу обратной матрицы:
=
=
(4)
При помощи теорем про раскладывание и аннулирование для определителей третьего порядка, несложно проверить, что
Нахождение обратной матрицы
Нужно найти обратную матрицу к матрице:
Решение будет в такой последовательности:
Шаг 1:
Вычислим определитель матрицы при помощи правила треугольников и получаем:
=
Как видите, , тогда существует обратная матрица:
Шаг 2:
Находим алгебраические дополнения элементов матрицы :
;
;
;
;
;
;
;
;
Шаг 3:
записываем новую матрицу по формуле (3):
Шаг 4:
По формуле (4) получим обратную матрицу:
=
=
=
Шаг 5:
Проверим, что
=
=
*
=
= =
=
=
=
В вышеописанном примере мы искали более сложную матрицу поэтапно. Давайте рассмотрим пример 2, который проще предыдущего.
Найти матрицу, обратную к матрице
Решение:
1)
2)
3)
4) =
*
5) =
*
*
=
*
=
= *
ОПРЕДЕЛЕНИЕ МАТРИЦЫ. ВИДЫ МАТРИЦ
Матрицей размером m×n называется совокупность m·n чисел, расположенных в виде
прямоугольной таблицы из m
строк и n столбцов. Эту таблицу
обычно заключают в круглые скобки. Например, матрица может иметь вид:
Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В.
В общем виде матрицу размером m×n записывают так

Числа,
составляющие матрицу, называются элементами
матрицы. Элементы матрицы удобно снабжать двумя индексами aij: первый указывает номер
строки, а второй – номер столбца. Например, a23 – элемент стоит во 2-ой строке, 3-м столбце.
Если в матрице
число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. В приведённых выше
примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая
матрица – её порядок 1.
Матрица, в
которой число строк не равно числу столбцов, называется прямоугольной. В примерах это первая матрица и третья.
Различаются также
матрицы, имеющие только одну строку или один столбец.
Матрица, у
которой всего одна строка , называется матрицей –
строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом.
Матрица, все
элементы которой равны нулю, называется нулевой
и обозначается (0), или просто 0. Например,

Главной диагональю квадратной матрицы назовём диагональ, идущую
из левого верхнего в правый нижний угол.
Квадратная
матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю,
называется треугольной матрицей.

Квадратная
матрица, у которой все элементы, кроме, быть может, стоящих
на главной диагонали, равны нулю, называется диагональной матрицей. Например, 
.
Диагональная
матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой
E. Например, единичная матрица 3-го порядка имеет вид 
ДЕЙСТВИЯ НАД МАТРИЦАМИ
Равенство матриц. Две матрицы A и B называются равными, если
они имеют одинаковое число строк и столбцов и их соответствующие элементы равны
aij = bij. Так если 

если a11 = b11, a12 = b12, a21 = b21 и a22 = b22.
Транспонирование. Рассмотрим произвольную матрицу A из m строк и n столбцов. Ей можно
сопоставить такую матрицу B из
n строк и m столбцов, у которой каждая
строка является столбцом матрицы A с
тем же номером (следовательно, каждый столбец является строкой матрицы A с тем же номером). Итак,
если 

Эту матрицу B называют транспонированной матрицей A, а переход от A к B транспонированием.
Таким образом, транспонирование – это
перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A, обычно обозначают AT.
Связь между матрицей A и её транспонированной
можно записать в виде .
Например. Найти матрицу транспонированную данной.
Сложение матриц. Пусть матрицы A и B состоят из одинакового
числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры.
Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах.
Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по
правилу, например,
или
Примеры. Найти сумму матриц:
.
— нельзя, т.к. размеры матриц различны.
.
Легко проверить,
что сложение матриц подчиняется следующим законам: коммутативному A+B=B+A и ассоциативному (A+B)+C=A+(B+C).
Умножение матрицы на число. Для того чтобы умножить
матрицу A на число k нужно каждый элемент
матрицы A умножить на это число.
Таким образом, произведение матрицы A на
число k есть новая матрица, которая
определяется по правилу 
.
Для любых чисел a и b и
матриц A и B выполняются равенства:
.
Примеры.
.
- Найти 2A-B, если
,
.
.
Найти C=–3A+4B.
Матрицу C найти нельзя, т.к. матрицы A и B имеют разные размеры.
Умножение матриц. Эта операция осуществляется по своеобразному
закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть
согласованы. Перемножать можно только те матрицы, у которых число столбцов
первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки
первой равна высоте столбца второй). Произведением
матрицы A не матрицу B называется новая матрица C=AB,
элементы которой составляются следующим образом:

Таким образом,
например, чтобы получить у произведения (т.е. в матрице C) элемент, стоящий в 1-ой
строке и 3-м столбце c13, нужно в 1-ой матрице взять
1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на
соответствующие элементы столбца и полученные произведения сложить. И другие
элементы матрицы-произведения получаются с помощью аналогичного произведения
строк первой матрицы на столбцы второй матрицы.
В
общем случае, если мы умножаем матрицу A = (aij) размера m×n на
матрицу B = (bij) размера n×p, то получим матрицу C
размера m×p, элементы которой вычисляются следующим образом: элемент cij получается в результате
произведения элементов i-ой строки матрицы A на соответствующие элементы j-го
столбца матрицы B и их сложения.
Из этого правила следует,
что всегда можно перемножать две квадратные матрицы одного порядка, в
результате получим квадратную матрицу того же порядка. В частности, квадратную
матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.
Другим важным
случаем является умножение матрицы–строки на матрицу–столбец, причём ширина
первой должна быть равна высоте второй, в результате получим матрицу первого
порядка (т.е. один элемент). Действительно,

Примеры.
- Пусть
Найти элементы c12, c23 и c21 матрицы C.
- Найти произведение матриц.
.
.
— нельзя, т.к. ширина
первой матрицы равна 2-м элементам, а высота второй – 3-м.- Пусть
Найти АВ и ВА.
Найти АВ и ВА.
, B·A – не имеет смысла.
Таким образом,
эти простые примеры показывают, что матрицы, вообще говоря, не перестановочны друг с другом, т.е. A∙B ≠ B∙A. Поэтому при умножении
матриц нужно тщательно следить за порядком множителей.
Можно
проверить, что умножение матриц подчиняется ассоциативному и дистрибутивному
законам, т.е. (AB)C=A(BC) и (A+B)C=AC+BC.
Легко также
проверить, что при умножении квадратной матрицы A на единичную матрицу E
того же порядка вновь получим матрицу A, причём AE=EA=A.
Можно
отметить следующий любопытный факт. Как известно произведение 2-х отличных от
нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение
2-х не нулевых матриц может оказаться равным нулевой матрице.
Например, если 
.
ПОНЯТИЕ ОПРЕДЕЛИТЕЛЕЙ
Пусть дана
матрица второго порядка – квадратная матрица, состоящая из двух строк и двух
столбцов 
Определителем второго порядка, соответствующим данной
матрице, называется число, получаемое следующим образом: a11a22 – a12a21.
Определитель обозначается
символом 
Итак, для того
чтобы найти определитель второго порядка нужно из произведения элементов
главной диагонали вычесть произведение элементов по второй диагонали.
Примеры. Вычислить определители второго порядка.
.
- Вычислить определитель матрицы D, если D= -А+2В и
Аналогично можно
рассмотреть матрицу третьего порядка и соответствующий ей определитель.
Определителем третьего порядка, соответствующим данной
квадратной матрице третьего порядка, называется число, обозначаемое и
получаемое следующим образом:

Таким образом,
эта формула даёт разложение определителя третьего порядка по элементам первой
строки a11, a12, a13 и сводит вычисление определителя третьего порядка к вычислению
определителей второго порядка.
Примеры. Вычислить определитель третьего порядка.
.
.
- Решите уравнение.
.
.
(x+3)(4x-4-3x)+4(3x-4x+4)=0.
(x+3)(x-4)+4(-x+4)=0.
(x-4)(x-1)=0.
x1 = 4, x2 = 1.
Аналогично можно ввести понятия определителей
четвёртого, пятого и т.д. порядков, понижая их порядок разложением по элементам
1-ой строки, при этом знаки «+» и «–» у слагаемых чередуются.
Итак, в отличие
от матрицы, которая представляют собой таблицу чисел, определитель это число,
которое определённым образом ставится в соответствие матрице.

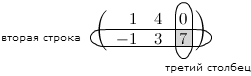
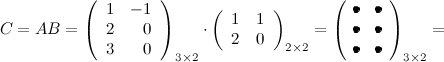
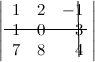





 .
. .
. Найти C=–3A+4B.
Найти C=–3A+4B.

 .
. .
.



 .
. .
. .
.