Как найти сближение велосипедистов

Задача 1. Автомобиль двигается со скоростью 80 км/ч. Сколько километров он проедет за 3 часа?

Решение

Если за один час автомобиль проезжает 80 километров, то за 3 часа он проедет в три раза больше. Чтобы найти расстояние, нужно скорость автомобиля (80км/ч) умножить на время движения (3ч)

80 × 3 = 240 км

Ответ: за 3 часа автомобиль проедет 240 километров.

Задача 2. На автомобиле за 3 часа проехали 180 км с одной и той же скоростью. Чему равна скорость автомобиля?

Решение

Скорость — это расстояние, пройденное телом за единицу времени. Под единицей подразумевается 1 час, 1 минута или 1 секунда.

Если за 3 часа автомобиль проехал 180 километров с одной и той же скоростью, то разделив 180 км на 3 часа мы определим расстояние, которое проезжал автомобиль за один час. А это есть скорость движения. Чтобы определить скорость, нужно пройденное расстояние разделить на время движения:

180 : 3 = 60 км/ч

Ответ: скорость автомобиля составляет 60 км/ч

Задача 3. За 2 часа автомобиль проехал 96 км, а велосипедист за 6 часов проехал 72 км. Во сколько раз автомобиль двигался быстрее велосипедиста?

Решение

Определим скорость движения автомобиля. Для этого разделим пройденное им расстояние (96км) на время его движения (2ч)

96 : 2 = 48 км/ч

Определим скорость движения велосипедиста. Для этого разделим пройденное им расстояние (72км) на время его движения (6ч)

72 : 6 = 12 км/ч

Узнаем во сколько раз автомобиль двигался быстрее велосипедиста. Для этого найдем отношение 48 к 12

Ответ: автомобиль двигался быстрее велосипедиста в 4 раза.

Задача 4. Вертолет преодолел расстояние в 600 км со скоростью 120 км/ч. Сколько времени он был в полете?

Решение

Если за 1 час вертолет преодолевал 120 километров, то узнав сколько таких 120 километров в 600 километрах, мы определим сколько времени он был в полете. Чтобы найти время, нужно пройденное расстояние разделить на скорость движения

600 : 120 = 5 часов

Ответ: вертолет был в пути 5 часов.

Задача 5. Вертолет летел 6 часов со скоростью 160 км/ч. Какое расстояние он преодолел за это время?

Решение

Если за 1 час вертолет преодолевал 160 км, то за 6 часов, он преодолел в шесть раз больше. Чтобы определить расстояние, нужно скорость движения умножить на время

160 × 6 = 960 км

Ответ: за 6 часов вертолет преодолел 960 км.

Задача 6. Расстояние от Перми до Казани, равное 723 км, автомобиль проехал за 13 часов. Первые 9 часов он ехал со скоростью 55 км/ч. Определить скорость автомобиля в оставшееся время.

Решение

Определим сколько километров автомобиль проехал за первые 9 часов. Для этого умножим скорость с которой он ехал первые девять часов (55км/ч) на 9

55 × 9 = 495 км

Определим сколько осталось проехать. Для этого вычтем из общего расстояния (723км) расстояние, пройденное за первые 9 часов движения

723 − 495 = 228 км

Эти 228 километров автомобиль проехал за оставшиеся 4 часа. Чтобы определить скорость автомобиля в оставшееся время, нужно 228 километров разделить на 4 часа:

228 : 4 = 57 км/ч

Ответ: скорость автомобиля в оставшееся время составляла 57 км/ч

Скорость сближения

Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.

Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причем скорость первого будет 100 м/м, а второго — 105 м/м, то скорость сближения будет составлять 100 + 105, то есть 205 м/м. Это значит, что каждую минуту расстояние между пешеходами будет уменьшáться на 205 метров

Чтобы найти скорость сближения, нужно сложить скорости объектов.

Предположим, что пешеходы встретились через три минуты после начала движения. Зная, что они встретились через три минуты, мы можем узнать расстояние между двумя пунктами.

Каждую минуту пешеходы преодолевали расстояние равное двухсот пяти метрам. Через 3 минуты они встретились. Значит умножив скорость сближения на время движения, можно определить расстояние между двумя пунктами:

205 × 3 = 615 метров

Можно и по другому определить расстояние между пунктами. Для этого следует найти расстояние, которое прошел каждый пешеход до встречи.

Так, первый пешеход шел со скоростью 100 метров в минуту. Встреча состоялась через три минуты, значит за 3 минуты он прошел 100 × 3 метров

100 × 3 = 300 метров

А второй пешеход шел со скоростью 105 метров в минуту. За три минуты он прошел 105 × 3 метров

105 × 3 = 315 метров

Теперь можно сложить полученные результаты и таким образом определить расстояние между двумя пунктами:

300 м + 315 м = 615 м

Задача 1. Из двух населенных пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 10 км/ч, а скорость второго — 12 км/ч. Через 2 часа они встретились. Определите расстояние между населенными пунктами

Решение

Найдем скорость сближения велосипедистов

10 км/ч + 12 км/ч = 22 км/ч

Определим расстояние между населенными пунктами. Для этого скорость сближения умножим на время движения

22 × 2 = 44 км

Решим эту задачу вторым способом. Для этого найдем расстояния, пройденные велосипедистами и сложим полученные результаты.

Найдем расстояние, пройденное первым велосипедистом:

10 × 2 = 20 км

Найдем расстояние, пройденное вторым велосипедистом:

12 × 2 = 24 км

Сложим полученные расстояния:

20 км + 24 км = 44 км

Ответ: расстояние между населенными пунктами составляет 44 км.

Задача 2. Из двух населенных пунктов, расстояние между которыми 60 км, навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 14 км/ч, а скорость второго — 16 км/ч. Через сколько часов они встретились?

Решение

Найдем скорость сближения велосипедистов:

14 км/ч + 16 км/ч = 30 км/ч

За один час расстояние между велосипедистами уменьшается на 30 километров. Чтобы определить через сколько часов они встретятся, нужно расстояние между населенными пунктами разделить на скорость сближения:

60 : 30 = 2 часа

Значит велосипедисты встретились через два часа

Ответ: велосипедисты встретились через 2 часа.

Задача 3. Из двух населенных пунктов, расстояние между которыми 56 км, навстречу друг другу выехали одновременно два велосипедиста. Через два часа они встретились. Первый велосипедист ехал со скоростью 12 км/ч. Определить скорость второго велосипедиста.

Решение

Определим расстояние пройденное первым велосипедистом. Как и второй велосипедист в пути он провел 2 часа. Умножив скорость первого велосипедиста на 2 часа, мы сможем узнать сколько километров он прошел до встречи

12 × 2 = 24 км

За два часа первый велосипедист прошел 24 км. За один час он прошел 24:2, то есть 12 км. Изобразим это графически

Вычтем из общего расстояния (56 км) расстояние, пройденное первым велосипедистом (24 км). Так мы определим сколько километров прошел второй велосипедист:

56 км − 24 км = 32 км

Второй велосипедист, как и первый провел в пути 2 часа. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:

32 : 2 = 16 км/ч

Значит скорость второго велосипедиста составляет 16 км/ч.

Ответ: скорость второго велосипедиста составляет 16 км/ч.

Скорость удаления

Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.

Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причем скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4+6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиться на 10 километров.

Чтобы найти скорость удаления, нужно сложить скорости объектов.

Так, за первый час расстояние между пешеходами будет составлять 10 километров. На следующем рисунке можно увидеть, как это происходит

Видно, что первый пешеход прошел свои 4 километра за первый час. Второй пешеход также прошел свои 6 километров за первый час. Итого за первый час расстояние между ними стало 4+6, то есть 10 километров.

Через два часа расстояние между пешеходами будет составлять 10×2, то есть 20 километров. На следующем рисунке можно увидеть, как это происходит:

Задача 1. От одной станции отправились одновременно в противоположных направлениях товарный поезд и пассажирский экспресс. Скорость товарного поезда составляла 40 км/ч, скорость экспресса 180 км/ч. Какое расстояние будет между этими поездами через 2 часа?

Решение

Определим скорость удаления поездов. Для этого сложим их скорости:

40 + 180 = 220 км/ч

Получили скорость удаления поездов равную 220 км/ч. Данная скорость показывает, что за час расстояние между поездами будет увеличиваться на 220 километров. Чтобы узнать какое расстояние будет между поездами через два часа, нужно 220 умножить на 2

220 × 2 = 440 км

Ответ: через 2 часа расстояние будет между поездами будет 440 километров.

Задача 2. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 16 км/ч, а скорость мотоциклиста — 40 км/ч. Какое расстояние будет между велосипедистом и мотоциклистом через 2 часа?

Решение

Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:

16 км/ч + 40 км/ч = 56 км/ч

Определим расстояние, которое будет между велосипедистом и мотоциклистом через 2 часа. Для этого скорость удаления (56км/ч) умножим на 2 часа

56 × 2 = 112 км

Ответ: через 2 часа расстояние между велосипедистом и мотоциклистом будет 112 км.

Задача 3. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Скорость велосипедиста 10 км/ч, а скорость мотоциклиста — 30 км/ч. Через сколько часов расстояние между ними будет 80 км?

Решение

Определим скорость удаления велосипедиста и мотоциклиста. Для этого сложим их скорости:

10 км/ч + 30 км/ч = 40 км/ч

За один час расстояние между велосипедистом и мотоциклистом увеличивается на 40 километров. Чтобы узнать через сколько часов расстояние между ними будет 80 км, нужно определить сколько раз 80 км содержит по 40 км

80 : 40 = 2

Ответ: через 2 часа после начала движения, между велосипедистом и мотоциклистом будет 80 километров.

Задача 4. Из пункта одновременно в противоположных направлениях отправились велосипедист и мотоциклист. Через 2 часа расстояние между ними было 90 км. Скорость велосипедиста составляла 15 км/ч. Определить скорость мотоциклиста

Решение

Определим расстояние, пройденное велосипедистом за 2 часа. Для этого умножим его скорость (15 км/ч) на 2 часа

15 × 2 = 30 км

На рисунке видно, что велосипедист прошел по 15 километров в каждом часе. Итого за два часа он прошел 30 километров.

Вычтем из общего расстояния (90 км) расстояние, пройденное велосипедистом (30 км). Так мы определим сколько километров прошел мотоциклист:

90 км − 30 км = 60 км

Мотоциклист за два часа прошел 60 километров. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:

60 : 2 = 30 км/ч

Значит скорость мотоциклиста составляла 30 км/ч.

Ответ: скорость мотоциклиста составляла 30 км/ч.

Задача на движение объектов в одном направлении

В предыдущей теме мы рассматривали задачи в которых объекты (люди, машины, лодки) двигались либо навстречу другу другу либо в противоположных направлениях. При этом мы находили различные расстояния, которые изменялись между объектами в течении определенного времени. Эти расстояния были либо скоростями сближения либо скоростями удаления.

В первом случае мы находили скорость сближения — в ситуации, когда два объекта двигались навстречу друг другу. За единицу времени расстояние между объектами уменьшалось на определенное расстояние

Во втором случае мы находили скорость удаления — в ситуации, когда два объекта двигались в противоположных направлениях. За единицу времени расстояние между объектами увеличивалось на определенное расстояние

Но объекты также могут двигаться в одном направлении, причем с различной скоростью. Например, из одного пункта одновременно могут выехать велосипедист и мотоциклист, причем скорость велосипедиста может составлять 20 километров в час, а скорость мотоциклиста — 40 километров в час

На рисунке видно, что мотоциклист впереди велосипедиста на двадцать километров. Связано это с тем, что в час он преодолевает на 20 километров больше, чем велосипедист. Поэтому каждый час расстояние между велосипедистом и мотоциклистом будет увеличиваться на двадцать километров.

В данном случае 20 км/ч являются скоростью удаления мотоциклиста от велосипедиста.

Через два часа расстояние, пройденное велосипедистом будет составлять 40 км. Мотоциклист же проедет 80 км, отдалившись от велосипедиста еще на двадцать километров — итого расстояние между ними составит 40 километров

Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.

В приведенном выше примере, скорость удаления составляет 20 км/ч. Её можно найти путем вычитания скорости велосипедиста из скорости мотоциклиста. Скорость велосипедиста составляла 20 км/ч, а скорость мотоциклиста — 40 км/ч. Скорость мотоциклиста больше, поэтому из 40 вычитаем 20

40 км/ч − 20 км/ч = 20 км/ч

Задача 1. Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 120 км/ч, а скорость автобуса 80 км/ч. Какое расстояние будет между ними через 1 час? 2 часа?

Решение

Найдем скорость удаления. Для этого из большей скорости вычтем меньшую

120 км/ч − 80 км/ч = 40 км/ч

Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 2 часа в два раза больше:

40 × 2 = 80 км

Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через два часа — 80 км.

Рассмотрим ситуацию в которой объекты начали свое движение из разных пунктов, но в одном направлении.

Пусть имеется дом, школа и аттракцион. От дома до школы 700 метров

Два пешехода отправились в аттракцион в одно и то же время. Причем первый пешеход отправился в аттракцион от дома со скоростью 100 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 80 метров в минуту. Какое расстояние будет между пешеходами через 2 минуты? Через сколько минут после начала движения первый пешеход догонит второго?

Ответим на первый вопрос задачи — какое расстояние будет между пешеходами через 2 минуты?

Определим расстояние, пройденное первым пешеходом за 2 минуты. Он двигался со скоростью 100 метров в минуту. За две минуты он пройдет в два раза больше, то есть 200 метров

100 × 2 = 200 метров

Определим расстояние, пройденное вторым пешеходом за 2 минуты. Он двигался со скоростью 80 метров в минуту. За две минуты он пройдет в два раза больше, то есть 160 метров

80 × 2 = 160 метров

Теперь нужно найти расстояние между пешеходами

Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (700м) прибавить расстояние, пройденное вторым пешеходом (160м) и из полученного результата вычесть расстояние, пройденное первым пешеходом (200м)

700 м + 160 м = 860 м

860 м − 200 м = 660 м

Либо из расстояния от дома до школы (700м) вычесть расстояние, пройденное первым пешеходом (200м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (160м)

700 м − 200 м = 500 м

500 м + 160 м = 660 м

Таким образом, через две минуты расстояние между пешеходами будет составлять 660 метров

Попробуем ответить на следующий вопрос задачи: через сколько минут после начала движения первый пешеход догонит второго?

Давайте посмотрим какой была ситуация в самом начале пути — когда пешеходы еще не начали своё движение

Как видно на рисунке, расстояние между пешеходами в начале пути составляло 700 метров. Но уже через минуту после начала движения расстояние между ними будет составлять 680 метров, поскольку первый пешеход двигается на 20 метров быстрее второго:

100 м × 1 = 100 м

80 м × 1 = 80 м

700 м + 80 м − 100 м = 780 м − 100 м = 680 м

Через две минуты после начала движения, расстояние уменьшится еще на 20 метров и будет составлять 660 метров. Это был наш ответ на первый вопрос задачи:

100 м × 2 = 200 м

80 м × 2 = 160 м

700 м + 160 м − 200м = 860 м − 200 м = 660 м

Через три минуты расстояние уменьшится еще на 20 метров и будет уже составлять 640 метров:

100 м × 3 = 300 м

80 м × 3 = 240 м

700 м + 240 м − 300м = 940 м − 300 м = 640 м

Мы видим, что с каждой минутой первый пешеход будет приближáться ко второму на 20 метров, и в конце концов догонит его. Можно сказать, что скорость равная двадцати метрам в минуту является скоростью сближения пешеходов. Правила нахождения скорости сближения и удаления при движении в одном направлении идентичны.

Чтобы найти скорость сближения при движении в одном направлении, нужно из большей скорости вычесть меньшую.

А раз изначальные 700 метров с каждой минутой уменьшаются на одинаковые 20 метров, то мы можем узнать сколько раз 700 метров содержат по 20 метров, тем самым определяя через сколько минут первый пешеход догонит второго

700 : 20 = 35

Значит через 35 минут после начала движения первый пешеход догонит второго. Для интереса узнаем сколько метров прошел к этому времени каждый пешеход. Первый двигался со скоростью 100 метров в минуту. За 35 минут он прошел в 35 раз больше

100 × 35 = 3500 м

Второй шел со скоростью 80 метров в минуту. За 35 минут он прошел в 35 раз больше

80 × 35 = 2800 м

Первый прошел 3500 метров, а второй 2800 метров. Первый прошел на 700 метров больше, поскольку он шел от дома. Если вычесть эти 700 метров из 3500, то мы получим 2800 м

Рассмотрим ситуацию в которой объекты движутся в одном направлении, но один из объектов начал своё движение раньше другого.

Пусть имеется дом и школа. Первый пешеход отправился в школу со скоростью 80 метров в минуту. Через 5 минут вслед за ним в школу отправился второй пешеход со скоростью 100 метров в минуту. Через сколько минут второй пешеход догонит первого?

Второй пешеход начал свое движение через 5 минут. К этому времени первый пешеход уже отдалился от него на какое-то расстояние. Найдём это расстояние. Для этого умножим его скорость (80 м/м) на 5 минут

80 × 5 = 400 метров

Первый пешеход отдалился от второго на 400 метров. Поэтому в момент, когда второй пешеход начнет свое движение, между ними будут эти самые 400 метров.

Но второй пешеход двигается со скоростью 100 метров в минуту. То есть двигается на 20 метров быстрее первого пешехода, а значит с каждой минутой расстояние между ними будет уменьшáться на 20 метров. Наша задача узнать через сколько минут это произойдет.

Например, уже через минуту расстояние между пешеходами будет составлять 380 метров. Первый пешеход к своим 400 метрам пройдет еще 80 метров, а второй пройдет 100 метров

Принцип здесь такой-же, как и в предыдущей задаче. Расстояние между пешеходами в момент движения второго пешехода необходимо разделить на скорость сближения пешеходов. Скорость сближения в данном случае равна двадцати метрам. Поэтому, чтобы определить через сколько минут второй пешеход догонит первого, нужно 400 метров разделить на 20

400 : 20 = 20

Значит через 20 минут второй пешеход догонит первого.

Задача 2. Из двух сел, расстояние между которыми 40 км, одновременно в одном направлении выехали автобус и велосипедист. Скорость велосипедиста 15 км/ч, а скорость автобуса 35 км/ч. Через сколько часов автобус догонит велосипедиста?

Решение

Найдем скорость сближения

35 км/ч − 15 км/ч = 20 км/ч

Определим через часов автобус догонит велосипедиста

40 : 20 = 2

Ответ: автобус догонит велосипедиста через 2 часа.

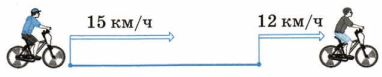
Используя рисунок, вычислите скорость сближения или скорость удаления велосипедистов и укажите характер изменения расстояния.
1)

2)

3)

4)

Задачи на движение навстречу друг другу (встречное движение) — один из трех основных видов задач на движение.

Если два объекта движутся навстречу друг другу, то они сближаются:

Чтобы найти скорость сближения двух объектов, движущихся навстречу друг другу, надо сложить их скорости:  

   

Скорость сближения больше, чем скорость каждого из них.

Скорость, время и расстояние связаны между собой формулой пути:

   

Рассмотрим некоторые задачи на встречное движение.

Задача 1

Два велосипедиста выехали навстречу друг другу. Скорость одного из низ 12 км/ч, а другого — 10 км/ч. Через 3 часа они встретились. Какое расстояние было между ними в начале пути?

Решение:

Условие задач на движение удобно оформлять в виде таблицы:

	v, км/ч	t, ч	s, км
I велосипедист	12	3	?
II велосипедист	10	3	?

1) 12+10=22 (км/ч) скорость сближения велосипедистов

2) 22∙3=66 (км) было между велосипедистами в начале пути.

Ответ: 66 км.

Задача 2

Два поезда идут навстречу друг другу. Скорость одного из них 50 км/ч, скорость другого —  60 км/ч. Сейчас между ними 440 км. Через сколько часов они встретятся?

Решение:

	v, км/ч	t, ч	s, км
I поезд	60	?	?
II поезд	50	?	?

1) 60+50=110 (км/ч) скорость сближения поездов

2) 440:110=4 (ч) время, через которое поезда встретятся.

Ответ: через 4 ч.

Задача 3.

Два пешехода находились на расстоянии 20 км друг от друга. Они вышли одновременно навстречу друг другу и встретились через 2 часа. Скорость одного пешехода 6 км/ч. Найти скорость другого пешехода.

	v, км/ч	t, ч	s, км
I пешеход	6	2	?
II пешеход	?	2	?

1) 20:2=10 (км/ч) скорость сближения пешеходов

2) 10-6=4 (км/ч) скорость другого пешехода.

Ответ: 4 км/ч.

Два велосипедиста выехали из двух пунктов навстречу друг другу.Когда первый проехал 1км 180м,второй проехал 820м.На какое расстояние сблизились велосипедисты? Чтобы решить эту хитрую задачку, необходимо просто сложить два отрезка пути, которые преодолел первый велосипедист и второй велосипедист. Итак мы складываем 1800 метров + 820 метров. Получаем 2000 метров, или целых 2 километра — именно на такое расстояние сблизились велосипедисты между собой. система выбрала этот ответ лучшим дольф­аника [379K] 8 лет назад  Обычно я всегда говорю, чтобы сначала представили, а лучше на бумаге нарисовали условие. Когда видишь, то легче сообразить какие цифры надо складывать или что с ними вообще надо делать. Оба велосипедиста едут, оба сближаются, в принципе они делают одно и тоже, только различие заключается в разной скорости велосипедистов, но это не важно. Так вот убирая расстояния двух ездоков, мы поймем сколько они проехали вместе. Надо сложить две цифры, тогда выйдет общая сумма километров. Сложение не сложное, всего две тысячи километров выходит. Можно с клеточками в тетради поразбираться. тогда еще масштаб легче освоить будет. ворчу­нов [106K] 9 лет назад  По условию задачи велосипедисты едут друг навстречу другу, поэтому расстояние между ними постоянно уменьшается в результате сближения. Поэтому, чтобы найти сколько метров осталось между ними или насколько они сблизились надо сложить пройденный (проеденный) каждым велосипедистом ими путь. По нашему условию в системе СИ (следует помнить об обязательном преобразование заданных значений к одной размерности) складываем 1180+820 метров и получаем 2000 метров. Это и будет ответом данной задачи — 2000 метров или 2 километра — расстояние на которое сблизились велосипедисты, выехавшие из двух пунктов навстречу друг другу. Возможно даже они проскочили друг друга или вовсе не встретились, но если учесть условие задачи, то конечно они сблизились друг другу настолько сколько они в сумме проехали и ответ с вместе с решением задачи будет выглядеть так. 1180+820 = 2000 метров. решение задачи будет выглядеть именно так, потому что автор не указывает отправные точки и какое расстояние между ними, а просто подтверждает, что они выехали навстречу друг другу. Roxri­te [79.1K] 8 лет назад  Для удобства сначала нужно перевести километры в метры: 1км 180м = 1180 метров. Каждый велосипедист начал своё движение от своего места, значит первый из них создал точку начала, второй — точку конца этого пути. Следовательно, чтобы выяснить расстояние их сближения нужно сложить их проехавший путь. 1180 м + 820 м = 2000 м. Ответ: 2000 метров (2 километра). Лолоч­ка611 [15.4K] 8 лет назад  Для того, чтобы решить эту не сложную задачку по математике нужно сложить километраж расстояния, которое проехал каждый из велосипедистов навстречу друг к другу: 1 км 180 м + 820 м = 1180 м + 820 м = 2000 м или 2 км. Правильный ответ: на 2 км велосипедисты стали ближе друг к другу. PRAVD­A911 [13.4K] 8 лет назад  Дано:Два велосипедиста выехали из двух пунктов навстречу друг другу.Когда первый проехал 1км 180м,второй проехал 820м.На какое расстояние сблизились велосипедисты? — правильный ответ на данную задачу будет — 2 километра или 2000 метров, так как мы сложим их общий пробег. [поль­зоват­ель забло­киров­ан] [54.4K] 8 лет назад  Решение данной задачи состоит из сложения пройденной обоими велосипедистами расстояния и получением ответа на задачу — 1180 метров плюс 820 метров равняется 2000 метров или два километра. Общее расстояние сближения равно двум километрам или 2000 метров. HotMi­lk [67.6K] 8 лет назад  Задача не сложная. Так как велосипедисты двигаются друг другу навстречу ,значит надо сложить расстояние которое они проехали . По условию задачи первый велосипедист проехал 1 км 180м ,а второй проехал 820 м. Складывая эти два значения получим 2 км. Mirra-Mi [58.7K] 8 лет назад  Ответ: велосипедисты, выехавшие друг другу на встречу, сблизились на то расстояние, которое они проехали. То есть необходимо сложить вместе путь пройденный одним велосипедистом с путем другого велосипедиста. 1180 м + 820 м = 2000 м = 2 км. Marus­ya112 [34.8K] 8 лет назад  Правильный ответ будет 2 километров. Надо одну тысячу сто восемьдесят метров прибавить восемьсот двадцать метров будет равно две тысячи метров. исходя из этого правольный ответ велосипедисты сблизятся на 2 километре haler­on [8.8K] 8 лет назад  нужно суммировать их так называемый пробег , если это сделать то мы имеем ровно 2000 м или 2 км , они стали ближе друг другу на это растояние , и это является правильным ответом на поставленный вами вопрос. Copyr­kina [4.9K] 9 лет назад  На 2 километра (1180м+820м=2000метров). Или я не права? Они едет навстречу, значит складываем их пройденный путь, и получаем насколько километром они ближе к друг другу… Как-то так, мне кажется ЮлияЮ­личка [19.4K] 9 лет назад  По-моему, они сблизились на расстояние, равное 1 км 180 м + 820 м = 2 км. Знаете ответ?