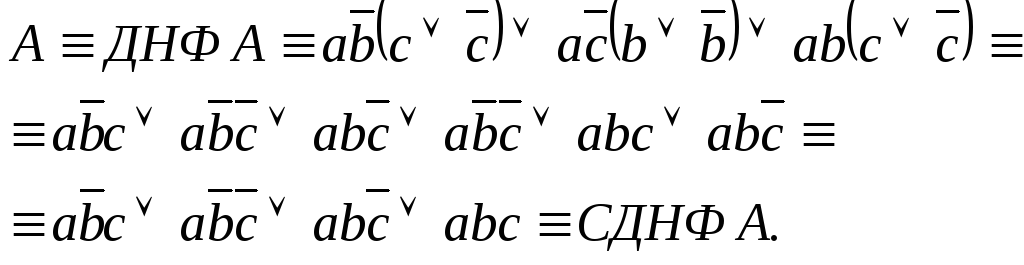Как найти сднф двумя способами

Что такое СДНФ 

Нормальная форма логической формулы характеризуется тем, что для нее не свойственны эквивалентность, отрицание формул неэлементарного типа и знаки импликации.

Существует две формы нормального типа: КНФ (конъюнктивная нормальная форма) и ДНФ (дизъюнктивная нормальная форма).

Определение

СДНФ — совершенная дизъюнктивная нормальная форма формулы. СДНФ — способ написания функции алгебры логики в качестве логического выражения.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

СДНФ формулы — это равнозначная ей формула, которая представляет собой дизъюнкцию элементарных конъюнкций, при которых функция достигает показателя «1».

ДНФ выглядит следующим образом:

((A;wedge;overline B;wedge;C);vee;(B;wedge;C))

СДНФ обладает некоторыми определенными свойствами:

  • включает различные элементарные конъюнкции;
  • все логические слагаемые формулы содержат все переменные, которые входят в функцию F;
  • ни в одном логическом слагаемом не содержится переменная и её отрицание.

К СДНФ возможно привести любую формулу алгебры логики. Исключение составляет только тождественно ложная формула. СДНФ можно получить как используя таблицы истинности, так и через равносильные преобразования.

Примечание

При построении таблицы истинности важно помнить, что логические переменные со значением «0» необходимо брать с отрицанием.

Что такое СКНФ

Определение

СКНФ — совершенная конъюнктивная нормальная форма. Формулу можно назвать таковой, когда она — конъюнкция неповторяющихся элементарных дизъюнкций.

КНФ имеет вид:

((A;vee;overline B;vee;C);wedge;(A;vee;C))

Формула должна соответствовать нескольким условиям, чтобы называться СКНФ:

  • в ней отсутствуют одинаковые элементарные дизъюнкции;
  • дизъюнкции не содержат одинаковые переменные;
  • все дизъюнкции содержат каждую переменную из входящих в конъюнктивную нормальную функцию такого типа.

Правила построения по таблице истинности

Дизъюнктивная форма

Если функция равна 1, то для всех наборов переменных, при которых это происходит, записывается произведение. Однако переменные, которые имеют значение 0, берутся с отрицанием.

Конъюнктивная форма

Когда функция равна 0, то для всех наборов переменных, при которых это происходит, записывается сумма. Однако переменные, которые имеют значение 1, берутся с отрицанием.

Алгоритм приведения к СДНФ и СКНФ

Рассмотрим логическую функцию в виде таблицы истинности.

Таблица 1

 

Алгоритм построения СДНФ по таблице истинности выглядит следующим образом:

  1. Отметить наборы переменных, значение функции F на которых равно 1.
  2. Записать для всех отмеченных наборов конъюнкцию всех переменных так: если значение некоторой переменной в этом наборе равняется 1, в конъюнкцию включается сама переменная. В случае противного результата, в конъюнкцию включается ее отрицание.
  3. Связать полученные конъюнкции операциями дизъюнкции.

Построим совершенную ДНФ:

Таблица 2

 

И как результат получим следующую СДНФ:

(F(x_1,;x_2,;x_3);=;(overline{x_1}wedgeoverline{x_2}wedgeoverline{x_3});vee(overline{x_1};wedge;overline{x_2};wedge;x_3);vee(x_1;wedge;overline{x_2};wedge;overline{x_3});vee;(x_1;wedge;overline{x_2};wedge;x_3);vee;(x_1;wedge;x_2;wedge;x_3))

Алгоритм построения СКНФ по таблице истинности выглядит следующим образом:

  1. Отметить в таблице истинности наборы переменных, значение функции F на которых равно 0.
  2. Записать для всех отмеченных наборов дизъюнкцию всех переменных — в том случае, когда значение некоторой переменной в этом наборе равняется 0, в дизъюнкцию включается сама переменная, если происходит наоборот, то в дизъюнкцию включается ее отрицание.
  3. Связать полученные дизъюнкции операциями конъюнкции.

Построим совершенную КНФ:

Таблица 3

 

И как результат получим следующую СКНФ:

(F(x_1,;x_2,;x_3);=;(x_1;vee;overline{x_2};vee;x_3);wedge;(x_1;vee;overline{x_2};vee;overline{x_3});wedge;(overline{x_1};vee;overline{x_2};vee;x_3))

Рассмотрев алгоритмы построения СДНФ и СКНФ ясно, что в случае подавляющей части наборов значений переменных функция равна 0, то значительно легче построить и СДНФ для получения ее формулы, а в обратном случае — СКНФ.

Доказательство эквивалентности

Эквивалентность — понятие, означающее, что две и более формул представляют одну и ту же функцию. Для обозначения эквивалентности могут использоваться следующие знаки: ( equiv , = , Leftrightarrow .)

Доказать эквивалентность формул можно двумя способами.

  1. Первый заключается в построении и сравнении таблиц истинности обеих функций. В этом случае результат будет истинным только в том случае, когда оба высказывания либо ложны, либо истинны.
  2. Второй вариант — метод эквивалентных преобразований. Суть этого метода —  построение цепи эквивалентных формул на основе ранее доказанных эквивалентностей. 

Далее следуют примеры с некоторыми эквивалентными преобразованием в булевой алгебре и новыми эквивалентностями, которые возможно получить с их помощью. 

Поглощение

(x;vee;xy;=;x)

(x(x;vee;y);=;x;)

Доказательство эквивалентности:

(x;vee;xy;=;x;cdot;l;vee;xy;=;x(l;vee;y);=;x)

(x(x;vee;y);=;xx;vee;xy;=;x;vee;xy;=;x)

Склеивание

(xy;vee;xoverline y;=;x)

Доказательство эквивалентности:

(xy;vee;xoverline y;=;x(y;vee;overline y);=;x;cdot;l;=;x)

Обобщенное склеивание

(xz;vee;yoverline z;vee;xy;=;xz;vee yoverline z)

Доказательство эквивалентности

(xz;vee;yoverline z;vee;xy;=;xz;vee yoverline z;vee;xyz;vee;xyoverline z;=;xz;vee;yoverline z)

Расщепление

(x;vee;overline xy;=;x;vee;y)

Доказательство эквивалентности

(x;vee;overline xy;=;xy;vee;xoverline y;vee;overline xy;=;xy;vee;xoverline y;vee;xy;vee;overline xy;=;x;cdot;l;;vee;y;cdot;l;=;x;vee;y)

Примеры с решением

Задача №1

Приведите к СКНФ (((((Arightarrow B)rightarrowoverline A)rightarrowoverline B)rightarrowoverline C)).

Через применение закона де Моргана и правила( x;rightarrow;y;=;overline x;vee;y) упростим выражения:

(F;=;((((A;rightarrow;B);rightarrow;overline A);rightarrowoverline B);rightarrow;overline C);=;(((overline A;vee;B);rightarrow;overline A);rightarrow;overline B);rightarrowoverline C;);=)

(=;((((overline A;vee;B);rightarrowoverline A);rightarrowoverline B);rightarrow;overline C);=;((overline{((overline A;vee;B)};vee;overline A);rightarrowoverline B);rightarrowoverline C);=)

(=(((overline A;vee;B);vee;overline A);rightarrow;overline B);rightarrow;overline C);=((overline{(overline{(overline Avee B)};vee;overline A;)};vee;overline B);rightarrow;overline C);=)

(=;(overline{(overline{(overline{(overline A;vee;B)};vee;overline A)};vee;overline B)};vee;overline C);=;(((A;vee;B);vee;overline A);vee;overline B);vee;overline C;=)

(=;((overline{(overline A;vee;B)};vee;overline A);wedge;B);vee;overline C;=;(((A;wedge;overline B);vee;overline A);wedge B);vee;overline C;=)

(=((Aoverline B;vee;overline A);vee;overline A);wedge;B);vee;overline C;=(((A;wedge;overline B);vee;overline A);wedge;B);vee;overline C;=)

(=;((Aoverline B;vee;overline A);wedge;B);vee;overline C;=;(Aoverline BB;vee;overline AB);vee;overline C;=;(0;vee;overline AB);vee;overline C;=;overline AB;vee;overline C)

Далее приведем выражение к КНФ:

(F;=;overline AB;vee;overline C;;=;(overline A;vee;overline C);wedge;(B;vee;overline C))

Далее приведем выражение к СКНФ:

(F;=;(overline A;vee;overline C);wedge;(B;vee;overline C);=;(overline A;vee:overline C;vee;Boverline B);wedge;(Aoverline A;vee;B;v;overline C);=)

(=;(overline A;vee;overline C;vee;B);wedge;(A;vee;B;vee;overline C);wedge;(overline A;vee;overline C;vee;overline B);wedge;(overline A;vee;B;;overline C))

Задача №2

Используя эквивалентные преобразования, постройте ДНФ функции (f(widetilde x^n))

(f(widetilde x^3) = (overline{x_1}x_2;oplus;x_3);cdot;(x_1x_3;rightarrow;x_2))

Преобразуем функцию:

(f(widetilde x^3) = (overline{x_1}x_2;oplus;x_3);cdot;(x_1x_3;rightarrow;x_2) = ((overline{x_1}x_2;cdot;overline{x_3};);vee;(overline{overline{x_1}x_2};cdot;x_3));cdot;(overline{x_1x_3};vee;x_2);=)

(=;((overline{x_1}x_2overline{x_3});vee;((overline{overline{x_1}};vee;overline{x_2});x_3);cdot;(overline{x_1};vee;overline{x_3};vee;x_2);=;((overline{x_1}x_{2;}overline{x_3});vee;((x_1;vee;overline{x_2});x_3);cdot;(overline{x_1};vee;overline{x_3};vee;x_2);=)

(=;(overline{x_1}x_2overline{x_3};vee;x_1x_3;vee;overline{x_2}x_3);cdot;(overline{x_1};vee;overline{x_3};vee;x_2);=)

(=(overline{x_1}x_2overline{x_3};cdot(x_1vee x_3vee x_2);vee;x_1x_3;cdot;(overline{x_1};vee;overline{x_3};vee;x_2);vee;overline{x_2}x_3;cdot;(overline{x_1};vee;overline{x_3};vee;x_2));=)

(=;(overline{x_1}x_2overline{x_3};vee;(x_1;x_3overline{x_1};vee;x_1x_3overline{x_3};vee;x_1x_3x_2);vee;(overline{x_2}x_3overline{x_1};vee;overline{x_2}x_3overline{x_3};vee;overline{x_2}x_3x_2);=)

(=;(overline{x_1}x_2overline{x_3};vee;0;vee;0;vee;x_1x_2x_3;vee;overline{x_1}overline{x_2}x_3;vee;0;vee;0);=)

(=;overline{x_1}x_2overline{x_3};vee;x_1x_2x_3;vee;overline{x_1}overline{x_2}x_3)

Источник

Для любой логической формулы можно построить бесконечное количество равносильных ей формул. Для этого потребуется произвести некоторое количество тождественных преобразований. Одной из главных задач в алгебре логики является нахождение канонических форм формул. Проще говоря таких, которые построены по одному канону (правилу).

Форма представления какой-либо логической функции будет считаться нормальной, если она выражена через конъюнкцию, дизъюнкцию, а также отрицание переменных. Среди всех нормальных форм можно выделить совершенно нормальные. Это тот случай, когда функция может быть записана только одним единственным способом.

Классы СКНФ и СДНФ

В при решении задач в алгебре логики особая роль отводится классам конъюнктивных и дизъюнктивных совершенно нормальных форм. Они основаны на стандартных понятиях элементарной конъюнкции и дизъюнкции.

Определение 1 — 2

Элементарной конъюнкцией принято называть формулу в том случае, когда она представляет собой конъюнкцию любого количества переменных, которые берутся без отрицания либо с отрицанием. При этом одночленной элементарной конъюнкцией считается только одна единственная переменная либо ее отрицание.

Элементарной дизъюнкцией называют формулу при условии, что она будет являться дизъюнкцией некоторого любого количества переменных и отрицаний, при этом она может быть и одночленной.

СКНФ

Форма любой логической формулы нормального типа не может содержать знаки эквивалентности, импликации, а также отрицания неэлементарных формул. Она может существовать только в двух видах:

  • КНФ – конъюнктивная нормальная форма, представляющая собой конъюнкцию нескольких дизъюнкций. К примеру, [(A vee bar{B} vee C) wedge(A vee C)];
  • ДНФ – дизъюнктивная нормальная форма, которая является дизъюнкцией нескольких конъюнкций. К примеру, [(A wedge bar{B} wedge C) vee(A wedge C)].

Определение 3

Совершенной конъюнктивной нормальной формой (СКНФ) называют КНФ, удовлетворяющую нескольким условиям:

  1. В ней не содержится двух и более элементарных дизъюнкций;
  2. Во всех дизъюнкциях отсутствуют одинаковые переменные;
  3. Каждая ДНФ содержит в себе все переменные из входящих в нее КНФ.

Любую булеву формулу, не являющуюся тождественной истиной, можно представить в виде СКНФ.

Правила построения СКНФ

В алгебре логики для любого набора переменных, при котором конечное значение функции становится нулевым, можно записать сумму. При этом переменные, имеющие числовые значение больше единицы, должны браться с отрицательным знаком.

Построение должно осуществляться по следующему алгоритму:

  1. В таблице нужно отметить такие наборы переменных, при которых [f=1].
  2. Для каждого выбранного набора переменных записываем КНФ, при этом если значение какой-либо из них равно 1, то она включается в неизменном виде, иначе – ее отрицание.
  3. На последнем этапе все полученные конъюнкции следует связать операциями дизъюнкции.

СНДФ

Определение 4

Совершенной дизъюнктивной нормальной формой (СНДФ) называют удовлетворяющую нескольким условиям ДНФ. Всего должно выполняться три условия:

  1. В ДНФ не должно содержаться двух и более одинаковых СКНФ.
  2. Ни в одной из конъюнкций не должно содержаться одинаковых переменных.
  3. В каждой элементарной КНФ должны содержаться все переменные, входящих в нее ДНФ, при этом их порядок должен полностью совпадать.

Любую булеву формулу в алгебре логики, не являющуюся тождественно ложной, можно представить в виде СНДФ, но только в одном единственном виде.

Правила построения СДНФ

Если существует определённый набор переменных, при котором значение функции равно единице, то можно записать произведения, учитывая, что переменные, значение которых больше нуля, нужно брать с отрицанием.

Алгоритм построения будет следующим:

  1. В таблице отмечаются все те наборы переменных, при которых [f=0]
  2. Для каждого отмеченного набора всех переменных записывается ДНФ, при этом если значение какой-либо из них равно нулю, то включается сама переменная, в любом другом случае ее нужно инвертировать.
  3. В конце все полученные дизъюнкции связываются друг с другом операциями конъюнкции.

Нет времени решать самому?

Наши эксперты помогут!

Примеры нахождения СКНФ и СДНФ

Рассмотрим несколько примеров нахождения СКНФ и СДНФ с помощью данных таблицы истинности.

Примеры 1 — 2

Необходимо по таблице истинности записать логическую функцию.

Примеры нахождения СКНФ и СДНФ 1

Решение. Для того чтобы выполнить задачу будем использовать правило построения СДНФ.

Примеры нахождения СКНФ и СДНФ 2

Получим СДНФ, которая имеет следующий вид:

[Fleft(x_{1}, x_{2}, x_{3}right)=left(overline{x_{1}} wedge overline{x_{2}} wedge overline{x_{3}}right) veeleft(overline{x_{1}} wedge overline{x_{2}} wedge x_{3}right) veeleft(x_{1} wedge overline{x_{2}} wedge overline{x_{3}}right) veeleft(x_{1} wedgeright.left.overline{x_{2}} wedge x_{3}right) veeleft(x_{1} wedge x_{2} wedge x_{3}right)]
Далее будем действовать согласно правилу построения СКНФ:

Примеры нахождения СКНФ и СДНФ 3

В результате получим:

[Fleft(x_{1}, x_{2}, x_{3}right)=left(x_{1} wedge overline{x_{2}} wedge x_{3}right) wedgeleft(x_{1} wedge overline{x_{2}} wedge overline{x_{3}}right) wedgeleft(overline{x_{1}} wedge overline{x_{2}} wedge x_{3}right)]

Требуется представить функцию, которая задана в таблице в виде СДНФ и СКНФ.

Примеры нахождения СКНФ и СДНФ 4

Решение: Для начала запишем в СНДФ заданную логическую функцию. Чтобы было проще, добавим еще один вспомогательный столбец. Руководствуемся правилом составления СДНФ и учитываем, что требуется ввести знак отрицания, если значение переменной будет нулевым. Это нужно для того, чтобы они не превратили в нули основной функции значение конъюнкции.

Примеры нахождения СКНФ и СДНФ 5

Значения, которые получились во вспомогательном столбце соединяем знаком дизъюнкции, в результате чего получаем искомую логическую функцию, которая примет следующий вид:

[Fleft(x_{1}, x_{2}, x_{3}, x_{4}right)=(bar{x} wedge bar{y} wedge z wedge f) veeleft(overline{x_{1}} wedge overline{x_{2}} wedge overline{x_{3}} wedge overline{x_{4}}right) veeleft(overline{x_{1}} wedge x_{2} wedge x_{3} wedgeright.left.x_{4}right) veeleft(x_{1} wedge overline{x_{2}} wedge overline{x_{3}} wedge overline{x_{4}}right)]

После этого потребуется записать логическую функцию в СКНФ. Для этого используем правило ее составления и вводим знаки отрицания для тех переменных, значение которых равно 1. Если пренебречь инвертированием единичных значений, то они могут превратить ДНФ в единицы основных функций.

Примеры нахождения СКНФ и СДНФ 6

Все полученные нами значения во вспомогательном столбце соединяем знаком конъюнкции и в итоге получаем логическую функцию в следующем виде.
[Fleft(x_{1}, x_{2}, x_{3}, x_{4}right)=left(x_{1} vee x_{2} vee x_{3} vee x_{4}right) wedgeleft(x_{1} vee x_{2} vee x_{3} vee overline{x_{4}}right) wedgeleft(x_{1} vee x_{2} veeright.\left.overline{x_{3}} vee x_{4}right) wedgeleft(x_{1} vee overline{x_{2}} vee x_{3} vee overline{x_{4}}right) wedgeleft(x_{1} vee overline{x_{2}} vee overline{x_{3}} vee x_{4}right) wedgeleft(overline{x_{1}} vee x_{2} vee x_{3} veeright.\left.overline{x_{4}}right) wedgeleft(overline{x_{1}} vee x_{2} vee overline{x_{3}} vee x_{4}right) wedgeleft(overline{x_{1}} vee x_{2} vee overline{x_{3}} vee overline{x_{4}}right) wedgeleft(overline{x_{1}} vee overline{x_{2}} vee x_{3} vee x_{4}right) wedge\left(overline{x_{1}} vee overline{x_{2}} vee x_{3} vee overline{x_{4}}right) wedgeleft(overline{x_{1}} vee overline{x_{2}} vee overline{x_{3}} vee x_{4}right) wedgeleft(overline{x_{1}} wedge overline{x_{2}} wedge overline{x_{3}} wedge overline{x_{4}}right)]
После рассмотрения примеров построения СДНФ и СКНФ с использованием таблицы истинности, стал понятен принцип построения логических функций.

Источник
Автор статьи

Диана Загировна Филиппенкова

Эксперт по предмету «Информатика»

Задать вопрос автору статьи

Нормальная форма логической формулы не содержит знаков импликации, эквивалентности и отрицания неэлементарных формул.

Нормальная форма существует в двух видах:

  1. конъюнктивная нормальная форма (КНФ) — конъюнкция нескольких дизъюнкций, например, $left(Avee overline{B}vee Cright)wedge left(Avee Cright)$;

  2. дизъюнктивная нормальная форма (ДНФ) — дизъюнкция нескольких конъюнкций, например, $left(Awedge overline{B}wedge Cright)vee left(Bwedge Cright)$.

СКНФ

Совершенная конъюнктивная нормальная форма (СКНФ) — это КНФ, удовлетворяющая трем условиям:

  • не содержит одинаковых элементарных дизъюнкций;

  • ни одна из дизъюнкций не содержит одинаковых переменных;

  • каждая элементарная дизъюнкция содержит каждую переменную из входящих в данную КНФ.

Любая булева формула, которая не является тождественно истинной, может быть представлена в СКНФ.

Правила построения СКНФ по таблице истинности

Для каждого набора переменных, при котором функция равна 0, записывается сумма, причем переменные, которые имеют значение 1, берутся с отрицанием.

СДНФ

Совершенная дизъюнктивная нормальная форма (СДНФ) — это ДНФ, удовлетворяющая трем условиям:

  • не содержит одинаковых элементарных конъюнкций;

  • ни одна из конъюнкций не содержит одинаковых переменных;

  • каждая элементарная конъюнкция содержит каждую переменную из входящих в данную ДНФ, к тому же в одинаковом порядке.

Любая булева формула, которая не является тождественно ложной, может быть представлена в СДНФ, к тому же единственным образом.

Правила построения СДНФ по таблице истинности

Для каждого набора переменных, при котором функция равна 1, записывается произведение, причем переменные, которые имеют значение 0 берут с отрицанием.

Примеры нахождения СКНФ и СДНФ

Пример 1

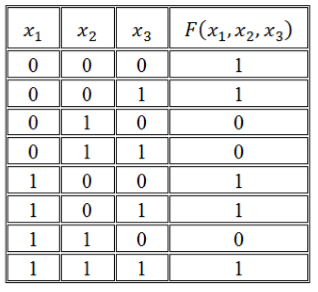
Записать логическую функцию по ее таблице истинности:

Рисунок 1.

Решение:

Воспользуемся правилом построения СДНФ:

Рисунок 2.

Получим СДНФ:

[Fleft(x_1, x_2, x_3right)=left(overline{x_1}wedge overline{x_2}wedge overline{x_3}right)vee left(overline{x_1}wedge overline{x_2}wedge x_3right)vee left(x_1wedge overline{x_2}wedge overline{x_3}right)vee left(x_1wedge overline{x_2}wedge x_3right)vee left(x_1wedge x_2wedge x_3right)]

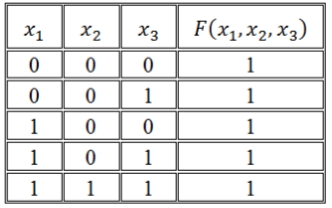
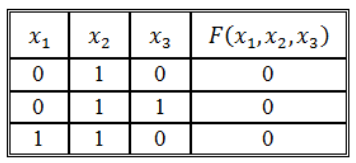
Воспользуемся правилом построения СКНФ:

Рисунок 3.

Получим СКНФ:

[Fleft(x_1, x_2, x_3right)=left(x_1vee overline{x_2}vee x_3right)wedge left(x_1vee overline{x_2}vee overline{x_3}right)wedge left(overline{x_1}vee overline{x_2}vee x_3right)]

«Построение СКНФ и СДНФ по таблице истинности» 👇

Пример 2

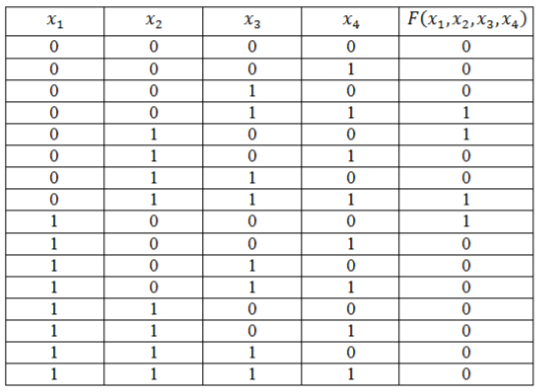
Функция задана таблицей истинности:

Рисунок 4.

Представить эту функцию в виде СДНФ и СКНФ.

Решение:

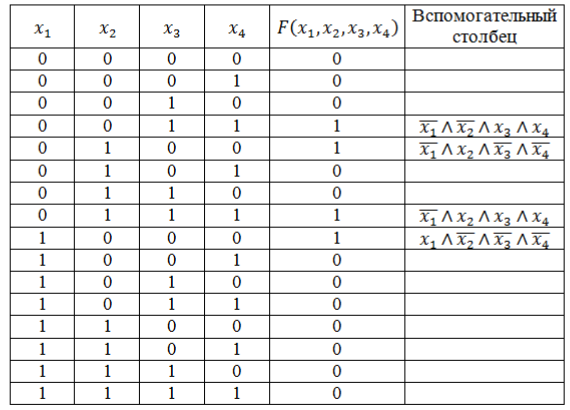
  1. Запишем логическую функцию в СДНФ. Для удобства решения добавим к таблице вспомогательный столбец.

    Используя правило составления СДНФ не забываем вводить знак отрицания для переменных со значением 0. Инвертировать нулевые значения переменных обязательно, т.к. иначе они превратят значения конъюнкций в нули основной функции.

    Рисунок 5.

    Полученные во вспомогательном столбце конъюнкции соединим знаком дизъюнкции и получим искомую логическую функцию в виде СДНФ:

    [Fleft(x_1,x_2,x_3,x_4right)=left(overline{x}wedge overline{y}wedge zwedge fright)vee left(overline{x_1}wedge x_2wedge overline{x_3}wedge overline{x_4}right)vee left(overline{x_1}wedge x_2wedge x_3wedge x_4right)vee left(x_1wedge overline{x_2}wedge overline{x_3}wedge overline{x_4}right).]

  2. Запишем логическую функцию в СКНФ.

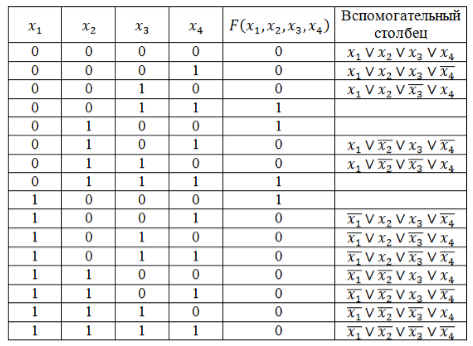
    Используя правило составления СКНФ не забываем вводить знак отрицания для переменных со значением 1. Инвертировать единичные значения переменных обязательно, т.к. иначе они превратят значения дизъюнкций в единицы основной функции.

    Рисунок 6.

    Полученные во вспомогательном столбце дизъюнкции соединим знаком конъюнкции и получим искомую логическую функцию в виде СКНФ:

    [Fleft(x_1,x_2,x_3,x_4right)=left(x_1vee x_2vee x_3vee x_4right)wedge left(x_1vee x_2vee x_3vee overline{x_4}right)wedge left(x_1vee x_2vee overline{x_3}vee x_4right)wedge left(x_1vee overline{x_2}vee x_3vee overline{x_4}right)wedge left(x_1vee overline{x_2}vee overline{x_3}vee x_4right)wedge left(overline{x_1}vee x_2vee x_3vee overline{x_4}right)wedge left(overline{x_1}vee x_2vee overline{x_3}vee x_4right)wedge left(overline{x_1}vee x_2vee overline{x_3}vee overline{x_4}right)wedge left(overline{x_1}vee overline{x_2}vee x_3vee x_4right)wedge left(overline{x_1}vee overline{x_2}vee x_3vee overline{x_4}right)wedge left(overline{x_1}vee overline{x_2}vee overline{x_3}vee x_4right)wedge left(overline{x_1}vee overline{x_2}vee overline{x_3}vee overline{x_4}right).]

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Определение 1.
Функцией
алгебры логики n
переменных называется
любая функция n
переменных
,
аргументы которой принимают два значения
1 и 0, и сама функция принимает одно из
двух значений: 1 или 0.

Всякая формула
алгебры логики есть функция алгебры
логики. Тождественно истинная и то
тождественно ложная формулы есть
постоянные функции.

Можно показать,
что всякую функцию алгебры логики можно
представить в виде формулы логики, и
это представление таково:

(*)

Формулу (*) можно
преобразовать к формуле, которая содержит
только элементарные переменные
высказывания и обладает следующими
свойствами совершенства (или свойствами
(С)):

1) каждое логическое
слагаемое формулы содержит все переменные,
входящие в функцию
;

2) все логические
слагаемые формулы различны;

3) ни одно логическое
слагаемое формулы не содержит одну и
ту же переменную и её отрицание;

4) ни одно логическое
слагаемое формулы не содержит одну и
ту же переменную дважды.

С помощью таблицы
истинности, определяющей функцию
,
легко получить соответствующую формулу
алгебры логики, обладающего свойствами
(С).
Действительно, для каждого набора
значений переменных на котором функция
принимает значение 1, запишем конъюнкцию
элементарных переменных высказываний,
взяв за член конъюнкции,
если значениена указанном наборе значений переменных
есть 1, и отрицание,
если значениеесть 0. дизъюнкция всех полученных таким
образом конъюнкции и будет искомой
формулой.

Определение 2.
Элементарной
конъюнкцией
n
переменных
называется конъюнкция переменных или
их отрицаний.

Определение 3.
Дизъюнктивной
нормальной формой (ДНФ) формулы A
называется
равносильная ей формула, представляющая
собой дизъюнкцию элементарных конъюнкции.

Определение 4.
Совершенной
дизъюнктивной нормальной формой (СДНФ)
формулы A
называется
ДНФ A,
обладающая свойствами (С).

СДНФ A
можно получить двумя способами: а) с
помощью таблицы истинности (см. выше);
б) с помощью равносильных преобразований.

Правило получения
СДНФ из формулы A
с помощью
равносильных преобразований.

1. Для формулы A
получаем
любую ДНФ.

2. Из ДНФ A
путём
равносильных преобразований получаем
СДНФ, последовательно добиваясь
выполнения четырёх свойств СДНФ:

1) Пусть B
есть слагаемое
ДНФ, не содержащее
.
Тогда надо заметить слагаемоеB
в ДНФ A
на слагаемое
.

2) Если в ДНФ A
встретится
два не одинаковых слагаемых
,
то лишнее нужно отбросить, так как.

3) Если в некоторое
слагаемое B
в ДНФ A
переменная
входит дважды, то лишнюю переменную
надо отбросить, так как.

4) Если слагаемое
B
в ДНФ A
содержит
конъюнкцию
,
то лишнюю переменную надо отбросить,
так как,
и следовательно,,
а ложное высказывание из дизъюнкции
можно выбросить (в силу равносильности).

Определение 5.
Элементарной
дизъюнкцией n
переменных
называется дизъюнкция переменных или
их отрицаний.

Определение 6.
Конъюнкция
нормальной формой
(КНФ) формулы А
называется равносильная ей формула,
представляющая собой конъюнкцию
элементарных дизъюнкций.

Определение 7.
Совершенной
конъюнктивной нормальной формой формулы
А (СКНФ А),
называется КНФ А,
удовлетворяющая четырем свойствам:

1) все элементарные
дизъюнкции, входящие в КНФ А,
содержат все переменные;

2) все элементарные
дизъюнкции, входящие в КНФ А,
различны;

3) каждая элементарная
дизъюнкция, входящая в КНФ А,
содержит переменную один раз;

4) ни одна элементарная
дизъюнкция, входящая в КНФ А,
не содержит переменную и её отрицание.

СКНФ А
можно получить двумя способами: а) с
помощью таблицы истинности (используя
закон двойственности
,
получаем с помощью таблицы истинности,
и, взяв отрицание
,
получаем СКНФА);
б) с помощью равносильных преобразований.

Правило получения
СКНФ из формулы А
с помощью
равносильных преобразований.

1. Для формулы А
получаем любую КНФ.

2. Из КНФ А
путём равносильных преобразований
получаем СКНФ А,
последовательно добиваясь выполнения
четырёх свойств СКНФ.

1) Если элементарная
дизъюнкция В,
входящая в КНФ А,
не содержит переменную
,
тогда заменяемВ
на
.

2) Если в некоторую
элементарную дизъюнкцию В
переменная
,
входит дважды, то лишнюю переменную
нужно отбросить, так как.

3) Если КНФ А
содержит две одинаковых элементарных
дизъюнкции, то одну можно отбросить,
так как
.

4) Если в элементарную
дизъюнкцию входит пара
,
то её можно отбросить, так как,
а истинное высказывание из конъюнкции
можно выбросить (в силу равносильности).

Пример 1.
Найти формулу, определяющую функцию
Ф(x,y,z),
по заданной таблице истинности:

x

y

z

Ф(x,y,z)

1

1

1

1

1

1

0

0

1

0

1

0

1

0

0

0

0

1

1

1

0

1

0

1

0

0

1

1

0

0

0

1

Решение. Используя
правило получения формулы алгебры
логики из таблицы истинности для функции
Ф(x,y,z),
получим:

.

Упростив эту
формулу, получим:

Таким образом,
искомой формулой, определяющей функцию
Ф(x,y,z),
можно считать
,
или,
или какую-нибудь другого из равносильных
формул.

Пример 2. Следующую
формулу привести к СДНФ, предварительно
приведя её равносильными преобразованиями
к ДНФ:
.

Решение.

Ответ:
.

Пример 3. Для
формулы из примера 2 найти СДНФ путём
составления таблицы истинности.

Решение. Составим
таблицу истинности для формулы
.

a

b

C

bc

ab

A

1

1

1

1

1

1

1

1

1

0

0

1

1

1

1

0

1

0

0

1

1

1

0

0

0

0

1

1

0

1

1

1

0

0

0

0

1

0

0

0

1

0

0

0

1

0

0

1

0

0

0

0

0

0

1

0

Тогда
.

Пример 4. Для
формулы из примера 2 найти СКНФ путём
равносильных преобразований, предварительно
приведя ее к КНФ.

Решение.
Из примера 2: .Далее

.

Ответ:
.

Пример 5.
Для формулы из примера 2 найти СКНФ,
записав предварительно ДНФ её отрицание,
а потом воспользовавшись формулой
двойственности.

Решение.
.

Все формулы алгебры
логики делятся на три класса: 1) тождественно
истинные; 2) тождественно ложные; 3)
выполнимые.

Формулу А
называют выполнимой,
если она принимает значение 1 хотя бы
на одном наборе значений входящих в неё
переменных и не является тождественно
истиной.

Теореме. Для
того, чтобы формула алгебры логики была
тождественно истинна (ложна), необходимо
и достаточно любая элементарная
дизъюнкция (конъюнкция), входящая в КНФ
А (ДНФ
А),
содержала переменную и её отрицание.

Пример 6. Будет
ли формула
тождественно
истинной, тождественно ложной или
выполнимой?

Решение. Приведём
пример к какой-либо нормальной форме:

Получение ДНФ не
является тождественно ложной, так как
каждая элементарная конъюнкция не
содержит переменную и её отрицание.
Следовательно, исходная формула
тождественно истинна или выполнима.
Преобразуем данную формулу к КНФ.

Это произведение
не является тождественно истинным, так
как элементарная сумма не тождественно
истинна, следовательно, она выполнима.

1.34. По
таблице истинности найдите формулы,
определяющие функции
,,,,
и придайте им более простой вид:

x

y

z

1

1

1

0

1

1

1

1

1

0

1

1

1

0

1

0

1

1

0

0

1

1

0

0

1

0

0

1

0

1

1

0

0

0

0

0

1

0

0

1

1

0

0

0

1

1

0

1

1

0

0

0

0

0

0

0

1.35. Пусть
— булевая функция, которая принимает
значение 1 тогда и только тогда, когда
точно одна из переменных принимает
значение 1. Составьте таблицу для функциии выразите эту функцию через основные
логические операции.

1.36. Назовём
функцией большинства
булеву
функцию от трёх переменных, значения
которой принимает большинство переменных.

а) Составьте
таблицу, определяющую функцию большинства
и выразите эту функцию через основные
операции.

б) Упростите
выражение
.

1.37. Булева
функции
называется двойственной по отношению
к булевой функции,
если

.

Для каждой
булевой функции от двух переменных
найдите двойственную ей булеву функцию.

1.38. Булева
функции
называется:

а) сохраняющей 0,
если
;

б) сохраняющей 1,
если
.

Среди булевых
функции от одной и двух переменных найти
все функции, сохраняющие 1, и все функции,
сохраняющие 0.

1.39. Для
следующих формул найти СДНФ и СКНФ,
каждую двумя способами (путём равносильности
преобразований и используя таблицы
истинности):

1)
;

2)
;

3) ;

4)
;

5)
;

6)
;

7)
;

8)
;

9)
;

10)
.

1.40. Найдите
СДНФ для всякой тождественно истинной
формулы, содержащей: 1) одно переменное,
2) два переменных, 3) три переменных.

1.41. Найдите
СКНФ для всякой тождественно истинной
формулы, содержащей: 1) одно переменное,
2) два переменных, 3) три переменных.

1.42. Докажите
равносильность формул
и
сравнением
их совершенно нормальных форм (конъюктивных
или дизъюктивных).

1.43. Найдите более простой вид формул,
имеющих следующие совершенные нормальные
формы:

1)
;

2)
;

3)
;

4)
).

1.44. Используя критерий тождественной
истиннос­ти и тождественной ложности
формулы, установить бу­дет ли данная
формула тождественно истинной,
тожде­ственно ложной или выполнимой:

1)
;

2)
;

3)
;

4)
;

5)
;

6)
.

Источник

    • 6. Канонические формы логических формул, СКНФ и СДНФ

6. Канонические формы логических формул, СКНФ и СДНФ

Канонические формы логических формул

Всякая логическая формула определяет некоторую булевую функцию. С другой стороны, для всякой булевой функции можно записать бесконечно много формул, ее представляющих. Одна из основных задач алгебры логики — нахождение канонических форм (т. е. формул, построенных по определенному правилу, канону), а также наиболее простых формул, представляющих булевы функции.

Если логическая функция выражена через дизъюнкцию, конъюнкцию и отрицание переменных, то такая форма представления называется нормальной. Среди нормальных форм выделяют такие, в которых функции записываются единственным образом. Их называют совершенными.

Особую роль в алгебре логики играют классы дизъюнктивных и конъюнктивных совершенных нормальных форм. В их основе лежат понятия элементарной дизъюнкции и элементарной конъюнкции. 

Формулу называют элементарной конъюнкцией, если она является конъюнкцией одной или нескольких переменных, взятых с отрицанием или без отрицания. Одну переменную или ее отрицание считают одночленной элементарной конъюнкцией.

Формула называется элементарной дизъюнкцией, если она является дизъюнкцией (быть может, одночленной) переменных и отрицаний переменных.

ДНФ И СДНФ

Формула называется дизъюнктивной нормальной формой (ДНФ), если она является дизъюнкцией неповторяющихся элементарных конъюнкций. ДНФ записываются в виде: А1 v А2 v … v Аn , где каждое Аn — элементарная конъюнкция.

Формула А от k переменных называется совершенной дизъюнктивной нормальной формой (СДНФ), если: 
1.А является ДНФ, в которой каждая элементарная конъюнкция есть конъюнкция k переменных х1, х2, …, xk, причем на i-м месте этой конъюнкции стоит либо переменная хi либо ее отрицание;
2. Все элементарные конъюнкции в такой ДНФ попарно различны. 

Например:       А = х1 & НЕ х2 v х1 & х2

Совершенная дизъюнктивная нормальная форма представляет собой формулу, построенную по строго определенным правилам с точностью до порядка следования элементарных конъюнкций (дизъюнктивных членов) в ней. 

Она является примером однозначного представления булевой функции в виде формульной (алгебраической) записи.

Теорема о СДНФ 

Пусть f(x1 х2, …, хn) – булева функция от n переменных, не равная тождественно нулю. Тогда существует совершенная дизъюнктивная нормальная форма, выражающая функцию f. 

Алгоритм построения СДНФ по таблице истинности:

1.В таблице истинности отмечаем наборы переменных, на которых значение функции f = 1. 
2.Записываем для каждого отмеченного набора конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае – ее отрицание. 
3.Все полученные конъюнкции связываем операциями дизъюнкции.

КНФ И СКНФ
 

Формула называется конъюнктивной нормальной формой (КНФ), если она является конъюнкцией неповторяющихся элементарных дизъюнкций. КНФ записываются в виде: А1 & А2 & … & Аn , где каждое Аn – элементарная дизъюнкция. 

Формула А от k переменных называется совершенной конъюнктивной нормальной формой (СКНФ), если:
1. А является КНФ, в которой каждая элементарная дизъюнкция есть дизъюнкция k переменных x1, х2, …, хk, причем на i-м месте этой дизъюнкции стоит либо переменная xi, либо ее отрицание;
2. Все элементарные дизъюнкции в такой КНФ попарно различны. 

Например: А = (х1 v НЕ х2) & (х1 v х2) 

Теорема о СКНФ 

Пусть f(x1 х2, …, хn) – булева функция от n переменных, не равная тождественно нулю. Тогда существует совершенная конъюнктивная нормальная форма, выражающая функцию f.

Алгоритм построения СКНФ по таблице истинности:

1.В таблице истинности отмечаем наборы переменных, на которых значение функции f = 0.
2.Записываем для каждого отмеченного набора дизъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 0, то в дизъюнкцию включаем саму переменную, в противном случае – ее отрицание.
3.Все полученные дизъюнкции связываем операциями конъюнкции.

Из алгоритмов построения СДНФ и СКНФ следует, что если на большей части наборов значений переменных функция равна 0, то для получения ее формулы проще построить СДНФ, в противном случае – СКНФ. 

Пример

Построить формулу для функции f(x1, х2, х3), заданной таблицей истинности:

 x1  x2  x3  F
 0  0  0  0
 0  0  1  0
 0  1  0  1
 0  1  1  0
 1  0  0  1
 1  0  1  1
 1  1  0  0
 1  1  1  0

Решение 

На большей части наборов значений переменных функция равна 0, поэтому проще построить СДНФ

 x1  x2  x3  F
 0  0  0  0
 0  0  1  0
 0  1  0  1
 0  1  1  0
 1  0  0  1
 1  0  1  1
 1  1  0  0
 1  1  1  0

F(x1,х2,х3) =  x1 & х2 & х3 v x1 & х2 & х3 v x1 & х2 & х3.

ć

Неизвестный пользователь,

27 янв. 2013 г., 06:26
Источник

Понравилась статья? Поделить с друзьями:
  • Металлиди как найти дорожку
  • Мертвое море как найти на карте
  • Как найти клиентов для эйвон
  • Как найди камеру на компьютер
  • Как найти розу симс 4