Что такое СДНФ
Нормальная форма логической формулы характеризуется тем, что для нее не свойственны эквивалентность, отрицание формул неэлементарного типа и знаки импликации.
Существует две формы нормального типа: КНФ (конъюнктивная нормальная форма) и ДНФ (дизъюнктивная нормальная форма).
Определение
СДНФ — совершенная дизъюнктивная нормальная форма формулы. СДНФ — способ написания функции алгебры логики в качестве логического выражения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
СДНФ формулы — это равнозначная ей формула, которая представляет собой дизъюнкцию элементарных конъюнкций, при которых функция достигает показателя «1».
ДНФ выглядит следующим образом:
((A;wedge;overline B;wedge;C);vee;(B;wedge;C))
СДНФ обладает некоторыми определенными свойствами:
- включает различные элементарные конъюнкции;
- все логические слагаемые формулы содержат все переменные, которые входят в функцию F;
- ни в одном логическом слагаемом не содержится переменная и её отрицание.
К СДНФ возможно привести любую формулу алгебры логики. Исключение составляет только тождественно ложная формула. СДНФ можно получить как используя таблицы истинности, так и через равносильные преобразования.
Примечание
При построении таблицы истинности важно помнить, что логические переменные со значением «0» необходимо брать с отрицанием.
Что такое СКНФ
Определение
СКНФ — совершенная конъюнктивная нормальная форма. Формулу можно назвать таковой, когда она — конъюнкция неповторяющихся элементарных дизъюнкций.
КНФ имеет вид:
((A;vee;overline B;vee;C);wedge;(A;vee;C))
Формула должна соответствовать нескольким условиям, чтобы называться СКНФ:
- в ней отсутствуют одинаковые элементарные дизъюнкции;
- дизъюнкции не содержат одинаковые переменные;
- все дизъюнкции содержат каждую переменную из входящих в конъюнктивную нормальную функцию такого типа.
Правила построения по таблице истинности
Дизъюнктивная форма
Если функция равна 1, то для всех наборов переменных, при которых это происходит, записывается произведение. Однако переменные, которые имеют значение 0, берутся с отрицанием.
Конъюнктивная форма
Когда функция равна 0, то для всех наборов переменных, при которых это происходит, записывается сумма. Однако переменные, которые имеют значение 1, берутся с отрицанием.
Алгоритм приведения к СДНФ и СКНФ
Рассмотрим логическую функцию в виде таблицы истинности.
Алгоритм построения СДНФ по таблице истинности выглядит следующим образом:
- Отметить наборы переменных, значение функции F на которых равно 1.
- Записать для всех отмеченных наборов конъюнкцию всех переменных так: если значение некоторой переменной в этом наборе равняется 1, в конъюнкцию включается сама переменная. В случае противного результата, в конъюнкцию включается ее отрицание.
- Связать полученные конъюнкции операциями дизъюнкции.
Построим совершенную ДНФ:
И как результат получим следующую СДНФ:
(F(x_1,;x_2,;x_3);=;(overline{x_1}wedgeoverline{x_2}wedgeoverline{x_3});vee(overline{x_1};wedge;overline{x_2};wedge;x_3);vee(x_1;wedge;overline{x_2};wedge;overline{x_3});vee;(x_1;wedge;overline{x_2};wedge;x_3);vee;(x_1;wedge;x_2;wedge;x_3))
Алгоритм построения СКНФ по таблице истинности выглядит следующим образом:
- Отметить в таблице истинности наборы переменных, значение функции F на которых равно 0.
- Записать для всех отмеченных наборов дизъюнкцию всех переменных — в том случае, когда значение некоторой переменной в этом наборе равняется 0, в дизъюнкцию включается сама переменная, если происходит наоборот, то в дизъюнкцию включается ее отрицание.
- Связать полученные дизъюнкции операциями конъюнкции.
Построим совершенную КНФ:
И как результат получим следующую СКНФ:
(F(x_1,;x_2,;x_3);=;(x_1;vee;overline{x_2};vee;x_3);wedge;(x_1;vee;overline{x_2};vee;overline{x_3});wedge;(overline{x_1};vee;overline{x_2};vee;x_3))
Рассмотрев алгоритмы построения СДНФ и СКНФ ясно, что в случае подавляющей части наборов значений переменных функция равна 0, то значительно легче построить и СДНФ для получения ее формулы, а в обратном случае — СКНФ.
Доказательство эквивалентности
Эквивалентность — понятие, означающее, что две и более формул представляют одну и ту же функцию. Для обозначения эквивалентности могут использоваться следующие знаки: ( equiv , = , Leftrightarrow .)
Доказать эквивалентность формул можно двумя способами.
- Первый заключается в построении и сравнении таблиц истинности обеих функций. В этом случае результат будет истинным только в том случае, когда оба высказывания либо ложны, либо истинны.
- Второй вариант — метод эквивалентных преобразований. Суть этого метода — построение цепи эквивалентных формул на основе ранее доказанных эквивалентностей.
Далее следуют примеры с некоторыми эквивалентными преобразованием в булевой алгебре и новыми эквивалентностями, которые возможно получить с их помощью.
Поглощение
(x;vee;xy;=;x)
(x(x;vee;y);=;x;)
Доказательство эквивалентности:
(x;vee;xy;=;x;cdot;l;vee;xy;=;x(l;vee;y);=;x)
(x(x;vee;y);=;xx;vee;xy;=;x;vee;xy;=;x)
Склеивание
(xy;vee;xoverline y;=;x)
Доказательство эквивалентности:
(xy;vee;xoverline y;=;x(y;vee;overline y);=;x;cdot;l;=;x)
Обобщенное склеивание
(xz;vee;yoverline z;vee;xy;=;xz;vee yoverline z)
Доказательство эквивалентности
(xz;vee;yoverline z;vee;xy;=;xz;vee yoverline z;vee;xyz;vee;xyoverline z;=;xz;vee;yoverline z)
Расщепление
(x;vee;overline xy;=;x;vee;y)
Доказательство эквивалентности
(x;vee;overline xy;=;xy;vee;xoverline y;vee;overline xy;=;xy;vee;xoverline y;vee;xy;vee;overline xy;=;x;cdot;l;;vee;y;cdot;l;=;x;vee;y)
Примеры с решением
Задача №1
Приведите к СКНФ (((((Arightarrow B)rightarrowoverline A)rightarrowoverline B)rightarrowoverline C)).
Через применение закона де Моргана и правила( x;rightarrow;y;=;overline x;vee;y) упростим выражения:
(F;=;((((A;rightarrow;B);rightarrow;overline A);rightarrowoverline B);rightarrow;overline C);=;(((overline A;vee;B);rightarrow;overline A);rightarrow;overline B);rightarrowoverline C;);=)
(=;((((overline A;vee;B);rightarrowoverline A);rightarrowoverline B);rightarrow;overline C);=;((overline{((overline A;vee;B)};vee;overline A);rightarrowoverline B);rightarrowoverline C);=)
(=(((overline A;vee;B);vee;overline A);rightarrow;overline B);rightarrow;overline C);=((overline{(overline{(overline Avee B)};vee;overline A;)};vee;overline B);rightarrow;overline C);=)
(=;(overline{(overline{(overline{(overline A;vee;B)};vee;overline A)};vee;overline B)};vee;overline C);=;(((A;vee;B);vee;overline A);vee;overline B);vee;overline C;=)
(=;((overline{(overline A;vee;B)};vee;overline A);wedge;B);vee;overline C;=;(((A;wedge;overline B);vee;overline A);wedge B);vee;overline C;=)
(=((Aoverline B;vee;overline A);vee;overline A);wedge;B);vee;overline C;=(((A;wedge;overline B);vee;overline A);wedge;B);vee;overline C;=)
(=;((Aoverline B;vee;overline A);wedge;B);vee;overline C;=;(Aoverline BB;vee;overline AB);vee;overline C;=;(0;vee;overline AB);vee;overline C;=;overline AB;vee;overline C)
Далее приведем выражение к КНФ:
(F;=;overline AB;vee;overline C;;=;(overline A;vee;overline C);wedge;(B;vee;overline C))
Далее приведем выражение к СКНФ:
(F;=;(overline A;vee;overline C);wedge;(B;vee;overline C);=;(overline A;vee:overline C;vee;Boverline B);wedge;(Aoverline A;vee;B;v;overline C);=)
(=;(overline A;vee;overline C;vee;B);wedge;(A;vee;B;vee;overline C);wedge;(overline A;vee;overline C;vee;overline B);wedge;(overline A;vee;B;;overline C))
Задача №2
Используя эквивалентные преобразования, постройте ДНФ функции (f(widetilde x^n))
(f(widetilde x^3) = (overline{x_1}x_2;oplus;x_3);cdot;(x_1x_3;rightarrow;x_2))
Преобразуем функцию:
(f(widetilde x^3) = (overline{x_1}x_2;oplus;x_3);cdot;(x_1x_3;rightarrow;x_2) = ((overline{x_1}x_2;cdot;overline{x_3};);vee;(overline{overline{x_1}x_2};cdot;x_3));cdot;(overline{x_1x_3};vee;x_2);=)
(=;((overline{x_1}x_2overline{x_3});vee;((overline{overline{x_1}};vee;overline{x_2});x_3);cdot;(overline{x_1};vee;overline{x_3};vee;x_2);=;((overline{x_1}x_{2;}overline{x_3});vee;((x_1;vee;overline{x_2});x_3);cdot;(overline{x_1};vee;overline{x_3};vee;x_2);=)
(=;(overline{x_1}x_2overline{x_3};vee;x_1x_3;vee;overline{x_2}x_3);cdot;(overline{x_1};vee;overline{x_3};vee;x_2);=)
(=(overline{x_1}x_2overline{x_3};cdot(x_1vee x_3vee x_2);vee;x_1x_3;cdot;(overline{x_1};vee;overline{x_3};vee;x_2);vee;overline{x_2}x_3;cdot;(overline{x_1};vee;overline{x_3};vee;x_2));=)
(=;(overline{x_1}x_2overline{x_3};vee;(x_1;x_3overline{x_1};vee;x_1x_3overline{x_3};vee;x_1x_3x_2);vee;(overline{x_2}x_3overline{x_1};vee;overline{x_2}x_3overline{x_3};vee;overline{x_2}x_3x_2);=)
(=;(overline{x_1}x_2overline{x_3};vee;0;vee;0;vee;x_1x_2x_3;vee;overline{x_1}overline{x_2}x_3;vee;0;vee;0);=)
(=;overline{x_1}x_2overline{x_3};vee;x_1x_2x_3;vee;overline{x_1}overline{x_2}x_3)
Диана Загировна Филиппенкова
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Нормальная форма логической формулы не содержит знаков импликации, эквивалентности и отрицания неэлементарных формул.
Нормальная форма существует в двух видах:
-
конъюнктивная нормальная форма (КНФ) — конъюнкция нескольких дизъюнкций, например, $left(Avee overline{B}vee Cright)wedge left(Avee Cright)$;
-
дизъюнктивная нормальная форма (ДНФ) — дизъюнкция нескольких конъюнкций, например, $left(Awedge overline{B}wedge Cright)vee left(Bwedge Cright)$.
СКНФ
Совершенная конъюнктивная нормальная форма (СКНФ) — это КНФ, удовлетворяющая трем условиям:
-
не содержит одинаковых элементарных дизъюнкций;
-
ни одна из дизъюнкций не содержит одинаковых переменных;
-
каждая элементарная дизъюнкция содержит каждую переменную из входящих в данную КНФ.
Любая булева формула, которая не является тождественно истинной, может быть представлена в СКНФ.
Правила построения СКНФ по таблице истинности
Для каждого набора переменных, при котором функция равна 0, записывается сумма, причем переменные, которые имеют значение 1, берутся с отрицанием.
СДНФ
Совершенная дизъюнктивная нормальная форма (СДНФ) — это ДНФ, удовлетворяющая трем условиям:
-
не содержит одинаковых элементарных конъюнкций;
-
ни одна из конъюнкций не содержит одинаковых переменных;
-
каждая элементарная конъюнкция содержит каждую переменную из входящих в данную ДНФ, к тому же в одинаковом порядке.
Любая булева формула, которая не является тождественно ложной, может быть представлена в СДНФ, к тому же единственным образом.
Правила построения СДНФ по таблице истинности
Для каждого набора переменных, при котором функция равна 1, записывается произведение, причем переменные, которые имеют значение 0 берут с отрицанием.
Примеры нахождения СКНФ и СДНФ
Пример 1
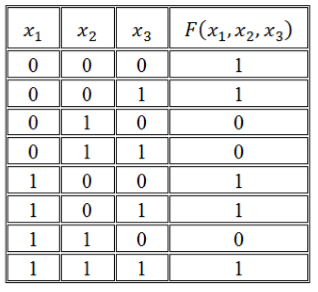
Записать логическую функцию по ее таблице истинности:
Рисунок 1.
Решение:
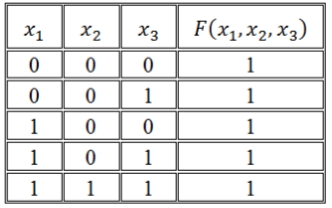
Воспользуемся правилом построения СДНФ:
Рисунок 2.
Получим СДНФ:
[Fleft(x_1, x_2, x_3right)=left(overline{x_1}wedge overline{x_2}wedge overline{x_3}right)vee left(overline{x_1}wedge overline{x_2}wedge x_3right)vee left(x_1wedge overline{x_2}wedge overline{x_3}right)vee left(x_1wedge overline{x_2}wedge x_3right)vee left(x_1wedge x_2wedge x_3right)]
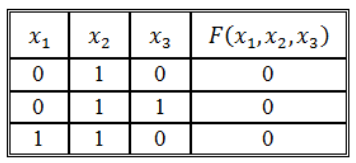
Воспользуемся правилом построения СКНФ:
Рисунок 3.
Получим СКНФ:
[Fleft(x_1, x_2, x_3right)=left(x_1vee overline{x_2}vee x_3right)wedge left(x_1vee overline{x_2}vee overline{x_3}right)wedge left(overline{x_1}vee overline{x_2}vee x_3right)]
«Построение СКНФ и СДНФ по таблице истинности» 👇
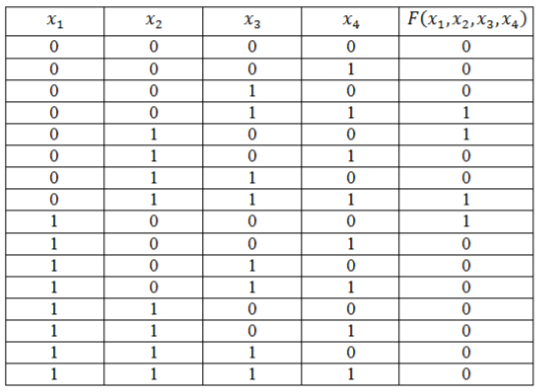
Пример 2
Функция задана таблицей истинности:
Рисунок 4.
Представить эту функцию в виде СДНФ и СКНФ.
Решение:
-
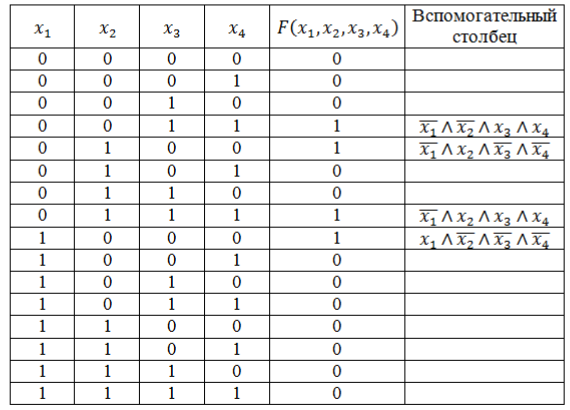
Запишем логическую функцию в СДНФ. Для удобства решения добавим к таблице вспомогательный столбец.
Используя правило составления СДНФ не забываем вводить знак отрицания для переменных со значением 0. Инвертировать нулевые значения переменных обязательно, т.к. иначе они превратят значения конъюнкций в нули основной функции.
Рисунок 5.
Полученные во вспомогательном столбце конъюнкции соединим знаком дизъюнкции и получим искомую логическую функцию в виде СДНФ:
[Fleft(x_1,x_2,x_3,x_4right)=left(overline{x}wedge overline{y}wedge zwedge fright)vee left(overline{x_1}wedge x_2wedge overline{x_3}wedge overline{x_4}right)vee left(overline{x_1}wedge x_2wedge x_3wedge x_4right)vee left(x_1wedge overline{x_2}wedge overline{x_3}wedge overline{x_4}right).]
-
Запишем логическую функцию в СКНФ.
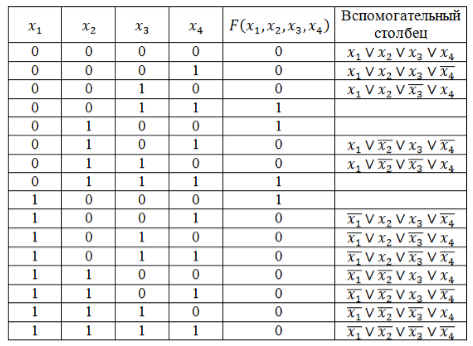
Используя правило составления СКНФ не забываем вводить знак отрицания для переменных со значением 1. Инвертировать единичные значения переменных обязательно, т.к. иначе они превратят значения дизъюнкций в единицы основной функции.
Рисунок 6.
Полученные во вспомогательном столбце дизъюнкции соединим знаком конъюнкции и получим искомую логическую функцию в виде СКНФ:
[Fleft(x_1,x_2,x_3,x_4right)=left(x_1vee x_2vee x_3vee x_4right)wedge left(x_1vee x_2vee x_3vee overline{x_4}right)wedge left(x_1vee x_2vee overline{x_3}vee x_4right)wedge left(x_1vee overline{x_2}vee x_3vee overline{x_4}right)wedge left(x_1vee overline{x_2}vee overline{x_3}vee x_4right)wedge left(overline{x_1}vee x_2vee x_3vee overline{x_4}right)wedge left(overline{x_1}vee x_2vee overline{x_3}vee x_4right)wedge left(overline{x_1}vee x_2vee overline{x_3}vee overline{x_4}right)wedge left(overline{x_1}vee overline{x_2}vee x_3vee x_4right)wedge left(overline{x_1}vee overline{x_2}vee x_3vee overline{x_4}right)wedge left(overline{x_1}vee overline{x_2}vee overline{x_3}vee x_4right)wedge left(overline{x_1}vee overline{x_2}vee overline{x_3}vee overline{x_4}right).]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Известно два способа задания логических
функций: с помощью формулы и с помощью
таблицы истинности. По формуле легко
составляется таблица. На практике при
конструировании различных электронных
устройств часто возникает обратная
задача – от таблицы истинности перейти
к формуле, чтобы на ее основе построить
функциональную схему.
Введем следующие определения:
Элементарной
конъюнкцией называется конъюнкция
нескольких переменных, взятых с отрицанием
или без отрицания, причем среди переменных
могут быть одинаковые.
Элементарной
дизъюнкцией называется дизъюнкция
нескольких переменных, взятых с отрицанием
или без отрицания, причем среди переменных
могут быть одинаковые.
Всякую дизъюнкцию
элементарных конъюнкций назовем
дизъюнктивной нормальной формой (ДНФ).
Всякую конъюнкцию
элементарных дизъюнкций назовем
конъюнктивной нормальной формой (КНФ).
Совершенной
дизъюнктивной нормальной формой (СДНФ)
называется ДНФ, в которой нет одинаковых
элементарных конъюнкций и все конъюнкции
состоят из одного и того же набора
переменных, в который каждая переменная
входит только один раз (возможно, с
отрицанием).
Совершенной
конъюнктивной нормальной формой (СКНФ)
называется КНФ, в которой нет одинаковых
элементарных дизъюнкций и все дизъюнкции
состоят из одного и того же набора
переменных, в который каждая переменная
входит только один раз (возможно, с
отрицанием).
Приведем примеры формул, соответствующих
и не соответствующих этим определениям:
|
НАЗВАНИЕ
В |
Формула,
соответствующая |
ФОРМУЛА,
НЕ ОПРЕДЕЛЕНИЮ |
|
Элементарная дизъюнкция |
|
|
|
Элементарная конъюнкция |
|
|
|
ДНФ |
|
ДНФ |
|
КНФ |
|
КНФ |
|
СДНФ |
|
|
|
СКНФ |
|
|
Любую функцию,
кроме констант 0 и 1, можно представить
в виде как СДНФ, так и СКНФ.
Этот факт является теоремой алгебры
логики. Из него следует, что любая формула
(кроме констант 0 и 1) может быть преобразован
к виду как СДНФ, так и СКНФ. Константа 0
может быть представлена только СКНФ
(),
а константа 1 – только СДНФ ().
Из вышесказанного следует, что если
надо построить формулу некоторой функции
по таблице истинности этой функции, то
всегда можно получить СКНФ или СДНФ
этой функции.
Алгоритм получения
СДНФ по таблице истинности:
-
Отметить те строчки таблицы истинности,
в последнем столбце которых стоят 1:
-
X
Y
F(X,Y)
0
0
0
0
1
1*
1
0
1*
1
1
0
-
Выписать для каждой отмеченной строки
конъюнкциювсех переменных следующим
образом: если значение некоторой
переменной в данной строкеравно 1,
то в конъюнкцию включатьсаму эту
переменную, еслиравно 0, то ееотрицание:
– для 2-й строки;
– для 3-й строки.
-
Все полученные конъюнкции связать в
дизъюнкцию:
.
Алгоритм получения
СКНФ по таблице истинности:
-
Отметить те строки таблицы истинности,
в последнем столбце которых стоит 0:
-
X
Y
F(X,Y)
0
0
0*
0
1
1
1
0
1
1
1
0*
-
Выписать для каждой отмеченной строки
дизъюнкциювсех переменных следующим
образом: если значение некоторой
переменной в данной строкеравно 0,
то в дизъюнкцию включатьсаму эту
переменную, еслиравно 1, то ееотрицание:
– для 1-й строки;
– для 4-й строки.
-
Все полученные дизъюнкции связать в
конъюнкцию:
.
Покажем, что полученные по двум алгоритмам
СДНФ и СКНФ эквивалентны. Преобразуем
СКНФ по правилам алгебры логики:
.
Примечание: для нахождения
формулы по таблице истинности рекомендуется
использовать тот из двух алгоритмов, в
котором в таблице помечается меньше
строк.
-
ТИПОВЫЕ ЛОГИЧЕСКИЕ
УСТРОЙСТВА ЭВМ.
К типовым логическим устройствам ЭВМ
относятся сумматоры, полусумматоры,
триггеры, счетчики, регистры, шифраторы,
дешифраторы.
-
СУММАТОРЫ.
Сумматор является
основным узлом арифметико-логического
устройства ЭВМ и служит для суммирования
чисел посредством поразрядного сложения.
Сумматор выполняет сложение многозначных
двоичных чисел. Он представляет собой
последовательное соединение одноразрядных
двоичных сумматоров, каждый из которых
осуществляет сложение в одном разряде.
При этом если сумма двух цифр в данном
разряде больше или равна основанию
используемой системы счисления, то
возникает перенос старшего разряда в
соседний сумматор.
Одноразрядный сумматор должен иметь
два выхода: для суммы и для переносимого
значения. У него может быть два или три
(для складываемых значений и значения
переноса) входа.
Одноразрядный
двоичный сумматор на два входа и два
выхода называется одноразрядным
полусумматором.
Одноразрядный
двоичный сумматор на три входа и два
выхода называется одноразрядным
сумматором на три входа.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Что нужно знать о СДНФ — основные сведения
Содержание:
-
Что такое СДНФ
- Краткая теория
- Построение СДНФ по таблице истинности
- Алгоритм построения СДНФ для булевой функции
-
Пример построения СДНФ
- Примеры СДНФ для некоторых функций
-
Алгоритм приведения к СДНФ (как решать выражения с СДНФ)
- Поглощение
- Склеивание
- Обобщенное склеивание
- Расщепление
- Примеры для самостоятельного нахождения СДНФ/СКНФ
Что такое СДНФ
Совершенная дизъюнктивная нормальная форма (или сокращенно СДНФ) — один из вариантов представления функции из раздела алгебры логики (или булевой функции) в форме логического выражения. Является также частным случаем дизъюнктивной нормальной функции (или сокращенно ДНФ), которая удовлетворяет таким трем условиям:
- в ней не существует одинаковых слагаемых (или элементарных конъюнкций);
- в каждом слагаемом не существует повторяющихся переменных;
- каждое слагаемое содержит в своем составе все переменные, от которых зависит значение булевой функции (каждая переменная может входить в слагаемое либо в инверсной, либо в прямой формах).
Любая булева формула, которая не является тождественно ложной, способна быть приведена к СДНФ. Более того, единственным способом, то есть для любой выполнимой функции в алгебре логики есть собственная СДНФ, притом единственная.
Примечание 1
Булева формула — формула из логики высказываний. В нее могут входить логические переменные, а также пропозициональные связки, такие как конъюнкцию ((«vee»)), дизъюнкцию ((«wedge»)), отрицание ((«neg»)) и иные.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Краткая теория
ДНФ является «суммой произведений». Более того, в качестве алгебраического действия «умножения» будет выступать операция И (то есть конъюнкция), а алгебраическим действием «сложения» выступает операция ИЛИ (то есть дизъюнкция). Сомножителями можно считать разные переменные, более того они могут входить в произведение как в инверсном, так и в прямом виде.
Представим пример простой ДНФ:
(F(A,B,C,D,E)=overline{A}B+Aoverline{B}E+Boverline{C}D)
В структуре ДНФ могут быть повторяющиеся слагаемые, а в структуре каждого слагаемого могут находиться повторяющиеся сомножители. К примеру:
(F(A,B,C,D,E)=overline{A}Boverline{B}+Aoverline{B}EA+Boverline{C}D+Boverline{C}D)
С точки зрения алгебры подобное клонирование лишено всякого смысла, потому что в булевой алгебре действие «умножения» любого выражения на само себя, а также действие сложения выражения с самим собой не изменяет результата ((x+x=x; xtimes{x}=x)). Действие сложения выражения со своей инверсией, а также умножение на свою инверсию производит константы ((x+overline{x}=1; xtimes{overline{x}}=0)).
Возможно удалить из последнего выражения повторяющиеся сомножители и слагатели таким способом:
(F(A,B,C,D,E)=overline{A}BB+Aoverline{B}EA+Boverline{C}D+Boverline{C}D=overline{A}times(Boverline{B})+(AA)times{B}E+Boverline{C}D=overline{A}times0+Aoverline{B}E+Boverline{C}D=Aoverline{B}E+Boverline{C}D.)
Из-за этого ДНФ, у которых наблюдаются повторяющиеся слагаемые и сомножители используются часто только для вспомогательных целей, к примеру, в процессе аналитического преобразования алгебраических выражений.
СДНФ — каноническая форма реализации булевой функции в формате ДНФ. В ней повторы сомножителей и слагаемых запрещаются. Более того, в каждом слагаемом должны быть все переменные (в инверсной и прямой форме).
Приведем пример СДНФ:
(F(A,B,C,D,E)=overline{A}BCDE+Aoverline{B}Coverline{D}E+ABoverline{C}Doverline{E})
Значение СДНФ проявляется в том, что:
- для каждой определенной функции СДНФ обладает единичным и однозначным характером;
- СДНФ обладает точным соответствием с таблицей истинности функции. Каждое слагаемое СДНФ будет соответствовать одной графе в таблице истинности, в которой функция равняется единице. Так получится, что количество слагаемых в СДНФ будет равно числу единичных значений, которые способна принимать булева функция в собственной области определения;
- СДНФ можно просто получить, исходя из таблицы истинности функции;
- СДНФ крайне удобна как базовое выражение для минимизации функции, просто в ней находятся слагаемые, которые пригодные для «склейки».
({displaystyle F(A,B,C,D,E)={bar {A}}BCDE+A{bar {B}}C{bar {D}}E+AB{bar {C}}D{bar {E}}.}2). Алгоритмы построения СДНФ
Построение СДНФ по таблице истинности
Что нужно делать, чтобы найти СДНФ по таблице истинности? Основная схема построения:
- В таблице истинности нужно отметить конкретный список переменных, на которых значение функции будет равно единице.
- Для каждого найденного набора нужно записать конъюнкцию абсолютно всех переменных по такому правилу: если значение некоторой переменной будет равно единицы, то в конъюнкцию можно включить саму переменную или же ее отрицание.
- Далее нужно полученные конъюнкции связать операциями дизъюнкции.
Примечание 2
Таблица истинности — вид таблицы, который описывает логическую функцию, отражающую все значения функции с помощью вероятных значений аргументов функции. Таблица сформирована из n+1 столбцов и (2^{n}), где n будет числом используемых переменных. В таблице истинности в первых n-столбцах записывают все величины аргументов функции, а в n+1 столбце записываются значения функции, которая она принимает на этом наборе аргументов.
Алгоритм построения СДНФ для булевой функции
Булева функция (или по-другому логическая функцияфункция в алгебре логики) от n переменных — отображение (B^{n}rightarrow{B}), где (B={0,1}) является булевым множеством.
Элементы булева множества 0 и 1 обычно рассматривают в качестве логических значений «ложно» и «истинно». В общем случае их рассматривают в качестве формальных символов, которые не обладают конкретным смыслом. Элементы декартова произведения (B^{n}) можно назвать булевыми векторами. Множество булевых функций от каждого числа переменных обычно обозначают (P^{2}), а от n переменных — (P^{2}(n)). Булевы функции носят свои названия по имени известного английского математика Джорджа Буля.
Так выглядел Джордж Буль:
Теорема 1
Для любой булевой функции (f(overrightarrow{x})), которая не равна тождественному нулю, есть СДНФ, которая задает ее.
Доказательство этой теоремы:
Для каждой булевой функции будет выполняться такое соотношение, которое называют в алгебре разложением Шеннона:
(f(overrightarrow{x})=neg{x_{i}}wedge{f}(x_{1},…,x_{i-1},0,x_{i+1},…,x_{n})vee{x_{i}}wedge{f}(x_{1},…,x_{i-1},1,x_{i+1},…,x_{n}).)
Такое соотношение просто проверить при помощи подстановки возможных значений (x_{i} (0 ) и (1)). Данная формула помогает вынести (x_{i}) за знак функции. Шаг за шагом вынося (x_{1}, x_{2}, x_{n}) за знак (f(overrightarrow{x})), можно получить такую формулу: (f(overrightarrow{x})=neg{x_1}wedge{neg{x_2}}wedge…wedge{neg{x_n-1}}wedge{neg{x_n}}wedge{f}(0,0,…,0,0)vee{neg{x_1}}wedge{neg{x_2}}wedge…wedge{neg}x_{n-1}wedge{x_n}wedge{f}(0,0,…,0,1)vee…vee{x_1}wedge{x_2}wedge…wedge{x_n-1}wedge{neg}x_nwedge{f}(1,1,…,1,0)vee{x_1}wedge{x_2}wedge…wedge{x_n-1}wedge{x_n}wedge{f}(1,1,…,1)).
Из-за использования этого соотношения к каждой из переменных увеличивается число конъюнктов в два раза. Так для функции от n переменных получается (2^{n}) возможных наборов величин n переменных. Если на каком-то наборе (f(overrightarrow{x})=0), тогда весь соответствующий конъюнкт будет также равняться нулю и из представления этой функции он может быть исключен. Если (f(overrightarrow{x})=1), тогда в конъюнкте значение функции возможно опустить. В итоге для произвольной функции была построена СДНФ.
Пример построения СДНФ
Представим пример построения СДНФ для медианы
- В таблице истинности отметим список переменных, на которых значение функции будет равным единице.
|
x |
y |
z |
(langle{x,y,z}rangle) |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
- Для каждого выбранного набора нужно записать конъюнкцию для всех переменных по такому правилу: если значение некоторой переменной — единица, то в конъюнкции включают собственно переменную или же ее отрицание.
|
x |
y |
z |
(langle{x,y,z}rangle) |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 ((neg{x}wedge{y}wedge{z})) |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 ((xwedge{neg{y}}wedge{z})) |
|
1 |
1 |
0 |
1 ((xwedge{y}wedge{neg{z}})) |
|
1 |
1 |
1 |
1 ((xwedge{y}wedge{z})) |
- Полученные конъюнкции связываются действиями дизъюнкции. Так (langle{x,y,z}rangle=(xwedge{y}wedge{z})wedge{(neg{x}wedge{y}wedge{z})}wedge{(xwedge{neg{y}}wedge{z})}vee(xwedge{y}wedge{neg{z}})).
Примеры СДНФ для некоторых функций
Стрелка Пирса будет такой: (xdownarrow{y}=(neg{x}wedge{neg}y)).
Примечание 3
Стрелка Пирса — бинарная логическая операция, булева функция над двумя переменными.
Исключающее или: (xoplus{y}oplus{z}=(overline{x}wedgeoverline{y}wedge{z})vee(overline{x}wedge{y}wedgeoverline{z})vee(xwedgeoverline{y}wedgeoverline{z})vee(xwedge{y}wedge{z})).
Совершенная дизъюнктивная нормальная форма формулы (A (x_{1}, x_{2},…, x_{n})) носит название ДНФ, которая обладает такими свойствами:
- в ней не существует одинаковых дизъюнктивных элементов;
- ни одна элементарная конъюнкция не обладает двумя одинаковыми высказываниями;
- ни одна элементарная конъюнкция не обладает высказыванием вместе с отрицанием;
- в каждой элементарной конъюнкции есть либо (x_{i}), или же (overline{x}_{i}, где i=1, n).
Первое и последнее свойства можно считать достаточными и необходимыми для того, чтобы ДНФ превратилась в СДНФ. Так данные условия дают возможность сформировать алгоритм получения СДНФ из ДНФ:
- Если у какой-нибудь элементарная конъюнкция нет высказывания (x_{i}), тогда можно заменить его выражением (Bwedge(x_{i}vee{overline{x_{i}}})=(Bwedge{x_{i}})vee(Bwedge{overline{x_{i}}}).
- Если в полученном выражении окажутся одинаковые элементарные конъюнкции, тогда лишние будут опущены.
- Если в некоторых элементарных конъюнкциях будут совпадать высказывания, тогда лишние будут опущены.
- Нужно удалить элементарные конъюнкции, в которых находятся высказывания вместе с отрицанием.
Если все элементарные конъюнкции будут таковыми, то есть вся формула будет ложной, тогда она не будет обладать СДНФ.
Формула будет носить название дизъюнктивной нормальной формы (ДНФ) в случае, когда она будет дизъюнкцией неповторяющихся элементарных конъюнкций. ДНФ будет записан в форме: (A_{1}vee{A_{2}}vee…vee{A_n}), где каждое (A_{n}) будет элементарной конъюнкцией.
Алгоритм приведения к СДНФ (как решать выражения с СДНФ)
Существует несколько способов приведения к СДНФ. Первый способ носит название аналитического. Можно привести к СДНФ так:
- Нужно привести формулу при помощи равносильных преобразований к ДНФ.
- Далее — удалить члены дизъюнкции, которые содержат переменную вместе с отрицанием (если подобные будут).
- Из подобных членов дизъюнкции (если подобные будут) нужно удалить все, кроме единственного.
- Из подобных членов каждой конъюнкции (если подобные будут) нужно удалить все, кроме единственного.
- Если в определенной конъюнкции не появляется переменная (x_{i}) из числа переменных, которые входят в исходную формулу, то следует добавить к данной конъюнкции член (x_{i}vee{overline{x_i}}).
- Далее нужно использовать закон дистрибутивности конъюнкции относительно дизъюнкции.
- Если в итоговой дизъюнкции будут одинаковые члены, тогда нужно удалить все подобные члены, кроме единственного.
Пример 1
Нужно привести такие формулы к СДНФ при помощи равносильных преобразований:
- ((xvee{y})(xvee{overline{y}}));
- (x(overline{y}vee{z}));
- ((xrightarrow{y})xy).
Решение.
- ((xvee{y})(xvee{overline{y}})=x=x(yvee{overline{y}})=xyvee{x}overline{y})
- (x(overline{y}vee{z})=xoverline{y}vee{xz}=xoverline{y}(zvee{overline{z}})vee{xz}(yveeoverline{y})=mid5mid=xoverline{y}zvee{x}overline{yz}vee{xzy}vee{xzoverline{y}=xoverline{y}}zvee{x}overline{yz}vee{xyz})
- ((xrightarrow{y})xy=(overline{x}vee{y})xy=overline{x}xyvee{yxy}=xy.)
Второй способ приведения СДНФ называется табличным. Для приведения нужно составить таблицу истинности для этой функции. Представим алгоритм приведения:
- Нужно построить таблицу значений формулы.
- Нужно рассмотреть исключительно такие строки, в которых величины формулы будут равны единице.
- Нужно убедиться, что каждой строке будет соответствовать конъюнкции всех аргументов (без повторений).
- Аргумент, который принимает значение 0, должен входить в конъюнкцию с отрицанием, значение единицы должно быть без отрицания.
- Так следует образовать дизъюнкцию всех конъюнкций.
Пример 2
Решение
Первое уравнение — [F=x(overline{y}vee{z})]. Нужно построить таблицу истинности для данной формулы.
|
№/н |
x |
y |
z |
[overline{y}] |
[overline{y}vee{z}] |
[F=x(overline{y}vee{z})] |
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
1 |
1 |
0 |
|
2 |
0 |
1 |
0 |
0 |
0 |
0 |
|
3 |
0 |
1 |
1 |
0 |
1 |
0 |
|
4 |
1 |
0 |
0 |
1 |
1 |
1 |
|
5 |
1 |
0 |
1 |
1 |
1 |
1 |
|
6 |
1 |
1 |
0 |
0 |
0 |
0 |
|
7 |
1 |
1 |
1 |
0 |
1 |
1 |
Нужно рассматривать исключительно наборы 4, 5 и 7, потому что только на данных наборах формула принимает величину, которая равняется единице. У СДНФ будет следующий вид: [F=xoverline{yz}vee{x}overline{y}zvee{xyz}].
Для второго уравнения [F=(xrightarrow{y})xy] нужно построить таблицу истинности.
|
№н |
x |
y |
[xoplus{y}] |
[F=(xoplus{y})frown{x}frown{y}] |
|
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
0 |
|
2 |
1 |
0 |
0 |
0 |
|
3 |
1 |
1 |
1 |
1 |
СДНФ (1): №3: F=xy.
Также стоит упомянуть алгоритм приведения СКНФ (совершенная конъюнктивная нормальная форма):
- Нужно отметить в таблице истинности список переменных, величины функции F на которых будет равно 0.
- Нужно записать для всех списков отмеченных дизъюнкцию всех переменных — в том случае, когда величина некоторой переменной в данном наборе будет равно 0, в дизъюнкцию включается собственно переменная, если происходит обратная ситуация, тогда в дизъюнкцию включается отрицание.
- Нужно связать дизъюнкции операциями конъюнкции.
- Доказательство эквивалентности
определение 3
Эквивалентность — алгебраический термин, который обозначает, что две и более формул представляют одну и ту же функцию. Для того, чтобы обозначить эквивалентность нужно использовать такие математические знаки: [equiv], [=], [Leftrightarrow].
Для доказательства эквивалентности формул возможно воспользоваться следующими способами:
- Первый способ — сравнение и построение таблиц истинности обеих функций. В данной случае итоги будут носить истинных характер только тогда, когда оба высказывания либо истинны, либо ложны.
- Второй способ — метод эквивалентных преобразований. Смысл данного метода состоял в построении цепи эквивалентности формул на базе ранее доказанных эквивалентностей.
Рассмотрим примеры с некоторыми эквивалентными преобразованиями в области булевой алгебры, а также новыми эквивалентностями, которые можно получить при помощи этих преобразований.
Поглощение
[xvee{xy}=x];
[x(xvee{y})=x].
Доказательство эквивалентности:
[xvee{xy}=xtimes{l}vee{xy}=x(lvee{y})=x]
[x(xvee{y})=xxvee{xy}=xvee{xy}=x]
Склеивание
[xyvee{x}overline{y}=x]
Доказательство эквивалентности:
[xyvee{x}overline{y}=x(yvee{overline{y}})=xtimes{l}=x]
Обобщенное склеивание
[xzvee{y}overline{z}vee{xy}=xzvee{y}overline{z}]
Доказательство эквивалентности:
[xzvee{y}overline{z}vee{x}y=xzvee{y}overline{z}vee{xyz}vee{xy}overline{z}=xzvee{y}overline{z}]
Расщепление
[xveeoverline{x}y=xvee{y}]
Доказательство эквивалентности:
[xveeoverline{x}y=xyvee{x}overline{y}veeoverline{x}y=xyvee{x}overline{y}vee{xy}veeoverline{x}y=xtimes{l}vee{y}times{l}=xvee{y}].
Примеры для самостоятельного нахождения СДНФ/СКНФ
задача 1
Нужно привести к СКНФ следующее уравнение: [((((Arightarrow{B})rightarrowoverline{A})rightarrowoverline{B})rightarrowoverline{C})].
При помощи использования закона де Моргана, а также правила [xrightarrow{y}=overline{x}vee{y}] можно упростить выражение:
[F=((((Arightarrow{B})rightarrowoverline{A})rightarrowoverline{B})rightarrowoverline{C})=(((overline{A}vee{B})rightarrowoverline{A})rightarrowoverline{B})rightarrowoverline{C})]=[((((overline{A}vee{B})rightarrowoverline{A})rightarrowoverline{B})rightarrowoverline{C})=((((overline{A}vee{B})veeoverline{A})rightarrowoverline{B})rightarrowoverline{C})]=[(((overline{A}vee{B})veeoverline{A})rightarrowoverline{B})rightarrowoverline{C})=((((overline{A}vee{B})veeoverline{A})veeoverline{B})rightarrowoverline{C})]=[((((overline{A}vee{B})veeoverline{A})veeoverline{B})veeoverline{C})=(((Avee{B})veeoverline{A})veeoverline{B})veeoverline{C}]=[(((overline{A}vee{B})veeoverline{A})\wedge{B})veeoverline{C}=(((Awedgeoverline{B})veeoverline{A})wedge{B})vee{C}]=[((Aoverline{B}veeoverline{A})veeoverline{A})wedge{B})veeoverline{C}=(((Awedgeoverline{B})veeoverline{A})wedge{B})veeoverline{C}]=[((Aoverline{B}veeoverline{A})wedge{B})veeoverline{C}=(Aoverline{B}Bveeoverline{A}B)veeoverline{C}=(0veeoverline{A}B)veeoverline{C}=overline{A}Bveeoverline{C}].
Нужно привести выражение к КНФ:
[F=overline{A}Bveeoverline{C}=(overline{A}veeoverline{C})wedge(Bveeoverline{C})]
Производим сокращение к СКНФ:
[F=(overline{A}veeoverline{C})wedge(Bveeoverline{C})=(overline{A}veeoverline{C}vee{B}overline{B})wedge(Aoverline{A}vee{B}veeoverline{C}]=[(overline{A}veeoverline{C}vee{B})wedge(Avee{B}veeoverline{C})wedge(overline{A}veeoverline{C}veeoverline{B})wedge(overline{A}vee{B}overline{C})]
задача 2
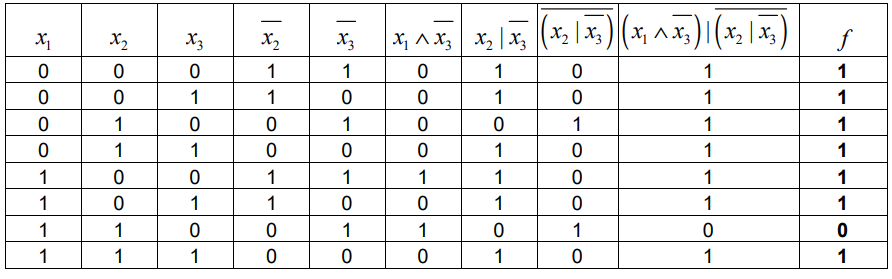
Задается булева функция [f(x_{1},x_{2},x_{3})=overline{x_{2}}vee((x_{1}wedgeoverline{x_{3}}mid(overline{x_{2}midoverline{x_{3}}}))]. Необходимо построить таблицу истинности, найти двоичную форму F булевой функции и привести ее к СДНФ.
Решение:
Сделаем таблицу истинности:
Источник: matburo.ru
Двоичная форма функции: F=(11111101). Так СДНФ будет: [overline{x_{1}}overline{x_{2}}overline{x_{3}}veeoverline{x_{1}}overline{x_{2}}{x_{3}}veeoverline{x_{1}}{x_{2}}overline{x_{3}}veeoverline{x_{1}}{x_{2}}{x_{3}}vee{x_{1}}overline{x_{2}}overline{x_{3}}vee{x_{1}}overline{x_{2}}{x_{3}}vee{x_{1}}{x_{2}}{x_{3}}]
СДНФ. Теорема о представлении в виде СДНФ. Построение СДНФ по таблице
ДНФ
Простой конъюнкцией или конъюнктом называется конъюнкция одной или нескольких переменных или их отрицаний, причём каждая переменная встречается не более одного раза.
Простая конъюнкция
- полная, если в неё каждая переменная { или её отрицание } входит ровно 1 раз;
- монотонная, если она не содержит отрицаний переменных.
ДНФ { Дизъюнктивная Нормальная Форма } — нормальная форма, в которой булева функция имеет вид дизъюнкции нескольких простых конъюнктов.
Пример ДНФ: $f(x,y,z) = (x land y) lor (y land neg { z } )$
СДНФ
СДНФ { Совершенная Дизъюнктивная Нормальная Форма } — это такая ДНФ, которая удовлетворяет условиям:
- в ней нет одинаковых простых конъюнкций
- каждая простая конъюнкция полная
Пример СДНФ: $f(x,y,z) = (x land neg { y } land z) lor (x land y land neg { z } )$
Теорема: Для любой булевой функции $f(vec { x } )$, не равной тождественному нулю (), существует СДНФ, ее задающая.
Доказательство:
Для любой булевой функции выполняется следующее соотношение, называемое разложением Шеннона.
$f(vec { x } ) = neg x_i wedge f(x_1, dots ,x_ { i-1 } ,0,x_ { i+1 } , dots ,x_n) vee x_i wedge f(x_1, dots ,x_ { i-1 } ,1,x_ { i+1 } , dots ,x_n)$
Данное соотношение легко проверить подстановкой всевозможных значений $x_i$ { $0$ и $1$ } . Эта формула позволяет выносить $x_i$ за знак функции. Последовательно вынося $x_1$, $x_2$,.., $x_n$ за знак $f(vec { x } )$, получаем следующую формулу :
$ f(vec { x } ) = neg x_1 wedge neg x_2 wedge …wedge neg x_ { n-1 } wedge neg x_n wedge f(0,0,…,0,0)~vee~$
$neg x_1 wedge neg x_2 wedge … wedge neg x_ { n-1 } wedge x_n wedge f(0,0,…,0,1) ~vee~ $ $dots $ $~vee~ x_1 wedge x_2 wedge … wedge x_ { n-1 } wedge neg x_n wedge f(1,1,…,1,0) ~vee~ $ $x_1 wedge x_2 wedge … wedge x_ { n-1 } wedge x_n wedge f(1,1,…,1) $
Так как применение данного соотношения к каждой из переменных увеличивает количество конъюнктов в два раза, то для функции от $n$ переменных мы имеем { { { $2^ { n } $ } } } конъюнктов. Каждый из них соответствует значению функции на одном из { { { $2^ { n } $ } } } возможных наборов значений $n$ переменных. Если на некотором наборе $f(vec { x } )=0$, то весь соответствующий конъюнкт также равен нулю и из представления данной функции его можно исключить. Если же $ f(vec { x } )=1$, то в соответствующем конъюнкте само значение функции можно опустить. В результате для произвольной функции была построена СДНФ.
Алгоритм построения СДНФ по таблице истинности
- В таблице истинности отмечаем те наборы переменных, на которых значение функции равно 1.
- Для каждого отмеченного набора записываем конъюнкцию всех переменных по следующему правилу: если значение некоторой переменной есть 1, то в конъюнкцию включаем саму переменную, иначе ее отрицание.
- Все полученные конъюнкции связываем операциями дизъюнкции.
Пример построения СДНФ для медианы
-
В таблице истинности отмечаем те наборы переменных, на которых значение функции равно 1.
x y z $langle x,y,z rangle$ 0 0 0 0 0 0 1 0 0 1 1 0 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 1 -
Для каждого отмеченного набора записываем конъюнкцию всех переменных по следующему правилу: если значение некоторой переменной есть 1, то в конъюнкцию включаем саму переменную, иначе ее отрицание.
x y z $ langle x,y,z rangle $ 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 $(neg { x } land y land z)$ 1 0 0 0 1 0 1 1 $(x land neg { y } land z)$ 1 1 0 1 $(x land y land neg { z } )$ 1 1 1 1 $(x land y land z)$ -
Все полученные конъюнкции связываем операциями дизъюнкции. $ langle x,y,z rangle = (x land y land z) lor (neg { x } land y land z) lor (x land neg { y } land z) lor (x land y land neg { z } )$
Примеры СДНФ для некоторых функций
Стрелка Пирса: $x downarrow y = (neg { x } land neg { y } )$
Исключающее или: $x oplus y oplus z = (overline { x } land overline { y } land z) lor (overline { x } land y land overline { z } ) lor (x land overline { y } land overline { z } ) lor (x land y land z)$
Совершенной дизъюнктивной нормальной формой формулы $A(x_1,x_2,…,x_n)$ называется ДНФ, обладающая следующими свойствами:
а } в ней нет одинаковых дизъюнктивных элементов;
б } ни одна элементарная конъюнкция не содержит двух одинаковых высказываний;
в } ни какая элементарная конъюнкция не содержит высказывание вместе с ее отрицанием;
г } в каждой элементарной конъюнкции содержится либо $X_i$, либо $overline { X } _i$, где $i = 1, n$.
Условие а } – г } являются необходимыми и достаточными для того, чтобы ДНФ стала СДНФ. В свою очередь эти условия дают возможность составить алгоритм получения СДНФ из ДНФ:
1) если какая-нибудь элементарная конъюнкция не содержит высказывание $X_i$, то заменим выражением $Bwedge (X_ivee overline { X } _i) equiv (Bwedge X_i)vee (Bwedge overline { X } _i)$;
2) если в полученном выражении окажутся одинаковые элементарные конъюнкции, то лишние опускаются;
3) если в некоторых элементарных конъюнкциях окажутся одинаковые высказывания, то лишние опускаются;
4) удаляем элементарные конъюнкции, в которых содержатся высказывания вместе с их отрицанием.
Если все элементарные конъюнкции окажутся таковыми, т.е. вся формула будет ложной, то она не будет иметь СДНФ.
Если все элементарные конъюнкции окажутся таковыми, т.е. вся формула будет ложной, то она не будет иметь СДНФ.
Формула называется дизъюнктивной нормальной формой { ДНФ } , если она является дизъюнкцией неповторяющихся элементарных конъюнкций. ДНФ записываются в виде: $A_1vee A_2vee …vee A_n$ , где каждое $A_n$ — элементарная конъюнкция.
Формула $A$ от $k$ переменных называется совершенной дизъюнктивной нормальной формой { СДНФ } , если:
-
$A$ является ДНФ, в которой каждая элементарная конъюнкция есть конъюнкция $k$ переменных $x_1,x_2,…,x_k$, причем на $i$-м месте этой конъюнкции стоит либо переменная $x_i$ либо ее отрицание;
-
Все элементарные конъюнкции в такой ДНФ попарно различны.
Например: $A = x_1 wedge$ НЕ $x_2 vee x_1 wedge x_2$
Совершенная дизъюнктивная нормальная форма представляет собой формулу, построенную по строго определенным правилам с точностью до порядка следования элементарных конъюнкций { дизъюнктивных членов } в ней.
Она является примером однозначного представления булевой функции в виде формульной { алгебраической } записи.
Теорема о СДНФ: Пусть $f(x_1 x_2, …, x_n)$ – булева функция от n переменных, не равная тождественно нулю. Тогда существует совершенная дизъюнктивная нормальная форма, выражающая функцию $f$.
Алгоритм построения СДНФ по таблице истинности:
- В таблице истинности отмечаем наборы переменных, на которых значение функции $f = 1$.
- Записываем для каждого отмеченного набора конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае – ее отрицание.
- Все полученные конъюнкции связываем операциями дизъюнкции.