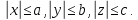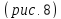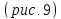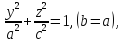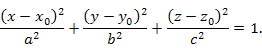Эллипсоиды
Определение эллипсоида
Эллипсоидом называется поверхность, определяемая в некоторой прямоугольной системе координат каноническим уравнением
(4.46)
где — положительные параметры, удовлетворяющие неравенствам
.
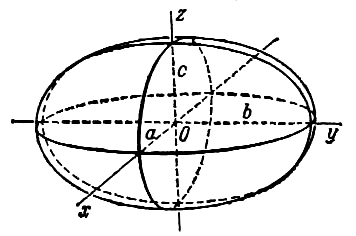
Если точка принадлежит эллипсоиду (4.46), то координаты точек
при любом выборе знаков также удовлетворяют уравнению (4.46). Поэтому эллипсоид (4.46) симметричен относительно координатных плоскостей, координатных осей и начала координат. Начало координат называют центром эллипсоида (4.46). Шесть точек
пересечения эллипсоида с координатными осями называются его вершинами, а три отрезка координатных осей, соединяющих вершины, — осями эллипсоида. Оси эллипсоида, принадлежащие координатным осям
, имеют длины
соответственно. Если
, то число
называется большой полуосью, число
— средней полуосью, число
— малой полуосью эллипсоида. Если полуоси не удовлетворяют условиям
, то уравнение (4.46) не является каноническим. Однако при помощи переименования неизвестных можно всегда добиться выполнения неравенств
.
Плоские сечения эллипсоида
Подставляя в уравнение (4.46), получаем уравнение
линии пересечения эллипсоида с координатной плоскостью
. Это уравнение в плоскости
определяет эллипс Линии пересечения эллипсоида с другими координатными плоскостями также являются эллипсами. Они называются главными сечениями (главными эллипсами) эллипсоида.
Рассмотрим теперь сечение эллипсоида плоскостью, параллельной какой-нибудь координатной плоскости, например . Подставляя
, где
— произвольная постоянная (параметр), в уравнение (4.46), получаем
(4.47)
При уравнение не имеет действительных решений (правая часть уравнения отрицательная, а левая неотрицательная), т.е. плоскость
не пересекает эллипсоид. При
уравнение (4.47) имеет нулевое решение
. Следовательно, плоскости
касаются эллипсоида в его вершинах
. При
, разделив обе части уравнения (4.47) на
, получаем уравнение эллипса
полуосями
. Следовательно, сечение эллипсоида плоскостью
при
представляет собой эллипс.
Плоские сечения дают возможность составить полное представление о виде эллипсоида (рис.4.40,а).
Эллипсоиды вращения
Эллипсоид, у которого две полуоси равны, называется эллипсоидом вращения (или сфероидом). Такой эллипсоид является поверхностью вращения. Например, если , то линии (4.47) при
являются окружностями. Следовательно, сечения эллипсоида плоскостями
представляют собой окружности с центрами на оси аппликат. Такую поверхность можно получить, вращая вокруг оси
эллипс
заданный в плоскости
(рис.4.41,а).
Если , то все сечения эллипсоида (4.46) плоскостями
при
будут окружностями с центрами на оси абсцисс. Такой эллипсоид можно получить, вращая вокруг оси
эллипс
(рис.4.41,б).
Если все полуоси эллипсоида равны , то он представляет собой сферу
радиуса
, которую можно получить, например, вращая окружность такого же радиуса вокруг любого диаметра.
Эллипсоид, у которого полуоси попарно различны , называется трехосным (или общим).
Замечания 4.8.
1. Плоскости определяют в пространстве основной прямоугольный параллелепипед, внутри которого находится эллипсоид (см. рис.4.40,б). Грани параллелепипеда касаются эллипсоида в его вершинах.
2. Эллипсоид можно определить, как геометрическое место точек, получаемое в результате трех сжатий (растяжений) сферы единичного радиуса к трем взаимно перпендикулярным плоскостям.
3. Начало канонической системы координат является центром симметрии эллипсоида, координатные оси — осями симметрии эллипсоида, координатные плоскости — плоскостями симметрии эллипсоида.
В самом деле, если точка принадлежит эллипсоиду, то точки с координатами
при любом выборе знаков также принадлежат эллипсоиду, поскольку их координаты удовлетворяют уравнению (4.46).
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
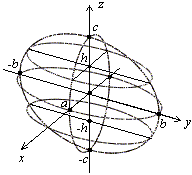
Эллипсоид
(рис.7) (от «эллипс»
и греч. «eidos» — вид) — замкнутая
центральная поверхность
второго порядка. Эллипсоид имеет
центр симметрии –

осями. Точки пересечения координатных
осей с эллипсоидом называются его
вершинами. Сечения эллипсоида плоскостями
являются эллипсами (в частности, всегда
можно указать круговые сечения эллипсоида).
Каноническое уравнение эллипсоида имеет
вид:
—
сфера.
В
сечении эллипсоида плоскостью,
перпендикулярной любой из координатных
осей, получается эллипс.
Форма эллипсоида.
Исследуем
форму эллипсоида. Из уравнения 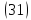
ограничены:
Эллипсоид
обладает тремя плоскостями симметрии,
тремя осями симметрии и центром симметрии.
Ими служат соответственно координатные
плоскости, координатные оси и начало
координат.
Для
выяснения формы эллипсоида рассмотрим
его сечения плоскостями. Найдем линию
пересечения эллипсоида с плоскостью

Так как любая точка плоскости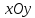
нулевую третью координату,
то координаты точек эллипсоида на
плоскости
уравнению:
Получаем,
что линия пересечения является эллипсом
с полуосями 
Рис.
8.
Сечение
плоскостью
Аналогично,
сечение в плоскости 
дает эллипс:
с
полуосями 

а сечение плоскостью
с
полуосями
Рис.9.
Сечения эллипсоида координатными
плоскостями
Нарисованный
«каркас» из сечений уже дает
представление об эллипсоиде. Но чтобы
выяснить, как ведет себя поверхность
между нарисованными кривыми, рассмотрим
сечение эллипсоида плоскостью

Эта плоскость параллельна плоскости
пересекает ось
точке
Уравнения этой линии:
Очевидно,
что если

то ни одна точка пространства не может
удовлетворять этой системе: в левой
части первого уравнения стоит
неотрицательное число, а в правой —
отрицательное.
Если

то в сечении получим лишь одну точку

зависимости от знака
Пусть
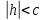
Тогда первое уравнение преобразуем к
виду:
то
есть к виду:
где
Уравнение

эллипсу, задаваемому уравнением
с коэффициентом подобия
полуосями

Ясно, что сечение плоскостью
таким же эллипсом, расположенным
симметрично первому относительно
плоскости
Нарисуем эти сечения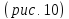
Рис.10.
Дополнительные сечения эллипсоида
Таким
образом, весь эллипсоид составлен из
эллипсов, лежащих в плоскостях,
параллельных плоскости
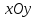
подобных эллипсу в плоскости

эллипсоида:
Рис.11.
Эллипсоид
Так
же, как для эллипса, точки пересечения
эллипсоида с координатными осями
называются вершинами эллипсоида, центр
симметрии — центром эллипсоида. Числа

полуосями. Если полуоси попарно различны,
то эллипсоид называется трехосным.
Если
две полуоси равны друг другу, то эллипсоид
называется эллипсоидом вращения.
Эллипсоид вращения может быть получен
вращением эллипса вокруг одной из осей.
Например, если

то все сечения эллипсоида плоскостями
будут окружностями. Сам эллипсоид может
быть получен из эллипса:
лежащего
в плоскости

при вращении его вокруг оси
Рис.12.
Эллипсоид
вращения
Конев В.В. Кривые и поверхности второго порядка
Поверхности второго порядка
Эллипсоид
Эллипсоидом называется поверхность, которая в некоторой декартовой системе координат описывается уравнением

Это равенство называется каноническим уравнением эллипсоида. Величины a, b и c называются полуосями эллипсоида.
Эллипсоид может быть получен равномерным сжатием или растяжением сферы вдоль трёх взаимно перпендикулярных осей. Говоря иначе, уравнение эллипсоида получается из уравнения сферы масштабным преобразованием
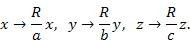
Если центр эллипсоида находится в точке 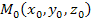
Рис. 10. Любая плоскость пересекает поверхность эллипсоида по эллипсу.
(Для изменения цвета и формы эллипсоида поместите курсор указателя мыши в область рисунка).
Эллипсоид, все оси которого различны, называется трехосным.
Если какие-либо две оси эллипсоида одинаковы, то эллипсоид называют сфероидом.
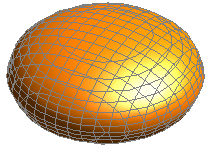
Рис. 11. Сфероиды.
Сфероид представляет собой поверхность, образованную вращением половины дуги эллипса вокруг оси, соединяющей концы этой дуги. Пусть, например, b = c. Тогда эллипсоид
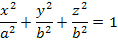
образован вращением верхней половины дуги эллипса, представленного на рисунке 4, вокруг оси 0x.
Рис. 12. Эллипс с полуосями a и b, расположенный в плоскости x0y.
Если a = b = c, то эллипсоид вырождается в сферу радиуса a.

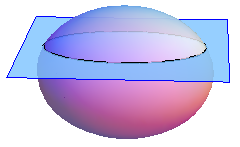
Рис. 13. Сечение эллипсоида произвольной плоскостью дает эллипс.
Любое сечение эллипсоида плоскостью — эллипс. А бывает ли сечение, являющееся окружностью?
Если рассматривать эллипсоид вращения — взяли эллипс и провращали вокруг одной из осей, — то, конечно,
окружности имеются: в сечении, перпендикулярном оси вращения. Эллипсоиды вращения Архимед ассоциировал
со сжатой сферой и называл «сфероид»: вытянутый сфероид, если вращали вокруг большой оси эллипса;
сплюснутый сфероид, если вращали вокруг малой оси.
Если сферу сжать по всем трём направлениям, то получается эллипсоид с тремя различными полуосями $a$, $b$, $c$.
Каноническое уравнение такого эллипсоида в декартовых координатах, совпадающих с осями сжатия:
$frac{x^2}{a^2}+frac{y^2}{b^2}+frac{z^2}{c^2}=1$. Есть ли на его поверхности окружности?
Эллипсоидом
называется поверхность, которая в некоторой
системе декартовых прямоугольных координат
определяется уравнением
(1).
Уравнение (1) называется каноническим
уравнением эллипсоида. Величины a,
b, c суть полуоси эллипсоида (рис. 1). Если все
они различны, эллипсоид называется трехосным; в
случае, когда какие-нибудь две из них одинаковы,
эллипсоид называется вытянутым, при a=b>c — сжатым. В случае, когда a=b=c, эллипсоид представляет
собой сферу.
Гиперболоидами называются
поверхности, которые в некоторой системе
декартовых прямоугольных координат
определяются уравнениями
, (2)
. (3)
Гиперболоид, определяемый уравнением
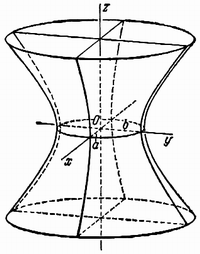
(2), называется однополостным (рис. 2); гиперболоид,
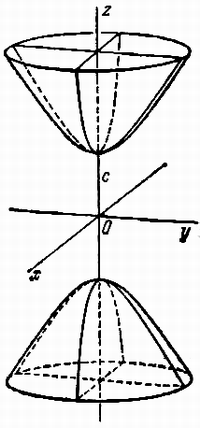
определяемый уравнением (3), — двуполостным (рис. 3);
уравнения (2) и (3) называются каноническими
уравнениями соответствующих гиперболоидов.
Величины a, b, c называются
полуосями гиперболоида. В случае однополостного
гиперболоида, заданного уравнением (2), только
первые из них (а и b) показаны
на рис. 2. В случае двуполостного гиперболоида,
заданного уравнением (3), одна из них (именно, с)
показана на рис. 3. Гиперболоиды, определяемые
уравнениями (2) и (3), при a=b
являются поверхностями вращения.
Параболоидами называются поверхности,
которые в некоторой системе декартовых
прямоугольных координат определяются
уравнениями
, (4)
, (5)
где p и q — положительные числа,
называемые параметрами параболоида. Параболоид,
определяемый уравнением (4), называется
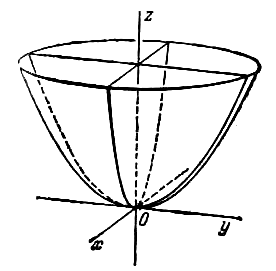
эллиптическим (рис. 4); параболоид, определяемый
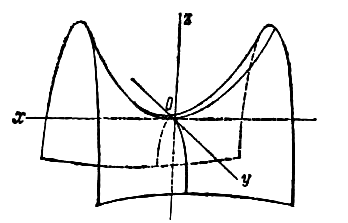
уравнением (5), — гиперболическим (рис. 5). Уравнения
(4) и (5) называют каноническими уравнениями
соответствующих параболоидов. В случае, когда p=q, параболоид, определяемый
уравнением (4), является поверхностью вращения
(вокруг Oz).
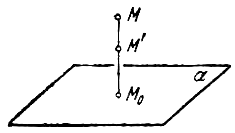
Рассмотрим теперь преобразование
пространства, которое называется равномерным
сжатием (или равномерным растяжением).
Выберем какую-нибудь плоскость;
обозначим ее буквой
. Зададим, кроме
того, некоторое положительное число q. Пусть М — произвольная точка
пространства, не лежащая на плоскости
,
— основание
перпендикуляра, опущенного на плоскость
из точки М. Переместим точку М по прямой
в
новое положение
так, чтобы имело
место равенство
и чтобы после перемещения точка
осталась с той же стороны от плоскости
,
где она была первоначально (рис. 6). Точно так же мы
поступим со всеми точками пространства, не
лежащими на плоскости
; точки, которые
расположены на плоскости
, оставим на своих
местах. Таким образом, все точки пространства, за
исключением тех, что лежат на плоскости
,
переместятся; при этом расстояние от каждой
точки до плоскости
изменится в
некоторое определенное число раз, общее для всех
точек. Описываемое сейчас перемещение точек
пространства называется его равномерным сжатием
к плоскости
; число q
носит название коэффициента сжатия.
Пусть дана некоторая поверхность F; при равномерном сжатии
пространства точки, которые ее составляют,
переместятся и в новых положениях сотавят
поверхность F’. Будем
говорить, что поверхность F’
получено из F в результате
равномерного сжатия пространства. Оказывается,
что многие поверхности второго порядка (все,
кроме гиперболического параболоида) можно
получить в результате равномерного сжатия из
поверхностей вращения).
ПРИМЕР. Доказать, что произвольный
трехосный эллипсоид
может быть получен из сферы
в результате двух последовательных
равномерных сжатий пространства к координатным
плоскостям: к плоскости Oxy с
коэффициентом сжатия
и к плоскости Oxz с коэффициентом сжатия
.
ДОКАЗАТЕЛЬСТВО. Пусть производится
равномерное сжатие пространства к плоскости Oxy с коэффициентом
и
пусть
— точка, в которую переходит при этом
точка
. Выразим координаты x’,
y’, z’ точки М’ через координаты x, y, z точки М. Так как прямая MM’ перпендикулярна к плоскости Oxy, то x’=x, y’=y.
С другой стороны, так как расстояние от точки М’
до плоскости Oxy равно
расстоянию от точки М до этой плоскости,
умноженному на число
, то
.
Таким образом, мы получаем искомые
выражения:
,
,
(6)
или
,
,
(7)
Предположим, что M(x; y; z)
— произвольная точка сферы
.
Заменим здесь x, y, z
их выражениями (7); получим
,
откуда
.
Следовательно, точка M’(x’;
y’; z’) лежит на эллипсоиде вращения.
Аналогично, мы должны осуществить сжатие
пространства к плоскости Oxz
по формулам
,
,
;
тогда получим трехосный эллипсоид и
именно тот, уравнение которого дано в условии
задачи.
Отметим еще, что однополостный
гиперболоид и гиперболический параболоид суть
линейчатые поверхности, то есть они состоят из
прямых; эти прямые называются прямолинейными
образующими указанных поверхностей.
Однополостный гиперболоид
имеет две системы прямолинейных
образующих, которые определяются уравнениями:
,
;
,
,
где
и
— некоторые
числа, не равные одновременно нулю.
Гиперболический параболоид
также имеет две системы прямолинейных
образующих, которые определяются уравнениями
,
;
,
.
Конической поверхностью, или конусом,
называется поверхность, которая описывается
движущейся прямой (образующей) при условии, что
эта прямая проходит через постоянную точку S и пересекает некоторую
определенную линию L. Точка S называется вершиной конуса;
линия L — направляющей.
Цилиндрической поверхностью, или
цилиндром, называется поверхность, которая
описывается движущейся прямой (образующей) при
услвоии, что эта прямая имеет постоянное
направление и пересекает некоторую определенную
линию L (направляющую).