Как найти сечение параллелограмма плоскостью

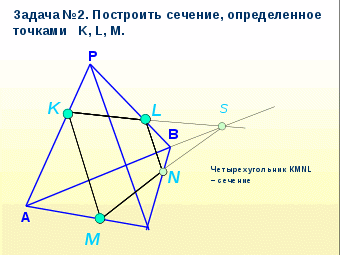
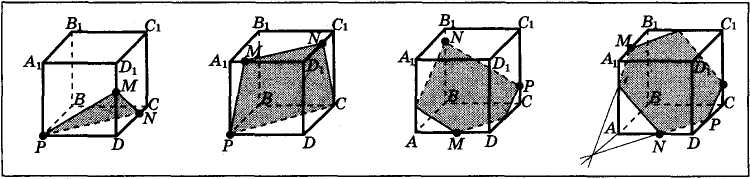
Урок по теме

« Построение сечений параллелепипеда»

Предмет  геометрия

Класс  10

Учебно-методическое обеспечение: учебник « Геометрия 10-11»  автор Л.С. Атанасян. Методические рекомендации к учебнику авторы С.М.Саакян, В.Ф. Бутузов

Оборудование и материалы для урока: Компьютер, проектор, экран, презентация для сопровождения урока, дидактический материал, копир-ответы , карточки-бланки для ответов учащихся, модели куба и прямоугольного параллелепипеда

Цели урока:

    1. Определить виды сечений параллелепипеда

2.Установить взаимосвязь между видом сечения и расположением точек на ребрах параллелепипеда

     3.Научиться строить сечения

Задачи урока

1. Обучающие: 

— Закрепить определение секущей плоскости и сечения многогранника  плоскостью;

— Отработать алгоритм построения сечения параллелепипеда плоскостью.

1. Развивающие:

— продолжить формирование пространственного воображения и математической речи;

— развивать аналитическое мышление при выработке алгоритма построения точки пересечения прямой и плоскости и сечений многогранников.

1. Воспитывающие:

— вырабатывать умение осознанно трудиться над поставленной целью;

— воспитывать культуру общения , графическую культуру.

.

Тип урока: комбинированный

Структура урока:

1. Организационный момент.
2. Проверка домашнего задания. Повторение.
3. Изучение нового материала.
4. Закрепление.
5. Самостоятельная работа.
6. Итог урока.
7. Комментарии к домашнему заданию.
8. Рефлексия

                                                 Ход урока :

1. Организационный момент   .            Приветствие уч-ся и гостей

Я и мои ребята  рады приветствовать вас. Думаем , что  у вас хорошее настроение и  оно конечно же передастся ребятам  и они будут работать спокойно и продуктивно

2.Вступительное слово учителя

Раздел стереометрии, изучающий сечения геометрических тел позволяет «заглянуть внутрь» предметов, познакомиться с их свойствами; значительно облегчает выполнение ряда заданий не только по математике, но и по физике, биологи и географии. Решение задач на построение сечений многогранников способствует развитию у человека пространственного представления и пространственного мышления  т.е. развивает геометрическую фантазию.

 На предыдущем уроке мы строили сечение тетраэдра плоскостью.

Тема сегодняшнего урока «Построение сечений параллелепипеда» (слайд 1)

3.Повторение изученного материала .Проверка домашнего задания.

Прежде чем мы будем учиться  строить сечения  параллелепипеда, проверим выполнение домашнего задания. Кто выполнил компьютерный вариант? Пожалуйста…№105..(настройка презентации).

Чертеж к задаче № 75

      А мы  в это время повторим некоторые вопросы теории, без которых нам не обойтись при построении сечений параллелепипеда.

1. Что такое секущая плоскость многогранника? 
2.  (Секущей плоскостью многогранника называют любую плоскость, по обе стороны от которой имеются точки данного многогранника)

1. Что такое сечение многогранника?

      (Секущая плоскость пересекает грани многогранника по отрезкам.    Многоугольник, сторонами которого являются эти отрезки, называется сечением  многогранника)

1. А где лежат вершины этого многоугольника?

         (на ребрах многогранника)

1.  Какие многоугольники мы получали при построении сечений тетраэдра?

          ( треугольники и четырехугольники).

Проверить выполнение домашнего задания  Комментарии презентации

Проверка правильности выполнения чертежа к задаче №75 и фронтальная работа по плану решения задачи.

                               4.Изучение нового материала.

Целью построения сечений является нахождение линий пересечения секущей плоскости с гранями , т. е. следы по которым плоскость пересекает грани многогранника.    А как можно задать секущую плоскость?

            ( Вовлечение учащихся в поисковую деятельность.)

1. Смоделируйте  как можно задать секущую плоскость(3 точками, прямой и не лежащей на ней точкой, 2 параллельными прямыми, 2 пересекающимися прямыми)

1. Мы на уроке  рассмотрим задачи на построение сечений, заданных тремя точками                                                  («живая геометрия»)

Как вы думаете а какие многоугольники мы можем получить при построении сечений параллелепипеда?

 ( треугольники и 4 -, 5 -и 6-угольники)

       Можем ли получить 7-угольное сечение? Почему?

( Нет, поскольку у параллелепипеда имеется только шесть граней, поэтому в сечении  не может получиться многоугольник с числом сторон, большим шести)

     Итак, мы предположили, что в сечении параллелепипеда получатся треугольники, четырехугольники, 5 и 6-угольники, нам это предположение нужно проверить, поэтому цели нашего урока (слайд 2)

1. Определить виды сечений параллелепипеда
2. Установить взаимосвязь между видом сечения и расположением точек на ребрах параллелепипеда
3. Научиться строить сечения параллелепипеда.

Во время урока мы будем работать с различными видами параллелепипеда, в том числе и с кубом – как прямоугольным параллелепипедом с равными ребрами .

    Начнем с треугольного сечения. Подумайте, как нужно расположить 3 точки на ребрах параллелепипеда, чтобы получить треугольное сечение?             (смоделировать и заслушать ответы учащихся)

(на ребрах исходящих из одной вершины или  расположенных в 3 вершинах).

    Выполним построение сечения треугольной формы (слайд )

 ( Комментарии учащихся и построение аналогичного сечения в тетради, двое у доски -разное расположение точек)

    Как нужно расположить 3 точки, чтобы получить 4-угольное сечение?

 (на  параллельных ребрах).

Ребята,  при выполнении этого задания хочу напомнить вам  следующее  очень важное условие (слайд 4)

Если секущая плоскость пересекает две противоположные грани параллелепипеда по отрезкам, то эти отрезки параллельны .(Запишем это утверждение)

    С учетом этого условия построим сечение, проходящее через точки М, N, K (слайд 5).

     Построение сечения происходит с  комментированием учащихся.  

         ( продемонстрировать изменение узлов и диагональное сечение)

Построение в тетрадях и у доски сечений по заданным точкам (точки задать на слайде)

    Переходим к следующим двум сечениям: 5 и 6 –угольным.

Расположим точки как показано на рисунке. Давайте продумаем план построения .                        ( обсуждение с учащимися).

Построим  сечение, заданное точками ????  (слайд 5тиуг . сеч.)

 Какой многоугольник вы  получили  (пятиугольник….  

Сколько  параллельных сторон у пятиугольника?…)

5.Работа в парах. Поисковая деятельность

( Постарайтесь изобразить шестиугольное сечение)-работают

6. Защита проектов

    Два  ученика изображают 6-угольные сечения на доске.

Мы изобразили 6-иугольные сечения ,а теперь давайте их построим

 (слайд    ,  учитель объясняет ход построения.

Найти две точки сечения , лежащие в самой грани не всегда удается, поэтому нас вполне удовлетворят  две точки сечения, лежащие в плоскости, а не в самой грани, поэтому нахождение этих точек выходит за пределы чертежа)

Ребята, а как проверить, правильно ли выполнен чертеж? (параллельность противоположных сторон шестиугольника) посмотрите в тетрадь своего соседа…

 А вот в пространстве…. ( анимация сечения куба  « Живая геометрия»)

 Для построения данного сечения использовался  метод «следов», заключающийся в нахождении точки пересечения прямой и плоскости по заданным двум точкам этой прямой и их проекциям на плоскость.

 А теперь включите свою геометрическую фантазию и постарайтесь правильно определить какой  многоугольник является сечением какой фигуры?( работа со слайдом)

Есть ли ошибки на чертежах?  (работа со слайдом)

Все эти замечания прошу учесть при выполнении самостоятельной работы.

7. Закрепление изученного материала. ( в это время проверка д. з.)

  Самостоятельная работа(2 варианта)

Учащиеся выполняют с.р. на заранее подготовленных чертежах, а затем проверяют при помощи копир-слайда    

Сечения при этом закрашивают  различными цветами . (затем это используется при анализе урока- тест Люшера)

      В процессе решения задач учащимся было предложено выделить построенное сечения в понравившейся им цветовой гамме. Методика ЦВ выявляет не только осознанное, субъективное отношение испытуемого к цветовым эталонам, но также неосознанные реакции на них, что позволяет считать метод глубинным проективным. Исходя из символики цветов и накопленного в многолетней практике опыта, структурное значение каждого цвета, выбираемого на первых позициях, описано Максом Люшером следующим образом:

1. зеленый – упорство, целеустремленность, волевое,усилие, эластичное напряжение, высокий уровень притязания, стремление к самовыражению;
2. красный – выражение жизненной силы, воли к победе, стремление к успеху, потребность в достижении самоутверждении;
3. желтый – раскованность, потребность в эмоциональной активности, стремление к новому и расширение возможностей;
4. синий – состояние покоя, эмоциональная стабильность, тенденция к эмоциональному комфорту;
5. серый – тенденция к пассивности, потребность в отдыхе, социальная отгороженность;
6. фиолетовый – потребность в уходе от реальной действительности, нереальные требования к жизни, мечтательность, индивидуальность;
7. коричневый – потребность снижения тревожности, ощущение физиологического дискомфорта, стресс;
8. черный – отказ, неприятие, огорчение, протест против существующего положения вещей,                           потребность в независимости, негативизм по отношению к любым авторитетам

8. Д.З .№110,112 из учебника « Геометрия 10-11» Атанасян Л.С.( слайд 12)и

Индивидуальное задание- задачи на карточках разного цвета- разного уровня сложности.

9. Итог урока

10.Рефлексия

.

Метод сечений, широко известный своей универсальностью, применяется в некоторых разделах черчения, физики, теоретической механики, сопротивления материалов, гидравлике и других естественных науках и технических дисциплинах.

Построение сечений используют в строительном деле, машиностроении. В качестве диагностики заболеваний в медицине широко применяют метод компьютерной томографии, основанный на получении при помощи рентгеновских аппарата снимков — сечений человеческого тела. Этим же методом пользуются историки и археологи для исследования некоторых объектов. Например, чтобы не испортить саркофаг и при этом посмотреть его содержимое. Для этого при помощи томографа делают множество снимков — поперечных сечений саркофагов, суммируя которые получают необходимую информацию.

Широко применяют сечения и в ювелирном деле. Чтобы придать камню нужную форму, мастер подвергает бесформенный драгоценный камень рассечению различными плоскостями. Эти плоскости выбираются не спонтанно, а таким образом, чтобы луч, падающий на камень, создавал его сияние, многократно отразившись от его граней. Изменяя угол наклона «секущих плоскостей» и их положения мастер добивается неповторимой игры света и радужных переливов на гранях камня.

Таким образом, интерес к задачам на построение сечений обусловлен не только их красотой и оригинальностью методов решения, но и их практической ценностью

11 Спасибо за работу (слайд )

Сечения геометрических фигур имеют различные формы. У параллелепипеда сечение всегда представляет собой прямоугольник или квадрат. Оно имеет ряд параметров, которые могут быть найдены аналитическим способом.

Инструкция

Через параллелепипед можно провести четыре сечения, которые представляют собой квадраты или прямоугольники. Всего он имеет два диагональных и два поперечных сечения. Как правило, они имеют разные размеры. Исключением является куб, у которого они одинаковы.
Перед тем как строить сечение параллелепипеда, составьте представление о том, что представляет собой эта фигура. Существует два вида параллелепипедов — обычный и прямоугольный. У обычного параллелепипеда грани располагаются под некоторым углом к основанию, а у прямоугольного они перпендикулярны ему. Все грани прямоугольного параллелепипеда представляют собой прямоугольники или квадраты. Из этого следует,что куб — это частный случай прямоугольного параллелепипеда.

У любого сечения параллелепипеда есть определенные характеристики. Основными из них являются площадь, периметр, длины диагоналей. Если из условия задачи известны стороны сечения или какие-либо иные его параметры, этого достаточно, чтобы найти его периметр или площадь. По сторонам определяются также диагонали сечений. Первый из этих параметров — площадь диагонального сечения.
Для того чтобы найти площадь диагонального сечения, нужно знать высоту и стороны основания параллелепипеда. Если даны длина и ширина основания параллелепипеда, то диагональ найдите по теореме Пифагора:
d=?a^2+b^2.
Найдя диагональ и зная высоту параллелепипеда, вычислите площадь сечения параллелепипеда:
S=d*h.

Периметр диагонального сечения тоже можно вычислять по двум величинам — диагонали основания и высоте параллелепипеда. В этом случае вначале найдите две диагонали (верхнего и нижнего оснований) по теореме Пифагора, а затем сложите с удвоенным значением высоты.

Если провести плоскость, параллельную ребрам параллелепипеда, можно получить сечение-прямоугольник, сторонами которого являются одна из сторон основания параллелепипеда и высота. Площадь этого сечения найдите следующим образом:
S=a*h.
Периметр этого сечения найдите аналогичным образом по следующей формуле:
p=2*(a+h).

Последний случай возникает, когда сечение проходит параллельно двум основаниям параллелепипеда. Тогда его площадь и периметр равны значению площади и периметра оснований, т.е.:
S=a*b — площадь сечения;

Портфолио учителя математики НОУ СОШ «ЛАДА» Лисуновой Г.В.

Тема: « Построение сечений тетраэдра и параллелепипеда».

Предмет
: геометрия Класс:
10 Используемые педагогические технологии:
технология проектного обучения, информационные технологии. Тема урока
: Построение сечений тетраэдра и параллелепипеда Тип урока
: урок закрепления и развития знаний. Формы работы на уроке
: фронтальная, индивидуальная Список используемых источников и программно-педагогических средств:

Л.С. Атанасян. Геометрия. 10-11 классы,- М: Просвещение, 2006г.

В. Н. Литвиненко. Задачи на развитие пространственных представлений. Книга для учителя. — М.: Просвещение, 1991.

Г. Прокопенко. Методы решения задач на построение сечений многогранников. 10 класс. ЧПГУ, г. Челябинск. Еженедельная учебно-методическая газета «Математика» 31/2001.

А. Мордкович. Семинар девятый. Тема: Построение сечений многогранников (позиционные задачи). Еженедельное приложение к газете «Первое сентября». Математика. 3/94.

Мультимедийный интерактивный курс «Открытая математика. Стереометрия.» Физикон

«Живая геометрия»

Цели: Образовательные:

Проверить знание теоретического материала о многогранниках (тетраэдр, параллелепипед).

Продолжить формирование умения анализировать чертеж, выделять главные элементы при работе с моделью многогранника, намечать ход решения задачи, предвидеть конечный результат.

Отработать навыки решения задач на построение сечений многогранников.

Развивать графическую культуру и математическую речь.

Формировать навыки использования компьютерных технологий на уроках геометрии.

Развивающие:

Развивать познавательный интерес учащихся.

Формировать и развивать у учащихся пространственное воображение.

Воспитательные:

Воспитывать самостоятельность, аккуратность, трудолюбие.

Воспитывать умения работать индивидуально над задачей.

Воспитывать волю и настойчивость для достижения конечных результатов.

Техническое обеспечение:

Компьютер с установленными программами «Живая геометрия», Power Point, мультимедиапроектор.

Раздаточный материал:

Бланки-карточки с заданиями для практической работы, бланки-карточки с ответами для взаимопроверки, опоры – памятки, презентация по теме «Аксиомы стереометрии, следствия из них», презентация ученика «Построение сечений параллелепипеда», цветные карандаши.

Структура урока.

Ход урока:

1)Приветствие. Организационный момент.

2) Постановка цели и задачи урока.

Задачи на построение сечений в многогранниках занимают заметное место в курсе стереометрии. Их роль обусловлена тем, что решение этого вида задач способствует усвоению аксиом стереометрии, следствий из них, развитию пространственных представлений и конструктивных навыков. Умение решать задачи на построение сечений являет-ся основой изучения почти всех тем курса стереометрии. При решении многих стереометрических задач используют сечения многогранников плоскостью. На предыдущих уроках мы с вами познакомились с аксиомами стереометрии, следствиями из аксиом и с теоремами о параллельности прямых и плоскостей в пространстве. Мы рассмотрели алгоритмы построения несложных сечений куба, тетраэдра и параллелепипеда. Эти сечения, как правило, задавались точками, расположенными на ребрах или гранях многогранника. Сегодня на уроке мы с вами повторим геометрические утверждения, позволяющие сформулировать правила построения сечений. А также научимся применять эти знания при решении задачи на построение сечения тетраэдра и параллелепипеда плоскостью, проходящей через три данные точки, такие, что никакие три из этих точек не лежат в одной грани.

3) Повторение изученного материала с использованием презентации.

Давайте повторим некоторые вопросы теории.

Что такое секущая плоскость? Как можно задать секущую плоскость? Что такое сечение тетраэдра (параллелепипеда)? Какие многоугольники мы получали при построении сечений тетраэдра? А какие многоугольники мы можем получить при построении сечений параллелепипеда? Давайте повторим аксиомы стереометрии, следствия из них и способы задания плоскости (презентация 1, слайды 1-10)

4) Актуализация опорных знаний.

Презентация ученика «Построение сечений параллелепипеда».

Теперь давайте вспомним алгоритм построения сечения тетраэдра на примере двух задач (презентация 1, слайды 11-12).

(построение комментируется пошагово учителем).
— Пащенко Алексей с помощью своей презентации напомнит нам об алгоритмах построения сечений параллелепипеда (презентация 2, слайды 1-5)

(ученик демонстрирует слайды, комментируя последовательность построения)
— А сейчас с помощью программы «Живая геометрия» мы «оживим» пространство на примере сечения куба. Программа позволяет вращать многогранник, что позволит вам увидеть сечение со всех сторон.

5) Практическая работа на построение сечений с последующей взаимопроверкой.

Ученики получают бланки-карточки для практической работы (приложение 1)

Малая наполняемость
класса (5 человек), достаточно большое количество посадочных мест, а также последующая взаимопроверка позволяет выполнение работы одного варианта. На бланках также расположено несколько различных примеров построения сечений. У каждого ученика на парте опора-памятка (приложение 2).

Практическая работа состоит из 12 заданий разного уровня сложности. 5-7 правильно выполненных заданий – оценка «3», 8-10 заданий — оценка «4», 11-12 заданий — оценка «5»

6) Взаимопроверка.

Ученики меняются листами с практической работой, получают для проверки бланки с ответами (приложение 3)

. Проверяют работы друг друга, отмечая правильно построенные сечения.

7) Домашнее задание.

В качестве домашнего задания я попрошу вас решить задачи, аналогичные задачам в практической работе, но на построение сечений тетраэдра. Каждому предлагается выполнить по 4 задания (приложение 4)

Задания имеют три уровня сложности.

Рефлексия.

Итак, подведем итог, чему мы научились сегодня на уроке? — Какие теоретические положения нам часто приходилось использовать? — Какие ошибки были допущены при решении задач? Как вы их устранили? — Кому приходилось возвращаться к задаче несколько раз? — Где в практической деятельности вам пригодится сегодняшний урок? На этапе рефлексии деятельности учащиеся анализируют, где и почему были допущены ошибки, каким способом они были исправлены, повторяют алгоритмы, вызвавшие затруднения, оценивают свою деятельность на уроке.

9) Итог урока.

В завершение урока учащиеся с помощью учителя фиксируют степень соответствия поставленной цели и результатов деятельности. Выставляются оценки.

Практическая работа по построению сечений параллелепипеда. Приложение 1

Приложение 2

Опора-памятка

Аксиома
1
. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и причем только одна. Аксиома
2
. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. Аксиома
3
. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Следствия из аксиом:

Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. Через две пересекающиеся прямые проходит плоскость, и притом только одна.

Способы задания плоскости:

Приложение 3

Ответы к практической работе.

Вот такая вот задача по геометрии про прямоугольный параллелепипед и плоскость:

В прямоугольном параллелепипеде ABCDA1B1C1D1 известны ребра AA1 = 6, AB = 6, AD = 3 корня из 13. Найдите площадь сечения параллелепипеда плоскостью AMK, где точки М и К делят ребра BB1 и CC1 в отношении 1:2, считая от прямой ВС
.

Для её решения этой задачи нужно просто представить то, что нам дано по условию и понять, что нужно найти. Рекомендую условие разбивать на части и каждую часть рассматривать отдельно. Сейчас я покажу, как это делается.

Читаем с самого начала: «В прямоугольном параллелепипеде…»
— всё, достаточно. И так, у нас есть прямоугольный параллелепипед — трехмерная геометрическая фигура, которую лучше всего нарисовать на листочке бумаги. Вот как выглядит прямоугольный параллелепипед на рисунке. В жизни это обычная коробка для обуви.

Дальше написано «…ABCDA1B1C1D1…» —
это так обозначаются вершины прямоугольного параллелепипеда. Если показывать условие задачи на коробке из-под обуви, то можно обойтись и без обозначений. Но ни один фокусник не вылезет к вам из задачника с коробкой под мышкой. Вот и приходится вводить обозначения вершин, чтоб можно было понятно написать о том, что у нас есть и что нужно найти. Донышко коробки, оно же основание параллелепипеда, обозначаются буквами без цифр, крышка обозначается буквами с цифрами. Одинаковые буквы располагаем друг над другом.

«…известны ребра AA1 = 6, AB = 6, AD = 3 корня из 13.»
Вот теперь мы можем прямо на рисунке подписать длину этих ребер. Смотрим на буквы, я выделил эти три ребра синим цветом.

Фактически нам даны размеры параллелепипеда. И хотя на рисунке длина ребер не совсем соответствует условию, ничего страшного. На алгебру решения это нисколько не влияет. Мы не используем рисунок для графического решения задачи. Он нам нужен только для того, чтобы понять ход решения. Одинаковые задачи для параллелепипедов самых разных размеров будут иметь одинаковый ход решения. В конце только числа разные будут получаться.

Ничего не понятно. Откуда взялись точки М и К? После этих слов в условии задачи ещё что-то написано. По этому пропускаем этот фрагмент и читаем дальше.

«…где точки М и К делят ребра BB1 и CC1 в отношении 1:2…»
Ага, вот и точки появились. Ребра на рисунке мы можем найти, но как их разделить «… в отношении 1:2…»
? Всё очень просто. Вспоминаем детский сад. «Разделите отрезок на три равные части и возьмите одну часть» — это очень простая задача, с которой справится даже ребенок. А мы уже взрослые. Как узнать, на сколько частей нужно делить? Выражение «Разделить в отношении 1:2»
равнозначно выражению «Разделить на 3 части»
. Ведь 1+2=3. Длина всех вертикальных ребер равна 6 см. Одна часть будет равна 6/3=2 см. Нам нужно взять одну часть. Но какую? Нижнюю, верхнюю или среднюю? Читаем дальше условие задачи: «…считая от прямой ВС»
. Почему ребро ВС вдруг превратилось в прямую? Математики, как заправские карточные шулеры, очень любят подменять одни понятия другими, превращая простую задачу в настоящий ребус. Вот из-за таких ребусов многие ненавидят математику. Прямая ВС совпадает с ребром ВС и находится они на нижнем основании прямоугольного параллелепипеда, на донышке коробки. По этому мы берем нижнюю треть вертикальных граней. Обозначаем нужные точки на рисунке.

Всё условие задачи мы разобрали до конца и теперь самое время вернуться к пропущенному фрагменту: «Найдите площадь сечения параллелепипеда плоскостью AMK…»
. Через точки М и К можно провести целое море плоскостей. Все они будут вращаться на отрезке МК, как шашлык на шампуре.

Нас же интересует только та плоскость, которая проходит через точку А. Такая плоскость всего одна. Поскольку отрезок МК параллелен ребру ВС, а тот в свою очередь параллелен ребру АD, значит наша плоскость проходит через это ребро. В сечении у нас получается прямоугольник АDМК, расположенный под углом к основанию.

Нам нужно найти площадь этого прямоугольника (на рисунке он закрашен голубеньким). Одна сторона у нас есть, нужно найти длину другой стороны. Если посмотреть на зелененький треугольник, то вторая сторона прямоугольника окажется гипотенузой прямоугольного треугольника АВМ. По теореме дедушки Пифагора мы без труда найдем длину этой гипотенузы. Как видите, детская задачка на два действия.

Вот только меня терзают смутные сомнения, что кто-то где-то запутался. Если для точек М и К брать не одну часть от ребер ВВ1 и СС1, а две части, тогда длина гипотенузы получается равной двум корням из тринадцати. При вычислении площади сечения число тринадцать вылезает из-под корня и площадь получается равной 78 сантиметров в квадрате. Явно кто-то ошибся. Либо математики при составлении своего ребуса, либо я не правильно расшифровал изящную словесность этого ребуса. Вот видите к чему могут приводить бездарные попытки казаться умнее, чем ты есть на самом деле. Это относится как ко мне, так и к математикам. Кстати, если бы в условии было указано соотношение 2:1, то и я бы правильно решил эту задачу и получил ответ без квадратного корня.

Для секущей плоскости А1МК решение получается очень даже красивое. Та же теорема Пифагора для зеленого треугольничка, та же площадь прямоугольника.

P.S. Рисовать картинки можно на бумаге. Я картинки рисую на компьютере для того, чтобы и вам их показывать. Вы тоже можете так делать. Берете заготовку прямоугольного параллелепипеда и разрисовываете её под условия своей задачи. Тогда находить решение вам будет гораздо проще. Если у вас есть ноутбук и он перегревается от вашего чрезмерного усердия, тогда охлаждающая подставка поможет вам избавиться от проблем. Работает такая подставка от самого ноутбука и подключается к нему через USB разъем. Никаких розеток с собою носить не нужно. Очень удобно и практично.

Пошаговое построение сечения параллелепипеда

Построение сечения методом следов — это поэтапное отыскание точек, принадлежащих одной и той же плоскости грани и одновременно плоскости сечения, то есть прямым, проходящим через точки, принадлежащие сечению. Метод подходит для использования тогда, когда следы секущей плоскости и прямые граней многогранника пересекаются в области чертежа, то есть если сечение параллельно или почти параллельно основанию, этот метод построения не подойдет.

Задача 1.

Построить сечение параллелепипеда плоскостью, проходящей через точки  .

Шаг 1. Чезез точки и , которые принадлежат одной грани, и, следовательно, одной плоскости, проводим прямую. Точки этой прямой все принадлежат секущей плоскости. Точка лежит в плоскости основания, поэтому неплохо бы найти найти точку прямой , которая также принадлежала бы основанию. Для этого проводим прямую , и находим точку ее пересечения с прямой — .

Шаг 2. Проводим прямую , принадлежащую плоскости основания. Находим точку пересечения этой прямой ребра — .

Шаг 3. Точка лежит в задней грани, поэтому надо бы найти точку прямой , которая принадлежала бы плоскости задней грани. Для этого проведем прямую , которая принадлежит как плоскости основания, так и плоскости задней грани, и найдем точку ее пересечения с прямой — . Через две точки задней грани проводим прямую , и находим место пересечения этой прямой с ребром — .

Шаг 4. Окончание построения. Соединяем полученные точки отрезками, и строим многоугольник сечения.

Задача 2.

Построить сечение параллелепипеда плоскостью, проходящей через точки 

Шаг 1. Точки и лежат в одной плоскости, можно соединить их прямой. Прямая пересечет ребро в точке .

Шаг 2. Точки и также лежат в одной плоскости. Соединяем их прямой и отыскиваем точку пересечения ею ребра — .

Шаг 3. Найдем точку секущей плоскости, принадлежащую передней грани, чтобы затем через эту точку и точку можно было бы тоже провести след секущей плоскости. Для того, чтобы найти такую точку, проведем луч и найдем его пересечение с прямой — ведь обе эти прямые принадлежат плоскости верхней грани. Точка пересечения — точка . Точки и можно соединить отрезком.

Шаг 4. Находим точку пересечения отрезком ребра — точку .

Шаг 5. После этого соединяем отрезками полученные точки и закрашиваем многоугольник сечения.

Задача 3.

Построить сечение параллелепипеда плоскостью, проходящей через точки 

Шаг 1. Построим прямую , это можно сделать, так как обе точки принадлежат одной грани. Точка принадлежит грани основания, поэтому нужна точка в этой плоскости.

Шаг 2. Для того, чтобы найти точку, одновременно принадлежащую и секущей плоскости, и плоскости нижней грани, продолжим прямую и найдем точку ее пересечения с прямой — .

Шаг 3. Проводим прямую и находим точку пересечения этой прямой с ребром — точка .

Шаг 4. Теперь надо найти точку в плоскости передней  грани, потому что в этой плоскости у нас уже есть точка — точка . Для того, чтобы найти такую точку, продлим прямую  и найдем пересечение этой прямой с прямой — точка .

Шаг 5. Проводим прямую , отыскиваем точки пересечения ею ребер — точку , и ребра — точку .

Шаг 6. Соединяем точки и получаем многоугольник сечения.

Окончательный вид сечения с другого ракурса:

Задача 4.

Построить сечение параллелепипеда плоскостью, проходящей через точки  . Точка в задней грани.

Шаг 1.  Проводим прямую через две точки одной плоскости — и .  Определяем точку пересечения данной прямой ребра — .

Шаг 2. Продолжение прямой пересечется с продолжением прямой — так как обе прямые принадлежат плоскости задней грани. Точка также принадлежит задней грани, но также и боковой. А в боковой грани у нас есть точка , и тогда можно провести прямую .

Шаг 3. Точка — точка пересечения прямой ребра . Продлим также ребро и найдем пересечение прямой и прямой — точку , которая принадлежит плоскости основания.

Шаг 4. Соединяем Точки и плоскости основания, определяем точку пересечения данной прямой с ребром — точку . Соединяем полученные точки отрезками. Штрихуем полученный многоугольник сечения.

Окончательный вид сечения с другого ракурса: