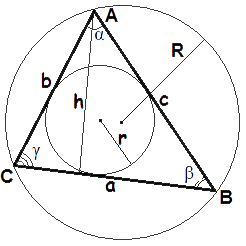Как найти секущую в треугольнике

Свойство секущих

Теорема

Для каждой из секущих, проведённых из одной точки, произведение длины секущей на длину её внешней части есть величина постоянная.

Дано : окружность (O; R), AB и AC — секущие,

AB∩окр. (O; R)=F, AC∩окр. (O; R)=K

Рассмотрим треугольники ABK и ACF.

∠ABK=∠ACF (как вписанные углы, опирающиеся на одну дугу FK).

Следовательно, треугольники ABK и ACF подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

По основному свойству пропорции:

Что и требовалось доказать.

II способ

1) Проведём отрезки FK и BC.

2) Так как четырёхугольник BFKC — вписанный в окружность, то сумма его противолежащих углов равна 180º:

∠BCK+∠BFK=180º. Следовательно, ∠BFK=180º-∠BCK.

3) ∠AFK+∠BFK=180º (как смежные). Отсюда,

4) Рассмотрим треугольники ABC и AKF.

У них ∠ACB=∠AFK (так как ∠AFK=∠BCK по доказанному), ∠A — общий угол. Следовательно, треугольники ABC и AKF — подобны (по двум углам).

Что и требовалось доказать .

При решении задач будем использовать свойство секущих, а также запомним полученные в ходе доказательства теоремы факты о подобии треугольников, образованных секущими. Причем подобие треугольников ABC и AKF можно доказывать как приведённым выше способом, так и опираясь на свойство секущих.

Треугольник. Формулы и свойства треугольников.

Типы треугольников

По величине углов

По числу равных сторон

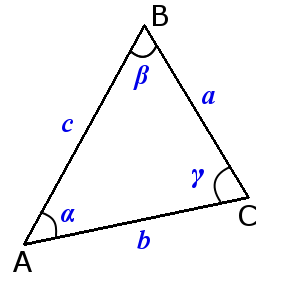
Вершины углы и стороны треугольника

Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°:

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

если α > β , тогда a > b

если α = β , тогда a = b

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

a + b > c
b + c > a
c + a > b

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

a	=	b	=	c	= 2R
sin α	sin β	sin γ

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 — 2 bc · cos α

b 2 = a 2 + c 2 — 2 ac · cos β

c 2 = a 2 + b 2 — 2 ab · cos γ

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β

b = a cos γ + c cos α

c = a cos β + b cos α

Формулы для вычисления длин сторон треугольника

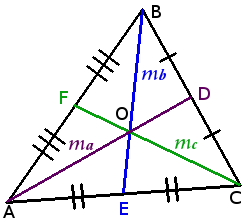
Медианы треугольника

Свойства медиан треугольника:

В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

Медиана треугольника делит треугольник на две равновеликие части

Треугольник делится тремя медианами на шесть равновеликих треугольников.

Формулы медиан треугольника

Формулы медиан треугольника через стороны

m_a = 1 2 √ 2 b 2 +2 c 2 — a 2

m_b = 1 2 √ 2 a 2 +2 c 2 — b 2

m_c = 1 2 √ 2 a 2 +2 b 2 — c 2

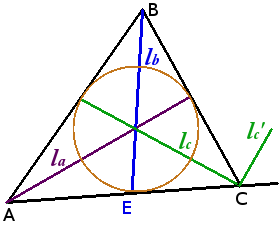
Биссектрисы треугольника

Свойства биссектрис треугольника:

Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны:

l_a = 2√ bcp ( p — a ) b + c

l_b = 2√ acp ( p — b ) a + c

l_c = 2√ abp ( p — c ) a + b

где p = a + b + c 2 — полупериметр треугольника

Формулы биссектрис треугольника через две стороны и угол:

l_a = 2 bc cos α 2 b + c

l_b = 2 ac cos β 2 a + c

l_c = 2 ab cos γ 2 a + b

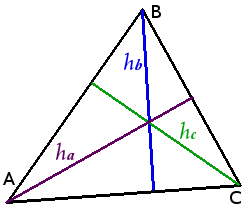
Высоты треугольника

Свойства высот треугольника

Формулы высот треугольника

h_a = b sin γ = c sin β

h_b = c sin α = a sin γ

h_c = a sin β = b sin α

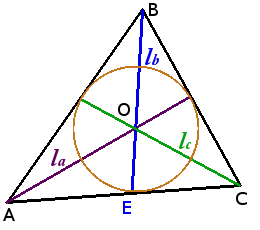
Окружность вписанная в треугольник

Свойства окружности вписанной в треугольник

Формулы радиуса окружности вписанной в треугольник

r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )

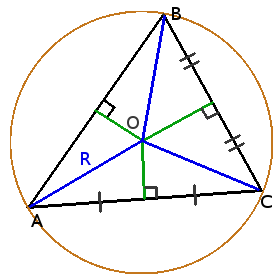
Окружность описанная вокруг треугольника

Свойства окружности описанной вокруг треугольника

Формулы радиуса окружности описанной вокруг треугольника

R = S 2 sin α sin β sin γ

R = a 2 sin α = b 2 sin β = c 2 sin γ

Связь между вписанной и описанной окружностями треугольника

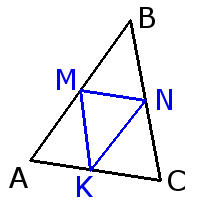
Средняя линия треугольника

Свойства средней линии треугольника

MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC

MN || AC KN || AB KM || BC

Периметр треугольника

Периметр треугольника ∆ ABC равен сумме длин его сторон

Формулы площади треугольника

Формула Герона

Равенство треугольников

Признаки равенства треугольников

Первый признак равенства треугольников — по двум сторонам и углу между ними

Второй признак равенства треугольников — по стороне и двум прилежащим углам

Третий признак равенства треугольников — по трем сторонам

Подобие треугольников

∆MNK => α = α ₁, β = β ₁, γ = γ ₁ и AB MN = BC NK = AC MK = k ,

где k — коэффициент подобия

Признаки подобия треугольников

Первый признак подобия треугольников

Второй признак подобия треугольников

Третий признак подобия треугольников

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Тема: «Применение конструкций треугольник-окружность в решении задач геометрии»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

Департамент образования города Москвы

Государственное образовательное учреждение

высшего профессионального образования

МОСКОВСКИЙ ИНСТИТУТ ОТКРЫТОГО ОБРАЗОВАНИЯ

Факультет повышения квалификации

слушателя факультета повышения квалификации

педагогических кадров отделения «Математика»

Ивакина Нелля Павловна

Тема: «Применение конструкций треугольник-окружность в решении задач геометрии»

Заведующий кафедрой математики

к.ф.-м.н. Ященко Иван Валериевич

«04» апреля 2014г.

г. Москва – 2014г.

Вспомогательные конструкции и их свойства…………………………… 5

Треугольник и секущая, теорема Менелая ……………………………5

Треугольник и точка, теорема Чевы …………………………………. 7

Вписанный угол. Теорема синусов …………………………….………9

Окружность и касательная, окружность и секущая. Теоремы о свойствах секущих …………………………………………….….……11

Основные конструкции……………………………………………….….…14

2.1 Треугольник и описанная окружность………………………….….….14

2.2 Частные случаи: прямоугольный, равнобедренный и равносторонний треугольник ………………………………………………………….……. 15

Треугольник и вписанная (вневписанная) окружность……….………17

Задачи для самостоятельного решения. ………………………….………21

Список использованной литературы …………………………………………23

Введение

При решении многих задач планиметрии возникают различные конфигурации, в которых участвуют треугольник и окружность. Знание наиболее распространенных комбинаций и их свойств позволяет получать короткие и красивые решения сложных на первый взгляд задач. К таким конструкциям в первую очередь относятся «треугольник и описанная окружность», «треугольник и вписанная окружность», которые довольно подробно изучаются в школьном курсе, в меньшей степени изучаются конструкции «треугольник и вневписанная окружность», «треугольник и окружность, проходящая через две его вершины», «треугольник и окружность, касающаяся двух его сторон» и другие.

Взгляд на планиметрию через призму конструкций дает учащимся возможность по-новому посмотреть на хорошо знакомый материал и связать его с новыми знаниями, укрепив их через практическое применение к решению задач.

Предлагаемые темы рассчитаны на школьников 10-11 классов, при подготовке к сдаче ЕГЭ (выполнения заданий С4).

Цель данных занятий:

познакомить старшеклассников с различными конструкциями, в которых участвуют треугольник и окружность и свойствами этих конструкций,

научить находить эти конструкции в ходе исследования условий задачи и применять нужные свойства для получения решения.

Требования к уровню усвоения содержания предмета

Старшеклассники должны знать:

основные конструкции, описанные выше и связанные с ними факты и теоремы,

ряд вспомогательных конструкций: «треугольник и секущая», «окружность и касательная», «треугольник и точка», «окружность и секущая» и их свойства.

Старшеклассники должны уметь:

определять, какие конструкции возникают в геометрических задачах,

применять подходящие свойства этих конструкций для поиска решения.

1. Вспомогательные конструкции и их свойства

В этой части мы рассмотрим некоторые важные конфигурации, в которых участвуют треугольник, окружность, прямая или угол.

1.1 Треугольник и секущая, теорема Менелая

Секущей будем называть прямую, которая пересекает некоторую геометрическую фигуру: треугольник, окружность, угол и т.п. Иногда удобно брать не только точки пересечения фигуры и секущей, но и некоторые дополнительные точки: например, точку пересечения прямой, на которой лежит сторона треугольника и секущей.

Рассмотрим секущую треугольника. К ней относится одна замечательная теорема: теорема Менелая, которая связывает отношения длин отрезков, на которые секущая делит стороны треугольника.

Теорема Менелая. Пусть пересечен прямой, не параллельной стороне А C и пересекающей две его стороны А B и ВС соответственно в точках C ₁ и А₁, а прямую А C в точке B ₁ тогда

(1)

Справедлива также обратная теорема Менелая.

Теорема, обратная теореме Менелая. В треугольнике АВС точки А₁, В₁, С₁ принадлежат прямым ВС, АС, АВ соответственно, тогда если

,

Упражнение 1. Докажите теорему Менелая. (Указание: опустите на секущую перпендикуляры из вершин треугольника и рассмотрите пары получившихся подобных прямоугольных треугольников. Заменив в (1) отношения гипотенуз на отношения соответствующих катетов и выполнив сокращения, получите нужный результат.)

Упражнение 2. Докажите теорему, обратную теореме Менелая. (Указание: воспользуйтесь методом «от противного». Предположите, что, например, точка A ₁ не лежит на секущей. Тогда секущая пересечет сторону BC в некоторой точке A ₂, для которой выполнена прямая теорема Менелая. Далее самостоятельно получите противоречие.)

Решение

Построим треугольник DEF , где D , E , F – середины сторон, AB , AC и BC соответственно.

(по теореме Менелая)

Значит, по обратному утверждению теоремы Менелая точки K , L и M лежат на одной прямой, что и требовалось доказать.

1.2 Треугольник и точка, теорема Чевы

Второй интересной конструкцией, которую мы рассмотрим, является треугольник, у которого три отрезка, проведенных из вершин на противоположные стороны или их продолжения, пересекаются в одной точке.

Свойства этой конструкции описывает теорема Чевы.

Т
еорема Чевы. В произвольном треугольнике АВС на сторонах ВС, СА, АВ или их продолжениях взяты соответственно точки А₁, В₁, С₁. Если прямые АА₁, ВВ₁, СС₁ пересекаются в некоторой внутренней точке Z треуголь­ника АВС то выполнено условие

. (2)

Так же, как и в случае теоремы Менелая, для теоремы Чевы справедливо обратное утверждение.

Теорема, обратная теореме Чевы. Если в произвольном треугольнике АВС на сторонах ВС, СА, АВ или их продолжениях взяты соответственно точки А₁, В₁, С₁, для которых выполнено условие

,

то прямые АА₁, ВВ₁, СС₁ пересекаются в одной точке.

Упражнение 4. Докажите теорему Чевы. (Указание: попробуйте записать условие теоремы Менелая для треугольников ABB ₁ и B ₁ BC и секущих CC ₁ и AA ₁, а затем исключите из этих равенств «лишние» отрезки.)

Упражнение 5. Докажите теорему, обратную теореме Чевы. (Указание: вновь используйте метод доказательства «от противного».)

Упражнение 6. Решите задачу. На медиане СМ треугольника АВС дана точка Р, через которую проведены прямые АР и ВР, пересекающие стороны ВС и АС треугольника в точках А₁ и В₁ соответственно. Докажите, что если АА₁ равно ВВ₁, то данный треугольник равнобедренный.

Решение.

По теореме Чевы

Если АА₁ = ВВ₁, то эта трапеция равнобокая, то есть АВ₁ = А₁В.

Тогда по теореме Чевы В₁С = А₁С,

а значит АС = АВ₁ + В₁С = А₁С + А₁В = ВС, то есть ∆АВС равнобедренный.

1.3 Вписанный угол. Теорема синусов

Свойства угла, вписанного в окружность, подробно изучаются в школьном курсе геометрии. Тем не менее, эта конструкция достойна отдельного упоминания, так как из нее можно получить очень полезное доказательство теоремы синусов.

Теорема о вписанном угле. Величина угла, вписанного в окружность, равна половине величины центрального угла, опирающегося на ту же дугу.

Теорема синусов. В произвольном треугольнике отношения длин сторон треугольника к синусам противолежащих углов есть постоянная величина, равная диаметру описанной вокруг этого треугольника окружности.

Упражнение 7. Докажите теорему синусов. (Указание: воспользуйтесь рисунком и выразите длину хорды (стороны треугольника) через радиус окружности и величину центрального угла.)

Упражнение 8. Решите задачу. В треугольнике АВС , АВ =4, ВС =3, точки А ₁ , В ₁ , С ₁ – основания высот треугольника АВС. Найдите радиус окружности, описанной вокруг треугольника А В ₁ С _1.

Решение.

Для сокращенной записи введем обозначение ∟АВС = β. Получаем ∟А В₁С_{1 =} β и ∟С В₁А₁ = β. Следовательно, ∟А₁В₁С₁ = 2 β. По теореме синусов, радиус описанной окружности ∆ А₁В₁С₁ равен

.

По условию, , чтобы найти R, остается вычислить А ₁ В ₁ С ₁ . Найдем АС по теореме косинусов:

АС 2 =АВ 2 +ВС 2 -2АВ ·ВС· , АС 2 =4 2 +3 2 -2·4·3· = 17, АС = . Значит А ₁ С ₁ = и окончательно получаем:

Ответ:

1.4 Окружность и касательная, окружность и секущая. Теоремы о свойствах секущих

Вспомогательная конструкция «окружность – секущая» часто встречается в разных задачах. Более того, она связана с важным понятием «степень точки относительно окружности».

Мы рассмотрим только несколько конструкций, которые для удобства собраны на одном чертеже.

Перечислим некоторые их свойства.

Свойство 1. Длины отрезков касательных, проведенных к одной окружности из одной точки M равны ( MT 2 = MO 2 — R 2 ).

Свойство 2. Произведения отрезков двух секущих к одной окружности равны ( MA MB = MC MD ).

Свойство 3. Произведение отрезков внешней секущей равно квадрату отрезка касательной, проведенной из той же точки ( MA MB = MT 2 = MO 2 — R 2 ).

Далее рассмотрим случай, когда точка расположена внутри окружности.

Свойство 4. (аналог свойства 2) Произведения отрезков двух секущих к одной окружности равны ( MA MB = MC MD ).

С
войство 5. (аналог свойства 3) Произведение отрезков внутренней секущей равно разности квадратов радиуса и расстояния от точки до центра окружности ( MA MB = R 2 — MO 2 ).

Упражнения 9-13. Докажите свойства 1-5.

Упражнение 14. Решите задачу. В окружности радиуса 17 проведена хорда АВ длины 30. Точка С лежит на хорде АВ так, что АС:ВС = 1:3. Найдите радиус окружности, касающейся данной окружности и касающейся хорды АВ в точке С.

Решение. 1). Пусть О –центр данной окружности радиуса 17, а r – искомый радиус окружности, касающийся данной окружности и касающийся ее хорды АВ в точке С. Возможны лишь два случая расположения этой окружности:

а) окружность и точка О лежат по одну сторону от хорды АВ.

б) окружность и точка О лежат по разные стороны от хорды АВ.

2) Пусть точке Р – центр окружности, радиус которой мы ищем, а точка К – точка касания этой окружности с данной. Точка РК = СР = r , СР _┴ АВ.

Т

ак как точка касания двух окружностей принадлежит прямой, соединяющей их центры, то точки О, Р, К лежат на одной прямой. Поэтому ОК = ОР + РК, ОР = ОК – РК = 17 – r .

Из треугольника СРО по теореме косинусов имеем:

ОР 2 =СР 2 +СО 2 -2СР·СО· cos ∟ОСР

289 – 34r = CO 2 — 2r· СО ·cos∟ ОСР

r

= (289 – СО 2 ) : (34 — 2·СО· cos ∟ОСР) (*)
Пусть М – середина хорды АВ, тогда ОМ _┴ АВ, и из ∆СОМ и ∆ВОМ имеем: СО 2 = СМ 2 + ОМ 2 ,

ОМ 2 = ВО 2 — ВМ 2 = 17 2 -15 2 = 64 ⇒ СО 2 = СМ 2 + 64.

Так как АС = 1/3ВС , то АС = 1/4 АВ = 15/2, СМ = АМ – АС = 15 – 15/2 = 15/2.

Итак СО 2 = (15/2) 2 + 64 = 481/4.

Поскольку ∟ОСР = 90 о — ∟ОСМ, то СО· cos ∟ОСР = СО· sin ∟ОСМ = ОМ = 8

Итак, r = (289 – 481/4) : (34 — 2·8) = 75/8

∟ ОСР = 90 о + ∟ОСМ, поэтому получаем

r = (289 – СО 2 ) : (34 + 2·СО· cos ∟ОСР) =

Ответ: 27/8 или 75/8

2. Основные конструкции

В этой части мы рассмотрим основные конструкции, которые образуют треугольник и окружность.

2.1 Треугольник и описанная окружность

Центр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника.

У остроугольного треугольника эта точка находится внутри, у прямоугольного – на середине гипотенузы, а у тупоугольного – вне треугольника.

Упражнение 15. Докажите, что если два треугольника имеют общую сторону, то прямая, проходящая через центры описанных окружностей этих треугольников делит такую сторону пополам (проходит через середину стороны).

Из теоремы о вписанном угле следует, что из центра описанной окружности каждая сторона видна под углом, в два раза большем, чем противолежащий угол треугольника. Используйте это свойство для решения следующего упражнения.

Упражнение 16. Выразить стороны треугольника через его углы и радиус описанной окружности.

Упражнение 17. Докажите для произвольного треугольника следующую формулу: , здесь a , b и c – стороны, R – радиус описанной окружности, S – площадь треугольника. (Указание: используйте выражение для стороны c из предыдущего упражнения и формулу для площади треугольника .)

2.2 Частные случаи: прямоугольный, равнобедренный и равносторонний треугольник

Как уже отмечалось выше, у прямоугольного треугольника центр описанной окружности лежит на середине гипотенузы. Отсюда следует, что радиус описанной вокруг прямоугольного треугольника окружности равен половине его гипотенузы.

Справедлива также следующая теорема.

Теорема. Если радиус описанной окружности некоторого треугольника равен половине длины одной из его сторон, то этот треугольник – прямоугольный.

Упражнение 18. Докажите теорему. (Указание: покажите, что центр описанной окружности лежит на середине стороны треугольника, и найдите синус противоположного угла с помощью теоремы синусов.)

Рассмотрим теперь равнобедренный треугольник. Так как высота, проведенная к основанию такого треугольника, одновременно является серединным перпендикуляром и биссектрисой, то центр описанной окружности лежит на высоте (или ее продолжении).

Упражнение 19. Выразите отношение радиуса описанной окружности равнобедренного треугольника к его высоте через угол при вершине этого треугольника.

Рассмотрим, наконец, равносторонний или правильный треугольник. В этом треугольнике высоты являются медианами, биссектрисами и серединными перпендикулярами. Поэтому центр описанной окружности совпадает с точкой пересечения медиан.

Так как точка пересечения медиан делит каждую из них в отношении 2 к 1 считая от вершины, то радиус описанной окружности равен двум третьим от высоты. Таким образом, , где a – сторона треугольника.

Упражнение 20. Выразите высоту, сторону и площадь равностороннего треугольника через радиус описанной окружности.

2.3 Треугольник и вписанная (вневписанная) окружность

Центр вписанной окружности лежит на пересечении биссектрис внутренних углов треугольника. Радиус этой окружности и точки касания можно определить, опустив перпендикуляр из центра на сторону. Довольно распространенной является такая ошибка: за точку касания окружности и стороны принимают точку пересечения стороны и биссектрисы.

Рассмотрим некоторые свойства вписанного треугольника.

П
усть x , y , z – отрезки, на которые точки касания вписанной окружности делят стороны треугольника. Эти отрезки можно выразить через стороны треугольника, решив следующую систему уравнений:

Упражнение 21. Докажите, что отрезки, соединяющие вершины треугольника с точками касания вписанной окружности, лежащими на противоположных сторонах, пересекаются в одной точке.

Упражнение 22. Решите задачу. В треугольнике АВС: АВ = 12, АС = 9,

ВС = 6. На прямой ВС взята точка D так, что В D : D С = 1 :7. В треугольнике А D С и А D В вписаны окружности, касающиеся прямой А D в точках Е и F . Найдите длину отрезка EF .

Решение. Так как BD CD , то возможны только два случая расположения точки D на прямой BC .

а) Точка D лежит на отрезке ВС.

б) Точка D лежит на продолжении стороны ВС за точку В.

Из соотношения ВD : DС = 1 :7 имеем:

В случае а) BD = 1/8 BC = 3/4, CD = 7 BD = 21/4.

В случае б) BD = 1/7 DC , BC = 6/7 DC ⇒ BD = 1/6 BC = 1, CD = 7 BD = 7.

Получаем DF = (AD+BD-AB)/2, DE = (AD+CD-AC)/2.

Таким образом, EF = DE — DF , EF = ( CD – AC – BD + AB )/2.

В случае а) EF = (21/4 – 9 — 3/4 + 12)/2 = 1/2·15/2 = 15/4

В случае б) EF = (7 – 9 – 1 + 12)/2 = 9/2

Ответ: 3,75 или 4,5.

Если вписанные окружности всем хорошо знакомы, то вневписанными встречаются реже. Поясним, чем они отличаются от вписанных.

Итак, центр вневписанной окружности лежит вне треугольника. Это точка пересечения биссектрис одного внутреннего и двух внешних углов треугольника.

Вневписанная окружность касается одной стороны и продолжений двух других сторон треугольника. Для треугольника существует три вневписанных окружности. (На рисунке изображены вписанная и вневписанная окружности. Хорошо видно, что точки касания этих окружностей со стороной треугольника не совпадают.)

Упражнение 23. Выразите длины отрезков касательных, проведенных из вершин треугольника к вневписанной окружности, через длины сторон этого треугольника. (Указание: используйте метод, который был применен к вписанной окружности.)

Найдем выражения для радиусов вписанной и вневписанных окружностей. Начнем со случая вписанной окружности. « Разрежем» треугольник на три треугольника так, как показано на рисунке. Каждый из них имеет высоту, равную радиусу вписанной окружности. Сумма площадей трех треугольников равна площади большого:

.

Отсюда легко получить формулу для вычисления радиуса вписанной окружности:

.

Радиусы вневписанных окружностей можно получить аналогично. Представим площадь треугольника ABC так:

.

Далее применим те же рассуждения, что и ранее. В результате получим следующую формулу:

.

Упражнение 24. Докажите, что прямые, соединяющие вершины треугольника с точками касания сторон или продолжений сторон этого треугольника с вневписанной окружностью, пересекаются в одной точке. (Указание: используйте теорему Чевы.)

3 Задачи для самостоятельного решения.

1. Две окружности внешне касаются в точке А, ВС — их общая внешняя касательная. Доказать, что .

2. Две окружности пересекаются в точках А и В. Точки А и В лежат по разные стороны от прямой l , которая пересекает окружности соответственно в точках С, D, Е и М. Доказать, что сумма углов DBE и САМ равна 180°.

3. Две окружности пересекаются в точках А и В. Прямые l ₁ и l ₂ параллельны, причем l ₁ проходит через точку А и пересекает окружности в точках Е и К, а l ₂ про­ходит через точку В и пересекает окружности в точках М и Р. Доказать, что четырехугольник ЕКМР — параллелограмм.

4. Из точки М проведены к окружности с центром в точке О касательные МА и МВ. Прямая l касается окружности в точке С и пересекает МА и МВ соответственно в точках D и Е. Доказать, что: а) периметр треугольника MDE не зависит от Выбо­ра точки С; б) угол DOE не зависит от выбора точки С.

5. Точки А, В, С и D делят окружность на части, отношение которых 1 : 3 : 5 : 6. Найти углы между касательными к окружности, проведенными в точках А, В, С и D.

6. Две равные окружности внешне касаются друг друга и третьей окружности, радиус которой равен 8 см. Отрезок, соединяющий точки касания двух равных ок­ружностей с третьей, равен 12 см. Найти радиусы равных окружностей.

7. Общая хорда двух пересекающихся окружностей равна а и служит для одной окружности стороной правильного вписанного шестиугольника: а для другой ­вписанного квадрата. Найти расстояние между центрами окружностей.

8. Две окружности радиусами, и R касаются внешним образом. Найти дли­ну их общей внешней касательной.

9. Две окружности радиусами r и R касаются внешним образом. Прямая 1 пересекает окружности в точках А, В, С и D так, что АВ = ВС = CD. Найти AD.

10. Две окружности, радиусы которых относятся как 1 : 3, касаются внешним образом, длина их общей внешней касательной см. Найти периметр фигуры, образованной внешними касательными и внешними дугами окружностей.

11. Из внешней точки к окружности проведены секущая длиной 48 см и каса­тельная, длина которой составляет от внутреннего отрезка секущей. Найти ра­диус окружности, если известно, что секущая удалена от центра на расстояние 24 см.

12. Общая внешняя касательная двух внешне касающихся окружностей составляет с линией центров угол а. Найти отношение радиусов.

13. Из точки А, расположенной вне круга с центром О, проведены секущие АВС и АМК (В и М — ближайшие к А точки окружности, лежащие на секущих). Найти ВС, если известно, что и секущая АМК проходит через центр окружности.

14. Две окружности пересекаются в точках А и В. Через точку А проведены отрезки АС и AD, каждый из которых, являясь хордой одной окружности, касается другой окружности. Доказать, что АС 2 . BD = AD 2 . B С.

15. АВ и CD — взаимно перпендикулярные пересекающиеся хорды окружно­сти радиуса R. Доказать, что АС 2 + BD 2 = 4R 2 .

16. Доказать, что сумма квадратов расстояний от точки М, взятой на диаметре окружности, до концов любой из параллельных этому диаметру хорд есть для дан­ной окружности постоянная величина.

17. Две окружности внешне касаются в точке С, АВ — их общая внешняя ка­сательная. Найти радиусы, если АС = 8 см, ВС = 6 см.

18. Окружности радиусами R и касаются внешним образом. Из центра мень­шей окружности под углом 30° к линии центров проведен отрезок длиной 2R. Найти длины тех частей отрезка, которые лежат вне окружностей.

19. Окружности радиусами а и b имеют внутреннее касание (а b ), причем центр большей окружности лежит вне меньшей окружности. Хорда АВ большей окружности касается меньшей окружности и образует с общей касательной к окруж­ностям угол . Найти АВ.

20. В правильном треугольнике АВС на сторонах АВ и АС взяты точки М и К так, что АМ : МВ = 2 : 1, АК : КС = 1 : 2. Доказать, что отрезок КМ равен радиусу окружности, описанной около треугольника АВС.

Список использованной литературы

Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Геометрия. 10-11 классы: учеб. Для общеобразоват. учреждений: базовый и профил. уровни– 18-е изд. – М.: Просвещение, 2009. – 255 с.

Гусев В.А., Кожухов И.Б., Прокофьев А.А. Геометрия. Полный справочник. – М.: Махаон, 2006. – 320 с.

Лаппо Л.Д., Филонов А.Н. Математика. Экспресс-курс подготовки к ЕГЭ: учебное пособие. – М.: Издательство «Экзамен», 2004. – 96с.

Мальцев Д.А. Математика. Все для ЕГЭ 2011. Часть 1: учебно-методическое пособие. – Ростов н/Д: Издатель Мальцев Д.А.; М.: НИИ школьных технологий, 2010. – 221 с.

Мельникова Н.Б. Геометрия: Дидакт. Метериалы для 10-11 кл. общеобразоват. Учреждений. – 2-е изд. –М.: Мнемозина, 1999. – 272 с.

Полонский В.Б., Рабинович Е.М., Якир М.С. Учимся решать задачи по геометрии. Учеб.-метод. пособие. – К. «Магистр», 1996, – 256 стр.

Потоскуев Е.В., Звавич. Л.И. Геометрия. 10 кл.: учеб. для общеобразоват. учреждений с углубл. и профильным изучением математики /– 3-е изд. – М.: Дрофа, 2005. – 223 с.

Потоскуев Е.В., Звавич. Л.И. Геометрия. 11 кл.: учеб. для общеобразоват. учреждений с углубл. и профильным изучением математики – 3-е изд. – М.:Дрофа, 2003. – 368 с.

Прасолов В.В. Задачи по планиметрии: Учебное пособие. – 5-е изд., испр. И доп. –М.: МЦНМО: ОАО «Московские учебники», 2006. – 640с.

Прокофьев А.А. Пособие по геометрии для подготовительных курсов (планиметрия). – 4-е изд. перераб. и доп. – М.:МИЭТ, 2007, 232 стр.

Шарыгин И.Ф. Геометрия. 10-11 классы: учеб. Для общеобразоват. заведений. – М.: Дрофа, 1999. – 208 с

Шарыгин И.Ф. Сборник задач по геометрии. 5000 задач с ответами / И.Ф.

Теорема

(Свойство секущих)

Для каждой из секущих, проведённых из одной точки, произведение длины секущей на длину её внешней части есть величина постоянная.

Дано: окружность (O; R), AB и AC — секущие,

AB∩окр. (O; R)=F, AC∩окр. (O; R)=K

Доказать:

AB ∙ AF=AC ∙ AK

Доказательство:

I способ

Рассмотрим треугольники ABK и ACF.

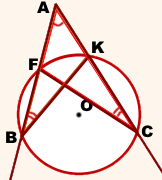
∠A — общий угол;

∠ABK=∠ACF (как вписанные углы, опирающиеся на одну дугу FK).

Следовательно, треугольники ABK и ACF подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

   

По основному свойству пропорции:

   

Что и требовалось доказать.

II способ

1) Проведём отрезки FK и BC.

2) Так как четырёхугольник BFKC — вписанный в окружность, то сумма его противолежащих углов равна 180º:

∠BCK+∠BFK=180º. Следовательно, ∠BFK=180º-∠BCK.

3) ∠AFK+∠BFK=180º (как смежные). Отсюда,

∠AFK=180º-∠BFK=180º-(180º-∠BCK)=180º-180º+∠BCK=∠BCK,

то есть ∠AFK=∠BCK.

4) Рассмотрим треугольники ABC и AKF.

У них ∠ACB=∠AFK (так как ∠AFK=∠BCK по доказанному), ∠A — общий угол. Следовательно, треугольники ABC и AKF — подобны (по двум углам).

Отсюда,

   

Что и требовалось доказать.

При решении задач будем использовать свойство секущих, а также запомним полученные в ходе доказательства теоремы факты о подобии треугольников, образованных секущими. Причем подобие треугольников ABC и AKF можно доказывать как приведённым выше способом, так и опираясь на свойство секущих.

[{Large{text{Основные сведения}}}]

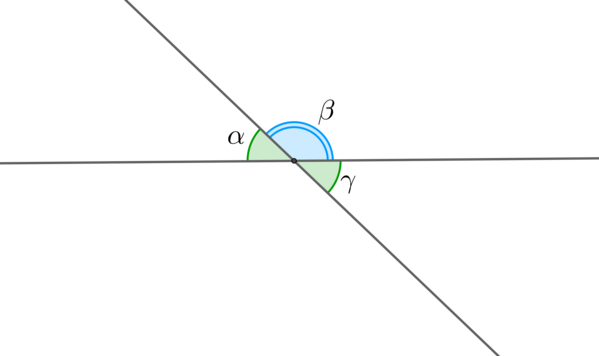
Определения

Угол – это геометрическая фигура, состоящая из точки и двух лучей, выходящих из этой точки. Градусная мера угла может принимать значения от (0^circ) до (180^circ) включительно.

Угол (alpha) называется острым, если (0^circ<alpha<90^circ), прямым – если (alpha=90^circ), тупым – если (90^circ<alpha<180^circ), и развернутым – если (alpha=180^circ).

Биссектриса угла – это луч, выходящий из вершины угла и делящий угол пополам.

Смежные углы – это два угла, у которых общая вершина и одна общая сторона, а две другие стороны образуют прямую.

Вертикальные углы – это два угла, образованные пересечением двух прямых и не являющиеся смежными.

Теорема

Смежные углы (alpha) и (beta) в сумме дают (180^circ).

Определения

Треугольник – это геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой (называемых вершинами треугольника), и отрезков, соединяющих эти точки (называемых сторонами треугольника). Треугольник со своей внутренностью будем сокращенно называть также треугольником.

Теоремы: признаки равенства треугольников

1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

2. Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.

3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
 

Определение

Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

Две прямые называются перпендикулярными, если угол между ними равен (90^circ).

Перпендикуляр из точки к прямой – это отрезок, соединяющий данную точку с точкой на прямой, проведенный под углом (90^circ).

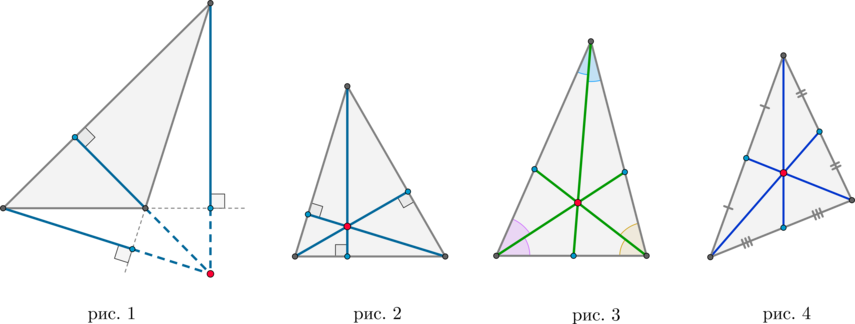
Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.

Замечание

Если в треугольнике один угол тупой, то высоты, опущенные из вершин острых углов, упадут не на сторону, а на продолжение стороны (рис. 1).

Теорема

[{Large{text{Параллельные прямые}}}]

Определение

Две различные прямые на плоскости называются параллельными, если они не пересекаются.

Замечание

Заметим, что на плоскости существует три вида взаимного расположения прямых: совпадают, пересекаются и параллельны.

Аксиома параллельных прямых

Через точку, не лежащую на данной прямой, проходит единственная прямая, параллельная данной.

Следствия из аксиомы

1. Если прямая пересекает одну из параллельных прямых, то она пересекает и другую прямую.

2. Две прямые, параллельные третьей прямой, параллельны.

Теоремы: признаки параллельности прямых

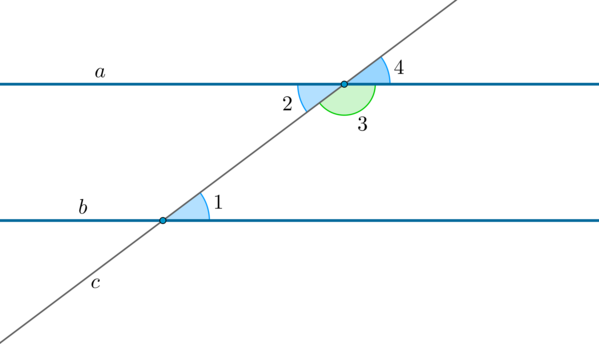
1. Если при пересечении двух прямых (a) и (b) секущей (c) накрест лежащие углы равны: (angle 1=angle 2), то такие прямые параллельны.

2. Если при пересечении двух прямых (a) и (b) секущей (c) сумма односторонних углов (angle 1) и (angle 3) равна (180^circ), то такие прямые параллельны.

Теоремы: свойства параллельных прямых

1. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

2. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна (180^circ).

3. Если две параллельные прямые пересечены секущей, то соответственные углы равны.
 

[{Large{text{Углы треугольника}}}]

Определения

Треугольник называется остроугольным, если все его углы острые.

Треугольник называется тупоугольным, если один его угол тупой (остальные — острые).

Треугольник называется прямоугольным, если один его угол прямой (остальные — острые).

Теорема

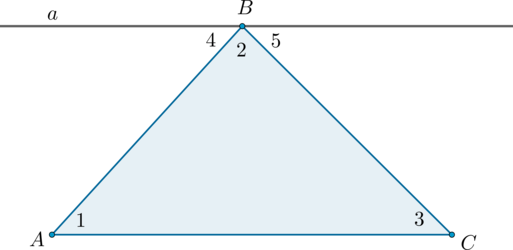
Сумма внутренних углов треугольника равна (180^circ).

Доказательство

Рассмотрим произвольный треугольник (ABC) и покажем, что (angle A +
angle B + angle C = 180^circ).

Углы (1) и (4) являются накрест лежащими углами при пересечении параллельных прямых (a) и (AC) секущей (AB), а углы (3) и (5) – накрест лежащими углами при пересечении тех же параллельных прямых секущей (BC). Поэтому [begin{aligned}
&angle 4 = angle 1, angle 5 = angle 3. qquad qquad qquad
(1)
end{aligned}]

Очевидно, сумма углов (4, 2) и (5) равна развёрнутому углу с вершиной (B), то есть (angle 4 + angle 2 + angle 5 = 180^circ). Отсюда, учитывая равенства ((1)), получаем: (angle 1 + angle 2 + angle 3 = 180^circ).

Определение

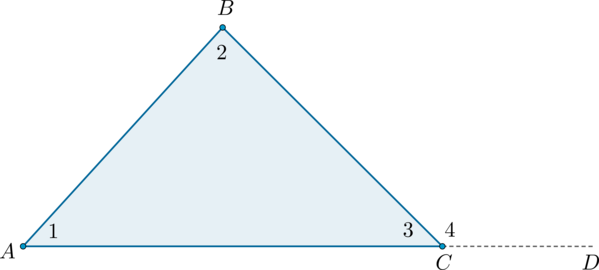
Внешний угол треугольника – это угол, смежный с каким-нибудь внутренним углом треугольника.

Теорема

Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним: (angle BCD=angle BAC+angle ABC).

Доказательство

Угол (4) – внешний угол треугольника, смежный с углом (3). Так как (angle 4 + angle 3 = 180^circ), а по теореме о сумме углов треугольника (angle 1 + angle 2 + angle 3 = 180^circ), то (angle 4 = angle 1 + angle 2), что и требовалось доказать.
 

[{Large{text{Равнобедренный треугольник}}}]

Определения

Треугольник называется равнобедренным, если две его стороны равны.
Эти стороны называются боковыми сторонами треугольника, а третья сторона — основанием.

Треугольник называется равносторонним, если все его стороны равны.
Равносторонний треугольник, очевидно, является и равнобедренным.

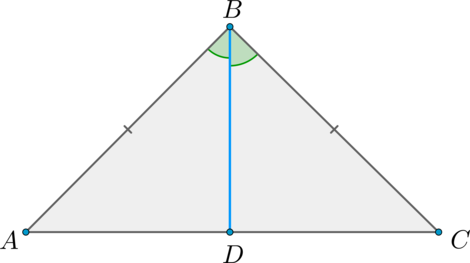
Теорема

В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.

Доказательство

Пусть (ABC) – равнобедренный треугольник, (AB = BC), (BD) – биссектриса (проведённая к основанию).

Рассмотрим треугольники (ABD) и (BCD): (AB = BC), (angle ABD =
angle CBD), (BD) – общая. Таким образом, (triangle ABD =
triangle BCD) по двум сторонам и углу между ними.

Кроме того, в равных треугольниках против равных сторон лежат равные углы, а (AB = BC), следовательно, [begin{aligned}
&angle ADB = angle CDB, qquad qquad qquad (2)
end{aligned}] но (angle ADB + angle CDB = angle ADC) – развёрнутый, следовательно, (angle ADB + angle CDB = 180^circ), откуда при учёте ((2)): (angle ADB = 90^circ = angle CDB), то есть (BD) – высота.

Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Теорема

В равнобедренном треугольнике углы при основании равны.

Доказательство

Проведем биссектрису (BD) (см. рисунок из предыдущей теоремы). Тогда (triangle ABD=triangle CBD) по первому признаку, следовательно, (angle A=angle C).

Теоремы: признаки равнобедренного треугольника

1. Если в треугольнике два угла равны, то треугольник равнобедренный.

2. Если в треугольнике высота является медианой или биссектрисой, то треугольник равнобедренный.
 

Теорема о соотношении между сторонами и углами треугольника

В треугольнике против большей стороны лежит больший угол.

В треугольнике против большего угла лежит большая сторона.

Теорема: неравенство треугольника

В треугольнике сумма любых двух сторон больше третьей стороны.

Другая формулировка: в треугольнике разность любых двух сторон меньше третьей стороны.
 

[{Large{text{Прямоугольный треугольник}}}]

Определения

В прямоугольном треугольнике большая сторона (то есть сторона, лежащая напротив прямого угла) называется гипотенузой.
Две другие стороны называются катетами.

Теоремы: свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна (90^circ).

2. В прямоугольном треугольнике катет, лежащий против угла (30^circ), равен половине гипотенузы.

Подобные треугольники

3 октября 2022

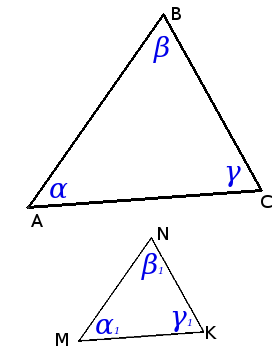
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны соответственным сторонам другого.

Подобные треугольники — ключевая тема геометрии 8 класса. Они будут преследовать нас до самого конца школы. И сегодня мы разберём всё, что нужно знать о них.

План такой:

1. Основное определение
2. Лемма о подобных треугольниках
3. Свойства подобных треугольников
4. Разбор задач

1. Основное определение

Определение. Треугольники называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны соответственным сторонам другого.

Рассмотрим треугольники $ABC$ и $MNK$:

У них есть равные углы: $angle A=angle M$, $angle B=angle N$, $angle C=angle K$. И пропорциональные стороны:

[frac{AB}{MN}=frac{BC}{NK}= frac{AC}{MK}= frac{color{red}{3}}{color{red}{2}}]

Следовательно, треугольники $ABC$ и $MNK$ подобны. Записывается это так:

[Delta ABCsim Delta MNK]

Число $k={color{red}{3}}/{color{red}{2}};$ называется коэффициентом подобия. К нему мы ещё вернёмся.

Пропорциональные стороны подобных треугольников (например, $AB$ и $MN$, либо $BC$ и $NK$) в некоторых учебниках называют сходственными. На практике этот термин применяется редко. Мы будем говорить просто «соответственные стороны».

Дальше идёт очень важное замечание.

1.1. Обозначение подобных треугольников

В геометрии один и тот же треугольник можно называть по-разному. Например, $Delta ABC$, $Delta BCA$ или $Delta CAB$ — это всё один и тот же треугольник. То же самое касается и углов.

Но в подобных треугольниках есть негласное правило:

При обозначении подобных треугольников порядок букв выбирают так, чтобы равные углы перечислялись в одной и той же последовательности.

Вернёмся к нашим треугольникам $ABC$ и $MNK$:

Поскольку $anglecolor{red}{A}=anglecolor{red}{M}$ и $anglecolor{blue}{B}=anglecolor{blue}{N}$, можно записать $Deltacolor{red}{A}color{blue}{B}Csim Deltacolor{red}{M}color{blue}{N}K$. Или $Delta Ccolor{red}{A}color{blue}{B}sim Delta Kcolor{red}{M}color{blue}{N}$. Но никак не $Deltacolor{red}{A}color{blue}{B}Csim Delta Kcolor{red}{M}color{blue}{N}$.

Да, это негласное правило. И если вы нарушите последовательность букв, это не ошибка. Никто не снизит вам за это баллы. А если снизит — добро пожаловать на апелляцию.

Правильная запись позволяет быстро и безошибочно выписывать пропорциональные стороны треугольников. Рассмотрим два подобных треугольника:

[Delta ABCsim Delta MNK]

Берём две первые буквы из каждого треугольника: ${AB}/{MN};$. Затем две последние буквы: ${BC}/{NK};$. Наконец, вычёркиваем «центральную» букву: ${AC}/{MK};$.

Приравниваем полученные три дроби:

[frac{AB}{MN}=frac{BC}{NK}=frac{AC}{MK}]

Вот и всё! Даже рисунок не нужен! Этот приём настолько прост и эффективен, что его в обязательном порядке изучают на моих занятиях, курсах и вебинарах.

В будущем мы увидим, что подобные треугольники чаще всего ищут как раз для составления таких пропорций.

2. Лемма о подобных треугольниках

Подобные треугольники появляются всякий раз, когда прямая, параллельная стороне треугольника, пересекает его стороны.

Теорема 1. Прямая, пересекающая две стороны треугольника и параллельная третьей стороне, отсекает треугольник, подобный исходному.

Доказательство. Рассмотрим треугольник $ABC$. Пусть прямая $MNparallel AB$ отсекает треугольник $MNC$:

Докажем, что $Delta ABCsim Delta MNC$. Рассмотрим треугольники $ABC$ и $MNC$. У них есть общий угол $ACB$.

Углы $ABC$ и $MNC$ — соответственными при $MNparallel AB$ и секущей $BC$. Следовательно, они равны: $angle ABC=angle MNC$.

Аналогично равны углы $BAC$ и $NMC$. Следовательно, треугольники $ABC$ и $MNC$ имеют три соответственно равных угла.

Докажем теперь, что соответственные стороны пропорциональны. Т.е. докажем пропорцию

[frac{AB}{MN}=frac{BC}{NC}=frac{AC}{MC}]

Рассмотрим угол $ACB$. Параллельные прямые $AB$ и $MN$ пересекают стороны этого угла. По теореме о пропорциональных отрезках:

[frac{AC}{MC}=frac{BC}{NC}]

Это равенство — второе в искомом:

[frac{AB}{MN}= color{red}{frac{BC}{NC}=frac{AC}{MC}}]

Осталось доказать первое равенство. Дополнительное построение: прямая $KNparallel AC$:

Поскольку $AMparallel KN$ (по построению) и $AKparallel MN$ (по условию), четырёхугольник $AKNM$ — параллелограмм. Поэтому $AK=MN$.

Рассмотрим угол $ABC$. Параллельные прямые $AC$ и $KN$ пересекают стороны этого угла. По теореме о пропорциональных отрезках:

[frac{AB}{AK}=frac{BC}{NC}]

Учитывая, что $AK=MN$, получаем

[frac{AB}{MN}=frac{BC}{NC}=frac{AC}{MC}]

Итак, соответственные углы треугольников $ABC$ и $MNC$ равны, а их стороны пропорциональны. Следовательно, по определению подобных треугольников

[Delta ABCsim Delta MNC]

Что и требовалось доказать.

Эта лемма — не признак подобия. Это самостоятельная теорема, которая ускоряет решение многих задач.

Признаки подобия разобраны в отдельном уроке — см. «Признаки подобия треугольников».

Частный случай этой леммы — средняя линия. Она отсекает треугольник со сторонами в два раза меньше, чем у исходного:

Оформляется это так. Поскольку $AM=MC$ и $BN=NC$, то $MN$ — средняя линия треугольника $ABC$. Следовательно, прямые $AB$ и $MN$ параллельны, откуда

[Delta ABCsim Delta MNC]

3. Свойства подобных треугольников

Два важнейших свойства: связь периметров и связь площадей.

3.1. Периметры подобных треугольников

Теорема 2. Отношение периметров подобных треугольников равно коэффициенту подобия.

Доказательство. Рассмотрим подобные треугольники $ABC$ и $MNK$:

Запишем равенство из определения подобия. Поскольку $Delta ABCsimDelta MNK$, стороны этих треугольников пропорциональны:

[frac{AB}{MN}=frac{BC}{NK}=frac{AC}{MK}=color{red}{k}]

Здесь число $color{red}{k}$ — коэффициент подобия. Полученное тройное равенство можно переписать так:

[frac{AB}{MN}=color{red}{k}; frac{BC}{NK}=color{red}{k}; frac{AC}{MK}=color{red}{k}]

Или, что то же самое:

[begin{align}AB&=color{red}{k}cdot MN \ BC &=color{red}{k}cdot NK \ AC &=color{red}{k}cdot MK \ end{align}]

Периметр треугольника $MNK$:

[{{P}_{Delta MNK}}=MN+NK+MK]

Периметр треугольника $ABC$:

[begin{align}{{P}_{Delta ABC}} &=AB+BC+CD= \ &=color{red}{k}cdot MN+color{red}{k}cdot NK+color{red}{k}cdot MK= \ &=color{red}{k}cdot left( MN+NK+MK right)= \ &=color{red}{k}cdot {{P}_{Delta MNK}} end{align}]

Итого получаем равенство

[{{P}_{Delta ABC}}=color{red}{k}cdot {{P}_{Delta MNK}}]

Обычно именно в таком виде это равенство и применяют. Но можно записать его и как отношение:

[frac{{{P}_{Delta ABC}}}{{{P}_{Delta MNK}}}=color{red}{k}]

В любом случае, мы получили отношение, которое и требовалось доказать.

3.2. Площади подобных треугольников

Теорема 3. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Доказательство. Первые шаги очень похожи на доказательство предыдущей теоремы. Вновь рассмотрим подобные треугольники $ABC$ и $MNK$:

Поскольку $Delta ABCsimDelta MNK$, углы $ABC$ и $MNK$ равны. Следовательно, равны синусы этих углов:

[begin{align}angle ABC &=angle MNK=color{blue}{alpha} \ sin angle ABC &=sin angle MNK=sin color{blue}{alpha} end{align}]

Кроме того, стороны подобных треугольников пропорциональны:

[frac{AB}{MN}=frac{BC}{NK}=frac{AC}{MK}=color{red}{k}]

В частности, из этого равенства следует, что

[frac{AB}{MN}=color{red}{k}; frac{BC}{NK}=color{red}{k}]

Или, что то же самое:

[begin{align}AB &= color{red}{k}cdot MN \ BC &= color{red}{k}cdot NK \ end{align}]

Площадь треугольника $MNK$:

[{{S}_{Delta MNK}}=frac{1}{2}cdot MNcdot NKcdot sin color{blue}{alpha} ]

Площадь треугольника $ABC$:

[begin{align}{{S}_{Delta ABC}} &=frac{1}{2}cdot ABcdot BCcdot sincolor{blue}{alpha} = \ &=frac{1}{2}cdotcolor{red}{k}cdot MNcdotcolor{red}{k}cdot NKcdot sincolor{blue}{alpha} = \ &={color{red}{k}^{2}}cdot frac{1}{2}cdot MNcdot NKcdot sin alpha = \ &={color{red}{k}^{2}}cdot {{S}_{Delta MNK}} end{align}]

Получаем равенство

[{{S}_{Delta ABC}}={color{red}{k}^{2}}cdot {{S}_{Delta MNK}}]

Перепишем в виде отношения:

[frac{{{S}_{Delta ABC}}}{{{S}_{Delta MNK}}}={color{red}{k}^{2}}]

Что и требовалось доказать.

Для доказательства теоремы мы использовали формулу площади треугольника:

[{{S}_{Delta }}=frac{1}{2}absin alpha ]

Тригонометрию проходят после подобия, поэтому мы опираемся на ещё не изученный материал.

Впрочем, ничто не мешает взять уже известную формулу:

[{{S}_{Delta }}=frac{1}{2}ah]

Здесь $a$ — сторона треугольника, $h$ — высота, проведённая к этой стороне. Дело в том, что высоты в подобных треугольниках тоже пропорциональны. И не только высоты. Назовём это Свойством 3.3.:)

3.3. Элементы подобных треугольников

Теорема 4. Отношение высот, биссектрис и медиан, проведённых к соответствующим сторонам подобных треугольников, равно коэффициенту подобия.

Проиллюстрируем это на высотах. Пусть треугольники $ABC$ и $MNK$ подобны:

В этом случае высоты $CDbot AB$ и $KLbot MN$ относятся как

[frac{CD}{KL}=frac{AB}{MN}= color{red}{k}]

Для доказательства этой теоремы нужно знать признаки подобия. Поэтому оставим его до следующего урока. А сейчас переходим к задачам.

4. Задачи на подобие

Здесь разобрано пять задач на подобие треугольников. Все они довольно простые. За сложными задачами добро пожаловать в задачник.:)

Задача 1. Готовые треугольники

Известно, что треугольники $ABC$ и $MNK$ подобны, причём $angle A=angle M$, $angle B=angle N$, $angle C=angle K$. Кроме того, стороны $AB=6$, $BC=7$, $AC=10$ и $MN=9$. Найдите стороны $NK$ и $MK$.

Решение. Построим треугольники $ABC$ и $MNK$, отметим известные стороны:

Из условия $Delta ABCsim Delta MNK$ следует, что верно равенство

[frac{AB}{MN}=frac{BC}{NK}=frac{AC}{MK}]

Подставим в это равенство всё, что нам известно:

[frac{color{red}{6}}{color{red}{9}}=frac{color{red}{7}}{NK}=frac{color{red}{10}}{MK}]

Опустим последнюю дробь и получим пропорцию

[frac{color{red}{6}}{color{red}{9}}=frac{color{red}{7}}{NK}]

Найдём сторону $NK$:

[NK=frac{color{red}{9}cdot color{red}{7}}{color{red}{6}}=10,5]

Аналогично, убирая среднюю дробь, получим пропорцию

[frac{color{red}{6}}{color{red}{9}}=frac{color{red}{10}}{MK}]

Найдём сторону $MK$:

[NK=frac{color{red}{9}cdot color{red}{10}}{color{red}{6}}=15]

Ответ: $NK=10,5$, $MK=15$.

Задача 2. Прямая, параллельная стороне

Прямая, параллельная стороне $AC$ треугольника $ABC$, пересекает сторону $AB$ в точке $D$, а сторону $BC$ — в точке $E$. Найдите:

а) Отрезок $BD$, если $AB=16$, $AC=20$, $DE=15$.

б) Отрезок $AD$, если $AB=28$, $BC=63$, $BE=27$.

Решение. Для начала построим рисунок. Он будет общий для обоих пунктов.

Из условия следует, что прямая $DE$ пересекает стороны треугольника $ABC$:

Поскольку $DEparallel AC$, по лемме о подобных треугольниках прямая $DE$ отсекает от треугольника $ABC$ новый треугольник, подобный исходному:

[Delta ABCsim Delta DBE]

Из подобия треугольников $ABC$ и $DBE$ следует равенство

[frac{AB}{DB}=frac{BC}{BE}=frac{AC}{DE}]

Решаем пункт а). Подставляем в это равенство всё, что нам известно:

[frac{color{red}{16}}{DB}=frac{BC}{BE}=frac{color{red}{20}}{color{red}{15}}]

Вычёркиваем среднюю дробь и получаем пропорцию

[frac{color{red}{16}}{DB}=frac{color{red}{20}}{color{red}{15}}]

Отсюда легко найти $DB$ (или, что то же самое, $BD$):

[DB=frac{color{red}{16}cdotcolor{red}{15}}{color{red}{20}}=12]

Аналогично решаем пункт б). Подставляем в исходное равенство известные величины:

[frac{color{red}{28}}{DB}=frac{color{red}{63}}{color{red}{27}}=frac{AC}{DE}]

Первые две дроби образуют пропорцию, из которой вновь легко найти $DB$:

[DB=frac{color{red}{28}cdotcolor{red}{27}}{color{red}{63}}=12]

Осталось найти $AD$:

[begin{align}AD &=AB-BD= \ &=color{red}{28}-color{red}{12}=16 end{align}]

Ответ: а) $BD=12$; б) $AD=16$.

Важное замечание по работе с пропорциями. Ни в коем случае не нужно перемножать числа в числителе.

Напротив: нужно разложить их на множители и сократить!

Взгляните:

[DB=frac{color{red}{28}cdotcolor{red}{27}}{color{red}{63}}=frac{4cdotcolor{blue}{7}cdot 3cdotcolor{green}{9}}{color{blue}{7}cdotcolor{green}{9}}=12]

Так вы сэкономите время, избежите умножения столбиком и защитите себя от множества ошибок. Никогда не умножайте большие числа, если дальше их нужно будет сокращать.

Задача 3. Доказательство подобия

Точки $M$ и $K$ — середины сторон $CD$ и $AD$ квадрата $ABCD$ соответственно. Докажите, что треугольники $MDK$ и $BCD$ подобны.

Решение. Сделаем первоначальный рисунок по условию задачи:

Здесь нет прямых, параллельных сторонам треугольника, поэтому лемма о подобных треугольниках не поможет. Докажем подобие по определению.

Сначала разберёмся с углами. Поскольку $ABCD$ — квадрат, и $KD=MD$ — половина стороны квадрата, треугольники $MDK$ и $BCD$ — прямоугольные и равнобедренные.

Все острые углы треугольников $MDK$ и $BCD$ равны 45°. Можем записать это так:

[begin{align}angle BCD &=angle MDK={90}^circ \ angle CBD &=angle DMK={45}^circ \ angle CDB &=angle DKM={45}^circ \ end{align}]

Дополнительное построение: диагональ квадрата $color{red}{AC}$:

Рассмотрим треугольник $ACD$. Отрезок $KM$ — средняя линия, поэтому $KM={color{red}{AC}}/{2};$. С другой стороны, $AC=BD$ как диагонали квадрата. Поэтому верно равенство

[frac{KM}{BD}=frac{KM}{color{red}{AC}}=frac{1}{2}]

Но тогда выполняется следующее равенство:

[frac{MD}{BC}=frac{DK}{CD}=frac{MK}{BD}=frac{1}{2}]

А это вместе с равенством углов как раз и означает, что треугольники $MDK$ и $BCD$ подобны:

[Delta MDKsim Delta BCD]

Доказательство завершено.

Мы доказали подобие треугольников по определению. Если пользоваться признаками подобия, всё будет намного быстрее. Но пока мы не вправе пользоваться этими признаками.

Задача 4. Вписанный ромб

В треугольник $ABC$ вписан ромб $BDEK$ так, как показано на рисунке. Найдите сторону ромба, если $AB=10$, $BC=15$.

Решение. Пусть искомая сторона ромба равна $color{red}{x}$. Из условия задачи получим такой рисунок:

Зная, что $AB=10$ и $BC=15$, выразим $AK$ и $CD$:

[begin{align}AK &=10-color{red}{x} \ CD &=15-color{red}{x} \ end{align}]

Далее рассмотрим треугольник $ABC$. Поскольку $BDEK$ — ромб, то $KEparallel BC$. По лемме о подобных треугольниках имеем:

[Delta ABCsim Delta AKE]

В подобных треугольниках подобные стороны пропорциональны, поэтому

[frac{AB}{AK}=frac{BC}{KE}=frac{AC}{AE}]

Подставим в это равенство всё, что нам известно или выражено через $color{red}{x}$:

[frac{10}{10-color{red}{x}}=frac{15}{color{red}{x}}=frac{AC}{AE}]

Последняя дробь оказалась бесполезной. Вычеркнем её и получим пропорцию:

[frac{10}{10-color{red}{x}}=frac{15}{color{red}{x}}]

Применяем основное свойство пропорции и уравнение:

[begin{align}10cdotcolor{red}{x} &=15cdot left( 10- color{red}{x} right) \ 2cdotcolor{red}{x} &=3cdot left( 10- color{red}{x} right) \ &cdots\ color{red}{x} &=6 end{align}]

Это и есть искомая сторона ромба. Она равна $color{red}{x}=6$.

Ответ: $BD=6$.

Задача 5. Свойства биссектрисы

В треугольнике $ABC$ стороны $AB=8$, $BC=12$, угол $ABC={120}^circ $. Отрезок $BD$ — биссектриса. Найдите длину $BD$.

Решение. Из условия задачи можно сделать вот такой рисунок:

Поскольку $BD$ — биссектриса угла в треугольнике, точка $D$ делит сторону $AC$ на отрезки, пропорциональные сторонам $AB$ и $BC$. Это можно записать так:

[frac{AD}{CD}=frac{AB}{CB}=frac{color{red}{8}}{color{red}{12}}=frac{color{red}{2}}{color{red}{3}}]

Обозначим пропорциональные отрезки переменными. Пусть $AD=color{blue}{2x}$, $CD=color{blue}{3x}$.

Дополнительное построение: прямая $DMparallel AB$:

Рассмотрим угол $ACB$. Поскольку $DMparallel AB$, по теореме о пропорциональных отрезках получаем, что

[frac{BM}{CM}=frac{AD}{CD}=frac{color{red}{2}}{color{red}{3}}]

Вновь обозначим пропорциональные отрезки переменными. Пусть $BM=color{blue}{2y}$, $CM=color{blue}{3y}$. Но тогда

[BC=BM+MC=color{blue}{5y}=color{red}{12}]

Получаем, что $color{blue}{y}=color{red}{2,4}$. Отсюда легко найти длину $BM$:

[BM=color{blue}{2y}=2cdotcolor{red}{2,4}= color{red}{4,8}]

Далее заметим, что если угол $ABC$ равен 120°, то

[angle ABD=angle CBD={60}^circ ]

С другой стороны, прямые $AB$ и $MD$ параллельны по построению. Прямая $BD$ — секущая для этих параллельных прямых.

Следовательно, углы $ABD$ и $BDM$ — внутренние накрест лежащие, поэтому

[angle BDM=angle ABD={60}^circ ]

Рассмотрим треугольник $BDM$. В нём есть два угла по 60°. Следовательно, это равносторонний треугольник:

[BD=BM=color{red}{4,8}]

Мы нашли длину отрезка $BD$. Задача решена.

Ответ: $BD=4,8$.

Итак, с определением разобрались. В следующем уроке разберём признаки подобия.:)

Смотрите также:

1. Как применяется теорема косинусов и подобие треугольников для решения широкого класса задач в планиметрии.
2. Теорема менелая
3. Комбинаторика в задаче B6: легкий тест
4. Введение системы координат
5. Четырехугольная пирамида: как найти координаты вершин
6. Нестандартная задача B5 на площадь круга