Золотой и серебряный треугольник
Как и по какому принципу творятся и живут тело вечного Космоса и многообразные части его тела?
«[Тело космоса] было искусно устроено так, чтобы получать пищу от собственного тления, осуществляя все свои действия и состояния в себе самом и само через себя… Ибо такому телу из семи родов движения он уделил соответствующий род, а именно тот, который ближе всего к уму и разумению. Поэтому он заставил его единообразно вращаться в одном и том же месте, в самом себе, совершая круг за кругом, а остальные шесть родов движения были устранены»[1]. (*Остальные шесть родов движений, как объясняется в примечании, – это вперед, назад, направо, налево, вверх и вниз, связанные с развитием деятельности органов живых существ, зависимых от окружающего мира).
АЛЬТЕРНАТИВНОЕ ГЕОМЕТРИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ «ЗОЛОТОЙ» ПРОПОРЦИИ.
Чем принципиально отличается новое геометрическое решение задачи «золотой» пропорции от традиционно существующего решения (Рис. 1)?
Рис. 1. Исполнение «золотого сечения» отрезка АВ в современной геометрии.
В осуществленном мной решении задачи, отрезок прямой не просто делится на гармоничные части, а он рассматривается, как некая изначальная «порождающая модель» (по Платону). Произвольный отрезок прямой посредством круговых движений сам себя делит на гармоничные части и одновременно является всеобщей мерой бесконечного многообразия форм самоорганизующегося космоса, «космических идей» (отношений) и всех реально существующих частей космоса, «в том числе, конечно и человека… его души и тела». Разумеется, выразить данный тезис одним и даже сотней рисунков невозможно. Поскольку, «Триалектика» — это новый метод познания и наука о началах, то моя задача сужается к тому, чтобы показать принципиально новый метод решения задачи «золотых сечений», а не только его результаты.
Понятно, что, воображая непрерывное круговое движение некой реальной пространственной субстанции, мы не в состоянии моделировать реальность ее форм и беспрерывность ее вращения и кручения посредством циркуля. Посредством циркуля и линейки мы моделируем идеальные, а не реальные формы бытия, их относительные масштабы, разные количественные и пространственные отношения, моделируем идеальные отношения, в согласии с которыми, возможно, они и существуют.
Сравним рисунки альтернативных методов решения задачи.
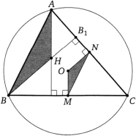
Рис. 2. Альтернативное геометрическое исполнение
«золотого сечения» отрезка АВ.
ЗОЛОТОЕ СЕЧЕНИЕ ОТРЕЗКА «АВ». НОВЫЙ МЕТОД РЕШЕНИЯ (Рис. 2).
Порядок геометрического решения задачи «золотого» сечения отрезка АВ:
1. Раствором циркуля равному АВ = α чертим окружность с центром в точке А. Таким образом, изначально абстрактный отрезок АВ (алгебраическое решение «Беседа 1»), в новом геометрическом решении «золотого сечения» отрезка обретает статус «порождающей модели». Он становится мерой конкретного круга. То есть АВ становится радиусом – r конкретного круга с центром в точке А.
2. Продолжим отрезок АВ до пересечения его с окружностью в точке Р. Таким образом, ВР = 2r – диаметр окружности.
3. Не меняя раствора циркуля, ставим его ножку в точку Р и чертим дугу до пересечения ее с окружностью в точках Н и Т.
4. Соединяем точки В, Н и Т прямыми линиями и, таким образом получаем первую и основную, по мнению многих, сакральную геометрическую фигуру – равносторонний треугольник, сторона НТ которого в точке О делит радиус круга пополам и сама также делится пополам.
5. Раствором циркуля ОВ восстанавливаем перпендикуляр к диаметру круга в точке А до пересечения его с окружностью в точках E и J. АЕ = r.
6. Раствором циркуля ОЕ чертим дугу от точки Е до пересечения ее с отрезком АВ в точке М.
7. Раствором циркуля РМ чертим дугу от точки М до пересечения ее с окружностью в точке С.
8. Раствором циркуля АМ чертим окружность и отмечаем замечательные точки пересечения L и F.
9. Соединяем прямыми линиями, полученные в результате кругового движения, замечательные точки, где ВР ≈ 1,4142135r – сторона вписанного квадрата. Отрезки АО = ОР = 0,5r, ОМ = ОЕ и РС = РМ – по построению.
Прежде чем приступить к вычислению длин интересующих нас отрезков, приведем замечательную подсказку Платона к нашим построениям и вычислениям:
«Итак, нам приходится отдать предпочтение двум треугольникам, как таким, из которых составлено тело огня и (трех) прочих тел: один из них равнобедренный, а другой таков, что в нем квадрат большей стороны в три раза больше квадрата меньшей» [2].
Таким образом, в итоге круговых движений был построен равнобедренный треугольник ЕОМ (ОМ = ОЕ), разделенный на два прямоугольных треугольника: ОАЕ и МАЕ и равнобедренный прямоугольный треугольник ВАЕ. В согласии с теоремой Пифагора, произведем вычисления сторон названных треугольников:
Так как ОМ = ОЕ, то АМ = ОМ – АО; АМ = 1,1180339r – 0,5r ≈ 0,6180339r.
Отрезок РМ = ОМ + ОР = АМ + АВ;
РМ = 1,1180339r + 0,5r ≈ 0,6180339r + r ≈ 1,6180339r.
МВ = АВ – АМ = r – 0,6180339r ≈ 0,3819661r.
Таким образом, была доказана, скажем так, «не четко сформулированная» Платоном теорема. Любой произвольно взятый отрезок прямой, можно разделить на пропорциональные части «золотых» сечений, мерой круговых вращений самого отрезка.
ОНТОЛОГИЧЕСКИЙ СМЫСЛ МЕРЫ ОТРЕЗКА РАВНОГО 1,6180339……α, при исполнении золотого сечения отрезка АВ, как показано на Рис. 1 нам выяснить не удалось, поскольку такой отрезок отсутствует на рисунке. В этом мы полагаем главный недостаток геометрического решения задачи (Рис. 2). Рис.3 устраняет, указанный недостаток. Но не только в этом и, главным образом, не в этом проявляется достоинство геометрического решения данной фундаментальной задачи! Решая ее в русле разгадок сакральных смыслов, имеющихся в сочинениях Платона, мы приоткрываем новый, более богатый мир геометрии «золотых» геометрических фигур и «золотых» отношений между их сторонами, периметрами и площадями. Для этого произведем еще несколько вычислений на базе Рис. 2.
Таким образом, построен по данному отрезку АВ вписанный прямоугольный треугольник. Такая задача на построение ставится и решается в геометрии впервые. Но не в этом – ценность ее постановки и решения. Ценность ее – в параметрах построенного треугольника, у которого одна сторона (гипотенуза) равна 2АВ, один катет является стороной правильного вписанного пятиугольника, а другой катет – мера «золотого сечения» ≈ 1,6180339r. При этом замечательной точкой F катет РС делится в отношениях «золотого сечения»:
FC : FP = r : 0,6180339r ≈ 1,6180339; FP : PC = 0,6180339r : 1,6180339r ≈ 0,381966.
« ЗОЛОТОЙ» И «СЕРЕБРЯННЫЙ» ТРЕУГОЛЬНИКИ РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА.
Стороны «золотого» ΔАЕМ соответственно равны:
сторона АЕ = r – сторона правильного, вписанного в данный круг 6-угольника;
сторона – сторона правильного, вписанного в данный круг 5-угольника;
сторона АМ ≈ 0,6180339r – сторона правильного, вписанного в данный круг 10-угольника.
Площади «золотого» и «серебряного» треугольников относятся как их основания: SАЕМ : SАЕО = АМ : АО. Подставив их значения, вычислим:
(0,5•0,6180339) : (0,5•0,5) = 0,6180339 : 0,5; 1,2360676 = 1,2360676.
Стороны «серебряного» ΔОАЕ – суть числа: АЕ = r = 1 – число триединой меры; ОЕ = 1,1180339 – число основания «золотого сечения»; АО = 0,5 – «вещественное» число [3].
«ЗОЛОТОЕ СЕЧЕНИЕ» ПЛОЩАДИ РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА
Стороны ВМЕ замечательны тем, что сторона ВЕ равна стороне вписанного квадрата, а МЕ равна стороне вписанного пятиугольника в круг с центром А. Сторона ВМ ≈ 0,382r. Площадь ΔВМЕ составляет пятую часть площади РСВ (0,951 : 0,190 ≈ 5).
Произведем вычисление площадей указанных треугольников:
Площадь ΔВАЕ равна 0,5•АВ•АЕ = 0,5r 2 ;
Площадь АЕМ равна 0,5•АМ•АЕ = 0,5•0,6180339r r ≈ 0,309r 2 ;
Площадь ВМЕ равна 0,5r 2 – 0,309r 2 ≈ 0,19098r 2 .
Произведем вычисление отношений между площадями указанных треугольников:
0,309r 2 : 0,5r 2 ≈ 0,618; 0,191r 2 : 0,5r 2 ≈ 0,382; 0,309r 2 : 0,191r 2 ≈ 1,618 и т.д.
ГЕОМЕТРИЧЕСКОЕ ЧИСЛО ФИЗИЧЕСКОЙ КОНСТАНТЫ ТОНКОЙ СТРУКТУРЫ
Размышляя о мудрости некоторых мер теоретической и экспериментальной физики, в 2001 г. я писал: «Постоянная тонкой структуры или постоянная электромагнитной связи α = (137) -1 = 1/137 = 0,007299270072992700729 — число с тайной. Она фигурирует почти во всех уравнениях электродинамики, но никто до сих пор, не знает, почему она равна именно 1/137 Никто не смог предложить теоретическую формулу для α, объясняющую эту величину, и выводящую ее из известных законов физики. Эмпирических формул за истекшие СТО лет от дней открытия этого таинственного числа было предложено немало. Но эмпирические формулы не объясняют физической сути, стоящей за ними. Экспериментальное значение данной постоянной равно 1/137,03604 = 0,007297350390452 и отличается от значения 1/137… Тайна его откроется, когда наступит тому время» [4].
Обращаю внимание читателя на отрезок LO (Рис.3). Его длина равна:
LO = АL – AO ≈ 0,6180339r – 0,5r ≈ 0,1180339r. Если учесть то, что некая изначальная мера Платоновой «порождающей модели» бытия порождает иерархию фрактальной геометрии и фрактальной физики, то геометрически можно с высокой точностью вычислить безразмерную величину постоянной тонкой структуры или постоянной электромагнитной связи.
Если фрактальный отрезок будет равен 10 -1 LO, тогда
1,6180339r : 0,01180339r ≈ 137,08213 – безразмерная физическая константа тонкой структуры или электромагнитной связи α = 1 :137,08213 ≈ 0,0072948…
Построенная геометрическая «порождающая модель» тонкой структуры отличается от экспериментальной физической безразмерной константы на (137,08213 – 137,03604) ≈ 0,04609.
Таким образом, полученные данные, проведенных мной исследований, дают основание предполагать, что реально существуют и более тонкие лучевые (волновые) структуры по сравнению с электромагнитными.
Наступило время и тайна приоткрылась.
ЛИТЕРАТУРА:
- Платон. Собр. соч. в 4-х т. «Мысль», М., 1994. Т.3, с. 436-437.
- Платон. Собр. соч. в 4-х т. «Мысль», М., 1994. Т.3, с. 457-458.
- Сергиенко П.Я. Триалектика: новое понимание мира. Пущино – 1995., с.19-30.
- Сергиенко П.Я. Триалектика. О мерах мудрости и мудрости мер. 82 с. Пущино – 2001.с. 75 – 76.
- Сергиенко П.Я. Синтетическая геометрия триалектики. 27с. Пущино – 2003
- Сергиенко П.Я. Начала. Триалектика сакральной геометрии. 32с. Пущино – 2005
Золотое и серебряное сечение: в чем различия?
Серебрянное сечение: что это такое, чем отличается от золотого.
Золотое сечение – это определенная закономерность, соотношение чисел, при котором большее число относится к меньшему так же, как сумма этих чисел к большему из них. Его можно встретить во многих арт-объектах, особенно в работах древних архитекторов, скульпторов и художников. Сегодня в художественных школах и академиях наставники сознательно рекомендуют ученикам и студентам использовать в своих работах «золотую пропорцию».
Золотое сечение применяют не только в искусстве, но и в точных науках, например в биологии, физике и математике. Возможно, вы не знали, но помимо широко известного уже упомянутого соотношения существуют и другие, так называемые «металлические» сечения, которые практически не изучены и редко применяются на практике. Можно сказать, что при повсеместном использовании золотого другие металлические соотношения отходят на задний план.
Благодаря стараниям двух сингапурских студентов-математиков постепенно все внимание мира вновь возвращается к «металлическим» константам, которые включают, кроме золотого сечения, все корни квадратного уравнения x² — nx = 1 для положительных значений n. Постепенно увеличивающиеся значения уравнения называются серебряным, бронзовым и другими «металлическими» сечениями.
Золотое сечение гораздо более известно, и мы ассоциируем его с раковиной наутилуса гораздо чаще, чем с фактическим представлением о том, что оно на самом деле воплощает. Согласно перефразированному студентами утверждению древнегреческого математика Евклида, «прямая линия обрезается в соответствии с золотым сечением, когда отношение всей линии к более длинному сегменту равно отношению более длинного сегмента к более короткому».
Другими словами, схема пропорциональных отрезков образует золотое сечение, причем «золотые» отрезки постепенно уменьшаются. В своей статье студенты предлагают ознакомиться с интерактивным графиком, где вы можно проследить зависимость спирали от изменения значений n в режиме онлайн.
Каждая пара смежных целых чисел имеет свою собственную «металлическую пропорцию», которая является собирательным названием для полного набора корней, включающих и золотое сечение. Поясним на примерах: золотое сечение – это средняя пропорция между 1 и 2, серебряное – между 2 и 3, и так вплоть до фермического (химический элемент с порядковым номером 100 в таблице Менделеева) и даже дальше.
Как мы уже говорили, золотое сечение тесно связано с эстетикой и красотой, поэтому активно используется всеми деятелями искусства – от дизайнеров интерьера до кинематографистов. Также не стоит забывать, что «золотая пропорция» переплетается со знаменитой последовательностью Фибоначчи (1, 1, 2, 3, . ), в которой первые два числа равны либо 1 и 1, либо 0 и 1, а каждое последующее равно сумме двух предыдущих чисел.
Таким образом, соотношение прогрессивных членов последовательности приближается к золотому сечению. Математики из Сингапура утверждают, что и у серебряного сечения есть собственный ряд чисел, называемый последовательностью Пелля. Фактически, можно сказать, что каждая последующая «металлическая пропорция» в свою очередь имеет собственную последовательность с соответствующими математическими закономерностями.
Точно так же, как логарифмическую спираль связывают с золотым сечением, для других металлов тоже существуют свои аналоги. Например, используя «золотое» соотношение, вы рисуете прямоугольник, затем вычеркиваете квадрат со сторонами, равными короткой стороне исходной фигуры. Оставшуюся часть вы поворачиваете на 90 градусов и получаете новый прямоугольник для деления в соответствии с «золотой пропорцией».
И так далее до самой бесконечности. Этот же прямоугольник можно разделить и с помощью других «металлических» соотношений. В каждом из случаев вы вычеркиваете необходимое количество квадратов в соответствии со значениями «металлической пропорции». Например, деля прямоугольник с помощью серебряного сечения, вы вычеркиваете два квадрата и получаете новый, уменьшенный по «серебряной» пропорции прямоугольник.
На данный момент золотое сечение является наиболее известной и широко используемой закономерностью. Однако мы не можем отрицать тот факт, что явления, связанные с «золотой пропорцией», масштабируются и по другим металлическим соотношениям. Нужно лишь немного времени на более тщательное изучение и огласку, и весь мир заговорит и о других «металлах».
Исследование золотых фигур
Разделы: Математика
«Хороший учитель обязан понимать, что никакую задачу нельзя исчерпать до конца. Этот взгляд он должен прививать и своим ученикам».
Д. Пойа
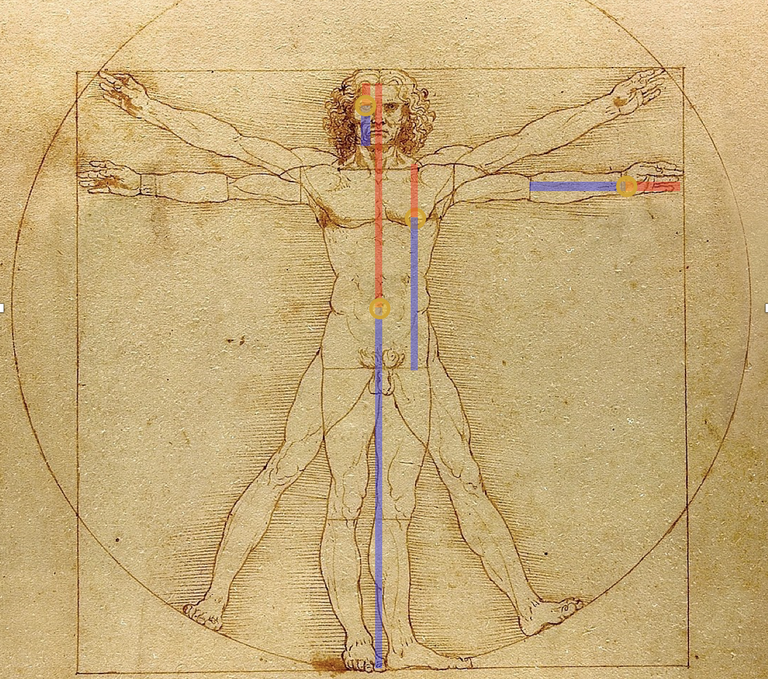
В жизни каждого человека присутствует математика. Она используется в самых разнообразных профессиях – математика нужна инженеру, военному, биологу, художнику, можно сказать, что она нужна всем. Великий художник Леонардо да Винчи был один из тех, кто заинтересовался знаменитым золотым сечением. Он много внимания уделял изучению золотого деления. Производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении; поэтому он дал этому делению название золотое сечение.
Золотое сечение интересно тем, что оно позволяет показать связь математики с другими науками, с искусством. А также помогает исследовать золотой треугольник и золотую пирамиду; рассмотреть геометрические задачи, связанные с золотыми фигурами.
Золотое сечение – это деление отрезка на две части. Таким образом, что большая его часть относится к меньшей части как весь отрезок относится к большой части.

Рис. 1.
=
или
, откуда
Иногда золотым сечением называют отношение, 

Число, обратное φ обозначают Ф:
Ф=
Отметим некоторые равенства, связывающие Ф и φ , которые нам впоследствии пригодятся:
1-
Ф, 1+Ф=
История золотого сечения.
Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамсеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.
В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.
В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др.. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне и они были известны только посвященным.
Великий астроном XVI в. Иоган Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение). Кеплер называл золотую пропорцию продолжающей саму себя «Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности».
ЗОЛОТОЙ ПРЯМОУГОЛЬНИК.
Если построить квадрат со стороной АВ=а, найти середину М отрезка АВ и провести дугу окружности радиусом МС с центром в точке М до пересечения с продолжением стороны АВ в точке Е, то точка В разделит отрезок АЕ в крайнем и среднем отношении.
Чтобы убедиться в этом, заметим, что по теореме Пифагора
Прямоугольник АЕFD со сторонами АЕ=φАD называется золотым прямоугольником. Четырехугольник АВСD − квадрат. Нетрудно видеть, что прямоугольник ВЕFС также золотой, поскольку BC=a=φВЕ. Это обстоятельство сразу наводит на мысль о дальнейшем разбиении прямоугольника ВЕFС.
Можно ли считать, что прямоугольник с отношением сторон, равным φ, выглядит изящнее, чем прямоугольники с отношением сторон, скажем, 2:1, 3:2 или 5:7? Чтобы ответить на этот вопрос, были проведены специальные эксперименты. Результаты их не вполне убедительны, но все же свидетельствуют о некотором предпочтении, отдаваемом золотому сечению.
ЗОЛОТОЙ ТРЕУГОЛЬНИК И ЕГО ИССЛЕДОВАНИЕ.
Золотым треугольником будем называть равнобедренный треугольник, отношение основания которого к боковой стороне равно φ Одним из таких треугольников является треугольник с боковой стороной Ф и основанием 1; именно его мы в дальнейшем будем называть золотым. Проведем исследование золотого треугольника.
Углы золотого треугольника.
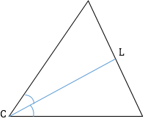
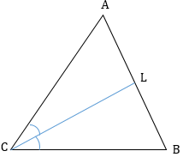
В треугольнике АВС выберем на стороне ВС точку D так, чтобы АD=1 (такую точку легко построить, проведя окружность с центром в точке А и радиусом АС). Из подобия треугольников АВС и АDС получаем:
или
, откуда DС=
Поскольку ВС=Ф, DС=φ, то, учитывая равенство Ф=
5
,
В последствии нам встретятся выражения, содержащие 

=
.
Найдем в золотом треугольнике:
- медиану, проведенную к боковой стороне;
- высоту, проведенную к основанию;
- площадь;
- высоту, проведенную к боковой стороне;
Пусть треугольник АВС − золотой. Для нахождения медианы воспользуемся формулой 
где

Найдем высоту ВН: ВН=Ф
Площадь треугольника АВС будет равна: S=
Пусть – высота, проведенная к стороне ВС. Возьмем на стороне ВС точку 


Применение золотого треугольника при решении задач.
Найти длины диагоналей правильного 10-угольника со стороной, равной 1.
Решение. Правильный 10-угольник имеет 4 вида диагоналей, на рисунке показано по одному представителю этих четырех множеств. Найдем их длины. Проще всего найти длину отрезка AF. Для этого найдем величину внутреннего угла правильного 10-угольника: 
Найдем длину диагонали АС. Из треугольника АВС имеем:
= 2
2
) =2(1+
)= 4
= 2+Ф,
откуда АС=
Найдем длину диагонали AD. В равнобоковой трапеции АВСD углы при основании равны 

AD=
.
Длину диагонали АЕ можно найти разными способами.
Способ 1. Будем искать ее из треугольника AEF. В этом треугольнике медиана ЕО равна половине стороны AF, поэтому треугольник AEF-прямоугольный. Тогда АЕ= AF
Способ 2. Заметим, что высота золотого треугольника EOF является средней линией треугольника AEF. Поскольку эта высота равна 
Ответ: 2Ф, 

ЗОЛОТАЯ ПИРАМИДА И ЕЕ ИССЛЕДОВАНИЕ.
Пирамида называется золотой, если каждая её грань − золотой треугольник.
Исследование золотой пирамиды.
Различные способы нахождения объёма золотой пирамиды.
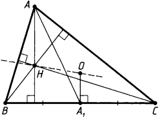
I способ: объем пирамиды находим по формуле 
Пусть DABC-данная пирамида,DH − ее высота. Плоскость ADH пересекает ребро ВС в точке М, причем ВМ=СМ. Треугольник ADM − равнобедренный.
Опустим на его основание AD высоту МК. Из подобия треугольников AHD и AKM будем иметь:
.
Поставим в это равенство известные нам числа:
МК= 
АМ= 
DH=



II способ:

длины противоположных ребер,
расстояние между ними, – угол между ними;


III способ:
Объем золотой пирамиды – это объем прямоугольного параллелепипеда минус объем четырех маленьких пирамид с ребрами длиной 1,


Применение золотой пирамиды при решении задач.
Найдем площадь поверхности золотой пирамиды.
=
= 4
Золотое сечение в картине Леонардо да Винчи «Джоконда»
Портрет Моны Лизы привлекает тем, что композиция рисунка построена на»золотых треугольниках» (точнее на треугольниках, являющихся кусками правильного звездчатого пятиугольника).
Золотая спираль в картине Рафаэля «Избиение младенцев»
В отличии от золотого сечения ощущение динамики, волнения проявляется, пожалуй, сильней всего в другой простой геометрической фигуре – спирали. Многофигурная композиция, выполненная в 1509 – 1510 годах Рафаэлем, когда прославленный живописец создавал свои фрески в Ватикане, как раз отличается динамизмом и драматизмом сюжета. Рафаэль так и не довел свой замысел до завершения, однако, его эскиз был гравирован неизвестным итальянским графиком Маркантинио Раймонди, который на основе этого эскиза и создал гравюру» Избиение младенцев». На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции −точки, где пальцы воина сомкнулись вокруг лодыжки ребенка, − вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Если естественным образом соединить эти куски кривой пунктиром, то с очень большой точностью получается . золотая спираль! Это можно проверить, измеряя отношение длин отрезков, высекаемых спиралью на прямых, проходящих через начало кривой.
Мы не знаем, рисовал ли на самом деле Рафаэль золотую спираль при создании композиции » Избиение младенцев» или только»чувствовал» её. Однако с уверенностью можно сказать, что гравер Раймонди эту спираль увидел.
Об этом свидетельствуют добавленные им новые элементы композиции, подчеркивающие разворот спирали в тех местах, где она у нас обозначена лишь пунктиром. Эти элементы можно увидеть на окончательной гравюре Раймонди: арка моста, идущая от головы женщины, − в левой части композиции и лежащее тело ребенка − в ее центре.
Нельзя не увидеть золотой треугольник и золотую пирамиду в ограненных драгоценных камнях. Многие гранильщики стараются придать бриллиантам форму тетраэдра, куба, октаэдра или икосаэдра. Но эти замечательные тела еще и потому красивы, что в основе их пропорциональных линий лежит золотая пропорция. Многие материалы, и не только драгоценные камни, состоят из мельчайших частиц, которые имеют форму многогранника. Такие вещества называются кристаллами. Соль, лед, песок, графит и т. д. состоят из кристаллов. Внутреннее устройство кристалла представляется в виде кристаллической решетки, в ячейках которых размещены по законам симметрии одинаковые мельчайшие частицы.
Литература:
- Большая Российская энциклопедия. М., «Научное издательство», 2007.
- Т. Каменева, А. Козлов. Золотой треугольник в задачах. М., 2007.
- Журнал «Математика в школе», 1993, № 3.
- Ковалев Ф.В. Золотое сечение в живописи. К.: Высшая школа, 1989.
- «Математика – Энциклопедия для детей» М.: Аванта +, 1998.
- Волошинов А.В. «Математика и искусство». М.: Мир, 1979.
http://1gai.ru/publ/524487-zolotoe-i-serebrjanoe-sechenie-v-chem-razlichija.html
http://urok.1sept.ru/articles/653727
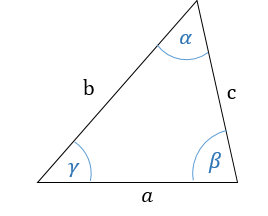
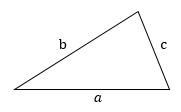
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
СВОЙСТВА ТРЕУГОЛЬНИКА:
1. Сумма углов в треугольнике равна α + β + γ = 180°.
2. Против большей стороны находится больший угол; против меньшего угла находится меньшая сторона. Отсюда следует, что если:
a < b < c, то α < β < γ и наоборот.
3. Сумма длин двух любых сторон треугольника всегда больше длины третьей стороны:
a + b > c.
Если это правило не выполняется — треугольник не существует.
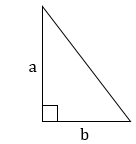
4. Формулы площади треугольника:
|
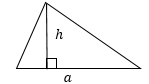
1 (через высоту) |
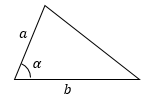
2 (через две стороны и синус угла между ними) |
3 (формула Герона) |
|
|
|
|
|
|
|
|
|
Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне. |
Площадь треугольника равна половине произведения его сторон на синус угла между ними. |
Площадь треугольника равна квадратному корню из произведения его полупериметра на разности полупериметра и каждой из его сторон. |
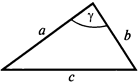
5. Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
с² = а² + b² – 2ab · cosγ
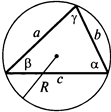
6. Теорема синусов: Отношения сторон треугольника к синусам противоположных им углов равны. Это отношение равно 2R, где R — радиус описанной окружности.
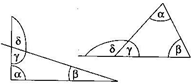
7. Внешний угол треугольника — δ, является смежным с одним из внутренних углов (сумма = 180°). Из этого следует, что внешний угол равен сумме двух внутренних, но не смежных с ним, углов треугольника (α + β = δ).
ВИДЫ ТРЕУГОЛЬНИКОВ:
Треугольники бывают:
- остроугольными (если все его углы острые),
- тупоугольными (если один из его углов тупой),
- прямоугольными (если один из его углов прямой).
Треугольник называется:
- равнобедренным, если две его стороны равны;
- равносторонним, если все три стороны равны;
- разносторонним, если все его стороны разные.
ЭЛЕМЕНТЫ ТРЕУГОЛЬНИКА:
БИССЕКТРИСА
Биссектриса ― луч, который соединяет вершину треугольника с противоположной стороной, при этом разделяя угол на две равные части.
Свойства биссектрисы треугольника:
1. Все три биссектрисы треугольника пересекаются в одной точке. Эта точка — центр вписанной в треугольник окружности.
2. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные двум другим сторонам.
3. Формулы для биссектрисы треугольника. Если а и b — стороны треугольника, γ — угол между ними, l — биссектриса треугольника, проведённая из вершины этого угла, а а’ и b’ — отрезки, на которые биссектриса делит третью сторону треугольника, то
МЕДИАНА
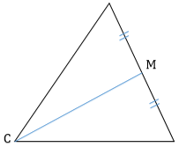
Медиана ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Свойства медианы треугольника:
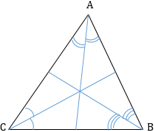
1. Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и точкой пересечения делятся в отношении 2 к 1, считая от вершины.
- Медиана разбивает треугольник на два равновеликих (по площади) треугольника.
- Треугольник делится тремя медианами на шесть равновеликих треугольников.
- В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.
- Формула для медианы треугольника. Если стороны треугольника a и b, mc — медиана треугольника, проведённая к стороне c, то
ВЫСОТА
Высота — перпендикуляр, опущенный из вершины треугольника на противоположную сторону (точнее, на прямую, содержащую противоположную сторону).
В зависимости от типа треугольника высота может содержаться:
- внутри треугольника (для остроугольного треугольника),
- совпадать с его стороной (являться катетом прямоугольного треугольника),
- проходить вне треугольника (для тупоугольного треугольника).
Свойства высоты треугольника:
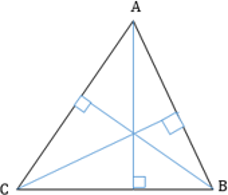
1. Все три высоты треугольника пересекаются в одной точке, которая называется ортоцентром.
2. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.
3. Если в треугольнике две высоты равны, то треугольник — равнобедренный.
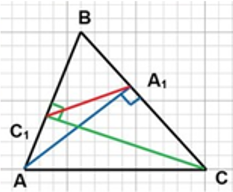
4. Если CC₁ и АА₁ — высоты треугольника АВС, то треугольник ВА₁С₁ подобен треугольнику АВС, причём коэффициент подобия равен cos B.
Сложные теоремы:
5. Если Н — точка пересечения высот треугольника AВС, а О — центр его описанной окружности, то отрезок АН вдвое больше расстояния от точки О до середины стороны ВС. То есть AH = 2OM.
6. Если Н — точка пересечения высот треугольника AВС, М — точка пересечения медиан треугольника AВС, а О — центр его описанной окружности, то точки О, H и М лежат на одной прямой (прямая Эйлера), причём точка М лежит на отрезке ОН и ОМ : МН = 1 : 2.
СРЕДИННЫЙ ПЕРПЕНДИКУЛЯР
Срединный перпендикуляр треугольника — прямая, перпендикулярная стороне треугольника и проходящая через его середину.
Все три срединных перпендикуляра треугольника пересекаются в одной точке, которая является центром описанной около треугольника окружности.
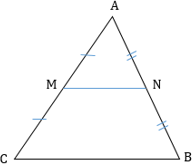
СРЕДНЯЯ ЛИНИЯ
Средняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника
Свойства средней линии треугольника:
- Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине:
MN||BC,MN = 1/2 BC
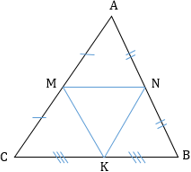
- В любом треугольнике три средних линии, при пересечении которых образуются 4 равных треугольника, подобных исходному с коэффициентом 1/2.
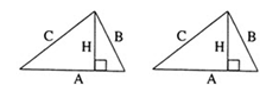
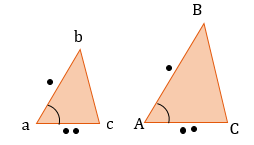
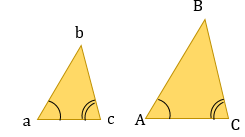
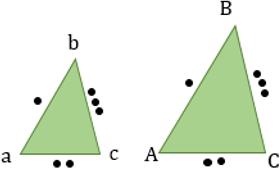
ПОДОБИЕ И РАВЕНСТВО ТРЕУГОЛЬНИКОВ
|
Подобные треугольники |
Равные треугольники |
|
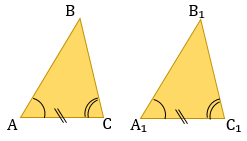
Треугольники подобны, если их углы равны. В подобных фигурах сохраняется отношение между соответствующими сторонами и другими линейными величинами (высоты, медианы, биссектрисы и периметры): Также сохраняется внутреннее отношение длин: |
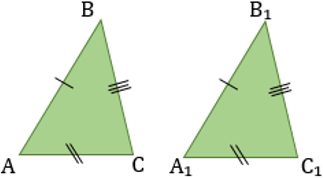
Два треугольника равны, если у них соответствующие стороны равны и соответствующие углы равны (треугольники равны, если их можно совместить наложением). |
|
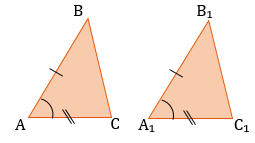
Признаки подобия треугольников: 1. По двум пропорциональным сторонам и углу между ними: 2. 3. По двум равным углам (тогда и третьи тоже будут равны) 4. 5. По трем пропорциональным сторонам: |
Признаки равенства треугольников: 1. По двум сторонам и углу между ними: 2. По стороне и двум прилежащим к ней углам. 3. По трем сторонам. |
ОСОБЫЕ ТРЕУГОЛЬНИКИ И ИХ СВОЙСТВА:
«Особенными», то есть обладающими какими — то дополнительными свойствами, считаются:
- равнобедренный,
- равносторонний
- прямоугольный треугольники.
РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК
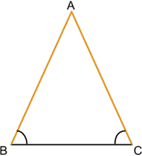
Равнобедренный треугольник ― это треугольник, у которого две стороны равны (АВ = АС).
Равные стороны (АВ и АС) в таком треугольнике называются боковыми, а оставшаяся третья сторона (ВС) ― основанием.
Свойства равнобедренного треугольника:
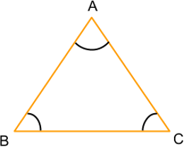
1. Углы при основании равны (∠АВС = ∠АСВ).
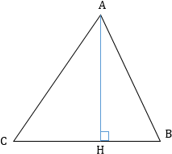
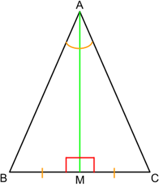
2. Медиана, проведённая к основанию, является биссектрисой и высотой. То есть она не только делит противолежащую сторону пополам (ВМ = МС), но и падает на неё под углом 90°, а кроме того делит угол, из которого выходит, пополам (∠ВАМ = ∠МАС).
Посмотрим на пример конкретной задачи. В равнобедренном треугольнике внешний угол равен 80°, необходимо найти все углы треугольника. Сразу возникает вопрос ― внешний угол при каком угле треугольника? Предположим, что это внешний угол при угле В (с нашего первого рисунка). Но в таком случае выходит, что сам ∠В = 100° (по сумме смежных углов). Значит, и ∠С = 100°, так как треугольник равнобедренный. Но тогда сумма только двух углов получается 200°, чего быть никак не может. Значит, речь идёт о внешнем угле при угле А треугольника. Тогда ∠А = 100°, а ∠В = ∠С = 40°.
РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК
Равносторонний треугольник ― треугольник, у которого все три стороны равны
Свойства равностороннего треугольника:
1. Кроме равенства сторон в таком треугольнике равны и все углы (каждый из которых по 60° ― так как 180°/3 = 60°).
2. Медиана, проведённая из любого угла, будет являться биссектрисой и высотой (другими словами, равносторонний треугольник с любой стороны является равнобедренным).
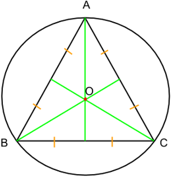
1. Центры вписанной и описанной окружностей совпадают.
2. Формулы 2 и 3 для площади треугольника превращаются в одну формулу:
— Через синус (так как все стороны равны и каждый угол равен 60°):
— Формула Герона (так как все стороны равны):
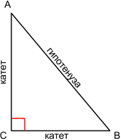
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Прямоугольный треугольник ― треугольник, у которого один угол равен 90° (собственно, это и есть прямой угол, дающий название всему треугольнику). Сторона, лежащая против такого угла, называется гипотенузой (АВ), а две другие стороны ― катетами (АС и ВС).
Свойства прямоугольного треугольника:
1. В любом прямоугольном треугольнике гипотенуза всегда больше катета (против большего угла лежит большая сторона, и наоборот).
2. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов
АВ2 = АС2 + ВС2
Теорема, обратная теореме Пифагора: Если для сторон произвольного треугольника выполняется отношение АВ2= АС2 + ВС2, то треугольник является прямоугольным.
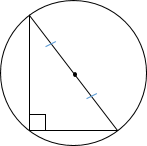
3. Центр описанной вокруг прямоугольного треугольника окружности всегда лежит на середине гипотенузы (доказательство: прямой ∠С становится вписанным, а против вписанного угла в 90° всегда лежит диаметр ― значит, гипотенуза является диаметром).
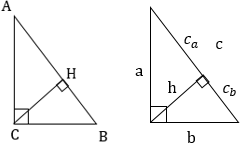
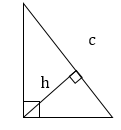
Высота, проведенная к гипотенузе, разбивает треугольник на два подобных прямоугольных треугольника, каждый из которых подобен исходному треугольнику
4. Высота, проведенная к гипотенузе, равна:
- Произведению катетов, деленному на гипотенузу
- Среднему геометрическому из произведений отрезков, на которые гипотенуза делится высотой
5. Медиана, проведенная к гипотенузе равна половине гипотенузы, то есть радиусу описанной около треугольника окружности.
6. Формулы площади прямоугольного треугольника:
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
Площадь прямоугольного треугольника равна половине произведения его катетов. |
Площадь прямоугольного треугольника равна половине произведения гипотенузы на опущенную к ней высоту. |
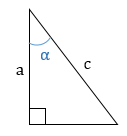
Площадь прямоугольного треугольника равна половине произведения его катета, гипотенузы и синуса угла между ними. |
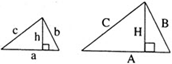
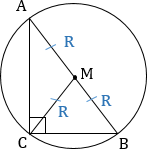
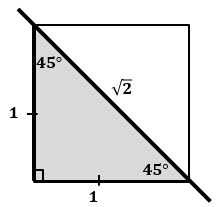
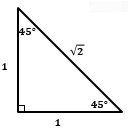
ЗОЛОТОЙ И СЕРЕБРЯНЫЙ ТРЕУГОЛЬНИКИ:
|
Серебряный треугольник — треугольник с углами 45°, 45° и 90° (разрубленный по диагонали квадрат) Отношение сторон в серебряном треугольнике: |
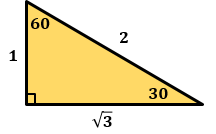
— треугольник с углами 30°, 60° и 90°. Отношение сторон в золотом треугольнике: |
From Wikipedia, the free encyclopedia
«Silver triangle» redirects here. For other uses, see Kepler triangle.

Silver rectangle |
|
| Representations | |
|---|---|
| Decimal | 2.4142135623730950488… |
| Algebraic form | 1 + √2 |
| Continued fraction |  |
| Binary | 10.01101010000010011110… |
| Hexadecimal | 2.6A09E667F3BCC908B2F… |
Silver ratio within the octagon
In mathematics, two quantities are in the silver ratio (or silver mean)[1][2] if the ratio of the smaller of those two quantities to the larger quantity is the same as the ratio of the larger quantity to the sum of the smaller quantity and twice the larger quantity (see below). This defines the silver ratio as an irrational mathematical constant, whose value of one plus the square root of 2 is approximately 2.4142135623. Its name is an allusion to the golden ratio; analogously to the way the golden ratio is the limiting ratio of consecutive Fibonacci numbers, the silver ratio is the limiting ratio of consecutive Pell numbers. The silver ratio is denoted by δS.
Mathematicians have studied the silver ratio since the time of the Greeks (although perhaps without giving a special name until recently) because of its connections to the square root of 2, its convergents, square triangular numbers, Pell numbers, octagons and the like.
The relation described above can be expressed algebraically:
or equivalently,
The silver ratio can also be defined by the simple continued fraction [2; 2, 2, 2, …]:
The convergents of this continued fraction (2/1, 5/2, 12/5, 29/12, 70/29, …) are ratios of consecutive Pell numbers. These fractions provide accurate rational approximations of the silver ratio, analogous to the approximation of the golden ratio by ratios of consecutive Fibonacci numbers.
The silver rectangle is connected to the regular octagon. If a regular octagon is partitioned into two isosceles trapezoids and a rectangle, then the rectangle is a silver rectangle with an aspect ratio of 1:δS, and the 4 sides of the trapezoids are in a ratio of 1:1:1:δS. If the edge length of a regular octagon is t, then the span of the octagon (the distance between opposite sides) is δSt, and the area of the octagon is 2δSt2.[3]
Calculation[edit]
For comparison, two quantities a, b with a > b > 0 are said to be in the golden ratio φ if,
However, they are in the silver ratio δS if,
Equivalently,
Therefore,
Multiplying by δS and rearranging gives
Using the quadratic formula, two solutions can be obtained. Because δS is the ratio of positive quantities, it is necessarily positive, so,
Properties[edit]
If one cuts two of the largest squares possible off of a silver rectangle one is left with a silver rectangle, to which the process may be repeated…
Silver spirals within the silver rectangle
Number-theoretic properties[edit]
The silver ratio is a Pisot–Vijayaraghavan number (PV number), as its conjugate 1 − √2 = −1/δS ≈ −0.41 has absolute value less than 1. In fact it is the second smallest quadratic PV number after the golden ratio. This means the distance from δ n
S to the nearest integer is 1/δ n
S ≈ 0.41n. Thus, the sequence of fractional parts of δ n
S, n = 1, 2, 3, … (taken as elements of the torus) converges. In particular, this sequence is not equidistributed mod 1.
Powers[edit]
The lower powers of the silver ratio are
The powers continue in the pattern
where
For example, using this property:
Using K0 = 1 and K1 = 2 as initial conditions, a Binet-like formula results from solving the recurrence relation
which becomes
Trigonometric properties[edit]
The silver ratio is intimately connected to trigonometric ratios for π/8 = 22.5°.
So the area of a regular octagon with side length a is given by
See also[edit]
- Metallic means
- Ammann–Beenker tiling
References[edit]
- ^ Vera W. de Spinadel (1999). The Family of Metallic Means, Vismath 1(3) from Mathematical Institute of Serbian Academy of Sciences and Arts.
- ^ de Spinadel, Vera W. (1998). Williams, Kim (ed.). «The Metallic Means and Design». Nexus II: Architecture and Mathematics. Fucecchio (Florence): Edizioni dell’Erba: 141–157.
- ^ Kapusta, Janos (2004), «The square, the circle, and the golden proportion: a new class of geometrical constructions» (PDF), Forma, 19: 293–313.
Further reading[edit]
- Buitrago, Antonia Redondo (2008). «Polygons, Diagonals, and the Bronze Mean», Nexus Network Journal 9,2: Architecture and Mathematics, p.321-2. Springer Science & Business Media. ISBN 9783764386993.
External links[edit]
- Weisstein, Eric W. «Silver Ratio». MathWorld.
- «An Introduction to Continued Fractions: The Silver Means Archived 2018-12-08 at the Wayback Machine», Fibonacci Numbers and the Golden Section.
- «Silver rectangle and its sequence» at Tartapelago by Giorgio Pietrocola
Что мы делаем. Каждая страница проходит через несколько сотен совершенствующих техник. Совершенно та же Википедия. Только лучше.
Золотой треугольник (геометрия)
Из Википедии — свободной энциклопедии
Пентаграмма. Каждый угол является золотым треугольником. Фигура также содержит пять золотых гномонов, которые получаются соединением двух несмежных углов с центральным пятиугольником.
Золотой треугольник[1] — это равнобедренный треугольник, в котором две боковые (равные) стороны находятся в золотой пропорции с основанием:
Золотые треугольники можно обнаружить в развёртках некоторых звёздчатых форм додекаэдра и икосаэдра.
Также, тот же треугольник обнаруживается в вершинах пентаграммы.
Угол при вершине равен
Из того, что сумма углов треугольника равна 180°, получаем, что углы при основании равны 72°[1].
Золотой треугольник можно найти также в десятиугольнике, если соединить две смежные вершины с центром. Полученный треугольник будет золотым, поскольку:
180(10-2)/10=144° является внутренним углом десятиугольника, и деление его отрезком, соединяющим вершину с центром, даст половину, 144/2=72[1].
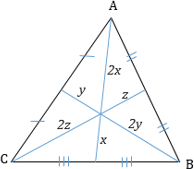
Золотой треугольник также замечателен уникальным соотношением углов 2:2:1[2].
Логарифмическая спираль
Последовательность золотых треугольников можно вписать в логарифмическую спираль. (Начиная с большого треугольника) делим угол при основании пополам, получаем следующую точку[3].
Процесс деления может продолжаться бесконечно, создавая бесконечно много золотых треугольников. Логарифмическую спираль можно провести через полученные вершины. Эта спираль известна также как равноугольная спираль. Термин предложил Рене Декарт: «Если провести прямую из полюса к любой точке на кривой, она пересечёт кривую всегда под одним и тем же углом»[4].
Золотой гномон
Золотой треугольник разбит на два треугольника Робинсона — золотой треугольник и золотой гномон.
Тесно связан с золотым треугольником золотой гномон, тупоугольный равнобедренный треугольник, в котором отношение длины равных (коротких) сторон к длине третьей стороны (основанию) является обратным к золотому отношению. Золотой гномон является уникальным треугольником с пропорцией углов 1:1:3. Его острые углы составляют 36°, то же значение, что и у угла при вершине золотого треугольника.
Расстояние AX и СX равны φ, что видно на рисунке. «Золотой треугольник имеет отношение основания к стороне, равное золотому отношению φ, в то время как золотой гномон имеет отношение боковой стороны к основанию, равное тому же золотому отношению» [5].


Плитки (сверху) и семь возможных типов вершин (снизу) в мозаике Пенроуза типа P2
Золотой треугольник может быть разрезан на золотой треугольник и золотой гномон. То же самое верно для золотого гномона. Золотой гномон и золотой треугольник с их равными сторонами (сторона гномона равна стороне треугольника) также являются тупым и острым треугольниками Робинсона[2].
Эти равнобедренные треугольники могут быть использованы для получения мозаик Пенроуза. Плитки Пенроуза состоят из «змеев» и «дротиков». «Змей» представляет собой дельтоид, состоящий из двух золотых треугольников, а «дротик» — дельтоид, состоящий из двух золотых гномонов.
См. также
- Золотое сечение
- Золотой прямоугольник
- Золотой ромб
- Треугольник Кеплера
- Лютня Пифагора[en]
- Мозаика Пенроуза
- Пентаграмма
Примечания
- ↑ 1 2 3 Elam, 2001.
- ↑ 1 2 Tilings Encyclopedia Архивная копия от 24 мая 2009 на Wayback Machine
- ↑ Huntley, 1970.
- ↑ Livio, 2002.
- ↑ Loeb, 1992.
Литература
- Kimberly Elam. Geometry of Design. — New York: Princeton Architectural Press, 2001. — ISBN 1-56898-249-6.
- H.E. Huntley. The Divine Proportion: A Study In Mathematical Beauty. — New York: Dover Publications Inc, 1970. — ISBN 0-486-22254-3.
- Mario Livio. The Golden Ratio: The Story of Phi, The World’s Most Astonishing Number. — Broadway Books, 2002. — ISBN 0-7679-0815-5.
- Arthur Loeb. Concepts and Images: Visual Mathematics. — Boston: Birkhäuser Boston, 1992. — ISBN 0-8176-3620-X.
Ссылки
- Weisstein, Eric W. Golden triangle (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Golden gnomon (англ.) на сайте Wolfram MathWorld.
- Robinson triangles at Tilings Encyclopedia
Эта страница в последний раз была отредактирована 24 февраля 2022 в 10:11.
Как только страница обновилась в Википедии она обновляется в Вики 2.
Обычно почти сразу, изредка в течении часа.
$begingroup$
Reading through geometric algorithms and code, I’ve encountered a term I’m not familiar with, and even the mighty google has not been that helpful:
What is a sliver triangle ?
From what i understand it’s a triangle that is almost flat (ie its minimum height is small). But i didn’t find a valid information source.
asked Aug 10, 2011 at 10:33
$endgroup$
$begingroup$
Your interpretation is correct.
In terms of mesh generation slivers can cause problems, in particular when applying Delaunay triangulation in 3D (with tetrahedrons instead of triangles), you most likely end up with many slivers.
In this setting, slivers are usually defined by having much smaller area/volume than its circumcircle. In 2D this would be equivalent to having a small angle between two edges, but this doesn’t hold for tetrahedrons.
answered Aug 10, 2011 at 11:24
$endgroup$
3
$begingroup$
According to Computer graphics dictionary by Roger T. Stevens (Google books link):
«A sliver polygon is a polygon whose area is so thin that its interior does not contain a distinct span for each scan line. In other words, instead of each scan line having a beginning and and ending pixel, each of which defines one side of the polygon, each scan line has only one pixel that may be the beginning or ending pixel.»
answered Aug 10, 2011 at 11:01
Hans LundmarkHans Lundmark
51.6k7 gold badges86 silver badges144 bronze badges
$endgroup$
$begingroup$
As an additional example of situations where a «sliver triangle» might cause trouble, Velvel Kahan shows in this article (he uses «needle» instead of «sliver» though) how Heron’s usual formula for computing the area of a triangle from side lengths can give bad results in inexact arithmetic when implemented naïvely (as well as other neat stuff I won’t get into here).
answered Aug 11, 2011 at 3:22
$endgroup$
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.






 =
=  или
или  , откуда
, откуда


 Ф, 1+Ф=
Ф, 1+Ф= 



 или
или  , откуда DС=
, откуда DС= 
 ,
, 
 =
= .
.





 = 2
= 2 2
2 ) =2(1+
) =2(1+ )= 4
)= 4 = 2+Ф,
= 2+Ф,
 .
.




 .
.

 длины противоположных ребер,
длины противоположных ребер,  расстояние между ними, – угол между ними;
расстояние между ними, – угол между ними;



 =
= 
 = 4
= 4 
























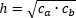




 Золотой треугольник
Золотой треугольник












![delta _{S}^{-1}=1delta _{S}-2=[0;2,2,2,2,2,dots ]approx 0.41421](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b990f8c24f259f20e790b19bc7a0964ffca4856)
![{displaystyle delta _{S}^{0}=0delta _{S}+1=[1]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3f43698a8899ad582f4858848f9a3128e6bc7c0)
![{displaystyle delta _{S}^{1}=1delta _{S}+0=[2;2,2,2,2,2,dots ]approx 2.41421}](https://wikimedia.org/api/rest_v1/media/math/render/svg/246db5a8c15bcfe70b7e8097f24316e50622feb3)
![{displaystyle delta _{S}^{2}=2delta _{S}+1=[5;1,4,1,4,1,dots ]approx 5.82842}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f21030c1b14c77c31ad8abb6aacd680e678fbbac)
![{displaystyle delta _{S}^{3}=5delta _{S}+2=[14;14,14,14,dots ]approx 14.07107}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a027dc6a0219d4911b34b55f89eb6be29eb4a01)
![delta_S^4 = 12delta_S + 5 = [33;1,32,1,32,dots] approx 33.97056](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8048daeeaf27de5d7ca01933e4f756099aec1e2)


![{displaystyle delta _{S}^{5}=29delta _{S}+12=[82;82,82,82,dots ]approx 82.01219}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc4032d19efdd0c8dfea44966c3f25ef2c19e510)








