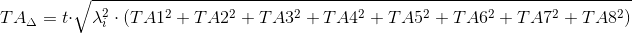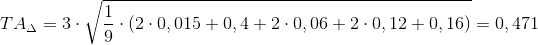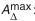Расчет размерных цепей
Обратная задача
теоретико-вероятностный метод
Теоретико-вероятностный метод — метод расчета, учитывающий рассеяние размеров
и вероятность различных сочетаний отклонений составляющих звеньев размерной цепи.
Применение теории вероятностей позволяет расширить допуски составляющих размеров
и тем самым облегчить изготовление деталей при практически ничтожном риске
несоблюдения предельных значений замыкающего размера.
Формулы
1. Определение характеристик составляющих звеньев размерной цепи
1.1.
Допуск i-го звена размерной цепи определим по формуле:
| T(A i ) = Es(A i ) — Ei(A i ) | (1) |
где
Es(A i ) – верхнее отклонение звена;
Ei(A i ) – нижнее отклонение звена;
i – индекс звена;
1.2.
Середину поля допуска i-го звена определим по формуле:
 |
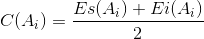(2) |
2. Определение характеристик замыкающего звена
2.1.
Номинальное значение замыкающего звена AΔ определим по формуле:
 |
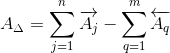(3) |
где
A j – номинальный размер любого увеличивающего звена;
A q – номинальный размер любого уменьшающего звена;
j – индекс увеличивающего звена;
q – индекс уменьшающего звена;
n – число увеличивающих звеньев;
m – число уменьшающих звеньев;
2.2.
Допуск замыкающего звена AΔ определим по формуле:
 |
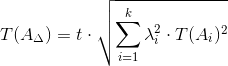(4) |
где
Т(А i ) – допуск любого составляющего звена;
k – число звеньев размерной цепи;
λ — коэффициент относительного рассеяния.
Зависит от принятого закона распределения размера:
— для нормального распределения(Гаусса) λ 2 = 1/9,
— для закона треугольника(Симпсона) λ 2 = 1/6,
— для закона равной вероятности λ 2 = 1/3.
t — коэффициент риска, определяющий количество бракованных деталей;
| p | 32 | 23 | 16 | 9 | 4,6 | 2,1 | 0,94 | 0,51 | 0,27 | 0,1 |
|---|---|---|---|---|---|---|---|---|---|---|
| t | 1 | 1,2 | 1,4 | 1,7 | 2 | 2,3 | 2,6 | 2,8 | 3 | 3,3 |
2.3.
Координата середины поля допуска замыкающего звена определяется по формуле:
 |
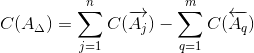(5) |
где
C(A j ) — координата середины поля допуска любого увеличивающего звена;
C(A q ) — координата середины поля допуска любого уменьшающего звена;
2.4. Предельные отклонения замыкающего звена.
2.4.1
Верхнее отклонение замыкающего звена Es(AΔ) определим по формуле:
 |
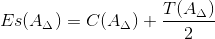(6) |
где
C(A Δ) — координата середины поля допуска замыкающего звена
T(A Δ) — допуск замыкающего звена;
2.4.2.
Нижнее отклонение замыкающего звена Ei(AΔ) определим по формуле:
 |
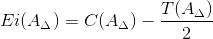(7) |
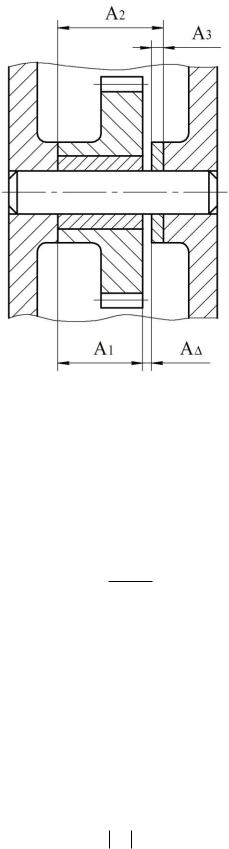
Пример
Задание:
Требуется проверить наличие и величину зазора AΔ.
Определить допуск и предельные отклонения размера замыкающего звена (см. рис. 1) по теоретико-вероятностному методу, приняв t=3, λ2 = 1/9,
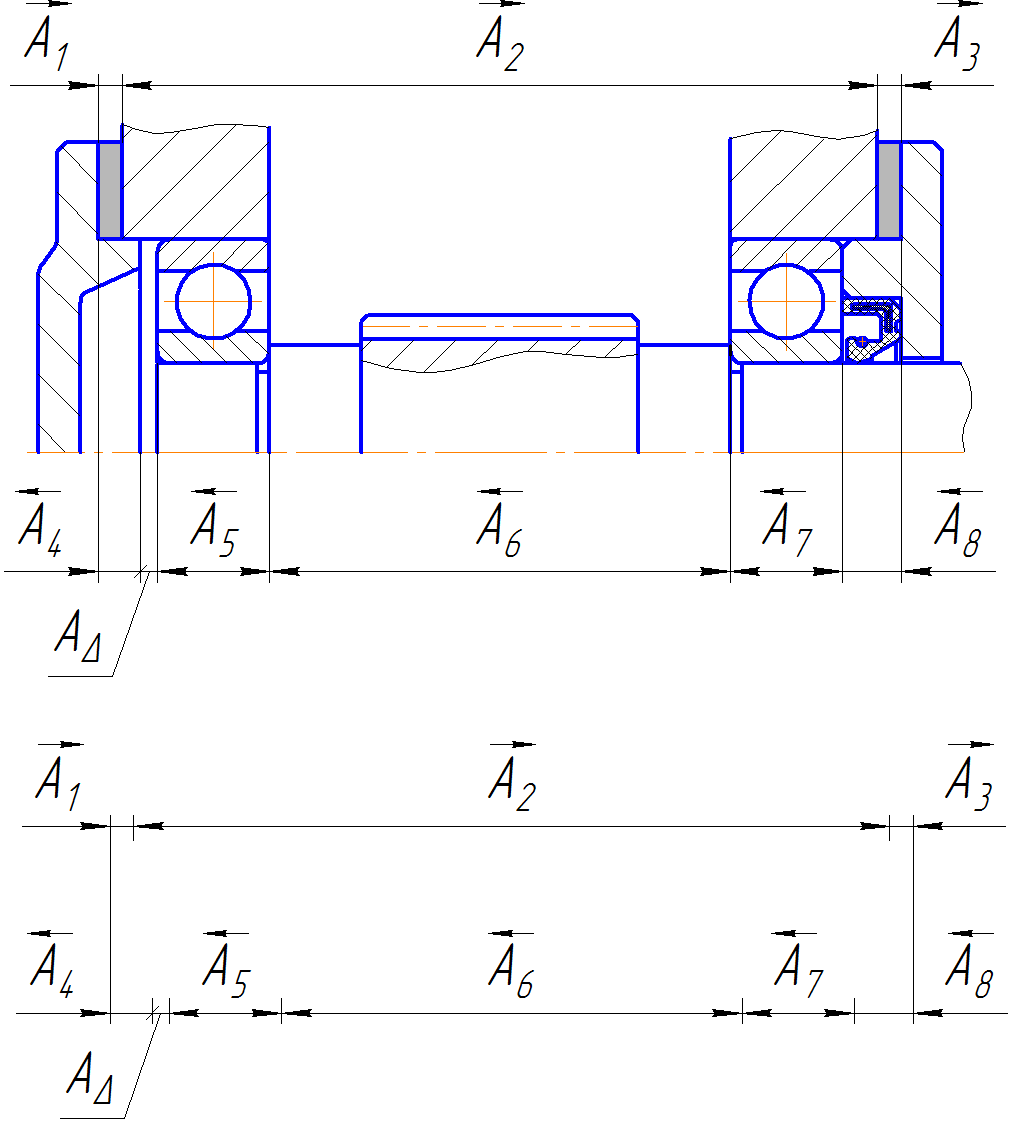
Рисунок 1 – Сборочная размерная цепь.
Исходные данные:
Звенья размерной цепи:
Допуски и координаты середины поля допуска составляющих звеньев определены по формулам
(1) и (2).
| A1 = 1-0,015 (мм); | Т(A1)=0,015 (мм); | C(A1) = -0,0075 (мм); | ||||
|
Т(A2)=0,4 (мм); | C(A2) = 0,15(мм); | ||||
| A3 = 1-0,015 (мм); | Т(A3)=0,015 (мм); | C(A3) = -0,0075 (мм); | ||||
| A4 = 10-0,06 (мм); | Т(A4)=0,06 (мм); | C(A4) = -0,03 (мм); | ||||
| A5 = 19-0,12 (мм); | Т(A5)=0,12 (мм); | C(A5) = -0,06 (мм); | ||||
|
Т(A6)=0,16 (мм); | C(A6) = -0,16 (мм); | ||||
| A7 = 19-0,12 (мм); | Т(A7)=0,12 (мм); | C(A7)= -0,06 (мм); | ||||
| A8 = 10-0,06 (мм); | Т(A8)=0,06 (мм); | C(A8)= -0,03 (мм); |
Увеличивающие звенья: A1, A2, A3;
Уменьшающие звенья: A4, A5, A6, A7, A8;
Замыкающее звено: AΔ
Решение:
1. Номинальный размер замыкающего звена
Номинальный размер замыкающего звена AΔ определим по формуле
.
Для заданной размерной цепи формула (3) принимает вид:
AΔ = A1 + A2 + A3 — (A4 + A5 + A6 + A7 + A8)
AΔ = 1 + 206 + 1 — (10 + 19 + 150 + 19 + 10) = 0(мм)
2. Допуск замыкающего звена
Допуск замыкающего звена AΔ определим по формуле
.
Для заданной размерной цепи формула (4) принимает вид:
3. Координаты середины поля допуска замыкающего звена
Координату середины поля допуска замыкающего звена определим по формуле
:
Для заданной размерной цепи формула (5) принимает вид:
С(AΔ) = С(A1) + С(A2) + С(A3) — (С(A4) + С(A5) + С(A6) + С(A7) + С(A8))
С(AΔ) = (-0,0075) + 0,15 + (-0,0075) — ((-0,03) + (-0,06) + (-0,16) + (-0,06) + (-0,03)) = 0,475 (мм)
4. Предельные отклонения замыкающего звена
4.1. Верхнее отклонение замыкающего звена EsAΔ определим по формуле
EsAΔ = 0,475 + 0,5·0,471 = 0,71(мм)
4.2. Нижнее отклонение замыкающего звена EiAΔ определим по формуле
EiAΔ = 0,475 — 0,5·0,471 = 0,24(мм)
Расчет размерных цепей онлайн. Обратная задача.
Замыкающее звено:
Выведем уравнения, необходимые для определения предельных отклонений замыкающего размера. При расчете удобно использовать координату середины поля допуска (Л ) и половину допуска ГЛ/2 (рис. 11.3), [c.253]
Подставим в уравнения (11.10) и (11.11) значения предельны.ч отклонений, выраженных через координату середины поля допуска в уравнениях (П.6) и (11.7) [c.254]
Если одно из предельных отклонений составляющего размера равно нулю, его допуск равен абсолютному значению второго отклонения, а координата середины поля допуска равна половине этого допуска со знаком, который имеет второе отклонение. [c.255]
По формуле (11.12) находим координату середины поля допуска замыкающего размера , (Л ) = А,) + (А,) — (Л,.,) + (Л J (Л,) = (70 + [c.255]
Координатой середины поля допуска A d называется разность между средним и номинальным размерами [c.215]
Сущность метода максимума-минимума (прямая задача). Исходя из установленных требований к величине замыкающего звена, определяются номинальные размеры, отклонения, допуски и координаты середины полей допусков составляющих звеньев. ГОСТ 16320—70 рекомендует решать прямую задачу способом равных допусков. Порядок решения прямой задачи следующий. [c.231]
На основании задания, расчетов, опыта и т. п. устанавливаются номинальный размер, отклонения, допуск и координата середины поля допуска замыкающего звена. [c.231]
Координаты середин полей допусков составляющих звеньев за исключением увязывающего определяются по формуле [c.232]
Координата середины поля допуска увязывающего звена определяется по формуле [c.232]
И. Определяются координаты середины полей допусков составляющих звеньев [c.234]
Координата середины поля допуска увязывающего звена [c.234]
Порядок решения обратной задачи следующий. Исходя нз установленных размеров, отклонений и координат середин полей допусков составляющих звеньев определяются величина отклонения и координаты середины поля допуска замыкающего звена. 234 [c.234]
Координаты середины полей допусков составляющих звеньев определяем по формуле (12.22) Д В = —0,2 Д В = 0 Д В = —0,1 Д В = 0,25. [c.237]
По формуле (12.13) определяем координаты середины поля допуска увязывающего звена Д Вд = —0,05. [c.237]
Определим координаты середин полей допусков составляющих звеньев ДВ, = +0,15 ДВз = 0 АВ4 = +0,15 ДВ = 0,15 ДВц = —0,05 ДВ = О ДВ9 = +0,1 ДВв = -0,1 ДВ, = —0,075 ДВ = —0,05 ДВ =+0,15. [c.237]
Координату середины поля допуска замыкающего звена определяем по формуле (12.21) Д В = 0,175. [c.237]
Далее находим координату середины поля допуска А и половину поля допуска S [c.34]
Координаты середины поля допуска 0 0 0 0 0 0 0 0 [c.42]
Координата середины поля допуска — расстояние от середины поля допуска до границы номинального размера. Обозначается буквой А с индексом 0, около которого ставится порядковый номер или условное обозначение звена (фиг. 12,6). [c.56]
Координаты середины поля допуска [c.58]
Координата середины поля допуска замыкающего или исходного звена [c.59]
Рассчитать по формулам табл. 3 номинальные размеры, координаты середин полей допусков и величины допусков на все звенья, составляющие каждую из размерных цепей. [c.61]
Для проверки правильности расчета и установления номиналов, координат середин полей допусков и величин допусков могут служить формулы [c.63]
В рабочих чертежах допуски задаются в виде предельных отклонений от номинального размера возьмем для расстояния между торцами втулок фартука координату середины поля допуска равной , д,., =0.3 мм тогда координата середины ноля допуска для размера ширины зубчатого колеса определяется из формулы (5) [c.70]
Сопоставление с требуемой величиной допуска показывает, что допуски н координаты середин полей допусков рассчитаны и установлены правильно. [c.73]
Коэффициент относительной асимметрии может быть отличен от нуля и в том случае, если исходное распределение (рассматриваемое вне зависимости от поля допуска) симметрично, но ось симметрии его смещена в поле допуска относительно координаты середины поля допуска Дц. Коэффициент относительной асимметрии отображает и несимметричность исходного распределения и несимметричность расположения исходного распределения в воле допуска. В частном случае возможна и взаимная компенсация этих двух несимметричностей (при противоположном направлении их), приводящая к значению коэффициента относительной асимметрии а = 0. [c.38]
Погрешностью закрепления называется разность предельных расстояний измерительной базы относительно установленного на размер инструмента в результате приложения к обрабатываемым заготовкам зажимного усилия. Для партии заготовок погрешность равна нулю, если величина смещения хотя и велика, но постоянна в этом случае координата середины поля допуска выполняемого размера может быть скорректирована настройкой станка. [c.311]
Обозначения б — допуск X — выборочное среднее 5 — выборочное среднее квадратическое отклонение Вер — среднее значение признака качества (например, координата середины поля допуска) т — выборочный эксцесс. [c.337]
В выводе уравнений для определения предельных отклонений замыкающего звена введена важная предпосылка о координате середины поля допуска E A ) (рис. 5.2). [c.203]
Координата середины поля допуска замыкающего звена записывается [c.203]
Координату середины поля допуска замыкающего размера определяем из формулы (3.3) [c.204]
Координата середины поля допуска замыкающего звена рассчитывается следующим образом [c.94]
ГОСТ 16319—80 устанавливает обозначения верхнего (Е ) и нижнего Дн (Е ) предельных отклонен]]] , а также координаты середины поля допуска Дс ( с) (обозначения, укази[]]]ые в скобках, разрешается применять наряду с ос-ноиными). [c.253]
| Фиг. 6. Теоретическая точностная диаграмма с зоной AjMj допускаемого разброса настроек / —/ и (/) — /) — настройка по верхнему пределу 2—2 и (2) — (2) — настройка по нижнему пределу До—координата середины поля допуска J — половина поля допуска. |  |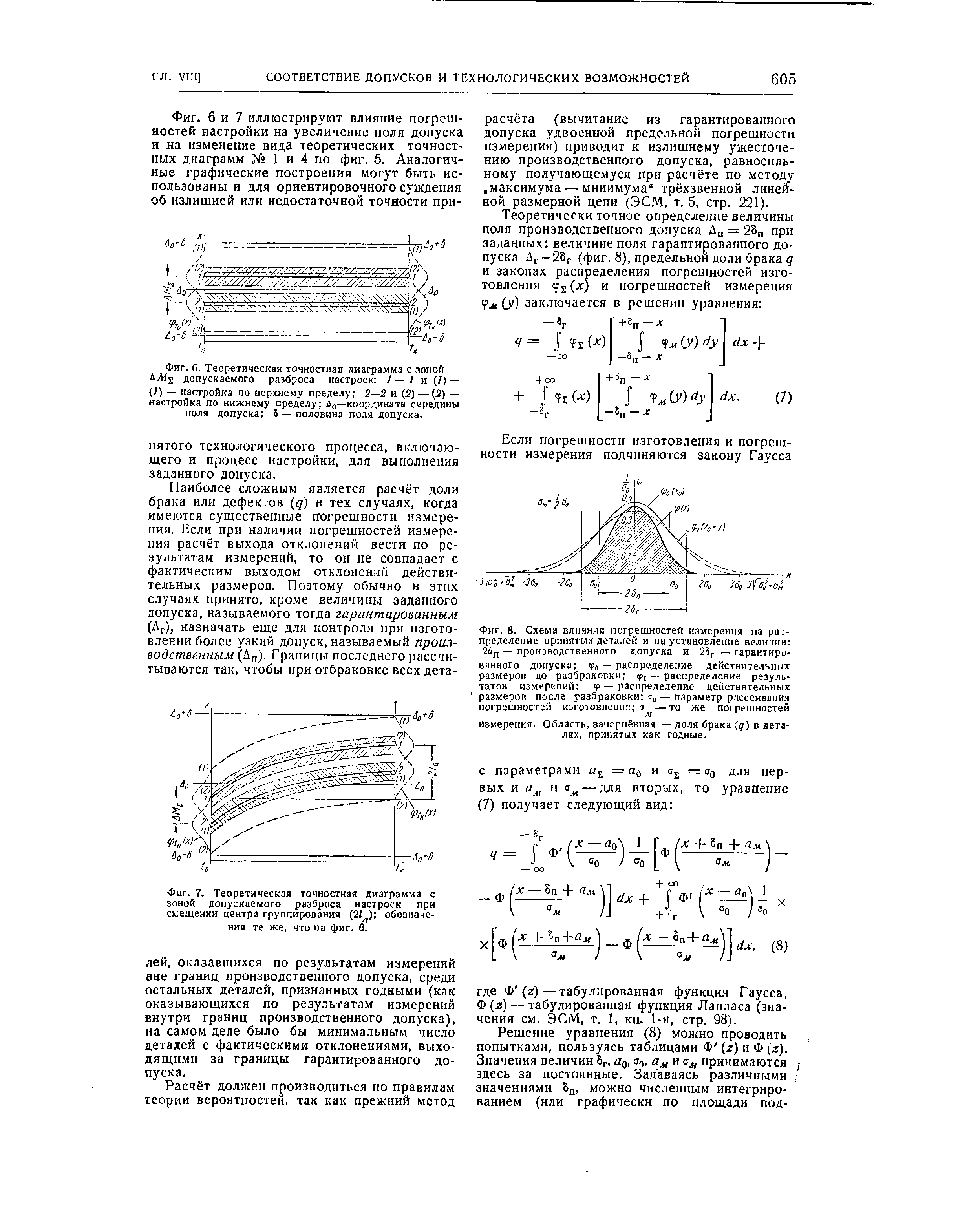
Раегчитанные величины допусков проставляют на чертежах у соответствующих номиналов с учетом координат середин полей допусков. Выполнение деталью (или деталями) функции компенсатора отмечается на чертеже соответствующей надписью. [c.69]
Зависимость вероятного брака деталей от коэффициентов точности и настроенности технологических процессов. Точность геометрических параметров детали обычно задает конструктор она количественно определяется полем допуска согласно чертежам или техническим условиям. Поле допуска определяется интервалом значений размера х от х,, — 5 до Хд -(- 5, где Хд — координата середины поля допуска 5 — половина поля допуска (рис. 4). Технологическая точность количественно определяется законом распределения суммарной по-грещности обработки. [c.79]
Примеры расчетов допусков (прямая задача)
Пример 1. Задача: обеспечить требуемый зазор между торцами зубчатого колеса и проставочного кольца механизма (рис. 4.39).
Рис 4.39. Схема размерной цепи
Замыкающим звеном является размер А , связывающий торцы зубчатого колеса и проставочного кольца. Из служебного назначения механизма следует, что минимальный зазор должен быть равен 0, а максимальный – 0,2 мм. Следовательно, поле допуска на зазор будет равно:
ТА =0,2-0=0,2 мм,
а координата середины поля допуска:
oA 0,22 0 0,1мм
Уравнение размерной цепи, определяющей величину зазора, согласно рис. 29
А =-А1+А2-А3
Задача решается пятью методами достижения требуемой точности замыкающего звена с целью их сопоставления.
1. Метод полной взаимозаменяемости При этом методе должно быть соблюдено условие
m 1
Ai TAi TA i 1
в линейной размерной цепи |ξAi| = 1.
Учитывая степень сложности достижения требуемой точности составляющих звеньев, устанавливаем подбором: TAI=0,03 мм, ТAi =0,15 мм, ТAi =0,02 мм.
Принимаем координаты середин полей допусков oAi= — 0,015 мм, oAi = +0,075 мм.
Координату середины поля допуска третьего звена находим из уравнения:
|
n |
m 1 |
|||||||||||||
|
оА oAi |
oAi |
oA1 oA2 oA3 |
||||||||||||
|
i 1 |
n 1 |
|||||||||||||
|
0,1=0,015+0,075- |
oAi |
|||||||||||||
|
Следовательно, |
oAi = — 0,01 мм. |
|||||||||||||
|
Правильность назначения допусков проверяем по формулам (7), (8) настоящего пособия, |
||||||||||||||
|
представив значения oAΔ и ТAΔ соответственно через |
oAi и ТAi установленные при расчете допусков: |
|||||||||||||
|
TA |
0,015 0,075 0,01 |
0,03 0,15 0,02 |
0; |
|||||||||||
|
HA |
oA |
|||||||||||||
|
2 |
2 |
|||||||||||||
|
TA |
0,015 0,075 0,01 |
0,03 0,015 0,02 |
0,3мм |
|||||||||||
|
BA |
oA |
|||||||||||||
|
2 |
2 |
|||||||||||||
Сопоставление с условиями задачи показывает, что допуски установлены верно.
2. Метод неполной взаимозаменяемости
Задаем значения коэффициента риска t и относительного среднего квадратического отклонения λАi .
Допустим, что в данном случае риск Р=1%, при котором t =2,57, экономически оправдан.
Полагая, что условия изготовления деталей таковы, что распределение отклонений размеров будет близким к закону Гаусса, принимаем: λ2Ai = 1/9.
Учитывая трудности достижения требуемой точности каждого составляющего звена, устанавливаем подбором следующие величины полей допусков: TA1=0,1 мм; TA2= 0,20 мм; TA3= 0,06 мм.
Правильность подбора допусков можно проверить по формуле (4):
|
m 1 |
||||
|
Т А t |
Ai2 2AiTAi2 |
2,57 |
1/ 9(0,12 0,22 0,062 ) 0,2мм |
|
|
i 1 |
Устанавливаем следующие координаты середин полей допусков: oA1 = 0; oA2 = 0,l мм.
Значение oA3 находим из уравнения:
oAΔ=- oA1+ oA2— oA3
0,1=0+0,1- oA3;
oA3=0
Правильность установленных допусков может быть проверена по формулам:
|
n |
m 1 |
m 1 |
2 |
||||||||
|
TAi |
|||||||||||
|
BAi |
( oAi |
oAi ) t |
Ai2 2Ai |
( |
) 0,10 0,1 0мм |
||||||
|
i 1 |
n 1 |
i 1 |
2 |
||||||||
|
n |
m 1 |
||||||||||
|
m 1 |
2 |
||||||||||
|
TAi |
|||||||||||
|
BAi |
( oAi |
oAi ) t |
Ai2 2Ai |
( |
) 0,1 0,1 0,2мм |
||||||
|
i 1 |
n 1 |
i 1 |
2 |
||||||||
|
Предельные отклонения размеров составляющих звеньев: |
|||||||||||
|
A 0,05, A 0,2 , |
A 0,03. |
||||||||||
|
1 |
2 |
3 |
|||||||||
|
3. |
Метод групповой взаимозаменяемости |
При решении задачи методом групповой взаимозаменяемости, прежде всего необходимо установить число групп, на которые должны быть рассортированы детали после изготовления, и значение производственного допуска замыкающего звена.
Допустим, что расширение TAΔ в три раза в данном случае является экономически обоснованным, в связи с чем число групп п равно 3.
Таким образом, T΄AΔ+TAΔ*n=0,2*3=0,6 мм
При расчете допусков должно быть соблюдено условие
|
k |
m 1 |
|||||||
|
i |
Ti |
i |
Ti |
|||||
|
i 1 |
k 1 |
|||||||
|
где Ti |
и Ti |
– допуски увеличивающих и уменьшающих звеньев. Согласно этому условию |
T΄A2= T΄A1+ T΄A3=1/2 T΄AΔ
Отсюда
T΄A2=1/2 T΄AΔ=0,3мм
и
T΄A1+ T΄A3=1/2 T΄AΔ=0,3мм
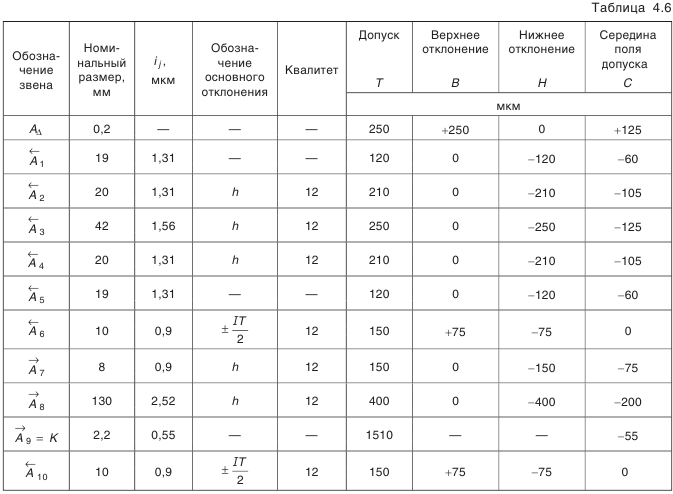
Сообразуясь со степенью сложности изготовления деталей, установим T΄AΔ = 0,24 мм и T΄A3 =0,06 мм. Устанавливаем поля допусков и координаты их середин для деталей каждой группы (табл.
4.6).
|
Таблица 4.6 |
|||||||||
|
Группа |
T΄A1 |
oA1 |
oA2 |
oA3 |
TA3 |
oA3 |
TAΔ |
||
|
oAΔ |
|||||||||
|
I |
0,08 |
-0,04 |
0,1 |
+0,05 |
0,02 |
-0,01 |
0,2 |
+0,1 |
|
|
II |
0,08 |
+0,04 |
0,1 |
+0,15 |
0,02 |
+0,01 |
0,2 |
+0,1 |
|
|
III |
0,08 |
+0,12 |
0,1 |
+0,25 |
0,02 |
+0,03 |
0,2 |
+0,1 |
|
При назначении координат середин полей допусков уравнение
должно быть следующего вида oAΔ=- oA1+ oA2— oA3
Две последние колонки табл. 3 показывают, что при соединении деталей в каждой из групп требуемые пределы зазора будут обеспечены.
Предельные отклонения размеров составляющих звеньев приведены в табл. 4.7.
Таблица 4.7
|
Группа |
А1 |
А2 |
А3 |
|
I |
— 0,08 |
+ 0,1 |
— 0,02 |
|
+0,2 |
|||
|
II |
+ 0,08 |
+0,02 |
|
|
+0,1 |
|||
|
+0,16 |
+ 0,3 |
+ 0,04 |
|
|
III |
|||
|
+ 0,08 |
+ 0,2 |
+0,02 |
|
4. Метод пригонки Для достижения требуемой точности зазора методом пригонки выберем в качестве
компенсирующего звена размер А3 проставочного кольца, изменение которого проще всего осуществить.
Установим на составляющие звенья экономически целесообразные значения полей допусков и координаты их середин (табл. 4.8.).
Таблица 4.8
|
Звено |
T΄Ai |
Δ΄oAi |
|
А1 |
0,3 |
— 0,15 |
|
А2 |
0,4 |
+ 0,2 |
|
А3 |
0,1 |
+ 0,25 |
Тогда производственный допуск замыкающего звена расширится до значения:
|
m1 |
|||||
|
Т |
0,3 0,4 0,1 0,8мм |
||||
|
А |
AiTAi |
i1
Наибольшая величина компенсации может быть равной
|
δК= T΄AΔ — TAΔ =0,8-0,2=0,6 мм. |
||||||||
|
Для того, чтобы создать на звене A3 |
необходимый для пригонки слой материала, в координату |
|||||||
|
середины поля допуска этого звена следует ввести поправку к |
||||||||
|
K |
0,6 |
(0,15 0,2 0,25) 0,1 0,3мм |
||||||
|
K |
oA |
|||||||
|
2 |
oA |
2 |
||||||
Поэтому следует установить
oAз=0,25+0,3=0,55 мм.
Предельные отклонения размеров составляющих звеньев:
0,6 A1 0,3 ; А2 0,4 ; А3 0,5
5. Метод регулирования с применением неподвижного компенсатора Выберем в качестве компенсатора то же звено, что было взято при решении задачи по методу
|
пригонки, |
и |
установим |
следующие |
допуски |
Т’Ai |
: |
|||||||||
|
0,2 – для звена Аi; 0,4 – для звена А2; 0,05 – для звена Аз. |
|||||||||||||||
|
В размерной цепи А компенсации подлежат отклонения только звеньев А1 |
и А2, которые в |
||||||||||||||
|
сумме могут составлять |
|||||||||||||||
|
m 2 |
|||||||||||||||
|
Т |
Ai |
T |
T |
T |
0,2 0,4 0,6мм |
||||||||||
|
A |
Ai |
A1 |
A2 |
i 1
Всоответствии с этим наибольшая величина компенсации будет
δК= T΄AΔ — TAΔ =0,6-0,2=0,4 мм.
Число ступеней компенсаторов вычисляют по формуле
|
N T |
T |
||||
|
T |
|||||
|
A |
|||||
|
A комп |
|||||
|
В данной задаче |
|||||
|
N |
0,6 |
4 |
|||
|
0,2 |
0,05 |
С целью упрощения расчета размеров компенсаторов рекомендуется назначать координаты середин полей допусков составляющих звеньев так, чтобы совместить одну из границ расширенного поля допуска замыкающего звена с соответствующей границей его поля допуска, заданного служебным назначением изделия.
В связи с этим, при совмещении нижних границ полей допусков замыкающего звена (рис. 4.40.), необходимо соблюсти условие:
|
нА нА ; |
||||||||||
|
Т |
||||||||||
|
А |
нА |
; |
||||||||
|
оА |
2 |
|||||||||
|
Т |
||||||||||
|
нА |
А |
; |
||||||||
|
оА |
2 |
|||||||||
|
0 |
0,6 |
0,3мм |
||||||||
|
оА |
2 |
|||||||||
Поскольку компенсации подлежат отклонения звеньев А1 и А2, то в расчете координат середин полей допусков компенсатор участвовать не должен.
Координата середины его поля допуска должна быть установлена независимо от координат середин полей допусков составляющих звеньев А1 и А2. С целью упрощения расчета размеров компенсаторов рекомендуется задавать координату середины поля допуска компенсирующего звена равной половине его поля допуска со знаком минус.
В данной задаче
|
Т |
0,05 |
0,025мм |
|||||||
|
А3 |
|||||||||
|
оА3 |
2 |
2 |
|||||||
|
Таким образом, |
|||||||||
|
0,3мм |
|||||||||
|
оА |
оА1 |
оА2 |
Установим
Δ΄oA1 = — 0,1 мм и Δ΄oA2 =0,2 мм.
При установленных координатах середин полей допусков звеньев А1 и А2 после допуска Т‘А займет относительно заданного поля допуска ТА положение, показанное на рис. 4.40.
При величине ступени компенсации, равной
ТА -Ткомп= 0,2-0,05=0,15 мм
и числе групп компенсаторов N=4, поле производственного допуска Т‘А будет разбито на четыре зоны с границами, показанными на рис. 30. Отклонения, возникающие в пределах той или иной зоны, должны компенсироваться путем постановки в изделие соответствующего поставочного кольца (компенсатора).
Размер компенсатора первой ступени равен его номинальному размеру. Размеры компенсаторов каждой следующей ступени будут отличаться от размеров компенсаторов предшествующей ступени на величину ступени компенсации.
Рис. 4.40
С учетом допуска на изготовление компенсаторов их размеры будут:
I ступень . . . Л3-0,05 мм;
II ступень . . . (А3+0,15)-0,05 мм;
III ступень . . . (А3+ 0,30)-0,05 мм;
IV ступень . . . (A3+0,45)-0,05 мм.
При задании размеров компенсаторов разницу в номиналах целесообразно перенести на координаты середин полей их допусков. Тогда размеры компенсаторов должны быть равны:
А3-0,05 мм – для I ступени;
0,15
А3 0,10 мм – для II ступени;
0,30
А3 0,25 мм – для III ступени;
0,45
А3 0,40 мм – для IV ступени.
На рис. 4.40 можно видеть, как осуществляется компенсация отклонений, находящихся в различных зонах Т’А .
Если координаты середин полей допусков составляющих звеньев А1и А2 установлены произвольно, то при определении размера компенсаторов первой ступени необходимо внести поправку в координату середины поля допуска компенсирующего звена
|
К |
, |
||||||||
|
К |
2 |
оА |
|||||||
|
n |
m 1 |
||||||||
|
оА |
oAi |
oAi |
|||||||
|
i 1 |
n 1 |
причем значения ‘oAi установлены произвольно.
Если компенсатор является увеличивающим звеном, поправку Δ’к вносят со своим знаком, а если уменьшающим звеном – с противоположным знаком.
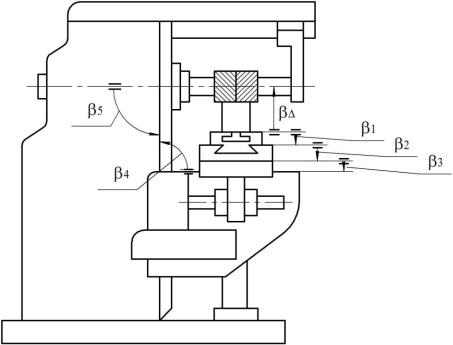
Пример 2. Задача: рассчитать и установить допуски на относительные повороты поверхностей деталей универсально-фрезерного станка с целью обеспечения требуемой параллельности рабочей плоскости стола оси вращения шпинделя.
Исходя из назначения станка, на замыкающее звено установлен допуск TβΔ =0,03/300 мм. При этом указано, что повороты рабочей плоскости стола и оси вращения шпинделя могут быть направлены только в сторону оси вращения шпинделя. Считая положительным направление поворота против часовой стрелки, согласно служебному назначению станка следует установить oβΔ= +0,015/300 мм. Выявляем размерную цепь, при помощи которой решается поставленная задача (рис.
4.41.).
При расчетах допусков на поворот поверхностей удобно использовать следующий прием. Поскольку допуски на поворот поверхностей задают в виде линейной величины, отнесенной к соответствующей длине, их следует вначале привести к общему знаменателю. Это позволит во время расчета не учитывать его и использовать методику и формулы, служащие для расчета линейных допусков. После расчета допусков отброшенный знаменатель следует восстановить.
Рис. 4.41. Схема технологической размерной цепи фрезерного станка
Рассчитаем среднюю величину допуска Тср:
Тср Т 0,006 / 300мм m 1
Полученная величина говорит о том, что детали универсально-фрезерного станка изготовить в пределах этого допуска не представляется экономически возможным.
Поэтому отказываемся от использования достижения требуемой точности методом полной взаимозаменяемости. Рассмотрим возможность использования метода неполной взаимозаменяемости.
Предварительно примем следующие исходные данные. Будем считать, что при изготовлении станков отклонения, получаемые на деталях, будут иметь характер рассеяния, близкий к закону Симпсона (треугольника), для которого величина коэффициента относительного среднего
квадратического отклонения i2 16 . Зададимся возможным риском Р=10%, чему соответствует t =1,65. Подставляя перечисленные данные в формулу, получаем:
|
Т ср |
Т |
0,03 |
0,0199 / 300мм |
||||||||
|
m 1 |
1 |
||||||||||
|
t |
i2 i2 |
1,65 |
5 |
||||||||
|
6 |
|||||||||||
|
i 1 |
|||||||||||
или, округляя, будем иметь Tср~ 0,02/300 мм. Считая полученное значение Tср приемлемым и учитывая трудности изготовления и монтажа отдельных деталей, установим следующие значения допусков: Tβ5 =0,03/300 мм — на поворот оси вращения шпинделя относительно направляющих станины (отклонение от перпендикулярности) ;
Tβ4=0,02/300 мм – на отклонение от перпендикулярности направляющих консоли, по которым перемещается каретка, относительно направляющих которыми консоль скользит по станине;
Tβ3=0,01/300 мм – на отклонение от параллельности верхней поверхности каретки относительно ее направляющих;
Tβ2= 0,02/300 мм и Tβ1=0,02/300 мм.
Проверим правильность установленных допусков по формуле
|
m 1 |
1 |
1 |
1 |
1 |
1 |
|||||||||||||||||||
|
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
|||||||||||||||||
|
Т t |
i |
iT i |
1,65 |
*0,02 |
*0,02 |
*0,01 |
*0,02 |
*0,03 |
||||||||||||||||
|
6 |
6 |
6 |
6 |
|||||||||||||||||||||
|
i 1 |
6 |
|||||||||||||||||||||||
|
1,65 0,0003647 |
0,0315 / 300мм |
Как видно, возможные отклонения замыкающего звена несколько больше установленного допуска (0,03/300 мм). Следовательно, процент риска также будет превосходить ранее избранный (Р- 10%).
Вычислим его:
|
t |
T |
||||||||||||||||||||
|
m 1 |
|||||||||||||||||||||
|
2 |
2 |
2 |
|||||||||||||||||||
|
i |
iT i |
||||||||||||||||||||
|
i 1 |
|||||||||||||||||||||
|
0,03 |
1,58 |
||||||||||||||||||||
|
1 |
0,022 |
1 |
0,022 |
1 |
0,022 |
1 |
0,022 |
1 |
0,032 |
||||||||||||
|
6 |
6 |
6 |
6 |
6 |
|||||||||||||||||
Этому значению t соответствует возможный риск 10,5%. Считаем, что на такой риск можно пойти, и в соответствии с этим принимаем установленные допуски.
Поскольку поворот поверхности стола должен быть направлен к оси вращения шпинделя, необходимо установить для каждого звена координату середины поля допуска и ее знак. Значения координат середин полей допусков устанавливаются с помощью уравнения.
o o 1 o 2 o 3 o 4 o 5
Если принять, что оси поворота поверхностей деталей расположены слева (рис. 4.42.), то координаты середин полей допусков звеньев β1; β2 β3 β4 будут иметь знак «+», а звена β5 – знак «-», Принимаем значения координат середин полей допусков равными:
оβ1 =0,01/300; оβ2=0,01/300;
оβ3= 0,005/300; оβ4= 0,0 1/300.
Рис. 4.42. Схема к назначению допустимых отклонений от параллельности
Координату середины поля допуска пятого звена находим из уравнения
o o 1 o 2 o 3 o 4 o 5 ; оβ5= — 0,02/300
Для того, чтобы убедиться в правильности установленных величии допусков и координат середин их полей, проверяем верхнее и нижнее предельные отклонения замыкающего звена размерной цепи по формулам:
|
m 1 |
2 |
2 |
T i |
2 |
|||||||||
|
n |
m 1 |
i |
i |
( |
) |
; |
|||||||
|
2 |
|||||||||||||
|
В ( o i |
o i ) t |
i 1 |
|||||||||||
|
i 1 |
n 1 |
||||||||||||
|
n |
m 1 |
m 1 |
2 2 |
T i |
2 |
||||||||
|
H ( o i |
o i ) t |
i |
i |
( |
) |
||||||||
|
2 |
|||||||||||||
|
i 1 |
n 1 |
i 1 |
|||||||||||
Подставляя в формулы значения установленных полей допусков: координат их середин и принятое значение t =l,58, получим:
|
B 0,01 0,01 0,05 0,01 ( 0,02) |
|||||||||||||||||
|
1,58 |
1 |
(0,01)2 |
1 |
(0,01)2 |
1 |
(0,05)2 |
1 |
(0,01)2 |
1 |
(0,015)2 |
|||||||
|
6 |
6 |
6 |
6 |
6 |
|||||||||||||
0,15 0,015 0,03 / 300;H 0,015 0,015 0
Определяем допуск замыкающего звена и координату его середины по формулам:
T B H 0,03 0 0,03/ 300мм
|
o |
B H |
0,03 0 |
0,015 / 300мм |
||
|
2 |
2 |
||||
Сопоставляя с условиями задачи видим, что допуски и координаты середин полей допусков установлены верно.
Пример 3. Задача: установить допуски на операционные (линейные) размеры (рис. 4.435,а), обеспечивающие получение размеров 50±0,1 и 60-0,3 детали. Деталь изготовляется по следующему маршруту.
Операция 1. Подрезка торцов и зацентровка заготовки валика на фрезерно-центровальном станке (рис. 4.43,б).
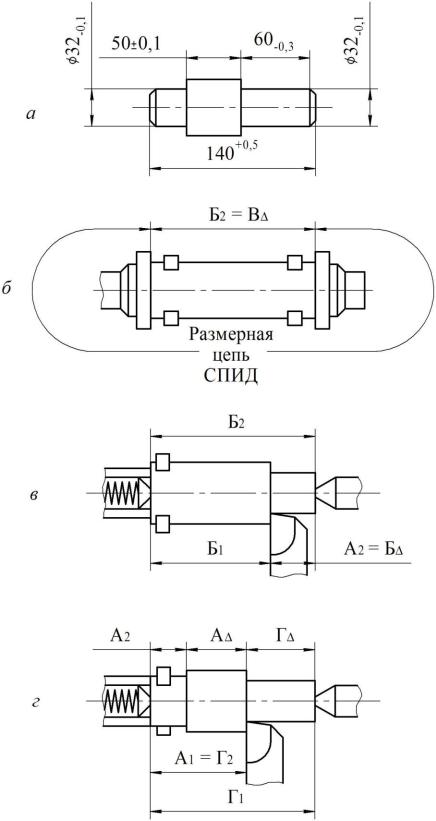
Рис. 4.43.
Операция 2. Токарная обработка валика с одного конца с установкой валика в центрах (передний центр–плавающий, рис. 4.43,в).
Операция 3. Токарная обработка валика с другого конца при аналогичной схеме базирования
(рис. 4.43,г).
В спроектированном технологическом процессе размер 50 мм окончательно получается на третьей операции и является замыкающим звеном размерной цепи А:
А=А1-А2
вкоторой звено А2 – размер, полученный на второй операции. Рассматривая его как замыкающее звено размерной цепи Б, имеем
А2=Б =-Б1+Б2
Б2 – размер, полученный на первой операции, где он является замыкающим звеном размерной цепи В системы СПИД (Б2 = В ). Размер 60 мм также получается на третьей операции. На рис. 4.5, г видно, что он является замыкающим звеном размерной цепи Г:
Г =Г1-Г2
и образуется одновременно с размером А . Так как Г1 — В , а Г2=А1 то
Г =В – А1
Таким образом, для обеспечения требуемой точности размеров 50 и 60 мм необходимо рассмотреть систему параллельно связанных размерных цепей:
А =А1-А2
А2=Б =-Б1+Б2
Г =В – А1
Учитывая, что более жесткие требования предъявлены к точности размера 50, установим допуски на звенья размерных цепей А и Б, применив метод неполной взаимозаменяемости и, приняв
|
2 |
1/ 9; |
||||||||
|
i |
|||||||||
|
Р 0,27%; |
|||||||||
|
(t 0) |
|||||||||
|
Исходя из значения ТА =0,2 мм, зададим ТAI =0,1 мм и ТА2 =0,17 мм. |
|||||||||
|
Проверка: |
|||||||||
|
m 1 |
1 |
||||||||
|
Т А t |
Ai2 2AiTAi2 |
3 |
(0,12 |
0,172 ) 0,2мм |
|||||
|
i 1 |
9 |
Поскольку ТБ =ТА2 =0,17 мм, установим ТБ1=0,1 мм и ТБ2=0,14 мм.
Проверка:
Т Б 3
19 (0,12 0,142 ) 0,17мм
Из ранее сказанного следует, что ТБ =ТА2 =0,14 мм.
Проверим теперь, обеспечивают ли установленные допуски требуемую точность размера Г
Т Г t 
i2 (TB2 TA21 ) 3
19 (0,142 0,12 ) 0,17мм
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Метод полной взаимозаменяемости
1. В зависимости от служебного назначения машины или ее механизмов устанавливают на исходные звенья каждой из размерных цепей требуемые величины номинальных размеров и величины допусков на расстояния и повороты, форму и чистоту поверхностей, ограничивающих исходное звено.
2. По величине номинального размера исходного звена рассчитывают величины номиналов всех звеньев размерной цепи по формулам (20), (21).
3. Исходя из величины координаты середины поля допуска, определяют среднюю величину координат середин полей допусков всех звеньев размерной цепи. Среднюю величину корректируют для использования стандартных величин и учета конструктивных особенностей и размеров соответствующих деталей, пользуясь формулами (26) и (27).
4. Исходя из величины допусков исходного звена, по формуле (28) рассчитывают среднюю величину допусков всех звеньев размерной цепи. Если порядок этой величины окажется экономически приемлемым для решения размерной цепи методом полной взаимозаменяемости, ее корректируют в ту или другую сторону в зависимости от конструктивных особенностей и размеров деталей, а также и для использования стандартных величин допусков и посадок. Правильность установленных таким образом величин допусков проверяют по формуле (15).
Величины допусков на общие звенья берутся наименьшими из всех полученных в результате независимого расчета всех параллельно-связанных размерных цепей.
5. Установленные в результате расчета и корректировки величины допусков записывают в виде предельных отклонений у соответствующих номинальных размеров с учетом координат середин полей допусков.
6. Производят контрольный расчет правильности установленных величин номиналов и предельных значений по формулам (1), (2), (7) и (8) (расчет на максимум и минимум).
7. Проверенные величины номинальных размеров и предельных отклонений вносят в рабочие чертежи. 8. В случае, если средняя величина допусков, рассчитанная по формуле (28), окажется экономически непригодной или практически неосуществимой, от решения размерной цепи методом полной взаимозаменяемости следует отказаться.
Метод неполной (ограниченной) взаимозаменяемости (с использованием вероятностных расчетов)
1. Производят расчет величины номинальных размеров и середин полей допусков так же, как указано в пп. 1, 2, 3 метода полной взаимозаменяемости.
2. Производят расчет и корректировку величин допусков по методике, указанной выше, с той разницей, что для определения средней величины допуска используют формулу (29). Величина t имеет в зависимости от принятого процента риска Р следующие значения:
Значение величины λ’ выбирают в зависимости от возможного1 закона распределения размеров каждого из звеньев: а) при распределении по закону равной вероятности (равномерное распределение) λ’ = 1/3;
б) при распределении по закону равнобедренного треугольника λ’ = 1/8; в) при распределении по нормальному или близкому к нему закону λ’ =1/9.
Значением λ’ = 1/8 следует пользоваться и в тех случаях, когда возможный закон распределения размера звена неизвестен. Точность результатов расчета по формуле (29) повышается с увеличением количества звеньев в размерной цепи. Наименьшее значение m, при котором еще можно пользоваться формулой (29) с достаточным для практики приближением, может быть принято в зависимости от величины λ’:
3. Установленные в результате расчета и корректировки величины допусков записывают в виде предельных отклонений у соответствующих номинальных размеров с учетом координат середин полей допусков.
4. Производят контрольный расчет правильности установленных величин номиналов и предельных отклонений.
5. При решении нескольких размерных цепей одной и той же машины или ее механизмов методом неполной взаимозаменяемости общий процент риска подсчитывается по формуле
где q1, q2, … , qs— процент риска (в долях единицы) первой, второй, . . , 5-й размерной цепи.
Метод групповой взаимозаменяемости (сборки с предварительной сортировкой деталей)
1. Производят расчет величин номиналов так же, как и в методе полной взаимозаменяемости.
2. Величины расчетных допусков, найденные по формуле (28), берут равными для всех звеньев размерной цепи и увеличивают в п раз для получения экономичных величин производственных допусков, т. е. принимают б’= nб. При этом следует ограничиваться наименьшей возможной величиной п, так как при обработке деталей необходимо допуски на относительный поворот поверхностей, их форму и чистоту выдержать в пределах расчетных величин.
3. Полученные величины производственных допусков в виде предельных отклонений проставляют на чертежах у соответствующих номинальных размеров с учетом координат середин полей допусков.
Метод пригонки
1. Производят расчет величин номиналов и середин полей допусков аналогично тому, как было указано для метода полной взаимозаменяемости.
2. Выбирают компенсирующее звено, не являющееся общим нескольким размерным цепям (чтобы не вносить ошибки во все пара/тлельно связанные размерные цепи), и звено, пригонка которого при прочих равных условиях наименее трудоемка и наиболее удобна.
3. Рассчитывают среднюю величину допуска по формуле (28). Путем соответствующей корректировки устанавливают экономичные величины допусков на все звенья.
4. Подсчитывают наибольшую возможную величину компенсации по формуле (33), в которой бΔ’—возможная величина допуска замыкающего звена при экономичных величинах допусков на все звенья: бΔ — требуемая величина допуска замыкающего звена.
5. Для обеспечения пригонки у всех размерных цепей за счет выбранного компенсирующего звена изменяют номинальную величину последнего в соответствии с системой расположения поля допуска исходного звена.
Величины измененного номинала компенсирующего звена определяют по таблице 4. В ней даны схемы элементарно простой трехзвенной цепи, к которой может быть приведена любая многозвенная размерная цепь путем суммирования отдельно увеличивающих и уменьшающих звеньев и замены каждой из этих сумм одним суммарным звеном.
Сначала по таблице 4 находят систему расположения поля допуска у исходного звена (по вертикали), затем в зависимости от того, является ли выбранное компенсирующее звено увеличивающим или уменьшающим, находят соответствующий горизонтальный ряд. В пересечении находятся схема и расчетная формула для определения номинала компенсирующего звена. Величины установленных допусков наносят на чертеж в виде предельных отклонений с учетом координат середин полей допусков.
Метод регулировки
1. Производят расчет величин номиналов и середин полей допусков так же, как и при методе полной взаимозаменяемости.
2. Выбирают компенсирующее звено, которое не должно являться общим нескольким размерным цепям, с таким расчетом, чтобы изменение его величины регулировкой подвижного или установкой неподвижного компенсатора было наиболее простым и экономичным.
3. Рассчитывают среднюю величину допуска бср по формуле (28) и путем корректировки устанавливают экономичные величины допусков на все звенья.
4. Подсчитывают наибольшую возможную величину бк, компенсации.
5. При наличии в размерной цепи звеньев, величина которых может меняться в процессе эксплуатации машин, определяют величину б изм этих изменений для последующей компенсации.
6. Рассчитывают максимальную величину необходимого перемещения подвижного компенсатора или наибольшую возможную величину компенсации’ при неподвижном компенсаторе по формуле
Рисунок 41
7. Разрабатывают конструкцию периодически или непрерывно автоматически действующего подвижного или неподвижного компенсатора.
8. При включении в размерную цепь неподвижного компенсатора рассчитывают необходимое количество ступеней размеров его по формуле (35).
9. Устанавливают размеры и подсчитывают количество необходимых не
подвижных компенсаторов в каждой из групп. При этом, если характер распределения величины компенсирующего звена неизвестен, количество неподвижных компенсаторов в каждой из групп — принимают одинаковым.
При известном характере распределения или когда его можно предвидеть (например по характеру распределения подобных звеньев). количество неподвижных компенсаторов в каждой из групп принимают пропорциональным участкам площади под кривой распределения между соответствующими ступенями размеров (рисунок 41).
В тех случаях, когда в качестве неподвижного компенсатора используется набор прокладок, их количество определяют по формуле (35).
10. Рассчитанные величины, допусков проставляют на чертежах у соответствующих номиналов с учетом координат середин долей допусков. Выполнение детально »(и л и деталями) функции компенсатора отмечается на чертеже соответствующей надписью. Иногда разрабатывают специальные, схемы, на которых указываются все компенсаторы, предусмотренные конструкцией, последовательность и направление их возможных перемещений (рисунок 42).
Рисунок 42. Зубострогальный полуавтомат для нарезания конических зубчатых колес:
1— компенсатор, обеспечивающий согласование осн развода суппортов с осью шпинделя по высоте;
2 — компенсатор для установки расстояния от центра до зеркала резцовой бабки 210 мм;
3 — компенсатор для устранения зазора между кронштейном резцовой бабки и прижимной шайбой;
4 — компенсатор, обеспечивающий правильное зацепление рейки, закрепленной на плите, с шестерней на делительной бабке;
5 — компенсатор, обеспечивающий одновременное соединение гидро- цилиндра с плитой и с кронштейном делительной бабки;
6 — станина;
7 — коробка подач;
8 — резцовая бабка;
9 — кронштейн резцовой бабки;
10 — кронштейн плиты;
11 — шаблон;
12— делительная бабка;
13 — каретка делительной бабки;
14 — кронштейн;
15 — гидроцилиндр.
Расчетные формулы.
Построение и расчет размерных цепей
Основные термины и определения
Рассмотрим фрагмент конструкции (рис. 4.1).
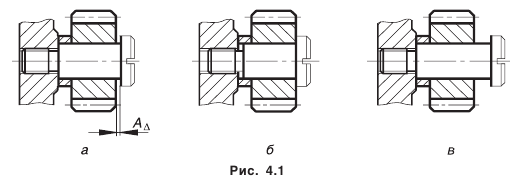
Для свободного вращения зубчатого колеса на оси необходим зазор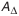 
. Величина получается автоматически при сопряжении деталей, контуры которых выделены. Если размеры их выполнены неверно (рис. 4.1 6, в), то либо зазора не будет вовсе, либо он будет слишком большой, что сделает невозможным нормальное функционирование узла.
Установим те размеры деталей, которые при сборке автоматически создадут необходимый зазор (рис. 4.2). Обозначив размеры деталей, которые влияют на зазор , мы тем самым построим размерную цепь.
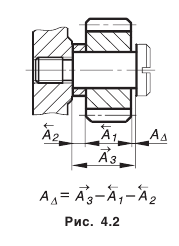
Размерной цепью называется совокупность размеров, непосредственно участвующих в решении поставленной задачи и образующих замкнутый контур (ГОСТ 16319-80).
По виду задач, в решении которых участвуют цепи, они делятся на конструкторские, технологические и измерительные.
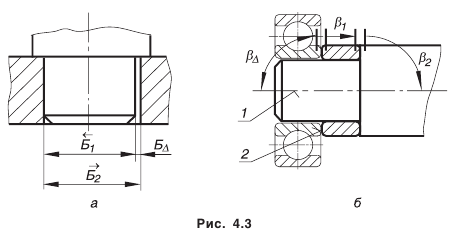
Конструкторские размерные цепи решают задачу по обеспечению точности при конструировании. Они устанавливают связь размеров детали в изделии. На рис. 4.3 приведены примеры сборочных размерных цепей.
На рис. 4.3, а приведена элементарная сборочная размерная цепь, решающая задачу обеспечения точности сопряжения двух деталей. На рис 4.3, 6 тоже показана сборочная цепь, которая решает задачу обеспечения перпендикулярности поверхности 2 к оси 1, необходимой для базирования подшипника качения.
Технологические размерные цепи решают задачу по обеспечению точности при изготовлении машин. Они устанавливают связь размеров деталей на разных этапах технологического процесса. На рис. 4.4, а изображена деталь с размерами, которые следует выдержать при изготовлении. Последовательность получения размеров приведена на рис. 4.4, 6, в, г. На основании предложенного маршрута обработки построена технологическая размерная цепь (см. рис 4.4, д). При обработке детали выдерживаются размеры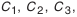 
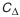
а размер 
получается автоматически.
Измерительные размерные цепи решают задачу обеспечения точности при измерении. Они устанавливают связь между звеньями, которые влияют на точность измерения.
Размеры, образующие размерную цепь, называются звеньями. В зависимости от расположения звеньев, цепи делятся на плоские (звенья расположены в одной или параллельных плоскостях) и пространственные. В зависимости от вида звеньев различают линейные размерные цепи (звеньями являются линейные размеры, рис. 4.2, 4.3, а) и угловые (рис. 4.3, б). Звенья линейной размерной цепи обозначают какой-либо одной прописной буквой русского алфавита с соответствующим числовым индексом, звенья угловых цепей — строчной буквой греческого алфавита.
Любая размерная цепь состоит из составляющих звеньев и одного замыкающего. Замыкающее звено (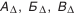
и т. д.) — то звено, которое непосредственно не выдерживается, а получается в результате выполнения размеров составляющих звеньев.
Составляющие звенья делятся на увеличивающие и уменьшающие. Увеличивающие звенья
— те, с увеличением которых замыкающее звено увеличивается, а уменьшающие
— те, с увеличением которых замыкающее звено уменьшается. При правильном определении увеличивающих и уменьшающих звеньев стрелки над буквами должны указывать движение в одном направлении по замкнутому контуру размерной цепи.
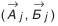
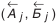
Принципы построения конструкторских размерных цепей
Перед тем как построить размерную цепь, следует выявить замыкающее звено, которое, допустим, определяет нормальное функционирование механизма. Размер или предельное отклонение замыкающего звена назначают или рассчитывают исходя из условий работы и (или) требуемой точности.
Например, размер и предельные отклонения 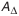(см. рис. 4.2) принимаются такими, которые обеспечивали бы свободное вращение зубчатого колеса при минимальном возможном смещении его вдоль оси. Несовпадение вершины делительного конуса конической шестерни с осью вращения конического колеса (рис. 4.7, а, б) определяется степенью точности зубчатых колес, а его предельные значения находятся по соответствующему стандарту.
В курсовом проекте замыкающее звено и допуск на него уже заданы. Надо только установить, между какими деталями стоит размер замыкающего звена, а затем связать эти детали цепью размеров.
Например, на рис. 4.5, б размер замыкающего звена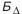 
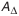
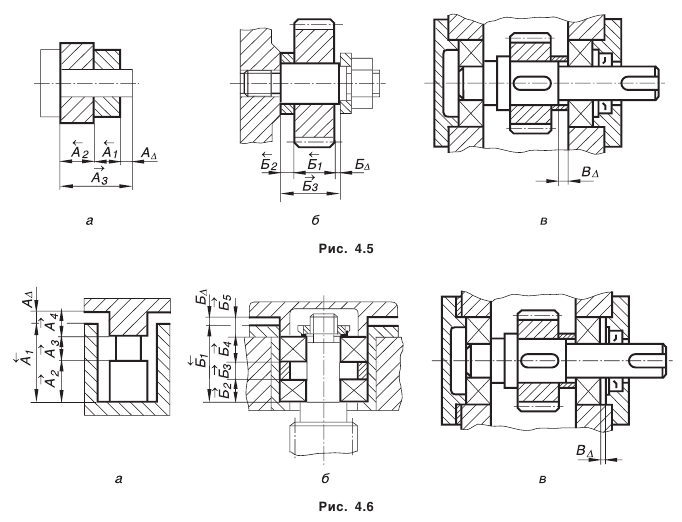
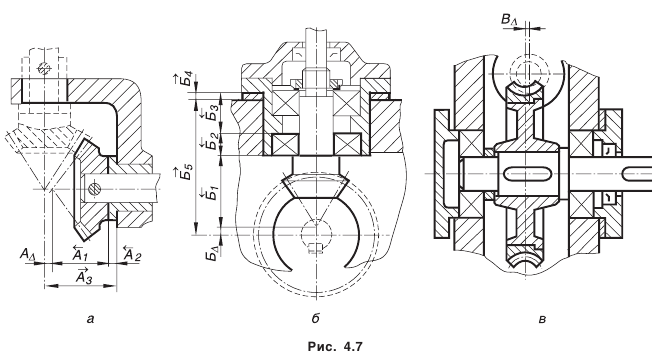
стоит между осью и торцом зубчатого колеса; на рис. 4.7, а стоит между осью отверстия в корпусе и вершиной делительного конуса конического колеса и т. д.
Рассмотрим наиболее типичные варианты сборочных размерных цепей’. Первый вид размерных цепей приведен на рис. 4.5, второй — на рис. 4.6, третий — на рис. 4.7.
При построении размерных цепей следует руководствоваться их основными свойствами:
• цепь должна быть замкнута;
• размер любого звена сборочной цепи должен относиться к элементам одной и той же детали; исключением является замыкающее звено, которое всегда соединяет элементы разных деталей;
• цепь должна быть проведена наикратчайшим способом, т. е. деталь своими элементами должна входить в размерную цепь только один раз.
Основные соотношения размерных цепей
Размерная цепь всегда замкнута. На основании этого свойства существует зависимость, которая связывает номинальные размеры звеньев. Для плоских размерных цепей с номинальными звеньями она имеет следующий вид:
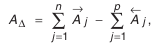
где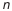 
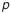
и 
— число увеличивающих и уменьшающих звеньев в размерной цепи соответственно.
Для определения зависимости, которая связывает допуски звеньев в размерной цепи, найдем вначале наибольшее значение замыкающего звена:
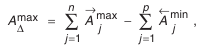
затем наименьшее значение:
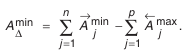
Вычтем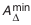 
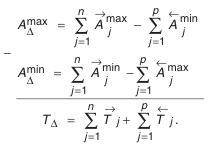
из 
Окончательно получим:
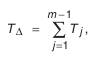
где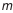 
— количество звеньев размерной цепи, включая замыкающее звено.
Из формулы (4.2) следует, что разброс размеров замыкающего звена равен сумме разбросов размеров составляющих звеньев. Поэтому, чтобы обеспечить наибольшую точность замыкающего звена, размерная цепь должна состоять из возможно меньшего числа звеньев, т. е. необходимо при конструировании машин и проектировании технологических процессов соблюдать принцип наикратчайшей размерной цепи. Аналогичным образом находится верхнее отклонение замыкающего звена:
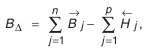
нижнее отклонение:
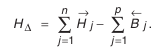
Координата середины поля допуска замыкающего звена рассчитывается следующим образом:
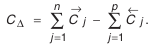
Если известны размеры и поля допусков, составляющих звеньев размерной цепи, то по формулам (4.1 )-(4.5) можно определить все параметры замыкающего звена.
Расчет размерных цепей
Обычно при конструировании возникает необходимость определить параметры составляющих звеньев размерной цепи при известном замыкающем звене. Решением данной задачи может быть большое количество вариантов сочетаний допусков и предельных отклонений составляющих звеньев. лишь бы они удовлетворяли основным соотношениям.
Обычно в прикидочных расчетах пользуются способом равных допусков, т. е.:
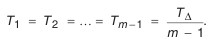
При большой разнице в номинальных размерах составляющих звеньев такой способ является некорректным, так как к большим звеньям будут предъявляться более жесткие требования по точности.
Смысл корректного расчета размерной цепи заключается в том, чтобы допуски на составляющие звеньев размерной цепи были бы одного или двух ближайших квалитетов.
Известно, что допуск есть произведение единицы допуска на коэффициент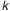 
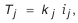
. Это справедливо и для любого звена размерной цепи:
где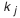 
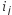
— число единиц допуска (величина постоянная для одного квалитета);
— единица допуска, характеризующая ту часть допуска, которая меняется с изменением размера.
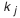
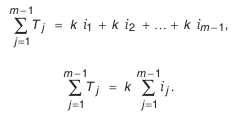
Итак, чтобы добиться одинаковых требований к точности изготовления составляющих звеньев, необходимо, чтобы коэффициенты были бы одинаковыми у всех звеньев. Просуммируем допуски составляющих звеньев размерной цепи:
Подставим полученную зависимость в формулу (4.2):
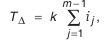
откуда
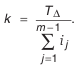
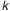
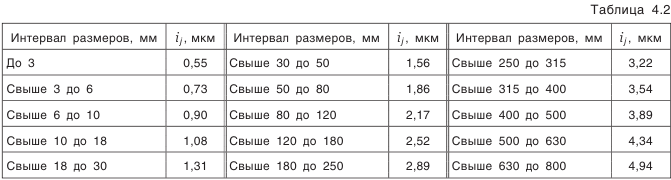
Значение характеризует точность, с которой следует получать все составляющие звенья размерной цепи. Рассчитанное по формуле значение к в общем случае не будет соответствовать строго определенному квалитету, поэтому для назначения допусков на соответствующие звенья выбирают ближайшие квалитеты по табл. 4.1.
Значения единицы допуска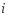 
для размеров до 800 мм приведены в табл. 4.2.
Обеспечить заданную точность замыкающего звена можно несколькими методами (ГОСТ 16320-80).
Метод полной взаимозаменяемости
Метод, при котором требуемая точность замыкающего звена размерной цепи получается при любом сочетании размеров составляющих звеньев. При этом предполагают, что в размерной цепи одновременно могут оказаться все звенья с предельными значениями, причем в любом из двух наиболее неблагоприятных сочетаний (все увеличивающие звенья с верхними предельными размерами, а уменьшающие с нижними, или наоборот). Такой метод расчета, который учитывает эти неблагоприятные сочетания, называется методом расчета на максимум — минимум.
Пример
На рис. П.8.2 изображен фрагмент конструкции, у которой необходимо обеспечить при сборке осевой зазор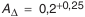 
между торцом крышки и наружным кольцом подшипника. Осевой зазор необходим для компенсации тепловых деформаций деталей, возникающих во время работы узла.
Требуется назначить допуски и отклонения на составляющие звенья для обеспечения 100% годности собираемых механизмов при любом сочетании размеров составляющих звеньев.
Допуски и отклонения на ширину подшипниковых колец и монтажную высоту подшипников качения, входящих в размерную цепь, назначать условно, как и на другие детали.
Решение
- Определение номинальных размеров составляющих звеньев.
Номинальные размеры стандартных деталей, например подшипников качения, находят по соответствующим стандартам. Остальные размеры составляющих звеньев, кроме звена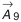 
, определяют непосредственно по чертежу узла.
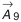
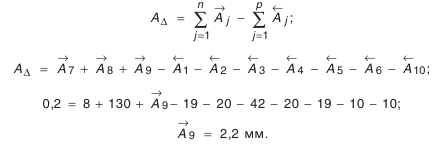
Для нахождения номинального размера воспользуемся зависимостью (4.1):
- Определение средней точности размерной цепи.
По формуле (4.7.) найдем значение :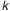
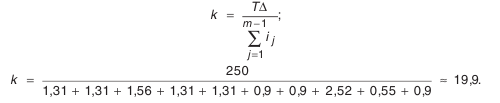
Найденное число единиц допуска лежит в пределах стандартных значений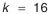 
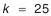
(7-й ква-литет) и 
(8-й квалитет). Отсюда следует, что часть звеньев должна изготавливаться по
7-му квалитету, а часть — по 8-му. При этом следует назначать допуски таким образом, чтобы допуск звена 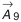лежал в пределах между 7-м и 8-м квалитетами либо соответствовал одному из этих квалитетов.
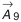
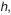
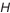
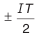
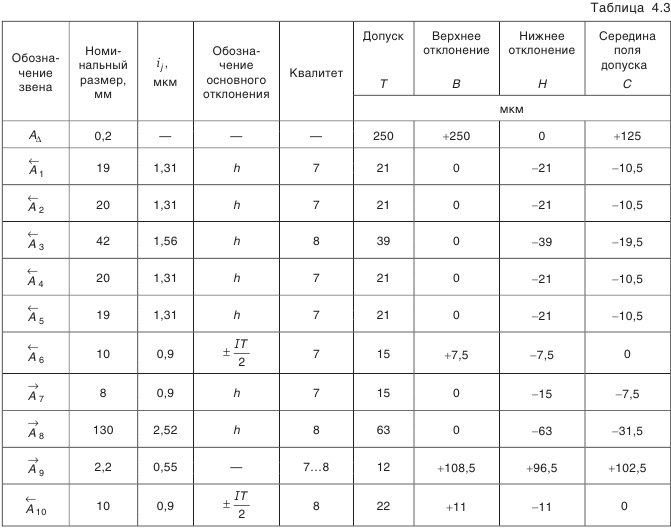
Предельные отклонения на составляющие звенья, кроме , рекомендуется назначать на размеры, относящиеся к валам — по 
относящиеся к отверстиям — по 
; на остальные — 
, т. е. симметричные предельные отклонения. 2
Результаты поэтапных расчетов внесены в табл. 4.3.
- Определение допуска звена
. Воспользуемся формулой (4.2):
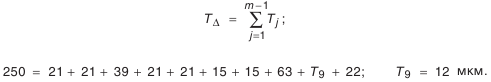
- Определение предельных отклонений звена . Из формулы (4.3):
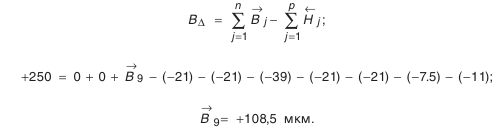
Из формулы (4.4):
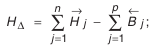
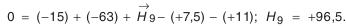
- Проверка.
Чтобы убедиться в правильности проведенных расчетов, воспользуемся зависимостью (4.5) для координат середины полей допусков:
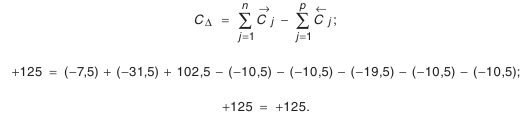
Это говорит о правильности проведенных вычислений.
Метод неполной взаимозаменяемости
Это метод, при котором требуемая точность замыкающего звена размерной цепи получается не при любых сочетаниях, а при ранее обусловленной части сочетаний размеров составляющих звеньев.
Сборка осуществляется без пригонки, регулировки и подбора звеньев.
Метод исходит из предположения, что сочетание действительных размеров составляющих звеньев в изделии носит случайный характер и вероятность того, что все звенья с самыми неблагоприятными сочетаниями окажутся в одном изделии, весьма мала.
Такой метод расчета, который учитывает рассеяние размеров и вероятность их различных сочетаний, называется вероятностным методом расчета. Другими словами, метод допускает малый процент изделий, у которых замыкающее звено выйдет за рамки поля допуска. При этом расширяются допуски составляющих цепь размеров, и тем самым снижается себестоимость изготовления деталей.
Задачей расчета является назначение допусков на составляющие звенья, соответствующих одинаковой степени точности.
Учитывая случайный характер сочетаний действительных размеров деталей в изделии, воспользуемся уравнением для определения дисперсии суммы независимых случайных величин:
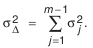
Допустим, что погрешность всех звеньев изменяется по закону нормального распределения, а границы рассеяния размеров для составляющих звеньев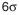 
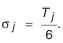
совпадают с границами полей допусков, тогда:
Для замыкающего звена допустим, что:
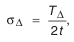
где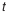 
— коэффициент риска.
Тогда:
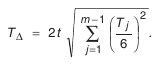
Обозначим через
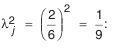
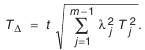
Формула (4.8) устанавливает связь между допуском на замыкающий размер и допусками на составляющие звенья.
Для того чтобы добиться одинаковой точности составляющих звеньев размерной цепи, воспользуемся известной формулой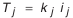 
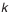
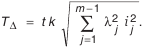
и подставим ее в выражение (4.8). Потребуем, чтобы 
у всех звеньев были одинаковыми, тогда:
Окончательно получим:
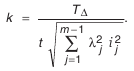
Значение 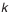характеризует точность, с которой следует изготовить все составляющие звенья размерной цепи при заданных условиях.
При обработке деталей разброс размеров у них может распределяться и не по закону Гаусса. В этом случае можно также воспользоваться формулой (4.9), только при этом следует поставить другие значения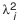 
.
Если предполагается, что рассеяние размеров близко, например, к закону Симпсона, то
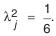
При неизвестном характере рассеяния размеров рекомендуется принимать закон равной вероятности с
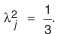
На основании предельных теорем теории вероятностей независимо от характера рассеяния размеров составляющих звеньев разброс размеров замыкающего звена размерной цепи будет близок к закону нормального распределения.
В зависимости от принятого процента риска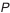 
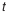
значения выбирают из ряда, приведенного в табл. 4.4.
Пример
Вероятностный метод расчета рассмотрим на том же узле (см. рис. П.8.2). По техническим требованиям необходимо обеспечить осевой зазор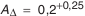 
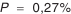
. Требуется назначить допуски и отклонения на составляющие звенья при 
и нормальном законе распределения рассеяния размеров составляющих звеньев (процент брака и закон распределения студент выбирает сам).
Допуски и отклонения на ширину подшипниковых колец и монтажную высоту подшипников качения, входящих в размерную цепь, назначать условно, как и на другие детали.
Решение
- Определение номинальных размеров составляющих звеньев.
Этот пункт решения задачи полностью соответствует первому пункту при расчете на максимум — минимум.
- Определение средней точности размерной цепи. Воспользуемся зависимостью (4.9):
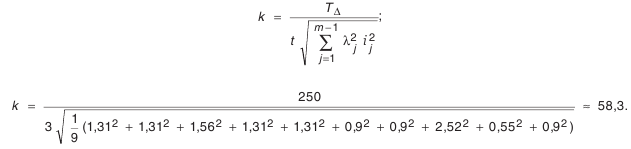
Найденное число единиц допуска лежит ближе к стандартному значению 
, что соответствует 10-му квалитету. Допуски на все звенья назначаются по 10-му квалитету. 3. Определение истинного процента брака. Из формулы (4.8):
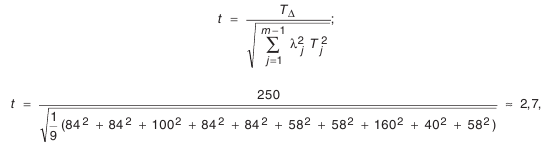
что соответствует 0.693% брака (значения процента брака определяется по табл. П.7.1 приложения).
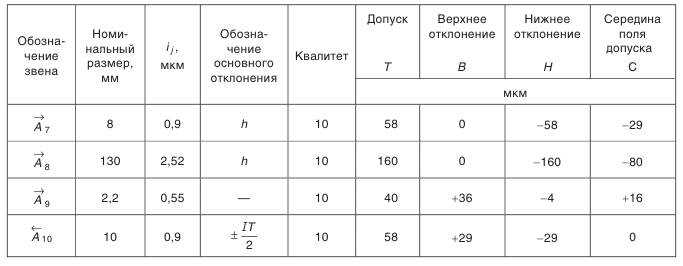
Полагаем, что такой процент брака нас устраивает. Если же количество брака мы сочли бы чрезмерным, тогда необходимо было бы допуски на ряд звеньев назначить по 9-му квалитету. Результаты поэтапных расчетов внесены в табл. 4.5.
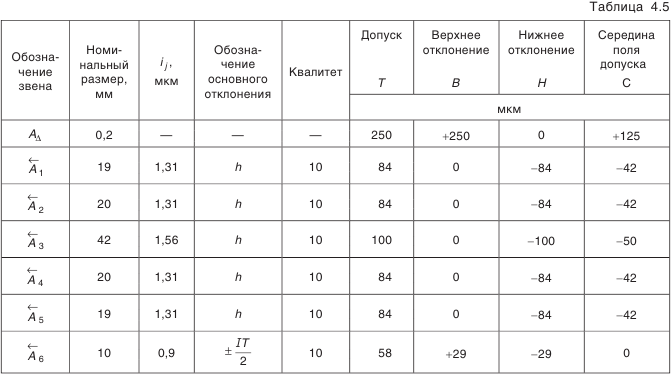
- Определение предельных отклонений звена .
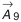
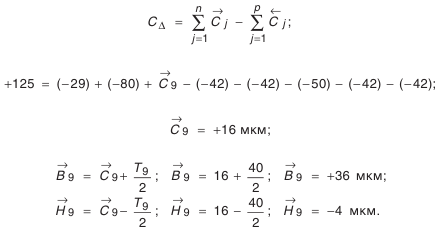
Вначале определим координату середины поля допуска звена по формуле (4.5):
Метод пригонки
Это метод, при котором требуемая точность замыкающего звена размерной цепи достигается изменением размера компенсирующего звена путем снятия с компенсатора слоя металла. Его суть состоит в том, что допуски на составляющие звенья назначаются по экономически приемлемым квалитетам, например по 12-14-му квалитетам. Получающийся после этого у замыкающего звена избыток поля рассеяния при сборке устраняют за счет компенсатора.
Смысл расчета заключается в определении припуска на пригонку, достаточного для компенсации величины превышения предельных значений замыкающего звена и вместе с тем наименьшего для сокращения объема пригоночных работ.
Роль компенсатора обычно выполняет деталь, наиболее доступная при разборке механизма, несложная по конструкции и неточная, например прокладки, шайбы, проставочные кольца и т. п.
Пример
Определить размеры заготовки компенсатора 
для размерной цепи (см. рис. П.8.2, приложение 8). Замыкающее звено должно быть 
.
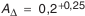
Решение
- Определение номинальных размеров составляющих звеньев.
Этот пункт решения задачи полностью соответствует первому пункту при расчете на максимум — минимум.
- Выбор и назначение допусков на составляющие звенья.
Считаем, что для размеров звеньев экономически приемлемым является 12-й квалитет. Назначаем по этому квалитету допуски на все размеры, кроме допусков на монтажную высоту шариковых радиальных подшипников, которые условно принимаются по табл. П.7.2 приложения 7, и на звено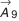 
, которое выбрали в качестве компенсатора.
- Определение наибольшей величины компенсации. По формуле (4.2):
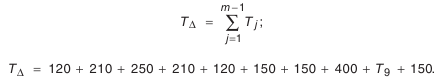
Нетрудно заметить, что сумма допусков составляющих звеньев значительно превосходит допуск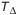 
, т. е. колебание размера замыкающего звена от изделия к изделию значительно увеличится.
Наибольшая расчетная компенсация избыточного колебания размера замыкающего звена:
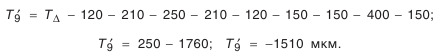
Следовательно, при самом неблагоприятном сочетании размеров надо с компенсатора снять слой материала толщиной 1,51 мм, чтобы замыкающее звено попало в предписанные пределы. Результаты расчетов представлены в табл. 4.6.
- Определение предельных размеров компенсатора звена .
Вначале определим координату середины поля допуска звена :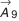
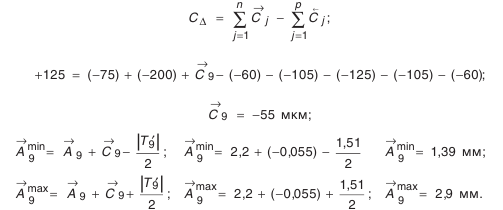
- Определение размера заготовки компенсатора.
Исполнительный размер заготовки компенсатора определяется его наибольшей величиной, так как в прочих случаях он будет подгоняться.
Для изготовления компенсатора на него надо назначить приемлемый допуск, например, по тому же 12-му квалитету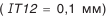 
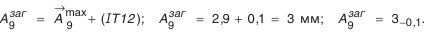
, но так, чтобы его наименьший размер был не менее 2,9 мм:
Метод регулирования с применением неподвижного компенсатора
Это метод, при котором требуемая точность замыкающего звена размерной цепи достигается изменением компенсирующего звена без снятия слоя металла.
Его суть состоит в том, что избыток поля рассеивания замыкающего звена устраняют путем подбора компенсатора из некоторого количества компенсаторов, заранее изготовленных с различными размерами.
Смысл расчета заключается в определении наименьшего количества компенсаторов в комплекте.
Пример
Определить размеры компенсационных прокладок в комплекте для размерной цепи (см. рис. П.8.2, приложение 8). Замыкающее звено должно быть
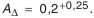
Решение
Прежним порядком (см. метод пригонки) устанавливаем номинальные размеры и назначаем допуски на составляющие звенья размерной цепи. Рассчитываем величину компенсации
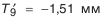
и наименьший размер компенсатора в комплекте
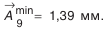
- Определение числа компенсаторов в комплекте.
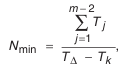
где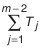 
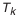
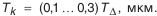
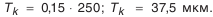
— сумма допусков всех составляющих звеньев без допусков на компенсатор; 
— допуск на отдельный компенсатор в комплекте. Допуск на отдельный компенсатор выбирается в пределах:
Принимаем
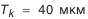
(10-й квалитет);
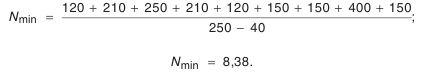
Найденное число компенсаторов в комплекте следует всегда округлять в бблыиую сторону, так как по формуле (4.10) определяется наименьшее число компенсаторов.
Принимаем:
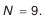
- Величина ступени компенсации.
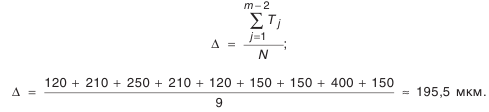
- Размеры компенсаторов в комплекте.
Эта лекция взята со страницы лекций по допускам и посадкам:
Допуски и посадки: ГОСТы и особенности применения
Возможно вам будут полезны эти страницы:
