В этом уроке будем учиться строить эпюры для балок, работающих на поперечный изгиб — эпюры поперечных сил и изгибающих моментов. Важно уметь правильно построить и проанализировать эти эпюры, потому что большинство современных инженерных сооружений состоят из элементов, которые работают на изгиб.
В статье рассмотрим 2 примера: один попроще — консольная балка, загруженная сосредоточенными силами и моментом, другой посложнее — двухопорная балка, загруженная распределённой нагрузкой.
Чтобы освоить материал этого урока, уже нужно знать, как определяются опорные реакции. Умеешь — отлично, но если же нет, то можешь изучить этот урок.
Подробно рассматривать в этом уроке нахождения реакций не будем, я буду приводить только их расчёт.
Поперечные силы и изгибающие моменты
При поперечном изгибе, в поперечных сечениях балки, возникает два внутренних силовых фактора (ВСФ) – поперечная сила (Q) и изгибающий момент (Mизг).


Наша задача, научиться определять их и строить эпюры. Чтобы потом, используя полученные эпюры, можно было проводить различные расчёты. Например, подбирать размеры поперечных сечений балки или проверять прочность балки, если эти размеры уже заданы и т. д.
Поперечные силы и изгибающие моменты определяются с помощью метода сечений. Когда балка мысленно рассекается на две части. Затем действие частей балки друг на друга заменяется внутренними силовыми факторами (ВСФ) – поперечными силами и изгибающими моментами. Потом путём рассмотрения равновесия одной из частей находятся ВСФ.
Если пока не очень понятно — это нормально, когда начнём это всё делать на практике, ты обязательно всё поймёшь!
Обозначения поперечных сил и изгибающих моментов
Теперь поговорим по поводу обозначений для поперечных сил и изгибающих моментов. Как правило, задачи в сопромате, и механике в целом, решаются относительно каких-то координатных осей. А поперечные силы и изгибающие моменты, имеют индексы в зависимости от выбранной системы координат.
Например, если выбрать следующие обозначения для координатных осей:

То, поперечная сила, будет обозначаться, как Qy (параллельна оси y), а изгибающий момент, как Mx (поворачивает относительно оси x). Это наиболее частый вариант. Однако, можно встретить обозначения – Qy, Mz или Qz, Mx. Самые ленивые, предпочитают подписывать данные величины, как просто Q и M. Как видишь, здесь всё зависит от предпочтений твоего преподавателя. Чтобы изучая этот урок, ты не привыкал (- а) к каким-то индексам, т. к. твой преподаватель тебя всё равно будет учить по-своему, я решил использовать в статье для поперечной силы, просто букву – Q, а для изгибающего момента – Mизг. Такое обозначение изгибающего момента, тоже используется часто, а сам индекс «изг» нужен, чтобы не путать внутренний – изгибающий момент, с внешними моментами, которые почти всегда подписываются просто буквой – M.
Расчётная схема балки
Также нужно понимать, что когда мы рассчитываем поперечные силы и изгибающие моменты, мы считаем их непросто для какой-то линии:

А подразумеваем, что мы рассчитываем некоторый элемент конструкции — балку, которая обязательно имеет некоторую форму, либо для которой впоследствии будет рассчитана эта форма, в зависимости от целей расчёта.
К примеру, балка может иметь прямоугольное поперечное сечение:

Если в расчётах эпюр при растяжении (сжатии) или кручении, форма стержня указывалась явно, и в этом был определённый смысл, так как те стержня имели ступенчатую форму – разную жёсткость на участках. То здесь, как правило, балки имеют одинаковое сечение, по всей длине, поэтому для экономии времени, балку показывают в виде такой линии. Затем, после построения эпюр, традиционно, для балки либо подбирается поперечное сечение из условия прочности, либо проверяется прочность уже заданного сечения.
Правила знаков для поперечных сил и изгибающих моментов
В этом разделе поговорим о правилах знаков для поперечных сил и изгибающих моментов. Для примера возьмём самую простую расчётную схему — консольную балку, загруженную сосредоточенной силой (F).
Расчётная схема

Предположим, что нужно определить поперечную силу и изгибающий момент в каком-то поперечном сечении. Пока не будем строить никаких эпюр, а просто поставим перед собой простейшую задачу — рассчитать внутренние силовые факторы (Q и Мизг) для одного, конкретного сечения. Например, рассмотрим сечение в заделке (А).
Чтобы вычислить внутренние силовые факторы для этого сечения, нужно учесть всю внешнюю нагрузку, либо справа от сечения, либо слева. Если учитывать нагрузку справа — нужно учесть силу F, а если учитывать нагрузку слева — нужно учесть тогда реакции в заделке. Чтобы не вычислять реакции, пойдём по короткому пути и учтём всю нагрузку — справа.
Правило знаков для поперечных сил
Поперечная сила в сечении будет равна алгебраической сумме всех внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.
А знаки внешних сил определяются следующим образом — если внешняя сила, относительно рассматриваемого сечения, стремится повернуть:
• ПО часовой стрелке, то её нужно учесть с «плюсом»;

• ПРОТИВ часовой стрелки — учитываем её с «минусом».

Таким образом, для нашего случая, поперечная сила в сечении A будет равна:
Правило знаков для изгибающих моментов
Изгибающий момент в сечении будет равен алгебраической сумме всех моментов внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.
Перед тем как поговорить о правилах знаков для изгибающих моментов. Необходимо понять ещё одну особенность — когда на балку действует какая-то внешняя нагрузка, балка деформируется. При деформации балки принято различать «верхние волокна» и «нижние волокна», относительно линии (нейтральной оси), проходящей через центр тяжести поперечного сечения балки.

Одни волокна при поперечном изгибе, будут растягиваться, а другие сжиматься.

В нашем случае, «верхние волокна», как видишь, будут растянуты, а нижние – сжаты.
На основании этой особенности, часто используется следующее правило для изгибающих моментов — если момент силы стремится растянуть:
• верхние волокна, то учитываем его с «минусом»;

• нижние волокна, то нужно учесть его с «плюсом».

Не забываем, что мы ведём расчёт моментов, поэтому все силы нужно умножать на соответствующие плечи.
Таким образом, в нашем случае, изгибающий момент в сечении A будет равен:
Если на балку действуют сосредоточенные моменты, то правило знаков аналогичное:


Сосредоточенные моменты, конечно, уже не нужно ни на что умножать. Например, для верхней схемы, изгибающий момент в сечении A будет равен:
Как построить эпюры поперечных сил и изгибающих моментов ?
В пределах участков, и эпюра Q и эпюра M меняются по определённому закону. Границами участков являются точки приложения сил, моментов, а также начало и конец распределённой нагрузки (будем рассматривать во второй задаче). Поэтому, чтобы построить эпюры в пределах участка, сначала необходимо написать уравнения, которые будут описывать изменение поперечных сил и изгибающих моментов в пределах участка. А затем, подставляя в уравнения координаты начала и конца участка, получить значения на эпюрах в характерных точках, и построить эпюры на участке. Рассчитав таким образом все участки, можно построить эпюры для балки.
Чувствую, опять перегрузил тебя информацией…давай лучше, наконец, посмотрим, как это всё делается на практике 😉
Построение эпюр для консольной балки
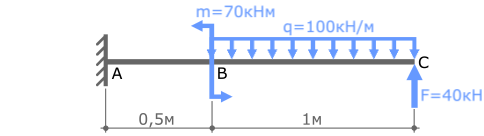
В качестве первого примера, возьмём консольную балку, жёстко закреплённую с левого торца и загруженной следующим образом:

Будем рассчитывать балку справа налево.
Рассмотрим первый участок
Обозначим некоторое сечение 1-1 на расстоянии x1, от свободного торца балки, при этом x1 будет находиться в диапазоне: 0 ≤ x1 ≤ 4м.

Так как расчёт выполняется справа налево, то в уравнениях необходимо учесть всю нагрузку, которая находится правее рассматриваемого сечения. Как видишь, на этом участке действует всего лишь одна сила F. Её и будем учитывать.
Поперечные силы на первом участке
Сила F, относительно сечения 1-1, поворачивает ПО часовой стрелке, поэтому с учётом правила знаков, записываем её с «плюсом»:
Как видишь, поперечная сила будет постоянна на первом участке:
Уже можем отразить это на эпюре поперечных сил:

Изгибающие моменты на первом участке
Теперь запишем уравнение для изгибающих моментов. Сила F растягивает верхние волокна, поэтому с учётом правила знаков, нужно учесть момент силы F со знаком «минус»:
Здесь уже изгибающие моменты будут меняться по линейному закону. Как я уже писал, чтобы построить эпюру изгибающих моментов на участке, нужно вычислить значения на границах участка:

Откладываем полученные значения:

Расчёт второго участка
Переходим ко второму участку. Также будем рассматривать некоторое сечение 2-2, на расстоянии x2 от начала участка (0 ≤ x2 ≤ 6м). Здесь также нужно учесть ВСЮ нагрузку, которая находится справа от сечения 2-2.

Поперечные силы на втором участке
Теперь на участке будут действовать 2 силы (сосредоточенный момент — M, никак не влияет на эпюру поперечных сил), учитываем их с учётом правила знаков:
Теперь можем показать окончательную эпюру поперечных сил:

Изгибающие моменты на втором участке
Для изгибающих моментов, с учётом правила знаков, второе уравнение будет выглядеть следующим образом:
Вычисляем значения на границах второго участка:

Показываем окончательную эпюру изгибащих моментов:

Проверка построенных эпюр
Балку можно рассчитать и слева направо. При этом очевидно, должны получаться те же эпюры. Давай проверим себя и рассчитаем эту балку с другой стороны.
Определение реакций в жёсткой заделке
Первым делом, нам потребуется определить реакции в заделке:

Расчёт эпюр поперечных сил и изгибающих моментов
Рассчитываем все участки теперь слева направо:

Ожидаемо, получили те же эпюры поперечных сил и изгибающих моментов:

Причём не обязательно считать все участки балки только слева направо или справа налево. Можно считать балку с разных сторон:

Такой подход позволяет минимизировать расчёт: когда балка имеет много расчётных участков. Как раз так и будем считать вторую двухопорную балку.
Эпюра моментов со стороны растянутых или сжатых волокон
По построенной эпюре можно явно сказать, какие волокна балки будут растянуты, а какие сжаты. Это очень полезная информация, при проведении прочностных расчётов.
Причем сама эпюра была построенна со стороны растянутых волокон:

Однако, студентов некоторых специальностей учат строить эпюры, с другой стороны – со стороны сжатых волокон:

Как видишь, в первом случае, отрицательные значения на эпюре моментов откладываются выше нулевой линии, а во втором – ниже. При этом правила знаков для расчета эпюр и сами расчёты не меняются. Обычно эпюры «на растянутых волокнах» строят студенты — строители, а эпюры «на сжатых волокнах» строятся студентами машиностроительных специальностей. В конечном счёте с какой стороны ты будешь строить эпюры, будет зависеть от твоего преподавателя, как он учит. В своих уроках я буду строить эпюры моментов со стороны растянутых волокон.
Учёт распределённой нагрузки
Перед тем как пойдём дальше и рассмотрим вторую задачу – двухопорную балку, нужно научиться работать с распределённой нагрузкой.
Давай рассмотрим ещё одну простенькую схему — консольную балку, загруженную распределённой нагрузкой:

Определение поперечной силы и изгибающего момента в сечении A
Чтобы определить поперечную силу в сечении A, первым делом нужно «свернуть» распределённую нагрузку (q) до сосредоточенной силы. Для этого нужно интенсивность нагрузки (q) умножить на длину участка действия нагрузки.
После чего получим силу — ql, приложенную ровно посередине участка, на котором действует распределённая нагрузка:

Тогда поперечная сила QA будет равна:
Изгибающий момент Mизг, A будет равен:

Расчёт эпюр поперечных сил и изгибающих моментов
Для написания уравнений для расчёта эпюр рассмотрим сечение 1-1:

Уравнение для поперечных сил будет следующее:
Рассчитаем значения на эпюре поперечных сил:


Уравнение для изгибающих моментов будет следующее:

Тогда значения на эпюре будут такими:


На участке с распределённой нагрузкой, на эпюре изгибающих моментов всегда будет либо выпуклость, либо вогнутость. Так как эпюра на этом участке будет меняться по квадратичному закону.
Если эпюра моментов откладывается со стороны растянутых волокон, распределённая нагрузка будет направлена «внутрь вогнутости» (выпуклости) эпюры изгибающих моментов:

Если же эпюра моментов откладывается со стороны сжатых волокон, то наоборот:

Построение эпюр для двухопорной балки
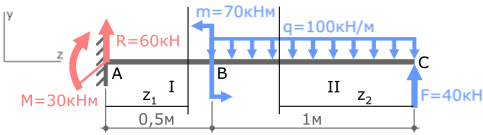
А теперь давай рассмотрим более сложную схему – двухопорную балку, загруженную всеми типами нагрузок:

Определим реакции опор:

Рассчитываем первый участок:
Строим эпюры на первом участке:

Определение экстремума на эпюре моментов
Так как эпюра поперечных сил пересекает нулевую линию на первом участке, это значит, что в месте пересечения — на эпюре изгибающих моментов будет экстремум — точка, в которой эпюра моментов часто имеет наибольшее значение. Это значение, обязательно следует рассчитывать, потому — что экстремумы часто являются не только максимальными значениями в пределах участка, но и для всей балки в целом. Поэтому так важно, вычислять это значение, для дальнейшего проведения прочностных расчётов.
Чтобы найти экстремум, сначала нужно найти координату, где эпюра поперечных сил пересекает нулевую линию. Для этого уравнение для поперечных сил нужно приравнять к нулю:
Отсюда найти значение координаты:

Затем подставить это значение в уравнение для изгибающих моментов:

Теперь можем указать экстремум на эпюре:

Расчет эпюр на остальных участках
Расчёты остальных участков не вижу смысла комментировать, потому что здесь будет применяться всё то, о чём я уже рассказывал по ходу урока. Поэтому просто приведу решение:
Определение экстремума:


Оценка правильности построенных эпюр поперечных сил и изгибающих моментов
И напоследок хочу рассказать как можно проверить себя – оценить правильность построенных эпюр визуально. Собственно так, как проверяют эпюры — преподаватели, ведь они не проверяют у всех студентов каждое уравнение, каждый знак или цифру, т.к. это бы занимало слишком много времени.
Вот несколько признаков, правильно построенных эпюр:
- На эпюре поперечных сил, в местах приложения сосредоточенных сил, должны быть скачки на величину этих сил.
- На эпюре изгибающих моментов, в местах приложения сосредоточенных моментов, должны быть скачки на величину этих моментов.
- Эпюра поперечных сил, на участках без распределённой нагрузки, должна быть постоянна. А на участках, где действует распределённая нагрузка – меняться по линейному закону.
- Эпюра изгибающих моментов, на участках без распределённой нагрузки, должна меняться по линейному закону или быть постоянна (если действуют только сосредоточенные моменты). А на участках, где действует распределённая нагрузка – иметь вогнутость или выпуклость.
Пример решения задачи на построение эпюры внутренних изгибающих моментов Mx для стальной консольной балки нагруженной сосредоточенной силой F, моментом m и равномерно распределенной нагрузкой q.
Задача
Рассмотрим порядок построения эпюры изгибающих моментов Mx для консольной балки закрепленной в жесткой заделке.
Другие примеры решений >
Помощь с решением задач >
Пример решения
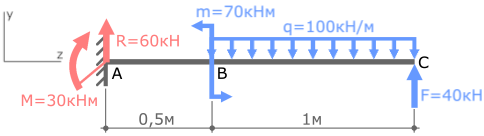
Ранее для данной балки уже были рассмотрены примеры определения опорных реакций и построения эпюры поперечных сил Qy.
Покажем найденные опорные реакции и выбранную систему координат.
Для построения эпюры изгибающих моментов Mx запишем их выражение по каждому силовому участку и рассчитаем их значения на границах участков. При этом воспользуемся методом сечений.
Наш видеоурок построения эпюр внутренних силовых факторов для балки:
Другие видео
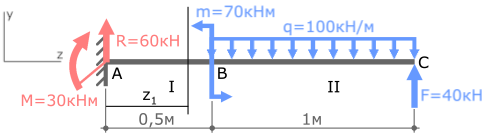
Нумерацию силовых участков балки, сечения и другие вспомогательные обозначения примем из расчета эпюры Qy.
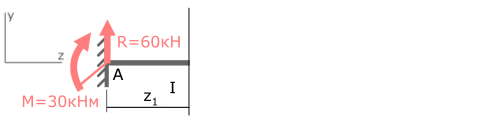
Рассмотрим I силовой участок:
Выбрав левую часть балки, отбросим ненадолго правую, и запишем имеющиеся данные.
I с.у. (AB) 0 ≤ z1≤ 0,5м
Внутренний изгибающий момент в указанном сечении равен сумме всех внешних моментов, воздействующих на рассматриваемую часть балки.
Здесь на момент в рассматриваемом сечении влияют только опорные реакции M и R, то есть сумма моментов состоит из двух слагаемых.
По правилу знаков момент, который стремится сжать верхние слои балки, принимается положительным, следовательно:
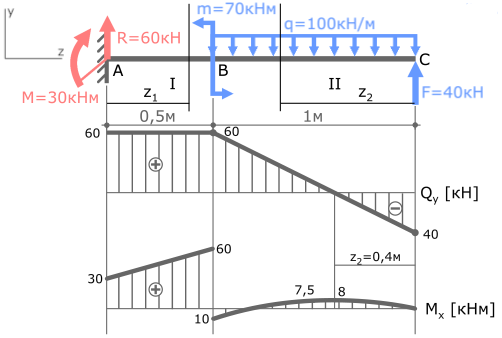
MxI=Σmi=M+R∙z1=30+60z1
В выражении переменная z1 в первой степени, поэтому эпюра Mx на первом участке будет иметь вид прямой линии.
Рассчитаем значения MxI на границах участка, т.е. при z1=0 и при z1=0,5м
MxI (z1=0)=30кНм
MxI (z1=0,5м)=60кНм
Переходим на второй силовой участок:
Рассекаем балку в произвольном месте участка и рассматриваем её правую часть.
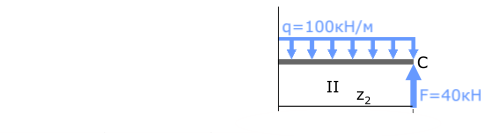
Эта часть балки изгибается силой F и распределенной нагрузкой q.
II с.у. (BC) 0 ≤ z2 ≤ 1м
MxII=Σmi=-q∙z2(z2/2)+F∙z2= -50∙z22+40∙z2
Получено выражение с переменной z2 во второй степени, значит, эпюра Mx на втором участке будет иметь вид параболы.
Видео про построение эпюр:
Другие видео
Для построения параболы требуется как минимум три точки. Этими точками будут значения Mx на границах и в середине II силового участка, то есть при z2=0, z2=1м и z2=0,5м.
MxII(z2=0)=0
MxII(z2=0,5м)=7,5кНм
MxII(z2=1м)= -10кНм
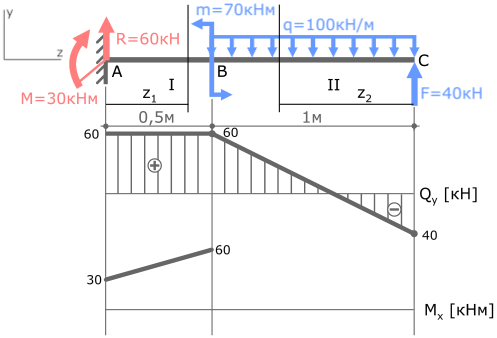
По полученным данным строим эпюру изгибающих моментов Mx (готовую эпюру Qy перенесем из ранее рассмотренной задачи)
I с.у. (AB) 0 ≤ z1 ≤ 0,5м.
MxI=30+60z1 (прямая)
MxI(z1=0)=30кНм
MxI(z1=0,5м)=60кНм
II с.у. (BC) 0 ≤ z2 ≤ 1м
MxII= -50z22+40z2 (парабола)
MxII(z2=0)=0
MxII(z2=0,5м)=7,5кНм
MxII(z2=1м)= -10кНм
Прежде чем соединять отмеченные точки эпюры параболой, обратите внимание на эпюру поперечных сил Qy.
Qy — первая производная от Mx. Поэтому в том месте, где Qy пересекает базовую линию (т.е. Qy=0) на эпюре Mx будет экстремум.
Видео про расчет экстремума эпюры:
Другие видео
Рассчитаем значение экстремума эпюры Mx на II участке балки.
Для этого:
- Выражение QyII приравняем к нулю
QyII=100z2-40=0 - Выразим из него z2
z2=40/100=0,4м - Подставим z2 в выражение для MxII
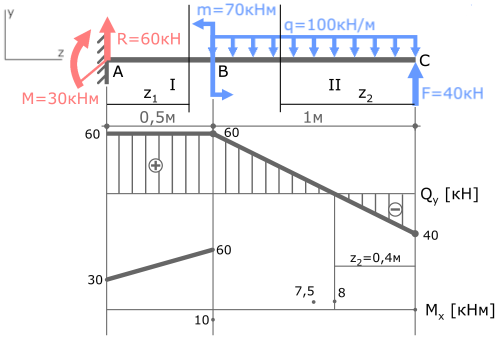
MxIIэкстр(z2=0,4м)= -50∙0,42+40∙0,4=8кНм
Отметив эту точку в области эпюры где Qy=0 соединим ее с тремя другими параболой.
Эпюра изгибающих моментов построена. Проверка эпюры Mx.
Расчеты на прочность >
Другие примеры решения задач >
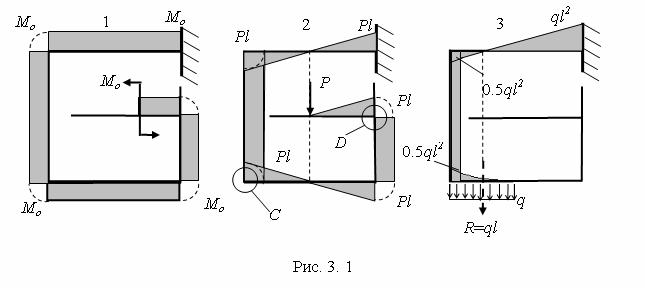
3. ПРАВИЛА ПОСТРОЕНИЯ ЭПЮР ВНУТРЕННИХ УСИЛИЙ M ,Q, N
Процедура построения ординат эпюры M
|
Для построения ординаты эпюры M в каком |
либо сечении стержня |
|
|
необходимо выполнить следующие две операции. |
||
|
1. С помощью уравнения равновесия |
∑M = 0 |
для левой отсеченной |
|
слева |
||
|
части стержневой системы (или ∑M = 0 |
для правой части) подсчитать |
|
|
справа |
численное значение изгибающего момента в сечении.
2. Отложить найденное численное значение в виде ординаты перпендикулярно оси стержня со стороны растянутого волокна стержня.
Численное значение изгибающего момента в сечении равно численному значению алгебраической суммы моментов всех сил, действующих на стержневую систему с любой одной из сторон сечения, взятых относительно точки на оси сечения.
Как устанавливается растянутое волокно в сечении, продемонстрировано на примере консоли ломаного очертания при ее загружении тремя видами нагрузки (рис. 3.1). Ординаты соответствующих трех эпюр M построены на растянутой стороне стержней, образующих консоль.
Признаки правильного вида эпюры M
При указанном правиле построения ординат эпюры M эта эпюра имеет следующие свойства.
44
1.На участке прямого стержня, свободном от нагрузки, эпюра прямолинейна.
2.На участке распределенной нагрузки она очерчена кривой линией, выпуклой в сторону действия нагрузки. Когда нагрузка равномерно распределена, кривая является параболой второй степени.
3.В точке приложения сосредоточенной силы эпюра имеет излом, острие которого направлено в сторону действия силы.
4.В точке приложения сосредоточенного момента эпюра имеет скачок в ординатах, равный величине момента.
5.В сечении, находящемся на границе незагруженного участка стержня и участка, загруженного распределенной нагрузкой, кривая линия эпюры плавно (без излома) переходит в прямолинейную эпюру, которая является касательной
ккриволинейному участку.
Эти свойства используют для контроля построенных эпюр M .
Правило знаков для ординат эпюр M
При построении ординат эпюры M со стороны растянутого волокна стержня вручную, знак ординаты не требовался. Однако при численном расчете на ПК, каждой ординате эпюры M присваивается знак. Используется знак эпюры M и при построении по ней эпюры Q .
В данном учебном пособии приводится правило знаков, принятое для ординат эпюр M в программе SCAD [2 − 5].
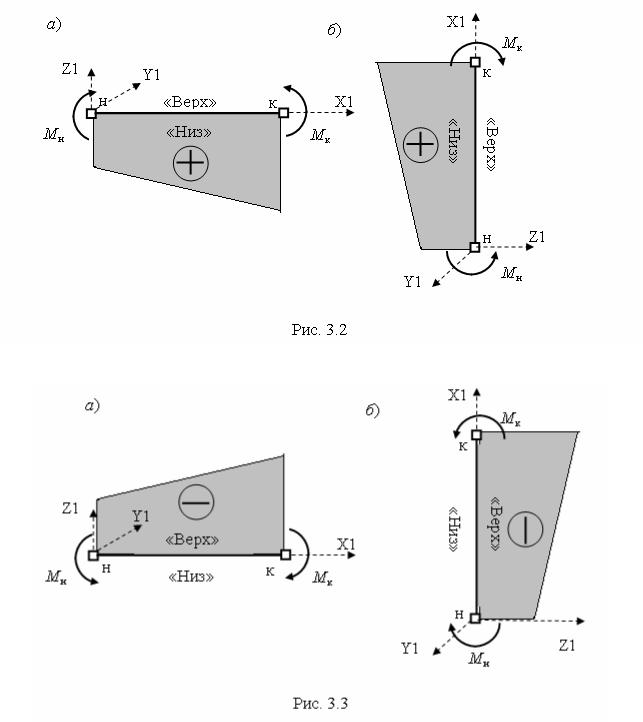
Если растянуто «нижнее» волокно стержня, то ордината откладывается от оси стержня «вниз» и ей присваивается знак «+»
(рис. 3. 2).
Если же растянуто «верхнее» волокно стержня, то ордината откладывается от оси стержня «вверх» и ей присваивается знак « – » (рис. 3.3).
«Нижним» волокном стержня в программе SCAD считается волокно стержневого конечного элемента (КЭ) типа «Стержень плоской рамы», находящееся со стороны отрицательных ординат оси Z1 местной системы осей координат (МСК), а «верхним» – со стороны положительных ординат оси Z1 (см. рис. 3.2, 3.3).
Примечание. При ручном подсчете алгебраической суммы моментов всех сил с одной стороны от сечения для определения изгибающего момента в сечении стержня, рекомендуется сразу ставить знаки слагаемых моментов в соответствии с этим правилом знаков. Тогда ордината изгибающего момента получится со своим знаком в соответствии с принятым правилом и может быть отложена от оси стержня по этому правилу.
45
Построение эпюры М на элементе стержня свободном от нагрузки
Из приведенных выше свойств эпюры M (признаков правильной эпюры)
известно, что если на конечном элементе стержня нет внешней нагрузки, то эпюра изгибающих моментов на нем будет прямолинейной. Для ее построения достаточно вычислить ординаты только в конечных сечениях такого элемента.
Примечание. В программе SCAD для получения ординат изгибающих моментов на КЭ загруженных распределенной нагрузкой «по умолчанию» может быть назначено вычисление для нескольких, например, трех сечений КЭ: в начале (н), в середине (с) и в конце (к) конечных элементов (начальное сечение «н» связано с началом оси X1 в МСК).
46
Тогда с целью сокращения выходных результатов для КЭ без нагрузки в их пределах
в разделе Назначения [2 − 5] на инструментальной панели необходимо нажать кнопку 
На рис. 3.2, 3.3 концевые сечения стержня обозначены узлами « н » и « к » МСК. После назначения для расчета усилий в отмеченных элементах только двух сечений, в программе SCAD в соответствующей таблице усилий [2 − 5] будут выдаваться значения изгибающих моментов M н (M1) и M к (M 2 ) только в узлах «н» (1) и «к» (2) (со своими
знаками в МСК).
При оцифровке ординат эпюры моментов, которая выполняется при нажатии кнопки

Построение эпюры М на элементе стержня при действии по его длине равномерно распределенной нагрузки
Если по всей длине КЭ расположена равномерно распределенная нагрузка, то эпюра изгибающих моментов на нем будет иметь вид параболы с выпуклостью направленной в сторону действия нагрузки.
Примечание. В программе SCAD с помощью процедуры, которая только что была рассмотрена по назначению для вычисления изгибающих моментов только в двух сечениях КЭ, можно назначить вычисление моментов в ряде сечений между узлами « н » и « к » элемента в МСК.
Для приближенного построения параболы достаточно вычислить ординаты эпюры M в трех сечениях КЭ: в начале «н», в середине «с» и в конце «к». В результирующей таблице усилий программы SCAD эти сечения обозначены соответственно 1, 2, 3. В программе SCAD вычисление моментов в указанных сечениях может быть обеспечено по умолчанию. Однако, если по какой-то причине у расчетчика оказались известными только две ординаты эпюры M по концам элемента ( M н и M к), то можно легко вычислить
ординату M c в среднем сечении, применив принцип независимости действия сил.
Пример. Вырежем (по узлам «н» (1) и «к» (3) МСК) из стержневой системы элемент, загруженный равномерно распределенной нагрузкой интенсивностью q (рис. 3.4,а).
Рассмотрим его, как балку на двух опорах, под действием внутренних усилий по концам элемента и распределенной нагрузки (рис. 3.4,б). Добавление указанных трех опорных связей не влияет на усилия в элементе, так как в вырезанном состоянии он находится в равновесии, поэтому в добавленных связях усилия (реакции) будут нулевыми.
Изгибающий момент M c в среднем сечении элемента (см. рис. 3.4, б) можно вычислить как сумму средней ординаты (рис. 3.4, в) линейной эпюры моментов (линии
47
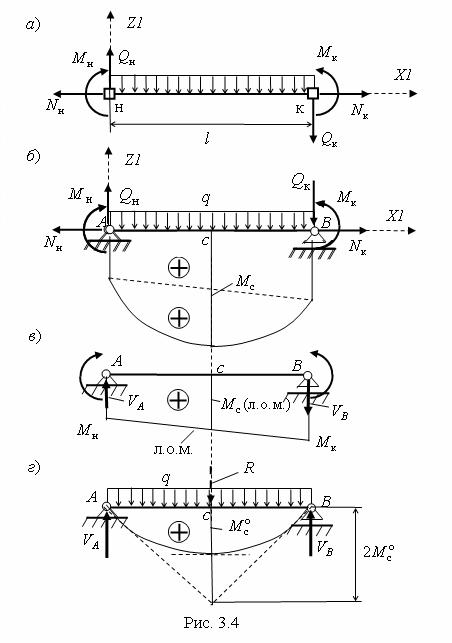
опорных моментов, или ЛОМ) M c (лом) = 0.5(M н +M к ) и средней ординаты Mco = ql2 / 8
параболической эпюры в простой балке на двух опорах от равномерно распределенной нагрузки (рис. 3.4, г):
|
M c =0.5(M н +M к ) +M co . |
(3.1) |
Обе суммируемые ординаты в рассмотренном примере положительны, так как они расположены снизу от оси балки. На рис. 3.5 показан вариант, когда ордината
M c (лом) =0.5(M н +M к ) отрицательна (ордината M co = ql 2 / 8 при указанном направлении нагрузки q положительна). Здесь же приведен графоаналитический способ построения параболической эпюры по трем ее суммарным ординатам ( M н, M с, M к ) и по трем
касательным к параболе в соответствующих концах ординат (отмечены крестиком).
Смысл этого графоаналитического способа будет понятен, если рассмотреть на рис. 3.4, г эпюру M (R) треугольной формы, показанную штриховыми линиями. Эпюра
48
Соседние файлы в предмете Теоретическая механика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Для двухопорной двутавровой балки (двутавр №12 по ГОСТ ГОСТ 8239-89) необходимо определить прогиб в середине пролета (сечение C), используя метод Мора — Верещагина. Данные для расчета указаны на схеме.
Ход выполнения расчета
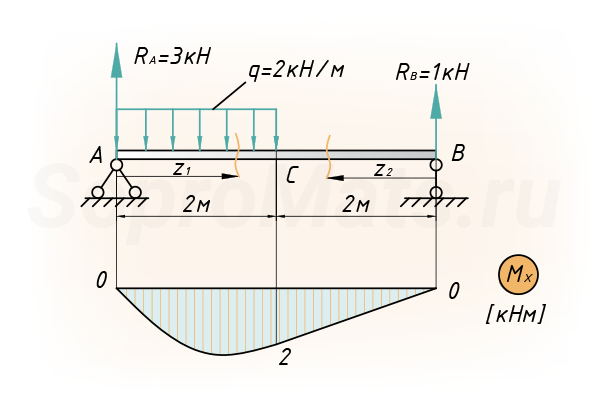
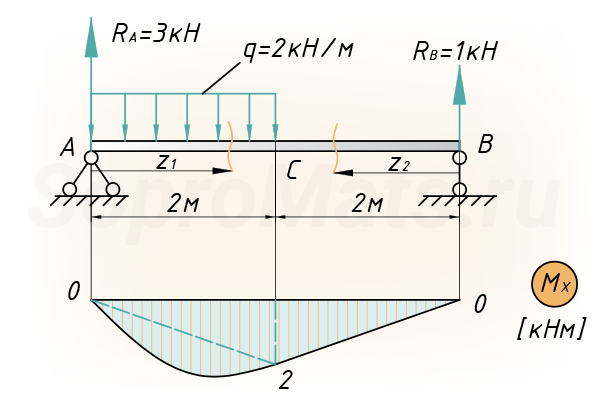
Сначала строим эпюру изгибающих моментов, для рассчитываемой балки:
Расслаиваем эпюру на простейшие фигуры:
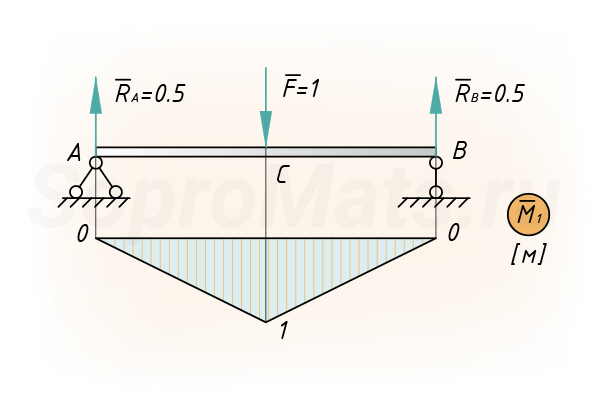
Построение единичной эпюры
Прикладываем единичное усилие по направлению искомого перемещения (в точке С) и строим от этой силы эпюры моментов:
Вычисление прогиба
Вычисляем прогиб сечения C по методу Мора — Верещагина (слева направо):
[ { V }_{ C }=frac { 1 }{ E{ I }_{ x } } (frac { q{ cdot 2 }^{ 3 } }{ 12 } cdot frac { 1 }{ 2 } cdot 1+frac { 1 }{ 2 } cdot 2cdot 2cdot frac { 2 }{ 3 } cdot 1+frac { 1 }{ 2 } cdot 2cdot 2cdot frac { 2 }{ 3 } cdot 1)=frac { 10кН{ м }^{ 3 } }{ 3E{ I }_{ x } } ]
По сортаменту двутавров выписываем значение момента инерции балки и вычисляем численное значение прогиба:
[ { I }_{ x }=350{ см }^{ 4 } ]
[ { V }_{ C }=frac { 10кН{ м }^{ 3 } }{ 3E{ I }_{ x } } =frac { 10cdot { 10 }^{ 9 }Нcdot { см }^{ 3 } }{ 3cdot 2cdot { 10 }^{ 7 }frac { Н }{ { см }^{ 2 } } cdot 350{ см }^{ 4 } } =0.476см ]
Задача. Расчет рамы. Для рамы построить эпюры продольных сил N, поперечных сил Q и изгибающих моментов М.
- Определим опорные реакции
Нанесем значения опорных реакций на расчетную схему.
2. Строим эпюру продольных сил N методом сечений. Имеем три характерных участка и три сечения на них.
Правило знаков продольных сил – продольная сила считается положительной, если сила растягивает стержень, и отрицательной, если сила сжимает стержень. Положительные значения откладываем влево от стойки и вверх от ригеля.
Строим эпюру продольных сил.
3. Строим эпюру поперечных сил Q методом сечений. Правило знаков – если сила относительно сечения направлена по часовой стрелке, то поперечная сила считается положительной и наоборот. Положительные значения откладываются влево от стоек и вверх от ригеля.
Строим эпюру поперечных сил
4. Строим эпюру изгибающих моментов М методом характерных точек. Расставляем точки: А – опора, В,С, — узлы рамы, D – свободный конец, К – середина равномерно распределенной нагрузки (точки экстремума при построении эп.Q не обнаружено). Эпюру М строим на сжатых волокнах (для машиностроительных специальностей), знак не ставим.
Строим эпюру моментов.
5. Вырезаем узлы С и В и проверяем их равновесие.
Узлы находятся в равновесии, значит эпюры построены верно.
Для балки с жесткой заделкой построить эпюры Q и М.
Расставляем сечения от свободного конца балки — в этом случае можно построить эпюры, не определяя опорных реакций. Рассматривать в каждом случае будем правую часть — справа от сечения. Сечения расставляем на характерных участках (между изменениями). По размерной нитке – 2 участка, 2 сечения.
Сечение 2-2 проходит по участку с равномерно распределенной нагрузкой, отмечаем размер z2 вправо от сечения до начала участка. Определяем поперечные силы в сечениях. Правило знаков см. — здесь.
Строим эпюру Q.
Построим эпюру М методом характерных точек. Расставляем точки на балке — это точки начала и конца балки (D,A), сосредоточенного момента (B), а также отметим в качестве характерной точки середину равномерно распределенной нагрузки (K) — это дополнительная точка для построения параболической кривой.
Определяем изгибающие моменты в точках. Правило знаков см. — здесь.
Момент в т. В будем определять следующим образом. Сначала определим:
Теперь:
Точку К возьмем в середине участка с равномерно распределенной нагрузкой.
Строим эпюру M. Участок АВ – параболическая кривая (правило «зонтика»), участок ВD – прямая наклонная линия.
Для балки определить опорные реакции и построить эпюры изгибающих моментов (М) и поперечных сил (Q).
- Обозначаем опоры буквами А и В и направляем опорные реакции RА и RВ.
Составляем уравнения равновесия.
Проверка
Записываем значения RА и RВ на расчетную схему.
2. Построение эпюры поперечных сил методом сечений. Сечения расставляем на характерных участках (между изменениями). По размерной нитке – 4 участка, 4 сечения.
сеч. 1-1 ход слева.
Сечение проходит по участку с равномерно распределенной нагрузкой, отмечаем размер z1 влево от сечения до начала участка. Длина участка 2 м. Правило знаков для Q — см. здесь.
Строим по найденным значением эпюру Q.
сеч. 2-2 ход справа.
Сечение вновь проходит по участку равномерно распределенной нагрузкой, отмечаем размер z2 вправо от сечения до начала участка. Длина участка 6 м.
Строим эпюру Q.
сеч. 3-3 ход справа.
сеч. 4-4 ход справа.
Строим эпюру Q.
3. Построение эпюры М методом характерных точек.
Характерная точка – точка, сколь-либо заметная на балке. Это точки А, В, С, D, а также точка К, в которой Q=0 и изгибающий момент имеет экстремум. Также в середине консоли поставим дополнительную точку Е, поскольку на этом участке под равномерно распределенной нагрузкой эпюра М описывается кривой линией, а она строится, как минимум, по 3 точкам.
Итак, точки расставлены, приступаем к определению в них значений изгибающих моментов. Правило знаков — см. здесь.
Участки NA, AD – параболическая кривая (правило «зонтика» у механических специальностей или «правило паруса» у строительных ), участки DС, СВ – прямые наклонные линии.
Момент в точке D следует определять как слева, так и справа от точки D. Сам момент в эти выражения не входит. В точке D получим два значения с разницей на величину m – скачок на его величину.
Теперь следует определить момент в точке К (Q=0). Однако сначала определим положение точки К, обозначив расстояние от нее до начала участка неизвестным х.
Т. К принадлежит второму характерному участку, его уравнение для поперечной силы (см. выше)
Но поперечная сила в т. К равна 0, а z2 равняется неизвестному х.
Получаем уравнение:
Теперь, зная х, определим момент в точке К с правой стороны.
Строим эпюру М. Построение выполним для механических специальностей, откладывая положительные значения вверх от нулевой линии и используя правило «зонтика».
Для заданной схемы консольной балки требуется построить эпюры поперечной силы Q и изгибающего момента M, выполнить проектировочный расчет, подобрав круглое сечение.
Материал — дерево, расчетное сопротивление материала R=10МПа, М=14кН·м,q=8кН/м
Строить эпюры в консольной балке с жесткой заделкой можно двумя способами — обычным, предварительно определив опорные реакции, и без определения опорных реакций, если рассматривать участки, идя от свободного конца балки и отбрасывая левую часть с заделкой. Построим эпюры обычным способом.
1. Определим опорные реакции.
Равномерно распределенную нагрузку q заменим условной силой Q= q·0,84=6,72 кН
В жесткой заделке три опорные реакции — вертикальная, горизонтальная и момент, в нашем случае горизонтальная реакция равна 0.
Найдем вертикальную реакцию опоры RA и опорный момент МA из уравнений равновесия.
2. Строим эпюру поперечных сил.
На первых двух участках справа поперечная сила отсутствует. В начале участка с равномерно распределенной нагрузкой (справа) Q=0, в заделеке — величине реакции RA.
4.Проектировочный расчет, то есть подбор размеров поперечного сечения.
Максимальный изгибающий момент с эпюры М=14 кН·м. Определим осевой момент сопротивления сечения
Таким образом, подбираем сечение с диаметром 25 см.
Требуется построить эпюры Q и M и подобрать стальную балку двутаврового поперечного сечения при расчетном сопротивлении R=160 МПа.
1.Определение реакций:
Сумма моментов относительно опор:
Опора А:
Опора В:
Сумма проекций всех сил на ось У (проверка):
2.Записываем уравнения Q и M для каждого из участков в общем виде, при этом учитываем знаки.
1) Первый участок:
2) Второй участок:
3) Третий участок:
3.Проектировочный расчет, то есть подбор размеров поперечного сечения.
Подобрать стальную балку двутаврового поперечного сечения при R=160 МПа:
С эпюры берем максимальный момент:
По сортаменту подбираем двутавр № 20 с
Двутавр можно взять чуть меньше, при условии, что перенапряжение составляет меньше 5%:
Для заданной балки требуется построить эпюры Q и M, найти Mmax и сделать проектировочный расчет — подобрать деревянную балку круглого поперечного сечения. Расчетное сопротивление материала Ru=10 МПа.
1.Определение реакций:
Сумма проекций всех сил на ось z:
Сумма проекций всех сил на ось y:
Сумма моментов относительно точки А:
После нахождения опорных реакций следует выполнить проверку, использовав уравнение равновесия (сумма моментов относительно любой выбранной точки должна быть равна нулю).
2. Записываем уравнения Q и M для каждого из участков в общем виде, при этом учитываем знаки.
Q — поперечная сила, считается положительной, если стремится повернуть рассматриваемую часть балки по часовой стрелке.
M— изгибающий момент, считается положительным, если растягивает нижние волокна.
1)Первый участок:
2) Второй участок:
3) Третий участок:
Следует отметить ,что на втором и третьем участке для построения плавной кривой потребуются дополнительные точки, в которых следует посчитать значение изгибающего момента.
3.Проектировочный расчет, то есть подбор размеров поперечного сечения.
Подберем деревянную балку круглого поперечного сечения при Ru=10 МПа
С эпюры берем максимальный момент и рассчитываем требуемый осевой момент сопротивления, после чего вычисляем необходимый диаметр балки.
Задача 1. Построить эпюры Q и M в балке с шарниром.
1. Определим опорные реакции. Для определения опорных реакций используем свойство шарнира – момент в нем как от левых, так и от правых сил равен 0.
Если рассмотреть левую часть, то в уравнении будут присутствовать две неизвестные RА и МА. Значит, следует рассмотреть правую часть (из него найдем RВ).
Теперь из него найдем МА
Следующее уравнение из него найдем RА
2. Строим эпюру Q.
Участок первый — АС, смотрим левую часть
Участок второй — СВ, смотрим правую часть
3. Строим эпюру М
Определим момент в точке, где Q=0 (момент имеет экстремум), это момент в точке К, т.е. МК , для этого определим положение точки К.
Это уравнение первого участка, на котором находится точка К
в точке К
Строим эпюры. Задача решена.
Задача 2. Построить эпюры Q и M в балке с шарниром.
1. Определим опорные реакции. Для определения опорных реакций используем свойство шарнира – момент в нем как от левых, так и от правых сил равен 0.
Если рассмотреть правую часть, то в уравнении будут присутствовать две неизвестные Rд и Rв. Значит, следует рассмотреть левую часть.
Знак «-» говорит о том, что реакция RВ направлена в обратную сторону.
Проверка:
2. Построение эпюры Q.
Участок первый — ЕА, смотрим левую часть
Участок второй — АС, смотрим левую часть
Участок третий — СВ, смотрим левую часть
Участок четвертый — ВД, смотрим правую часть
3. Построение эпюры М
Т.к. точки экстремума на эп.Q не наблюдается, определяем изгибающий момент в середине участка ВД
Строим эпюры, задача решена.
Задача 1. Построить эпюры внутренних усилий для рамы ( рис.а).
Дано: F=30кН, q=40 кН/м, М=50кНм, а=1,8м, h=2м.
Решение.
Для рассматриваемой рамы опорные реакции можно не определять, поскольку будем рассматривать участки, идя от свободных концов рамы к заделке.
Вычислим значения внутренних усилий N, Q и М в характерных сечениях рамы. Правило знаков для поперечных сил Q и изгибающих моментов М такие же,как в балках. Эпюры моментов построим на сжатых волокнах. Для продольной N, силы правило знаков: растягивающая сила – положительна, сжимающая – отрицательна.
Участок ВС: (сжаты нижние волокна).
(сжаты нижние волокна).
Участок DC: 
Участок СК: (сжаты левые волокна)
(сжаты левые волокна)
На рисунке — эпюры нормальных (продольных) сил — (б), , поперечных сил — (в) и изгибающих моментов — (г).
Проверка равновесия узла С:
Задача 2 Построить эпюры внутренних усилий для рамы (рис. а).
Дано: F=30кН, q=40 кН/м, М=50кНм, а=3м, h=2м.
Определим опорные реакции рамы:
Из этих уравнений найдем:
Поскольку значения реакции RK имеет знак минус, на рис. а изменяется направление данного вектора на противоположное, при этом записывается RK=83,33кН.
Определим значения внутренних усилий N, Q и М в характерных сечениях рамы:
Участок ВС:
(сжаты правые волокна).
Участок CD:
(сжаты правые волокна);
(сжаты правые волокна).
Участок DE:
(сжаты нижние волокна);
(сжаты нижние волокна).
Участок КС
(сжаты левые волокна).
Построим эпюры нормальных (продольных) сил (б), поперечных сил (в) и изгибающих моментов (г).
Рассмотрим равновесие узлов D и Е
Из рассмотрения узлов Dи Е видно, что они находятся в равновесии.
Задача 3. Для рамы с шарниром построить эпюры внутренних усилий.
Дано: F=30кН, q=40 кН/м, М=50кНм, а=2м, h=2м.
Решение. Определим опорные реакции. Следует отметить ,что в обеих шарнирно-неподвижных опорах по две реакции. В связи с этим следует использовать свойство шарнира С — момент в нем как от левых ,так и от правых сил равен нулю. Рассмотрим левую часть.
Уравнения равновесия для рассматриваемой рамы можно записать в виде:
Из решения данных уравнений следует:
На схеме рамы направление действия силы НВ изменяется на противоположное (НB=15кН).
Определим усилия в характерных сечениях рамы.
Участок BZ:
(сжаты левые волокна).
Участок ZC:
(сжаты левые волокна);
Участок КD:
(сжаты левые волокна);
(сжаты левые волокна).
Участок DС:
(сжаты нижние волокна);
Определение экстремального значения изгибающего момента на участке CD :
(сжаты верхние волокна).
Строим эпюры внутренних усилий. Проверяем равновесие узлов рамы.
Узлы C и D находятся в равновесии.
Построение эпюр М и Q в балке с жесткой заделкой с определенными опорными реакциями. Построение методом характерных точек.
1. Построение эпюры поперечных сил. Для консольной балки (рис. а) характерные точки: А – точка приложения опорной реакции VA; С – точка приложения сосредоточенной силы; D, B– начало и конец распределенной нагрузки. Для консоли поперечная сила определяется аналогично двухопорной балке. Итак, при ходе слева:
Для проверки правильности определения поперечной силы в сечениях пройдите балку аналогичным образом, но с правого конца. Тогда отсеченными будут правые части балки. Помните, что правило знаков при этом изменятся. Результат должен получиться тот же. Строим эпюру поперечной силы (рис,б).
2. Построение эпюры моментов
Для консольной балки эпюра изгибающих моментов строится аналогично предыдущему построению.Характерные точки для этой балки (см. рис. а) следующие: А – опора; С — точка приложения сосредоточенного момента и силы F; D и В — начало и конец действия равномерно распределенной нагрузки. Поскольку эпюра Qx на участке действия распределенной нагрузки нулевую линию не пересекает, для построения эпюры моментов на данном участке (параболическая кривая) следует выбрать произвольно дополнительную точку для построения кривой, к примеру в середине участка.
Ход слева:
Ходом справа находим MB = 0.
По найденным значениям строим эпюру изгибающих моментов (см. рис. в).
Построение эпюр М и Q в балке на двух опорах с определенными опорными реакциями. Построение методом характерных точек.
1. Построение эпюры Qу. Из теоретического курса известно, что на участке балки с равномерно распределенной нагрузкой эпюра Qу ограничивается наклонной прямой, а на участке, на котором нет распределенной нагрузки, — прямой, параллельной оси, поэтому для построения эпюры поперечных сил достаточно определить значения Qу в начале и конце каждого участка. В сечении, соответствующем точке приложения сосредоточенной силы, поперечная сила должна быть вычислена чуть левее этой точки (на бесконечно близком расстоянии от нее) и чуть правее ее; поперечные силы в таких местах обозначаются соответственно .
Строим эпюру Qу методом характерных точек, ходом слева. Для большей наглядности отбрасываемую часть балки на первых порах рекомендуется закрывать листом бумаги. Характерными точками для двухопорной балки (рис. а) будут точки C и D – начало и конец распределенной нагрузки, а также A и B – точки приложения опорных реакций, E– точка приложения сосредоточенной силы. Проведем мысленно ось y перпендикулярно оси балки через точку С и не будем менять ее положение, пока не пройдем всю балку от C до E. Рассматривая левые отсеченные по характерным точкам части балки, проецируем на ось y действующие на данном участке силы с соответствующими знаками. В результате получаем:
Для проверки правильности определения поперечной силы в сечениях можно пройти балку аналогичным образом, но с правого конца. Тогда отсеченными будут правые части балки. Результат должен получиться тот же. Совпадение результатов может служить контролем построения эпюры Qу. Проводим нулевую линию под изображением балки и от нее в принятом масштабе откладываем найденные значения поперечных сил с учетом знаков в соответствующих точках. Получим эпюру Qу (рис. б).
Построив эпюру, обратите внимание на следующее: эпюра под распределенной нагрузкой изображается наклонной прямой, под ненагруженными участками — отрезками, параллельными нулевой линии, под сосредоточенной силой на эпюре образуется скачок, равный значению силы. Если наклонная линия под распределенной нагрузкой пересекает нулевую линию, отметьте эту точку, то это точка экстремума, и она является теперь для нас характерной, согласно дифференциальной зависимости между Qу и Мx, в этой точке момент имеет экстремум и его нужно будет определить при построении эпюры изгибающих моментов. В нашей задаче это точка К. Сосредоточенный момент на эпюре Qу себя никак не проявляет, так как сумма проекций сил, образующих пару, равна нулю.
2. Построение эпюры моментов.Строим эпюру изгибающих моментов, как и поперечных сил, методом характерных точек, ходом слева. Известно, что на участке балки с равномерно распределенной нагрузкой эпюра изгибающих моментов очерчивается кривой линией (квадратичной параболой), для построения которой надо иметь не менее трех точек и, следовательно, должны быть вычислены значения изгибающих моментов в начале участка, конце его и в одном промежуточном сечении. Такой промежуточной точкой лучше всего взять сечение, в котором эпюра Qу пересекает нулевую линию, т.е. где Qу= 0. На эпюре М в этом сечении должна находиться вершина параболы. Если же эпюра Qу не пересекает нулевую линию, то для построения эпюры М следует на данном участке взять дополнительную точку, к примеру, в середине участка (начала и конца действия распределенной нагрузки), помня, что выпуклостью парабола всегда обращена вниз, если нагрузка действует сверху вниз (для строительных специальностей). Существует правило «дождя», которое очень помогает при построении параболической части эпюры М. Для строителей это правило выглядит следующим образом: представьте, что распределенная нагрузка — это дождь, подставьте под него зонт в перевернутом виде, так чтобы дождь не стекал, а собирался в нем. Тогда выпуклость зонта будет обращена вниз. Точно так и будет выглядеть очертание эпюры моментов под распределенной нагрузкой. Для механиков существует так называемое правило «зонта». Распределенная нагрузка представляется дождем, а очертание эпюры должно напоминать очертания зонтика. В данном примере эпюра построена для строителей.
Если требуется более точное построение эпюры, то должны быть вычислены значения изгибающих моментов в нескольких промежуточных сечениях. Условимся для каждого такого участка изгибающий момент сначала определить в произвольном сечении, выражая его через расстояние х от какой-либо точки. Затем, давая расстоянию х ряд значений, получим значения изгибающих моментов в соответствующих сечениях участка. Для участков, на которых нет распределенной нагрузки, изгибающие моменты определяют в двух сечениях, соответствующих началу и концу участка, так как эпюра М на таких участках ограничивается прямой. Если к балке приложен внешний сосредоточенный момент, то обязательно надо вычислять изгибающий момент чуть левее места приложения сосредоточенного момента и чуть правее его.
Для двухопорной балки характерные точки следующие: C и D – начало и конец распределенной нагрузки; А – опора балки; В – вторая опора балки и точка приложения сосредоточенного момента; Е – правый конец балки; точка К, соответствующая сечению балки, в котором Qу = 0.
Ход слева. Правую часть до рассматриваемого сечения мысленно отбрасываем (возьмите лист бумаги и прикройте им отбрасываемую часть балки). Находим сумму моментов всех сил, действующих слева от сечения относительно рассматриваемой точки. Итак,
Прежде чем определить момент в сечении К, необходимо найти расстояние х=АК. Составим выражение для поперечной силы в данном сечении и приравняем его к нулю (ход слева):
Это расстояние можно найти также из подобия треугольников KLN и KIG на эпюре Qу (рис.б).
Определяем момент в точке К:
Пройдем оставшуюся часть балки ходом справа.
Как видим, момент в точке D при ходе слева и справа получился одинаковый – эпюра замкнулась. По найденным значениям строим эпюру. Положительные значения откладываем вниз от нулевой линии, а отрицательные – вверх (см. рис. в).