Как найти середину гипотенузы в прямоугольном треугольнике - Исправление недочетов и поиск решений вместе с Examum.ru

Свойства медианы в прямоугольном треугольнике с доказательствами

В этой статье мы рассмотрим свойства медианы в прямоугольном треугольнике, а также их доказательства.

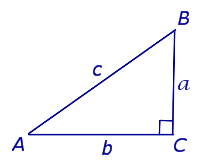
Медиана — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. Для прямоугольного треугольника это будут медианы, проведённые с острого угла к серединам катетов или с прямого к центру гипотенузы (рис. 1).

Свойства медианы в прямоугольном треугольнике

Медианы в прямоугольном треугольнике пересекаются в одной точке, а точка пересечения делит их в соотношении два к одному считая от вершины, из которой проведена медиана.
Медиана, проведённая из вершины прямого угла к гипотенузе, равна половине гипотенузы.
Медиана, проведённая к гипотенузе прямоугольного треугольника, является радиусом описанной окружности.

Доказательства свойств

Первое свойство

Доказать, что медианы в прямоугольном треугольнике пересекаются в одной точке и делятся в пропорции 2:1, считая от вершины.

Доказательство:

Рассмотрим прямоугольный треугольник ABC. Проведем две медианы AE и BD, которые пересекаются в точке X (рис. 2).

Середины отрезков AX и BX обозначим, соответственно, буквами F и G (рисунок 3).

Соединим между собой точки (D, F, G и E) и получим четырёхугольник DFGE (рис. 4).

Сторона DE этого четырёхугольника будет средней линией треугольника ABC. Согласно определению: отрезок, соединяющий середины двух сторон треугольника, является его средней линией. При этом по свойству средняя линия параллельна не пересекающейся с ней стороне и равна половине этой стороны, то есть.
DE || AB и DE = AB / 2.

Аналогично сторона FG треугольника AXB будет его средней линией.
FG || AB и FG = AB / 2

Отсюда следует, что отрезки DE и FG являются параллельными и равными. Следовательно, четырехугольник DFGE – параллелограмм (по признаку параллелограмма).

Так как диагонали параллелограмма в точке пересечения делятся пополам, то
FX=XE, GX=XD

Так как AF = FX (по построению), то и AF = FX = XE, аналогично DX = XG = GB.

Получается, что точка X делит обе медианы AE и BD в соотношении 2 к 1 считая от вершины треугольника.

Аналогично, мы сможем доказать, что точка пересечения 3-ей медианы, проведенной из прямого угла к гипотенузе, с медианой AE (или BD) будет делить ее в соотношении 2 к 1, считая от вершины. То есть наша 3-я медиана также пройдет через точку X. Отсюда следует, что все 3 наши медианы пересекаются в одной точке.

Что и требовалось доказать.

Второе свойство

Доказать, что медиана, проведённая с вершины прямого угла к гипотенузе, равна половине гипотенузы.

Доказательство:

Чтобы доказать это свойство рассмотрим прямоугольный треугольник ABC и проведём медиану к гипотенузе. Точку ее пересечения с гипотенузой обозначим буквой D (рис. 6).

Отразим симметрично наш треугольник ABC относительно отрезка AB (рисунок 7). В результате получим четырёхугольник AEBC, в котором AD=DB (поскольку CD медиана к стороне AB) и CD=DE (по построению). То есть диагонали четырехугольника AEBC пересекаются и точкой пересечения делятся пополам. Отсюда следует, что AEBC является параллелограммом (по признаку параллелограмма).

Один из признаков прямоугольника говорит о том, что параллелограмм является прямоугольником, если хотя бы один из его углов прямой. Поскольку ∠ACB прямой (по построению), то AEBC — прямоугольник.

Поскольку диагонали прямоугольника равны и в точке пересечения делятся пополам (свойство прямоугольника), то AB = CE и AD = DB = CD = DE.

Так как AB = AD + DB, AD = BD и СD = AD = BD, то получается, что медиана AD, проведенная к гипотенузе AB равна половине ее длины.

Что и требовалось доказать.

Третье свойство

Доказать, что медиана, проведённая к гипотенузе прямоугольного треугольника, является радиусом описанной окружности.

Доказательство:

Опишем вокруг прямоугольного треугольника ABC окружность.

Поскольку точка C уже лежит на окружности, то для того, чтобы доказать, что медиана CM является радиусом, нам надо доказать, что точка M – центр описанной окружности (т.е. равноудалена от нее).

Так как медиана делит отрезок пополам, а медиана проведенная к гипотенузе равна ее половине (согласно доказанному выше свойству), то точка M будет равноудалена от всех вершин треугольника, которые в свою очередь касаются окружности (рисунок 8).

Отсюда следует, что окружность, описанная вокруг прямоугольного треугольника ABC будет иметь центр на середине гипотенузы (в точке M), а медиана CM будет радиусом описанной окружности.

Что и требовалось доказать.

Понравилась статья, расскажите о ней друзьям:

Свойства прямоугольного треугольника

Треугольник, у которого один из углов равен 90°, называют прямоугольным треугольником. Сторону, лежащую против угла в 90°, называют гипотенузой , две другие стороны называют катетами .

Катеты прямоугольного треугольника

Длины катетов прямоугольного треугольника меньше длины гипотенузы.

Равнобедренным прямоугольным треугольником называют такой прямоугольный треугольник, у которого равны катеты.
Острые углы равнобедренного прямоугольного треугольника равны 45°.

Катет прямоугольного треугольника, лежащий против угла в 30° , равен половине гипотенузы.

Катет, равный половине гипотенузы

Если в прямоугольном треугольнике один из катетов равен половине гипотенузы, то этот катет лежит против угла в 30° .

Медиана, проведённая к гипотенузе прямоугольного треугольника

Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы.

Медиана треугольника, равная половине стороны, к которой она проведена

Если в треугольнике медиана равна половине стороны, к которой она проведена, то такой треугольник является прямоугольным.

Середина гипотенузы прямоугольного треугольника является центром описанной около него окружности.

Если в треугольнике центр описанной окружности лежит на одной из сторон, то этот треугольник является прямоугольным треугольником, а центр описанной окружности совпадает с серединой гипотенузы.

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

Обратная теорема Пифагора

Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник является прямоугольным

Фигура	Рисунок	Формулировка
Прямоугольный треугольник
Равнобедренный прямоугольный треугольник
Прямоугольный треугольник с углом в 30°

Определение прямоугольного треугольника:

Треугольник, у которого один из углов равен 90° , называют прямоугольным треугольником .

Сторону, лежащую против угла в 90° , называют гипотенузой , две другие стороны называют катетами .

Свойство катетов прямоугольного треугольника:

Длины катетов прямоугольного треугольника меньше длины гипотенузы.

Прямоугольный треугольник

Равнобедренный прямоугольный треугольник

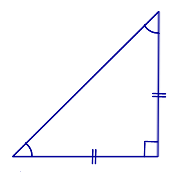
Определение равнобедренного прямоугольного треугольника:

Равнобедренным прямоугольным треугольником называют такой прямоугольный треугольник, у которого равны катеты.

Свойство углов прямоугольного треугольника:

Острые углы равнобедренного прямоугольного треугольника равны 45° .

Прямоугольный треугольник с углом в 30°

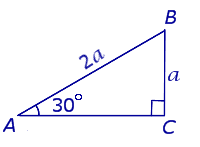
Свойство прямоугольного треугольника с углом в 30° :

Катет прямоугольного треугольника, лежащий против угла в 30° , равен половине гипотенузы.

Признак прямоугольного треугольника с углом в 30° :

Медиана, проведённая к гипотенузе прямоугольного треугольника

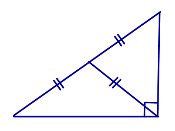
Свойство медианы, проведенной к гипотенузе прямоугольного треугольника:

Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы.

Признак прямоугольного треугольника:

Центр описанной окружности

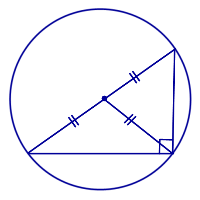
Свойство окружности, описанной около прямоугольного треугольника:

Середина гипотенузы прямоугольного треугольника является центром описанной около него окружности.

Признак прямоугольного треугольника:

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

Обратная теорема Пифагора:

Медиана в прямоугольном треугольнике

Медиана в прямоугольном треугольнике — это отрезок, который соединяет вершину треугольника и середину противоположной стороны, то есть вершину острого угла с серединой противолежащего катета или вершину прямого угла с серединой гипотенузы.

Все медианы прямоугольного треугольника пересекаются в одной точке и делятся этой точкой в отношении два к одному, считая от вершины:

Из всех медиан прямоугольного треугольника в задачах чаще всего речь идет о медиане, проведенной к гипотенузе. Это связано с ее свойствами.

Свойства медианы, проведенной к гипотенузе:

1) Медиана, проведенная к гипотенузе, равна половине гипотенузы.

(в следующий раз рассмотрим доказательство этого свойства)

2) Медиана, проведенная к гипотенузе, равна радиусу описанной около прямоугольного треугольника окружности.

Пользуясь свойствами прямоугольного треугольника, длины медиан прямоугольного треугольника можно выразить через катеты и острые углы.

Например:

12 Comments

Информация очень хорошая. Правда не помогла мне решить задачу, которую мой сын не решил на контрольной. приведу условие:
Из прямого угла треугольника проведена медиана на гипотенузу. Длина медианы 6см. Определить катеты.

Петр, данных для определения катетов недостаточно. Длина гипотенузы в 2 раза больше длины медианы — 12 см. Это всё, что можно сказать по данным условия.

не правда надо провести высоту из прямого угла дальше все получится. один катет равен 6 а второй 2 корня из 22

Сумма квадратов катетов равна квадрату гипотенузы. Проверим 6^2+(2*корень из 22)^2
=36+4*22=36+88=124. Квадрат гипотенузы 12^2=144

попробуйте составить уравнение,обозначив 1 из катетов через х а 2-ой катет обозначьте буквами…x^2+BC^2=12^2…да числа не очень,но это 1 способ..решаю дальше:BC^2=12^2-x^2
BC^2=11x
X^2+11X=144
X^2=12
x(1 катет)=корню из 12,а «-ой катет=11 корней из 12….решал на основе теоремы пифагора

задача имеет бесконечное кол-во решений. решение возможно только в виде формулы или графика, где описана зависимость между катетами и гипотенузой

Да просто треугольник медианой делится на два треугольника с одинаковыми катетами, а дальше как уже предлагалось выше Пифагор во спасение))

А кто вам сказал, что медиана в прямоугольном треугольнике является еще и высотой? Откуда у вас два треугольника с одинаковыми катетами?

Спасибо за понятное объяснение, но у нас задача немного другая.
В прямоугольном треугольнике АВС угол С= 90 градусов,медиана ВВ1 равна 10 см.Найдите медианы АА1 СС1, если известно, что АС=12 см.( используя т.Пифагора.

1) Рассмотрим треугольник BB1C. В нём угол С равен 90 градусов, BB1=10 см, B1C=6 см (так как BB1 — медиана). По теореме Пифагора находим BC: BC=8 см. 2) Рассмотрим треугольник AA1C. В нём угол С равен 90 градусов, AC=12 см, AA1=4 см (так как BB1 — медиана). По теореме Пифагора находим AA1: AA1=4√10 см.3) Из треугольника ABC по теореме Пифагора найдём AB: AB=4√13 см. 4) CC1=1/2 AB (как медиана, проведённая к гипотенузе), CC1=2√13 см.
Где-то так.

источники:

http://www.resolventa.ru/demo/traininggia.htm

Медиана в прямоугольном треугольнике

Источник

В данной публикации мы рассмотрим определение и свойства прямоугольного треугольника. Также разберем пример решения задачи для закрепления изложенного материала.

Определение прямоугольного треугольника
Свойства прямоугольного треугольника
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
Пример задачи

Определение прямоугольного треугольника

Прямоугольным называют треугольник, в котором один из трех углов является прямым, т.е. равным 90°.

AB и AC – катеты;
BC – гипотенуза.

Прямоугольный треугольник может быть равнобедренным – когда оба катета равны, а угол между каждым из них и гипотенузой составляет 45°.

Свойства прямоугольного треугольника

Свойство 1

Сумма двух острых углов прямоугольного треугольника равняется 90°.

α + β = 90°

Сумма всех углов любого треугольника составляет 180°. Т.к. один угол равен 90°, на два других, также, остается 90°.

Свойство 2

Катет прямоугольного треугольника, расположенный напротив угла в 30°, равняется половине его гипотенузы.

В нашем случае, катет AB лежит напротив ∠ACB = 30°. Следовательно:

Обратная формулировка:

Если длина одного из катетов прямоугольного треугольника в два раза меньше длины его гипотенузы, значит угол напротив этого катета равняется 30°.

Свойство 3

Терему Пифагора можно, также, отнести к свойствам прямоугольного треугольника. Согласно ее формулировке, сумма квадратов катетов (a и b) равняется квадрату гипотенузы (c).

a² + b² = c²

Таким образом, гипотенуза прямоугольного треугольника больше любого из его катетов.

Свойство 4

Медиана, опущенная на гипотенузу прямоугольного треугольника (проведенная из вершины прямого угла), равняется половине гипотенузы.

AD – медиана
AD = BD = DC

Свойство 5

Середина гипотенузы прямоугольного треугольника – это центр описанной вокруг него окружности.

Согласно свойству 4, рассмотренному выше, медиана BO равняется половине гипотенузы AC и, одновременно, радиусу окружности, описанной вокруг △ABC.

BO = AO = OC = R_окр.

Пример задачи

В качестве примера давайте рассмотрим второе свойство, представленное выше. Допустим у нас имеется прямоугольный треугольник ABC с прямым углом в вершине C. Катет BC расположен напротив угла в 30°. Нужно доказать, что BC в два раза меньше гипотенузы AB.

Решение

Нарисуем чертеж по условиям задачи, и зеркально отразим получившийся треугольник.

Получаем △ABD, в котором ∠BAD равен 60° (30° + 30°). Т.к. все три угла данного треугольника равны, он является равносторонним. Следовательно, AD = AB = BD.

Отрезки BC и CD равны между собой (зеркально отраженные), и каждый из них составляет половину BD. Как мы уже выяснили, BD равняется AB.

Таким образом, BC в два раза меньше AB (или AB = 2BC).

Источник

Прямоугольный треугольник, свойства, признаки и формулы.

Прямоугольный треугольник – это треугольник, в котором один угол прямой (то есть составляет 90°).

Прямоугольный треугольник (понятие, определение)

Признаки равенства прямоугольных треугольников

Свойства прямоугольного треугольника

Формулы прямоугольного треугольника

Остроугольный треугольник, прямоугольный треугольник, равнобедренный треугольник, равносторонний треугольник, тупоугольный треугольник

Прямоугольный треугольник (понятие, определение):

Прямоугольный треугольник – это треугольник, в котором один угол прямой (то есть составляет 90°).

Сторона, противоположная прямому углу, называется гипотенузой. Гипотенуза (с греч. ὑποτείνουσα – «натянутая») – это самая длинная сторона прямоугольного треугольника, противоположная прямому углу.

Стороны, прилегающие к прямому углу, называются катетами. Катет (с греч. κάθετος – «перпендикуляр, опущенный, отвесный») – одна из двух сторон прямоугольного треугольника, образующих прямой угол.

Для непрямоугольного треугольника гипотенуза и катеты не существуют.

Рис. 1. Прямоугольный треугольник

АВ, АС – катеты прямоугольного треугольника, ВС – гипотенуза прямоугольного треугольника, ∠ ВАС = 90°

Равнобедренный треугольник может быть прямоугольным (равнобедренным прямоугольным треугольником).

Равнобедренный прямоугольный треугольник — это треугольник, являющийся одновременно равнобедренным и прямоугольным. В этом треугольнике каждый острый угол равен 45°.

Признаки равенства прямоугольных треугольников:

Признаки равенства прямоугольных треугольников основаны и вытекают из общих признаков равенства треугольников.

1. Равенство по двум катетам.

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.

Рис. 2. Равенство прямоугольных треугольников по двум катетам

АВ = А₁В₁, АС = А₁С₁

2. Равенство по катету и прилежащему острому углу.

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.

Рис. 3. Равенство прямоугольных треугольников по катету и прилежащему углу

АВ = А₁В₁, ∠АВС = ∠А₁В₁С₁

3. Равенство по гипотенузе и острому углу.

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Рис. 4. Равенство прямоугольных треугольников по гипотенузе и острому углу

ВС = В₁С₁, ∠АВС = ∠А₁В₁С₁

4. Равенство по гипотенузе и катету.

Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Рис. 5. Равенство прямоугольных треугольников по гипотенузе и катету

ВС = В₁С₁, АС = А₁С₁

5. Равенство по катету и противолежащему острому углу.

Если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Рис. 6. Равенство прямоугольных треугольников по катету и противолежащему острому углу

АС = А₁С₁, ∠АВС = ∠А₁В₁С₁

Свойства прямоугольного треугольника:

1. В прямоугольном треугольнике сумма двух острых углов равна 90°.

2. В прямоугольном треугольнике катет, лежащий против угла в 30° , равен половине гипотенузы.

И наоборот, если в прямоугольном треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

Рис. 7. Прямоугольный треугольник с острым углом 30˚

b = c / 2

3. Теорема Пифагора:

Сумма квадратов катетов равна квадрату гипотенузы.

c² = a² + b² ,

где a, b – катеты, c – гипотенуза.

Рис. 8. Прямоугольный треугольник

4. В прямоугольном треугольнике центр описанной окружности – есть середина гипотенузы.

И соответственно радиус описанной окружности (R) равен половине гипотенузы.

где c – гипотенуза.

Рис. 9. Прямоугольный треугольник и описанная окружность

5. В прямоугольном треугольнике медиана, падающая на гипотенузу, равна половине гипотенузы.

Рис. 10. Прямоугольный треугольник и медиана, падающая на гипотенузу

АМ – медиана прямоугольного треугольника, падающая на гипотенузу, АМ = ВМ = МС, АМ = ВС/2

6. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника подобные исходному.

Рис. 11. Прямоугольный треугольник и высота, проведенная из вершины прямого угла

АВ/ВС = АН/АС = ВН/АВ

Формулы прямоугольного треугольника:

Пусть a и b – длины катетов прямоугольного треугольника, с – длина гипотенузы прямоугольного треугольника, h – высота прямоугольного треугольника, проведенная к гипотенузе (АН), R – радиус описанной окружности, r – радиус вписанной окружности (см. Рис. 9, 11, 12).

Формулы сторон прямоугольного треугольника (a, b, c) по теореме Пифагора:

c² = a² + b² ,

a² = c² – b² ,

b² = c² – a² .

Формула радиуса вписанной окружности (r):

Рис. 12. Прямоугольный треугольник и вписанная окружность

Формула радиуса описанной окружности (R):

Формулы площади (S) прямоугольного треугольника:

Формулы высоты (h)прямоугольного треугольника:

Квадрат

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Ромб

Коэффициент востребованности
31 133

Источник

$[AO:O{A_1} = BO:O{B_1} = CO:O{C_1} = 2:1.]$

Свойства медианы, проведенной к гипотенузе:

1) Медиана, проведенная к гипотенузе, равна половине гипотенузы.

$[C{C_1} = frac{1}{2}AB]$

(в следующий раз рассмотрим доказательство этого свойства)

2) Медиана, проведенная к гипотенузе, равна радиусу описанной около прямоугольного треугольника окружности.

Например:

$[C{C_1} = frac{1}{2}sqrt {A{C^2} + B{C^2}} ]$

$[C{C_1} = frac{{BC}}{{2sin angle A}}]$

$[C{C_1} = frac{{AC}}{{2cos angle A}}]$

$[A{A_1} = sqrt {A{C^2} + {A_1}{C^2}} = sqrt {A{C^2} + frac{1}{4}B{C^2}} ]$

$[B{B_1} = sqrt {B{C^2} + {B_1}{C^2}} = sqrt {B{C^2} + frac{1}{4}A{C^2}} ]$

и так далее.

Источник

Любой треугольник всегда можно представить как «сумму» или «разность» двух прямоугольных треугольников – достаточно провести высоту. Поэтому многие свойства произвольных треугольников и многоугольников следуют из свойств прямоугольного треугольника и высот произвольного треугольника.

В логике теорем | Для решения задач | Задачи | Комментарии

1 Дополнительное построение, ведущее к теореме о средней линии треугольника, трапеции и свойствам подобия треугольников.

Проводим из вершины прямого угла отрезок прямой, составляющий с катетом CA угол, равный углу CAB заданного прямоугольного треугольника ABC. В результате получим равнобедренный треугольник ACM с углами при основании alpha . Но другой треугольник, получающийся при таком построении, также будет равнобедренным, поскольку каждый его угол при основании равен d-alpha (по свойству углов прямоугольного треугольника и по построению — из прямого угла «вычли» угол alpha ). В силу того, что треугольники BMC и AMC равнобедренные с общей стороной MC имеем равенство MB=MA=MC, т.е. MC – медиана, проведенная к гипотенузе прямоугольного треугольника, и она равна половине гипотенузы.
Следствие 1. Середина гипотенузы является центром окружности, описанной вокруг этого треугольника, поскольку получилось, что середина гипотенузы равноудалена от вершин прямоугольного треугольника.
Следствие 2. Средняя линия прямоугольного треугольника, соединяющая середину гипотенузы и середину катета, параллельна противоположному катету и равна его половине.

PL08

Опустим в равнобедренных треугольниках BMC и AMC высоты MH и MG на основания. Поскольку в равнобедренном треугольнике, высота, опущенная на основание, является также и медианой (и биссектрисой), то MH и MG –линии прямоугольного треугольника, соединяющие середину гипотенузы с серединами катетов. По построению они оказываются параллельными противоположным катетам и равные их половинам, поскольку треугольники равны MHC и MGC равны (причем MHCG – прямоугольник). Этот результат является основанием для доказательства теоремы о средней линии произвольного треугольника и, далее, средней линии трапеции и свойства пропорциональности отрезков, отсекаемых параллельными прямыми на двух пересекающих их прямых.

2 Все прямоугольные треугольники с одинаковым острым углом — подобны. Взгляд на тригонометрические функции.

Треугольники со сторонами штрихованными и с не штрихованными подобны по равенству двух углов. Поэтому $frac{a'}{a}=frac{b'}{b}=frac{c'}{c},$ откуда

$frac{a'}{c'}=frac{a}{c},,frac{b'}{c'}=frac{b}{c},,frac{b'}{a'}=frac{b}{a}.$

Это значит, что указанные отношения зависят лишь от острого угла прямоугольного треугольника и по сути определяют его. Это одно из оснований появления тригонометрических функций:

$sinalpha=frac{a'}{c'}=frac{a}{c}=cosbeta,,cosalpha=frac{b'}{c'}=frac{b}{c}=sinbeta,$

$mathrm{tg}beta=frac{b'}{a'}=frac{b}{a}=mathrm{ctg}alpha.$

Часто запись тригонометрических функций угла в подобных прямоугольных треугольниках наглядней записи соотношений подобия !

3 Пример дополнительного построения — высота, опущенная на гипотенузу. Вывод теоремы Пифагора на основе подобия треугольников.

Опустим на гипотенузу AB высоту CH. Имеем три подобных треугольника ABC, AHC и CHB. Запишем выражения для тригонометрических функций:

$cosbeta=frac{c_1}{a}=frac{a}{c},,cosalpha=frac{c_2}{b}=frac{b}{c}.$

Отсюда видно, что . Складывая, получаем теорему Пифагора, поскольку :

1Все прямоугольные треугольники с одинаковым острым углом — подобны. Взгляд на тригонометрические функции.

$frac{a'}{c'}=frac{a}{c},,frac{b'}{c'}=frac{b}{c},,frac{b'}{a'}=frac{b}{a}.$

$sinalpha=frac{a'}{c'}=frac{a}{c}=cosbeta,,cosalpha=frac{b'}{c'}=frac{b}{c}=sinbeta,$

$mathrm{tg}beta=frac{b'}{a'}=frac{b}{a}=mathrm{ctg}alpha.$

2Пример дополнительного построения — высота, опущенная на гипотенузу. Вывод теоремы Пифагора на основе подобия треугольников.

$cosbeta=frac{c_1}{a}=frac{a}{c},,cosalpha=frac{c_2}{b}=frac{b}{c}.$

Отсюда видно, что . Складывая, получаем теорему Пифагора, поскольку :

Другое доказательство теоремы Пифагора см.в комментарии к задаче 4.

3Важный пример дополнительного построения – построение угла, равного одному из углов треугольника.

PL08

Задачи
Использование свойств подобия -1
Использование основных свойств — 2
Использование дополнительного построения 3-4

1234

Высота, опущенная из вершины прямого угла прямоугольного треугольника равна корню квадратном из длин отрезков, на которые она делит гипотенузу.

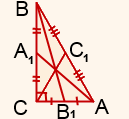
Найти геометрическое место точек (ГМТ) пересечения медиан всевозможных прямоугольных треугольников, гипотенуза АВ которых зафиксирована.

В неравнобедренном прямоугольном треугольнике из вершины прямого угла проведены медиана, биссектриса и высота.
а)Докажите, что биссектриса делит угол между медианой и высотой пополам.
б) Покажите, что верно и обратное, т.е. если из вершины С неравнобедренного треугольника проведена биссектриса, которая делит угол между медианой и высотой, проведенными из той же вершины, пополам, то угол С — прямой.

Доказательство утверждения а)

Доказательство утверждения б)

На гипотенузе прямоугольного треугольника как на стороне во внешнюю сторону построен квадрат. Докажите, что отрезок, соединяющий вершину прямого угла треугольника с центром квадрата, делит этот угол пополам.

Дополнительное построение

Исторические комментарии
Исчисление прямоугольных треугольников Виета и его интерпретация

Авторские учебные материалы для старшеклассников, студентов и аспирантов

Источник