Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно 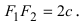
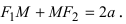
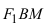
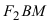
соответственно. Следовательно, согласно определению имеем
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 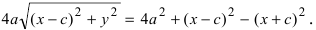
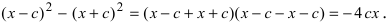
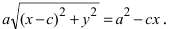
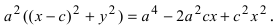
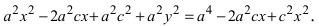
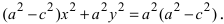
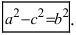
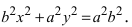
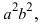
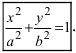
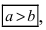
Определение: Найденные точки называются вершинами эллипса.
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если 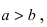
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству 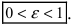
Если 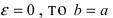
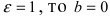
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр 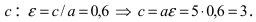
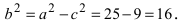
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса 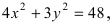
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
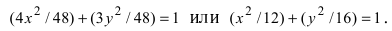
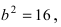
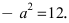
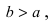
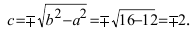
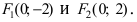
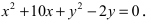
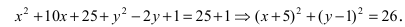
Построим в декартовой системе координат треугольник 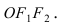
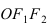
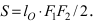
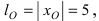
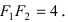
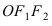
где 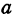
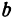
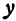
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное 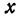
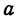
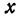
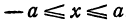
При 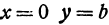
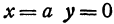
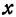

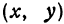
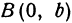
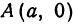
Полученная линия называется эллипсом. Число 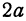
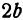
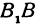
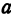
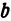
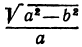
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Возьмем две плоскости, пересекающиеся под углом 
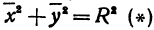
Пусть точка 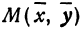
Обозначим проекцию точки 
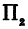
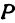
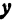
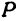

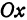
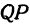
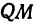
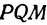
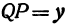
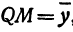
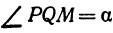
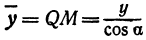

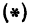
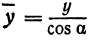
а это есть уравнение эллипса с полуосями 
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей 
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам 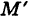
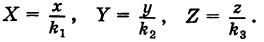
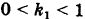
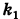
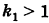
где 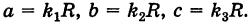
Величины 
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Окружностью называется замкнутая плоская кривая, все точки которой равноудалены от заданной точки (центра окружности). Расстояние от любой точки окружности (Pleft( right)) до ее центра называется радиусом . Центр окружности и сама окружность лежат в одной и той же плоскости. Уравнение окружности радиуса (R) с центром в начале координат ( каноническое уравнение окружности ) имеет вид
( + = ).
Уравнение окружности радиуса (R) с центром в произвольной точке (Aleft( right)) записывается как
( <left( right)^2> + <left( right)^2> = ).
Уравнение окружности, проходящей через три точки , записывается в виде: (left| <begin<*<20>> <+ > & x & y & 1\ & <> & <> & 1\ & <> & <> & 1\ & <> & <> & 1 end> right| = 0.\)
Здесь (Aleft( <,> right)), (Bleft( <,> right)), (Cleft( <,> right)) − три точки, лежащие на окружности.
Уравнение окружности в параметрической форме
( left < beginx &= R cos t \ y &= Rsin t end right., ;;0 le t le 2pi),
где (x), (y) − координаты точек окружности, (R) − радиус окружности, (t) − параметр.
Общее уравнение окружности
(A + A + Dx + Ey + F = 0)
при условии (A ne 0), (D^2 + E^2 > 4AF).
Центр окружности расположен в точке с координатами (left( right)), где
(a = — largefrac<<2A>>normalsize,;;b = — largefrac<<2A>>normalsize.)
Радиус окружности равен
(R = sqrt <largefrac<<+ — 4AF>><<2left| A right|>>normalsize> )
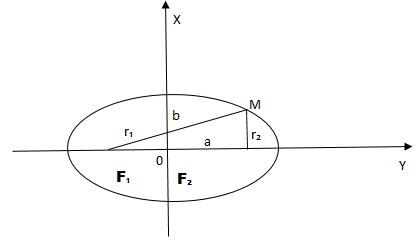
Эллипсом называется плоская кривая, для каждой точки которой сумма расстояний до двух заданных точек ( фокусов эллипса ) постоянна. Расстояние между фокусами называется фокусным расстоянием и обозначается через (2c). Середина отрезка, соединяющего фокусы, называется центром эллипса . У эллипса есть две оси симметрии: первая или фокальная ось, проходящая через фокусы, и перпендикулярная ей вторая ось. Точки пересечения этих осей с эллипсом называются вершинами . Отрезок, соединяющий центр эллипса с вершиной, называется полуосью эллипса . Большая полуось обозначается через (a), малая полуось − через (b). Эллипс, центр которого находится в начале координат, а полуоси лежат на координатных прямых, описывается следующим каноническим уравнением :
(largefrac<<>><<>>normalsize + largefrac<<>><<>>normalsize = 1.)
Сумма расстояний от любой точки эллипса до его фокусов постоянна:
( + = 2a),
где (), () − расстояния от произвольной точки (Pleft( right)) до фокусов () и (), (a) − большая полуось эллипса.
Соотношение между полуосями эллипса и фокусным расстоянием
( = + ),
где (a) − большая полуось эллипса, (b) − малая полуось, (c) − половина фокусного расстояния.
Уравнение эллипса в параметрической форме
( left < beginx &= acos t \ y &= bsin t end right., ;;0 le t le 2pi),
где (a), (b) − полуоси эллипса, (t) − параметр.
Общее уравнение эллипса
(A + Bxy + C + Dx + Ey + F = 0),
где ( — 4AC Общее уравнение эллипса, полуоси которого параллельны осям координат
(A + C + Dx + Ey + F = 0),
где (AC > 0).
Периметр эллипса
(L = 4aEleft( e right)),
где (a) − большая полуось эллипса, (e) − эксцентриситет, (E) − полный эллиптический интеграл второго рода.
Площадь эллипса
(S = pi ab)
Кривые второго порядка в математике с примерами решения и образцами выполнения
1) всякая прямая в прямоугольной системе координат определяется уравнением первой степени относительно переменных и ;
2) всякое уравнение первой степени в прямоугольной системе координат определяет прямую и притом единственную.
Мы займемся изучением линий, определяемых уравнениями второй степени относительно текущих
координат и :
Такие линии называются линиями (кривыми) второго порядка. Коэффициенты уравнения (1) могут принимать различные действительные значения, исключая одновременное равенство и нулю (в противном случае уравнение (1) не будет уравнением второй степени).
Окружность и ее уравнения
Как известно, Окружностью называется множество всех точек плоскости, одинаково удаленных от данной точки, называемой центром.
Пусть дана окружность радиуса с центром в точке требуется составить ее уравнение.
Возьмем на данной окружности произвольную точку
(рис. 38). Имеем
удовлетворяют координаты произвольной точки окружности. Более того, этому уравнению не удовлетворяют координаты никакой точки, не лежащей на окружности, так как и . Следовательно, (I) есть уравнение окружности радиуса с центром в точке . Если центр окружности находится на оси , т. е. если , то уравнение (I) примет вид
Если центр окружности находится на оси т. е. если то уравнение (I) примет вид
Наконец, если центр окружности находится в начале координат, т. е. если , то уравнение (I) примет вид
Пример:
Составить уравнение окружности радиуса с центром в точке .
Решение:
Имеем: . Подставив эти значения в уравнение (I), найдем .
Из изложенного выше следует, что уравнение окружности является уравнением второй степени относительно переменных и , как бы она ни была расположена в плоскости . Уравнение окружности (I) является частным случаем общего уравнения второй степени с
переменными
В самом деле, раскрыв скобки в уравнении (1), получим
Справедливо следующее утверждение: если в уравнении (5) , то Уравнение (5) определяет окружность.
Действительно, разделив уравнение (5) почленно на , получим:
Дополним группы членов, стоящие в скобках, до полного квадрата:
Положим Так как, по условию, то можно положить
Получим
Если в уравнении то оно определяет точку (говорят также, что окружность вырождается в точку). Если же то уравнению (5) не удовлетворяет ни одна пара действительных чисел (говорят также, что уравнение (5) определяет «мнимую» окружность).
Пример:
Найти координаты центра и радиус окружности
Решение:
Сравнивая данное уравнение с уравнением (1), находим: . Следовательно, .
Пример:
Установить, какое из уравнений:
определяет окружность. Найти координаты центра и радиус каждой из них.
Решение:
Первое уравнение не определяет окружность, потому что . Во втором уравнении . Однако и оно не определяет окружность, потому что . В третьем уравнении условия выполняются. Для окончательного вывода преобразуем его так:
Это уравнение, а следовательно, и уравнение 3), определяет окружность с центром и радиусом .
В четвертом уравнении также выполняются условия Однако преобразовав его к виду
, устанавливаем, что оно не определяет никакой линии.
Эллипс и его каноническое уравнение
Определение:
Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек той же плоскости, называемых фокусами, есть величина постоянная, большая расстояния между фокусами.
Составим уравнение эллипса, фокусы и которого лежат на оси
и находятся на одинаковом расстоянии от
начала координат (рис. 39).
Обозначив , получим Пусть произвольная точка эллипса. Расстояния называются фокальными радиусами точки . Положим
тогда, согласно определению эллипса, — величина постоянная и По формуле расстояния между двумя точками находим:
Подставив найденные значения и в равенство (1), получим уравнение эллипса:
Преобразуем уравнение (3) следующим образом!
Имеем: положим
последнее уравнение примет вид
Так как координаты и любой точки эллипса удовлетворяют уравнению (3),то они удовлетворяют уравнению (5).
Покажем, что справедливо и обратное: если координаты точки удовлетворяют уравнению (5) то она принадлежит эллипсу.
Пусть — произвольная точка, координаты которой удовлетворяют уравнению (5). Так как из (5)
то откуда
Подставив (6) в соотношения (2) и проведя необходимые упрощения, получим
Но так как то
т. е. точка действительно принадлежит эллипсу.
Уравнение (5) называется каноническим уравнением
эллипса.
Исследование формы эллипса по его уравнению
Определим форму эллипса по его каноническому
уравнению
1. Координаты точки не удовлетворяют уравнению (1), поэтому эллипс, определяемый этим уравнением не проходит через начало координат.
Найдем точки пересечения эллипса с осями координат. Положив в уравнении (1) , найдем Следовательно, эллипс пересекает ось в точках . Положив в уравнении (1) , найдем точки пересечения эллипса с осью :
(рис.40).
3. Так как в уравнение (1) переменные и входят только в четных степенях, то эллипс симметричен относительно координатных осей, а следовательно, и относительно начала координат.
4. Определим область изменения переменных и . В предыдущем параграфе (см. (7)) мы уже показали, что
Аналогично, переписав уравнение эллипса (1) в виде
получим откуда или
Таким образом, все точки эллипса находятся внутри прямоугольника, ограниченного прямыми
(см. рис, 40).
5. Переписав уравнение (1) соответственно в вида
мы видим, что при возрастании от 0 до величина убывает от до 0, а при возрастании от 0 до величина убывает от до 0. Эллипс имеет форму, изображенную на рис. 41.
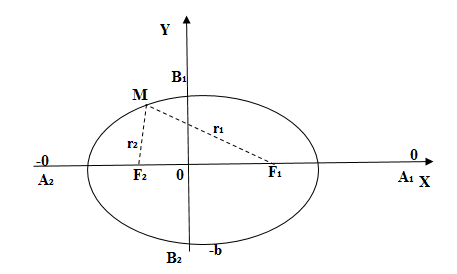
Точки пересечения эллипса с осями координат
называются вершинами эллипса. Отрезок называется
большой осью эллипса, а отрезок — малой осью. Оси являются осями симметрии эллипса, а точка — центром симметрии (или просто центром) эллипса.
Пример:
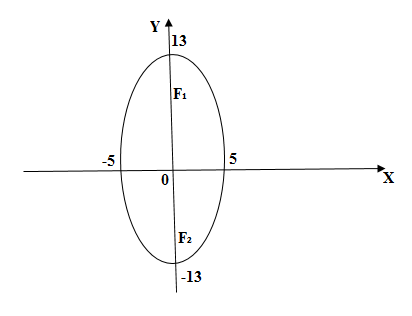
Определить длину осей и координаты фокусов эллипса
Решение:
Разделив обе части данного уравнения на 1176, приведем его к каноническому виду
Следовательно,
Пример:
Составить каноническое уравнение эллипса, если фокусное расстояние равно 10, а малая ось равна 6.
Решение:
Другие сведения об эллипсе
Мы рассмотрели эллипс, у которого Если же то уравнение
определяет эллипс, фокусы которого лежат на оси (рис. 42). В этом случае длина большой оси равна , а малой . Кроме того, связаны между собой равенством
Определение:
Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большой оси и обозначается буквой .
Если , то, по определению,
При имеем
Из формул (3) и (4) следует . При этом с
увеличением разности между полуосями и увеличивается соответствующим образом и эксцентриситет
эллипса, приближаясь к единице; при уменьшении разности между и уменьшается и эксцентриситет, приближаясь к нулю. Таким образом, по величине эксцентриситета можно судить о форме эллипса: чем больше эксцентриситет, тем более вытянут эллипс; чем меньше эксцентриситет, тем круглее эллипс. В частности, если и уравнение эллипса примет вид , которое определяет окружность с центром в начале координат. Таким образом, окружность можно рассматривать как частный случай эллипса, у которого полуоси равны между собой, а следовательно, эксцентриситет равен нулю.
Из рис. 43, на котором изображены эллипсы и окружность , хорошо видна зависимость формы эллипса от его эксцентриситета. В заключение поясним, как можно построить эллипс
Для этого на осях координат строим вершины эллипса . Затем из вершины (можно из ) радиусом, равным а, на большой оси делаем засечки (рис. 44). Это будут фокусы эллипса, потому что . Далее, берем нерастяжимую нить, длина которой равна , и закрепляем ее концы в найденных фокусах. Натягиваем нить
острием карандаша и описываем кривую, оставляя нить все время в натянутом состоянии.
Пример:
Составить каноническое уравнение эллипса, фокусы которого лежат на оси , если его большая ось равна 14 и
Решение. Так как фокусы лежат на оси , то По
формуле (2) находим:
Следовательно, искомое уравнение, будет
Гипербола и ее каноническое уравнение
Определение:
Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек той же плоскости, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Составим уравнение гиперболы, фокусы которой лежат на оси и находятся на одинаковом расстоянии от начала координат (рис. 45).
Обозначив получим , Пусть
— произвольная точка гиперболы.
Расстояния называются фокальными радиусами точки . Согласно определению гиперболы
где — величина постоянная и Подставив
в равенство (1), получим уравнение гиперболы
Уравнение (2) можно привести к более простому виду; для этого преобразуем его следующим образом:
Имеем: . Положим
тогда последнее равенство принимает вид
Так как координаты и любой точки гиперболы удовлетворяют уравнению (2), то они удовлетворяют и уравнению (4).
Как и в случае эллипса (см. конец § 2), можно показать, что справедливо и обратное: если координаты точки удовлетворяют уравнению (4), то она принадлежит гиперболе.
Уравнение (4) называется каноническим уравнением гиперболы.
Исследование формы гиперболы по ее уравнению
Определим форму гиперболы по ее каноническому уравнению
1. Координаты точки (0; 0) не удовлетворяют уравнению (1), поэтому гипербола, определяемая этим уравнением, не проходит через начало координат.
2. Найдем точки пересечения гиперболы с осями координат. Положив в уравнении (1) , найдем . Следовательно, гипербола пересекает ось в точках . Положив в уравнение (1) , получим , а это означает, что система
не имеет действительных решений. Следовательно, гипербола не пересекает ось .
3. Так как в уравнение (1) переменные и входят только в четных степенях, то гипербола симметрична относительно координатных осей, а следовательно, и относительно начала координат.
4. Определим область изменения переменных и ; для этого из уравнения. (1) находим:
Имеем: или ; из (3) следует, что — любое действительное число. Таким образом, все точки гиперболы расположены слева от прямой и справа от прямой
5. Из (2) следует также, что
Это означает, что гипербола состоит из двух ветвей, одна из которых расположена справа от прямой , а другая слева от прямой .
Гипербола имеет форму, изображенную на рис. 46.
Точки пересечения гиперболы с осью называются вершинами гиперболы. Отрезок Рис. 46.
соединяющий вершины гиперболы, называется действительной осью. Отрезок , , называется мнимой осью. Число называется действительной полуосью, число — мнимой полуосью. Оси являются осями симметрии гиперболы. Точка пересечения осей симметрии называется центром гиперболы. У гиперболы (1) фокусы всегда находятся на действительной оси.
Пример:
Составить уравнение гиперболы, вершины которой находятся в точках , а расстояние между фокусами равно 14.
Решение:
Имеем: . По формуле находим
Следовательно, искомое уравнение будет
Пример:
Составить каноническое уравнение гиперболы с фокусами на оси , если длина ее действительной оси равна 16 и гипербола проходит через точку .
Решение:
Имеем: . Положив в уравнении (1) , получим
Другие сведения о гиперболе
Асимптоты гиперболы
Определение:
Прямая называется
асимптотой кривой при , если
Аналогично определяется асимптота при . Докажем, что прямые
являются асимптотами гиперболы
при
Так как прямые (2) и гипербола (3) симметричны относительно координатных осей, то достаточно рассмотреть только те точки указанных линий, которые расположены в первой четверти (рис. 47). Напишем уравнения прямых (2) и гиперболы (3), соответствую*
щие первой четверти:
Положив найдем:
Следовательно, прямые (2) являются асимптотами гиперболы (3).
Отметим, что асимптоты (2) совпадают с диагоналям прямоугольника, стороны которого параллельны осям и и равны соответственно и , а его центр находится в начале координат. При этом ветви гиперболы расположены внутри вертикальных углов,
образуемых асимптотами, и приближаются сколь угодно близко к асимптотам (рис.48).
Пример:
Составить уравнение гиперболы, проходящей через точку и, имеющей асимптоты
Решение:
Из данных уравнений асимптот имеем:
Заменив в уравнении гиперболы переменные и координатами точки и его найденным значением, получим:
Следовательно, искомое уравнение будет
Эксцентриситет гиперболы
Определение:
Эксцентриситетом гиперболы называется отношение расстояния между фокусами
к длине действительной оси и обозначается буквой :
Из формулы (§ 5) имеем поэтому
Пример:
Найти эксцентриситет гиперболы .
Решение:
По формуле (5) находим
Равносторонняя гипербола
Гипербола называется равносторонней, если длины ее полуосей равны между собой, т. е. . В этом случае уравнение гиперболы принимает вид
Равносторонняя гипербола определяется одним пара*
метром и асимптотами являются биссектрисы координатных углов:
У всех равносторонних гипербол один и тот же эксцентриситет:
Так как асимптоты равносторонней гиперболы взаимно перпендикулярны, их можно принять за оси новой системы координат полученной в результате поворота осей старой системы вокруг начала координат на угол (рис.49).
Составим уравнение равносторонней гиперболы относительно новой системы координат . Для этого воспользуемся формулами
(4) § 3 гл. 2:
Положив , получим:
Учитывая равенство (6), получим
Уравнение (8) называется уравнением равносторонней гиперболы, отнесенной к своим асимптотам.
Из уравнения (8) следует, что переменные — величины обратно пропорциональные. Таким образом, равносторонняя гипербола, отнесенная к своим асимптотам, представляет собой график обратно пропорциональной зависимости.
Пример:
Составить каноническое уравнение
равносторонней гиперболы, проходящей через точку .
Решение:
Заменив в уравнении (6) переменные координатами точки , получим:
Следовательно, искомое уравнение будет
Парабола и ее каноническое уравнение
Определение:
Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и от данной прямой, не проходящей через данную точку и
называемой директрисой.
Составим уравнение параболы, фокус которой лежит на оси , а
директриса параллельна оси и удалена от нее на такое же расстояние, как и фокус от начала координат (рис.50).
Расстояние от фокуса до директрисы называется параметром параболы и обозначается через . Из рис. 50 видно, что следовательно, фокус имеет координаты , а уравнение директрисы имеет вид , или
Пусть — произвольная точка параболы. Соединим точки
и и проведем . Непосредственно из рис. 50 видно, что
а по формуле расстояния между двумя точками
согласно определению параболы
Уравнение (1) является искомым уравнением параболы. Для упрощения уравнения (1) преобразуем его следующим образом:
Последнее уравнение эквивалентно
Координаты точки параболы удовлетворяют уравнению (1), а следовательно, и уравнению (3).
Покажем, что справедливо и обратное: если координаты точки удовлетворяют уравнению (3), то она принадлежит параболе.
Но так как из (3) , и в левой части последнего уравнения можно оставить знак «плюс», т. е. оно является исходным уравнением параболы (1).
Уравнение (3) называется каноническим уравнением параболы.
Исследование формы параболы по ее уравнению
Определим форму параболы по ее каноническому уравнению
1. Координаты точки удовлетворяют уравнению (1), следовательно, парабола, определяемая этим уравнением, проходит через начало координат.
2. Так как в уравнение (1) переменная входит только в четной степени, то парабола симметрична относительно оси абсцисс.
Так как . Следовательно, парабола расположена справа от оси .
4. При возрастании абсциссы ордината изменяется от , т. е. точки параболы неограниченно удаляются как от оси , так и от оси .
Парабола имеет форму, изображенную на рис. 51.
Ось является осью симметрии параболы. Точка пересечения параболы с осью симметрии называется вершиной параболы. Отрезок называется фокальным радиусом точки .
5. Если фокус параболы лежит слева от оси , а директриса справа от нее, то ветви параболы расположены слева от оси (рис. 52, а). Уравнение такой параболы имеет вид
Координаты ее фокуса будут ; директриса определяется уравнением .
6. Если фокус параболы имеет координаты , а директриса задана уравнением , то ветви параболы направлены вверх (рис. 52,6), а ее уравнение имеет вид
7. Наконец, если фокус параболы имеет координаты а директриса задана уравнением , то ветви параболы направлены вниз (рис. 52, в), а ее уравнение имеет вид
Пример:
Дана парабола . Найти координаты ее фокуса и составить уравнение директрисы.
Решение:
Данная парабола симметрична относительно оси , ветви направлены вверх. Сравнивая данное уравнение с уравнением (3), находим:
Следовательно, фокус имеет координаты , а уравнение директрисы будет , или .
Пример:
Составить уравнение параболы с вершиной в начале координат, директриса которой задана уравнением .
Решение:
Из условия задачи следует, что парабола симметрична относительно оси и ветви расположены слева от оси , поэтому искомое уравнение имеет вид . Так как и, следовательно,
Параллельный перенос параболы
Пусть дана парабола с вершиной в точке , ось симметрии которой параллельна оси , а ветви направлены вверх (рис. 53).
Требуется составить ее уравнение. Сделаем параллельный перенос осей координат, поместив начало в точке . Относительно новой системы координат парабола определяется уравнением
Чтобы получить уравнение данной параболы относительно старой системы, воспользуемся формулами преобразования прямоугольных координат при параллельном переносе;
Подставив значения из формул (2) в уравнение (1), получим
Преобразуем это уравнение следующим образом:
С уравнением параболы вида (5) читатель хорошо знаком по школьному курсу.
Пример 1. Составить уравнение параболы с вершиной в точке и с фокусом в точке .
Решение. Вершина и фокус данной параболы лежат на прямой, параллельной оси (у них абсциссы одинаковы), ветви параболы направлены вверх (ордината фокуса больше ординаты вершины), расстояние фокуса от вершины равно
Заменив в уравнении (3) и координатами точки и его найденным значением, получим:
Пример:
Дано уравнение параболы
Привести его к каноническому виду.
Решение:
Разрешив данное уравнение относительно переменной , получим
Сравнивая это уравнение с уравнением (5), находим Из формул (4) имеем:
следовательно, Подставляем найденные значения в уравнение (3):
Положив получим т. е, каноническое уравнение данной параболы.
Уравнения кривых второго порядка как частные случаи общего уравнения второй степени с двумя переменными
Выше было установлено, что уравнение окружности есть частный случай общего уравнения второй степени с переменными и :
Покажем, что и канонические уравнения эллипса, гиперболы и параболы являются частными случаями уравнения (1). В самом деле:
1) при и уравнение (1) примет вид
т. е. определяет эллипс;
2) при и уравнение (1) примет вид
т. е. определяет гиперболу;
3) при и уравнение (1) примет вид т. е. определяет параболу.
Дополнение к кривым второго порядка
Пусть задана кривая, определяемая уравнением второй степени
где — действительные числа; и одновременно не равны нулю. Эта кривая называется кривой второго порядка.
Приведем еще одно определение кривой второго порядка.
Геометрическое место точек плоскости, для которых отношение их расстояний до заданной точки, называемой фокусом, и до заданной прямой, называемой директрисой, есть величина постоянная, равная , является кривой 2-го порядка с эксцентриситетом, равным . Если , то кривая второго порядка — эллипс; — парабола; — гипербола.
Эллипс
Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек и этой плоскости, называемых фокусами, есть величина постоянная, равная . Если фокусы совпадают, то эллипс представляет собой окружность.
Каноническое уравнение эллипса: .
Если , то эллипс расположен вдоль оси ; если , то эллипс расположен вдоль оси (рис. 9а, 9б).
Если , то, сделав замену , перейдем в «штрихованную» систему координат, в которой уравнение будет иметь канонический вид:
Декартова прямоугольная система координат, в которой уравнение эллипса имеет канонический вид, называется канонической.
Точки пересечения эллипса с осями координат называются вершинами эллипса. Расстояния от начала координат до вершин и называются соответственно большой и малой полуосями эллипса.
Центр симметрии эллипса, совпадающий с началом координат, называется центром эллипса.
Если — расстояние от начала координат канонической системы координат до фокусов, то .
Отношение называется эксцентриситетом эллипса.
Расстояние от произвольной точки , лежащей на эллипсе, до каждого из фокусов является линейной функцией от ее абсциссы, т.е. .
С эллипсом связаны две замечательные прямые, называемые его директрисами. Их уравнения в канонической системе имеют вид .
Гипербола
Гиперболой называется геометрическое место точек плоскости, для которых абсолютная величина разности расстояний до двух фиксированных точек и этой плоскости, называемых фокусами, есть величина постоянная, равная (рис. 10).
Декартова прямоугольная система координат, в которой уравнение гиперболы имеет канонический вид, называется канонической. Каноническое уравнение гиперболы:
Ось абсцисс канонической системы пересекает гиперболу в точках, называемых вершинами гиперболы. Ось ординат не пересекает гиперболу. и называются вещественной и мнимой полуосями гиперболы. Центр симметрии гиперболы, совпадающий с началом координат, называется центром гиперболы.
Если — расстояние от начала координат канонической системы координат до фокусов гиперболы, то .
Отношение называется эксцентриситетом гиперболы.
Расстояние от произвольной точки , лежащей на гиперболе, до каждого из фокусов равно .
Гипербола с равными полуосями называется равносторонней.
Прямые с уравнениями в канонической системе называются асимптотами гиперболы.
Прямые называют директрисами гиперболы в канонической системе координат.
Парабола
Параболой называется геометрическое место точек плоскости, для которых расстояние до некоторой фиксированной точки этой плоскости равно расстоянию до некоторой фиксированной прямой, также расположенной в рассматриваемой плоскости (рис. 11).
Указанная точка называется фокусом параболы, а фиксированная прямая — директрисой параболы.
Система координат, в которой парабола имеет канонический вид, называется канонической, а ось — осью параболы.
Каноническое уравнение параболы:
Парабола проходит через начало канонической системы координат. Эта точка называется вершиной параболы.
Фокус параболы имеет координаты .
Директрисой параболы называется прямая в канонической системе координат.
Расстояние от произвольной точки параболы до фокуса равно .
Пример задачи решаемой с применением кривых второго порядка
Линия задана уравнением в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от до и придавая значения через промежуток ; 2) найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс — с полярной осью, привести его к каноническому виду; 3) по уравнению в декартовой прямоугольной системе координат определить, какая это линия.
Решение:
1) Вычисляя значения с точностью до сотых при указанных значениях , получим таблицу:
Используя полученные табличные значения, построим кривую в полярной системе координат (рис. 17).
2) Используя формулы перехода
из полярной в декартовую систему координат, получим: .
Возведем левую и правую части в квадрат: Выделим полный квадрат и приведем к каноническому виду: , где
3) Это эллипс, смещенный на вдоль оси .
Ответ: эллипс , где
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Возможно вам будут полезны эти страницы:
Кривая второго порядка и её определение
Кривая второго порядка — это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением
Окружность и ее уравнение
Окружностью называется геометрическое место точек, одинаково удаленных от одной точки, называемой центром.
Пользуясь этим определением, выведем уравнение окружности. Пусть радиус ее равен r, а центр находится в точке
О1(а; b). Возьмем на окружности произвольную точку М(х; у) (рис. 27).
По формуле расстояния между двумя точками можем написать:
или, после возведения обеих частей равенства в квадрат,
Так как точка М нами взята произвольно, а радиус r — величина постоянная, то равенство (1) справедливо для всех точек окружности, т. е. координаты любой ее точки удовлетворяют этому равенству. А если так, то равенство (1) нужно рассматривать как уравнение окружности.
В уравнении (1) а и b — координаты центра окружности, а х и у — текущие координаты.
Если положить а = 0, то уравнение (1) обратится в следующее:
и будет определять окружность с центром на оси Оу (рис. 28).
При b = 0 уравнение (1) примет вид
и будет определять окружность с центром на оси Ох (рис. 29).
Наконец, при а = 0 и b = 0 уравнение (1) преобразуется в следующее:
и будет определять окружность с центром в начале координат (рис. 30).
Можно построить окружность, имея ее уравнение. Пусть, например, требуется построить окружность
Перепишем это уравнение в следующем виде:
сравнивая это уравнение с(1), видим, что координаты центра окружности суть (2; — 3) и радиус ее r = 3. Построив
точку О1(2;—3), опишем из нее радиусом, равным 3 единицам масштаба, искомую окружность (рис. 31).
Уравнение окружности как частный вид общего уравнения второй степени
Раскрыв скобки в уравнении (1) , можем написать:
Умножив все члены последнего равенства на А, получим:
тогда уравнение (1) окружности примет вид
Уравнение (2) является частным случаем общего уравнения второй степени с двумя переменными. В самом деле, сравним уравнение (2) с общим уравнением второй степени с двумя переменными, имеющим, как известно, следующий вид:
Мы видим, что уравнение (2) отличается от уравнения (3) только тем, что у первого коэффициенты при х2 и у2 одинаковы и отсутствует член, содержащий произведение ху.
Таким образом, окружность определяется общим уравнением второй степени с двумя переменными, если в нем коэффициенты при х2 и у2 равны между собой и отсутствует член с произведением ху.
Обратно, уравнение вида (2), вообще говоря, определяет окружность. Убедимся в этом на примере. Пусть дано уравнение
Перепишем его в следующем виде:
и преобразуем двучлены, стоящие в скобках, в полные квадраты суммы и разности, прибавив к первому 4, ко второму 16. Чтобы равенство при этом не нарушилось, увеличим и правую часть его на сумму 4+16. Получим:
Последнее равенство является уравнением окружности, имеющей радиус, равный 5, и центр в точке О1(-2; 4).
Бывают однако случаи, когда уравнение (2) при некоторых значениях коэффициентов не определяет окружности; например, уравнению
удовлетворяют координаты единственной точки (0; 0), а уравнению
не удовлетворяют координаты ни одной точки, так как сумма квадратов действительных чисел не может иметь отрицательного значения.
Пример:
и хорда Найти длину этой хорды.
Решение:
Так как концы хорды являются общими точками окружности и хорды, то их координаты удовлетворяют как уравнению первой, так и уравнению второй линии. Поэтому, чтобы найти эти координаты, нужно решить совместно уравнения окружности и хорды. Подставив значение
в уравнение окружности, получим:
Находим значение у:
Итак, концами хорды служат точки с координатами (4; 3) и (6; 1).
По формуле расстояния между двумя точками можем определить искомую длину хорды
Эллипс и его уравнение
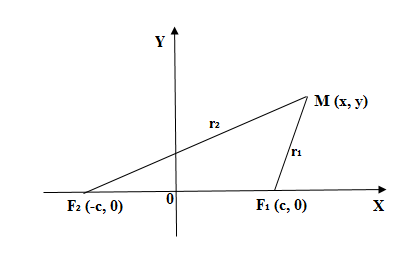
Эллипсом называется геометрическое место точек, сумма расстояний каждой из которых от двух данных точек, называемых фокусами, есть величина постоянная (и болыиая, чем расстояние между фокусами).
Пусть, например, на эллипсе взяты точки М1, M2, M3, М4 и т. д. (рис. 32). Если фокусы обозначить через F и F1, то согласно данному определению можно написать:
Геометрическое место точек, обладающих вышеуказанным свойствам (1), и есть эллипс.
На основании определения эллипса составим его уравнение. Для этого выберем систему координат следующим образом. За ось Ох примем прямую, проходящую через фокусы F и F1, а за ось Оу — прямую перпендикулярную
к FF1 и проведенную через середину отрезка FF1 (рис. 33). Обозначим расстояние F1F между фокусами через 2с, тогда координаты фокусов будут:
Возьмем на эллипсе произвольную точку М(х;у). Обозначим постоянную величину суммы расстояний каждой точки от фокусов через 2а, тогда
По формуле расстояния между двумя точками найдем:
Теперь равенство (2) перепишется следующим образом:
и будет представлять уравнение эллипса в принятой системе координат.
Упростим уравнение (3). Для этого перенесем один из радикалов в правую часть уравнения:
Возведем обе части этого равенства в квадрат:
Приведем подобные члены:
Сократив на 4 и снова возведя в квадрат обе части равенства, получим:
Перенесем все члены, содержащие х и у, в левую часть равенства, остальные члены — в правую:
Но согласно определению эллипса
Из последнего неравенства следует, что а потому эту разность можно обозначить через Подставив это обозначение в равенство (4), найдем:
Наконец, разделим все члены последнего равенства на окончательно получим:
где х и у — текущие координаты точек эллипса, а
Уравнение (6) и есть простейший вид уравнения эллипса *).
*) Уравнение (6) получилось в результате двукратного возведения в квадрат уравнения (3), благодаря чему, вообще говоря, возможно появление посторонних корней. Можно показать, что уравнение (6) не имеет посторонних корней, т. е. любая точка, координаты которой удовлетворяют уравнению (6), лежит на эллипсе.
Исследование уравнения эллипса
Определим сначала у из уравнения (5) :
Из того же уравнения (5) найдем:
Рассмотрим теперь равенства (1) и (2).
I. Пусть
*) | х | означает, что х берется по абсолютной величине; таким образом, запись | х |
Тогда каждому значению у, как мы видим из равенства (2), отвечают два значения х равные по абсолютной величине, но с разными знаками. Отсюда следует, что каждому значению у соответствуют на эллипсе две точки, симметричные относительно оси Оу.
Из сказанного заключаем: эллипс симметричен относительно координатных осей.
II. Найдем точки пересечения эллипса с осью Ох. Пусть
тогда из равенства (2) имеем:
Отсюда следует: эллипс пересекает ось Ох в двух точках, координаты которых (а; 0) и (— а; 0) (точки А и А1 на рис. 34).
III. Найдем точки пересечения эллипса с осью Оу. Пусть
тогда из равенства (1) имеем:
Отсюда заключаем, что эллипс пересекает ось Оу в двух точках, координаты которых (0; b) и (0; —b) (точки В и В1 на рис. 35).
IV. Пусть х принимает такие значения, что
тогда выражение под корнем в равенстве (1) будет отрицательным, и, следовательно, у будет иметь мнимые значения. А это значит, что не существует точек эллипса, абсциссы которых удовлетворяют условию (3), т. е. эллипс расположен внутри полосы, заключенной между прямыми х = + а и х = — а (рис. 34, прямые КL и РQ).
Если же положить
то из равенства (2) получим для х мнимые значения. Это говорит о том, что точки, удовлетворяющие условию (4), на эллипсе не лежат, т. е. эллипс заключен между прямыми у = + b и у = — b (рис. 35, прямые РК и QL .
Из сказанного следует, что все точка эллипса лежат внутри прямоугольника, стороны которого параллельны координатным осям и имеют длины, равные 2а и 2b, а диагонали пересекаются в начале координат (рис. 36).
Эллипс имеет форму, показанную на рис. 37, Точки A,, A1, В и В1 называются вершинами эллипса, а точка О — его центром. Отрезок А1А = 2а называется его большой осью, а отрезок В1В = 2b — малой осью, Отрезки FМ и F1М носят название фокальных радиусов точки М.
Эксцентриситет эллипса
Эксцентриситетом эллипса называется отношение расстояния между его фокусами к длине большой оси, т. e.
Эксцентриситет обычно обозначают буквой е. Таким образом,
Но согласно формуле (7)
Поэтому для определения эксцентриситета может служить
Так как 0 а уравнение (6) представляет эллипс, фокусы которого лежат на оси Оу; в этом случае его большая ось равна 2 b , а малая 2 а . В соответствии с этим формула (7) и формулы (1) и (2) настоящей лекции примут такой вид:
Пример:
Определить длину его осей, координаты вершин и фокусов, а также величину эксцентриситета.
Решение:
Разделив обе части данного уравнения на 400, получим:
Итак, большая ось эллипса а малая
Координаты вершин его будут:
Чтобы найти координаты фокусов, нужно узнать величину
Из равенства (7) имеем:
Следовательно, координаты фокусов будут:
Наконец, по формуле (1) настоящей лекции находим:
Связь эллипса с окружностью
Положим, что полуоси эллипса равны между собой, т. е. а = b, тогда уравнение эллипса примет вид
Полученное уравнение, как известно, определяет окружность радиуса, равного а.
Посмотрим, чему будет равен эксцентриситет в этом случае; полагая в формуле (2)
Отсюда заключаем, что окружность есть частный случай эллипса, у которого полуоси равны между собой, а следовательно, эксцентриситет равен нулю.
Гипербола и ее уравнение
Гиперболой называется геометрическое место точек, разность расстояний каждой из которых от двух данных точек, называемых фокусами, есть величина постоянная (эта постоянная берется по абсолютному значению, причем она меньше расстояния между фокусами и не равна нулю).
Пусть, например, точки М1, М2, M3, М4 лежат на гиперболе, фокусы которой находятся в точках F и F1 (рис. 39). Тогда, согласно данному выше определению, можно написать:
Пользуясь определением гиперболы, выведем ее уравнение.
Примем за ось Ох прямую, проходящую через фокусы F и F1 (рис. 40), а за ось Оу — прямую, перпендикулярную к отрезку F1F и делящую его пополам.
Положим F1F = 2c тогда координаты фокусов будут
Возьмем на гиперболе произвольную точку М(х; у) и обозначим величину разности расстояний каждой точки от фокусов через 2а; тогда
По формуле расстояния между двумя точками найдем:
и, заменив в равенстве (2) F1М и FМ их выражениями, напишем:
Это и есть уравнение гиперболы относительно выбранной системы координат, так как оно согласно равенствам (1) справедливо для любой ее точки.
*) Знак + берется в случае, если F1М > FМ , и знак —, если F1М
Возведем обе части уравнения в квадрат:
Приведем подобные члены:
Сократив на 4, снова возведем в квадрат обе части уравнения; получим:
Перенесем в левую часть члены, содержащие х и у, а остальные члены в правую:
Согласно определению гиперболы
При условии (5) разность имеет только положительное значение, а потому ее можно обозначить через
Сделав это в равенстве (4), получим:
Разделив последнее равенство на найдем окончательно:
где х и у— текущие координаты точек гиперболы, а
Равенство (7) представляет собой простейший вид уравнения гиперболы *).
*) Как и в случае эллипса, можно показать, что уравнение (7) равносильно уравнению (3), т. е. не имеет посторонних корней.
Исследование уравнения гиперболы
Из уравнения (6) имеем:
Из этого же уравнения (6) находим:
Исследуем уравнения (1) и (2) для выяснения геометрической формы гиперболы.
I. Найдем точки пересечения гиперболы с осью Ох. Для этого полагаем, у = 0 и из уравнения (2) получаем:
Отсюда следует: гипербола пересекает ось Ох в двух точках, координаты которых (а; 0) и (— а; 0) (рис. 41, точки А и А1).
II. Положим в уравнении (1)
тогда у получит мнимое значение, а это значит, что на гиперболе нет точек, удовлетворяющих условию (3). Следовательно, в полосе между прямыми х = + а и х = — а (прямые KL и РQ на рис. 41) нет точек гиперболы
III. Пусть
тогда из равенства (1) найдем для каждого х два действительных значения у, равных по абсолютной величине, но с противоположными знаками. А это значит, что каждому значению х, удовлетворяющему неравенству (4), соответствуют на нашей кривой две точки, симметричные относительно оси Ох.
Следовательно, гипербола симметрична относительно оси Ох.
С другой стороны, для каждого значения у из равенства (2) найдем два действительных значения х, равных по абсолютной величине, но противоположных по знаку, т. е. каждому значению у на гиперболе соответствуют две точки, симметричные относительно оси Оу.
Следовательно, гипербола 1 симметрична относительно оси Оу.
IV. Если в уравнении (1) давать х значения, заключенные между +a и то величина у будет изменяться от 0 до : т. е. в этом случае каждому значению х соответствуют на кривой две точки, симметричные относительно оси Ох и отстоящие друг от друга тем дальше, чем больше величина абсциссы. Таким образом, можно сказать, что гипербола имеет бесконечную ветвь, расположенную справа от прямой х = с.
Если же давать х значения, заключенные между — а и , то у будет изменяться опять от 0 до а это значит, что, как в предыдущем случае, гипербола имеет бесконечную ветвь, но идущую влево от прямой х = — а. Итак, гипербола есть кривая, состоящая из двух ветвей, простирающихся в бесконечность.
Из всего изложенного следует, что гипербола
состоит из двух симметричных относительно оси Оу бесконечных ветвей, одна из которых расположена справа от
прямой х = + а, а другая слева от прямой х = — а. Каждая из этих ветвей симметрична относительно оси Ох (рис. 42).
Точки А(а; 0) и А1(- а; 0) называются вершинами гиперболы, а точка О (0; 0) — ее центром.
Отрезок АА1 = 2а носит название действительной или вещественной оси гиперболы в отличие от оси ВВ1 = 2b, называемой мнимой *).
*) Отрезок ВВ1 = 2b называется мнимой осью, так как на нем нет точек гиперболы.
Отрезки F1М и FМ — фокальные радиусы точки М.
Эксцентриситет гиперболы
Эксцентриситетом гиперболы называется отношение расстояния между фокусами к длине вещественной оси, т. е.
Эксцентриситет гиперболы, так же как и для эллипса, обозначается буквой е:
Но согласно равенству (8)
поэтому формулу (1) можно представить в следующем виде:
Так как для гиперболы с > а , то дробь
а потому эксцентриситет гиперболы больше единицы.
Асимптоты гиперболы
Построим на осях гиперболы
прямоугольник LQRS со сторонами, равными 2а и 2b и проведем его диагонали LR и QS продолжив их по обе стороны (рис. 43).
Прямая LR проходит через начало координат, поэтому ее уравнение будет:
Но угловой коэффициент
Заменив в уравнении (1) найденным его значением, получим уравнение прямой LR в следующем виде:
Прямая QS также определяется уравнением (1), но угловой коэффициент ее будет уже другой, а именно:
Таким образом, уравнение прямой QS будет:
Обычно уравнения (2) и (3) записывают следующим образом:
Между прямыми, представленными уравнениями (4), и гиперболой существует связь; выясним ее.
Решим совместно способом подстановки уравнения (4) и
уравнение гиперболы
что невозможно, так как
Таким образом, прямые (4) х2 уа
и гипербола не имеют общих точек, т. е. прямые (4) не пересекают гиперболу.
Возьмем на прямой LR и на гиперболе точки М и N, расположенные в первом координатном углу и имеющие одну и ту же абсциссу. Ординатой точки М служит РМ; обозначим ее через Y в отличие от ординаты точки N которую обозначим буквой у. Из уравнения (2) можно написать:
Из уравнения гиперболы имеем:
и посмотрим, как она будет изменяться при возрастании абсциссы. Для этого умножим и разделим правую часть последнего равенства на выражение
Пусть величина х в равенстве (5) бесконечно возрастает, тогда знаменатель дроби также бесконечно растет, а сама дробь уменьшается, приближаясь к нулю. Таким образом, гипотенуза NМ и, следовательно, катет NT в прямоугольном треугольнике МNТ стремится к нулю. Из сказанного делаем вывод: при неограниченном возрастании абсциссы х гипербола приближается к прямой LR как угодно близко, нигде ее не пересекая.
Так как прямые LR и QS, а также точки гиперболы симметричны относительно оси Ох, то можно сказать, что и часть гиперболы, расположенная в четвертом координатном углу, как угодно близко подходит к прямой QS , нигде ее не пересекая.
Вывод, сделанный для правой ветви гиперболы, справедлив и для ее левой ветви благодаря той же симметричности прямых (4) и гиперболы относительно координатных осей.
называются асимптотами гиперболы.
Из сказанного в настоящей лекции можно сделать заключение, что гипербола расположена всеми своими точками внутри вертикальных углов, образуемых асимптотами, и нигде не выходит за их границы. Этим обстоятельством можно воспользоваться для построения гиперболы в случае, если не требуется точного, а достаточно только приближенного ее изображения; для этого, нарисив асимптоты, нужно провести плавную кривую линию, постепенно приближая ее к асимптотам.
Пример:
Дана гипербола
Узнать, лежит ли точка A(2; 1,5) на какой-либо ее асимптоте.
Решение:
Из данного уравнения имеем:
Следовательно, уравнения асимптот будут:
Так как точка А лежит согласно условию в первом координатном углу, то она может принадлежать только асимптоте, определяемой уравнением
Подставив в него вместо х и у координаты точки А, получим тождество:
Значит, точка А лежит на указанной асимптоте гиперболы.
Равносторонняя гипербола
Если в уравнении гиперболы
положим а = b то это уравнение примет вид
Уравнение (1) определяет гиперболу, у которой полуоси равны между собой. Такая гипербола называется равносторонней. Уравнения асимптот в этом случае будут:
так как отношение
Как видно из уравнения (2), угловые коэффициенты асимптот равны + 1 и —1 . Если обозначить углы, образуемые асимптотами с положительным направлением оси Ох, соответственно через а и а1 (рис. 44), то
Следовательно, угол между асимптотами будет:
Отсюда заключаем: асимптоты равносторонней гиперболы взаимно перпендикулярны.
Уравнение равносторонней гиперболы, отнесенной к асимптотам
Так как асимптоты равносторонней гиперболы взаимно перпендикулярны, то их можно принять за оси прямоугольной системы координат и рассматривать гиперболу по отношению к этим новым осям. Выведем уравнение равносторонней гиперболы для этого случая.
Пусть дана равносторонняя гипербола. Тогда ее уравнение по отношению к координатным осям Ох и Оу (рис. 45)
выразится, как было пока-* у зано в , в виде
Взяв на гиперболе произвольную точку М (х; у) и построив ее координаты, будем иметь:
Примем теперь за оси координат асимптоты гиперболы: ОХ— за ось абсцисс, ОY — за ось ординат. Опустив перпендикуляр МС на новую ось абсцисс, найдем:
Выразим новые координаты X н Y точки М через старые х и у. Для этого из точки А проведем и
Обратим внимание на то, что в образовавшихся прямоугольных треугольниках АМВ и АОD
как углы, образованные взаимно перпендикулярными прямыми. Но
Из рисежа имеем:
Перемножив равенства (2) и (3) и приняв во внимание равенство (1), получим:
Положим для краткости
тогда равенство (4) перепишется так:
где m— постоянная величина.
Таково уравнение равносторонней гиперболы, если за оси координат принять ее асимптоты.
Как видно из уравнения (5), переменные X и Y — величины обратно пропорциональные, а потому можно сказать, что равносторонняя гипербола ху = m представляет собой график обратно пропорциональной зависимости между переменными величинами.
Парабола и ее простейшее уравнение
Параболой называется геометрическое место точек, каждая из которых одинаково удалена от точки, называемой фокусом, и от прямой, называемой директрисой <при условии, что фокус не лежит на директрисе).
Пусть точки М1 М2, М3, М4 лежат на параболе (рис. 46).
Если точка F изображает фокус, а прямая АВ— директрису, то согласно данному выше определению можем написать:
Выведем уравнение параболы, пользуясь ее определением. Для этого выберем систему координат, приняв за ось Ох прямую, проведенную через точку F (фокус) перпендикулярно к директрисе АВ, а за
ось Оу — прямую, проходящую через середину отрезка КF перпендикулярно к последнему (рис. 47). Обозначим
тогда координаты фокуса F будут
Возьмем на параболе произвольную точку М(x; у) расстояния ее от фокуса F и от директрисы АВ будут выражаться соответственно отрезками FМ и МN. Согласно определению параболы, можем написать:
Применяя формулу расстояния между двумя точками и приняв во внимание, что точка N имеет координаты , найдем:
Заменив FМ и МN в равенстве (1) их выражениями, получим:
Это и есть уравнение параболы относительно выбранной системы координат, так как оно справедливо для любой ее точки.
Упростим уравнение (2). Для этого возведем обе части его в квадрат:
Приведя подобные члены, получим простейшее уравнение параболы
*) Можно показать, что уравнение (3) равносильно уравнению (2). Величина р называется параметром параболы.
Исследование уравнения параболы
Из уравнения (3) найдем:
Исследуем уравнение (1) для выяснения геометрической формы нашей кривой, полагая р > 0.
I. Положим
Отсюда следует: парабола проходит через начало координат.
II. Если х 0, то у имеет два действительных значения, равных по абсолютной величине, но с разными знаками. Это значит, что каждому положительному значению х на параболе соответствуют две точки, расположенные симметрично относительно оси Ох.
Следовательно, парабола симметрична относительно оси Ох.
IV. Пусть х неограниченно возрастает, тогда и будет неограниченно расти, т. е. точки параболы с перемещением вправо от оси Оу неограниченно удаляются вверх и вниз от оси Ох.
Итак, парабола состоит из бесконечных ветвей.
Вышеизложенное позволяет представить параболу, как показано на рис. 48.
Точка О называется вершиной параболы, отрезок FМ — фокальным радиусом точки М параболы, а бесконечная прямая Ох является ее осью симметрии.
Если директрису параболы поместить справа от начала координат, то фокус и ветви ее расположатся как показано на рисеже 49.
При этом абсциссы точек параболы будут удовлетворять условию
а потому ее уравнение примет вид:
Парабола может быть симметрична и относительно оси Оу в этом случае фокус ее будет лежать па оси ординат, а директрисой будет прямая, параллельная оси Ох. Как видно при этом условии координатные оси поменяются ролями, и уравнение параболы примет вид
если ветви ее направлены вверх (рис. 50), и
если ветви направлены вниз (рис. 51).
Пример:
Найти координаты ее фокуса и написать уравнение директрисы.
Решение:
Данная парабола симметрична относительно оси Ох и расположена направо от оси Оу. Из уравнения находим:
Расстояние фокуса от начала координат равно , поэтому абсцисса фокуса будет Итак, фокус находится в точке
Директрисой служит прямая, параллельная оси Оу и отстоящая от последней на расстоянии Следовательно,
уравнение директрисы параболы будет х = — 3.
Пример:
Фокус параболы с вершиной в начале координат лежит в точке F(0; —4). Написать уравнение этой параболы.
Решение:
Согласно условию данная парабола симметрична относительно оси Оу, а ветви ее направлены вниз, поэтому искомое уравнение найдется из (3). Так как
и уравнение параболы будет:
Уравнение параболы со смещенной вершиной и осью, параллельной оси Оу
Возьмем уравнения параболы (2) и (3) и запишем их в следующем виде:
Положив в уравнении (1)
Уравнение (2) определяет параболу, ветви которой направлены вверх, если А > О, вниз, если А
Возьмем на параболе произвольную точку М(х; у). Опустив из нее перпендикуляр МР на ось Ох, будем иметь:
Проведем через О1 прямые О1Х и QY, параллельные координатным осям Ох и Оу, и положим временно, что прямые О1Х и О1Y служат осями новой системы координат. Обозначим координаты точки М в этой системе через X и Y, т. е.
Уравнение параболы в новой системе координат напишется следующим образом:
Чтобы найти ее уравнение относительно прежних осей Ох и Оу, нужно X и Y выразить через х и y. Так как
Подставив в уравнение (3) найденные значения X и Y, получим:
Упростим уравнение (4); для этого раскроем в нем скобки.
тогда уравнение (5) примет вид
Это—уравнение параболы с вершиной, лежащей в любой точке плоскости, и с осью симметрии, параллельной оси Оу.
Рассмотрим частные случаи.
Пусть абсцисса вершины параболы a = 0; тогда величина В в равенстве (6) также будет нулем и уравнение (8) примет следующий вид:
Полученное уравнение определяет параболу, у которой вершина лежит на оси Оу, являющейся в то же время и ее осью симметрии (рис. 53).
Положим, что одна из точек параболы (исключая ее вершину) лежит в начале координат; тогда координаты (0; 0) должны удовлетворять уравнению (8). Заменив в нем х и у нулями, найдем С=0. В этом случае уравнение (8) получит вид
и будет определять параболу, проходящую через начало координат (рис. 54).
Заметим, что и уравнение (2) можно рассматривать как частный случай уравнения (8). Действительно, положив в равенствах (6) и (7)
вследствие чего уравнение (8) преобразуется в следующее:
Из сказанного следует, что парабола, у которой ось симметрии параллельна оси Оу или совпадает с ней, определяется уравнением
при любых значениях А, В и С, кроме А = 0.
Убедимся на примере, что справедливо и обратное утверждение: всякое уравнение вида (8) определяет параболу с осью симметрии, параллельной оси Оу.
Пусть дано уравнение
Преобразуем его следующим образом:
тогда уравнение (10) примет вид:
Уравнение (11) имеет такой же вид, как и уравнение (2), поэтому оно, а следовательно, и уравнение (9) определяют параболу, у которой ось симметрии параллельна оси Оу.
Для построения параболы, определяемой уравнением вида (8), можно использовать обычный прием, применяемый для вычерчивания графиков функций, а именно: дав х ряд значений, вычислить значения у, а затем, построив точки по найденным координатам, провести через них плавную линию.
Пример:
Решение:
Прежде всего найдем абсциссы точек пересечения данной параболы с осью Ох; положив у = 0, получим:
Так как найденные точки симметричны относительно оси параболы, то вершина последней, находясь на этой оси, имеет 0 + 4 0
абсциссу, равную ордината же ее
Этих трех точек достаточно для приближенного изображения параболы.
Для более точного ее представления нужны дополнительные точки. Составим следующую таблицу:
Построив эти точки и прозедя через них плавную линию, получим искомую параболу (рис. 55).
Пример:
Решение:
мнимые, а потому ось Ох не пересекает данную параболу. В этом случае следует найти абсциссы точек пересечения параболы с прямой
(-1 — свободный член данного уравнения параболы)
Решая для этой цели систему уравнений
Полученные точки симметричны относительно оси параболы, поэтому абсцисса ее вершины равна ордината же ее
Присоединим к этим точкам несколько дополнительных точек. Составим таблицу:
Конические сечения
Окружность, эллипс, гипербола и парабола определяются, как мы установили в предыдущих лекциях уравнениями второй степени относительно текущих координат; поэтому их называют кривыми второго порядка. Они были известны еще древним грекам, которые изучали эти кривые, рассматривая их как результат сечения прямого кругового конуса плоскостью в следующих четырех случаях.
I. Секущая плоскость перпендикулярна к оси конуса; в сечении получается окружность (рис. 57).
II. Секущая плоскость образует с осью конуса угол, не равный 90°, и пересекает все его образующие по одну сторону от вершины S; в сечении получается эллипс (рис. 58).
III. Секущая плоскость параллельна какой-либо образующей конуса; при этом получается кривая, называемая параболой (рис. 59).
IV. Секущая плоскость пересекает обе полости конуса; при этом получаются две бесконечные ветви, образующие гиперболу (рис. 60).
Окружность, эллипс, гипербола и парабола называются коническими сечениями.
Конические сечения изучались в древности исключительно геометрическим путем, что представляло большие трудности, и только со времени Декарта, давшего метод координат, изучение их значительно упростилось.
Кривая второго порядка и её вычисление
Уравнение линии. Кривые второго порядка. Окружность. Эллипс. Гипербола. Парабола. Приведение к каноническому виду.
Уравнение линии в декартовых и полярных координатах
В лекции 3 было введено понятие неявной функции, задаваемой уравнением вида F(x,y) = 0.
Определение 6.1. Множество точек плоскости, координаты которых удовлетворяют некоторому уравнению
(6.1) F(x;y) = 0
называется линией (плоской кривой).
Не всякое уравнение определяет линию. Например, уравнение x² + y² = -1 не определяет никакой линии. Кроме того, линия может состоять из отдельных точек. Так, например, уравнению x² + y² = 0 удовлетворяет только начало координат.
Линия не обязательно является графиком функции. Так, например, уравнение x² + y² = 1 определяет окружность с центром в начале координат и радиуса 1 (т.к. d = = 1, расстояние от начала координат равно 1). Однако это не будет графиком функции у от х, т.к. каждому х, |x| ≤ 1, соответствует два значения у: у = ±, т.е. линия задается двумя функциями у = (верхняя полуокружность) и у = — (нижняя полуокружность).
Уравнение произвольной окружности с центром в точке M(a;b) и радиусом R будет иметь вид:
(6.2) (х — а)² + (у- b)² = R²,
т.к. окружность радиусом R есть геометрическое место точек плоскости, находящихся на расстоянии R от центра, т.е. в соответствии с формулой ( 6.2) d = = R.
В частности, окружность с центром в начале координат, радиусом R, описывается уравнением
x² + y² = R².
Пример 6.1. Какую линию описывает уравнение x² + y² = Rx?
Решение: Перенося Rx в левую часть и выделяя полный квадрат, получаем:
x² + y² = Rx ⇔ X2 — Rx + у² = 0 ⇔ x² — Rx + ⇔
(х — ) + y² = .
Ответ: данное уравнение описывает окружность с центром в точке M(;0) и радиусом .
Линия может определяться на плоскости уравнением как в декартовых, так и в полярных координатах: F(; r) = 0. Если при этом зависимость r от обладает тем свойством, что каждому значению из области определения соответствует единственное значение r, то данная линия будет графиком функции r от : r = f().
Пример 6.2. Построить график функции, заданной в полярных координатах уравнением r = 2 sin3, ∈ (—∞; ∞).
Решение: Составим таблицу некоторых значений этой функции:
| 0 | ||||||||
| r | 0 | 1 | 2 | 1 | 0 | -2 |
Рис. 70. График функции r = 2 sin 3 в декартовых координатах
Далее, пользуясь тем, что из вида графика функции r = 2 sin 3, приведенного в декартовых координатах на рис. 70, следует, что неотрицательные значения г повторяются на промежутках ∈ [0; ], ∈ [;π], ∈ [-;] и т. д.. Отсюда заключаем, что если в полярных координатах построить график в секторе ∈ [0; ], то в секторах ∈ [; π], ∈ [— ; ] и т. д. вид графика будет аналогичный, а в секторах ∈ (; ), ∈ ;0) и т.д. графика не будет, т.к. там r Рис. 71. График функции r = 2 sin 3 в полярных координатах
Такой график называют называют “трехлепестковая роза”.
Кривые второго порядка:
Определение 6.2. Кривой второго порядка называется линия, определяемая в декартовых координатах уравнением:
(6.3) Ax² + 2Bxy + Cy² + 2Dx + 2Ey + F = O.
Здесь коэффициенты — действительные числа и, по крайней мере, одно из чисел A₁B или C не равно нулю. Удобство таких обозначений для коэффициентов (2В, 2D, 2Е) станет ясно позже.
Всего существует три ’’реальных” кривых второго порядка: эллипс, (окружность — частный случай эллипса) гипербола и парабола, не считая такие линии, как ’’пара пересекающихся прямых” (ху = 0), «пара параллельных прямых” ((x — у)² — 4), ’’точка” ((x — 5)² + (у — 1)² = 0), ’’прямая” (х — 1)² = 0) и ’’мнимые кривые” (x² + y² + 5 = 0), которым не соответствует ни одна точка.
Окружность
Ранее было получено уравнение ( 6.2) окружности с центром в точке M(а; b), радиусом R. Это уравнение вида ( 6.3), т.е. окружность есть кривая второго порядка — можно показать, что уравнение (6.3), в котором A = C и B = O c помощью дополнения до полного квадрата каждой группы членов Ax² + 2Dx и By² + 2Еу приводится к виду (6.2), определяющему окружность радиуса R, или к виду: (х — а)² + (у — b)² = -R², не определяющему линию при R ≠ 0. Покажем это на примере.
Пример:
Показать, что уравнение 2x² + 2y² — 4x + 8y — 13 = 0 определяет окружность.
Решение: Поделив обе части на 2, получим уравнение в виде: x² + y² — 2x + 4y — 6,5 = 0 или, выделяя полный квадрат: (x² — 2х + 1) + (у² + 4y + 4) = 11,5 ⇔ (х — 1)² + (у + 2)² =11,5. Мы получим уравнение окружности с центром M(1; —2) и радиусом R = √11,5.
Пример:
Показать, что уравнение х² + у² + 6х — 6у + 22 = 0 не определяет никакой линии.
Решение:
Аналогично предыдущему, выделяя полный квадрат, получаем: х² + у² + 6х — 6у + 22 = 0 ⇔ (х² + 6х + 9) + (у² — 6у + 9) = — 4 ⇔ (x + 3)² + (y — 3)² =-4.
Эллипс
Определение:
Эллипсом называется множество всех точек плоскости, сумма расстояний каждой из которых от двух данных точек этой плоскости, называемых фокусами, равна постоянной величине.
Обозначим фокусы F₁ и F₁, расстояние между ними 2с, а сумму расстояний до них от точек эллипса через 2а (2а > 2с). Выберем декартову систему координат как показано на рис. 72. По определению эллипса: MF₁ + MF₂ = 2а. Пользуясь формулой (2.6) получаем:
Рис. 72. Фокусы эллипса и гиперболы
Обозначив b² = a² — с² > 0, получаем: b²x² + a²y² — a²b² или:
(6.4)
Уравнение ( 6.4) называется каноническим уравнением эллипса, а и b — полуосями, а — большая полуось, b — малая, т.к. b = Рис. 73. Эллипс
Так как 2а > 2с, то ε т.е. тем меньше эллипс вытянут вдоль фокальной оси Ох. В пределе, при ε → 0,a = b и получается окружность x² + у² = а² радиусом а При этом с = = 0, т.е. F₁ — F₂ = 0. Если эллипс расположен так, что центр его симметрии находится в точке P(x₀; y₀), а полуоси параллельны осям координат, то, перейдя к новым координатам X = х — х₀, У = у — у₀, начало которых совпадает с точкой Р, а оси параллельны исходным (см. п. 2.8), получим, что в новых координатах эллипс описывается каноническим уравнением Уравнение такого эллипса в старых координатах будет:
(6.5)
Гипербола
Определение 6.4. Гиперболой называется множество всех точек плоскости, модуль разности расстояний каждой из которых от двух данных точек этой плоскости, называемых фокусами, равен постоянной величине.
Обозначим фокусы F₁ и F₂, расстояние между ними 2с, а модуль разности расстояний до них от точек гиперболы через 2a (2c > 2a > 0). Выберем декартову систему координат, как показано на рис. 72. По определению гиперболы: MF₁ — MF₂ = ±2а. Пользуясь формулой (2.6), аналогично тому, как это было сделано для эллипса, получаем:
= ±2a ⇒ (а² — c²)x² + a²y² = a²(a² — с²). Обозначив b² = с² — a² > 0 (сравните с выводом формулы ( 6.4) для эллипса), получаем: -b²x² + a²y² = -b²a², или:
Уравнение (6.6) называется каноническим уравнением гиперболы, а и b — полуосями, а — действительной полуосью, b — мнимой. Так как х и у входят в уравнение только в четных степенях, гипербола симметрична относительно осей Ox и Оу. Выразив у из уравнения ( 6.6), получаем: , |x| ≥ а, что означает, что гипербола состоит из двух симметричных половин, верхней у = и нижней у = — . При х = а у = 0, при возрастании х от 0 до +∞, у для верхней части возрастает от 0 до +∞. C учетом симметрии, получаем линию, изображенную на рис. 74.
Точки пересечения гиперболы с осью Ox (фокальной осью) называются ее вершинами A₂(а;0), A₁(-a;0). C осью ординат гипербола не пересекается, поэтому фокальная ось называется действительной осью (а — действительная полуось), а перпендикулярная ей ось — мнимой осью (b — мнимая полуось). Можно показать, что при неограниченном возрастании абсциссы точка гиперболы неограниченно приближается к прямой у = (изображена на рис. 74 пунктиром). Такая прямая, к которой неограниченно приближается некоторая линия, называется асимптотой. Из соображений симметрии вытекает, что у гиперболы две асимптоты: у = и у =-, изображенные на рис. 74 пунктиром. Прямоугольник, с центром в начале координат, со сторонами 2а и 2b, параллельными осям, называется основным. Асимптоты являются его диагоналями.
Рис. 74. Гипербола
Отношение называется эксцентриситетом гиперболы. Т.к. 2α 1. Эксцентриситет определяет форму гиперболы: чем меньше е, тем более вытянут в направлении фокальной оси ее основной прямоугольник (= = — 1 = ε² — 1). Если а = b, гипербола называется равносторонней (равнобочной). Для нее х² — у² = а², асимптоты: у = х, у = —х, ε = = √2. Если центр гиперболы (центр ее симметрии) находится в точке P(x₀; y₀), a оси параллельны осям координат, то, применяя параллельный перенос координат (п. 2.8), аналогично тому, как это было сделано для эллипса, получим уравнение гиперболы:
(6.7)
Уравнение асимптот такой гиперболы будет: у — y₀ =
Парабола
Определение:
Параболой называется множество всех точек плоскости, равноудаленных от данной точки F, называемой фокусом, и данной прямой d, называемой директрисой (F ∉ d).
Обозначим расстояние от фокуса до директрисы р. Эта величина называется параметром параболы. Выберем декартову систему координат как показано на рис. 75.
По определению параболы MF=MN. Из рис. 75. ясно, что:
Рис. 75. Фокус и директриса параболы
Приравнивая, получаем:
(6.8) у² = 2рх
Уравнение ( 6.8) называется каноническим уравнением параболы. Т.к. у входит в уравнение в четной степени, парабола симметрична относительно оси Ох. Выразив у из уравнения, получаем: у = , х ≥ 0. При х =0 у = 0, при возрастании х от 0 до +∞ у для верхней части возрастает от 0 до +∞. C учетом симметрии получаем линию, изображенную на рис. 76.
Ось симметрии параболы называется фокальной осью (ось Ox на рис. 76), точка пересечения пораболы с ней называется вершиной пораболы (точка О на рис. 76). Если вершина параболы находится в точке P(x₀; у₀), фокальная ось параллельна и одинаково направлена с осью Ox и расстояние от директрисы до фокуса равно Р, то с помощью параллельного переноса осей координат нетрудно получить уравнение такой параболы:
(6.9) (y — y₀)² = 2p(x -х₀)
Пример:
Найти фокус, директрису, фокальную ось для параболы у= 4x².
Рис. 76. Парабола
Решение:
Как известно, осью симметрии параболы у = х² является ось Оу, а вершиной — точка О, поэтому фокальной осью будет ось Оу, вершиной — начало координат.
Для определения фокуса и директрисы запишем уравнение данной параболы в виде: x² = y, откуда 2р =; р =. Поэтому фокус имеет координаты F(0; ), а директриса — уравнение у = — (см. рис. 77).
Рис. 77. График параболы у = 4х²
Понятие о приведении общего уравнения второго порядка к каноническому виду
Если в общем уравнении кривой второго порядка ( 6.3)
Ax² + 2Bxy + Cy² + 2Dx + 2Ey +F = 0
коэффициент 2B ≠ 0, то методами, которые будут изложены позже (лекция 34) это уравнение преобразуется к виду, в котором отсутствует член с произведением координат (т.е. 2В — 0).
Для приведения к каноническому виду уравнения ( 6.3), в котором 2В = 0, необходимо дополнить члены, содержащие х и у, до полных квадратов.
Если при этом (В = 0) А = С, то получится окружность (пример 6.3), точка или мнимая окружность (пример 6.4).
Если при этом (В = 0) A ≠ C и A ∙ C > 0, то получится эллипс (пример 6.8) или мнимый эллипс.
Если при этом (В = 0) A ≠ C и A ∙ C Рис. 78. Гипербола
Пример:
Приведите к каноническому виду уравнение и определите вид кривой: x² — 6x — 4y + 29 = 0.
Решение:
Выделим полный квадрат: x² — 6x — 4y + 29 = 0 ⇔ x² — 6x + 9 = 4y — 20 ⇔ (x — 3)² = 4(у — 5). Сделав замену координат X =х — 3, Y = у — 5 мы получим каноническое уравнение параболы X² = 4Y с осью OY и параметром р = 2. Таким образом исходная парабола имела вершину A(3; 5) и ось х = 3 параллельную оси Oy (рис. 79).
Пример:
Приведите к каноническому виду уравнение и определите вид кривой: x² + 4y² + 2x — 24y + 21 =0.
Решение:
Выделив полный квадрат, получим уравнение: (x + 1)² + 4(у — 3)² = 16. Сделав замену координат: X = х + 1, Y = y — 3, получим каноническое уравнение эллипса: X² + AY² ⇔ = 1 с параметрами а = 4, b = 2. Таким образом, исходный эллипс имел центр A( —1;3) и полуоси а = 4, b = 2 (рис. 80).
Рис. 79. Решение примера 6.7 Рис. 80. Решение примера 6.8
Решение заданий на тему: Кривые второго порядка
Пример:
Составьте уравнение окружности, имеющей центр 0(2; —5) и радиус R = 4.
Решение:
В соответствии с формулой (6.2) искомое уравнение имеет вид: (х — 2)² + (у + 5)² = 16.
Ответ: (х — 2)² + (у + 5)² = 16.
Пример:
Составьте уравнение эллипса, зная, что сумма полуосей равна 8 и расстояние между фокусами равно 8.
Решение:
Из условия имеем: a + b = 8, 2c = 8. C учетом того, что b² = а² — с², находим с = 4, а = 5, b = 3. Искомое уравнение эллипса будет: .
Ответ:
Пример:
Составьте уравнение гиперболы, зная, что фокусы F₁(10;0) и F₂(-10; 0) и что гипербола проходит через точку M(12; 3√5)
Решение:
Из условия имеем: с = 10, |MF₁ — MF₂|= 2а ⇔ 2а = ⇔ а = 8. C учетом того, что b² = с² — а², находим а = 8, с = 10, b = 6. Искомое уравнение гиперболы будет: .
Ответ: .
Пример:
Составьте уравнение параболы, зная, что фокус имеет координаты (5;0), а ось ординат является директрисой.
Решение:
Поскольку расстояние от директрисы параболы до ее полюса равно параметру р, а вершина находится на середине, из условия следует, что р = 5 и вершина расположена в точке A(2,5;0). Таким образом, в новых координатах X = х — 2,5; У = у каноническое уравнение параболы будет: Y² = 10Х, а в старых координатах: у² = 10(х — 2,5).
Ответ: y² = 10x — 25.
Пример:
Приведите к каноническому виду уравнение x² + y² — 2х + 6у — 5 = 0, определите вид кривой и ее параметры.
Решение:
Выделим полный квадрат: х² — 2х + у² + 6у — 5 = 0 ⇔ x² — 2x + 1 + у² + 6у + 9 — 1 — 9 — 5 = 0 ⇔ (х — 1)² + (у + 3)² = 15
В соответствии с формулой (6.2) это есть уравнение окружности с центром в точке A(1; -3), радиусом √5.
Ответ: (х — 1)² + (у + 3)² = 15.
Пример:
Приведите к каноническому виду уравнение x² + 4у² + 4х — 16у — 8 = 0, определите вид кривой и ее параметры:
Решение:
Выделим полный квадрат: x² + 4х + 4у² — 16y -8 = 0 ⇔ x²+4x + 4 + 4y²- 16y + 16-4-16-8 = 0 ⇔ (x + 2)² + 4(y²-4у+ 4) -28 ⇔ (х + 2)² + 4(y — 2)² = 28 ⇔ = 1. Сделав замену координат: X = x +2, Y = у — 2, в новых координатах получим уравнение эллипса с полуосями а = √28 и b = √7. Таким образом, в старых координатах эллипс имеет центр A(—2; 2) и полуоси а = 2√7 и b = √7.
Ответ: = 1.
Пример:
Приведите к каноническому виду уравнение x² + 2y² + 8x — 4 = 0, определите вид кривой и ее параметры.
Решение:
Выделим полный квадрат:
x²+2y²+8x-4 = 0 ⇔ x²+8x+16+2y²-16-4 =0 ⇔ (x+4)²+2y2-20 = 0 ⇔ =1
Сделав замену координат X = х + 4, Y — у, убеждаемся, что эта кривая — эллипс, с полуосями a = 2√5 и b = √10 и центром A(-4;0).
Ответ: =1
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Answering part of the question with code
How to find the center of an ellipse by coordinates of a pair of points on its curve.
This is a TypeScript function which is based on the excellent accepted answer by Sergey Illinsky above (which ends somewhat halfway through, IMHO). It calculates the center of an ellipse with given radii, given the condition that both provided points a and b must lie on the circumference of the ellipse. Since there are (almost) always two solutions to this problem, the code choses the solution that places the ellipse «above» the two points:
(Note that the ellipse must have major and minor axis parallel to the horizontal/vertical)
/**
* We're in 2D, so that's what our vertors look like
*/
export type Point = [number, number];
/**
* Calculates the vector that connects the two points
*/
function deltaXY (from: Point, to: Point): Point {
return [to[0]-from[0], to[1]-from[1]];
}
/**
* Calculates the sum of an arbitrary amount of vertors
*/
function vecAdd (...vectors: Point[]): Point {
return vectors.reduce((acc, curr) => [acc[0]+curr[0], acc[1]+curr[1]], [0, 0]);
}
/**
* Given two points a and b, as well as ellipsis radii rX and rY, this
* function calculates the center-point of the ellipse, so that it
* is "above" the two points and has them on the circumference
*/
function topLeftOfPointsCenter (a: Point, b: Point, rX: number, rY: number): Point {
const delta = deltaXY(a, b);
// Sergey's work leads up to a simple system of liner equations.
// Here, we calculate its general solution for the first of the two angles (t1)
const A = Math.asin(Math.sqrt((delta[0]/(2*rX))**2+(delta[1]/(2*rY))**2));
const B = Math.atan(-delta[0]/delta[1] * rY/rX);
const alpha = A + B;
// This may be the new center, but we don't know to which of the two
// solutions it belongs, yet
let newCenter = vecAdd(a, [
rX * Math.cos(alpha),
rY * Math.sin(alpha)
]);
// Figure out if it is the correct solution, and adjusting if not
const mean = vecAdd(a, [delta[0] * 0.5, delta[1] * 0.5]);
const factor = mean[1] > newCenter[1] ? 1 : -1;
const offMean = deltaXY(mean, newCenter);
newCenter = vecAdd(mean, [offMean[0] * factor, offMean[1] * factor]);
return newCenter;
}
This function does not check if a solution is possible, meaning whether the radii provided are large enough to even connect the two points!
Отстойные, но довольно быстрые, способы — через решение систем уравнений влоб. Типа, окружность по трем точкам, эллипс по восьми (?) точкам, перебираем комбинации все/случайным образом и усредняем результат. То, что предлагает mayorovp вторым пунктом. Почему отстойные — устойчивость плохая. Именно так мы делаем у себя — способы действительно отстойные и требуют костылей, но действительно быстрые. Разница между реальным центром и найденным таким способом намного меньше пикселя, но костылей действительно много. Например, отбирая треугольник при поиске окружности по 3-м точкам, нужно, чтобы все три точки были из разных четвертей окружности.
Я не рекомендую — кода много, а экономия оправдывает себя только на железе 20 летней давности, когда нужен околорилтайм. Для эллипса по-моему малореально вообще что-либо нормальное получить.
Универсальный способ — метод наименьших квадратов. То есть заставить компьютер подобрать такие параметры эллипса чтобы разница между эллипсом и нашими точками была минимальной. Лучше критерий сложно придумать — хотя иногда получается не то, что ожидаешь, но это скорее говорит о том, что исходные данные неправильные.
Алгоритм такой:
1. Выбираем подходящее уравнение эллипса.
2. Пишeм целевую функцию (сумма квадратов уравнения для каждой точки исходных данных). По необходимости добавляем к целевой функции дополнительные условия, типа невырождаемости эллипса в гиперболу. Типа, если условие нарушается, устремляем ее в бесконечность.
3. Выбираем минимизатор (градиентный спуск, нормальное уравнение т. д.)
4. Если результаты не устраивают по скорости или качеству, возвращаемся к п. 3 или к п. 1.
По поводу третьего пункта. В России почему-то считается, что МНК — это когда решение идет с помощью нормального уравнения (составляем матрицы и решаем (AtA)^-1*At*x=b без итераций в один присест). Это не так. Минимизировать можно каким угодно способом. Хоть генетическими алгоритмами. Нормальное уравнение хорошо тогда, когда член (AtA)^-1 получается маленькой квадратной матрицей. То есть когда параметров мало, а точек очень много. Систему уравнений для эллипса вообще к виду A*x-b=0 привести служно. Искать соответствующие статьи как это делается мне влом, поэтому я пойду влоб, в качестве минимизатора взяв стандартный матлабовский.
Используя формулы mayorovp.
%точки
xs = [1 2 3 4 5 6 7 8 9 10];
ys = [11 10 9 7 5 4 3 2 1 1];
%сначала приблизим окружностью - чтобы не вырождалось в гиперболу
%уравнение окружности
circ = @(xs, ys, x0, y0, Rsq) (xs - x0).^2 + (ys - y0).^2 - Rsq;
%целевая функция МНК
fitfunc1 = @(X) sum( ( circ(xs, ys, X(1), X(2), X(3)) ) .^2 );
%начальное приближение
x0 = mean(xs);
y0 = mean(ys);
R = 1;
result1 = fminsearch(fitfunc1, [x0 y0 R], optimset('display', 'iter'));
%уравнение эллипса
ellipse = @(xs, ys, x0, y0, A, B, C, F) A*(xs-x0).^2 + B*(xs-x0).*(ys-y0) + C*(ys-y0).^2 - F;
%целевая функция МНК
fitfunc2 = @(X) sum( ( ellipse(xs, ys, X(1), X(2), X(3), X(4), X(5), X(6))) .^2 );
%начальное приближение - найденная окружность
x0 = result1(1);
y0 = result1(2);
A = 1;
B = 0;
C = 1;
F = result1(3);
%сумма квадратов целевой функции для каждой точки
result = fminsearch(fitfunc2, [x0 y0 A B C F], optimset('display', 'iter'));
figure
hold on;
%изначальные точки
scatter(xs, ys,'b');
%эллипс
xs1 = -2:0.005:20;
ys1 = -2:0.005:20;
[xss yss] = meshgrid(xs1, ys1);
ell = abs(ellipse(xss(:), yss(:), result(1), result(2), result(3), result(4), result(5), result(6)) ) < 0.0001;
scatter(xss(ell), yss(ell),'r');
Российская кривая: коническое сечение 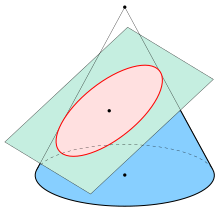


В математике, эллипс — это плоская кривая , окружающая два фокальные точки, так что для всех точек на кривой сумму двух расстояний до фокальных точек является постоянной. Таким образом, он обобщает круг , который представляет собой особый тип эллипса, в котором две точки фокусировки совпадают. Удлинение эллипса измеряется его эксцентриситетом e, числом от e = 0 (предельный случай окружности) до e = 1 (предельный случай бесконечного удлинения, больше не эллипс, а парабола ).
Эллипс имеет простое алгебраическое решение для своей площади, но только приближения для его периметра, для которого требуется интегрирование для получения точного решения.
Анали уравнение стандартного эллипса с центром в начале координат с шириной 2a и высотой 2b имеет вид:
- x 2 a 2 + y 2 b 2 = 1. { displaystyle { frac {x ^ {2 }} {a ^ {2}}} + { frac {y ^ {2}} {b ^ {2}}} = 1.}
Предполагая, что a ≥ b, фокусы равны (± c, 0) для c = a 2 — b 2 { displaystyle c = { sqrt {a ^ {2} -b ^ {2}}}}
- (x, y) = (a cos (t), b sin (t)) для 0 ≤ t ≤ 2 π. { displaystyle (x, y) = (a cos (t), b sin (t)) quad { text {for}} quad 0 leq t leq 2 pi.}
эллипсы являются закрытым типом конического сечения : плоская кривая, отслеживающая пересечение конуса с плоскостью (см. рисунок). Эллипсы имеют много общего с двумя другими формами конических сечений, параболами и гиперболами, обе из которых являются открытыми и неограниченными. Угловое поперечное сечение цилиндра также является эллипсом.
Эллипс также может быть определен в терминах одной точки фокусировки и линии за пределами эллипса, называемой направляющей : для всех точек на эллипсе отношение расстояния к фокус, расстояние до директрисы является постоянным. Это постоянное соотношение является упомянутым выше эксцентриситетом:
- e = ca = 1 — b 2 a 2 { displaystyle e = { frac {c} {a}} = { sqrt {1 — { frac {b ^ { 2}} {a ^ {2}}}}}}
.
Эллипсы распространены в физике, астрономии и инженерии. Например, орбита каждой планеты в солнечной системе представляет собой эллипс с Солнцем в одной точке фокусировки (точнее, фокус — это барицентр пары Солнце — планета). То же верно и для спутников, вращающихся вокруг планет, и для всех других систем двух астрономических тел. Формы планет и звезд часто хорошо описываются эллипсоидами. Круг, если смотреть под боковым углом, как эллипс: то есть эллипс — это изображение круга под параллельной или перспективной проекцией. Эллипс также является самой простой фигурой Лиссажу, образованной, когда горизонтальные и вертикальные движения синусоиды с одинаковой точностью: аналогичный эффект приводит к эллиптической поляризации света в оптика.
Имя λλειψις (élleipsis, «упущение») было дано Аполлонием Пергским в его Кониксах.
Содержание
- 1 Определение как геометрическое место точек
- 2 В декартовых координатах
- 2.1 Стандартное уравнение
- 2.2 Параметры
- 2.2.1 Главные оси
- 2.2.2 Линейный эксцентриситет
- 2.2.3 Эксцентриситет
- 2.2.4 Semi-latus rectum
- 2.3 Касательная
- 2.4 Сдвинутый эллипс
- 2.5 Общий эллипс
- 3 Параметрическое представление
- 3.1 Стандартное параметрическое представление
- 3.2 Рациональное представление
- 3.3 Наклон касательной как параметр
- 3.4 Общий эллипс
- 4 Полярные формы
- 4.1 Полярная форма относительно центра
- 4.2 Полярная форма относительно фокуса
- 5 Эксцентриситет и свойство директрисы
- 6 Свойство отражения от фокуса к фокусу
- 7 Сопряженные диаметры
- 7.1 Теорема Аполлония о сопряженных диаметрах
- 8 Ортогональные касательные
- 9 Рисование эллипсов
- 9.1 Построение точки де Ла Хира
- 9.2 Штифты Метод струн
- 9.3 Методы бумажной ленты
- 9.4 Аппроксимац ия соприкаса с кругами
- 9.5 Поколение Штейнера
- 9.6 Как гипотрохоида
- 10 вписанные углы и трехточечная форма
- 10.1 окружности
- 10.1.1 теорема вписанных углов для окружностей
- 10.1.2 трехточечная форма уравнения окружности
- 10.2 эллипсы
- 10.2.1 вписанные Теорема об углах для эллипсов
- 10.2.2 Трехточечная форма уравнения эллипса
- 10.1 окружности
- 11 Соотношение полюсов и полюсов
- 12 Метрические свойства
- 12.1 Площадь
- 12.2 Окружность
- 12.3 Кривизна
- 13 В геометрии треугольника
- 14 В виде плоских сечений квадрик
- 15 Приложения
- 15.1 Физика
- 15.1.1 Эллиптические отражатели и акустика
- 15.1.2 Планетарные орбиты
- 15.1.3 Гармонические осцилляторы
- 15.1.4 Просмотр фаз
- 15.1.5 Эллиптические шестерни
- 15.1.6 Оптика
- 15.2 Статистика и финансы
- 15.3 Компьютерная графика
- 15.4 Теория оптимизации
- 15.1 Физика
- 16 См. Также
- 17 Примечания
- 18 Ссылки
- 19 Внешние ссылки
Определение как геометрическое место точек
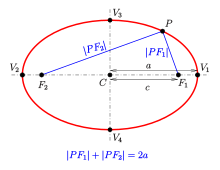
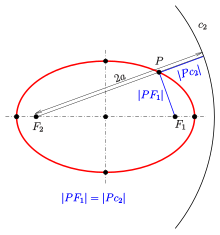
эллипс может быть определен геометрически как набор или геометрическое место точек на евклидовой плоскости:
- Даны две фиксированные точки F 1, F 2 { displaystyle F_ {1}, F_ {2}}
называется фокусами и расстояние 2 a { displaystyle 2a}
, больше, чем расстояние между фокусами, эллипс — это набор точек P { displaystyle P}
такие, что сумма расстояний | P F 1 |, | P F 2 | { displaystyle | PF_ {1} |, | PF_ {2} |}
равно 2 a { displaystyle 2a}
:E = {P ∈ R 2 ∣ | P F 2 | + | P F 1 | = 2 а}. { Displaystyle E = {P in mathbb {R} ^ {2} , mid , | PF_ {2} | + | PF_ {1} | = 2a } .}
Средняя точка C { displaystyle C}




Случай F 1 = F 2 { displaystyle F_ {1} = F_ {2}}
Уравнение | P F 2 | + | P F 1 | Знак равно 2 а { Displaystyle | PF_ {2} | + | PF_ {1} | = 2a}
- If c 2 { displaystyle c_ {2}}
— круг со средней точкой F 2 { displaystyle F_ {2}}
и радиусом 2 a { displaystyle 2a}
, тогда расстояние от точки P { displaystyle P}
до окружности c 2 { displaystyle c_ {2}}
равно расстояние до фокуса F 1 { displaystyle F_ {1}}
:
- | P F 1 | = | P c 2 |. { displaystyle | PF_ {1} | = | Pc_ {2} |.}
- | P F 1 | = | P c 2 |. { displaystyle | PF_ {1} | = | Pc_ {2} |.}
c 2 { displaystyle c_ {2}}

Используя сферы Данделина, можно доказать, что любое плоское сечение конуса с плоскостью является эллипсом, при условии, что плоскость не содержит вершины и имеет наклон меньше, чем у прямого на конусе.
В декартовых координатах
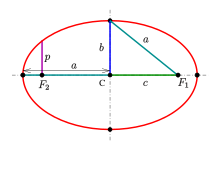
- a: большая полуось,
- b: малая полуось,
- c: линейный эксцентриситет,
- p: semi-latus rectum (обычно ℓ { displaystyle ell}
).
Стандартное уравнение
Стандартная форма эллипса в декартовых координатах предполагает, что начало координат находится в центре эллипса ось x — большая ось, и:
- фокусы — это точка F 1 = (c, 0), F 2 = (- c, 0) { displaystyle F_ {1} = (c, , 0), F_ { 2} = (- c, , 0)}
,
- вершинами являются V 1 = (a, 0), V 2 = (- a, 0) { displaystyle V_ {1} = (a, , 0), V_ {2} = (- a, , 0)}
.
для произвольной точки (x, y) { displaystyle (x, y)}




- (x — c) 2 + y 2 + (x + c) 2 + y 2 = 2 a. { displaystyle { sqrt {(xc) ^ {2} + y ^ {2}}} + { sqrt {(x + c) ^ {2} + y ^ {2}}} = 2a .}
Удаление радикалов подходящими квадратами и использованием b 2 = a 2 — c 2 { displaystyle b ^ {2} = a ^ {2} -c ^ {2}}
- x 2 a 2 + y 2 b 2 = 1, { displaystyle { frac {x ^ {2}} {a ^ {2}}} + { frac {y ^ {2}} {b ^ {2}}} = 1,}
или, решенное относительно y:
- y = ± baa 2 — x 2 = ± (a 2 — x 2) (1 — е 2). { displaystyle y = pm { frac {b} {a}} { sqrt {a ^ {2} -x ^ {2}}} = pm { sqrt { left (a ^ {2} — x ^ {2} right) left (1-e ^ {2} right)}}.}
Параметры ширины и высоты a, b { displaystyle a, ; b}




Из уравнения следует, что эллипс симметричен относительно осей координат и, следовательно, относительно начала координат.
Параметры
Главные оси
В этой статье большая и малая полуоси обозначаются a { displaystyle a}

В принципе, каноническое уравнение эллипса x 2 a 2 + y 2 b 2 = 1 { displaystyle { tfrac {x ^ {2 }} {a ^ {2}}} + { tfrac {y ^ {2}} {b ^ {2}}} = 1}




Линейный эксцентриситет
Это расстояние от центра к фокусу: c = a 2 — b 2 { displaystyle c = { sqrt {a ^ {2} -b ^ {2}}}}
Эксцентриситет
Эксцентриситет можно выразить как:
- e = ca = 1 — (ba) 2 { displaystyle e = { frac {c} {a}} = { sqrt {1- left ({ frac {b}) {a}} right) ^ {2}}}}
,
предположим г а>б. { displaystyle a>b.}

-lat7
Длина хорды, проходящей через один очаг, перпендикулярной большой оси, называется latus rectum. Половина ее составляет semi-latus rectum ℓ { displaystyle ell}
- ℓ знак равно b 2 a = a (1 — e 2). { Displaystyle ell = { frac {b ^ {2}} {a}} = a left (1-e ^ {2} right).}
Прямая полу-широта ℓ { displaystyle ell}
Касательная
Произвольная линия g { displaystyle g}


- x 1 a 2 x + y 1 b 2 y = 1. { displaystyle { frac {x_ {1}} {a ^ {2}}} x + { frac {y_ { 1}} {b ^ {2}}} y = 1.}
Векторное параметрическое уравнение касательной:
- x → = (x 1 y 1) + s (- y 1 a 2 Икс 1 б 2) { Displaystyle { vec {x}} = { begin {pmatrix} x_ {1} \ y_ {1} end {pmatrix}} + s { begin {pmatrix} ; ! — y_ {1} a ^ {2} \; x_ {1} b ^ {2} end {pmatrix}} }
с s ∈ R. { displaystyle s in mathbb {R} .}
Доказательство: Пусть (x 1, y 1) { displaystyle (x_ {1}, , y_ {1})}




- (x 1 + su) 2 a 2 + (y 1 + sv) 2 b 2 знак равно 1 ⟹ 2 s (x 1 ua 2 + y 1 vb 2) + s 2 (u 2 a 2 + v 2 b 2) = 0. { displaystyle { frac { left (x_ {1) } + su right) ^ {2}} {a ^ {2}}} + { frac { left (y_ {1} + sv right) ^ {2}} {b ^ {2}}} = 1 quad Longrightarrow quad 2s left ({ frac {x_ {1} u} {a ^ {2}}} + { frac {y_ {1} v} {b ^ {2}}} вправо) + s ^ {2} left ({ frac {u ^ {2}} {a ^ {2}}} + { frac {v ^ {2}} {b ^ {2}}} right) = 0 .}
- Тогда есть случаи:
- x 1 a 2 u + y 1 b 2 v = 0. { displaystyle { frac {x_ {1}} {a ^ {2}}} u + { frac {y_ {1}} {b ^ {2}}} v = 0.}
Затем строка g { displaystyle g}
и эллипс имеют только точка (x 1, y 1) { displaystyle (x_ {1}, , y_ {1})}
в общем, а g { displaystyle g}
— ка сательная. Касательное направление имеет перпендикулярный вектор (x 1 a 2 y 1 b 2) { displaystyle { begin {pmatrix} { frac {x_ {1}} {a ^ {2}}} { frac {y_ {1}} {b ^ {2}}} end {pmatrix}}}
, поэтому касательная линия имеет уравнение x 1 a 2 x + y 1 б 2 y = к { textstyle { frac {x_ {1}} {a ^ {2}}} x + { tfrac {y_ {1}} {b ^ {2}}} y = k}
для некоторых k { displaystyle k}
. <Времен738>(x 1, y 1) { displaystyle (x_ {1}, , y_ {1})}
находится на касательной и эллипсе, получаем k = 1 { displaystyle к = 1}
.
- x 1 a 2 u + y 1 b 2 v ≠ 0. { displaystyle { frac {x_ {1}} {a ^ {2}}} u + { frac {y_ {1) }} {b ^ {2}}} v neq 0.}
Тогда строка g { displaystyle g}
имеет вторую точку, общую с эллипсом, и является секансом.
- x 1 a 2 u + y 1 b 2 v = 0. { displaystyle { frac {x_ {1}} {a ^ {2}}} u + { frac {y_ {1}} {b ^ {2}}} v = 0.}
Используя (1), получаем, что (- y 1 a 2 x 1 b 2) { displaystyle { begin {pmatrix} -y_ {1} a ^ {2} x_ {1} b ^ {2} end {pmatrix}}}

Если (x 1, y 1) { displaystyle (x_ {1}, y_ {1})}



Сдвинутый эллипс
Если стандартный эллипс смещен так, чтобы его центр был (x ∘, y ∘) { displaystyle left (x _ { circ}, , y _ { circ} right)}
- (x — x ∘) 2 a 2 + (y — y ∘) 2 b 2 = 1. { displaystyle { frac { left (xx _ { circ} right) ^ {2}} {a ^ {2}}} + { frac { left (yy _ { circ} right)) ^ {2}} {b ^ {2}}} = 1 .}
Оси по-прежнему параллельны осям x и y.
Общий эллипс
В аналитической геометрии эллипс определяется как квадрика: набор точек (X, Y) { displaystyle (X, , Y)}
- AX 2 + BXY + CY 2 + DX + EY + F = 0 { displaystyle AX ^ {2} + BXY + CY ^ {2} + DX + EY + F = 0}
при условии B 2–4 AC < 0. {displaystyle B^{2}-4AC<0.}
Чтобы различать вырожденные случаи из невырожденного случая, пусть ∆ — детерминант
- ∆ = | A 1 2 B 1 2 D 1 2 B C 1 2 E 1 2 D 1 2 E F | = (AC — B 2 4) F + BED 4 — CD 2 4 — AE 2 4. { displaystyle Delta = { begin {vmatrix} A { frac {1} {2}} B { frac {1} {2}} D \ { frac {1} {2}} BC и { frac {1} {2}} E \ { frac {1} {2}} D { frac {1} {2}} EF end {vmatrix}} = left (AC — { frac {B ^ {2}} {4}} right) F + { frac {BED} {4}} — { frac {CD ^ {2}} {4}} — { frac {AE ^ {2}} {4}}.}
Тогда эллипс является невырожденным действительным эллипсом тогда и только тогда, когда C∆ < 0. If C∆>0, у нас есть мнимый эллипс, а если ∆ = 0, у нас есть точечный эллипс.
коэффициенты общих уравнений могут быть получены из известной большой полуоси a { displaystyle a}



- A = a 2 sin 2 θ + b 2 cos 2 θ B = 2 (b 2 — a 2) sin θ cos θ C = a 2 cos 2 θ + b 2 sin 2 θ D = — 2 A x ∘ — B y ∘ E = — B x ∘ — 2 C у ∘ F = A Икс ∘ 2 + В Икс ∘ Y ∘ + С Y ∘ 2 — а 2 б 2. { Displaystyle { begin {align} A = a ^ {2} sin ^ {2} theta + b ^ {2 } cos ^ {2} theta \ B = 2 left (b ^ {2} -a ^ {2} right) sin theta cos theta \ C = a ^ {2} cos ^ {2} theta + b ^ {2} sin ^ {2} theta D = — 2Ax _ { circ} -By _ { circ} \ E = — Bx _ { circ} -2Cy _ { circ} \ F = Ax _ { circ} ^ {2} + Bx _ { circ} y _ { circ} + Cy _ { circ} ^ {2} -a ^ {2} b ^ {2}. end {align}}}
Эти выражения могут быть получены из канонического уравнения x 2 a 2 + y 2 b 2 = 1 { displaystyle { tfrac {x ^ {2}} {a ^ {2 }}} + { tfrac {y ^ {2}} {b ^ {2}}} = 1}

- x = (X — x ∘) cos θ + (Y — y ∘) sin θ y = — (X — x ∘) sin θ + (Y — y ∘) cos θ. { Displaystyle { begin {выровнено} х = влево (X-х _ { circ} right) cos theta + left (Yy _ { circ} right) sin theta \ y = — left (Xx _ { circ} right) sin theta + left (Yy _ { circ} right) cos theta. end {align}}}
И наоборот, Параметры канонической формы могут быть получены из коэффициентов общей формы с помощью уравнений:
- a, b = — 2 (AE2 + CD 2 — BDE + (B 2 — 4 AC) F) ((A + C) ± (A — C) 2 + B 2) B 2 — 4 AC x ∘ = 2 CD — BEB 2 — 4 AC y ∘ = 2 AE — BDB 2 — 4 AC θ = {arctan (1 B (C — A — (A — C) 2 + B 2)) для B ≠ 0 0 для B = 0, A < C 90 ∘ for B = 0, A>C { displaystyle { begin {align} a, b = { frac {- { sqrt {2 { Big (} AE ^ {2} + CD ^ {2} -BDE + (B ^ {2} — 4AC) F { Big)} left ((A + C) pm { sqrt {(AC) ^ {2} + B ^ {2}}} right)}}} {B ^ {2} — 4AC}} \ x _ { circ} = { frac {2CD-BE} {B ^ {2} — 4AC}} \ [3pt] y _ { circ} = { frac {2AE- BD} {B ^ {2} -4AC}} \ [3pt] theta = { begin {cases} arctan left ({ frac {1} {B}} left (CA — { sqrt {(AC) ^ {2} + B ^ {2}}} right) right) { text {for}} B neq 0 \ 0 { text {for}} B = 0, A C \ end {case}} end {align}}}
Параметрическое представление
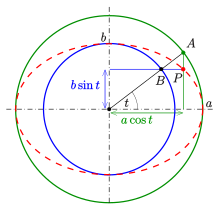

Δ u = 0,2 { displaystyle Delta u = 0, 2}

Стандартное параметрическое представление
Использование тригонометрические функции, параметрическое представление стандартного эллипса x 2 a 2 + y 2 b 2 = 1 { displaystyle { tfrac {x ^ {2}} {a ^ {2}}} + { tfrac {y ^ {2}} {b ^ {2}}} = 1}
- (x, y) = (a cos t, b sin t), 0 ≤ t < 2 π. {displaystyle (x,,y)=(acos t,,bsin t), 0leq t<2pi .}
Параметр t (который в астрономии называется эксцентрической аномалией ) не является углом (x (t), y ( t)) { displaystyle (x (t), y (t))}
Рациональное представление
С заменой u = tan (t 2) { textstyle u = tan left ({ frac {t} {2}} right) }
- cos t = 1 — u 2 U 2 + 1, T знак равно 2 uu 2 + 1 { displaystyle cos t = { frac {1- u ^ {2}} {u ^ {2} +1}} , quad sin t = { frac {2u} {u ^ {2} +1}}}
и рациональное параметрическое уравнение эллипса
- x (u) = a 1 — u 2 u 2 + 1 y (u) = 2 buu 2 + 1, — ∞ < u < ∞, {displaystyle {begin{aligned}x(u)=a{frac {1-u^{2}}{u^{2}+1}}\y(u)={frac {2bu}{u^{2}+1}}end{aligned}};,quad -infty
который покрывает любую точку эллипса x 2 a 2 + y 2 b 2 = 1 { displaystyle { tfrac {x ^ {2}} {a ^ {2}}} + { tfrac {y ^ {2}} {b ^ {2}}} = 1}

Для u ∈ [0, 1], { displaystyle u in [0, , 1 ],}![{displaystyle uin [0,,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c61b780db9ac550dd283876e16abe9c2cccdf8c3)

Рациональные представления конических сечений обычно используются в автоматизированном проектировании (см. кривая Безье ).
Наклон касательной как параметр
Параметрическое представление, в котором используется наклон m { displaystyle m}

- x → ′ (t) = (- грех t, b cos t) T → m = — ba cot t → cot t = — маб. { displaystyle { vec {x}} ‘(t) = (- a sin t, , b cos t) ^ { mathsf {T}} quad rightarrow quad m = — { frac { b} {a}} cot t quad rightarrow quad cot t = — { frac {ma} {b}}.}
С помощью тригонометрических формул получаем:
- cos t = детская кроватка t ± 1 + детская кроватка 2 t = — ma ± m 2 a 2 + b 2, sin t = 1 ± 1 + детская кроватка 2 t = b ± m 2 a 2 + b 2. { displaystyle cos t = { frac { cot t} { pm { sqrt {1+ cot ^ {2} t}}}} = { frac {-ma} { pm { sqrt { m ^ {2} a ^ {2} + b ^ {2}}}} , quad quad sin t = { frac {1} { pm { sqrt {1+ cot ^ {2) } t}}}} = { frac {b} { pm { sqrt {m ^ {2} a ^ {2} + b ^ {2}}}}}.}
Замена cos t { displaystyle cos t}

- c → ± (m) = ( — ma 2 ± m 2 a 2 + b 2, b 2 ± m 2 a 2 + b 2), m ∈ R. { displaystyle { vec {c}} _ { pm} (m) = left ( — { frac {ma ^ {2}} { pm { sqrt {m ^ {2} a ^ {2}) + b ^ {2}}}}}, ; { frac {b ^ {2}} { pm { sqrt {m ^ {2} a ^ {2} + b ^ {2}}}} right), , m in mathbb {R }.}
Здесь m { displaystyle m}



Уравнение касательной в точке c → ± (m) { displaystyle { vec {c}} _ { pm} (m)}



- y = mx ± m 2 a 2 + b 2. { displaystyle y = mx pm { sqrt {m ^ {2} a ^ {2} + b ^ {2}}} ;.}
Это описание касательных эллипса является важным инструментом для определения ортоптики эллипса. Ортоптическая статья содержит другое доказательство, без дифференциального исчисления и тригонометрических формул.
Общий эллипс

Другое определение эллипса использует аффинные преобразования :
- Любой эллипс является аффинным представлением единичной окружности с уравнением x 2 + y 2 = 1 { displaystyle x ^ {2} + y ^ {2} = 1}
.
- параметрическое представление
Аффинное преобразование евклидовой плоскости вид x → ↦ е → 0 + A x → { displaystyle { vec {x}} mapsto { vec {f}} ! _ {0} + A { vec {x}}}






- x → = p → (t) = f → 0 + f → 1 cos t + f → 2 sin t. { displaystyle { vec {x}} = { vec {p}} (t) = { vec {f}} ! _ {0} + { vec {f}} ! _ {1} cos t + { vec {f}} ! _ {2} sin t .}
Здесь f → 0 { displaystyle { vec {f}} ! _ {0}}

- вершины
Четыре вершины эллипса: p → (t 0), p → (t 0 ± π 2), p → (t 0 + π) { displaystyle { vec {p}} ( t_ {0}), ; { vec {p}} left (t_ {0} pm { tfrac { pi} {2}} right), ; { vec {p}} left (t_ {0} + pi right)}

- детская кроватка (2 t 0) = f → 1 2 — f → 2 2 2 f → 1 ⋅ f → 2. { displaystyle cot (2t_ {0}) = { гидроразрыв {{ vec {f}} ! _ {1} ^ {, 2} — { vec {f}} ! _ {2} ^ {, 2}} {2 { vec {f}} ! _ {1} cdot { vec {f}} ! _ {2}}}.}
(Если f → 1 ⋅ f → 2 = 0 { displaystyle { vec {f}} ! _ {1} cdot { vec {f}} ! _ {2} = 0}


- p → ′ (t) = — f → 1 sin t + f → 2 cos t. { displaystyle { vec {p}} , ‘(t) = — { vec {f}} ! _ {1} sin t + { vec {f}} ! _ {2} cos t .}
При параметре вершины t = t 0 { displaystyle t = t_ {0}}
- 0 = p → ′ (t) ⋅ (p → (t) — f → 0) = (- f → 1 sin t + f → 2 cos t) ⋅ (f → 1 cos t + f → 2 sin т). { displaystyle 0 = { vec {p}} ‘(t) cdot left ({ vec {p}} (t) — { vec {f}} ! _ {0} right) = left (- { vec {f}} ! _ {1} sin t + { vec {f}} ! _ {2} cos t right) cdot left ({ vec {f} } ! _ {1} cos t + { vec {f}} ! _ {2} sin t right).}
Расширение и применение тождеств cos 2 t — sin 2 t знак равно соз 2 T, 2 грех T соз T знак равно грех 2 t { displaystyle cos ^ {2} t- sin ^ {2} t = cos 2t, 2 sin t cos t = sin 2t}

- неявного представления
Решение параметрического представления для cos т, грех т { displaystyle ; cos t, sin t ;}

- det (x → — f → 0, f → 2) 2 + det (е → 1, x → — f → 0) 2 — det (f → 1, f → 2) 2 = 0 { displaystyle det ({ vec {x}} ! — ! { vec { f}} ! _ {0}, { vec {f}} ! _ {2}) ^ {2} + det ({ vec {f}} ! _ {1}, { vec { x}} ! — ! { Vec {f}} ! _ {0}) ^ {2} — det ({ vec {f}} ! _ {1}, { vec {f} } ! _ {2}) ^ {2} = 0}
.
- Определение эллипса в этом разделе дает параметрическое представление произвольноголипса, даже в пространстве, если можно f → 0, f → 1, е → 2 { displaystyle { vec {f}} ! _ {0}, { vec {f}} ! _ {1}, { vec {f}} ! _ {2}}
быть векторми в дизайне.
Полярные формы
Полярные формы относительно центра
Полярные координаты с центром в центре.
В полярных координатах, с началом в центре эллипса и с угловой координатой θ { displaystyle theta}
, измеренной от большой оси, уравнение эллипса имеет вид
- р (θ) знак равно ab (b соз θ) 2 + (грех θ) 2 знак равно б 1 — (е соз θ) 2 { displaystyle r ( theta) = { frac {ab} { sqrt {(b cos theta) ^ {2} + (a sin theta) ^ {2}}}} = { frac {b} { sqrt {1- (e cos theta) ^ { 2}}}}
- r (θ) = a (1 — e 2) 1 ± e cos θ { displaystyle r ( theta) = { frac {a (1-e ^ {2})} {1 pm e cos theta}}}
- r = a (1 — e 2) 1 — e cos (θ — ϕ). { displaystyle r = { frac {a (1-e ^ {2})} {1-e cos ( theta — phi)}}.}
- Для произвольной точки P { displaystyle P}
эллипса отношение расстояния до одного фокуса и соответствующей направляющей (см. Диаграмму) равно эксцентриситету:
- | P F 1 | | P l 1 | = | P F 2 | | P l 2 | = е = с а. { displaystyle { frac { left | PF_ {1} right |} { left | Pl_ {1} right |}} = { frac { left | PF_ {2} right |} { left | Pl_ {2} right |}} = e = { frac {c} {a}} .}
- | P F 1 | | P l 1 | = | P F 2 | | P l 2 | = е = с а. { displaystyle { frac { left | PF_ {1} right |} { left | Pl_ {1} right |}} = { frac { left | PF_ {2} right |} { left | Pl_ {2} right |}} = e = { frac {c} {a}} .}
- | P F 1 | 2 — с 2 а 2 | P l 1 | 2 = 0. { displaystyle left | PF_ {1} right | ^ {2} — { frac {c ^ {2}} {a ^ {2}}} left | Pl_ {1} right | ^ {2} = 0 .}
- Для любой точки F { displaystyle F}
(фокус), любая строка l { displaystyle l}
(directrix) не через F { displaystyle F}
и любое действительное число e { displaystyle e}
с 0 < e < 1, {displaystyle 0
эллипс — это геометрическое место точек, для которых отношение расстояний до точки и линии равно e, { displaystyle e, }
то есть:
- E = {P | | P F | | P l | = e}. { Displaystyle E = left {P left | { frac {| PF |} {| Pl |}} = e right. right }.}
- E = {P | | P F | | P l | = e}. { Displaystyle E = left {P left | { frac {| PF |} {| Pl |}} = e right. right }.}
- Доказательство
- (x — f) 2 + y 2 = e 2 (x + fe) 2 = (ex + f) 2 { displaystyle (xf) ^ {2 } + y ^ {2} = e ^ {2} left (x + { frac {f} {e}} right) ^ {2} = (ex + f) ^ {2}}
и x 2 (e 2-1) + 2 xf (1 + e) - y 2 = 0. { displaystyle x ^ {2} left (e ^ {2} -1 right) + 2xf (1 + e) -y ^ {2} = 0.}
- x 2 (e 2-1) + 2 px — y 2 = 0. { displaystyle x ^ {2} left (e ^ {2} -1 right) + 2px- y ^ {2} = 0.}
- (x — a) 2 a 2 + y 2 b 2 = 1, { displaystyle { frac {(xa) ^ {2}} {a ^ {2}}} + { frac {y ^ {2}} {b ^ {2}} = 1 ,}
- Общий эллипс
- (x — f 1) 2 + (y — f 2) 2 = e 2 (ux + vy + w) 2 u 2 + v 2. { displaystyle left (x-f_ {1} right) ^ {2} + left (y-f_ {2} right) ^ {2} = e ^ {2} { frac { left (ux + vy + w right) ^ {2}} {u ^ {2} + v ^ {2}}} .}
- Нормаль в точке P { displaystyle P}
делит пополам угол между линиями PF 1 ¯, PF 2 ¯ { displaystyle { overline { PF_ {1}}}, , { overline {PF_ {2}}}}
.
- Доказательство
- Приложение
- Передние параллельные хорд лежат на диаметре.
- Определение
- Два диаметра P 1 Q 1 ¯, P 2 Q 2 ¯ { displaystyle { overline {P_ {1} Q_ {1}}}, , { overline {P_ {2} Q_ {2}}}}
эллипса сопряжены, если касательные в точке P 1 { displaystyle P_ {1}}
и Q 1 { displaystyle Q_ { 1}}
параллельны P 2 Q 2 ¯ { displaystyle { overline {P_ {2} Q_ {2}}}}
.
- x → = p → (t) = f → 0 + f → 1 cos t + f → 2 sin t, { displaystyle { vec {x}} = { vec {p}} (t) = { vec {f}} ! _ {0} + { vec {f}} ! _ {1} cos t + { vec {f}} ! _ {2} sin t,}
- Пусть c 1 { displaystyle c_ {1}}
и c 2 { displaystyle c_ {2}}
быть половинками двух сопряженных диаметров (см. Диаграмму), тогда
- c 1 2 + c 2 2 = a 2 + b 2 { displaystyle c_ {1} ^ {2} + c_ {2} ^ {2} = a ^ {2} + b ^ {2}}
,
- треугольник, образованный c 1, c 2 { displaystyle c_ {1}, , c_ {2}}
, имеет постоянную площадь A Δ = 1 2 ab { textstyle A _ { Delta} = { frac {1} {2}} ab}
- параллелограмм касательных, примыкающих к данным сопряженным диаметром, имеет Площадь 12 = 4 пр. { displaystyle { text {Area}} _ {12} = 4ab .}
- c 1 2 + c 2 2 = a 2 + b 2 { displaystyle c_ {1} ^ {2} + c_ {2} ^ {2} = a ^ {2} + b ^ {2}}
- Доказательство
- p → (t) = (a cos t, b грех t) { displaystyle { vec {p}} (t) = (a cos t, , b sin t)}
.
- | c → 1 | 2 + | c → 2 | 2 знак равно ⋯ знак равно а 2 + Ь 2. { displaystyle left | { vec {c}} _ {1} right | ^ {2} + left | { vec {c}} _ {2} right | ^ {2} = cdots = a ^ {2} + b ^ {2} .}
- A Δ = 1 2 det (c → 1, c → 2) = ⋯ = 1 2 ab { displaystyle A _ { Дельта} = { frac {1} {2}} det left ({ vec {c}} _ {1}, , { vec {c}} _ {2} справа) = cdots = { frac {1} {2}} ab}
- Площадь 12 = 4 a b. { displaystyle { text {Area}} _ {12} = 4ab .}
- Нарисуйте две окружности в центре эллипса с радиусами a, b { displaystyle a, b}
и осями эллипса.
- Проведите линию через центр, которая пересекает два круга в точке A { displaystyle A}
и B { displaystyle B}
соответственно..
- Проведите линию через A { displaystyle A}
, которая параллельна малой оси, и линию через B { displaystyle B}
, которая параллельна большой оси. Эти линии пересекаются в точке эллипса (см. Диаграмму).
- Повторите шаги (2) и (3) с разными линиями через центр.
Метод де Ла Хира
Анимация метода
- (a cos t, b sin t) { displaystyle (a cos t, , b sin t)}
- Метод 1
- полосы бумаги длиной a + b { displaystyle a + b}
.
Конструкция бумажной ленты 1
Эллипсы с парой Туси. Два примера: красный и голубой.
Вариант метода 1 полосы бумаги
Анимация варианта метода 1 полосы бумаги
- Метод 2
- a полоска бумаги длиной a { displaystyle a}
.
Траммель Архимеда (принцип)
Эллипсограф из-за Бенджамина Брамера
Вариант метода бумажной полосы 2
- отмечает точку H = (a, b) { displaystyle H = (a, , b)}
и нарисуйте отрезок линии V 1 V 3, { displaystyle V_ {1} V_ {3} ,}
- нарисуйте линию через H { displaystyle H}
, которая перпендикулярна линии V 1 V 3, { displaystyle V_ {1} V_ {3} ,}
- пересечение точки этой линии с осями центрами соприкасающихся окружностей.
- Даны два карандаша B (U), B (V) { displaystyle B (U), , B (V)}
линий в двух точках U, V { displaystyle U, , V}
(все строки, содержащие U displaystyle U}
и V { displaystyle V}
соответственно) и проекционное, но не перспективное отображение π { displaystyle pi}
из B (U) { displaystyle B (U)}
на B (V) { displaystyle B (V)}
, то точки пересечения соответствующих прямых образуют невырожденное проективное коническое сечение.
- Для четырех точек P i = (xi, yi), i = 1, 2, 3, 4, { displaystyle P_ {i} = left (x_ {i}, , y_ {i} right), i = 1, , 2, , 3, , 4, ,}
(см. диаграмму) верно следующее утверждение:
- Четыре точки находятся на окружности тогда и только тогда, когда углы равны P 3 { displaystyle P_ {3}}
и P 4 { displaystyle P_ {4}}
равны.
- Чтобы измерить угол между двумя линиями с помощью уравнений y = m 1 Икс + d 1, Y знак равно м 2 Икс + d 2, м 1 ≠ м 2, { displaystyle y = m_ {1} x + d_ {1}, y = m_ {2} x + d_ {2}, m_ {1} neq m_ {2},}
используется частное:
- 1 + m 1 m 2 m 2 — m 1 = cot θ. { displaystyle { frac {1 + m_ {1} m_ {2}} {m_ {2} -m_ {1}}} = cot theta .}
- 1 + m 1 m 2 m 2 — m 1 = cot θ. { displaystyle { frac {1 + m_ {1} m_ {2}} {m_ {2} -m_ {1}}} = cot theta .}
- точки находятся на окружности, если и только если углы равны P 3 { displaystyle P_ {3}}
и P 4 { displaystyle P_ {4}}
равны. В терминах измерения угла выше это означает:
- (x 4 — x 1) (x 4 — x 2) + (y 4 — y 1) (y 4 — y 2) (y 4 — y 1) (x 4 — x 2) — (y 4 — y 2) (x 4 — x 1) = (x 3 — x 1) (x 3 — x 2) + (y 3 — y 1) (y 3 — y 2) (y 3 — y 1) (x 3 — x 2) — (y 3 — y 2) (x 3 — x 1). { displaystyle { frac {(x_ {4} -x_ {1}) (x_ {4} -x_ {2}) + (y_ {4} -y_ {1}) (y_ {4} -y_ {2 })} {(y_ {4} -y_ {1}) (x_ {4} -x_ {2}) — (y_ {4} -y_ {2}) (x_ {4} -x_ {1})} } = { frac {(x_ {3} -x_ {1}) (x_ {3} -x_ {2}) + (y_ {3} -y_ {1}) (y_ {3} -y_ {2})} {(y_ {3} -y_ {1}) (x_ {3} -x_ {2}) — (y_ {3} -y_ {2}) (x_ {3} -x_ {1})}}.}
- (x 4 — x 1) (x 4 — x 2) + (y 4 — y 1) (y 4 — y 2) (y 4 — y 1) (x 4 — x 2) — (y 4 — y 2) (x 4 — x 1) = (x 3 — x 1) (x 3 — x 2) + (y 3 — y 1) (y 3 — y 2) (y 3 — y 1) (x 3 — x 2) — (y 3 — y 2) (x 3 — x 1). { displaystyle { frac {(x_ {4} -x_ {1}) (x_ {4} -x_ {2}) + (y_ {4} -y_ {1}) (y_ {4} -y_ {2 })} {(y_ {4} -y_ {1}) (x_ {4} -x_ {2}) — (y_ {4} -y_ {2}) (x_ {4} -x_ {1})} } = { frac {(x_ {3} -x_ {1}) (x_ {3} -x_ {2}) + (y_ {3} -y_ {1}) (y_ {3} -y_ {2})} {(y_ {3} -y_ {1}) (x_ {3} -x_ {2}) — (y_ {3} -y_ {2}) (x_ {3} -x_ {1})}}.}
- Как следствие, получается уравнение для круга, определяемого тремя неколлинеарными точками P i = (xi, yi) { displaystyle P_ { i} = left (x_ {i}, , y_ {i} right)}
:
- (x — x 1) (x — x 2) + (y — y 1) (y — y 2) ( y — y 1) (x — x 2) — (y — y 2) (x — x 1) = (x 3 — x 1) (x 3 — x 2) + (y 3 — y 1) (y 3 — y 2) (y 3 — y 1) (x 3 — x 2) — (y 3 — y 2) (x 3 — x 1). { displaystyle { frac {({ color {red} x} -x_ {1}) ({ color {red} x} -x_ {2}) + ({ color {red} y} -y_ { 1}) ({ цвет {красный} y} -y_ {2})} {({ color {красный} y} -y_ {1}) ({ color {красный} x} -x_ {2}) — ({ color {red} y} -y_ {2}) ({ color {red} x} -x_ {1})}} = { frac {(x_ {3} -x_ {1}) ( x_ {3} -x_ {2}) + (y_ {3} -y_ {1}) (y_ {3} -y_ {2})} {(y_ {3} -y_ {1}) (x_ {3 } -x_ {2}) — (y_ {3} -y_ {2}) (x_ {3} -x_ {1})}}.}
- (x — x 1) (x — x 2) + (y — y 1) (y — y 2) ( y — y 1) (x — x 2) — (y — y 2) (x — x 1) = (x 3 — x 1) (x 3 — x 2) + (y 3 — y 1) (y 3 — y 2) (y 3 — y 1) (x 3 — x 2) — (y 3 — y 2) (x 3 — x 1). { displaystyle { frac {({ color {red} x} -x_ {1}) ({ color {red} x} -x_ {2}) + ({ color {red} y} -y_ { 1}) ({ цвет {красный} y} -y_ {2})} {({ color {красный} y} -y_ {1}) ({ color {красный} x} -x_ {2}) — ({ color {red} y} -y_ {2}) ({ color {red} x} -x_ {1})}} = { frac {(x_ {3} -x_ {1}) ( x_ {3} -x_ {2}) + (y_ {3} -y_ {1}) (y_ {3} -y_ {2})} {(y_ {3} -y_ {1}) (x_ {3 } -x_ {2}) — (y_ {3} -y_ {2}) (x_ {3} -x_ {1})}}.}
- (x — 2) x + y (y — 1) yx — (y — 1) (х — 2) знак равно 0 { displaystyle { frac {(x-2) x + y (y-1)} {yx- (y-1) (x-2)}} = 0}
, который можно переформатировать в (x — 1) 2 + (y — 1 2) 2 = 5 4. { displaystyle (x-1) ^ {2} + left (y — { tfrac {1} {2}} right) ^ {2} = { tfrac {5} {4}} .}
- (x → — x → 1) ⋅ (x → — x → 2) det (x → — x → 1, x → — x → 2) = (x → 3 — x → 1) ⋅ (x → 3 — x → 2) det (x → 3 — x → 1, x → 3 — x → 2). { displaystyle { frac { left ({ color {red} { vec {x}}} — { vec {x}} _ {1} right) cdot left ({ color {red}) { vec {x}}} — { vec {x}} _ {2} right)} { det left ({ color {red} { vec {x}}} — { vec {x }} _ {1}, { color {red} { vec {x}}} — { vec {x}} _ {2} right)}} = { frac { left ({ vec { x}} _ {3} — { vec {x}} _ {1} right) cdot left ({ vec {x}} _ {3} — { vec {x}} _ {2} right)} { det left ({ vec {x}} _ {3} — { vec {x}} _ {1}, { vec {x}} _ {3} — { vec { x}} _ {2} right)}}.}
- [1 y 1 — y 2 x 1 — x 2 x 1 — x 3 y 1 — y 3 1] [x ∘ y ∘] = [x 1 2 — x 2 2 + y 1 2 — y 2 2 2 (x 1 — x 2) y 1 2 — y 3 2 + x 1 2 — x 3 2 2 (y 1 — y 3)]. { displaystyle { begin {bmatrix} 1 { frac {y_ {1} -y_ {2}} {x_ {1} -x_ {2}}}\ { frac {x_ {1} -x_ {3)}} {y_ {1} -y_ {3}}} 1 end {bmatrix}} { begin {bmatrix} x _ { circ} y _ { circ} end {bmatrix}} = { begin {bmatrix} { frac {x_ {1} ^ {2} -x_ {2} ^ {2} + y_ {1} ^ {2} -y_ {2} ^ {2}} {2 (x_ {1} — x_ {2})}} \ { frac {y_ {1} ^ {2} -y_ {3} ^ {2} + x_ {1} ^ {2} -x_ {3} ^ {2}} {2 (y_ {1} -y_ {3})}} end {bmatrix}}.}
- r = (x 1 — x ∘) 2 + (y 1 — y ∘) 2 = (x 2 — x ∘) 2 + (y 2 — y) 2 = (x 3 — x ∘) 2 + ( у 3 — у) 2. { displaystyle r = { sqrt { left (x_ {1} -x _ { circ} right) ^ {2} + left (y_ {1} -y _ { circ} right) ^ {2}}} = { sqrt { left (x_ {2} -x _ { circ} right) ^ {2} + left (y_ {2} -y _ { circ} right) ^ {2}}} = { sqrt { left (x_ {3} -x _ { circ} right) ^ {2} + left (y_ {3} -y _ { circ} right) ^ {2}}}.}
- q = a 2 b 2 = 1 1 — e 2, { displaystyle { color {blue} q} = { frac {a ^ {2}} {b ^ {2}}} = { frac {1} {1-e ^ {2}}},}
- (x — x ∘) 2 + q (y — y ∘) 2 знак равно a 2, { displaystyle left (xx _ { circ} right) ^ {2} + { color {blue} q} , left (yy _ { circ} right) ^ {2} = a ^ {2},}
- Для этого семейства эллипсов вводится следующее q-аналог Измерение угла между двумя линиями с помощью соотношений y = m 1 x + d 1, y = m 2 Икс + d 2, м 1 ≠ м 2 { displaystyle y = m_ {1} x + d_ {1}, y = m_ {2} x + d_ {2}, m_ {1} neq m_ {2}}
используется частное:
- 1 + qm 1 m 2 m 2 — m 1. { Displaystyle { frac {1 + { color {blue} q} ; m_ {1} m_ {2}} {m_ {2} -m_ {1}}} .}
- 1 + qm 1 m 2 m 2 — m 1. { Displaystyle { frac {1 + { color {blue} q} ; m_ {1} m_ {2}} {m_ {2} -m_ {1}}} .}
- Дано четыре точка п i = (xi, yi), i = 1, 2, 3, 4 { displaystyle P_ {i} = left (x_ {i}, , y_ {i} right), i = 1, , 2, , 3, , 4}
, три из них на прямой (см. диаграмму).
- Четыре точки находятся на эллипсе с уравнением (Икс — Икс ∘) 2 + Q (Y — Y ∘) 2 = a 2 { displaystyle (xx _ { circ}) ^ {2} + { color {blue} q} , (yy _ { circ}) ^ {2} = a ^ {2}}
тогда и только тогда, когда углы в P 3 { displaystyle P_ {3}}
и P 4 { displaystyle P_ {4}}
равны в смысле измерения выше, то есть если
- (x 4 — x 1) (x 4 — x 2) + q (y 4 — y 1) (y 4 — y 2) (y 4 — y 1) (x 4 — x 2) — (y 4 — y 2) (x 4 — x 1) = (x 3 — x 1) (x 3 — x 2) + q (y 3 — y 1) (y 3 — y 2) (y 3 — y 1) (x 3 — x 2) — (y 3 — y 2) (х 3 — х 1). { displaystyle { frac {(x_ {4} -x_ {1}) (x_ {4} -x_ {2}) + { color {blue} q} ; (y_ {4} -y_ {1})) (y_ {4} -y_ {2})} {(y_ {4} -y_ {1}) (x_ {4} -x_ {2}) — (y_ {4} -y_ {2}) (x_ {4} -x_ {1})}} = { frac {(x_ {3} -x_ {1}) (x_ {3} -x_ {2}) + { color {blue} q} ; (y_ {3} -y_ {1}) (y_ {3} -y_ {2})} {(y_ {3} -y_ {1}) (x_ {3} -x_ {2}) — (y_ { 3} -y_ {2}) (x_ {3} -x_ {1})}} .}
- (x 4 — x 1) (x 4 — x 2) + q (y 4 — y 1) (y 4 — y 2) (y 4 — y 1) (x 4 — x 2) — (y 4 — y 2) (x 4 — x 1) = (x 3 — x 1) (x 3 — x 2) + q (y 3 — y 1) (y 3 — y 2) (y 3 — y 1) (x 3 — x 2) — (y 3 — y 2) (х 3 — х 1). { displaystyle { frac {(x_ {4} -x_ {1}) (x_ {4} -x_ {2}) + { color {blue} q} ; (y_ {4} -y_ {1})) (y_ {4} -y_ {2})} {(y_ {4} -y_ {1}) (x_ {4} -x_ {2}) — (y_ {4} -y_ {2}) (x_ {4} -x_ {1})}} = { frac {(x_ {3} -x_ {1}) (x_ {3} -x_ {2}) + { color {blue} q} ; (y_ {3} -y_ {1}) (y_ {3} -y_ {2})} {(y_ {3} -y_ {1}) (x_ {3} -x_ {2}) — (y_ { 3} -y_ {2}) (x_ {3} -x_ {1})}} .}
- Как следствие, уравнение для эллипса, определяемое тремя неколлинеарными точками P i = (xi, yi) { displaystyle P_ {i} = left (x_ {i }, , y_ {i} right)}
:
- (x — x 1) (x — x 2) + q (y — y 1) (y — y 2) (y — y 1) (x — x 2) — (y — y 2) (x — x 1) = (x 3 — x 1) (x 3 — x 2) + q (y 3 — y 1) (y 3 — y 2) (y 3 — y 1) (x 3 — x 2) — (y 3 — y 2) (x 3 — x 1). { displaystyle { frac {({ color {red} x} -x_ {1}) ({ color {red} x} -x_ {2}) + { color {blue} q} ; ({ color {red} y} -y_ {1}) ({ color {red} y} -y_ {2})} {({ color {red} y} -y_ {1}) ({ цвет {красный} x} -x_ {2}) — ({ color {red} y} -y_ {2}) ({ color {red} x} -x_ {1})}} = { frac { (x_ {3} -x_ {1}) (x_ {3} -x_ {2}) + { color {blue} q} ; (y_ {3} -y_ {1}) (y_ {3} -y_ {2})} {(y_ {3} -y_ {1}) (x_ {3} -x_ {2}) — (y_ { 3} -y_ {2}) (x_ {3} -x_ {1})}} .}
- (x — x 1) (x — x 2) + q (y — y 1) (y — y 2) (y — y 1) (x — x 2) — (y — y 2) (x — x 1) = (x 3 — x 1) (x 3 — x 2) + q (y 3 — y 1) (y 3 — y 2) (y 3 — y 1) (x 3 — x 2) — (y 3 — y 2) (x 3 — x 1). { displaystyle { frac {({ color {red} x} -x_ {1}) ({ color {red} x} -x_ {2}) + { color {blue} q} ; ({ color {red} y} -y_ {1}) ({ color {red} y} -y_ {2})} {({ color {red} y} -y_ {1}) ({ цвет {красный} x} -x_ {2}) — ({ color {red} y} -y_ {2}) ({ color {red} x} -x_ {1})}} = { frac { (x_ {3} -x_ {1}) (x_ {3} -x_ {2}) + { color {blue} q} ; (y_ {3} -y_ {1}) (y_ {3} -y_ {2})} {(y_ {3} -y_ {1}) (x_ {3} -x_ {2}) — (y_ { 3} -y_ {2}) (x_ {3} -x_ {1})}} .}
- (x — 2) Икс + 4 Y (Y — 1) Yx — (Y — 1) (X — 2) = 0 { Displaystyle { frac {(x-2) x + 4y (Y-1)} {yx- (y- 1) (x-2)}} = 0}
и после преобразования (x — 1) 2 2 + (y — 1 2) 2 1 2 = 1. { displaystyle { frac {(x-1) ^ {2}} {2}} + { frac { left (y — { frac {1} {2}} right) ^ {2}} { frac {1} { 2}}} = 1.}
- (x → — x → 1) ∗ (x → — x → 2) det (x → — x → 1, x → — x → 2) знак равно (x → 3 — x → 1) ∗ (x → 3 — x → 2) det (x → 3 — x → 1, x → 3 — x → 2), { displaystyle { frac { left ({ color {red} { vec {x}}} — { vec {x}} _ {1} right) * left ({ color {red} { vec { x}}} — { vec {x}} _ {2} right)} { det left ({ color {красный} { vec {x}}} — { vec {x}} _ { 1}, { color {red} { vec {x}}} — { vec {x}} _ {2} right)}} = { frac { left ({ vec {x}} _ {3} — { vec {x}} _ {1} righ t) * left ({ vec {x}} _ {3} — { vec {x}} _ {2} right)} { det left ({ vec {x}} _ {3} — { vec {x}} _ {1}, { vec {x}} _ {3} — { vec {x}} _ {2} right)}},}
- точка P 1 = (x 1, y 1) ≠ (0, 0) { displaystyle P_ {1} = left (x_ {1}, , y_ {1} right) neq (0, , 0)}
отображается в строке x 1 xa 2 + y 1 yb 2 = 1 { displaystyle { tfrac {x_ {1} x} {a ^ {2}}} + { tfrac {y_ {1} y} {b ^ {2}}} = 1}
, а не через центр эллипса.
- линию y = mx + d, d ≠ 0 { displaystyle y = mx + d, d neq 0}
на точку (- ma 2 d, б 2 d) { displaystyle left (- { tfrac {ma ^ {2}} {d}}, , { tfrac {b ^ {2}} {d}} справа)}
и
- строка x = c, c ≠ 0 { displaystyle x = c, c neq 0}
на точку (а 2 с, 0). { displaystyle left ({ tfrac {a ^ {2}} {c}}, , 0 right) .}
- Для точки (полюса) на эллипсе полярность является касательной в этой точке (см. Диаграмму: P 1, p 1 { displaystyle P_ {1}, , p_ {1}}
).
- Для полюса P { displaystyle P}
вне эллипса точки пересечения его полярные с эллипсом — это точки касания двух касательных, проходящих через P { displaystyle P}
(см. диаграмму: P 2, p 2 { displaystyle P_ {2}, , p_ {2}}
).
- Для точки внутри эллипса полярная точка не имеет общей точки с эллипсом (см. диаграмму: F 1, l 1 { displaystyle F_ {1}, , l_ {1 }}
).
- Точка пересечения двух поляр — это полюс линии, проходящей через их полюса.
- Фокусы (c, 0), { displaystyle (c, , 0),}
и (- c, 0) { displaystyle (-c, , 0)}
соответственно и директрисы x = a 2 c { displaystyle x = { tfrac {a ^ {2}} {c}}}
и x = — a 2 c { displaystyle x = — { tfrac {a ^ {2}} {c}}}
соответственно относятся к парам полюса и полюса.
- Эллипс = π ab { displaystyle A _ { text {ellipse}} = pi ab}
- Эллипс = ∫ — aa 2 b 1 — x 2 a 2 dx = ba ∫ — aa 2 a 2 — x 2 dx. { displaystyle { begin {align} A _ { text {ellipse}} = int _ {- a} ^ {a} 2b { sqrt {1 — { frac {x ^ {2}} {a ^ {2}}}}} , dx \ = { frac {b} {a}} int _ {- a} ^ {a} 2 { sqrt {a ^ {2} -x ^ { 2}}} , dx. end {align}}}
- A эллипс = ba π a 2 = π a b. { displaystyle A _ { text {ellipse}} = { frac {b} {a}} pi a ^ {2} = pi ab.}
- C = 4 a ∫ 0 π / 2 1 — е 2 грех 2 θ d θ = 4 a E (e) { displaystyle C , = , 4a int _ {0} ^ { pi / 2} { sqrt {1-e ^ {2} sin ^ {2} theta}} d theta , = , 4a , E (e)}
- E (e) = ∫ 0 π / 2 1 — е 2 грех 2 θ d θ { Displaystyle E (e) , = , int _ {0} ^ { pi / 2} { sqrt {1-e ^ {2} sin ^ {2} theta}} d theta}
- C = 2 π a [1 — (1 2) 2 e 2 — (1 ⋅ 3 2 ⋅ 4) 2 e 4 3 — (1 ⋅ 3 ⋅ 5 2 ⋅ 4 ⋅ 6) 2 e 6 5 — ⋯] = 2 π a [1 — ∑ n = 1 ∞ ((2 n — 1) !! (2 n) !!) 2 e 2 n 2 n — 1] = — 2 π a ∑ N знак равно 0 ∞ ((2 n — 1) !! (2 n) !!) 2 e 2 n 2 n — 1, { Displaystyle { begin {align} C = 2 pi a left [{1- left ({ frac {1} {2}} right) ^ {2} e ^ {2} — left ({ frac {1 cdot 3} {2 cdot 4}}) right) ^ {2} { frac {e ^ {4}} {3}} — left ({ frac {1 cdot 3 cdot 5} {2 cdot 4 cdot 6}} right) ^ {2} { frac {e ^ {6}} {5}} — cdots} right] \ = 2 pi a left [1- sum _ { n = 1} ^ { infty} left ({ frac {(2n-1) !!} {(2n) !!}} right) ^ {2} { frac {e ^ {2n}} { 2n-1}} right] \ = — 2 pi a sum _ {n = 0} ^ { infty} left ({ frac {(2n-1) !!} {(2n)! !}} right) ^ {2} { frac {e ^ {2n}} {2n-1}}, end {align}}}
- C = π (a + b) ∑ n = 0 ∞ ((2 n — 3) !! 2 nn !) 2 hn = π (a + b) [1 + h 4 + ∑ n = 2 ∞ ((2 n — 3) !! 2 nn!) 2 hn] = π (a + b) [1 + ∑ n = 1 ∞ ((2 n — 1) !! 2 nn!) 2 hn (2 n — 1) 2]. { displaystyle { begin {align} C = pi (a + b) sum _ {n = 0} ^ { infty} left ({ frac {(2n-3) !!} {2 ^ {n} n!}} right) ^ {2} h ^ {n} \ = pi (a + b) left [1 + { frac {h} {4}} + sum _ { n = 2} ^ { infty} left ({ frac {(2n-3) !!} {2 ^ {n} n!}} Right) ^ {2} h ^ {n} right] = pi (a + b) left [1+ sum _ {n = 1} ^ { infty} left ({ frac {(2n-1) !!} {2 ^ {n} n !}} right) ^ {2} { frac {h ^ {n}} {(2n-1) ^ {2}}} right]. end {align}}}
- C ≈ π [3 (a + b) — (3 a + b) (a + 3 b)] = π [3 (a + b) — 10 ab + 3 (a 2 + b 2) ] { displaystyle C приблизительно pi { biggl [} 3 (a + b) — { sqrt {(3a + b) (a + 3b)}} { biggr]} = pi { biggl [} 3 (a + b) — { sqrt {10ab + 3 left (a ^ {2} + b ^ {2} right)}} { biggr]}}
- C ≈ π ( а + б) (1 + 3 ч 10 + 4 — 3 ч). { displaystyle C приблизительно pi left (a + b right) left (1 + { frac {3h} {10 + { sqrt {4-3h}}}} right).}
- y = b 1 — x 2 a 2. { displaystyle y = b { sqrt {1 — { frac {x ^ {2}} {a ^ {2}}}}}.}
- s = — b ∫ arccos x 1 a arccos x 2 a 1 — (1 — a 2 b 2) sin 2 zdz. { displaystyle s = -b int _ { arccos { frac {x_ {1}} {a}}} ^ { arccos { frac {x_ {2}} {a}}} { sqrt {1 — left (1 — { frac {a ^ {2}} {b ^ {2}}} right) sin ^ {2} z}} , dz.}
- s знак равно — б [E (z | 1 — a 2 b 2)] arccos x 1 a arccos x 2 a { displaystyle s = -b left [E left (z ; { Biggl |} ; 1 — { frac {a ^ {2}} {b ^ {2}}} right) right] _ { arccos { frac {x_ {1}} {a}}} ^ { arccos { frac {x_ {2}} {a}}}}
- 2 π b ≤ C ≤ 2 π a, π (a + b) ≤ C ≤ 4 (a + b), 4 a 2 + b 2 ≤ C ≤ 2 π a 2 + b 2. { Displaystyle { begin {align} 2 pi b leq C leq 2 pi a, \ pi (a + b) leq C leq 4 (a + b), \ 4 { sqrt {a ^ {2} + b ^ {2}}} leq C leq { sqrt {2}} pi { sqrt {a ^ {2} + b ^ {2}}}. end {выровнен}}}
- ρ = a 2 b 2 (x 2 a 4 + y 2 b 4) 3 2 = 1 a 4 b 4 (a 4 y 2 + b 4 x 2) 3. { displaystyle rho = a ^ {2} b ^ {2} left ({ frac {x ^ {2}} {a ^ {4}}} + { frac {y ^ {2}} {b ^ {4}}} right) ^ { frac {3} {2}} = { frac {1} {a ^ {4} b ^ {4}}} { sqrt { left (a ^ { 4} y ^ {2} + b ^ {4} x ^ {2} right) ^ {3}}} .}
- ρ 0 = b 2 a = p, (± c 2 a | 0). { displaystyle rho _ {0} = { frac {b ^ {2}} {a}} = p , qquad left ( pm { frac {c ^ {2}} {a}} , { bigg |} , 0 right) .}
- ρ 1 = a 2 b, (0 | ± c 2 b). { displaystyle rho _ {1} = { frac {a ^ {2}} {b}} , qquad left (0 , { bigg |} , pm { frac {c ^ { 2}} {b}} right) .}
- эллипс Штейнера : эллипс, проходящий через вершины треугольника с центром в центроид,
- в эллипсах : эллипсы, соприкасающиеся со стороны треугольника. Особыми случаями являются эллипс Штейнера и эллипс Мандарта.
- Эллипсоид
- Эллиптический конус
- Эллиптический цилиндр
- Гиперболоид из одного листа
- Гиперболоид из двух листов
Эллипсоид
Эллиптический конус
Эллиптический цилиндр
Гиперболоид из одного листа
Гиперболоид из двух листов
- e = ra — rpra + rp = ra — rp 2 ara = (1 + e) arp = (1 — e) a { displaystyle { begin {align} e = { frac {r_ {a} -r_ {p}} {r_ {a} + r_ {p}}} = { frac {r_) {a} -r_ {p}} {2a}} \ r_ {a} = (1 + e) a \ r_ {p} = (1-e) a end {align}}}
- a = ra + rp 2 b = rarp ℓ = 2 1 ra + 1 rp = 2 rarpra + rp { displaystyle { begin {align} a = { frac {r_ {a} + r_) {p}} {2}} \ [2pt] b = { sqrt {r_ {a} r_ {p}}} \ [2pt] ell = { frac {2} {{ frac { 1} {r_ {a}}} + { frac {1} {r_ {p}}}}} = { frac {2r_ {a} r_ {p}} {r_ {a} + r_ {p}} } end {align}}}
.
- Из материала, который оптически анизотропный (двулучепреломляющий ), показатель преломления зависит от направления света. Зависимость может быть описана эллипсоидом индекс . (Если материал оптически изотропный, этот эллипсоид представляет собой сферу.)
- В твердотельных лазерах с лампой накачкой использовались отражатели эллиптической формы цилиндрической. для направления света от лампы накачки (коаксиально с одной фокальной осью эллипса) на стержень активной среды (коаксиально со второй фокальной осью).
- В лазерно-плазменном производстве используются источники света EUV В литографии микрочипа свет EUV генерируется плазмой, расположенной в первичном фокусе эллипсоидного зеркала, и предназначено во вторичном фокусе на представлении литографической машины.
- Рисование с использованием Безье
- Декартов овал, обобщение эллипса
- круговой и инконической
- Расстояние наибольшего сближения эллипсов
- Подгонка эллипса
- Эллиптические координаты, ортогональная система координат, основанная на семействах эллипсов и гипербол
- Эллиптических уравнение в частных производных
- Эллиптическое распределение в статистике
- Геодезические на эллипсоиде
- Большой эллипс
- Законы движения планет Кеплера
- n-эллипс, обобщение эллипса для n фокусов
- Овальный
- Сфероид, эллипсоид, полученный вращением эллипса вокруг его большой или малой оси
- Стадион (геометрия), двумерная геометрическая форма, построенная из прямоугольника с полукругами на паре противоположных сторон
- круговой эллипс Штейнера, уникальный эллипс, описывающий треугольник и d разделяет свой центроид
- Суперэллипс, обобщение эллипса, которое может выглядеть более прямоугольным или более «заостренным»
- Истинный, эксцентрический и означает аномалию
- Безант, WH (1907). «Глава III. Эллипс». Конические сечения. Лондон: Джордж Белл и сыновья. п. 50. CS1 maint: ref = harv (ссылка )
- Coxeter, HSM (1969). Введение в геометрию (2-е изд.). Нью-Йорк: Wiley. Стр. 115–9.
- Месерв, Брюс Э. (1983) [1959], Основные концепции геометрии, Дувр, ISBN 978-0-486-63415-9
- Миллер, Чарльз Д.; Лиал, Маргарет Л.; Шнайдер, Дэвид И. (1990). Основы алгебры колледжа (3-е изд.). Скотт Форесман / Литтл. Стр. 381. ISBN 978-0-673-38638-0 .
- Проттер, Мюррей Х.; Морри, Чарльз Б., младший (1970), Колледж по исчислению с аналитической геометрией (2-е изд.), Чтение: Аддисон-Уэсли, LCCN 76087042
Полярная форма относительно фокуса
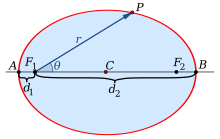
Если вместо этого мы будем использовать полярные координаты с началом в одном фокусе, с угловой координатой θ = 0 { displaystyle theta = 0}
где знак в знаменателе отрицательный, если направление ссылки θ = 0 { displaystyle theta = 0}
В немного более общем случае эллипса с одним фокусом в начале и другим фокусом в угловой координате ϕ { displaystyle phi}
Угол θ { displaystyle theta }

Эксцентриситет и свойство directrix
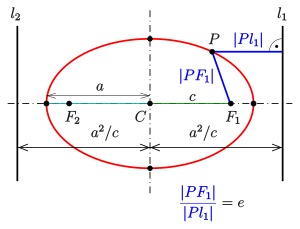
Каждая из двух линий, параллельных малой оси, и на расстоянии d = a 2 c = ae { displaystyle d = { frac {a ^ {2}} {c} } = { frac {a} {e}}}
Доказательство для пары F 1, l 1 { displaystyle F_ {1}, l_ {1}}


Второй случай доказывается аналогично.
Обратное также верно и может использоваться для определения эллипса (аналогично определению параболы):
Выбор e = 0 { displaystyle e = 0}
(выбор e = 1 { displaystyle e = 1}


Пусть F = (f, 0), e>0 { displaystyle F = (f, , 0), e>0}и предположим, что (0, 0) { displaystyle (0, , 0)}





Подстановка p = f (1 + e) { displaystyle p = f (1 + e)}
Это уравнение эллипса (e < 1 {displaystyle e<1}


Если e < 1 {displaystyle e<1}


который представляет собой уравнение эллипса с центром (a, 0) { displaystyle (a, , 0)}

Если фокус F = (f 1, f 2) { Displaystyle F = left (f_ {1}, , f_ {2} right)}

(В правой части уравнения используется нормальная форма Гессе линии для вычислений расстояния | P l | { displaystyle | Pl |}
Свойство отражения в фокусе
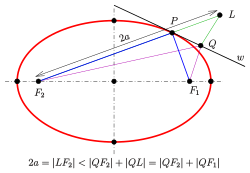
Эллипс следующим образом:
Потому что касательная перпендикулярная нормали, утверждение верно и для касательной и дополнительного угла угла между линиями к фокусам (см. Диаграмму).
Пусть L { displaystyle L}














Из диаграммы и неравенства треугольника видно, что 2 a = | L F 2 | < | Q F 2 | + | Q L | = | Q F 2 | + | Q F 1 | {displaystyle 2a=left|LF_{2}right|<left|QF_{2}right|+left|QLright|=left|QF_{2}right|+left|QF_{1}right|}



Лучи из одного фокуса отражаются эллипсом во втором положении. Это свойство имеет оптические и акустические приложения, аналогичные отражательные свойства параболы (см. шепчущая галерея ).
Сопряженные диаметры
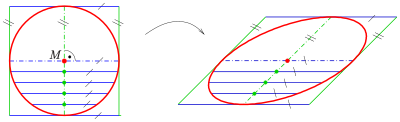
Окружность имеет следующее свойство:
Аффинное преобразование параллелизм и середины. прямой сегмент, поэтому это свойство верно для любого эллипса. орды и диаметр больше не ортогональны.)
Два диаметра d 1, d 2 { displaystyle d_ {1}, , d_ {2}}

Из диаграммы можно найти:
Сопряженные диаметры в эллипсе обобщают ортогональные диаметры в окружности.
В параметрическом уравнении для общего эллипса, приведенном выше,
любая пара точек p → (t), p → (t + π) { displaystyle { vec {p}} (t), { vec { p}} (t + pi)}

Теорема Аполлония о сопряженных диаметрах

Для эллипса с полуосями a, b { displaystyle a, , b}
Пусть эллипс имеет каноническую форму с параметрическим уравнением
Две точки c → 1 = p → (т), с → 2 знака равно п → (т + π 2) { displaystyle { vec {c}} _ {1} = { vec {p}} (т), { vec {c}} _ {2 } = { vec {p}} left (t + { frac { pi} {2}} right)}

Площадь треугольника, образованная c → 1, c → 2 { displaystyle { vec {c}} _ {1}, , { vec {c}} _ {2}}
и из диаграммы видно, что площадь параллелограмма в 8 раз больше, чем у A Δ { displaystyle A _ { Delta} }
Ортогональные касательные
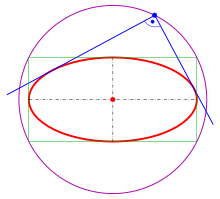
Для эллипса x 2 a 2 + y 2 b 2 = 1 { displaystyle { tfrac {x ^ {2}} {a ^ {2}}} + { tfrac {y ^ {2}} {b ^ {2}}} = 1}

Эта окружность называется ортоптической или направляющей окружностью эллипса (не путать с круговой направляющей, тип выше).
Рисование эллипсов
Эллипсы появляются в описательной геометрии как изображения (параллельная или центральная проекция) окружностей. Существуют различные инструменты для рисования эллипса. Компьютеры обеспечивают самый быстрый и точный метод рисования эллипса. Однако технические средства (эллипсографы ) для рисования эллипса без использования компьютера существуют. Принцип эллипсографов был известен греческим математикам, таким как Архимед и Проклос.
. Если эллипсограф недоступен, можно нарисовать эллипс, используя аппроксимацию четырьмя соприкасающимися кругами на вершины.
Для любого метода, ниже, необходимо знание осей и полуосей (или, что эквивалентно: фокусов и большой полуоси). Если это предположение не выполнено, необходимо знать как минимум два сопряженных диаметра. С помощью конструкции Ритца оси и полуоси могут быть восстановлены.
Построение точки де Ла Хира
Следующее построение отдельных точек эллипса связано с де Ла Хиром. Он основан на стандартном параметрическом представлении (a cos t, b sin t) { displaystyle (a cos t, , b sin t)}
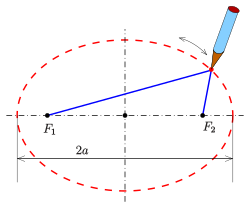
Метод булавок и цепочек
Характеристика эллипса как геометрического места точек, так что сумма расстояний до фокусов постоянна, приводит к методу рисования одного из двух булавки для рисования, веревка и карандаш. В этом методе булавки вставляются в бумагу в двух точках, которые становятся фокусами эллипса. На каждом конце к двум булавкам привязывается веревка; его длина после связывания составляет 2 a { displaystyle 2a}
Подобный метод рисования конфокальных эллипсов с замкнутой цепочкой был разработан ирландским епископом Чарльзом Грейвсом.
Методы бумажной ленты
Два следующих метода использования на параметрическом представлении (см.. параметрическое представление выше):
Технически это представление можно смоделировать двумя простыми способами. В обоих случаях центр оси и полуоси a, b { displaystyle a, , b}
Первый метод начинается с
Точка, где встречаются полуоси, отмечена P { displaystyle P}



Техническая реализация бумажной ленты может быть достигнута с помощью пары Туси (см. Анимацию). Устройство способно нарисовать любой эллипс с фиксированной суммой a + b { displaystyle a + b}
Вариант метода 1 с бумажной полоской использует наблюдение, что средняя точка N displaystyle N}







Второй метод начинается с
Одна отмечает точку, которая делит полосу на две части длиной b { displaystyle b}



Этот метод используется для нескольких эллипсографов (см. Раздел ниже).
Аналогичным способом способом 1 с бумажной полосой, можно найти вариант способа 2 с бумажной полосой (см. Диаграмму) путем разрезания части между осями пополам.
Большинство эллипсографов чертежей основы на второй метод бумажной ленты.

Аппроксимация соприкасаса разными кругами
Из метрических свойств, приведенных ниже, можно получить:
На схеме показан простой способ найти центры кривизны C 1 = (a — b 2 a, 0), С 3 знак равно (0, b — a 2 b) { displaystyle C_ {1} = left (a — { tfrac {b ^ {2}} {a}}, 0 right), , C_ {3} = left (0, b — { tfrac {a ^ {2}} {b}} right)}


(доказательство: простой расчет).
Центры остальных вершин находятся симметрично.
С помощью французской строительной кривой С помощью французской строительной кривой, которая имеет плавный контакт с соприкаса нашими кругами.
Поколение Штейнера

Следующий метод построения отдельных точек эллипса основан на генерации Штейнера конического сечения сечения :
Для генерации точек эллипс x 2 a 2 + y 2 b 2 = 1 { displaystyle { tfrac {x ^ {2}} {a ^ {2}}} + { tfrac {y ^ { 2}} {b ^ {2}}} = 1}



Р { Displaystyle P}









Генерация Штейнера также может быть определена для гипербол и парабол. Иногда его используют методом параллелограммы, потому что можно использовать другие точки, а не вершины, которые начинается с параллелограммы вместо прямоугольника.
Как гипотрохоиды
Эллипс является частным случаем гипотрохоиды , когда R = 2r, как показано на соседнем изображении. Частный случай движущегося круга с радиусом r { displaystyle r}

Вписанные углы и трехточечная форма
Круги
Круг с уравнением (x — x ∘) 2 + (Y — Y ∘) 2 знак равно р 2 { displaystyle left (xx _ { circ} right) ^ {2} + left (yy _ { circ} right) ^ {2} = r ^ {2}}


Обычно вписанные углы измеряются градусом или радианом θ, но здесь более удобно следующее измерение:
Теорема о вписанном угле для окружностей
Для четырех точек P i = (xi, yi), i = 1, 2, 3, 4, { displaystyle P_ {i} = left (x_ {i}, , y_ {i}) справа), i = 1, , 2, , 3, , 4, ,}
Сначала такт доступен только для хорд, не параллельных оси Y, но окончательная формула работает для любого аккорда.
Трехточечная форма уравнения круга
Например, для P 1 = (2, 0), п 2 знак равно (0, 1), п 3 знак равно (0, 0) { displaystyle P_ {1} = (2, , 0), ; P_ {2} = (0, , 1), ; P_ {3} = (0, , 0)}
Используя векторы, скалярные произведения и детерминанты, эту формулу можно упорядочить более четко, позволяя x → = (x, y) { displaystyle { vec {x} } = (x, , y)}
Центр круга (x ∘, y ∘) { displaystyle left (x _ { circ}, , y _ { circ } right)}
Радиус — это расстояние между любым из трех точек и центр.
Эллипсы
В этом разделе мы рассматриваем семейство эллипсов, определяемым уравнением (x — x ∘) 2 a 2 + (y — y ∘) 2 б 2 знак равно 1 { displaystyle { tfrac { left (xx _ { circ} right) ^ {2}} {a ^ {2}}} + { tfrac { left (yy _ { circ} right) ^ {2}} {b ^ {2}}} = 1}
и записать уравнение эллипса в виде:
где q фиксировано и x ∘, y ∘, a { displaystyle x _ { circ}, , y _ { circ}, , a}



Для этого семейства эллипсов вводится следующее q-аналог угловая мера, которая не является обычной угловой мера, которая не является обычной угловой меры θ:
Теорема о вписанном угле для эллипсов
Сначала такт доступны только для хорд, которые не параллельны оси y. Но окончательная формула работает для любого аккорда. Доказательство следует из простого вычисления. Для доказательства, что находится точка на эллипсе, можно предположить, что центр эллипса является началом координат.
Трехточечная форма уравнения эллипса
Например, для P 1 = (2, 0), P 2 = (0, 1), П 3 знак равно (0, 0) { Displaystyle P_ {1} = (2, , 0), ; P_ {2} = (0, , 1), ; P_ {3} = (0, , 0)}

Аналогично случаю круга уравнение можно записать более четко используя:
где ∗ { displaystyle *}
Отношение полюса к полюсу
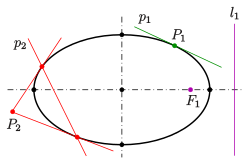
Любой эллипс можно описать в подходящей системе координат уравнением x 2 a 2 + y 2 b 2 = 1 { displaystyle { tfrac {x ^ { 2}} {a ^ {2}}} + { tfrac {y ^ {2}} {b ^ {2}}} = 1}



Это отношение между точками и линией является биекцией.
обратной функцией отображает
Такое отношение между точками и линиями, образованными коникой, называется полюсом -полярное отношение или полярность. Полюс — это точка, полярная линия.
Расчетным путем можно подтвердить следующие свойства полярно-полярного отношения эллипса:
Соотношения полюс-полярность существуют также для гипербол и парабол.
Свойства показателей
Все приведенные ниже свойства показателей относятся к эллипсу с уравнением x 2 a 2 + y 2 b 2 = 1 { displaystyle { frac {x ^ {2 }} {a ^ {2}}} + { frac {y ^ {2}} {b ^ {2}}} = 1}
Площадь
Область Эллипс { displaystyle A _ { text {ellipse}}}
где a { displaystyle a}







![{ displaystyle x in [-a, a],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb19e5015712fa6f6c57d3f334266c73d7782434)

![[-a,a]](https://wikimedia.org/api/rest_v1/media/math/render/svg/50ccbcece37f9ec0a4c6d396be3a143a0b76d5c1)
Второй интеграл — это площадь круга радиуса a, { displaystyle a,}

Эллипс, неявно определяемый A x 2 + B xy + C y 2 = 1 { displaystyle Ax ^ {2} + Bxy + Cy ^ {2} = 1}
Площадь также может быть выражена через эксцентриситет и длину большой полуоси как a 2 π 1 — e 2 { displaystyle a ^ { 2} pi { sqrt {1-e ^ {2}}}}
Окружность
Окружность C { displaystyle C}
где снова a { displaystyle a}


, которая в общем случае не является элементарной функцией.
Окружность эллипса может быть оценена в терминах E (e) { displaystyle E (e)}
точный бесконечный ряд :
где п! ! { displaystyle n !!}

Шриниваса Рамануджан дает два близких приближения для окружности в §16 «Модульных уравнений и приближения к π { displaystyle pi}
и
Ошибки этих приближений, полученные эмпирическим путем, имеют порядок h 3 { displaystyle h ^ {3}}

В более общем смысле, длина дуги части окружности как функция от угла наклона (или x-координат любых двух точек в верхней половине эллипса), дается неполным эллиптическим интегралом . Верхняя половина эллипса параметризуется как
Тогда длина дуги s { displaystyle s}


Это эквивалентно
где E (z ∣ m) { displaystyle E (z mid m)}
Обратная функция , создающая функцию длины дуги, задается некоторой угол эллиптической функции .
Некоторая нижняя и верхняя границы окружности канонического эллипса x 2 / a 2 + y 2 / b 2 = 1 { displaystyle x ^ {2} / a ^ {2} + y ^ {2} / b ^ {2 } = 1}

Здесь верхняя граница 2 π a { displaystyle 2 pi a}

Кривизна
Кривизна определяет как κ = 1 a 2 b 2 (x 2 a 4 + y 2 b 4) — 3 2, { displaystyle kappa = { frac {1} {a ^ {2} b ^ {2}}} left ({ frac {x ^ {2}} {a ^ {4}}} + { frac {y ^) {2}} {b ^ {4}}} right) ^ {- { frac {3} {2}}} ,}

Радиус кривизны в двух вершинах (± a, 0) { displaystyle ( pm a, 0)}
Радиус кривизны в двух совпадающих вершинах (0, ± b) { displaystyle (0, pm b)}
В геометрии треугольника
Эллипсы появляются в геометрии треугольника как
В виде плоских сечений квадрик
Эллипсы появляются как плоские с использованием следующих квадрик :
Приложения
Физика
Эллиптические отражатели и акустика
Если поверхность воды нарушается в одном фокусе эллиптического резервуара с водой, Круговые волны этого возмущения после отражения от стен одновременно сходятся к одной точке: второму фокусу. Это следствие того, что общая длина пути одинакова на любом пути отскока от стен между двумя фокусами.
Аналогично, если источник света помещен в один фокус эллиптического зеркала, все световые лучи в плоскости эллипса отражаются во втором фокусе. Так как никакая другая гладкая кривая не обладает таким свойством, ее можно использовать как альтернативное определение эллипса. (В частном случае круга с кругом в центре весь свет будет отражаться обратно к центру.) Если эллипс повернуть вдоль его большой оси, чтобы получить эллипсоидальное зеркало (в частности, вытянутый сфероид ), это свойство сохраняется для всех лучей, выходящих из источника. В качестве альтернативы можно использовать цилиндрическое зеркало с эллиптическим поперечным сечением для фокусировки света от линейной люминесцентной лампы вдоль линии бумаги; такие зеркала используются в некоторых сканерах документов.
Звуковые волны отражаются аналогичным образом, поэтому в большой эллиптической комнате человек, стоящий в одном фокусе, может замечательно хорошо слышать человека, стоящего в другом фокусе. Эффект еще более очевиден под сводчатой крышей, имеющей форму вытянутого сфероида. Такая комната называется камера шепота. Тот же эффект может быть использован с двумя отражателями, расположенными между ними, расположенными сфероидами. Примеры: Национальный скульптурный зал в Капитолии США (где Джон Куинси Адамс, как говорят, использует это свойство для прослушивания вопросов); Скиния мормонов на Храмовой площади в Солт-Лейк-Сити, Юта ; на выставке звука в Музее науки и промышленности в Чикаго ; напротив Университета Иллинойса в Урбане-Шампейн Аудитория Феллингера; а также в боковой камере дворца Карла V, в Альгамбре.
планетных орбитах
В 17 веке Иоганн Кеплер обнаружил, что орбиты, по которым путешествующие вокруг Солнца, соответственно, собой эллипсы с Солнцем [приблизительно] в одном фокусе, в его первом законе движения планет. Позже Исаак Ньютон объяснил это следствие своего всемирного тяготения.
В более общем плане, в гравитационной задаче двух тел, если два тела связаны друг с другом (то есть полная энергия отрицательна), их орбиты являются подобными эллипсами, при этом общем барицентр является одним из фокусов каждого эллипса. Другой фокус любого эллипса не имеет физического физического значения. Орбита одного тела в системе отсчета другого тела также является эллипсом, а другое тело находится в том же фокусе.
Кеплеровские эллиптические орбиты являются результатом любой радиально направленной силы притяжения, сила которой обратно пропорциональна квадрату расстояния. Таким образом, в принципе двух движущихся изображений заряженных частиц. (Этот вывод игнорирует потери из-за электромагнитного излучения и квантовых эффектов, которые становятся значительными, когда частицы движутся с высокой скоростью.)
Для эллиптические орбиты, полезные соотношения, включающие эксцентриситет e { displaystyle e}
где
Кроме того, с точки зрения ra { displaystyle r_ {a}}




Гармонические осцилляторы
Общее решение для гармонического осциллятора в двух или более измерениях также является эллипсом. Так обстоит дело, например, с длинным маятником, который может свободно двигаться в двух измерениях; массы, прикрепленной к фиксированной точке с помощью идеально упругой пружины ; или любого объекта, который движется под действием силы притяжения, который прямо пропорциональна его расстоянию от фиксированного аттрактора. Однако, в отличие от кеплеровских орбитов, эти «гармонические орбиты» имеют центр притяжения в геометрическом центре эллипса и имеют довольно простые уравнения движения.
Визуализация фазы
В электронике относительную фазу двух синусоидальных сигналов можно сравнить, подав их на вертикальный и горизонтальный входы осциллографа . Если изображение фигуры Лиссажу представляет собой эллипс, а не прямую линию, два совпадения по фазе.
Эллиптические шестерни
Две некруглые шестерни с одинаковым эллиптическим контуром, каждая из которых вращается вокруг одного фокуса и установлены под нужным углом, плавно поворачиваются, сохраняя при этом контакт раз. В качестве альтернативы они могут быть соединены цепью звеньев или ремнем привода ГРМ, или, в случае велосипеда, основная передняя звезда может быть эллиптической, или яйцевидная похожая на эллипс по форме. Такие эллиптические шестерни могут быть установлены в механическом оборудовании для эксплуатации угловой или крутящего момента за счет постоянного вращения ведущей оси или, в случае велосипеда, для обеспечения вращения кривошипа. скорость с обратным изменением скорости механическое преимущество.
Эллиптические велосипедные шестерни облегчают соскальзывание цепи с зубца при переключении передач.
Пример применения шестерни может быть устройство, которое наматывает резьбу на конический шпулька на прядильной машине. Шпулька должна наматываться быстрее, когда нить находится около вершины, чем когда она находится рядом с основанием.
Оптика
Статистика и финансы
В статистике двумерный случайный вектор (X, Y) вместе эллиптически распределен, если его контуры изоплотности — равных плотности плотности функция — это эллипсы. Эта концепция произвольное количество элементов случайного вектора, и в этом случае в общем случае контуры изоплотности представит собой эллипсоиды. Особым случаем является многомерное нормальное распределение. Эллиптические распределения важны в финансах, потому что, если нормы прибыли на национальном уровне распределены эллиптически, тогда все портфели могут полностью охарактеризовать их средним значением и дисперсией портфеля, то есть любыми портфелями с одинаковыми средним средним размером и дисперсией портфеля. return имеют идентичное распределение доходности портфеля.
Компьютерная графика
Рисование эллипса в виде графического примитива распространено в стандартных библиотеках отображения, таких как MacIntosh QuickDraw API и Direct2D в Windows. Джек Брезенхэм из IBM наиболее известным изобретением примитивов 2D-рисования, включая рисование линий и окружностей, с использованием только быстрых целочисленных операций, таких как сложение и переход по биту переноса. В 1967 году MLV Pitteway расширил алгоритм Брезенхэма для линий на коники. Еще одно эффективное обобщение для рисования эллипсов было изобретено в 1984 году Джерри Ван Акеном.
В 1970 году Дэнни Коэн представил на конференции «Компьютерная графика 1970» в Англии линейный алгоритм рисования эллипсов и окружностей. В 1971 г. Л. Б. Смит опубликовал аналогичные алгоритмы для всех конических сечений и доказал их хорошие свойства. Этим алгоритмам требуется всего несколько умножений и сложений для каждого события.
В компьютерной графике полезно использовать параметрическую формулировку, потому что плотность точек максимальна там, где больше всего кривизны. Таким образом, изменение наклона между каждой точкой невелико, снижает очевидную «неровность» приближения.
Составные кривые Безье также можно использовать для рисования эллипса с достаточной точностью, поскольку любой эллипс может быть истолкован как аффинное преобразование окружности. Сплайновые методы, применяемые для рисования круга круга, преподаватели для рисования эллипса, поскольку производящие кривые Безье ведут себя соответствующим образом при таких преобразованиях.
Теория оптимизации
Иногда бывает полезно найти минимальный ограничивающий эллипс для набора точек. Метод эллипсоида весьма полезен для решения этой проблемы.
См. Также
Примечания
Ссылки
Внешние ссылки
Эллипс – это замкнутая плоская кривая, сумма расстояний от каждой точки до двух точек равняется постоянной величине.
Что такое эллипс и фокусное расстояние
Эллипс – это множество точек плоскости, сумма расстояний которых от двух заданных точек, что называются фокусами, есть постоянная величина и равна .
Обозначим фокусы эллипса и
. Допустим, что расстояние
=
– фокусное расстояние.
Рис. 1
– фокусы .
;
,
– половина расстояния между фокусами;
– большая полуось;
– малая полуось.
Теорема:
Фокусное расстояние и полуоси связаны соотношением:
Если точка находится на пересечении эллипса с вертикальной осью,
(теорема Пифагора). Если же точка
находится на пересечении его с горизонтальной осью,
. Так как по определению сумма
– постоянная величина, то приравнивая получается:
.
Уравнение эллипса
Уравнение элиппса бывает двух видов:
- Каноническое уравнение эллипса.
- Параметрическое уравнение эллипса.
Сначала рассмотрим каноническое уравнение эллипса:
Уравнение описывает эллипс в декартовой системе координат. Если центр эллипсa в начале системы координат, а большая ось лежит на абсциссе, то эллипс описывается уравнением:
Если центр эллипсa смещен в точку с координатами
тогда уравнение:
Чтобы получить каноническое уравнение эллипса, разместим и
на оси
симметричной к началу координат. Тогда у фокусов будут такие координаты
и
(см. рис. 2).
Пусть – произвольная точка эллипса. Обозначим через
и
– расстояние от точки
к фокусам. Согласно с определением эллипса:
(1)
Рис. 2
Подставим в (1) ,
и освободимся от иррациональности, подняв обе части к квадрату, получим:
(подносим к квадрату обе части): ,
Обозначим: , получаем каноническое уравнение эллипса:
(2)
Отметим, что по известному свойству треугольника (сумма двух сторон больше третьей) из у нас получается
. Так как
, тогда
, и поэтому
.
Для построения эллипса обратим внимание, что если точка принадлежит эллипсу, то есть удовлетворяет уравнение (2), тогда точки
тоже удовлетворяют это уравнение: из
.
Точки – расположены симметрично относительно осей координат. Значит, эллипс – фигура, симметричная относительно координатных осей. Поэтому достаточно построить график в первой четверти, а тогда симметрично продолжить его.
Из уравнения (2) находим , для первой четверти
.
Если , тогда
. Если же
, тогда
. Точки
и
, а также симметричные с ними
,
– вершины эллипса, точка
– центр эллипса,
=
большая ось,
– малая ось эллипса.
Если первой четверти, тогда из
получается, что при возрастании
от
к
значение
падает от
к
. (рис. 3)
Параметрическое уравнение выглядит так:
Основные свойства эллипса
Рассмотрим основные свойства эллипса, которые необходимы для решения многих задач.
1. Угол между касательной к эллипсу и фокальным радиусом равен углу между касательной и фокальным радиусом
.
2. Уравнение касательной к эллипсу в точке с координатами
:
.
3. Если эллипс пересекается двумя параллельными прямыми, то отрезок, который соединяет середины отрезков образовавшихся при пересечении прямых и эллипса, всегда проходит через середину (центр) эллипсa. (При помощи данного свойства можно построить эллипс при помощи циркуля и линейка, а также найти центр эллипса).
4. Эволюта эллипсa – это астероида, которая растянута вдоль короткой оси.
5. Если вписать эллипс с фокусами и
у треугольника
, тогда выполняется соотношение:
=
Эксцентриситет эллипса
Эксентриситет эллипса – это величина отношения межфокусного расстояния к большей оси и после сокращения на обозначается
Значения эксентриситета характеризует степень “сплющенность” эллипса. Если , тогда
– получается круг. Если же
, тогда
– эллипс превращается в отрезок. В некоторых случаях
. Для фокальных радиусов приведём без доказательства такие формулы:
Рис. 3
Эллипс можно построить механическим способом. Из канонического уравнения нужно найти полуоси и
, тогда вычислим
– полуфокусное расстояние.
Строим фокусы и
на расстоянии один от другого
Концы не растянутой нити длиной
закрепляем в точках
и
. Натягивая остриём карандаша нитку, водим остриём по плоскости таким образом, чтобы нитка скользила по острию. Карандаш при этом опишет полуось. Оттягивая нить в противоположную сторону, начертим вторую половину эллипса.
Примеры решения задач
Задача
Задан эллипс уравнением и точки
. Необходимо:
- убедиться, что точки
и
лежат на эллипсе;
- найти полуоси эллипса и координаты его фокусов;
- найти расстояние от точки
к фокусам;
- убедиться, что сумма этих расстояний равна длине большой оси;
- найти эксентриситет эллипса.
Решение
1. Подставим координаты точки
в левую часть уравнения эллипса:
– точка
лежит на эллипсе. Аналогично для
:
точка
лежит на эллипсе.
2. С канонического и данного уравнения
эллипса выходит:
Из равенства
получается:
– полуфокусное расстояние. Координаты фокусов
и
.
3. Найдём фокальные радиусы точки :
4. Найдём сумму , что отвечает определению эллипса.
5. Эксцентриситет находится по формуле .
Задача
Найти оси, вершины и фокусы эллипса
Решение
Сведём обычное уравнение к каноническому:
,
. Вершины эллипса в точках
,
,
,
. Строим вершины на координатных осях и соединяем плавной линией (см. рис. 2). Так как в данном случае
больше, чем
, то эллипс, который вытянут вдоль оси
, находим полуфокусное расстояние
.
Фокусы в точках и
. (см. рис. 3)
Рис. 4
Найти оси, вершины и фокусы эллипса или
. Построить эллипс.
Сравнивая последнее уравнение с уравнением (2), у нас получается:
,
. Откуда находим оси эллипса:
,
и координаты вершин:
,
,
,
. Дальше из формулы:
. Значит, фокусами эллипса есть точки:
и
. Для построения эллипса отложим на осях
и
вершины
соответственно соединим их плавной линией, (см. задачу 1).
Замечание! Если в каноническом уравнении большей полуосью будет
, тогда фокусы эллипса будут расположены на оси
и тогда
.

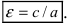
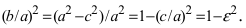
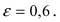
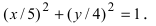
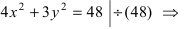


 .
. называется фокусами и расстояние 2 a { displaystyle 2a}
называется фокусами и расстояние 2 a { displaystyle 2a} равно 2 a { displaystyle 2a}
равно 2 a { displaystyle 2a}
 :
:

 ,
, .
.



 ,
,

 с s ∈ R. { displaystyle s in mathbb {R} .}
с s ∈ R. { displaystyle s in mathbb {R} .}

 Затем строка g { displaystyle g}
Затем строка g { displaystyle g} , поэтому касательная линия имеет уравнение x 1 a 2 x + y 1 б 2 y = к { textstyle { frac {x_ {1}} {a ^ {2}}} x + { tfrac {y_ {1}} {b ^ {2}}} y = k}
, поэтому касательная линия имеет уравнение x 1 a 2 x + y 1 б 2 y = к { textstyle { frac {x_ {1}} {a ^ {2}}} x + { tfrac {y_ {1}} {b ^ {2}}} y = k} для некоторых k { displaystyle k}
для некоторых k { displaystyle k} . <Времен738>(x 1, y 1) { displaystyle (x_ {1}, , y_ {1})}
. <Времен738>(x 1, y 1) { displaystyle (x_ {1}, , y_ {1})} .
. Тогда строка g { displaystyle g}
Тогда строка g { displaystyle g}





![{displaystyle {begin{aligned}a,b={frac {-{sqrt {2{Big (}AE^{2}+CD^{2}-BDE+(B^{2}-4AC)F{Big)}left((A+C)pm {sqrt {(A-C)^{2}+B^{2}}}right)}}}{B^{2}-4AC}}\x_{circ }={frac {2CD-BE}{B^{2}-4AC}}\[3pt]y_{circ }={frac {2AE-BD}{B^{2}-4AC}}\[3pt]theta ={begin{cases}arctan left({frac {1}{B}}left(C-A-{sqrt {(A-C)^{2}+B^{2}}}right)right){text{for }}Bneq 0\0{text{for }}B=0, A<C\90^{circ }{text{for }}B=0, A>C \ end {case}} end {align}}}](https://ru.wikibrief.org/wiki/%20//wikimedia.org/api/rest_v1/media/math/render/svg/acde65bb036f1c47ad935258399a696f50875a68)








 .
.



 .
. быть векторми в дизайне.
быть векторми в дизайне.
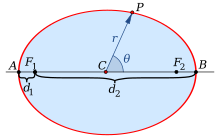 Полярные координаты с центром в центре.
Полярные координаты с центром в центре. 




 (фокус), любая строка l { displaystyle l}
(фокус), любая строка l { displaystyle l} эллипс — это геометрическое место точек, для которых отношение расстояний до точки и линии равно e, { displaystyle e, }
эллипс — это геометрическое место точек, для которых отношение расстояний до точки и линии равно e, { displaystyle e, } то есть:
то есть:

 и x 2 (e 2-1) + 2 xf (1 + e) - y 2 = 0. { displaystyle x ^ {2} left (e ^ {2} -1 right) + 2xf (1 + e) -y ^ {2} = 0.}
и x 2 (e 2-1) + 2 xf (1 + e) - y 2 = 0. { displaystyle x ^ {2} left (e ^ {2} -1 right) + 2xf (1 + e) -y ^ {2} = 0.}




 эллипса сопряжены, если касательные в точке P 1 { displaystyle P_ {1}}
эллипса сопряжены, если касательные в точке P 1 { displaystyle P_ {1}} и Q 1 { displaystyle Q_ { 1}}
и Q 1 { displaystyle Q_ { 1}} параллельны P 2 Q 2 ¯ { displaystyle { overline {P_ {2} Q_ {2}}}}
параллельны P 2 Q 2 ¯ { displaystyle { overline {P_ {2} Q_ {2}}}} .
.
 и c 2 { displaystyle c_ {2}}
и c 2 { displaystyle c_ {2}} ,
, , имеет постоянную площадь A Δ = 1 2 ab { textstyle A _ { Delta} = { frac {1} {2}} ab}
, имеет постоянную площадь A Δ = 1 2 ab { textstyle A _ { Delta} = { frac {1} {2}} ab}

 .
.

 и осями эллипса.
и осями эллипса. соответственно..
соответственно..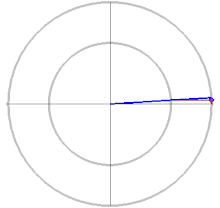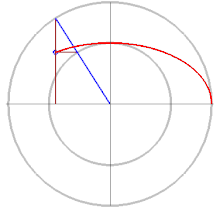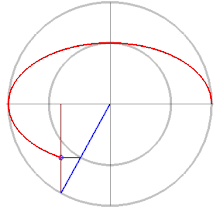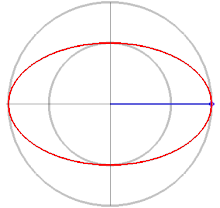


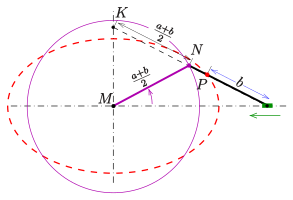


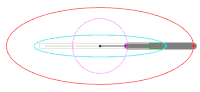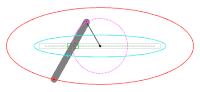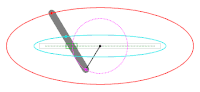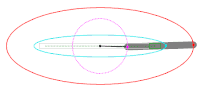
 и нарисуйте отрезок линии V 1 V 3, { displaystyle V_ {1} V_ {3} ,}
и нарисуйте отрезок линии V 1 V 3, { displaystyle V_ {1} V_ {3} ,}
 , которая перпендикулярна линии V 1 V 3, { displaystyle V_ {1} V_ {3} ,}
, которая перпендикулярна линии V 1 V 3, { displaystyle V_ {1} V_ {3} ,} линий в двух точках U, V { displaystyle U, , V}
линий в двух точках U, V { displaystyle U, , V} (все строки, содержащие U displaystyle U}
(все строки, содержащие U displaystyle U} и V { displaystyle V}
и V { displaystyle V} соответственно) и проекционное, но не перспективное отображение π { displaystyle pi}
соответственно) и проекционное, но не перспективное отображение π { displaystyle pi} на B (V) { displaystyle B (V)}
на B (V) { displaystyle B (V)} , то точки пересечения соответствующих прямых образуют невырожденное проективное коническое сечение.
, то точки пересечения соответствующих прямых образуют невырожденное проективное коническое сечение. и P 4 { displaystyle P_ {4}}
и P 4 { displaystyle P_ {4}} равны.
равны. используется частное:
используется частное:


 :
:

 , который можно переформатировать в (x — 1) 2 + (y — 1 2) 2 = 5 4. { displaystyle (x-1) ^ {2} + left (y — { tfrac {1} {2}} right) ^ {2} = { tfrac {5} {4}} .}
, который можно переформатировать в (x — 1) 2 + (y — 1 2) 2 = 5 4. { displaystyle (x-1) ^ {2} + left (y — { tfrac {1} {2}} right) ^ {2} = { tfrac {5} {4}} .}





 используется частное:
используется частное:

 , три из них на прямой (см. диаграмму).
, три из них на прямой (см. диаграмму). тогда и только тогда, когда углы в P 3 { displaystyle P_ {3}}
тогда и только тогда, когда углы в P 3 { displaystyle P_ {3}}

 и после преобразования (x — 1) 2 2 + (y — 1 2) 2 1 2 = 1. { displaystyle { frac {(x-1) ^ {2}} {2}} + { frac { left (y — { frac {1} {2}} right) ^ {2}} { frac {1} { 2}}} = 1.}
и после преобразования (x — 1) 2 2 + (y — 1 2) 2 1 2 = 1. { displaystyle { frac {(x-1) ^ {2}} {2}} + { frac { left (y — { frac {1} {2}} right) ^ {2}} { frac {1} { 2}}} = 1.}


 отображается в строке x 1 xa 2 + y 1 yb 2 = 1 { displaystyle { tfrac {x_ {1} x} {a ^ {2}}} + { tfrac {y_ {1} y} {b ^ {2}}} = 1}
отображается в строке x 1 xa 2 + y 1 yb 2 = 1 { displaystyle { tfrac {x_ {1} x} {a ^ {2}}} + { tfrac {y_ {1} y} {b ^ {2}}} = 1} , а не через центр эллипса.
, а не через центр эллипса. на точку (- ma 2 d, б 2 d) { displaystyle left (- { tfrac {ma ^ {2}} {d}}, , { tfrac {b ^ {2}} {d}} справа)}
на точку (- ma 2 d, б 2 d) { displaystyle left (- { tfrac {ma ^ {2}} {d}}, , { tfrac {b ^ {2}} {d}} справа)} и
и на точку (а 2 с, 0). { displaystyle left ({ tfrac {a ^ {2}} {c}}, , 0 right) .}
на точку (а 2 с, 0). { displaystyle left ({ tfrac {a ^ {2}} {c}}, , 0 right) .}
 ).
). ).
). ).
). и (- c, 0) { displaystyle (-c, , 0)}
и (- c, 0) { displaystyle (-c, , 0)} соответственно и директрисы x = a 2 c { displaystyle x = { tfrac {a ^ {2}} {c}}}
соответственно и директрисы x = a 2 c { displaystyle x = { tfrac {a ^ {2}} {c}}} и x = — a 2 c { displaystyle x = — { tfrac {a ^ {2}} {c}}}
и x = — a 2 c { displaystyle x = — { tfrac {a ^ {2}} {c}}} соответственно относятся к парам полюса и полюса.
соответственно относятся к парам полюса и полюса.





![{ displaystyle { begin {align} C = 2 pi a left [{1- left ({ frac {1} {2}} right) ^ {2} e ^ {2} - left ({ frac {1 cdot 3 } {2 cdot 4}} right) ^ {2} { frac {e ^ {4}} {3}} - left ({ frac {1 cdot 3 cdot 5} {2 cdot 4 cdot 6}} right) ^ {2} { frac {e ^ {6}} {5}} - cdots} right] \ = 2 pi a left [1- sum _ {n = 1} ^ { infty} left ({ frac {(2n -1) !!} {(2n) !!}} right) ^ {2} { frac {e ^ {2n}} {2n-1}} right] \ = - 2 pi a sum _ {n = 0} ^ { infty} left ({ frac {(2n-1) !!} {(2n) !!}} right) ^ {2} { frac {e ^ {2n }} {2n-1}}, end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e202a234c19a28620ecf9c6d260eb21b1bd7aa0)
![{ displaystyle { begin {align} C = pi (a + b) sum _ {n = 0} ^ { infty} left ({ frac {(2n-3) !!} {2 ^ {n} n!}} right) ^ {2} h ^ {n} \ = pi (a + b) left [ 1 + { frac {h} {4}} + sum _ {n = 2} ^ { infty} left ({ frac {(2n-3) !!} {2 ^ {n} n!} } right) ^ {2} h ^ {n} right] \ = pi (a + b) left [1+ sum _ {n = 1} ^ { infty} left ({ frac {(2n-1) !!} {2 ^ {n} n!}} right) ^ {2} { frac {h ^ {n}} {(2n-1) ^ {2}}} справа]. end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d29d8f31216e5d32400e99b04e75e242d987893)
![{ displaystyle C приблизительно pi { biggl [} 3 (a + b) - { sqrt {(3a + b) (a + 3b)}} { biggr]} = pi { biggl [} 3 (a + b) - { sqrt {10ab + 3 left (a ^ {2} + b ^ {2} right)}} { biggr]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86c8a7234c16af19a7338faafe61b4cf9a333f80)



![{displaystyle s=-bleft[Eleft(z;{Biggl |};1-{frac {a^{2}}{b^{2}}}right)right]_{arccos {frac {x_{1}}{a}}}^{arccos {frac {x_{2}}{a}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed75c6daa97d1f19f90b6a53c3441bf0e65601a2)










![{ displaystyle { begin {align} a = { frac {r_ {a} + r_ {p}} {2}} \ [2pt] b = { sqrt {r_ {a} r_ {p}} } \ [2pt] ell = { frac {2} {{ frac {1} {r_ {a}}} + { frac {1} {r_ {p}}}}} = { frac {2r_ {a} r_ {p}} {r_ {a} + r_ {p}}} end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08835a73be73e7094f529d4eff42804930898271) .
.