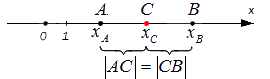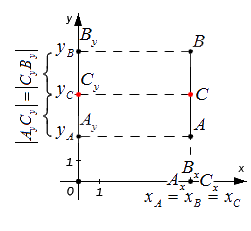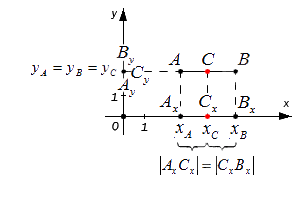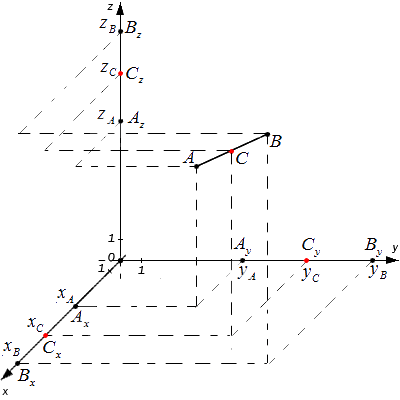Как найти середину отрезка на графике

Основное определение отрезка

Прямую АВ можно получить путем удлинения отрезка, который состоит из двух точек. Вследствие чего, можно сказать, что полученный отрезок АВ — это часть прямой, которая ограничена точками А и В. Отрезок объединяет обе точки, которые являются концами прямой, а также множество других точек, лежащих на отрезке.  

Например: дана точка К которая расположена между заданными отметками, следовательно, можно сказать, что данная точка лежит на этом отрезке.

Середина отрезка на координатной прямой

Заданы следующие параметры: координатная прямая Ox; точки А и В, которые не совпадают с данной прямой.

Заданным точкам соответствуют действительные числовые значения [x_{A}] и [x_{B}]. Координата С — это середина отрезка А и В. Исходя из этого нужно определить значение координаты [x_{C}] .

AB = |a — b|, где A и B — это произвольные точки, расстояние между которыми надо найти, то есть, найти длину отрезка AB, a и b — координаты точек.
Выражение |a — b| можно заменить выражением |b — a|, так как a — b и b — a являются противоположными числами и их модули равны.
Следовательно, чтобы найти расстояние между точками координатной прямой надо из координаты одной точки вычесть координату другой точки.

Середина отрезка на плоскости

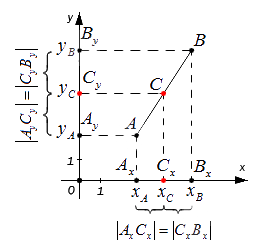
Зададим следующие параметры: прямоугольная система координат относительно заданной плоскости Oxy; две произвольно расположенные несовпадающие точки, для которых заданы координаты [mathrm{A}left(x_{A} y_{A}right)] и [Bleft(chi_{B} chi_{B}right)]. Точка C — это заданная середина отрезка АВ. Нужно вычислить координаты [x_{C}] и [y_{C}] относительно точки С.

Чтобы правильно проанализировать задачу, возьмем случай, когда точки A и В между собой не совпадают и расположены на одной координатной плоскости.

В свою очередь координатная плоскость является перпендикулярной относительной одной из осей.

Координаты отметок [A_{x} A_{y} B_{x} B_{y} C_{x} C_{y}] — это проекции точек А, В, С.

Согласно построению, все прямые можно назвать параллельными; прямые также параллельны между собой. Принимая во внимание данное свойство и теорему Фалеса из равенства А С   =   С В следуют, что все  равенства между собой равны. Также они в свою очередь свидетельствуют о том, что точка [C_{x}] – это середина отрезка [A_{x}] и [B_{x}], [C_{y}] а – середина отрезка [A_{y}] и [B_{y}].

Опираясь на полученное выражение получаем основное уравнение середины отрезка на координатной плоскости. 

[x_{c}=frac{x_{A}+x_{B}}{2}text { и } y_{c}=frac{y_{A}+y_{B}}{2}]

Данным набором формул можно использовать, когда точки А и B лежат на одной координатной плоскости или прямой. Которая соответственно перпендикулярна относительной одной из осей.

В данном случае координаты отрезка будут определяться по следующей формуле:

[x_{C}=frac{x_{A}+x_{B}}{2} text{ и } y_{c}=frac{y_{A}+y_{B}}{2}]

Параметры середины отрезка в пространстве

Для выведения основной формулы для решения подобного рода задач, нужно рассмотреть конкретный пример.

Дана система координат, две произвольные координатные точки с конкретными координатами [mathrm{A}left(A_{x} A_{y} A_{z}right)] и [mathrm{B}left(B_{chi} B_{y} B_{z}right)]. Нужно определить отметку точки C, которая в свою очередь будет являться серединой отрезка.

Согласно основной теоремы Фалеса, все равенства между собой являются равными. Следовательно, значение точек С будут являться серединами отрезков, каждой координатной плоскости, коих имеется три.

Можно составить и записать окончательную формулу для определения середины прямой при координатной плоскости, состоящей более чем двух осей.

[x_{c}=frac{x_{A}+x_{B}}{2} text{ и } y_{C}=frac{y_{A}+y_{B}}{2}, z_{c}=frac{z_{A}+z_{B}}{2}]

Данные формулы также можно применять в случаях, когда точки A и B расположены на одной из координатных прямых. Либо на прямой, которая перпендикулярна относительно одной из осей. Есть еще случай, когда точки расположены в одной координатной плоскости, которая перпендикулярна одной из координатных плоскостей.

Определение координат середины отрезка через координаты радиус-векторов его концов

Формулу для определения отметок середины отрезка, можно определить применяя алгебраическое правило решения векторных выражений.

Исходные данные: прямоугольная декартова система координат Oxy, точки с конкретно заданными координатами [mathrm{A}left(A_{x} A_{y}right)] и [text { B }left(B_{x} B_{y}right)].

Точка  C – это середина отрезка с точками А и В.

Согласно геометрическому правилу и определению, действия над векторами будет выглядеть следующим образом:

[overline{O C}=frac{1}{2} cdot(overline{O A}+overline{O B}).]

Координата С в данной ситуации — это значение, в которой пересекаются диагонали геометрической фигуры параллелограмм. Данная фигура построена на основании следующих векторов  [overline{O A}] и [overline{O B}], иными словами — это точка середины диагоналей.

Координатные показатели радиуса — это векторные показатели, которые  равны координатам, тогда будут верны и равенства: [overline{O A}left(x_{A} y_{A}right)] и [overline{O B}left(x_{B} y_{B}right)].

Выполним следующие действия над векторными значениями и получим следующие формулы:

[overline{O C}=frac{1}{2} cdot(overline{O A}+overline{O B})=left(frac{x_{A}+y_{B}}{2}, frac{y_{A}+y_{B}}{2}right).]

Следовательно, заданная координата С обладает данными:

[left(frac{x_{A}+y_{B}}{2}, frac{y_{A}+y_{B}}{2}right).]

Аналогичным образом определяется нахождение координат середины заданного отрезка в пространстве.

[Cleft(frac{x_{A}+y_{B}}{2}, frac{y_{A}+y_{B}}{2}, frac{z_{A}+z_{B}}{2}right)]

Примеры решения задачи, при нахождении точки середины отрезка

Была ли эта статья полезной?

Обновлено: 26.05.2023

В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.

Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .

Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .

Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .

Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B

И далее мы рассмотрим, как же определять координаты середины отрезка (точки C ) при заданных координатах концов отрезка ( A и B ), расположенных на координатной прямой или в прямоугольной системе координат.

Середина отрезка на координатной прямой

Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа x A и x B . Точка C – середина отрезка A B : необходимо определить координату x C .

Поскольку точка C является серединой отрезка А В , верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.

| А С | = | С В | ⇔ x C — x A = x B — x C

Тогда возможно два равенства: x C — x A = x B — x C и x C — x A = — ( x B — x C )

Из первого равенства выведем формулу для координаты точки C : x C = x A + x B 2 (полусумма координат концов отрезка).

Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных — несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A ( x A ) и B ( x B ):

Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.

Середина отрезка на плоскости

Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .

Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y — проекции точек A , B и C на оси координат (прямые О х и О y ).

Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:

x C = x A + x B 2 и y C = y A + y B 2

Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:

Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов A ( x A , y A ) и B ( x B , y B ) определяются как:

( x A + x B 2 , y A + y B 2 )

Середина отрезка в пространстве

Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A ( x A , y A , z A ) и B ( x B , y B , z B ) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .

A x , A y , A z ; B x , B y , B z и C x , C y , C z — проекции всех заданных точек на оси системы координат.

Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z

Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:

x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2

Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.

Определение координат середины отрезка через координаты радиус-векторов его концов

Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.

Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A ( x A , y A ) и B ( x B , x B ) . Точка C – середина отрезка A B .

Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т.е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = ( x A , y A ) , O B → = ( x B , y B ) . Выполним некоторые операции над векторами в координатах и получим:

O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2

Следовательно, точка C имеет координаты:

x A + x B 2 , y A + y B 2

По аналогии определяется формула для нахождения координат середины отрезка в пространстве:

C ( x A + x B 2 , y A + y B 2 , z A + z B 2 )

Примеры решения задач на нахождение координат середины отрезка

Исходные данные: на плоскости – точки с заданными координатами А ( — 7 , 3 ) и В ( 2 , 4 ) . Необходимо найти координаты середины отрезка А В .

Решение

Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .

x C = x A + x B 2 = — 7 + 2 2 = — 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2

Ответ: координаты середины отрезка А В — 5 2 , 7 2 .

Исходные данные: известны координаты треугольника А В С : А ( — 1 , 0 ) , В ( 3 , 2 ) , С ( 9 , — 8 ) . Необходимо найти длину медианы А М .

Решение

1. По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M :

x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + ( — 8 ) 2 = — 3

1. Поскольку теперь нам известны координаты обоих концов медианы (точки A и М ), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М :

A M = ( 6 — ( — 1 ) ) 2 + ( — 3 — 0 ) 2 = 58

Ответ: 58

Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 ( 1 , 1 , 0 ) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M ( 4 , 2 , — 4 ) . Необходимо рассчитать координаты точки А .

Решение

Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А : x M = x A + x C 1 2 ⇒ x A = 2 · x M — x C 1 = 2 · 4 — 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M — y C 1 = 2 · 2 — 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M — z C 1 = 2 · ( — 4 ) — 0 = — 8

В данной публикации мы рассмотрим, что такое середина отрезка, по какой формуле считаются ее координаты (в плоскости и пространстве). Также разберем примеры решения задач по этой теме.

Расчет координат середины отрезка

Серединой называется точка, лежащая на отрезке и находящаяся на одинаковом расстоянии от его концов.

Если концы отрезка и расположены в одной плоскости, то координаты его середины (точки C) считаются по формуле:

Если отрезок с концами и находится в трехмерном пространстве, координаты его середины рассчитываются следующим образом:

Примеры задач

Задание 1
Вычислим координаты точки C, которая является серединой отрезка AB, образованного точками и .

Решение:
В данном случае нам подойдут формулы для плоскости:
x_c = (5 + 11) / 2 = 8
y_c = (-2 + 10) / 2 = 4

Таким образом, точка C имеет координаты (8, 4).

Задание 2
Найдем координаты точки B, являющейся одним из концов отрезка AB. При этом известны координаты точки и середины отрезка – .

Решение:
Нужные нам формулы можно вывести из выражений для расчета координат середины отрезка:

Середина отрезка — это точка, которая лежит на отрезке и находится на равном расстоянии от конечных точек.

В геометрических задачах часто можно столкнуться с необходимостью найти середину отрезка заданного координатами точек его концов, например в задачах поиска медианы, средней линии, .

Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка.

Формулы вычисления расстояния между двумя точками:

• Формула вычисления координат середины отрезка с концами A( x_a , y_a ) и B( x_b , y_b ) на плоскости:

Примеры задач на вычисление середины отрезка

Примеры вычисления координат середины отрезка на плоскости

xc =	xa + xb	=	-1 + 6	=	5	= 2.5
2	2	2

yc =	ya + yb	=	3 + 5	=	8	= 4
2	2	2

Ответ: С(2.5, 4).

Найти координаты точки В, если известны координаты точки C(1; 5), середины отрезка AB и точки A(-1, 3).

Ответ: B(3, 7).

Примеры вычисления координат середины отрезка в пространстве

xc =	xa + xb	=	-1 + 6	=	5	= 2.5
2	2	2

yc =	ya + yb	=	3 + 5	=	8	= 4
2	2	2

zc =	za + zb	=	1 + (-3)	=	-2	= -1
2	2	2

Ответ: С(2.5, 4, -1).

Найти координаты точки В если известны координаты точки C(1, 5, 2), середины отрезка AB и точки A(-1, 3, 10).

Ответ: B(3, 7, -6).

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Определение 1. Отрезок (или отрезок прямой )− это часть прямой, ограниченная двумя точками.

Определение 2. Отрезок − это множество, состоящая из двух различных точек данной прямой и всех точек, лежащих между ними.

Точки, ограничивающие отрезки называются концами отрезка, а точки, которые находятся между концами отрезка называются внутренними точками.

На рисунке 1 отрезок выделен красным цветом. Точки A и B концы отрезка, а точки между ними − внутренние точки.

Обозначение отрезков

Отрезки обозначаются с помощью его конечных точек. Отрезок на рисунке 1 обозначается так: AB или BA. Порядок следования имен конечных букв не имеет значения.

Сравнение отрезков

Для сравнения отрезков нужно:

• Взять любую прямую и отметить на ней какую-нибудь точку.
• Отложить на прямой оба отрезка из отмеченной точки на прямой на одну и ту же сторону.

Если два других конца совместяться, то отрезки равны. Если же конец одного отрезка находится внутри другого, то длина первого отрезка меньше второго.

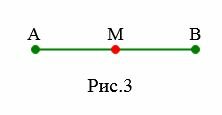
Пусть даны два отрезка AB и CD (Рис.2). Требуется сравнить эти отрезки, т.е. определить какой из них больше. Отложим эти отрезки на прямой a. Как видим, точка D находится внутри отрезка AB. Значит отрезок CD меньше отрезка AB. Это обозначается так: CD Определение 3. Точка отрезка,делящая его на два равных отрезка называется серединой отрезка.

На рисунке 3 ( small M ) является серединой отрезка ( small AB ) поскольку ( small AM = MB ).

Длина отрезка

Для определения длины отрезка его нужно сравнить с другим отрезком, принятым за единицу измерения.

В качестве единицы измерения можно взять, например, сантиметр. В этом случае для определения длины отрезка узнают, сколько раз в данном отрезке укладывается сантиметр. Этот показатель и является длиной отрезка выраженная в сантиметрах. Если длина отрезка AB равна трем сантиметрам, то пишут AB=3см.

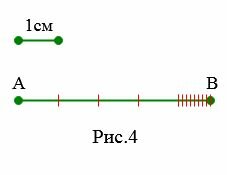
Если отрезок, принятый за единицу измерения не укладывается целое число раз в измеряемом отрезке, то его обычно делят на 10 равных частей и определяют сколько раз одна такая часть укладывается в остатке. Одна десятая часть сантиметра называется миллиметром. В итоге получаем длину отрезка в сантиметрах и миллиметрах.

На Рис.4 1см укладывается в отрезке AB 4 раза и в остатке укладывается ровно 8 одну десятую часть сантиметра. Поэтому можно писать: AB=4см 8мм или AB=4.8см.

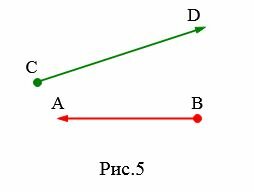
Направленный отрезок

Если для отрезка определить направление, то такой отрезок называется направленным отрезком. Направленный отрезок имеет начальную точку и конечную точку. В конечной точке направленного отрезка рисуют стрелку (Рис.5)

Для обозначения направленных отрезков сначала пишется начальная точка, а затем конечная точка. На рисунке 2 верхний направленный отрезок обозначают так: ( small overrightarrow ) а нижний отрезок так: ( small overrightarrow ) Направленный отрезок называют вектором.

Читайте также:

  

• Экг пропедевтика внутренних болезней кратко

  

• Цепь с параллельным соединением катушки и конденсатора кратко

  

• Онтогенез и гаметогенез кратко

  

• Элина быстрицкая биография кратко

  

• Документы подлежащие засекречиванию и рассекречиванию кратко

Гипермаркет знаний>>Математика>>Математика 8 класс. Полные уроки>>Геометрия: Координаты середины отрезка. Полные уроки

Тема урока

• Координаты середины отрезка.

Цели урока

• Расширить кругозор понятий.
• Познакомиться с новыми определениями и вспомнить некоторые уже изученные.
• Научиться применять свойства фигур при решении задач.
• Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
• Воспитательные — посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.

Задачи урока

• Проверить умение учащихся решать задачи.

План урока

1. Вступительное слово.
2. Повторение ранее изученного материала.
3. Координаты середины отрезка.
4. Логические задачи.

Вступительное слово

Перед тем как перейти к самому материалу по теме хотелось бы немного поговорить о отрезке не только как о математическим определении. Много ученых старались посмотреть на отрезок как то по другому, видели в нем нечто необычное. Некоторые талантливые художники заставляли геометрические фигуры передавать настроение и эмоции.

Есть множество теорий как цвет влияет на наше настроение и почему.

Цвет можно чувствовать, он тесно связан с нашими эмоциями. Окружающий нас цвет природы, архитектуры, растений, одежды исподволь влияет на наше настроение.

Как утверждают специалисты цветовая гама может воздействовать человека.

• Красный цвет может поднять настроение, придать сил.
• Розовый цвет символизируют мир и покой.
• Оранжевый — это теплый, беспокойный цвет, дающий энергию и поднимающий настроение.
• В императорском Китае желтый считался настолько священным цветом, что носить желтую одежду мог только император. Египтяне и майя считали желтый цветом Солнца и почитали его силу, поддерживающую жизнь. Желтые цветы могут взбодрить и порадовать, когда вы чувствуете себя неважно.
• Зеленый — целительный цвет. Вызывает ощущение равновесия и гармонии.
• Синий усиливает творческое начало.
• Фиолетовый — цвет задумчивости, духовности и покоя. Он связан с интуицией и заботой о других.
• Белый обычно считается цветом чистоты и невинности. Он также связан с вдохновением, озарением, духовностью и любовью.

Но сколько людей столько и мнений. У каждого своя правда.

Так же есть интересная теория как связана форма линии или отрезка с ее характером.

Форма, как и цвет, является свойством предмета. Форма – это внешние очертания видимого предмета, отражающие его пространственные аспекты (forma, в переводе с латинского, — наружный вид). Все, что окружает нас, имеет определенную форму. Понять и изобразить ее конструктивное строение и смысловую наполненность — задача художника. А нам, как зрителям, необходимо уметь читать изображение, расшифровывать характер и смысл различных форм. На листе бумаги и экране компьютера форма образуется при замыкании линии. Поэтому характер формы зависит от характера линии, которой она образована.

Какой из этих линий можно выразить спокойствие, злость, равнодушие, волнение, радость?

Однозначного ответа в данном случае быть не может. Например, колючая линия может выражать злость, злорадство или бурную радость, граничащую с безрассудством.

Какое настроение или эмоция соответствует каждой из этих линий?

Как форма зависит от характера линии, которой она образована? 

Повторение ранее изученного материала

Декартова система координат

И так эта система координат имеет два своих вполне оправданных названия. Первым из них является декартова, такое название она получила от фамилии своего автора. И второе не менее интересное и оправданное — прямоугольная система координат, происхождение такого имени становится понятным после первого взгляда на саму систему координат. Угол между двумя направляющими равен 90° такое угол зачастую называют прямым, откуда и пошло второе название.

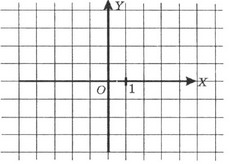
Горизонтальная ось называется осью ОХ, вертикальная — осью OY. Место пересечения осей ОХ и OY называется началом координат, которое также обозначают цифрой 0 (“ноль”). Каждая точка на координатной плоскости имеет свой точный адрес. Это пара чисел: первое число по оси ОХ, второе — по оси OY. Эти числа называются координатами точки. А чтобы не путать порядок следования координат, вспомните, как устроены наши дома: сначала мы заходим в нужный подъезд (по оси ОХ), а затем поднимаемся на нужный этаж (по оси ОУ).

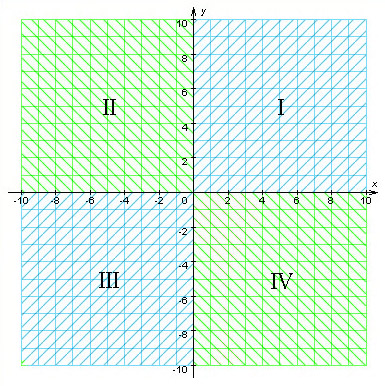
Оси координат разбивают плоскость на четыре части, которые называются координатными четвертями.

Если точка A лежит в координатном угле I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном угле II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном угле III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном угле IV, то точка A имеет положительную абсциссу и отрицательную ординату.

Прямоугольная система координат в пространстве

Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения одинаковы для всех осей. OX — ось абсцисс, OY — ось ординат, OZ — ось аппликат. Положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY, если этот поворот наблюдать со стороны положительного направления оси OZ. Такая система координат называется правой. Если большой палец правой руки принять за направление X, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси.

Координаты середины отрезка

Середина — центральная часть; место объекта, одинаково удалённое от его краев.

Что же такое отрезок?

Отрезком может называться одно из двух близких понятий в геометрии и математическом анализе.

Отрезок в геометрии

Отрезок прямой — это множество (часть прямой), состоящее из двух различных точек и всех точек, лежащих между ними. Отрезок прямой, соединяющий две точки A и B (которые называются концами отрезка), обозначается следующим образом — [A;B]. Если в обозначении отрезка опускаются квадратные скобки, то пишут «отрезок AB». Любая точка, лежащая между концами отрезка, называется его внутренней точкой. Расстояние между концами отрезка называют его длиной и обозначают как |AB|.

Направленный отрезок

Обычно у отрезка прямой неважно, в каком порядке рассматриваются его концы: то есть отрезки AB и BA представляют собой один и тот же отрезок. Если у отрезка определить направление, то есть порядок перечисления его концов, то такой отрезок называется направленным. Например, выше указанные направленные отрезки не совпадают. Особого обозначения у направленных отрезков нет — то, что у отрезка важно его направление обычно указывается особо.

Колючая линия

На протяжении многих столетий математики имели дело лишь с линиями, почти в каждой точке которых можно было провести касательную. Если и встречались исключения, то только в нескольких точках. В этих точках линия как бы ломалась, и потому их называли точками излома. В течение долгого времени ни-кто из математиков не верил, что может существовать непрерывная линия, целиком состоящая из зубцов, изломов и колючек. Велико было изумление, когда удалось построить такую линию, более того, функцию, график которой был такой колючей изгородью.

Первым это сделал Больцано. Но его работа осталась неопубликованной, и впервые такой пример опубликовал Вейерштрасс. Однако пример Вейерштрасса очень трудно изложить – он основан на теории тригонометрических рядов.

Середина отрезка

На плоскости

Координаты середины отрезка равны полусуммам координат его концов: если концы отрезка – A(x₁; y₁) и B(x₂; y₂), то координаты его середины –

В пространстве

Есть две произвольные точки A1(x₁;y₁;z₁) и A2(x₂;y₂;z₂). Тогда серединой отрезка A1A2 будет точка С с координатами x, y, z, где

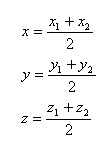
Деление отрезка в заданном отношении

Если x₁ и y₁ — координаты точки A, а x₂ и y₂ — координаты точки B, то координаты x и y точки C, делящей отрезок AB в отношении , определяются по формулам

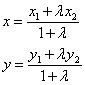
Если ,  то точка C(x, y) делит отрезок AB пополам, и тогда координаты x и y середины отрезка AB определяются по формулам

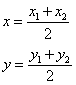
Площадь треугольника по известным координатам его вершин A(x₁, y₁), B(x₂, y₂), C(x₃, y₃) вычисляется по формуле.

Полученное с помощью этой формулы число следует взять по абсолютной величине.

Пример №1

Найдите середину отрезка АВ.

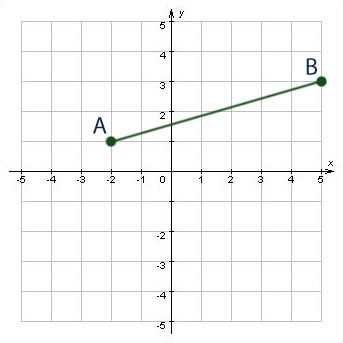
Решение:

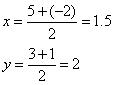
Ответ: Координаты середины отрезка равны (1.5;2)

Пример №2.

Найдите середину отрезка АВ.

[[Image:11062011 16.jpg|300px|Пример]

Решение:

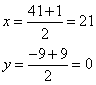
Ответ: Координаты середины отрезка равны (21;0)

Пример №3.

Найдите координаты точки С, если АС=5,5 а СВ=19,5.

А(1;7), В(43;-4)

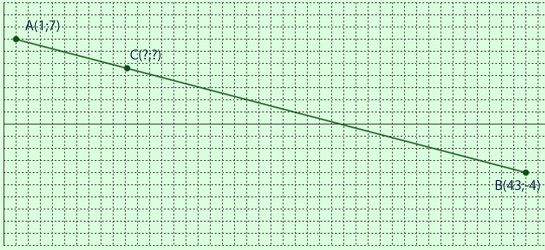
Решение:

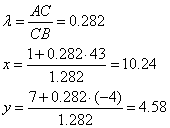
Ответ: Координаты точки С(10,24;4,58)

Задачи

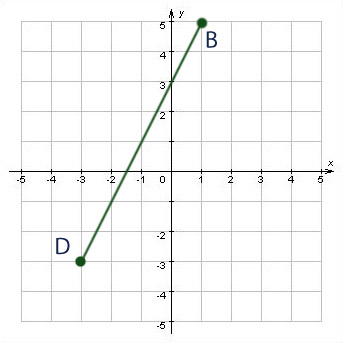
Задача №1

Найдите середину отрезка DB.

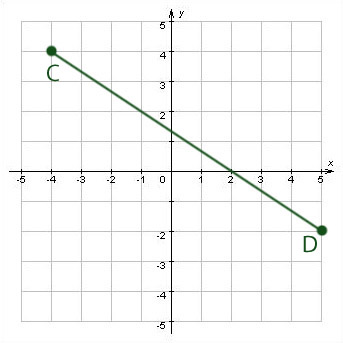
Задача №2.

Найдите середину отрезка CD.

Интересный факт

Как делают статуи.

Про многих знаменитых скульпторов рассказывают, что на вопрос, как удается делать столь замечательные статуи, следовал ответ: “Я беру глыбу мрамора и отсекаю от нее все лишнее”. В разных книгах это можно прочитать о Микеланджело, о Торвальдсене, о Родене.

Давид (Микеланджело)

Статуя Иисуса Христа в Рио–де–Жанейро

Тем же самым способом можно получить любую ограниченную плоскую геометрическую фигуру: надо взять какой-нибудь квадрат, в котором она лежит, а потом отсечь все лишнее. Однако отсекать надо не сразу, а постепенно, на каждом шагу отбрасывая кусочек, имеющий форму круга. При этом сам круг выбрасывается, а его граница – окружность – остается в фигуре.

На первый взгляд кажется, что так можно получить лишь фигуры определенного вида. Но все дело в том, что отбрасывают не один и не два круга, а бесконечное, точнее говоря, счетное множество кругов. Таким путем можно получить любую фигуру. Чтобы убедиться  в этом достаточно принять во внимание, что множество кругов, у которых рациональны и радиус и обе координаты центра, счетное.

А теперь чтобы получить любую фигуру, достаточно взять содержащий ее квадрат (глыбу мрамора) и обросить все круги указанного выше вида, которые не содержат ни одной точки нужной нам фигуры. Если же выбрасывать круги не из квадрата, а из всей плоскости, то описанным приемом можно получить и неограниченные фигуры.

Вопросы

1. Что такое отрезок?
   
2. С чего состоит отрезок?
3. Как можно найти середину отрезка?

Список использованных источников

1. Кузнецов А. В., учитель математики (5-9 класс), г. Киев
2. «Единый государственный экзамен 2006. Математика. Учебно-тренировочные материалы для подготовки учащихся/ Рособрнадзор, ИСОП – М.: Интеллект-Центр, 2006»
3. Мазур К. И. «Решение основных конкурсных задач по математике сборника под редакцией М. И. Сканави»
4. Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина «Геометрия, 7 – 9: учебник для общеобразовательных учреждений»

---

Над уроком работали

Кузнецов А. В.

Потурнак С.А.

Татьяна Проснякова

---

Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов  высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.

Предмети > Математика > Математика 8 класс

Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки

©  Автор системы образования 7W и Гипермаркета Знаний — Владимир Спиваковский

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.

Разработка — Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email:

В данной публикации мы рассмотрим, что такое середина отрезка, по какой формуле считаются ее координаты (в плоскости и пространстве). Также разберем примеры решения задач по этой теме.

Расчет координат середины отрезка

Серединой называется точка, лежащая на отрезке и находящаяся на одинаковом расстоянии от его концов.

AC = CB

Если концы отрезка A (x_a, y_a) и B (x_b, y_b) расположены в одной плоскости, то координаты его середины (точки C) считаются по формуле:

Если отрезок с концами A (x_a, y_a, z_a) и B (x_b, y_b, z_b) находится в трехмерном пространстве, координаты его середины рассчитываются следующим образом:

Примеры задач

Задание 1
Вычислим координаты точки C, которая является серединой отрезка AB, образованного точками A (5, -2) и B (11, 10).

Решение:
В данном случае нам подойдут формулы для плоскости:
x_c = (5 + 11) / 2 = 8
y_c = (-2 + 10) / 2 = 4

Таким образом, точка C имеет координаты (8, 4).

Задание 2
Найдем координаты точки B, являющейся одним из концов отрезка AB. При этом известны координаты точки A (7, 13) и середины отрезка – C (4, -3).

Решение:
Нужные нам формулы можно вывести из выражений для расчета координат середины отрезка:

x_b = 2x_c – x_a = 2 · 4 – 7 = 1
y_b = 2y_c – y_a = 2 · (-3) – 13 = -19

Следовательно, координаты B – (1, -19).